| ГОСТы, СНиПы Карта сайта TehTab.ru Поиск по сайту TehTab.ru | Навигация по справочнику TehTab.ru: главная страница / / Техническая информация/ / Математический справочник/ / Теория вероятностей и статистика / / Таблица. Нормированный интеграл вероятностей (нормированная функция Лапласа). Она же нормированная функция ошибок.
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Нашли ошибку? Есть дополнения? Напишите нам об этом, указав ссылку на страницу. | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
TehTab.ru Реклама на сайте | Обращаем ваше внимание на то, что данный интернет-сайт носит исключительно информационный характер. Информация, представленная на сайте, не является официальной и предоставлена только в целях ознакомления. Все риски за использование информаци с сайта посетители берут на себя. Проект TehTab.ru является некоммерческим, не поддерживается никакими политическими партиями и иностранными организациями. | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Лапласа — Энциклопедия по экономике
При нормальном распределении расчетные формулы для определения вероятности нахождения параметра х внутри поля допуска получаются с помощью нормированной функции Лапласа [c.
152] Из таблицы значений функции Лапласа. следует, что [c.153]
Расчет вероятности наступления завершающего события в заданный срок обычно совершенно необходим, когда установленный директивный срок Гд оказывается меньше рассчитанного срока наступления завершающего события Тс. Предполагая, что значение 7″с подчиняется закону нормального распределения, можно рассчитать эту вероятность следующим образом. Аргумент нормальной функции распределения вероятностей (функции Лапласа) [c.235]
Найдя Ф(х) по таблице значений функции Лапласа (табл. 5.1), определяют вероятность наступления завершающего события в заданный срок. Считается что вероятность Рк должна находиться в пределах 0,35 [c.42]
Предлагаются и другие критерии, например, пытаются свести проблему неопределенных факторов it проблеме случайных факторов, считая, что параметр у распределен равномерно на множестве (так называемый критерий Байеса — Лапласа). В задаче о полезных ископаемых предполагалось бы, что месторождения расположены равномерно по всей территории.
Такой подход навряд ли можно считать правомерным, поскольку выводы, полученные с его помощью, не имеют под собой логической основы. Впрочем, критерий Байеса — Лапласа не произвольнее критерия Гурвица.
[c.158]
Оптимистичный подход, подходы на основе критерия Гурвица, критерия Байеса — Лапласа и критерия Сэвиджа имеют в данном случае следующий вид [c.218]
В полидисперсных средах кривизна отдельных участков пленки пены неодинакова, и жидкость в пленке находится под различным давлением, определенным управлением Лапласа [c.27]
Функция Лапласа — нечетная, т.е. Ф(— г) = — Ф(—z). [c.59]
Доверительный интервал, доверительная вероятность и риск. Если случайная величина имеет нормальное распределение, то вероятность того, что ее значение появится в интервале (zo) около среднего значения зависит только от величины z, равной отношению отклонения Д от среднего значения и среднеквадратического отклонения z = Л/о. Интервал +Д называют доверительным интервалом, а соответствующую ему вероятность Р(г) — доверительной вероятностью, она равна при нормальном распределении функции Лапласа.
Риск выхода за этот интервал R(z) = [1 —
[c.59]
| Таблица 6.1 Значения интеграла вероятностей — функции Лапласа |
Уравнение Лапласа — Гаусса предполагает непрерывное изменение / и неограниченное возрастание п. Поэтому площадь нормальной кривой, заключенную между ординатами /, и t2, определяют, интегрируя функцию (7.7). [c.168]
Определитель квадратной матрицы п-го порядка (или определитель п-го порядка) при любом п определяется более сложно. Он может быть вычислен с помощью разложения по элементам строки или столбца (теоремы Лапласа) [c.262]
Значения функции Лапласа ф(х) = -==[ е 2/2dt [c.291]
Идентифицируемость модели 22 Интеграл вероятностей Лапласа 35 Интервальная оценка параметра 44 [c.300]
Принимаем, что плотность распределения смешанных случайных величин стремится к нормальному закону распределения.
Предельную точку кривой нормального распределения выражаем через функцию Лапласа [c.91]
Затем, используя функцию Лапласа, определяют такое-значение А, при котором [c.94]
Критерий Лапласа — ориентируйся на среднее [c.122]
Еще одним типом экспоненциального распределения, наряду с нормальным, является распределение Лапласа, плотность которого выражается формулой [c.38]
Как и распределение Гаусса, распределение Лапласа зависит от двух параметров (//, сг), [c.38]
Однако эксцесс распределения 8 — 6, то есть вдвое превышает эксцесс нормального распределения. Следовательно, распределение Лапласа островершинное, то есть имеет высокий пик и [c.38]
Распределение Лапласа можно использовать для описания логарифмов относительного изменения цен активов, зачастую с большим успехом, чем нормальное распределение. Однако, с еще большей точностью, реальные распределения вероятностей описывает обобщенное экспоненциальное распределение, которое будет также рассмотрено в этой главе.
[c.39]
Казалось бы, распределение Коши выглядит очень привлекательно для описания и моделирования случайных величин. Однако в действительности это не так. Свойства распределения Коши резко отличны от свойств распределения Гаусса, Лапласа и других экспоненциальных распределений. [c.39]
Выше в этой главе были рассмотрены два вида экспоненциальных распределений Гаусса и Лапласа. У них много общего они симметричны, зависят от двух параметров (//, сг), [c.41]
Обычно в справочниках распределения Гаусса, Лапласа и равномерное рассматриваются как разные распределения, хотя в излагаемой здесь концепции — это одно и тоже распределение. Единственным параметром, характеризующим форму (а значит и свойства) этих распределений является показатель ОС. [c.42]
С7 В этом современном виде теорема Байеса была на самом деле сформулирована Лапласом. Томасу Байесу принадлежит сама постановка задачи. Он сформулировал ее как обратную известной задаче Бернулли. Если Бернулли искал вероятность различных исходов бросания «кривой» монеты, то Байес, наоборот, стремился определить степень этой «кривизны» по эмпирически наблюдаемым исходам бросания монеты.
В его решении отсутствовала априорная вероятность.
[c.55]
Ф(х) — функция Лапласа, см. табл. 3.3 1), [c.139]
Для решения задачи в нулевом приближении используется преобразо-Лапласа-Карсона. Концентрации вещества в трубе и в окружающей [c.232]
В связи с этим необходимо использование специальных процедур и методов для отбора наиболее целесообразных вариантов. При этом мы не имеем полной информации о возможных действиях конкурентов. Рассмотренные задачи могут быть описаны с помощью «традиционных» методов принятия решений без использования численных значений вероятностей отдельных вариантов». Из них наиболее целесообразным является использование критериев Лапласа, Сэвиднея. Однако, для эффективного применения последних необходима разработка специальной методики определения возможных потерь от выбора неэффективного варианта стратегии. [c.96]
Мы рассмотрели несколько основных подходов к принятию решения в случае неопределенных факторов в изучаемой модели.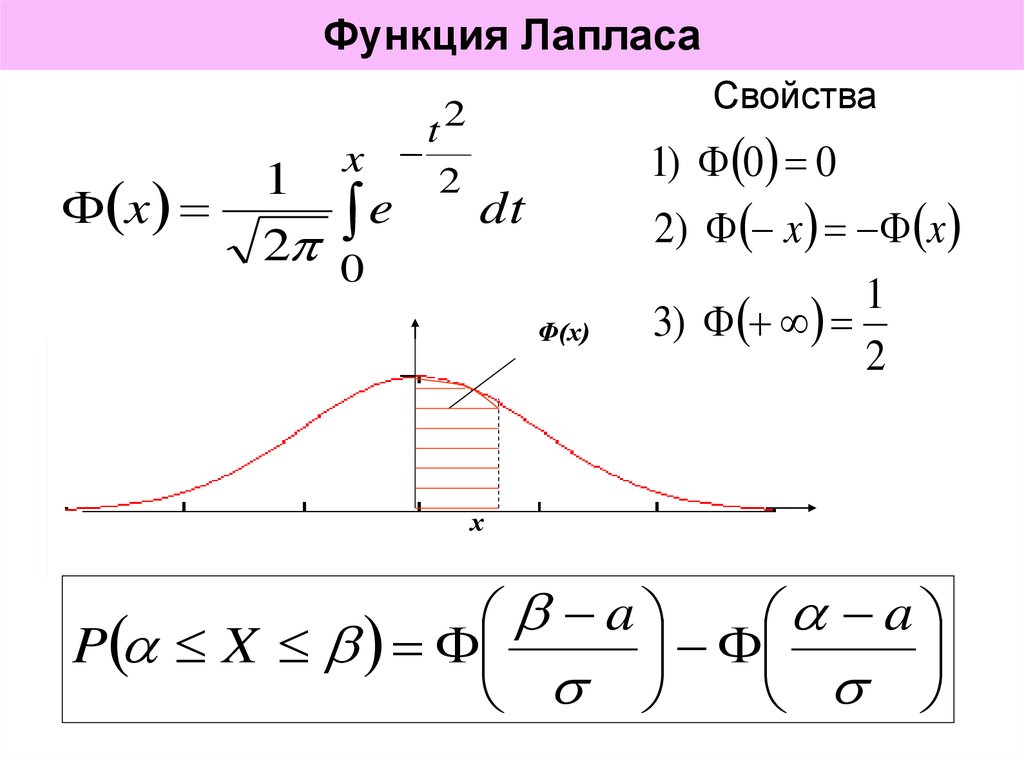
Можно привести примеры, когда все критерии принятия решения приводят к выбору одного и того же решения x e X, обычно же этого не происходит, каждый критерий приводит к своему решению (пример такого рода рассмотрен в следующей главе). Поэтому возникают дискуссии о том, какой критерий и когда предпочтительнее,. делаются попытки построить на основе нескольких критериев единственный. В частности, критерий Гурвица является таким объединением двух критериев. Предпринимались также попытки объединить критерий Гурвпца и критерий Байеса — Лапласа. Все получаемые критерии имеют высокую степень произвольности. По нашему мнению, единственным путем преодоления этих трудностей является многокритериальный подход, в котором ЛПР смогло бы рассмотреть варианты принимаемого решения, эффективные с точки зрения совокупности показателей, и выбрать среди них наиболее подходящий. Такой подход использован в примере, приведенном в следующей главе. Конечно, совокупность показателей при этом должна, быть не слишком велика.
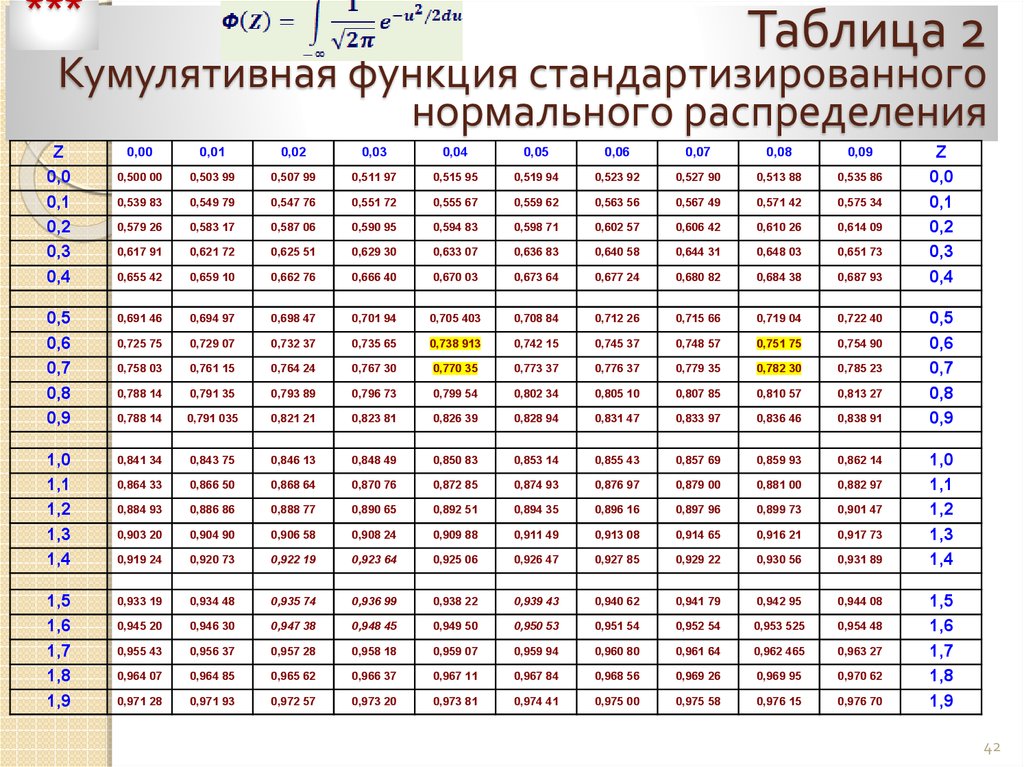[c.159]
Методы построения решения без участия ЛПР предлагается использовать в тех случаях, когда указывается направление улучшения значения критерия. При этом применяются методы типа максим инного или оптимистичного подхода, критериев Гурвица, Байеса — Лапласа и Сэвиджа, которые были подробно описаны и проиллюстрированы ранее. Напомним, что каждый из них обычно приводит к своему решению, так что об объективности выбора говорить навряд ли можно. [c.319]
Теория малых выборок разработана английским статистиком В. Госсетом (писавшим под псевдонимом Стьюдент) в начале XX в. В 1908 г. им построено специальное распределение, которое позволяет и при малых выборках соотносить / и доверительную вероятность F(t). При п > 100 таблицы распределения Стьюдента дают те же результаты, что и таблицы интеграла вероятностей Лапласа, при 30 малым выборкам относят выборки объемом менее 30 единиц (безусловно, большой считается выборка с объемом более 100 единиц). [c.190]
В условиях риска вместо критерия максимума выигрыша используется критерий максимума математического ожидания выигрыша.
Кроме того, в этой ситуации можно использовать критерий минимума математического ожидания риска (минимума среднего риска). Следует учитывать, что в теории статистических решений доказано, что стратегия (проект, вариант) наилучшая по критерию максимума среднего выиграша будет таковой и по критерию минимума среднего риска. В некоторых случаях при отсутствии надежной априорной информации о вероятностях возможных исходов, можно использовать принцип недостаточного освоения Лапласа, приняв значения этих вероятностей равными друг другу.
[c.284]
В качестве методологической основы используются методы полумарковских процессов и теории операционного исчисления. Данные методы позволяют свести решение, систем интегро-дифференциальных уравнений, описывающих эксплуатацию объектов связи, к решению систем алгебраических уравнений с последующим определением оригиналов полученных выражений для основных показателей надежности при помощи известных методов обращения. В случае, когда нахождение оригинала в явном виде затруднено, применяется усовершенствованный алгоритм численного обращения двумерного преобразователя Лапласа, в котором для оценки оригинала используются полиномы Лагерра.
Получено дальнейшее развитие подходов к формализации процесса эксплуатации технических объектов средств связи в виде аналитических выражений для основных показателей надежности,
[c.167]
Распределение Лапласа / Двойная экспонента
Распределения вероятностей > Распределение Лапласа
Что такое распределение Лапласа?
Распределение Лапласа , одно из самых ранних известных распределений вероятностей, представляет собой непрерывное распределение вероятностей, названное в честь французского математика Пьера-Симона Лапласа. Подобно нормальному распределению, это распределение унимодальное (один пик) и также является симметричным распределением. Однако оно имеет более острый пик, чем нормальное распределение.
Распределение Лапласа — это распределение разности двух независимых случайных величин с идентичными экспоненциальными распределениями (Leemis, n.d.). Он часто используется для моделирования явлений с тяжелыми хвостами или когда данные имеют более высокий пик, чем нормальное распределение.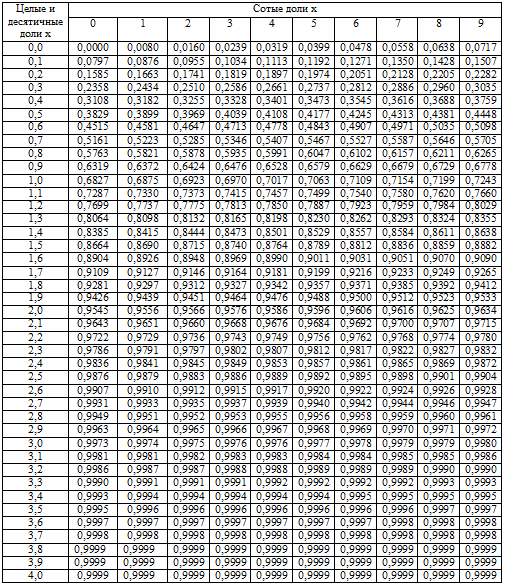
Это распределение является результатом двух экспоненциальных распределений, одного положительного и одного отрицательного; Его иногда называют двойным экспоненциальным распределением или , потому что оно выглядит как два экспоненциальных распределения, склеенных друг с другом.
ЛапласPDF.
Общая формула для функции плотности вероятности (PDF):
где:
- μ (любое действительное число) — параметр местоположения, а
- β (должно быть > 0) — параметр масштаба; это иногда называют разнообразием .
Параметры масштаба и местоположения
Форма распределения Лапласа определяется параметрами местоположения и масштаба. Следующее изображение было создано с помощью этого онлайн-калькулятора Casio (μ = 3, β = 0,7), который позволяет создавать различные файлы PDF и CDF для распространения.
Среднее, дисперсия, асимметрия, эксцесс
- Среднее (μ): μ
- Дисперсия (σ 2 ): 2β 2
- Асимметрия = 0
- Эксцесс = 6
(Härdle & Simar, 2015)
Классический одномерный Лаплас
Распределение Лапласа с параметром местоположения, равным нулю (т.
классическое одномерное распределение Лапласа . Функция для этой конкретной версии дистрибутива:
f(x) = e -|x| / 2.
Где e -x — экспоненциальная функция.
CDF
Кумулятивная функция распределения (CDF) распределения Лапласа находится с помощью исчисления; это интеграл PDF. Вы можете думать об интеграле как о площади под кривой. Это та же идея, что и нахождение площади под кривой для нахождения вероятностей в нормальном распределении.
Формула для CDF:
Где sgn — функция знака.
Для получения дополнительной информации о решении интегралов см.:
- Определенные интегралы (CalculusHowTo.com)
- Функция накопления (CalculusHowTo.com)
Программное обеспечение
Несмотря на то, что это одно из старейших распределений вероятностей, оно редко используется. Поэтому поиск функций для этого дистрибутива в популярном программном обеспечении, таком как Excel, может оказаться сложной задачей.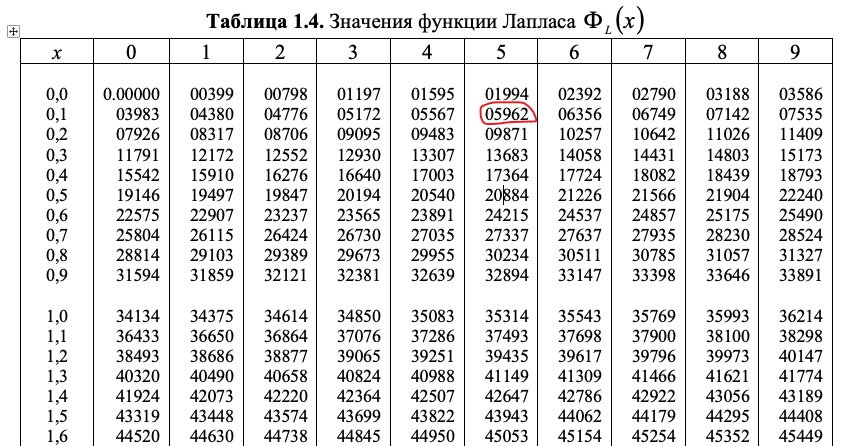
Однако многие пакеты статистического программного обеспечения предлагают опции, включая Maple и SPSS.
Посетите наш канал YouTube, где вы найдете сотни видеороликов со статистикой.
Ссылки
Хердле, В. и Симар, Л. (2015). Прикладной многомерный статистический анализ. Спрингер.
Лимис, Л. (без даты). Экспонента / Лаплас. Получено 10 января 2018 г. с: http://www.math.wm.edu/~leemis/chart/UDR/PDFs/ExponentialLaplace.pdf
Вайсштейн, Эрик В. «Распределение Лапласа». Из MathWorld — веб-ресурса Wolfram. http://mathworld.wolfram.com/LaplaceDistribution.html
УКАЗЫВАЙТЕ ЭТО КАК:
Стефани Глен . «Распределение Лапласа / Двойная экспонента» Из StatisticsHowTo.com : Элементарная статистика для всех нас! https://www.statisticshowto.com/laplace-distribution-double-exponential/
Нужна помощь с домашним заданием или контрольным вопросом? С Chegg Study вы можете получить пошаговые ответы на ваши вопросы от эксперта в данной области.
Ваши первые 30 минут с репетитором Chegg бесплатны!
Комментарии? Нужно опубликовать исправление? Пожалуйста, Свяжитесь с нами .
Домашняя страница калькулятора распределения ЛапласаСписок помощи по математике — — Быстрый переход по математике — Научный онлайн-калькулятор — Общая математика — Калькулятор дробейКалькулятор процентовКалькулятор квадратного корняКалькулятор факторингаУпрощение выраженийКалькулятор делителейКалькулятор множителейКалькулятор наибольшего общего множителя (НОК)Калькулятор наименьшего общего кратного (НОК)Калькулятор и проверка простых чиселВалидатор идеальных чиселВалидатор идеальных квадратных чисел-Интерполяция-Интерполяционный калькулятор — Алгебра и комбинаторика -Решатель уравненийРешатель квадратных уравненийРешатель систем уравненийКомбинаторикаПерестановкиПолиномыПолиномы -Сложение и вычитаниеПолиномы -Умножение и делениеПолиномы -Дифференцирование и интегрированиеПолиномы -Калькулятор четности (нечетные, четные, нет)Полиномы -Поиск корняПолиномы -Сгенерировать из корнейМатрицаМатрицаМатрица-детерминантКалькулятор Сложение, вычитание, умножение, исчисление, интегральный калькуляторОпределенный интегральный калькуляторПроизводный калькуляторЧисловая производная КалькуляторLimit CalculatorTaylor Series Expansion CalculatorTaylor Series Expansion Calculator-Plots and Geometry-2D Graphing Calculator3D Graphing Calculator-Complex Numbers and Trigonometry-Complex Number CalculatorTrigonometry Calculator-The Number Theory-Riemann Zeta Function CalculatorHurwitz Zeta Function CalculatorГенератор чисел БернуллиГенератор полиномов Бернулли-Статистика и вероятность -Калькулятор PDF QuantileCDF Calculator Deviation CalculatorVariance CalculatorKurtosis CalculatorSkewness Calculator- Descriptive Statistics Calculators -Matrix Central Moment CalculatorCorrelation Matrix CalculatorCovariance Matrix CalculatorMatrix Geometric Mean CalculatorMatrix Harmonic Mean CalculatorMatrix Interquartile Range CalculatorMatrix Kurtosis CalculatorMatrix Noncentral Moment CalculatorMatrix Mean CalculatorMatrix Maximum CalculatorMatrix Minimum CalculatorMatrix Median CalculatorMatrix Median Deviation CalculatorMatrix Mean Deviation CalculatorMatrix Quantile Calculator Matrix Quartile Skewness CalculatorMatrix Skewness CalculatorMatrix Standard Deviation CalculatorMatrix Variance CalculatorMatrix Variation Coefficient Calculator- Continuous Distributions Calculators -Beta Distribution CalculatorsChi-Square Distribution CalculatorsExponential Distribution CalculatorsGamma Distribution CalculatorsGumbel Distribution CalculatorsLaplace Distribution CalculatorsLognormal Distribution CalculatorsNormal (Gaussian) Distribution CalculatorsPareto Distribution CalculatorsRayleigh Distribution CalculatorsStudent t-Distribution CalculatorsUniform Distribution КалькуляторыКалькуляторы распределения Вейбулла-Калькуляторы дискретных распределений-Калькуляторы биномиального распределенияКалькуляторы геометрического распределенияКалькуляторы распределения ПуассонаКалькуляторы равномерного (дискретного) распределения
Электронная почта Печать
|
Распределение Лапласа — это непрерывное распределение вероятностей, названное в честь Пьера-Симона Лапласа.