 определение в
8.2).
Таблица приводится по источнику [5]. определение в
8.2).
Таблица приводится по источнику [5].
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| А.Д. Манита, 2001-2011 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Как найти критическое значение T в Excel
Всякий раз, когда вы проводите t-тест, в результате вы получаете тестовую статистику. Чтобы определить, являются ли результаты t-теста статистически значимыми, можно сравнить статистику теста с критическим значением T. Если абсолютное значение тестовой статистики больше критического значения Т, то результаты теста статистически значимы.
Критическое значение T можно найти с помощью таблицы распределения t или с помощью статистического программного обеспечения.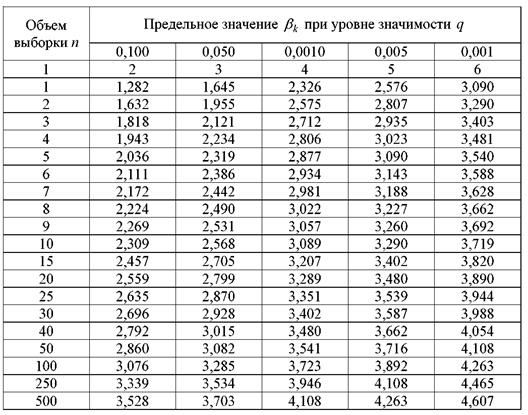
Чтобы найти критическое значение T, необходимо указать:
- Уровень значимости (обычно выбирают 0,01, 0,05 и 0,10).
- Степени свободы
- Тип теста (односторонний или двусторонний)
Используя эти три значения, вы можете определить критическое значение T для сравнения со статистикой теста.
Связанный: Как найти критическое значение Z в Excel
Как найти критическое значение T в ExcelExcel предлагает две функции для нахождения критического значения T.
Т.ОБР.Чтобы найти критическое значение T в Excel для одностороннего теста , вы можете использовать функцию T.ОБР.() , которая использует следующий синтаксис:
T.INV (вероятность, град_свободы)
- вероятность: уровень значимости для использования
- deg_freedom : Степени свободы
Эта функция возвращает критическое значение из распределения t для одностороннего теста на основе уровня значимости и предоставленных степеней свободы.
Чтобы найти критическое значение T в Excel для двустороннего теста , вы можете использовать функцию T.ОБР.2T() , которая использует следующий синтаксис:
T.INV.2T (вероятность, град_свободы)
- вероятность: уровень значимости для использования
- deg_freedom : Степени свободы
Эта функция возвращает критическое значение из распределения t для двустороннего теста на основе уровня значимости и предоставленных степеней свободы.
Примеры поиска критического значения T в ExcelВ следующих примерах показано, как найти критическое значение T для левостороннего, правостороннего и двустороннего критериев.
Левосторонний тестЧтобы найти критическое значение T для левостороннего критерия с уровнем значимости 0,05 и степенями свободы = 11, мы можем ввести в Excel следующую формулу: T.ОБР(0,05, 11)
Это возвращает значение -1,79588. Это критическое значение для левостороннего теста с уровнем значимости 0,05 и степенями свободы = 11.
Это критическое значение для левостороннего теста с уровнем значимости 0,05 и степенями свободы = 11.
Чтобы найти критическое значение T для правостороннего критерия с уровнем значимости 0,05 и степенями свободы = 11, мы можем ввести в Excel следующую формулу: ABS( T.ОБР(0,05, 11))
Это возвращает значение 1,79588.Это критическое значение для двустороннего теста с уровнем значимости 0,05 и степенями свободы = 11.
Двусторонний тестЧтобы найти критическое значение T для двустороннего критерия с уровнем значимости 0,05 и степенями свободы = 11, мы можем ввести в Excel следующую формулу: T.ОБР.2T(0,05, 11)
Это возвращает значение 2.200985.Это критическое значение для двустороннего теста с уровнем значимости 0,05 и степенями свободы = 11.
Обратите внимание, что это также соответствует числу, которое мы нашли бы в таблице распределения t с α = 0,05 для двух хвостов и DF (степени свободы) = 11.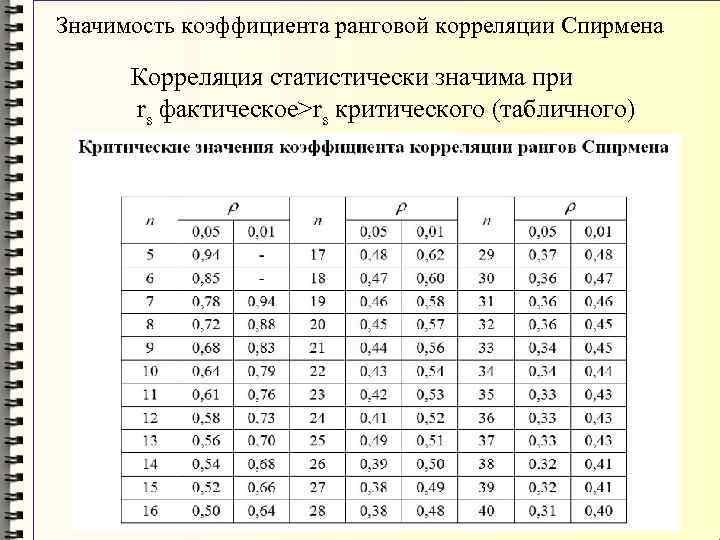
Обратите внимание, что обе функции T.ОБР () и T.ОБР.2T() в Excel выдают ошибку, если происходит одно из следующих событий:
- Если какой-либо аргумент не является числовым.
- Если значение вероятности меньше нуля или больше 1.
- Если значение для deg_freedomменьше 1.
Калькулятор критического значения T (калькулятор таблицы t)
Выберите тип вероятности, введите степень свободы и уровень значимости для расчета значения t с помощью нашего калькулятора значения t.
Калькулятор критического значения
Калькулятор критического значения T — это интерактивный статистический инструмент, который вычисляет значение t для односторонней и двусторонней вероятности. Кроме того, калькулятор критических значений также показывает сопоставленное значение t в таблице распределения Стьюдента для одного образца и двух образцов.
Какое значение t?
Значение T измеряет размер разницы относительно вариации данных выборки. В основном это расчетная разница, представленная в единицах стандартной ошибки.
- Если значение t больше, это свидетельствует о значительной разнице.
- Если значение t ближе к 0, , есть шансы, что существенной разницы не будет.
| Наименование типа | Формула Т -критического значения |
| Правоем | Q T, D (1 — α) | Q T, D (α) |
| Двухсторонний | ± Q T, D (1-α/2) |
, как можно найти значение. т?
Чтобы вычислить критическое значение t вручную (без использования калькулятора t ), следуйте приведенному ниже примеру.
Пример:
Рассчитать критическое значение t (одна решка и две решки) для уровня значимости 5% и 30 степеней свободы.
Решение:
Шаг 1: Определите значения.
Significance level = 5% = 5/100 = 0.05
Degree of freedom = 30
Step 2: Look for the significance level в верхней строке таблицы распределения t ниже (один хвост) и степени свободы (df) в левой части стола.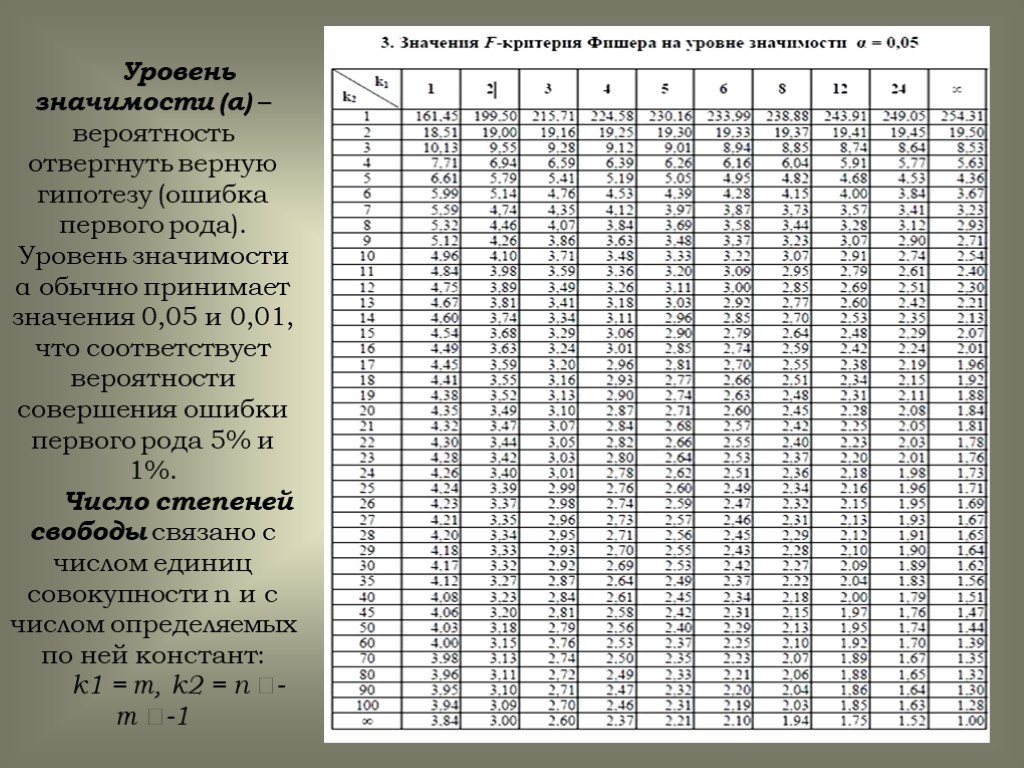 Получите соответствующее значение из таблицы.
Получите соответствующее значение из таблицы.
критическое значение T (одностороннее) = 1,6978
Критическое значение T (двусторонний +/-) = 2,0428
Используйте наш калькулятор таблицы t выше, чтобы быстро получить значения таблицы t.
Таблица T-распределения (односторонняя)
Таблица t для односторонней вероятности приведена ниже.
| DF | A = 0.1 | 0.05 | 0.025 | 0.01 | 0.005 | 0.001 | 0.0005 | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| ∞ | t a = 1.282 | 1.645 | 1.960 | 2,326 | 2,576 | 3,091 | 3,291 | ||||||||||
| 1 | 3.078 | 6.314 | 12.706 | 31.821 | 63.656 | 318. 289 289 | 636.578 | ||||||||||
| 2 | 1.886 | 2.920 | 4.303 | 6.965 | 9.925 | 22.328 | 31.600 | ||||||||||
| 3 | 1,638 | 2,353 | 3,182 | 4,541 | 5,841 | 10,214 | 12,91 | 10,214 | 12,91,24 | ||||||||
| 4 | 1.533 | 2.132 | 2.776 | 3.747 | 4.604 | 7.173 | 8.610 | ||||||||||
| 5 | 1.476 | 2.015 | 2.571 | 3.365 | 4.032 | 5.894 | 6.869 | ||||||||||
| 6 | 1,440 | 1,943 | 2,447 | 3,143 | 3,707 | 5.2051 | 3,707 | 5.2051 | 3,707 | 5.2051 | 3,707 | 5.2051 | 3,707 | 3,707 | 3,707 | .||
| 7 | 1.415 | 1.895 | 2.365 | 2.998 | 3.499 | 4.785 | 5.408 | ||||||||||
| 8 | 1.397 | 1.860 | 2.306 | 2.896 | 3.355 | 4.501 | 5.041 | ||||||||||
| 1,383 | 1,833 | 2,262 | 2,821 | 3,250 | 4,297 979 | 3,250 | 4,297 979797 | 3,250 | 4,297 9007 | 3,250 | 4,297 | 3,250 | 4.0051 | 4.781 | |||
| 10 | 1.372 | 1.812 | 2.228 | 2.764 | 3.169 | 4.144 | 4.587 | ||||||||||
| 11 | 1.363 | 1.796 | 2.201 | 2.718 | 3.106 | 4.025 | 4.437 | ||||||||||
| 12 | 1,356 | 1,782 | 2,179 | 2,681 | 3,055 | 2,681 | 3,055 | 2,681 | 3,055 | .4.318 | |||||||
| 13 | 1.350 | 1.771 | 2.160 | 2.650 | 3.012 | 3.852 | 4.221 | ||||||||||
| 14 | 1.345 | 1.761 | 2.145 | 2.624 | 2.977 | 3,787 | 4.140 | ||||||||||
| 15 | 1,341 | 1,753 | 2.131 | 2.602 | 2.9 2,91 | 2.602 | 2.9 2,9 2,98 2,131 | 2.602 | 2.9 2,131 | 2.602 | 2.47 | 3.733 | 4.073 | ||||
| 16 | 1.337 | 1.746 | 2.120 | 2.583 | 2.921 | 3.686 | 4.015 | ||||||||||
| 17 | 1.333 | 1.740 | 2.110 | 2.567 | 2.898 | 3.646 | 3.965 | ||||||||||
| 18 | 1.330 | 1.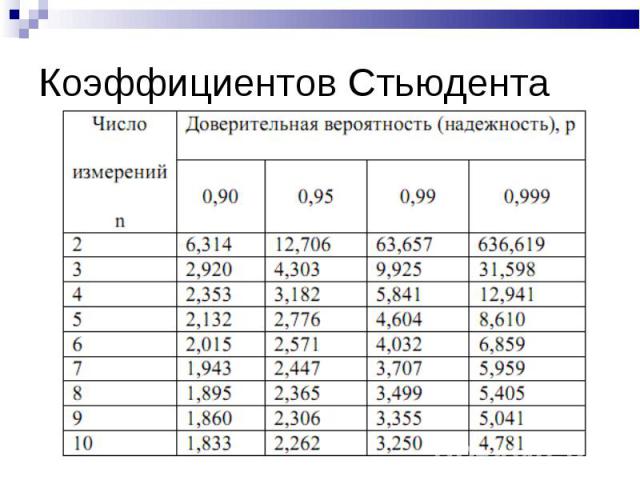 734 734 | 2.101 | 2.552 | 2.878 | 3.610 | 3.922 | ||||||||||
| 19 | 1.328 | 1.729 | 2.093 | 2.539 | 2.861 | 3.579 | 3.883 | ||||||||||
| 20 | 1.325 | 1.725 | 2.086 | 2.528 | 2.845 | 3,552 | 3,850 | ||||||||||
| 21 | 1,323 | 1,721 | 2,080 | 2,518 | 2,080 | ,5 2,518 9008 9008 | 2,080 | ,5 2,518 | 2,080 | 2,721 | 2,080 | 2,721 | .00512.831 | 3.527 | 3.819 | ||
| 22 | 1.321 | 1.717 | 2.074 | 2.508 | 2.819 | 3.505 | 3.792 | ||||||||||
| 23 | 1.319 | 1.714 | 2.069 | 2,500 | 2,807 | 3,485 | 3,768 | ||||||||||
| 24 | 1,318 | 1,711 | 2,064 | 1,711 | 2,064 | 1,711 | 2,064 | 1,711 | 2,064 | 0048 2.2.797 | 3.467 | 3.745 | |||||
| 25 | 1.316 | 1.708 | 2.060 | 2.485 | 2.787 | 3.450 | 3.725 | ||||||||||
| 26 | 1.315 | 1.706 | 2.056 | 2,479 | 2,779 | 3,435 | 3,707 | ||||||||||
| 27 | 1,314 | 1,703 | 148 2,0521,703 | 148 2,05291,703 | 148,052 9005 21,703 | 148,0521,703 | 148,0521,703 | 48,0521,703 2,052 | .00512.473 | 2.771 | 3.421 | 3.689 | |||||
| 28 | 1.313 | 1.701 | 2.048 | 2.467 | 2.763 | 3.408 | 3.674 | ||||||||||
| 29 | 1.311 | 1.699 | 2.045 | 2.462 | 2. 756 756 | 3.396 | 3.660 | ||||||||||
| 30 | 1.310 | 1.697 | 2.042 | 2.457 | 2.750 | 3.385 | 3.646 | ||||||||||
| 60 | 1.296 | 1.671 | 2.000 | 2.390 | 2.660 | 3.232 | 3.460 | ||||||||||
| 120 | 1.289 | 1.658 | 1,980 | 2,358 | 2,617 | 3.160 | 3,373 | ||||||||||
| 1000 | 1,282 | 414861,282 | 14861841,282 | 1486184.00511,962 | 2,330 | 2,581 | 3,098 | 3,300 |
T-распределение (два хвоста).
| DF | A = 0.2 | 0.10 | 0.05 | 0.02 | 0.01 | 0.002 | 0.001 |
|---|---|---|---|---|---|---|---|
| ∞ | t a = 1.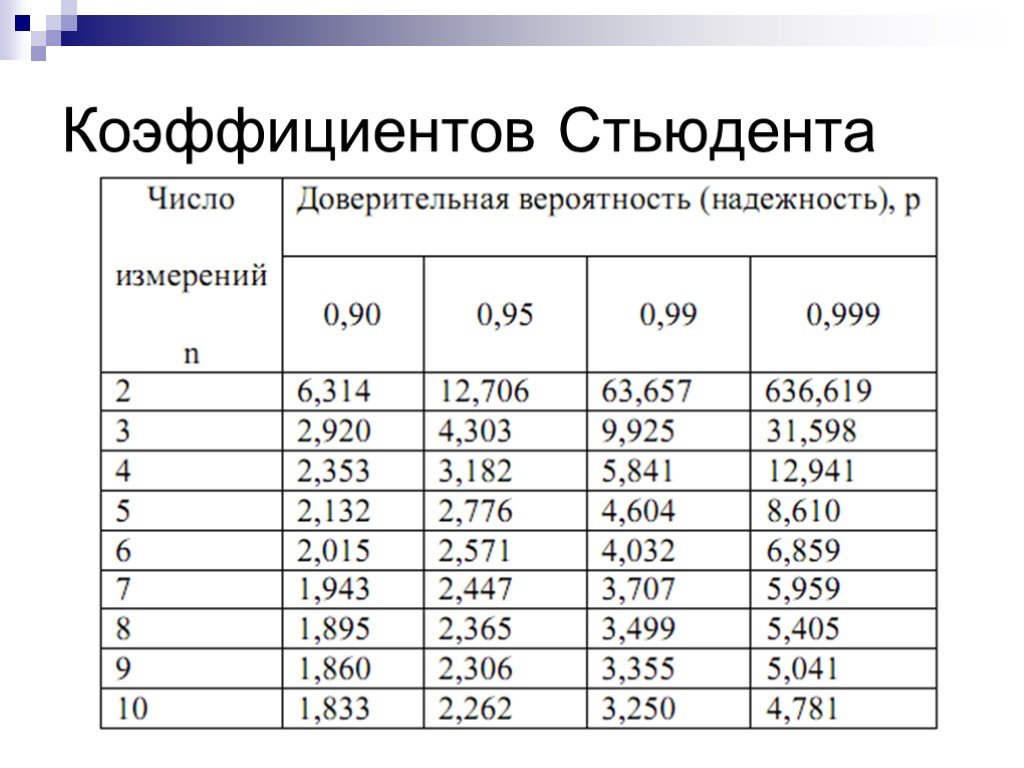 282 282 | 1.645 | 1.960 | 2.326 | 2.576 | 3.091 | 3.291 |
| 1 | 3.078 | 6.314 | 12.706 | 31.821 | 63.656 | 318.289 | 636.578 |
| 2 | 1.886 | 2,920 | 4.303 | 6.965 | 9,925 | 22,328 | 31,600 |
| 3 | 1,638 | ||||||
| 3 | 1,638 | ||||||
| 3 | 1,638 | ||||||
| 3.182 | 4.541 | 5.841 | 10.214 | 12.924 | |||
| 4 | 1.533 | 2.132 | 2.776 | 3.747 | 4.604 | 7.173 | 8.610 |
| 5 | 1.476 | 2.015 | 2.571 | 3.365 | 4.032 | 5.894 | 6.869 |
| 6 | 1.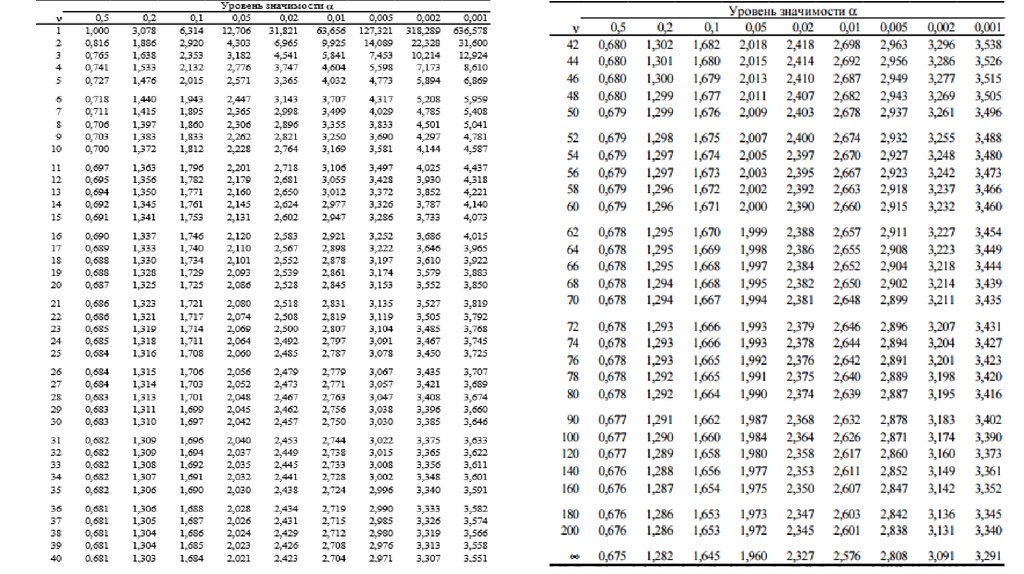 440 440 | 1.943 | 2.447 | 3.143 | 3.707 | 5.208 | 5.959 |
| 7 | 1.415 | 1.895 | 2.365 | 2.998 | 3.499 | 4.785 | 5.408 |
| 8 | 1,397 | 1,860 | 2,306 | 2,896 | 3,355 | 4,501 | 5,041 |
| 5 | ,383333333333333333333333333333333333333333333333333333333333333333333тели | 1.833 | 2.262 | 2.821 | 3.250 | 4.297 | 4.781 |
| 10 | 1.372 | 1.812 | 2.228 | 2.764 | 3.169 | 4.144 | 4.587 |
| 11 | 1,363 | 1,796 | 2,201 | 2,718 | 3,106 | 4,025 | 4,437 |
| 12 | 937|||||||
| 12 | |||||||
12 5 9370048 1.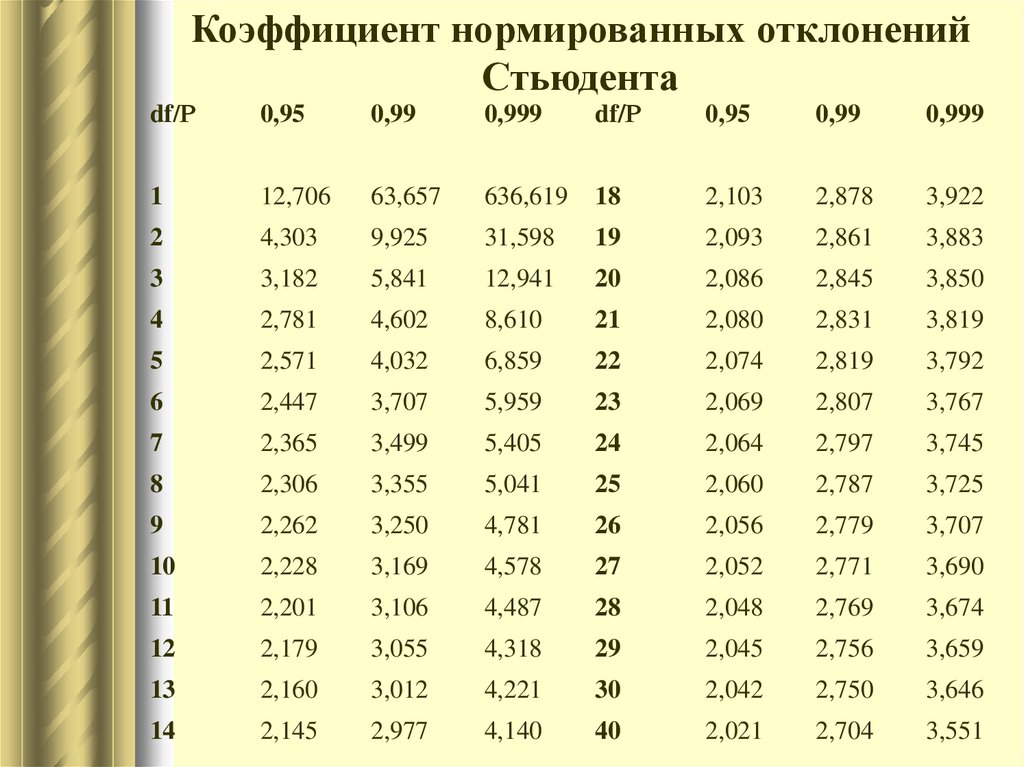 356 356 | 1.782 | 2.179 | 2.681 | 3.055 | 3.930 | 4.318 | |
| 13 | 1.350 | 1.771 | 2.160 | 2.650 | 3.012 | 3.852 | 4.221 |
| 14 | 1,345 | 1,761 | 2,145 | 2,624 | 2,977 | 3,787 | 4.140 |
| 4.140 | |||||||
| 4.140 | |||||||
| 4.140 | |||||||
| 0185 | 1.341 | 1.753 | 2.131 | 2.602 | 2.947 | 3.733 | 4.073 |
| 16 | 1.337 | 1.746 | 2.120 | 2.583 | 2.921 | 3.686 | 4.015 |
| 17 | 1,333 | 1,740 | 2,110 | 2,567 | 2,898 | 3,646 | 3,965 |
| 3,965 | |||||||
| 3,965 | |||||||
| 3,965 | |||||||
| 3,965 | |||||||
| 3,965 | |||||||
| 3,965 | 3,965 | ||||||
1. 330 330 | 1.734 | 2.101 | 2.552 | 2.878 | 3.610 | 3.922 | |
| 19 | 1.328 | 1.729 | 2.093 | 2.539 | 2.861 | 3.579 | 3.883 |
| 20 | 1.325 | 1.725 | 2.086 | 2.528 | 2.845 | 3.552 | 3.850 |
| 21 | 1.323 | 1.721 | 2.080 | 2.518 | 2.831 | 3.527 | 3.819 |
| 22 | 1.321 | 1.717 | 2.074 | 2.508 | 2.819 | 3.505 | 3.792 |
| 23 | 1.319 | 1.714 | 2.069 | 2.500 | 2.807 | 3.485 | 3.768 |
| 24 | 1.318 | 1.711 | 2. 064 064 | 2.492 | 2.797 | 3.467 | 3.745 |
| 25 | 1.316 | 1.708 | 2.060 | 2.485 | 2.787 | 3.450 | 3.725 |
| 26 | 1,315 | 1,706 | 2,056 | 2,479 | 2,779 | 3,435 | 3,707 | .0051
| 27 | 1.314 | 1.703 | 2.052 | 2.473 | 2.771 | 3.421 | 3.689 |
| 28 | 1.313 | 1.701 | 2.048 | 2.467 | 2.763 | 3.408 | 3.674 |
| 29 | 1.311 | 1.699 | 2.045 | 2.462 | 2.756 | 3.396 | 3.660 |
| 30 | 1.310 | 1.697 | 2.042 | 2.457 | 2.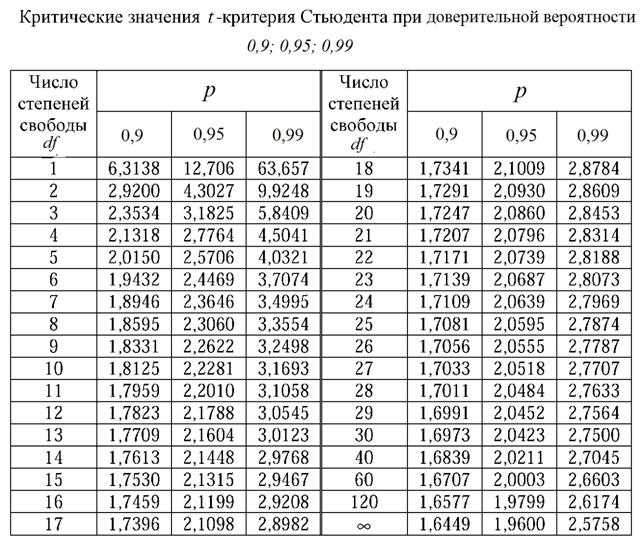 750 750 | 3.385 | 3.646 |
| 60 | 1.296 | 1.671 | 2.000 | 2.390 | 2.660 | 3.232 | 3,460 |
| 120 | 1,289 | 1,658 | 1,980 | 2,358 | 2.617 | 98 3,1603,168 2,3582.617 | 98 3,1603,168 3,358.00513.373 |
| ∞ | 1.282 | 1.645 | 1.960 | 2.326 | 2.576 | 3.091 | 3.291 |
T-Distribution Probability Calculator — MathCracker.com
Решатели Статистика
Инструкции: Используйте этот Калькулятор вероятности T-распределения для вычисления вероятностей t-распределения, используя форму ниже. Введите количество степеней свободы, связанных с t-распределением, и предоставьте подробную информацию о событии, для которого вы хотите вычислить вероятность:
Введите количество степеней свободы, связанных с t-распределением, и предоставьте подробную информацию о событии, для которого вы хотите вычислить вероятность:
Стьюдентное распределение — это тип непрерывного распределения вероятностей, которое принимает случайные значения на всей прямой. Основные свойства t-распределения:
- Он непрерывен (и, как следствие, вероятность получения какого-либо одного конкретного результата равна нулю)
- Он имеет форму «колокола», точно так же, как нормальные кривые имеют форму колокола.
- Он определяется одним параметром: количеством степеней свободы (df).
 Для одной выборки число степеней свободы равно df = n — 1, где n — объем выборки.
Для одной выборки число степеней свободы равно df = n — 1, где n — объем выборки. - Он симметричен относительно 0
- Распределение t «сходится» к стандартному нормальному распределению по мере того, как число степеней свободы (df) стремится к бесконечности (+∞).
Чтобы вычислить вероятности, связанные с t-распределением, мы можем либо использовать специализированное программное обеспечение, такое как Excel и т. д., либо мы можем использовать таблицы t-распределения (обычно доступные в учебниках по статистике колледжей. Использование t-распределения возникает при выполнении гипотезы тестирования (для случая, когда стандартное отклонение популяции неизвестно).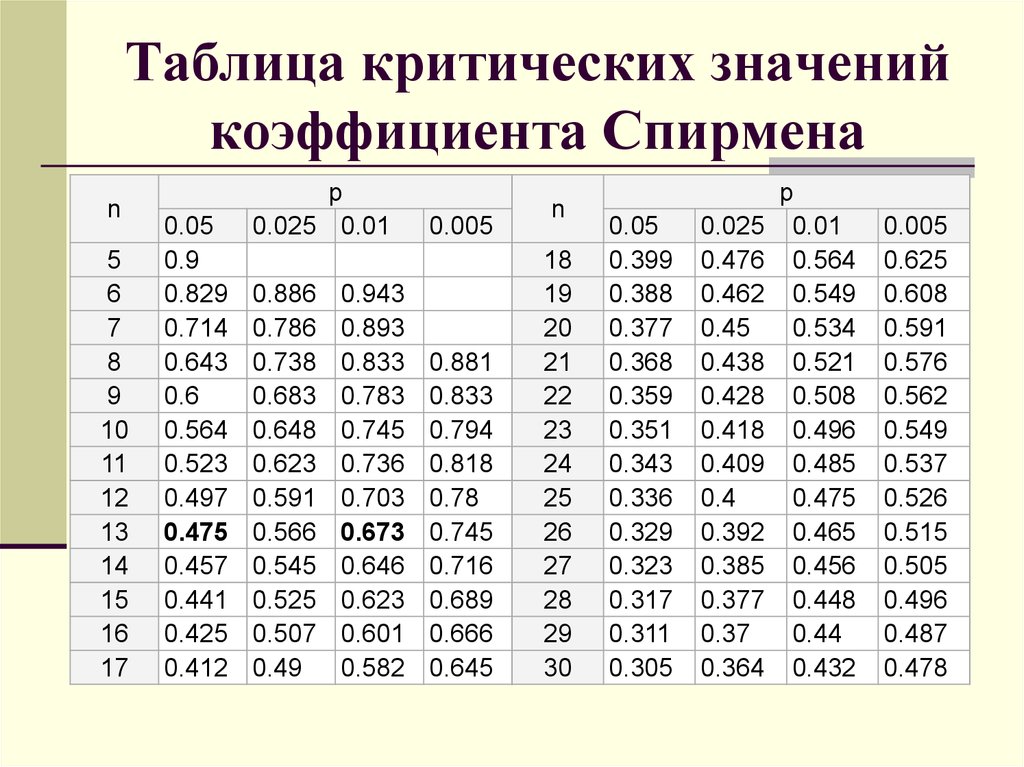
Как вам этот калькулятор Т-распределения
Этот калькулятор позволяет вам иметь калькулятор Т-распределения как для двустороннего, так и для левостороннего и двустороннего. Этот достигается путем выбора правильного типа события в форме выше.
Что означает Калькулятор площади t-распределения
Площадь t-распределения, как и всех вероятностных распределений, представляет собой вероятность того, что случайное четное происходит в области, для которой рассчитывается площадь. Другими словами, в данном случае площадь = вероятность.
Какова точность калькулятора распределения T
Это действительно зависит от того, какой инструмент вы используете для расчета. Например, если вы используете t-таблицы для вычисления t-распределения вероятностей, вы обнаружите, что они обычно имеют точность 4 цифры.
Теперь, когда вы используете наш калькулятор (или Excel), вы получаете точность около 15 цифр. Вы можете подумать, что это здорово и лучше, и это
на самом деле это так, только вы должны быть осторожны, отвечая на тесты и викторины, где они могут попросить вас пройти 9 раундов1503 промежуточный и
окончательные шаги, которые могут привести к ответам, которые могут отличаться от ответов, ожидаемых системой.
Вы можете подумать, что это здорово и лучше, и это
на самом деле это так, только вы должны быть осторожны, отвечая на тесты и викторины, где они могут попросить вас пройти 9 раундов1503 промежуточный и
окончательные шаги, которые могут привести к ответам, которые могут отличаться от ответов, ожидаемых системой.
Дополнительные калькуляторы для t-распределения
Это калькулятор для T-Distribution. Если вам необходимо работать с нормальным распределением, вас также могут заинтересовать наши калькулятор z-распределения . Кроме того, нормальная вероятность для выборок могла бы пригодиться, чтобы иметь дело с такими вещами, как центральная предельная теорема и тому подобное.
Применение: расчет вероятности
Вопрос : вычислить вероятность события (-1, 0,8) для t-распределения с 34 степенями свободы.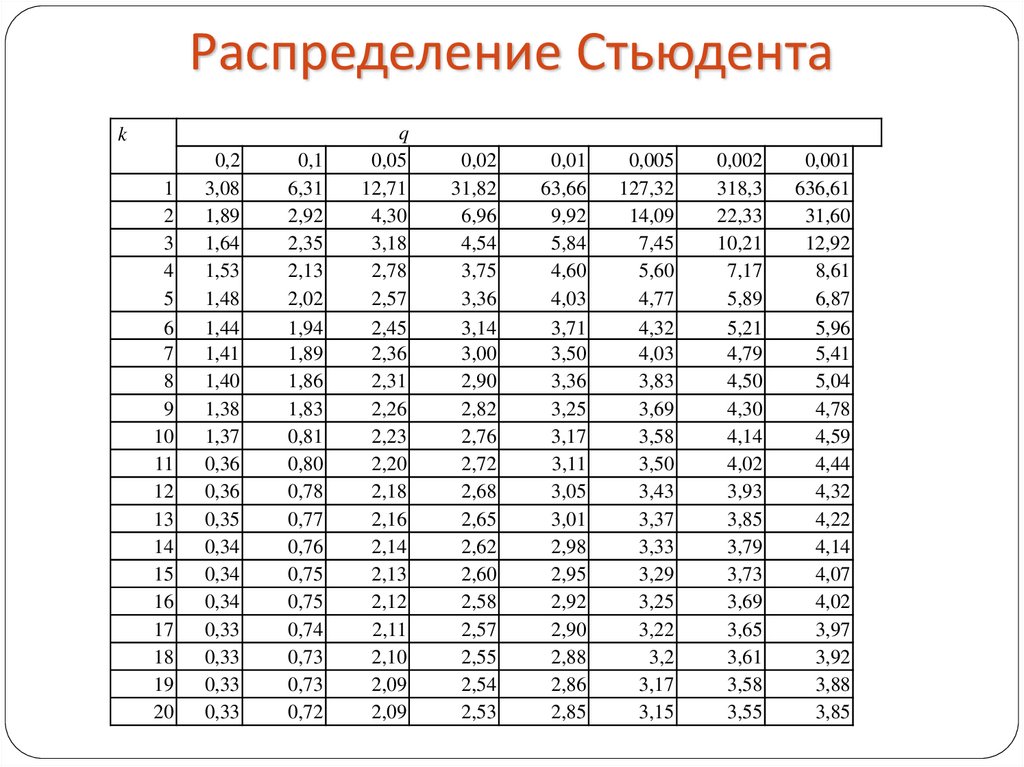

 0048 Левый хвост
0048 Левый хвост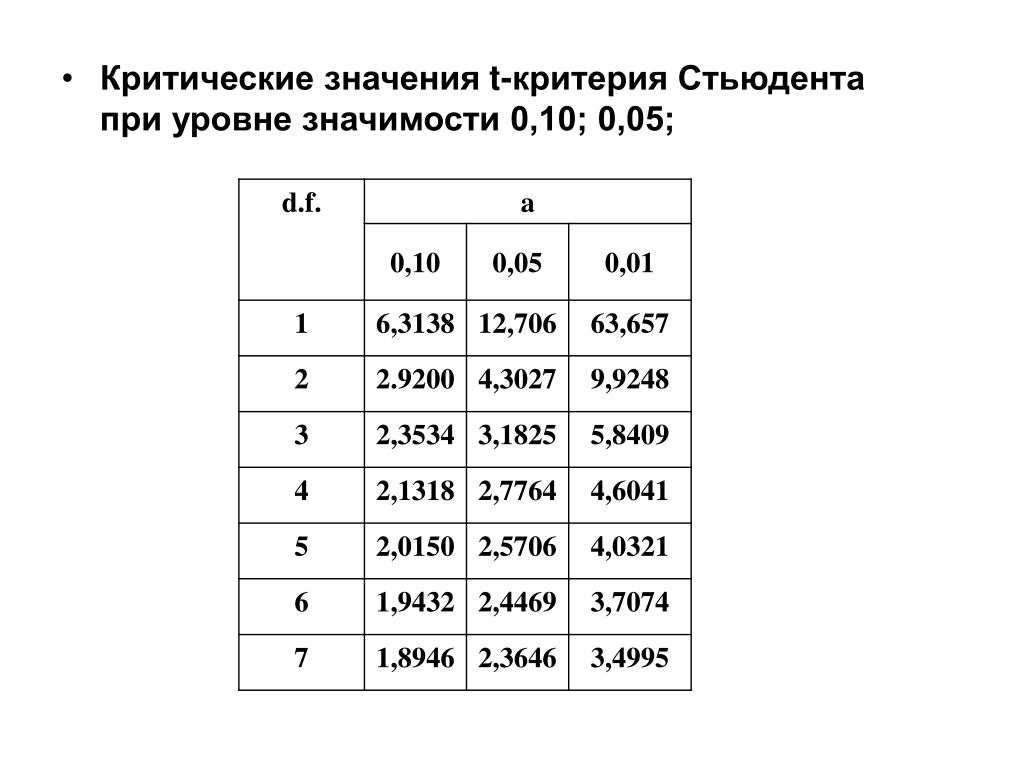 0048 5.959
0048 5.959 0048 3.930
0048 3.930 492
492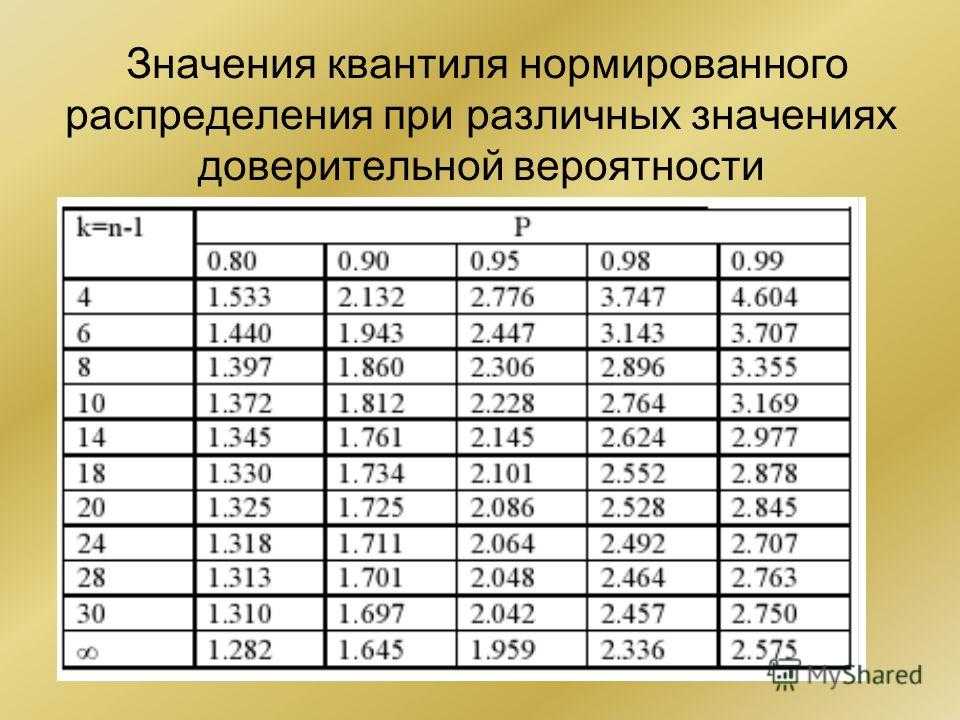 Для одной выборки число степеней свободы равно df = n — 1, где n — объем выборки.
Для одной выборки число степеней свободы равно df = n — 1, где n — объем выборки.