Таблица sin cos углов: Таблица синусов и косинусов

Косинус 0.5 какой угол. Связь с другими тригонометрическими функциями

Внимание!
К этой теме имеются дополнительные
материалы в Особом разделе 555.
Для тех, кто сильно «не очень…»
И для тех, кто «очень даже…»)

Прежде всего напомню простой, но очень полезный вывод из урока «Что такое синус и косинус? Что такое тангенс и котангенс?»

Вот этот вывод:

Синус, косинус, тангенс и котангенс накрепко связаны со своими углами. Знаем одно — значит, знаем и другое.

Другими словами, у каждого угла есть свой неизменный синус и косинус. И почти у каждого — свой тангенс и котангенс. Почему почти? Об этом ниже.

Это знание здорово помогает в учёбе! Существует масса заданий, где требуется перейти от синусов к углам и наоборот. Для этого существует таблица синусов. Аналогично, для заданий с косинусом — таблица косинусов. И, как вы уже догадались, существует таблица тангенсов и таблица котангенсов.

)

Таблицы бывают разные. Длинные, где можно посмотреть, чему равен, скажем, sin37°6’. Раскрываем таблицы Брадиса, ищем угол тридцать семь градусов шесть минут и видим значение 0,6032. Понятное дело, запоминать это число (и тысячи других табличных значений) совершенно не требуется.

В сущности, в наше время длинные таблицы косинусов синусов тангенсов котангенсов не особо-то и нужны. Один хороший калькулятор заменяет их полностью. Но знать о существовании таких таблиц не мешает. Для общей эрудиции.)

И зачем тогда этот урок?! — спросите вы.

А вот зачем. Среди бесконечного количества углов существуют особые, о которых вы должны знать всё . На этих углах построена вся школьная геометрия и тригонометрия. Это, своего рода, «таблица умножения» тригонометрии. Если вы не знаете, чему равен, например, sin50°, никто вас не осудит.) Но если вы не знаете, чему равен sin30°, будьте готовы получить заслуженную двойку…

Таких

особых углов тоже прилично набирается. Школьные учебники обычно любезно предлагают к запоминанию таблицу синусов и таблицу косинусов для семнадцати углов. Ну и, разумеется, таблицу тангенсов и таблицу котангенсов для тех же семнадцати углов… Т.е. предлагается запомнить 68 значений. Которые, между прочим, очень похожи между собой, то и дело повторяются и меняют знаки. Для человека без идеальной зрительной памяти — та ещё задачка…)

Мы пойдём другим путём. Заменим механическое запоминание на логику и смекалку. Тогда нам придётся зазубрить 3 (три!) значения для таблицы синусов и таблицы косинусов. И 3 (три!) значения для таблицы тангенсов и таблицы котангенсов. И всё. Шесть значений запомнить легче, чем 68, мне кажется…)

Все остальные необходимые значения мы будем получать из этих шести с помощью мощной законной шпаргалки — тригонометрического круга. Если вы не изучали эту тему, сходите по ссылочке, не ленитесь. Этот круг не только для этого урока нужен. Он незаменим

для всей тригонометрии сразу . Не пользоваться таким инструментом просто грех! Не хотите? Дело ваше. Заучивайте таблицу синусов. Таблицу косинусов. Таблицу тангенсов. Таблицу котангенсов. Все 68 значений для разнообразных углов.)

Итак, начнём. Для начала разобьём все эти особые углы на три группы.

Первая группа углов.

Рассмотрим первую группа углов из семнадцати особых . Это 5 углов: 0°, 90°, 180°, 270°, 360°.

Вот так выглядит таблица синусов косинусов тангенсов котангенсов для этих углов:

Угол х (в градусах)	0	90	180	270	360
Угол х (в радианах)	0
sin x	0	1	0	-1	0
cos x	1	0	-1	0	1
tg x	0	не сущ.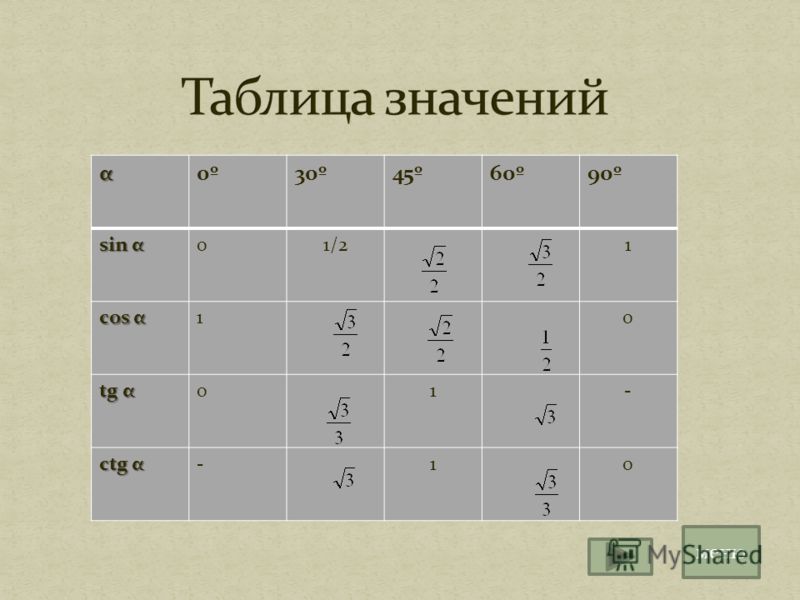	0	не сущ.	0
ctg x	не сущ.	0	не сущ.	0	не сущ.

Желающие запомнить — запоминайте. Но сразу скажу, что все эти единички и нолики очень путаются в голове. Гораздо сильнее, чем хочется.) Поэтому включаем логику и тригонометрический круг.

Рисуем круг и отмечаем на нём эти самые углы: 0°, 90°, 180°, 270°, 360°. Я эти углы отметил красными точками:

Сразу видно, в чём особенность этих углов. Да! Это углы, которые попадают точно на оси координат! Собственно, поэтому-то и путается народ… Но мы путаться не будем. Разберёмся, как находить тригонометрические функции этих углов без особого запоминания.

Кстати, положение угла в 0 градусов полностью совпадает с положением угла в 360 градусов.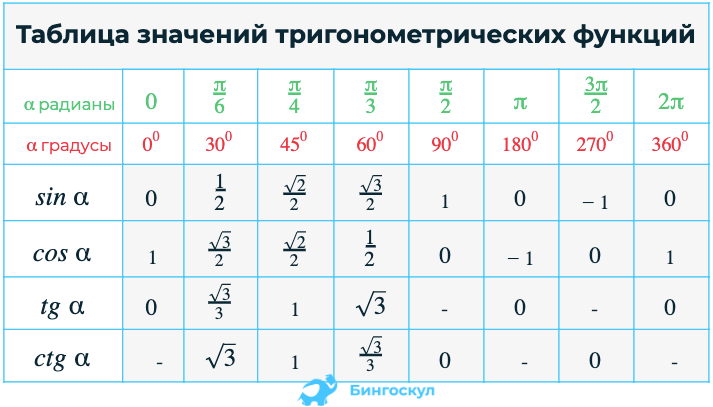

Это значит, что синусы, косинусы, тангенсы у этих углов совершенно одинаковы. Угол в 360 градусов я отметил, чтобы замкнуть круг.

Предположим, в сложной стрессовой обстановке ЕГЭ вы как-то засомневались… Чему равен синус 0 градусов? Вроде ноль… А вдруг единица?! Механическое запоминание такая штука. В суровых условиях сомнения грызть начинают…)

Спокойствие, только спокойствие!) Я подскажу вам практический приём, который выдаст стопроцентно правильный ответ и начисто уберёт все сомнения.

В качестве примера разберёмся, как чётко и надёжно определить, скажем, синус 0 градусов. А заодно, и косинус 0. Именно в этих значениях, как ни странно, частенько люди путаются.

Для этого на круге нарисуем произвольный угол х . В первой четверти, чтобы недалеко от 0 градусов было. Отметим на осях синус и косинус этого угла

х, всё чин-чинарём. Вот так:

А теперь — внимание! Уменьшим угол х , приблизим подвижную сторону к оси ОХ. Наведите курсор на картинку (или коснитесь картинки на планшете) и всё увидите.

Теперь включаем элементарную логику!. Смотрим и размышляем: как ведёт себя sinx при уменьшении угла х? При приближении угла к нулю? Он уменьшается! А cosx — увеличивается! Остаётся сообразить, что станет с синусом, когда угол схлопнется совсем? Когда подвижная сторона угла (точка А) уляжется на ось ОХ и угол станет равным нулю? Очевидно, и синус угла уйдёт в ноль. А косинус увеличится до… до… Чему равна длина подвижной стороны угла (радиус тригонометрического круга)? Единице!

Вот и ответ. Синус 0 градусов равен 0. Косинус 0 градусов равен 1. Совершенно железно и безо всяких сомнений!) Просто потому, что иначе

быть не может.

Совершенно аналогично можно узнать (или уточнить) синус 270 градусов, например. Или косинус 180. Нарисовать круг, произвольный угол в четверти рядышком с интересующей нас осью координат, мысленно подвигать сторону угла и уловить, чем станет синус и косинус, когда сторона угла уляжется на ось.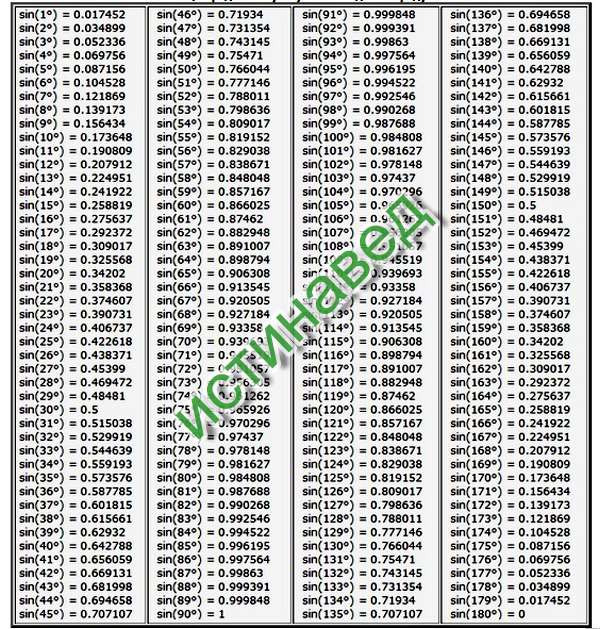 Вот и всё.

Как видите, для этой группы углов ничего заучивать не надо. Не нужна здесь таблица синусов… Да и таблица косинусов — тоже.) Кстати, после нескольких применений тригонометрического круга все эти значения запомнятся сами по себе. А если забудутся — нарисовал за 5 секунд круг и уточнил. Куда проще, чем звонить другу из туалета с риском для аттестата, правда?)

Что касается тангенса и котангенса — всё то же самое. Рисуем на круге линию тангенса (котангенса) — и всё сразу видно. Где они равны нулю, а где — не существуют. Что, не знаете про линии тангенса и котангенса? Это печально, но поправимо.) Посетили Раздел 555 Тангенс и котангенс на тригонометрическом круге — и нет проблем!

Если вы поняли, как чётко определить синус, косинус, тангенс и котангенс для этих пяти углов — я вас поздравляю! На всякий случай сообщаю, что вы теперь можете определять функции любых углов, попадающих на оси. А это и 450°, и 540°, и 1800°, и ещё бесконечное количество.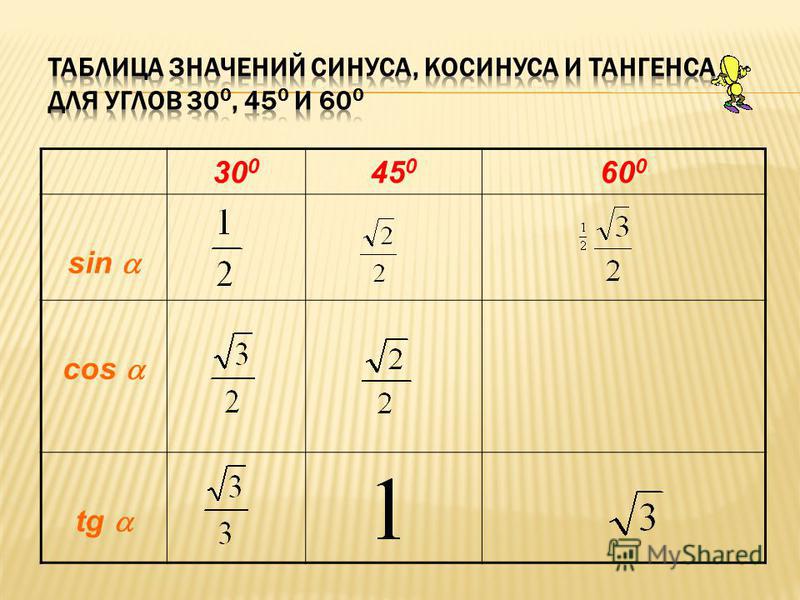 ..) Отсчитал (правильно!) угол на круге — и нет проблем с функциями.

Но, как раз, с отсчётом углов и случаются проблемы да ошибки… Как их избежать, написано в уроке: Как нарисовать (отсчитать) любой угол на тригонометрическом круге в градусах. Элементарно, но очень помогает в борьбе с ошибками.)

А вот урок: Как нарисовать (отсчитать) любой угол на тригонометрическом круге в радианах — покруче будет. В смысле возможностей. Скажем, определить на какую из четырёх полуосей попадает угол

вы сможете за пару секунд. Я не шучу! Именно за пару секунд. Ну конечно, не только 345 «пи»…) И 121, и 16, и -1345. Любой целый коэффициент годится для мгновенного ответа.

А если угол

Подумаешь! Верный ответ получается секунд за 10. Для любого дробного значения радианов с двойкой в знаменателе.

Собственно, этим и хорош тригонометрический круг. Тем, что умение работать с некоторыми углами он автоматически расширяет на бесконечное множество углов.

Итак, с пятью углами из семнадцати — разобрались.

Вторая группа углов.

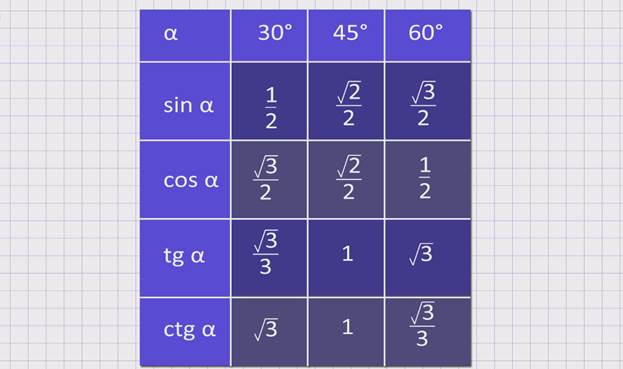
Следующая группа углов — это углы 30°, 45° и 60°. Почему именно эти, а не, к примеру, 20, 50 и 80? Да как-то сложилось так… Исторически.) Дальше будет видно, чем хороши эти углы.

Таблица синусов косинусов тангенсов котангенсов для этих углов выглядит так:

Угол х (в градусах)	0	30	45	60	90
Угол х (в радианах)	0
sin x	0				1
cos x	1				0
tg x	0		1		не сущ.
ctg x	не сущ.		1		0

Я оставил значения для 0° и 90° из предыдущей таблицы для завершённости картины.) Чтобы было видно, что эти углы лежат в первой четверти и возрастают. От 0 до 90. Это пригодится нам дальше.

Значения таблицы для углов 30°, 45° и 60° надо запомнить. Зазубрить, если хотите. Но и здесь есть возможность облегчить себе жизнь.) Обратите внимание на значения таблицы синусов этих углов. И сравните со значениями таблицы косинусов…

Да! Они одни и те же! Только расположены в обратном порядке. Углы возрастают (0, 30, 45, 60, 90) — и значения синуса возрастают от 0 до 1. Можете убедиться с калькулятором. А значения косинуса — убывают от 1 до нуля. Причём, сами значения одни и те же.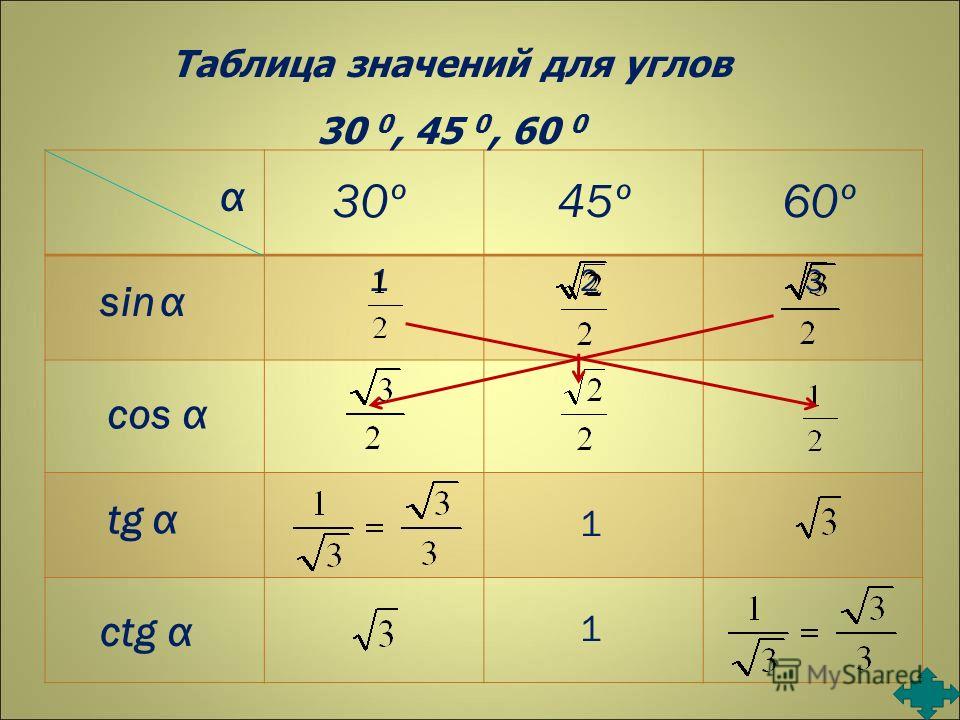 Для углов 20, 50, 80 так бы не получилось…

Отсюда полезный вывод. Достаточно выучить три значения для углов 30, 45, 60 градусов. И помнить, что у синуса они возрастают, а у косинуса — убывают. Навстречу синусу.) На половине пути (45°) они встречаются, т.е синус 45 градусов равен косинусу 45 градусов. А дальше опять расходятся… Три значения можно выучить, правда?

С тангенсами — котангенсами картина исключительно та же самая. Один в один. Только значения другие. Эти значения (ещё три!) тоже надо выучить.

Ну вот, практически всё запоминание и закончилось. Вы поняли (надеюсь), как определять значения для пяти углов попадающих на оси и выучили значения для углов 30, 45, 60 градусов. Всего 8.

Осталось разобраться с последней группой из 9 углов.

Вот эти углы:
120°; 135°; 150°; 210°; 225°; 240°; 300°; 315°; 330°. Для этих углов надо железно знать таблицу синусов, таблицу косинусов и т.д.

Кошмар, правда?)

А если добавить сюда углы, типа: 405°, 600°, или 3000° и много-много такого же красивого?)

Или углы в радианах? Например, про углы:

и многие другие, вы должны знать всё . °}=\)\(\frac{\sqrt{3}}{2}\)
\(\cos⁡\)\(\frac{π}{3}\) \(=\)\(\frac{1}{2}\)
\(\cos⁡2=-0,416…\)

Аргумент и значение

Косинус острого угла

Косинус острого угла можно определить с помощью прямоугольного треугольника — он равен отношению прилежащего катета к гипотенузе.

Пример :

1) Пусть дан угол и нужно определить косинус этого угла.

2) Достроим на этом угле любой прямоугольный треугольник.

3) Измерив, нужные стороны, можем вычислить косинус.

Косинус острого угла больше \(0\) и меньше \(1\)

Если при решении задачи косинус острого угла получился больше 1 или отрицательным, то значит где-то в решении есть ошибка.

Косинус числа

Числовая окружность позволяет определить косинус любого числа, но обычно находят косинус чисел как-то связанных с : \(\frac{π}{2}\) , \(\frac{3π}{4}\) , \(-2π\).

Например, для числа \(\frac{π}{6}\) — косинус будет равен \(\frac{\sqrt{3}}{2}\) .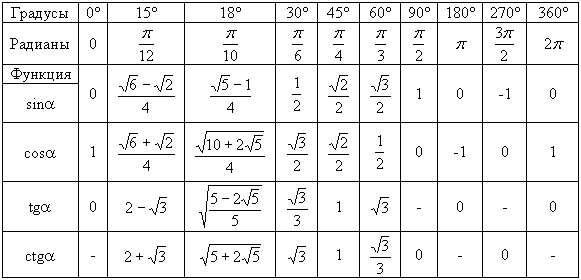 А для числа \(-\)\(\frac{3π}{4}\) он будет равен \(-\)\(\frac{\sqrt{2}}{2}\) (приблизительно \(-0,71\)).

Косинус для других часто встречающихся в практике чисел смотри в .

Значение косинуса всегда лежит в пределах от \(-1\) до \(1\). При этом вычислен косинус может быть для абсолютно любого угла и числа.

Косинус любого угла

Благодаря числовой окружности можно определять косинус не только острого угла, но и тупого, отрицательного, и даже большего, чем \(360°\) (полный оборот). Как это делать — проще один раз увидеть, чем \(100\) раз услышать, поэтому смотрите картинку.

Теперь пояснение: пусть нужно определить косинус угла КОА с градусной мерой в \(150°\). Совмещаем точку О с центром окружности, а сторону ОК – с осью \(x\). После этого откладываем \(150°\) против часовой стрелки. Тогда ордината точки А покажет нам косинус этого угла.

Если же нас интересует угол с градусной мерой, например, в \(-60°\) (угол КОВ ), делаем также, но \(60°\) откладываем по часовой стрелке.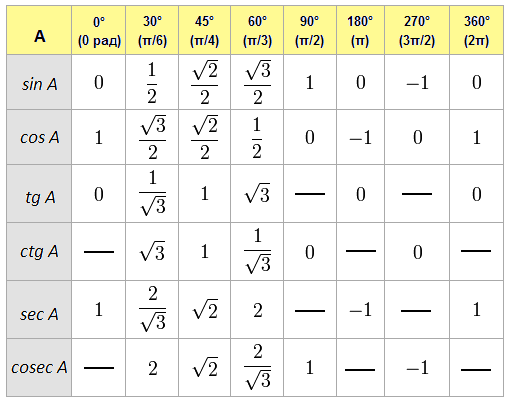

И, наконец, угол больше \(360°\) (угол КОС ) — всё аналогично тупому, только пройдя по часовой стрелке полный оборот, отправляемся на второй круг и «добираем нехватку градусов». Конкретно в нашем случае угол \(405°\) отложен как \(360° + 45°\).

Несложно догадаться, что для откладывания угла, например, в \(960°\), надо сделать уже два оборота (\(360°+360°+240°\)), а для угла в \(2640°\) — целых семь.

Стоит запомнить, что:

Косинус прямого угла равен нулю. Косинус тупого угла — отрицателен.

Знаки косинуса по четвертям

С помощью оси косинусов (то есть, оси абсцисс, выделенной на рисунке красным цветом) легко определить знаки косинусов по числовой (тригонометрической) окружности:

Там, где значения на оси от \(0\) до \(1\), косинус будет иметь знак плюс (I и IV четверти – зеленая область),
— там, где значения на оси от \(0\) до \(-1\), косинус будет иметь знак минус (II и III четверти – фиолетовая область).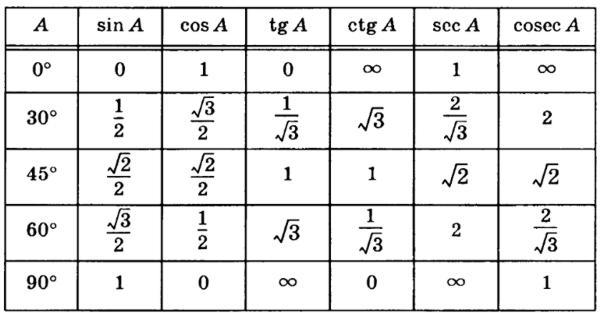 2⁡x}\)
— и синусом того же угла (или числа): формулой \(ctgx=\)\(\frac{\cos{x}}{\sin⁡x}\)
Другие наиболее часто применяемые формулы смотри .

Функция \(y=\cos{x}\)

Если отложить по оси \(x\) углы в радианах, а по оси \(y\) — соответствующие этим углам значения косинуса, мы получим следующий график:

График данной называется и обладает следующими свойствами:

Область определения – любое значение икса: \(D(\cos{⁡x})=R\)
— область значений – от \(-1\) до \(1\) включительно: \(E(\cos{x})=[-1;1]\)
— четная: \(\cos⁡(-x)=\cos{x}\)
— периодическая с периодом \(2π\): \(\cos⁡(x+2π)=\cos{x}\)
— точки пересечения с осями координат:
ось абсцисс: \((\)\(\frac{π}{2}\) \(+πn\),\(;0)\), где \(n ϵ Z\)
ось ординат: \((0;1)\)
— промежутки знакопостоянства:
функция положительна на интервалах: \((-\)\(\frac{π}{2}\) \(+2πn;\) \(\frac{π}{2}\) \(+2πn)\), где \(n ϵ Z\)
функция отрицательна на интервалах: \((\)\(\frac{π}{2}\) \(+2πn;\)\(\frac{3π}{2}\) \(+2πn)\), где \(n ϵ Z\)
— промежутки возрастания и убывания:
функция возрастает на интервалах: \((π+2πn;2π+2πn)\), где \(n ϵ Z\)
функция убывает на интервалах: \((2πn;π+2πn)\), где \(n ϵ Z\)
— максимумы и минимумы функции:
функция имеет максимальное значение \(y=1\) в точках \(x=2πn\), где \(n ϵ Z\)
функция имеет минимальное значение \(y=-1\) в точках \(x=π+2πn\), где \(n ϵ Z\).

Тригонометрическая таблица, значения, функции, шаги и примеры

Шаг 1

Таблица должна быть создана с верхней строкой, содержащей стандартные углы, такие как 0°, 30°, 45°, 60°, 90° , 180°, 270°, 360°, а первый столбец с левой стороны должен содержать все тригонометрические функции, такие как cos, sin cot, tan, sec и cosec.

Шаг 2

Получение значения sin

Чтобы найти значение всех степеней в sin, нужно разделить под корень из 0,1,2,3,4 соответственно. Например, 0/4 = 0

Следовательно, тригонометрическая таблица греха будет выглядеть следующим образом.

Уголки	0°	30°	45°	60°	90°	180°	270°	360°
Грех	0	1/2	1/√2	√3/√2	1	0	-1	0

Шаг 3

Получение значения cos

Значения углов cos являются обратными значениям углов sin.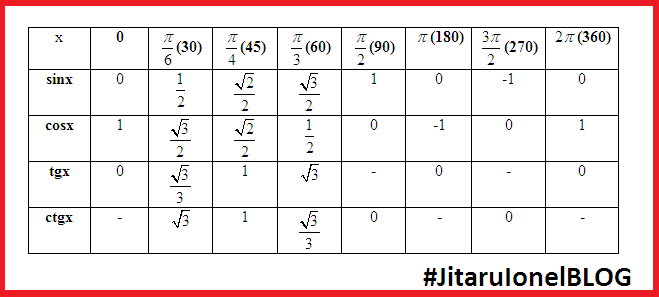 Для получения cos-значения нужно разделить на 4 в обратной последовательности от sin-значения. Например, чтобы получить значение cos 0°, шаг должен быть 4/4 = 1,9.0005

Следовательно, тригонометрическая таблица cos будет выглядеть следующим образом.

Уголки	0°	30°	45°	60°	90°	180°	270°	360°
Кос	1	√3/√2	1/√2	1/2	0	-1	0	1

Шаг 4

Получение значения тангенса

Значения тангенса угла представляют собой деление значений угла sin и угла cos. То есть tan = sin/cos. Например, если попытаться найти значение тангенса 0°, то нужно сделать следующее:

тангенс 0° = sin 0°/cos 0°

тангенс 0° = 0/1 = 0

Следовательно, тригонометрическая таблица тангенса будет выглядеть следующим образом.

Уголки	0°	30°	45°	60°	90°	180°	270°	360°
желтовато-коричневый	0	1/√3	1	√3		0		0

Шаг 5

Получение значения раскладушки

Значения угла раскладушки обратно пропорциональны значению tan. Например, значение cot 0° можно рассчитать как 1, деленное на значение tan 0°, чтобы найти значение cot 0°, нужно сделать следующее:

Детская кроватка 0° = 1/0 = не определена или бесконечна

Следовательно, тригонометрическая таблица детской кроватки будет следующей.

Уголки	0°	30°	45°	60°	90°	180°	270°	360°
кроватка		√3	1	1/√3	0		0

Шаг 6

Получение значения cosec

Значения угла cosec обратны значению sin во всех градусах соответственно.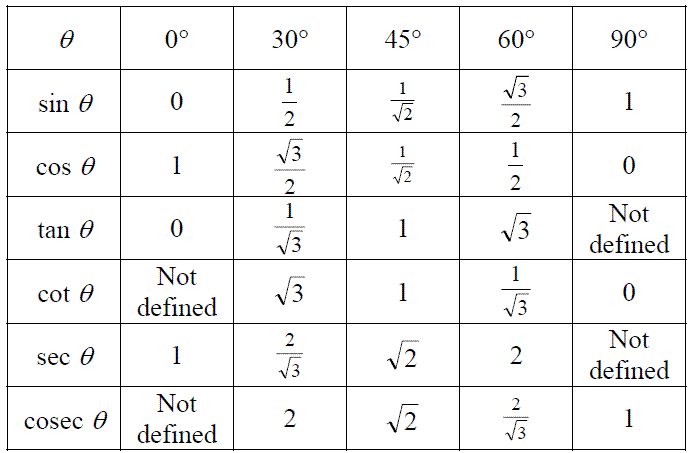 Например,

cosec 0° = 1/0 = Не определено или бесконечно

Следовательно, тригонометрическая таблица cosec будет следующей.

Уголки	0°	30°	45°	60°	90°	180°	270°	360°
косек		2	√2	2/√3	1		-1

Шаг 7

Получение значения секунды

Значения угла секунды являются просто обратными значениям угла косинуса во всех градусах соответственно. Например, сек 0° = 1/1 = 1

Таким образом, тригонометрическая таблица значения сек выглядит следующим образом.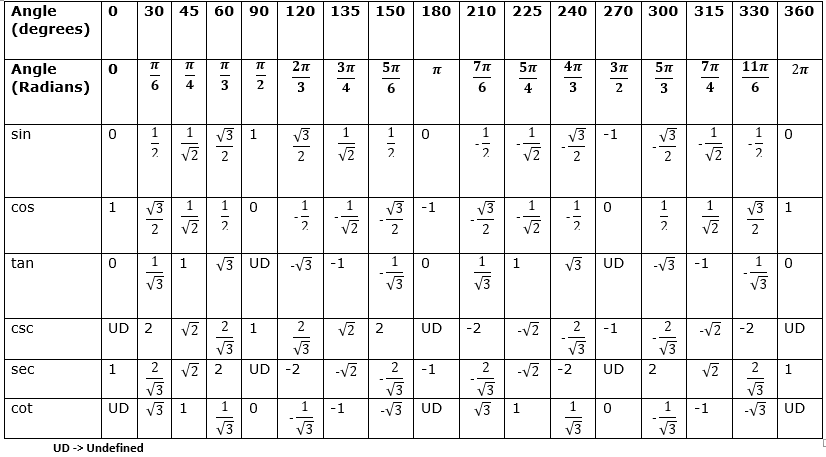

Уголки	0°	30°	45°	60°	90°	180°	270°	360°
сек	1	2√3	√2	2		-1		1

ZRD — Тригонометрические таблицы

ZRD — Тригонометрические таблицы
Ниже приведены три основные тригонометрические таблицы, которые при правильном применении опытным пользователем могут оказаться очень полезными.

Теорема Пифагора ниже

В любом прямоугольном треугольнике для любого угла: длина противоположной стороны = грех угла длина гипотенузы длина смежной стороны = cos угла длина гипотенузы длина противоположной стороны = тангенс угла длина прилегающей стороны Гипотенуза прямоугольного треугольника – это наибольшая сторона, лежащая против прямого угла. Прилегающая сторона – это сторона, которая находится между рассматриваемый угол и прямой угол. Противоположная сторона находится напротив рассматриваемого угла. sin = o/h  cos = a/h  tan = o/a Часто вспоминают: soh cah toa

График sin, cos и tan

Примечания:

Графики sin и cos имеют повторяющийся период 360°. Графики повторяются каждые 360°. График cos такой же, как график sin сдвинутый 90° вправо/влево. По этой причине sin(x) = cos(90 — x) и cos(x) = sin(90 — x). Cos — четная функция. Он симметричен относительно оси Y. Грех — странная функция.

График тангенса имеет асимптоты (линия, которая подходит очень близко, но не касается). Красные линии — асимптоты.

Эти графы подчиняются обычным законам преобразования графов.

Теорема Пифагора

В любом прямоугольном (один угол ровно 90 градусов) треугольнике квадрат длины гипотенузы (С — сторона, противолежащая прямому углу) равно сумме квадратов двух других сторон (A, B). Теорема Пифагора может быть выражена в виде уравнения Пифагора: A 2 + B 2 = C 2 C = квадратный корень из ( A 2 + B 2 ) A = квадратный корень из ( C 2 — B 2 ) B = квадратный корень из ( C 2 — A 2 )

Нахождение квадратных корней чисел без калькулятора
1. Оценка. Во-первых, подойдите как можно ближе, найдя два полных квадратных корня, между которыми находится ваше число.
2. Разделить — разделить ваше число на меньшее оценочное число.
3. Среднее — взять среднее из результата шага 2 и корень.
4. Используйте результат шага 3 или повторяйте шаги 2 и 3, пока не получите достаточно точное число.

Пример:
Извлеките квадратный корень из 10 с точностью до 2 знаков после запятой.

Решение:
1. 3 в квадрате = 9 и 4 в квадрате = 16, поэтому квадратный корень из 10 находится между 3 и 4.