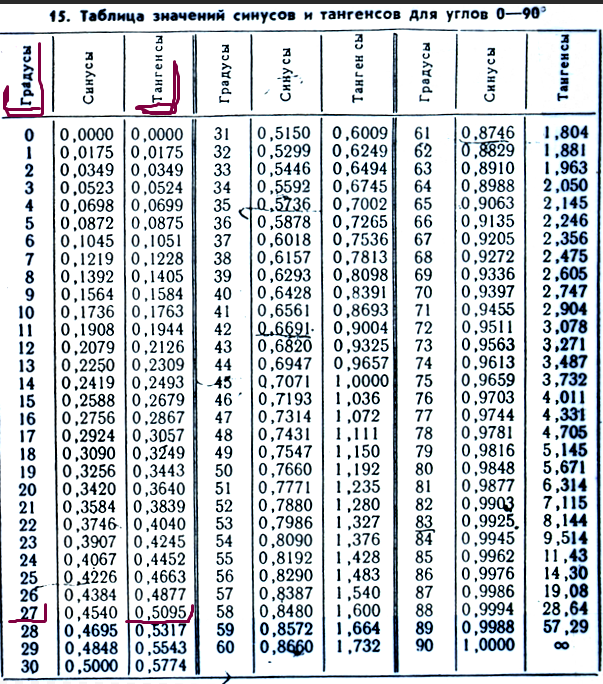
Таблица тангенсы углов: Тангенс угла! Как найти тангенс, формула, таблица?!

Содержание

Таблица тангенсов.

Таблица тангенсов — это записанные в таблицу посчитанные значения тангенсов углов от 0° до 360°. Используя таблицу тангенсов Вы сможете провести расчеты даже если под руками не окажется инженерного калькулятора. Чтобы узнать значение тангенса от нужного Вам угла достаточно найти его в таблице.

Вычислить тангенс угла

tg(°) = 0

Таблица тангенсов в радианах

α	0	π6	π4	π3	π2	π	3π2	2π
tg α	0	√33	1	√3	∞	0	∞	0

Таблица тангенсов углов от 0° до 180°

tg(0°) = 0
tg(1°) = 0.01746
tg(2°) = 0.03492
tg(3°) = 0.05241
tg(4°) = 0.06993
tg(5°) = 0.08749
tg(6°) = 0.1051
tg(7°) = 0.12278
tg(8°) = 0.14054
tg(9°) = 0.15838
tg(10°) = 0.17633
tg(11°) = 0.19438
tg(12°) = 0.

21256
tg(13°) = 0.23087
tg(14°) = 0.24933
tg(15°) = 0.26795
tg(16°) = 0.28675
tg(17°) = 0.30573
tg(18°) = 0.32492
tg(19°) = 0.34433
tg(20°) = 0.36397
tg(21°) = 0.38386
tg(22°) = 0.40403
tg(23°) = 0.42447
tg(24°) = 0.44523
tg(25°) = 0.46631
tg(26°) = 0.48773
tg(27°) = 0.50953
tg(28°) = 0.53171
tg(29°) = 0.55431
tg(30°) = 0.57735
tg(31°) = 0.60086
tg(32°) = 0.62487
tg(33°) = 0.64941
tg(34°) = 0.67451
tg(35°) = 0.70021
tg(36°) = 0.72654
tg(37°) = 0.75355
tg(38°) = 0.78129
tg(39°) = 0.80978
tg(40°) = 0.8391
tg(41°) = 0.86929
tg(42°) = 0.9004
tg(43°) = 0.93252
tg(44°) = 0.96569
tg(45°) = 1
tg(46°) = 1.03553
tg(47°) = 1.07237
tg(48°) = 1.11061
tg(49°) = 1.15037
tg(50°) = 1.19175
tg(51°) = 1.2349
tg(52°) = 1.27994
tg(53°) = 1.32704
tg(54°) = 1.37638
tg(55°) = 1.42815
tg(56°) = 1.48256
tg(57°) = 1.53986
tg(58°) = 1.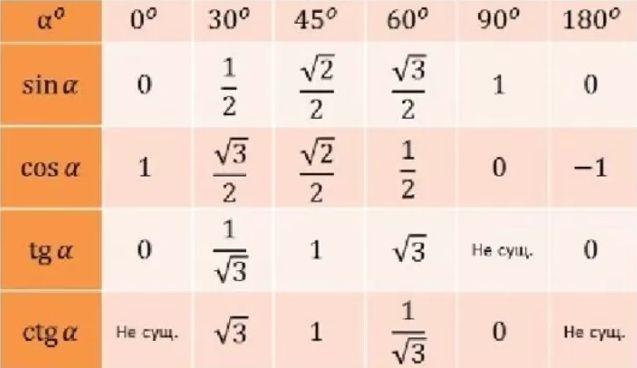

60033
tg(59°) = 1.66428
tg(60°) = 1.73205

tg(61°) = 1.80405
tg(62°) = 1.88073
tg(63°) = 1.96261
tg(64°) = 2.0503
tg(65°) = 2.14451
tg(66°) = 2.24604
tg(67°) = 2.35585
tg(68°) = 2.47509
tg(69°) = 2.60509
tg(70°) = 2.74748
tg(71°) = 2.90421
tg(72°) = 3.07768
tg(73°) = 3.27085
tg(74°) = 3.48741
tg(75°) = 3.73205
tg(76°) = 4.01078
tg(77°) = 4.33148
tg(78°) = 4.70463
tg(79°) = 5.14455
tg(80°) = 5.67128
tg(81°) = 6.31375
tg(82°) = 7.11537
tg(83°) = 8.14435
tg(84°) = 9.51436
tg(85°) = 11.43005
tg(86°) = 14.30067
tg(87°) = 19.08114
tg(88°) = 28.63625
tg(89°) = 57.28996
tg(90°) = ∞
tg(91°) = -57.28996
tg(92°) = -28.63625
tg(93°) = -19.08114
tg(94°) = -14.30067
tg(95°) = -11.43005
tg(96°) = -9.51436
tg(97°) = -8.14435
tg(98°) = -7.11537
tg(99°) = -6.31375
tg(100°) = -5.67128
tg(101°) = -5.14455
tg(102°) = -4.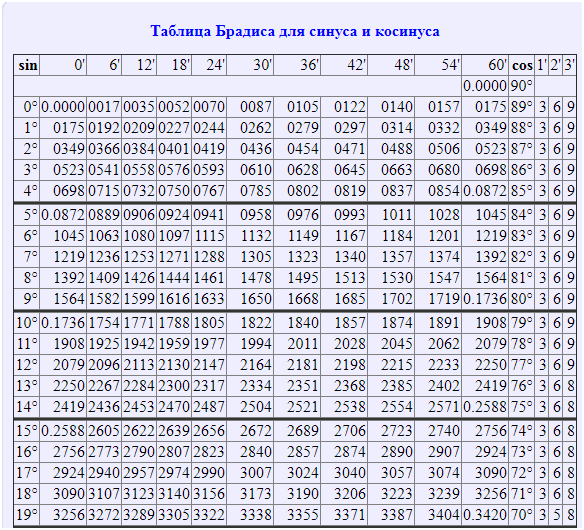70463
tg(103°) = -4.

33148
tg(104°) = -4.01078
tg(105°) = -3.73205
tg(106°) = -3.48741
tg(107°) = -3.27085
tg(108°) = -3.07768
tg(109°) = -2.90421
tg(110°) = -2.74748
tg(111°) = -2.60509
tg(112°) = -2.47509
tg(113°) = -2.35585
tg(114°) = -2.24604
tg(115°) = -2.14451
tg(116°) = -2.0503
tg(117°) = -1.96261
tg(118°) = -1.88073
tg(119°) = -1.80405
tg(120°) = -1.73205

tg(121°) = -1.66428
tg(122°) = -1.60033
tg(123°) = -1.53986
tg(124°) = -1.48256
tg(125°) = -1.42815
tg(126°) = -1.37638
tg(127°) = -1.32704
tg(128°) = -1.27994
tg(129°) = -1.2349
tg(130°) = -1.19175
tg(131°) = -1.15037
tg(132°) = -1.11061
tg(133°) = -1.07237
tg(134°) = -1.03553
tg(135°) = -1

tg(136°) = -0.96569
tg(137°) = -0.93252
tg(138°) = -0.9004
tg(139°) = -0.86929
tg(140°) = -0.8391
tg(141°) = -0.80978
tg(142°) = -0.78129
tg(143°) = -0.75355
tg(144°) = -0.72654
tg(145°) = -0.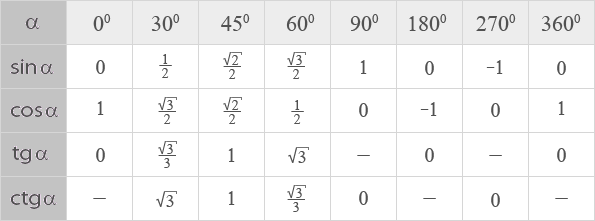

70021
tg(146°) = -0.67451
tg(147°) = -0.64941
tg(148°) = -0.62487
tg(149°) = -0.60086
tg(150°) = -0.57735
tg(151°) = -0.55431
tg(152°) = -0.53171
tg(153°) = -0.50953
tg(154°) = -0.48773
tg(155°) = -0.46631
tg(156°) = -0.44523
tg(157°) = -0.42447
tg(158°) = -0.40403
tg(159°) = -0.38386
tg(160°) = -0.36397
tg(161°) = -0.34433
tg(162°) = -0.32492
tg(163°) = -0.30573
tg(164°) = -0.28675
tg(165°) = -0.26795
tg(166°) = -0.24933
tg(167°) = -0.23087
tg(168°) = -0.21256
tg(169°) = -0.19438
tg(170°) = -0.17633
tg(171°) = -0.15838
tg(172°) = -0.14054
tg(173°) = -0.12278
tg(174°) = -0.1051
tg(175°) = -0.08749
tg(176°) = -0.06993
tg(177°) = -0.05241
tg(178°) = -0.03492
tg(179°) = -0.01746
tg(180°) = 0

Таблица тангенсов углов от 181° до 360°

tg(181°) = 0.01746
tg(182°) = 0.03492
tg(183°) = 0.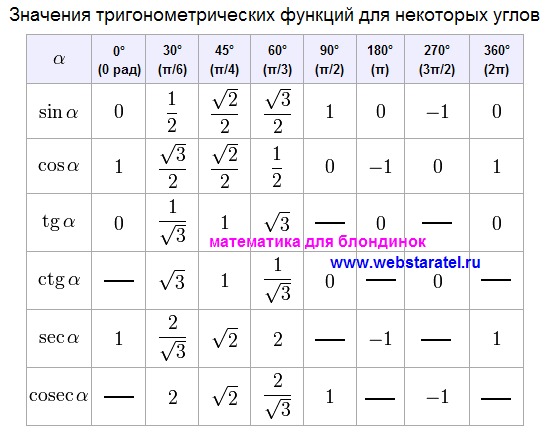

05241
tg(184°) = 0.06993
tg(185°) = 0.08749
tg(186°) = 0.1051
tg(187°) = 0.12278
tg(188°) = 0.14054
tg(189°) = 0.15838
tg(190°) = 0.17633
tg(191°) = 0.19438
tg(192°) = 0.21256
tg(193°) = 0.23087
tg(194°) = 0.24933
tg(195°) = 0.26795
tg(196°) = 0.28675
tg(197°) = 0.30573
tg(198°) = 0.32492
tg(199°) = 0.34433
tg(200°) = 0.36397
tg(201°) = 0.38386
tg(202°) = 0.40403
tg(203°) = 0.42447
tg(204°) = 0.44523
tg(205°) = 0.46631
tg(206°) = 0.48773
tg(207°) = 0.50953
tg(208°) = 0.53171

tg(209°) = 0.55431
tg(210°) = 0.57735
tg(211°) = 0.60086
tg(212°) = 0.62487
tg(213°) = 0.64941
tg(214°) = 0.67451
tg(215°) = 0.70021
tg(216°) = 0.72654
tg(217°) = 0.75355
tg(218°) = 0.78129
tg(219°) = 0.80978
tg(220°) = 0.8391
tg(221°) = 0.86929
tg(222°) = 0.9004
tg(223°) = 0.93252
tg(224°) = 0.96569
tg(225°) = 1
tg(226°) = 1.03553
tg(227°) = 1.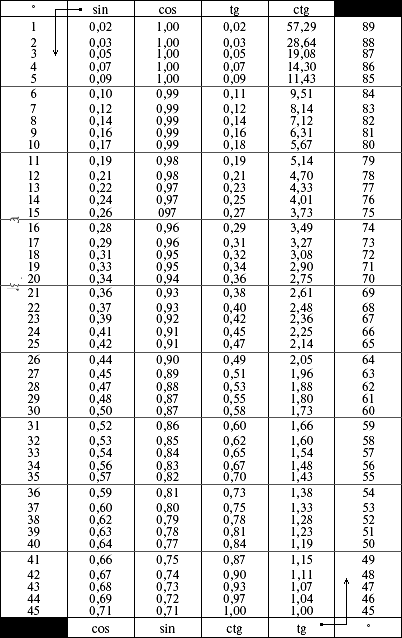

07237
tg(228°) = 1.11061
tg(229°) = 1.15037
tg(230°) = 1.19175

tg(231°) = 1.2349
tg(232°) = 1.27994
tg(233°) = 1.32704
tg(234°) = 1.37638
tg(235°) = 1.42815
tg(236°) = 1.48256
tg(237°) = 1.53986
tg(238°) = 1.60033
tg(239°) = 1.66428
tg(240°) = 1.73205

tg(241°) = 1.80405
tg(242°) = 1.88073
tg(243°) = 1.96261
tg(244°) = 2.0503
tg(245°) = 2.14451
tg(246°) = 2.24604
tg(247°) = 2.35585
tg(248°) = 2.47509
tg(249°) = 2.60509
tg(250°) = 2.74748
tg(251°) = 2.90421
tg(252°) = 3.07768
tg(253°) = 3.27085
tg(254°) = 3.48741
tg(255°) = 3.73205
tg(256°) = 4.01078
tg(257°) = 4.33148
tg(258°) = 4.70463
tg(259°) = 5.14455
tg(260°) = 5.67128
tg(261°) = 6.31375
tg(262°) = 7.11537
tg(263°) = 8.14435
tg(264°) = 9.51436
tg(265°) = 11.43005
tg(266°) = 14.30067
tg(267°) = 19.08114
tg(268°) = 28.63625
tg(269°) = 57.28996
tg(270°) = ∞
tg(271°) = -57.

28996
tg(272°) = -28.63625
tg(273°) = -19.08114
tg(274°) = -14.30067
tg(275°) = -11.43005
tg(276°) = -9.51436
tg(277°) = -8.14435
tg(278°) = -7.11537
tg(279°) = -6.31375
tg(280°) = -5.67128
tg(281°) = -5.14455
tg(282°) = -4.70463
tg(283°) = -4.33148
tg(284°) = -4.01078
tg(285°) = -3.73205
tg(286°) = -3.48741
tg(287°) = -3.27085
tg(288°) = -3.07768
tg(289°) = -2.90421
tg(290°) = -2.74748
tg(291°) = -2.60509
tg(292°) = -2.47509
tg(293°) = -2.35585
tg(294°) = -2.24604
tg(295°) = -2.14451
tg(296°) = -2.0503
tg(297°) = -1.96261
tg(298°) = -1.88073
tg(299°) = -1.80405
tg(300°) = -1.73205

tg(301°) = -1.66428
tg(302°) = -1.60033
tg(303°) = -1.53986
tg(304°) = -1.48256
tg(305°) = -1.42815
tg(306°) = -1.37638
tg(307°) = -1.32704
tg(308°) = -1.27994
tg(309°) = -1.2349
tg(310°) = -1.19175
tg(311°) = -1.15037
tg(312°) = -1.11061
tg(313°) = -1.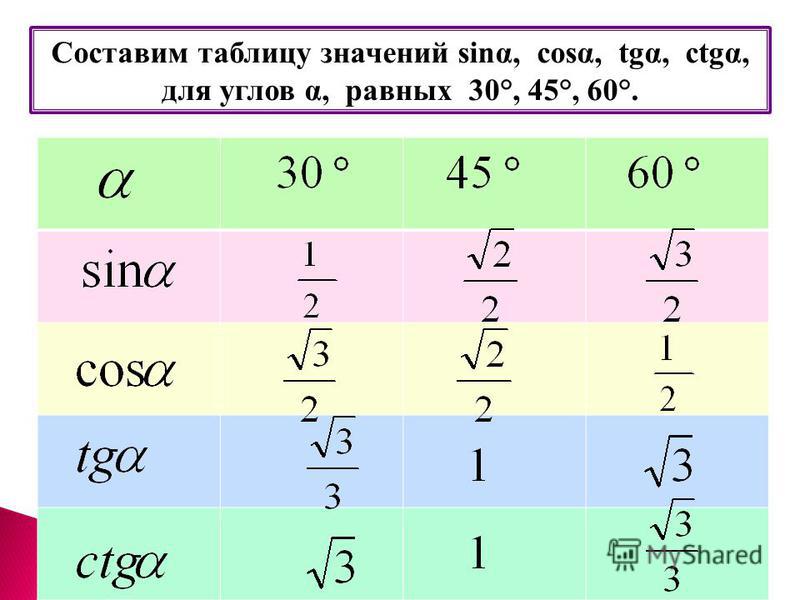

07237
tg(314°) = -1.03553
tg(315°) = -1
tg(316°) = -0.96569
tg(317°) = -0.93252
tg(318°) = -0.9004
tg(319°) = -0.86929
tg(320°) = -0.8391
tg(321°) = -0.80978
tg(322°) = -0.78129
tg(323°) = -0.75355
tg(324°) = -0.72654
tg(325°) = -0.70021
tg(326°) = -0.67451
tg(327°) = -0.64941
tg(328°) = -0.62487
tg(329°) = -0.60086
tg(330°) = -0.57735
tg(331°) = -0.55431
tg(332°) = -0.53171
tg(333°) = -0.50953
tg(334°) = -0.48773
tg(335°) = -0.46631
tg(336°) = -0.44523
tg(337°) = -0.42447
tg(338°) = -0.40403
tg(339°) = -0.38386
tg(340°) = -0.36397
tg(341°) = -0.34433
tg(342°) = -0.32492
tg(343°) = -0.30573
tg(344°) = -0.28675
tg(345°) = -0.26795
tg(346°) = -0.24933
tg(347°) = -0.23087
tg(348°) = -0.21256

tg(349°) = -0.19438
tg(350°) = -0.17633
tg(351°) = -0.15838
tg(352°) = -0.14054
tg(353°) = -0.12278
tg(354°) = -0.1051
tg(355°) = -0.08749
tg(356°) = -0.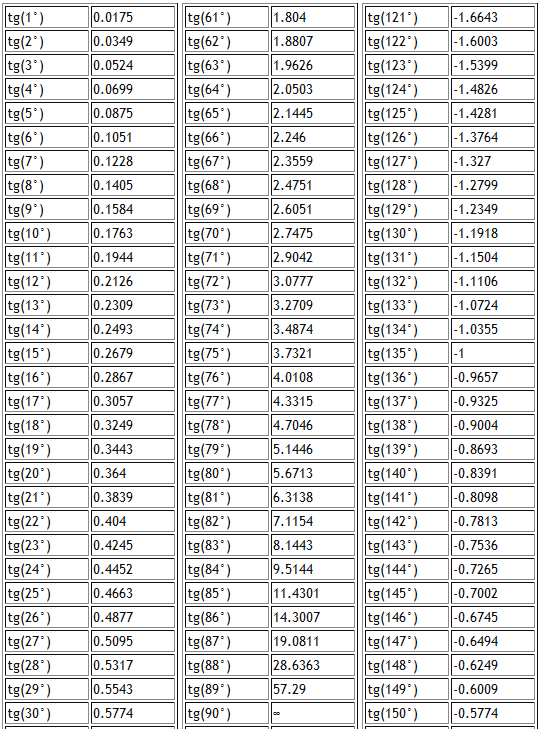

06993
tg(357°) = -0.05241
tg(358°) = -0.03492
tg(359°) = -0.01746
tg(360°) = 0

Таблицы значений тригонометрических функций Таблицу синусов Таблица косинусов Таблица котангенсов Сводная таблица тригонометрических функций

Тригонометрические формулы

Все таблицы и формулы

Любые нецензурные комментарии будут удалены, а их авторы занесены в черный список!

Калькулятор угла касательной

Создано Joanna Śmietańska, кандидатом наук

Отзыв Стивена Вудинга

Последнее обновление: 01 марта 2023 г.

Содержание:

Как найти угол касательной?
Свойства функции тангенса
Пример вычисления тангенса угла
Другие полезные тригонометрические калькуляторы
Часто задаваемые вопросы

Этот быстрый калькулятор угла тангенса поможет вам, когда вам интересно как найти угол касательной . Неважно, указан ли угол в вашей домашней работе в градусах, радианах или пи-радианах. Читайте ниже, чтобы узнать больше полезной информации о тангенсе угла .

Как найти угол касательной?

В тригонометрии или геометрии тангенс угла (просто обозначаемый как тангенс ) представляет собой длину стороны , противоположной углу, деленную на прилежащую сторону . Обратите внимание, что это относится только к прямоугольный треугольник . Звучит сложно? Не волнуйся. Давайте посмотрим на изображение, чтобы объяснить:

Если α\alphaα угол между сторонами bbb и ccc треугольника, то тангенс угла tan⁡(θ)\tan(\theta)tan(θ) равен отношение между противоположной стороной aaa и соседней стороной bbb.

tan⁡(θ)=ab\small{\tan(\theta) = \frac{a}{b}}tan(θ)=ba

Другое определение гласит, что тангенс представляет собой отношение функции синуса и функция косинуса , поэтому тангенс — это sin/cos 9соотношение 0022.

Свойства функции тангенса

Функция тангенса является одной из основных тригонометрических функций. График функции тангенса имеет ту особенность, что не имеет определенного значения при х = -π/2, π/2, -3π/2, 3π/2, 5π/2 и т. д. (или -90° , 90°, -270°, 270°, 450° и т.д. ).

В отличие от синуса или косинуса, функция тангенса имеет период π\piπ, поэтому ее значения повторяются через каждые π радиан .

💡 Проверьте сами! Попробуйте ввести угол π/2 (или 90° в градусах) в этот калькулятор угла тангенса и посмотрите, какое значение он вам даст.

Пример расчета тангенса угла

Если вы хотите найти тангенс заданного угла , введите градус в наш калькулятор тангенса угла или выполните следующие действия:

Определите гипотенузу в вашем треугольнике. Обычно это самая длинная сторона треугольника.
Измерьте две стороны , между которыми есть угол, и обозначьте их как aaa (противоположная) и bbb (прилежащая), например, a=21a = 21a=21 и b=8b = 8b=8.
Разделите aaa на bbb – a/b=21/8a/b = 21/8a/b=21/8 =2,63 = 2,63=2,63. Вы получите тангенс угла .

Другие полезные тригонометрические калькуляторы

Когда вы научитесь пользоваться калькулятором тангенса угла , ознакомьтесь с другими нашими тригонометрическими инструментами:

Тригонометрический калькулятор;
Калькулятор косинуса треугольника;
Калькулятор триггерного треугольника;
Калькулятор синус-косинус-тангенса; и
Калькулятор отношения тангенса.

Часто задаваемые вопросы

Касательная x/y?

Нет, тангенс угла равен y/x . Вы можете увидеть треугольники, где х — гипотенуза, х — прилежащая сторона в углу, а y — противолежащая сторона. Но тангенс угла есть отношение противоположные/смежные стороны, что в данном случае y/x .

Чему равен тангенс числа пи/4?

1 . Вы можете выразить pi/4 в радианах как 45° в градусах и tan(45°) = 1 . Поскольку угол pi/4 лежит между 0 и pi/2, функция тангенса положительна и равна 1 .

Джоанна Сметаньска, докторант

Тригонометрическая функция: тангенс

Проверка 19похожие калькуляторы тригонометрии 📐

ArccosArcsinArctan… еще 16

Geometry: The Tangent Ratio

Тригонометрия берет свое начало с расчетов первых математиков и астрономов. Они изучали отношения длин сторон прямоугольных треугольников и заметили некоторые интересные вещи. Например, они заметили, что всякий раз, когда отношение длины более короткого катета к длине более длинного катета составляет 7/10, угол, противоположный более короткому катету (то есть наименьший угол прямоугольного треугольника), всегда равен 35º. На рис. 20.1 показано несколько треугольников с отношением длины катетов 7/10. Обратите внимание, что все эти треугольники подобны. Каждый из них имеет прямой угол, и каждый из них имеет угол измерения 35º. По теореме о подобии AA (теорема 13.1) они подобны.

Рисунок 20.1 Три прямоугольных треугольника, каждый из которых имеет отношение длины более короткой стороны к длине более длинной стороны, равное ⁷ / ₁₀ .

Но это происходит не только с соотношением 7/10. Все прямоугольные треугольники с одинаковым отношением длины катетов будут подобны друг другу.

На рис. 20.2 показан типичный прямоугольный треугольник. Напомним, что ¯AB — гипотенуза треугольника. Если вы сосредоточитесь на BAC, то ¯BC — это сторона, противоположная BAC, а ¯AC — сторона, примыкающая к BAC. Если вы сосредоточили свое внимание на ABC, то противоположная сторона будет ¯AC, а соседняя сторона — ¯BC. Что хорошо в гипотенузе, так это то, что она всегда является стороной, противоположной прямому углу, и она никогда не меняется. Отношение длины противоположной стороны угла к длине прилежащей стороны в прямоугольном треугольнике называется 9.0173 тангенс угла. Напишите

tan BAC = ^BC / _AC

, когда вы хотите сказать «тангенс BAC — это отношение ^BC / _AC». Когда нет путаницы с вовлеченным углом, вы можете сократить это обозначение до

.
тангенс A = ^BC / _AC .
Рисунок 20.2 Прямоугольный треугольник ABC.
Обратите внимание, что в треугольнике на рис. 20.2 тангенс A = ^BC / _AC и tanB = ^AC / _BC . Эти отношения тангенсов обратны друг другу! Это означает, что если tan A > 1, tan B
Если отношение тангенсов угла равно 1, это означает, что длина противолежащей стороны равна длине прилежащей стороны. У вас есть треугольник с двумя катетами одинаковой длины. Вы видели этот треугольник раньше; это треугольник 45-45-90.
Если интерпретировать этот треугольник как объект (скажем, дерево), отбрасывающий тень на землю (как показано на рис. 20.3), то этот угол в 35º называется углом возвышения.
Solid Facts
В прямоугольном треугольнике тангенс угла равен отношению длины противолежащей стороны угла к длине прилежащей стороны.
Вы видели применение этой идеи ранее в этом разделе. Помните задачу о поиске высоты дерева в «Похожих треугольниках»? Вы решили эту задачу, используя подобные треугольники. У вас был треугольник, образованный деревом и его тенью, и у вас был треугольник, образованный вами и вашей тенью. Используя пропорции, вы смогли точно оценить высоту дерева.
Рисунок 20.3 Дерево, отбрасывающее тень на землю, можно интерпретировать как образующее прямоугольный треугольник.
Вы можете немного изменить ситуацию. Что, если бы вы не знали свой рост, но могли бы оценить угол возвышения?
Пример 1 : Предположим, у вас есть дерево, похожее на то, что показано на рис. 20.3. Вам говорят, что угол подъема равен 30º и что тангенс 30º = 0,577. Если тень дерева составляет 25 футов, оцените высоту дерева.
Решение : Вы знаете, что tan 30º = 0,577. Вы также знаете, что tan 30º = ^BC / _AC . Используя замену (и тот факт, что AC = 25), у вас есть
^BC / ₂₅ = .577
до н.э. = 25 (0,577) = 14,4 фута.
Касательная линия
Я использовал слово «тангенс» по отношению к линии, которая просто выходит за пределы окружности. Теперь я говорю о касательной угла. Использую ли я одно и то же слово в двух разных контекстах, потому что у меня закончились слова и я должен начать использовать одни и те же слова для разных идей? Или есть более глубокая связь, которая может стать более очевидной по ходу раздела?
Ранние математики рассчитывали таблицы значений тангенса различных функций.
No related posts.