Таблица тригонометрических значений обратных функций: Значения обратных тригонометрических функций. Таблица обратных тригонометрических функций.

Значения обратных тригонометрических функций. Таблица обратных тригонометрических функций.

• Альфашкола
• Статьи
• Значения обратных тригонометрических функций y=arcsin(x) и y=arccos(x)

Значения обратных тригонометрических функций \(arcsin(x)\) и \(arccos(x)\):

 

 

 Вычислим угол \(\alpha\) на  промежутке \([ -\frac{\pi }{2};\frac{\pi }{2}]\) , так как функция \(y=arcsin(x)\) обратная для функции \(y=sin(x)\) на отрезке \(y ∈[ − π / 2 , π / 2 ] \), где \(x ∈ [ − 1 , 1 ] \).

 Рассмотрим угол \( \sin \alpha =-\frac{\sqrt{3}}{2}\) . Нарисуем на оси \(oy\) значение \(-\frac{\sqrt{3}}{2}\). \(-\frac{\sqrt{3}}{2}\) соответсвует \({{\alpha }_{1}}=-\frac{\pi }{3}\) и \({{\alpha }_{2}}=-\frac{2\pi }{3}\), но промежуток \(\left[ -\frac{\pi }{2};\frac{\pi }{2} \right]\) включает только \({{\alpha }_{1}}=-\frac{\pi }{3}\).

Вывод: \(\arcsin \left( -\frac{\sqrt{3}}{2} \right)=-\frac{\pi }{3}\).

Функция арксинус нечетная, тогда \(\arcsin \left( -\frac{\sqrt{3}}{2} \right)=-\arcsin \frac{\sqrt{3}}{2}\).  \(\arcsin \frac{\sqrt{3}}{2}\) найдем, используя таблицу значений \(\sin \alpha =\frac{\sqrt{3}}{2} \) при \(\alpha =\frac{\pi }{3}\). Тогда окончательно имеем \( \arcsin \left( -\frac{\sqrt{3}}{2} \right)=-\frac{\pi }{3}\).

Больше уроков и заданий по математике вместе с преподавателями нашей онлайн-школы «Альфа». Запишитесь на пробное занятие уже сейчас!

Запишитесь на бесплатное тестирование знаний!

Нажимая кнопку «Записаться» принимаю условия Пользовательского соглашения и Политики конфиденциальности

Наши преподаватели

Далер Евгеньевич Мануилов

Репетитор по математике

Стаж (лет)

Образование:

Самаркандский Государственный Университет

Проведенных занятий:

Форма обучения:

Дистанционно (Скайп)

Зоя Юрьевна Духненко

Репетитор по математике

Стаж (лет)

Образование:

Душанбинский государственный педагогический институт им.

Т. Г. Шевченко

Проведенных занятий:

Форма обучения:

Дистанционно (Скайп)

Юлия Владимировна Горбанёва

Репетитор по математике

Стаж (лет)

Образование:

Челябинский государственный педагогический университет

Проведенных занятий:

Форма обучения:

Дистанционно (Скайп)

Предметы

• Математика
• Физика
• Химия
• Русский язык
• Английский язык
• Обществознание
• История России
• Биология
• География
• Информатика

Специализации

• Подготовка к ОГЭ по химии
• Подготовка к олимпиадам по физике
• Репетитор для подготовки к сочинению ЕГЭ по русскому
• Подготовка к ЕГЭ по английскому языку
• Репетитор для подготовки к ВПР по английскому языку
• Репетитор для подготовки к ВПР по русскому языку
• Репетитор для подготовки к ЕГЭ по обществознанию
• Подготовка к ОГЭ по биологии
• Подготовка к ЕГЭ по географии
• Подготовка к ОГЭ по географии

Похожие статьи

• Округление десятичных дробей
• Функция
• Площади трапеции
• Геометрическая прогрессия
• НИУ ВШЭ (Программная инженерия): проходной балл, отзывы
• РУДН: Геология
• Эллипс
• Решаем задачи на движение по окружности

Нажимая кнопку «Записаться» принимаю условия Пользовательского соглашения и Политики конфиденциальности

Текст с ошибкой:

Расскажите, что не так

Обратные тригонометрические функции

Арксинус

Рассмотрим на множестве $X=\left[-\frac{\pi }{2},\frac{\pi }{2}\right]$ функцию $y=sinx$. Она непрерывна и возрастает на множестве $X$ и отображает множество $X=\left[-\frac{\pi }{2},\frac{\pi }{2}\right]$ на множество $Y=[-1,1]$, поэтому по теореме о существовании обратной непрерывной монотонной функции у функции $y=sinx$ в множестве $Y$ существует обратная функция, которая также непрерывна и возрастает в множестве $Y=[-1,1]$ и отображает множество $[-1,1]$ на множество $\left[-\frac{\pi }{2},\frac{\pi }{2}\right]$. Эта обратная функция называется арксинусом и обозначается $x=arcsiny$.

В более привычной для нас записи имеем $y=arcsinx$. График функции арксинуса изображен на рисунке 1.

Рисунок 1. График функции арксинуса.

Арккосинус

Рассмотрим на множестве $X=\left[0,\pi \right]$ функцию $y=cosx$. Она непрерывна и убывает на множестве $X$ и отображает множество $X=\left[0,\pi \right]$ на множество $Y=[-1,1]$, поэтому по теореме о существовании обратной непрерывной монотонной функции у функции $y=cosx$ в множестве $Y$ существует обратная функция, которая также непрерывна и возрастает в множестве $Y=[-1,1]$ и отображает множество $[-1,1]$ на множество $\left[0,\pi \right]$. Эта обратная функция называется арккосинусом и обозначается $x=arccosy$.

В более привычной для нас записи имеем $y=arccosx$. График функции арккосинуса изображен на рисунке 2.

Рисунок 2. График функции арккосинуса.

Арктангенс

Рассмотрим на множестве $X=\left(-\frac{\pi }{2},\frac{\pi }{2}\right)$ функцию $y=tgx$. Она непрерывна и возрастает на множестве $X$ и отображает множество $X=\left(-\frac{\pi }{2},\frac{\pi }{2}\right)$ на множество $Y=R$, поэтому по теореме о существовании обратной непрерывной монотонной функции у функции $y=tgx$ в множестве $Y$ существует обратная функция, которая также непрерывна и возрастает в множестве $Y=R$ и отображает множество $R$ на множество $\left(-\frac{\eth }{2},\frac{\pi }{2}\right)$. Эта обратная функция называется арктангенсом и обозначается $x=arctgy$.

В более привычной для нас записи имеем $y=arctgx$. График функции арктангенса изображен на рисунке 3.

Рисунок 3. График функции арктангенса.

Арккотангенс

Рассмотрим на множестве $X=(0,\pi )$ функцию $y=ctgx$. Она непрерывна и убывает на множестве $X$ и отображает множество $X=(0,\pi )$ на множество $Y=R$, поэтому по теореме о существовании обратной непрерывной монотонной функции у функции $y=ctgx$ в множестве $Y$ существует обратная функция, которая также непрерывна и возрастает в множестве $Y=R$ и отображает множество $R$ на множество $(0,\pi )$. Эта обратная функция называется арккосинусом и обозначается $x=arcctgy$.

В более привычной для нас записи имеем $y=arcctgx$. График функции арккотангенса изображен на рисунке 4.

Рисунок 4. График функции арккосинуса.

Таблица значений обратных тригонометрических функций

Рисунок 5.

Пример 1

Используя график функции $y=arcsinx$ запишем основные свойства данной функции.

1. Область определения $\left[-1,1\right]$.
2. Область значения $\left[-\frac{\pi }{2},\frac{\pi }{2}\right]$.
3. Функция нечетна.
4. Функция непериодическая.
5. Функция проходит через начало координат.
6. Функция выше оси $Ox$ при $x\in (0,1]$.
7. Функция ниже оси $Ox$ при $x\in [-1,0)$.
8. Функция возрастает на всей области определения.
9. Функция непрерывна на всей области определения.

Исследование остальных трех обратных тригонометрических функций предоставляем читателю.

Обратные тригонометрические функции — формулы, графики, области значений и диапазоны

Обратные тригонометрические функции, как предмет изучения, тесно связаны с основными тригонометрическими функциями. Область определения и область значений тригонометрических функций преобразуются в область значений и область определения обратных тригонометрических функций. В тригонометрии мы узнаем о соотношениях между углами и сторонами в прямоугольном треугольнике. Точно так же у нас есть обратные тригонометрические функции. Основными тригонометрическими функциями являются sin, cos, tan, cosec, sec и cot. С другой стороны, обратные тригонометрические функции обозначаются как sin 9.0003 -1 х, cos ^-1 x, кроватка ^-1 x, тан ^-1 x, cosec ^-1 x, и sec ^-1

x.

Обратные тригонометрические функции имеют все формулы основных тригонометрических функций, которые включают сумму функций, двойную и тройную функции. Здесь мы попытаемся понять преобразование тригонометрических формул в обратные тригонометрические формулы.

1.	Что такое обратные тригонометрические функции?
2.	Обратные тригонометрические формулы
3.	График обратных тригонометрических функций
4.	Область определения и диапазон обратных тригонометрических функций
5.	Производные обратных триггерных функций
6.	Часто задаваемые вопросы об обратных тригонометрических функциях

Что такое обратные тригонометрические функции?

Обратные тригонометрические функции — это обратные функции, относящиеся к основным тригонометрическим функциям.

Базовую тригонометрическую функцию sin θ = x можно изменить на sin ^-1 x = θ. Здесь x может иметь значения в целых числах, десятичных дробях, дробях или показателях степени. Для θ = 30° имеем θ = sin ^-1 (1/2), где θ находится в диапазоне от 0° до 90°. Все тригонометрические формулы могут быть преобразованы в формулы обратной тригонометрической функции.

Обратные тригонометрические функции также известны как антитригонометрические функции/функции дуги/циклометрические функции. Обратные тригонометрические функции — это функции, обратные основным тригонометрическим функциям, которые представляют собой функции синуса, косинуса, тангенса, котангенса, секанса и косеканса. Обратные тригонометрические функции записываются с использованием префикса дуги, например arcsin(x), arccos(x), arctan(x), arccsc(x), arcsec(x), arccot(x). Обратные тригонометрические функции используются для нахождения угла треугольника по любой из тригонометрических функций. Он используется в различных областях, таких как геометрия, инженерия, физика и т.

д.

Рассмотрим функцию y = f(x) и x = g(y), тогда обратную функцию можно записать в виде g = f ^-1 ,

Это означает, что если y = f(x), то х = f ^-1 (у).

Пример обратной тригонометрической функции: x = sin ^-1 y.

Обратные тригонометрические формулы

Список обратных тригонометрических формул был сгруппирован по следующим формулам. Эти формулы помогают преобразовать одну функцию в другую, найти значения главных углов функций и выполнить многочисленные арифметические операции над этими обратными тригонометрическими функциями. Далее все основные формулы тригонометрических функций были преобразованы в формулы обратных тригонометрических функций и классифицируются здесь как следующие четыре набора формул.

• Произвольные значения
• Взаимные и дополнительные функции
• Сумма и разность функций
• Двойная и тройная функция

Формулы обратной тригонометрической функции для произвольных значений

Формула обратной тригонометрической функции для произвольных значений применима ко всем шести тригонометрическим функциям. Для обратных тригонометрических функций синуса, тангенса, косеканса отрицательные значения переводятся как отрицательные значения функции. А для функций косинуса, секанса, котангенса минусы домена переводятся как вычитание функции из значения π.

• sin ^-1 (-x) = -sin ^-1 x,x ∈ [-1,1]
• тангенс ^-1 (-x) = -тангенс ^-1 х, х ∈ R
• cosec ^-1 (-x) = -cosec ^-1 x, x ∈ R — (-1,1)
• cos ^-1 (-x) = π — cos ^-1 x, x ∈ [-1,1]
• сек ^-1 (-x) = π — сек ^-1 x, x ∈ R — (-1,1)
• детская кроватка ^-1 (-x) = π — детская кроватка ^-1 x, x ∈ R

Формулы обратной тригонометрической функции для обратных функций

Обратная тригонометрическая функция для обратных значений x преобразует заданную обратную тригонометрическую функцию в ее обратную функцию. Это следует из тригонометрических функций, где sin и косеканс обратны друг другу, тангенс и котангенс обратны друг другу, а cos и секанс обратны друг другу.

Обратная тригонометрическая формула арксинуса, арккосинуса и арктангенса также может быть выражена в следующих формах.

• sin ^-1 x = cosec ^-1 1/x, x ∈ R — (-1,1)
• cos ^-1 x = сек ^-1 1/x, x ∈ R — (-1,1)
• коричневый ^-1 x = детская кроватка ^-1 1/x, x > 0
  загар ^-1 х = — π + cot ^-1 х, х < 0

Формулы обратных тригонометрических функций для дополнительных функций

Сумма дополнительных обратных тригонометрических функций дает прямой угол. При тех же значениях x сумма дополнительных обратных тригонометрических функций равна прямому углу. Следовательно, дополнительные функции синуса-косинуса, тангенса-котангенса, секанса-косеканса дают в сумме π/2. Дополнительные функции, синус-косинус, тангенс-котангенс и секанс-косеканс, можно интерпретировать как 9.0015

• sin ^-1 x + cos ^-1 x = π/2, x ∈ [-1,1]
• загар ^-1 x ^{+ кроватка -1 x = π/2, x ∈ R}
• с ^-1 x + cosec ^-1 x = π/2, x ∈ R — [-1,1]

Сумма и разность формул обратной тригонометрической функции

Сумма и разность двух обратных тригонометрических функций могут быть объединены в одну обратную функцию в соответствии с приведенным ниже набором формул. Сумма и разность обратных тригонометрических функций были получены из формул тригонометрических функций sin(A + B), cos(A + B), tan(A + B). Эти формулы обратной тригонометрической функции можно использовать для дальнейшего вывода формул двойной и тройной функции.

• sin ^-1 x + sin ^-1 y = sin ^-1 (x. √ (1 — y ² ) + y√0 (1 — y ² ) + y√0
• sin ^-1 x — sin ^-1 y = sin ^-1 (x. √ (1 — y ² ) — y√(1 — x ² ))
• cos ^-1 x + cos ^-1 y = cos ^-1 (xy — √ (1 — x ² ).√(1 — ² ).√(2 900 2 4 )) 0 9

  4 )

• cos ^-1 x — cos ^-1 y = cos ^-1 (xy + √ (1 — x ² ).√(1 — ² ).√(1 — 9000 2 ⁴⁾⁾
• tan ^-1 x + tan ^-1 y = tan ^-1 (x + y)/(1 — xy), если xy < 1
• желтовато-коричневый ^-1 x + tan ^-1 y = tan ^-1 (x — y)/(1 + xy), если xy > — 1

Двойная формула обратной тригонометрической функции

Двойная обратная тригонометрическая функция может быть решена для получения одной тригонометрической функции в соответствии с приведенным ниже набором формул.

• 2sin ^-1 x = sin ^-1 (2x.√(1 — x ² ))

• 2 cos ^-1 x = cos ^-1 (2x ² — 1)

• 2tan ^-1 x = tan ^-1 (2x/1 — x ² )

Эти формулы получены из формул двойного угла тригонометрии.

Тройка формул обратной тригонометрической функции

Тройка обратных тригонометрических функций может быть решена для получения одной обратной тригонометрической функции в соответствии с приведенным ниже набором формул.

• 3sin ^-1 x = sin ^-1 (3x — 4x ³ )

• 3 cos ^-1 x = cos ^-1 (4x ³ — 3x)

• 3tan ^-1 x = tan ^-1 (3x — x ³ /1 — 3x ² )

Эти формулы напоминают формулы тройного угла тригонометрии и являются их производными.

Давайте изучим свойства обратных тригонометрических функций, используя их график, область определения и область значений в следующих разделах.

• Арксинус
• Арккосинус
• Арктангенс
• Арккотангенс
• Арксеканс
• Арккосеканс

График обратных тригонометрических функций

Мы можем построить графики различных обратных тригонометрических функций с их диапазоном главных значений. Здесь мы выбрали случайные значения для x в области соответствующих обратных тригонометрических функций. Мы поймем область и диапазон этих функций в следующих разделах.

Функция арксинуса

Функция арксинуса или функция обратного синуса, также обозначаемая как sin ^-1 x, является обратной функцией синуса. График обратной функции синуса приведен ниже.

Функция арккосинуса

Функция арккосинуса или функция обратного косинуса, также обозначаемая как cos ^-1 x, является обратной функцией косинуса. График обратной функции cos приведен ниже.

Функция арктангенса

Функция арктангенса или функция арктангенса, также обозначаемая как тангенс ^-1 x, является обратной функцией тангенса. График обратной функции тангенса приведен ниже.

Функция арккотангенса

Функция арккотангенса или функция арккотангенса, также обозначаемая как cot ^-1 x, является обратной функцией котангенса. График обратной функции кроватки показан ниже.

Функция арксеканс

Функция арксеканс или функция арксеканс, также обозначаемая как сек ^-1 x, является обратной функцией секущей. График обратной функции sec приведен ниже.

Функция арккосеканса

Функция арккосеканса или функция арккосеканса, также обозначаемая как cosec ^-1 x, является обратной функцией косеканса. График обратной функции cosec приведен ниже.

Область определения и диапазон обратных тригонометрических функций

Приведенные выше графики помогают нам сравнить и понять функции y = sin ^-1 x, y = cos ^-1 x, y = tan ^-1 x, y = cot ^-1 x, y = sec ^-1 x, и y = cosec ^-1 Икс. Область (значение x) функции представлена ​​по оси x, а диапазон (значение y) обратной тригонометрической функции представлен по оси y. В приведенной ниже таблице указаны область определения и диапазон главных значений обратных тригонометрических функций.

Обратный тригонометрический функция	Домен	Диапазон
Арксинус	[-1,1]	[-π/2,π/2]
Арккос	[-1,1]	[0,π]
Арктан	Р	(-π/2,π/2)
Арккот	Р	(0,π)
Арксек	(-∞,-1] ∪ [1,∞)	[0,π/2) ∪ (π/2,π ]
Арксск	(-∞,-1] ∪ [1,∞)	[-π/2,0) ∪ (0,π/2]

Производные обратных триггерных функций

Мы можем найти дифференцирование различных обратных тригонометрических функций, используя формулы дифференцирования. В следующей таблице приведены результаты дифференцирования обратных триггерных функций.

Обратные тригонометрические функции	крас./дв.
у = sin -1 (х), х ≠ -1, +1	1/√(1-x 2 )
у = cos -1 (х), х ≠ -1, +1	-1/√(1-x 2 )
у = тангенс -1 (х), х ≠ -i, +i	1/(1+x 2 )
у = детская кроватка -1 (х), х ≠ -i, +i	-1/(1+x 2 )
у = сек -1 (х), |х| > 1	1/[|х|√(х 2 -1)]
у = csc -1 (х), |х| > 1	-1/[|х|√(х 2 -1)]

Интегралы обратных тригонометрических функций

Здесь приведены интегральные формулы обратных тригонометрических функций. Чтобы узнать, как получить каждый из них, нажмите здесь.

Обратная тригонометрическая функция	Интеграл
∫ sin -1 x дх	x sin -1 x + √(1 — x²) + C
∫ cos -1 х дх	x cos -1 x — √(1 — x²) + C
∫ тангенс -1 х дх	x tan -1 x — (1/2) ln |1 + x²| + С
∫ csc -1 x дх	x csc -1 x + ln |x + √(x² — 1)| + С
∫ сек -1 х дх	x сек -1 x — ln |x + √(x² — 1)| + С
∫ кроватка -1 x дх	x детская кроватка -1 x + (1/2) ln |1 + x²| + С

☛ Связанные темы:

• Калькулятор обратных триггерных функций
• Тригонометрия
• Теорема Пифагора
• Обратные операции

Советы и рекомендации по обратным тригонометрическим функциям:

Некоторые из приведенных ниже советов будут полезны при решении и применении различных формул обратных тригонометрических функций.

• sin ^-1 (sin x) = x, когда -1 ≤ x ≤ 1 (для получения дополнительной информации нажмите здесь)
• sin(sin ^-1 x) = x, когда -π/2 ≤ x ≤ π/2.
• sin ^-1 x отличается от (sin x) ^-1 . Также (sin x) ^-1 = 1/sinx
• sin ^-1 x = θ и θ относятся к углу, который является главным значением этой обратной тригонометрической функции.

 

Решенные примеры на обратные тригонометрические функции

1. Пример 1: Найдите основное значение cos ^-1 (-1/2).

   Решение:

   Предположим, что x = cos ^-1 ( -1/2)

   Мы можем записать это как:

   cos х = -1/2

   Диапазон основной стоимости обратная триггерная функция cos ^-1 равна [0,π ].

   Таким образом, главное значение cos ^-1 (-1/2) равно 2π/3.

   Ответ: Следовательно, основное значение cos ^-1 (-1/2) равно 2π/3.

2. Пример 2: Найти значение sin ^-1 (1/2) — сек ^-1 (-2).

   Решение: sin ^-1 (1/2) — сек ^-1 (-2) = π/6 — (π — сек ^-1 2)
   = π/6 — (π — π/3) (Диапазон cos ⁻¹ (x) равен [0,π], мы можем найти x, используя x = cos ^-1 (1/2) = π /3)
   = π/6 — π + π/3
   = π/6 + π/3 – π
   = π/2 — π
   = -π/2

   Ответ: Следовательно, значение данного выражения равно -π/2

3. Пример 3: Найдите значение cos ^-1 (cos 13π/6).

   Решение: cos ^-1 (cos 13π/6) = cos ^-1 [cos(2π + π/6)]

   = cos ^-1 [cos π/6]

   5 = 9 π/6 (из формул обратных тригонометрических функций)

   Ответ: Значение cos ^-1 (cos 13π/6) равно π/6.

4. Пример 4: Найдите значение tan ^-1 (1) + cos ^-1 (-1/2) + sin ^-1 (-1/2).

   Решение:

   Используя формулы обратных триггерных функций,

   tan ^-1 (1) + cos ^-1 (-1/2) + sin ^-1 (-1/15)

   = π/4 + π — cos ^-1 (1/2) — sin ^-1 (1/2)

   = π/4 + π — π/3 — π/6

   = π/ 4 + π — π/2

   = π/4 + π/2

   = 3π/4

   Ответ: Следовательно, ответ равен 3π/4.

5. Пример 5: Найдите значение tan ^-1 (√3) — cot ^-1 (-√3).

   Решение:

   По обратным формулам триггера,

   тангенс ^-1 (√3) — раскладушка ^-1 (-√3)

   = тангенс ^{3 -1 — детская кроватка -1 (√3))}

   = коричневый ^-1 (√3) — π + детская кроватка ^-1 (√3)

   = π/3 — π + π/6

   = π/2 — π

   = -π/2

   Ответ: Следовательно, ответ равен -π/2.

перейти к слайдуперейти к слайдуперейти к слайдуперейти к слайдуперейти к слайду

Разложить сложные концепции с помощью простых визуальных средств.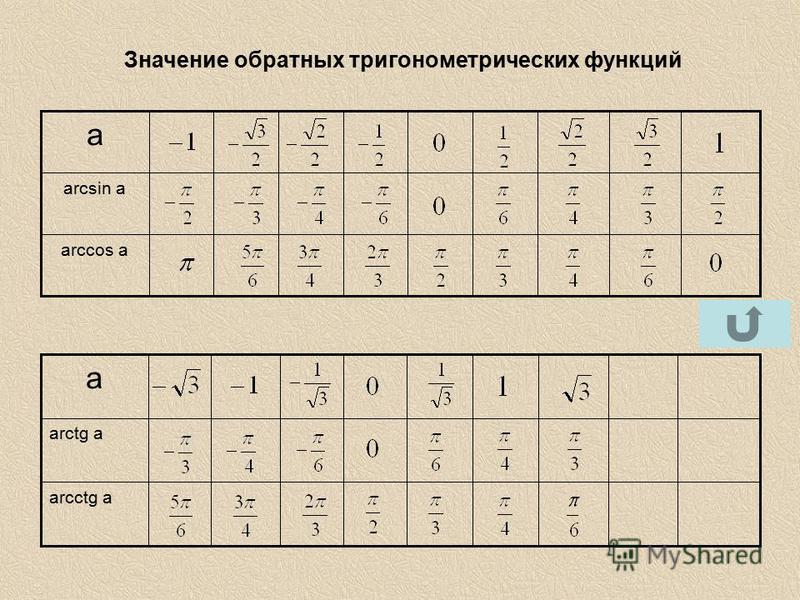

Математика больше не будет сложным предметом, особенно когда вы понимаете концепции с помощью визуализаций.

Запись на бесплатный пробный урок

Практические вопросы по обратным тригонометрическим функциям

 

перейти к слайдуперейти к слайду

Часто задаваемые вопросы об обратных тригонометрических функциях

Как найти обратную тригонометрическую функцию?

Обратные тригонометрические функции арксинуса, арккосинуса или арктангенса можно найти из основных тригонометрических соотношений. Например, если sin θ = x, то θ = sin ⁻¹ x. Таким же образом мы можем найти другие обратные функции триггера.

Для чего используются обратные тригонометрические формулы в обратной тригонометрии?

Формула обратной тригонометрической функции помогает найти угол для данной обратной тригонометрической функции сторон прямоугольного треугольника (sin ⁻¹ x = θ)

Как преобразовать обратную тригонометрическую функцию синуса в обратную к загару обратному?

Инверсия синуса преобразуется в инверсию тангенса с помощью одной из тригонометрических формул инверсии. Формула преобразования приведена ниже.
sin ⁻¹ x = tan ⁻¹ [x/√(1−x ² )]

Что такое тождества обратных тригонометрических функций для обратных функций?

Тождества обратной тригонометрической функции для обратных функций задаются следующим образом:

• sin ^-1 x = cosec ^-1 1/x
• cos ^-1 x = сек ^-1 1/x
• коричневый ^-1 x = детская кроватка ^-1 1/x

Что такое арксинус, арккосинус и арктангенс обратных тригонометрических функций?

Термины арксинус, арккосинус и арктангенс являются обратными отношениями тригонометрических соотношений sinθ, cosθ и tanθ.

• θ = sin ^-1 x
• θ = cos ^-1 y
• θ = тангенс ^-1 z

Что такое обратные тригонометрические формулы?

Обратные тригонометрические функции являются обратными функциями основных тригонометрических функций, таких как синус, косинус, тангенс, котангенс, секанс и косеканс. Некоторые основные обратные тригонометрические формулы приведены ниже:

• sin ^-1 (-x) = -sin ^-1 x
• тангенс ^-1 (-x) = -тангенс ^-1 x
• cosec ^-1 (-x) = -cosec ^-1 x
• , потому что ^-1 (-x) = π — потому что ^-1 x
• сек ^-1 (-x) = π — сек ^-1 x
• детская кроватка ^-1 (-x) = π — детская кроватка ^-1 x

Как вы решаете обратные триггерные функции?

Обратные тригонометрические функции можно решить, используя список обратных тригонометрических формул. Некоторые из этих формул,

• sin ^-1 x + sin ^-1 y = sin ^-1 (x. √ (1 — y 2

  ) + y√0 , если x и y ≥ 0 и x ² + y ² ≤ 1

• sin ^-1 x — sin ^-1 y = sin ^-1 (x. √ (1 — y ² ) — y√)(1 — x

  3 2 ), если x и y ≥ 0 и x

  ² + y ² ≤ 1
• cos ^-1 x + cos ^-1 y = cos ^-1 (xy — √ (1 — x ² ). √(1 — y ² )), если x и y ≥ 0 и x 2 ^{+ у 2 ≤ 1}
• sin ^-1 x + cos ^-1 x = π/2
• коричневый ^-1 x ^{+ детская кроватка -1 x = π/2}
• сек ^-1 х + косек ^-1 х = π/2

Что такое 6 обратных тригонометрических функций?

В тригонометрии есть шесть обратных тригонометрических функций. Эти функции задаются как sin ^-1 х, cos ^-1 x, кроватка ^-1 x, тан ^-1 x, cosec ^-1 x, и sec ^-1 x.

Что такое диапазон и область определения тригонометрической функции арккосинуса?

Функция арккосинуса записывается как cos ^-1 (x) или arccos(x). Обратные функции меняют местами значения x и y, таким образом, диапазон обратного косинуса составляет от 0 до pi, а область определения — от -1 до 1.

Как работать с функциями обратной тригонометрии

Автор: Мэри Джейн Стерлинг и

Обновлено: 26 марта 2016 г.

Рабочая тетрадь по тригонометрии для чайников

Изучить книгу Купить на Amazon

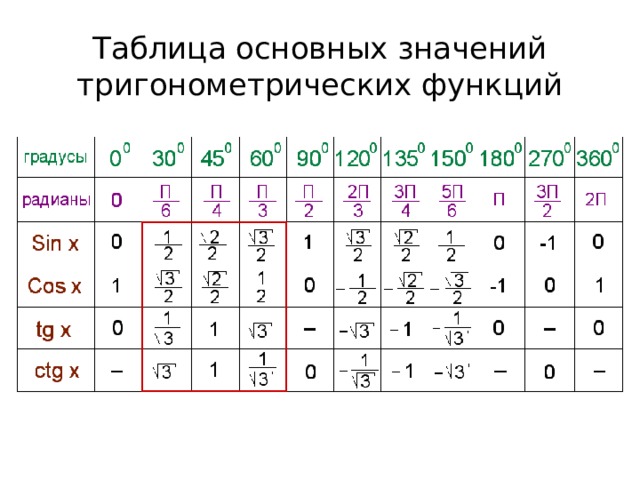
Самый простой способ работать с обратными триггерными функциями — иметь под рукой диаграмму с точными значениями функций. Когда речь идет об углах, отличных от наиболее распространенных или популярных, вы можете либо использовать таблицу, либо достать свой удобный научный калькулятор.

Когда вы много работаете с тригонометрией, вы быстро запоминаете основные углы и значения их функций. Вы также знаете, что синус и его величина положительны в QI и QII; косинус и его обратная величина положительны в QI и QIV; а тангенс и его обратная величина положительны в QI и QIII. Вооруженный основы , вы можете довольно быстро и эффективно находить значения функций, не прибегая к диаграмме или калькулятору.

В этом первом примере используется точное значение из диаграммы (или из памяти). Найти

1. Определите необходимый опорный угол, используя абсолютное значение ввода.

2. Используйте знак ввода, чтобы определить правильный квадрант.

   Потому что

   отрицательно, а из двух квадрантов диапазона косинус отрицателен в QII, ответом является угол в QII, опорный угол которого равен 45 градусам.

3. Определите правильный размер угла.

   Угол в стандартном положении в QII, опорный угол которого равен 45 градусам, равен

   .

В следующем примере используется арккотангенс. Найти

1. Определите необходимый опорный угол.

2. Используйте знак ввода, чтобы определить правильный квадрант.

3. Определите правильный размер угла.

   Все углы в QI совпадают с исходными углами, поэтому

Проблемы, с которыми вы столкнетесь, не всегда будут связаны с красивыми цифрами с самых распространенных точек зрения. Когда вы сталкиваетесь с неприятным маленьким десятичным значением, вам, возможно, придется использовать таблицу.