Таблица значений синуса, косинуса и т.д
Функция | Значения | |||||||||
| 00 | | 300 | | 450 | | 600 | | 900 | |
cosx | 1 | 0 | ||||||||
sinx | 0 | 1 | ||||||||
tgx | 0 | 1 | — | |||||||
| ctgx | — | 1 | 0 | |||||||
Соседние файлы в папке Теория по темам
- #
12.
 05.201515.87 Кб11Среднее арифметическое.doc
05.201515.87 Кб11Среднее арифметическое.doc - #
12.05.201518.43 Кб12Средняя линия.doc
- #
12.05.201522.53 Кб12Степенная функция.doc
- #
12.05.201528.16 Кб12Степень.doc
- #
12.05.201524.06 Кб11Сумма разность векторов.doc
- #
12.05.201530.72 Кб12Таблица значений синуса, косинуса и т.д..doc
- #
12.05.201519.46 Кб15Теорема Виета.doc
- #
12.05.201520.48 Кб20Теорема косинусов.doc
- #
12.05.201520.48 Кб16Трапеция.doc
- #
12.05.201522.02 Кб13Углы на плоскости.doc
- #
12.05.201518.43 Кб14Уравнение движения.doc
Мастер – класс по математике «Таблица значений основных тригонометрических функций» | Материал для подготовки к ЕГЭ (ГИА) по алгебре (9 класс) на тему:
Опубликовано 24. 01.2015 — 20:50 — Снопкова Ирина Владимировна
01.2015 — 20:50 — Снопкова Ирина Владимировна
Материал предназначен для преподавателей, работающих в 9-11 классах. Рассматривается способ запоминания таблицы значений основных тригонометрических функций.
Скачать:
Подписи к слайдам:
Переход от градусной меры угла к радианной
Проверь себя:
Ответы:
а)
б) 2
Прямоугольный треугольник
В
А С
Переход от радианной меры угла к градусной
Практическая работа
Задание 3.
Вычислите значение выражения:
а)
cos
+ sin 0 + sin
б)
tg
+ 3 sin — 2
cos
0
МАСТЕР-КЛАСС ПО МАТЕМАТИКЕ
«Таблица значений тригонометрических функций»
Автор: Снопкова Ирина Владимировна,
преподаватель математики
Задача нахождения значений синуса, косинуса, тангенса и котангенса путем применения известных формул сводится к нахождению значений
sin
α
, cos
α
,
tg
α
,
ctg
α
,
где
0
≤
α
≤
Практическая работа
Задание 2.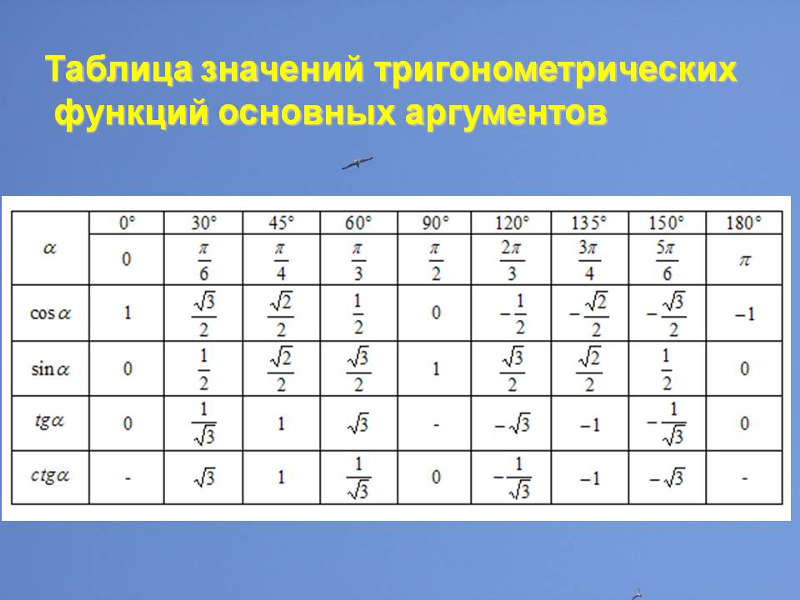 Найдите
Найдите
sin
, sin 0°, cos
.
Основные тригонометрические функции
В
А С
sin
α
=
cos
α
=
tg
α
=
ctg
α
=
таблиц
а значений тригонометрических функций
α
0
sin α
0
1
cos
α
1
0
tg α
0
1
—
ctg α
—
1
0
Элементы Прямоугольного треугольника
∠С =90° ( прямой угол)
∠ А=
α
(острый угол)
АВ –гипотенуза
АС – прилежащий катет
ВС –противолежащий катет
В
А
С
Практическая работа
Задание 1
.
Найдите
sin
;
sin
30
°
cos
45°.
tg
90°
Решение: воспользуемся таблицей значений тригонометрических функций
СПАСИБО ЗА РАБОТУ!
По теме: методические разработки, презентации и конспекты
Урок алгебры в 10 классе по теме: Преобразование сумм тригонометрических функций в произведение
Представлена технологическая карта урока с приложениями к уроку, а также добавлены файла электронного теста и презентация для интерактивной доски Mimio. ..
..
Урок алгебры в 10 классе по теме: «Нахождение значений тригонометрических функций от аркфункций»
…
Зачет №1 по алгебре и начала анализа 10 класса по теме «Числовая окружность, тригонометрические функции»
Материал зачетной работы предназначен для учащихся 10 класса заочной формы обучения и самообразования….
мастер-класс «Задание №23 ОГЭ. Построение графиков функций»
Здесь рассмотрено решение демоверсии 2019 года задание №23 и несколько заданий по разделам: построение парабол, построение гипербол, построение модульных функций, построение кусочно-непрерывных функци…
Разработка урока математики в 10 классе «Формулы суммы и разности тригонометрических функций»
Урок изучения новой темы….
31.03.2021 МСТ1 и 22.03.2021 ПК1 Домашняя контрольная работа по теме: » Свойства основных тригонометрических функций».
Задания:1.Вычислить значения выражения, составленных из тригонометрических функций, используя таблицу значений тригонометрических функций.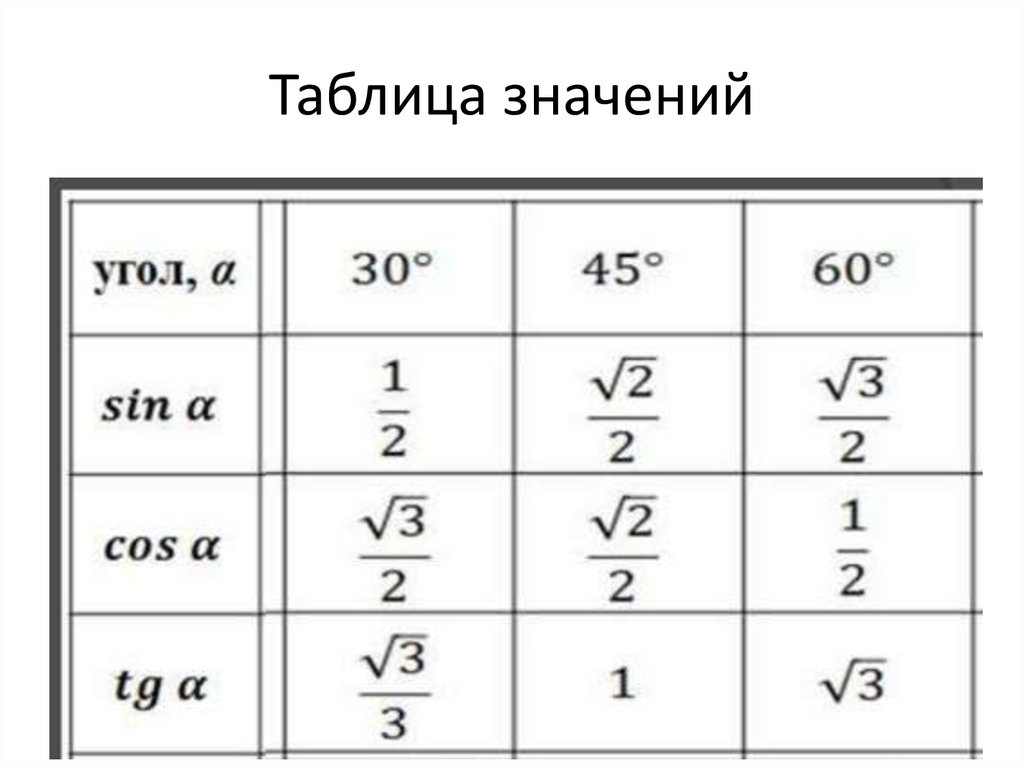 (№7)2. Выполнить перевод градусной меры угла в радианну…
(№7)2. Выполнить перевод градусной меры угла в радианну…
мастер-класс»Способ отбора корней в тригонометрическом уравнении»
Мастер — класс дло педагогов…
Поделиться:
Калькулятор тригонометрических отношений и таблица значений — хитрость для расчета
Зохеб Математика 8 класс, Математика 9 класс Тригонометрия 0
Вы можете либо использовать калькулятор, чтобы найти тригонометрические значения любых углов, либо также взглянуть на нашу таблицу значений, которая показывает значения только стандартных углов.
Калькулятор тригонометрических отношений/функций
Просмотр или загрузка таблицы значений тригонометрических отношений стандартных углов в формате PDF или изображения (JPEG)
Ищете ли вы Шестидесятеричная система или Круговая система Тригонометрическая таблица , эта таблица сделает работу.
Скачать в формате изображения | Скачать в формате PDF
Как легко запомнить значение тригонометрического отношения стандартных углов?
Какие стандартные углы?
Среднее значение стандартных углов здесь: 0°, 30°, 45°, 60°, 90°
Уловка для простого вычисления значения тригонометрического отношения синуса θ(Sin θ)
Разделите числа 0, 1, 2, 3 и 4 на 4 и получить их квадратный корень, чтобы получить значение синуса стандартных углов.
- sin 0° будет √( 0 ⁄ 4 ) = 0
- sin 30° будет √( 1 ⁄ 4 ) = 1 ⁄ 2
- sin 45° будет √( 2 ⁄ 4 ) = 1 ⁄ √2
- sin 60° будет √( 3 ⁄ 4 ) = √3 ⁄ 2
- sin 90° будет √( 4 ⁄ 4 ) = 1
Уловка для простого вычисления значения тригонометрического отношения косинуса θ(Cos θ)
стандартных углов cos ( 0°, 30°, 45°, 60°, 90°) = стандартных углов sin (90°, 60° , 45°, 30°, 0°) .
Итак, если вы запишете значения стандартных углов sin в обратном порядке, это даст вам значение стандартных углов cos.
- cos 0° = sin 90° = 1
- cos 30° = sin 60° = √3 ⁄ 2
- cos 45° = sin 45° = 1
- cos 60° = sin 30° = 1 ⁄ 2
- cos 90° = sin 0° = 0
Когда мы уже знаем значения Sin и Cos, легко получить значение тангенса θ (тег θ). Просто разделите значение Sin на Cos, чтобы получить значение Tan
Вот обучающее видео
- tan 0° = sin0° ⁄ cos0° = 0/1 = 0
- tan 30° = sin30° ⁄ cos30° = 1/2 / √3/2
- тангенс 45° = sin45° ⁄ cos45° = 1/√2 / 1/√2.
 = 1
= 1 - тангенс 60° = sin60° ⁄ cos60° = √3/2 / 1/2. = √3
- tan 90° = sin90° ⁄ cos90° = 1/0 = undefined (бесконечность)
Котангенс или cot θ: простой способ запомнить
стандартные углы cot ( 0°, 30°, 45°, 60°, 90°) = тангенс стандартные углы (90°, 60°, 45° , 30°, 0°)
Дело в том, что вам просто нужно написать значение тангенса снизу, которое будет значением cot.
- кроватка 0° = загар 90° = не определено (бесконечность)
- cot 30° = tan 60° = √3
- кроватка 45° = коричневая 45° = 1
- cot 60° = tan 30° = 1 ⁄ √3
- кроватка 90° = загар 0° = 0
Косеканс, или косеканс, или cos θ: Простой способ вычисления
Как мы уже узнали, как получить значение sin. все, что вам нужно сделать, это разделить 1 на значение sin, и вы получите значение cosec
- cosec 0° = 1 ⁄ sin0° = 1 ⁄ 0
- косек 30° = 1 ⁄ sin30° = 1 ⁄ 1/2 = 2
- cosec 45° = 1 ⁄ sin45° = 1 ⁄ 1/√2 = √2
- cosec 60° = 1 ⁄ sin60° = 1 ⁄ √3/2 = 2 ⁄ √3
- cosec 90° = 1 ⁄ sin90° = 1 ⁄ 1 = 1
секанс или сек θ: легко запомнить
сек стандартные углы ( 0°, 30°, 45°, 60°, 90°) = стандартных углов cosec напишите снизу значение cosec, которое будет значением sec.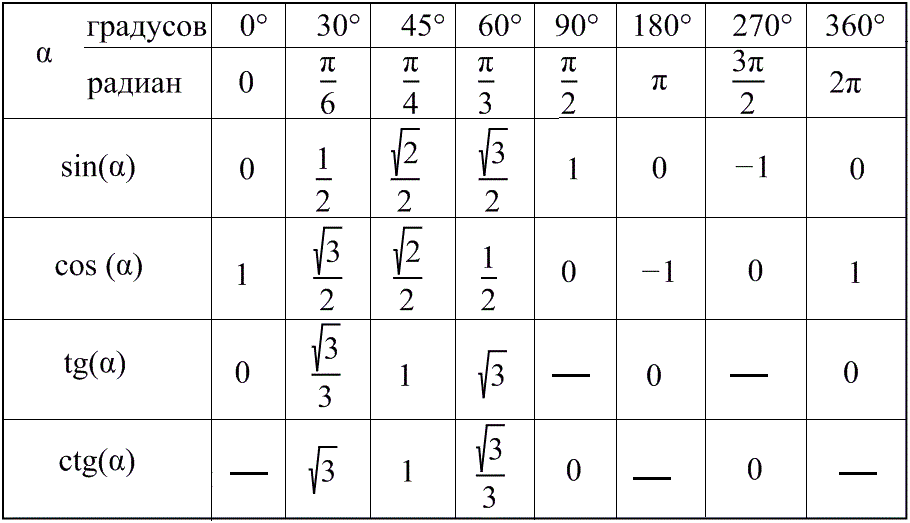

 05.201515.87 Кб11Среднее арифметическое.doc
05.201515.87 Кб11Среднее арифметическое.doc = 1
= 1