Таблицы истинности. Логические схемы. 10 класс
Похожие презентации:
Логические выражения и таблицы истинности
Логические выражения и таблицы истинности. Логика
Построение таблиц истинности для логических выражений
Таблицы истинности логических функций
Основы логики. 10 класс
Формы мышления. Алгебра высказываний. (10 класс)
Логические выражения и таблицы истинности
Формы мышления. Логика
Логические схемы
Решение логических задач 10 класс
1. Таблицы истинности. Логические схемы
Урок информатики.10 класс.
Сивова А.Ю., МОУ «Лицей №31» г. Саранск
2. Построим таблицу истинности для выражения F = (AvB)&(¬Av¬B).
Построим таблицу истинности длявыражения F = (AvB)&(¬Av¬B).
Количество строк = 22 (2 переменных) + 1
(заголовки столбцов) = 5.
Количество столбцов = 2 логические переменные
(А, В) + 5 логических операций (v, &, ¬, v,) = 7.

B
v
Сивова А.Ю., МОУ «Лицей №31» г. Саранск
9. Построение логических схем
Определить число логических переменных.Определить количество базовых логических операций и их
порядок.
Изобразить для каждой логической операции
соответствующий вентиль.
Соединить вентили в порядке выполнения логических
операций.
Сивова А.Ю., МОУ «Лицей №31» г. Саранск
Пример 1
Пусть X = истина, Y = ложь.
Составить логическую схему для следующего логического
выражения: F = X v Y & X.
Две переменные — X и Y.
Две логические операции:
2 1
X v Y & X.
1
Х
Y
0
0
1
&
1
v
Ответ: 1v 0 & 1 = 1.
Сивова А.Ю., МОУ «Лицей №31» г. Саранск
11. Пример 2 Постройте логическую схему, соответствующую логическому выражению F=X&Yv¬(YvX). Найдите значение логического выражения
Пример 2Постройте логическую схему, соответствующую логическому
выражению F=X&Yv¬(YvX).
Найдите значение логического выражения для
X=1, Y=0.
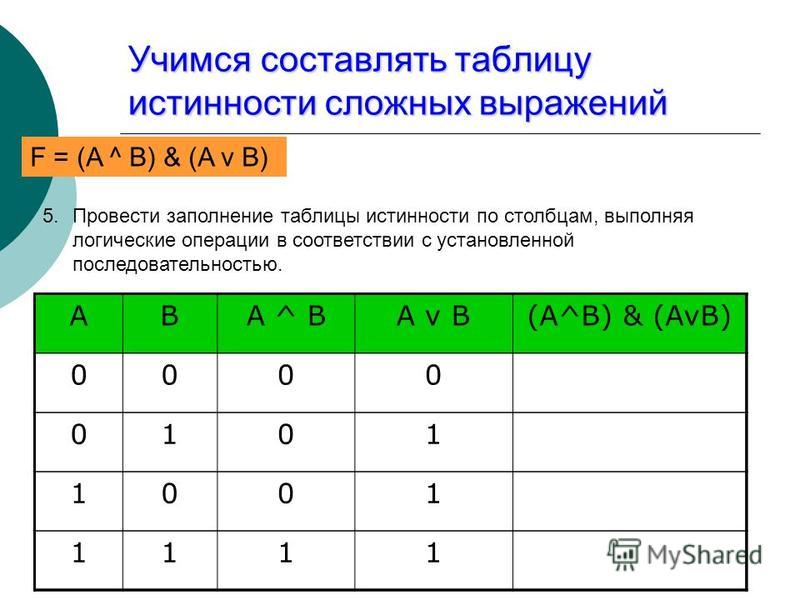
Переменных две: X и Y;
Логических операций четыре: конъюнкция, две дизъюнкции и
инверсия:
1 43 2
X&Yv ¬ (YvX)
Схему строим слева направо в соответствии с порядком
логических операций
1
0
1
0
&
11
v
0
¬
Сивова А.Ю., МОУ «Лицей №31» г. Саранск
v
0
№1
Составьте таблицы истинности для следующих логических выражений:
1. F=(X& Y)vZ.
2. F=X&YvZ.
3. F= ¬ (XvY) & (YvX).
4. F= ¬ ((XvY) & (ZvX)) & (ZvY).
5. F= A&B&C& D.
6. F= (AvB) & ( BvAvB).
№2
Постройте логическое выражение по логической схеме:
А
&
А
¬¬
¬
В
С
1
ВВ
¬
¬
Сивова А.Ю., МОУ «Лицей №31» г. Саранск
1
&
&
№3
Постройте логическую схему, соответствующую
логическому выражению, и найдите значение
логического выражения:
F = AvB& C, если А = 1, В=1, С=1 (1).
F = ¬ (AvB&C), если А=0, В=1, С=1 (1).
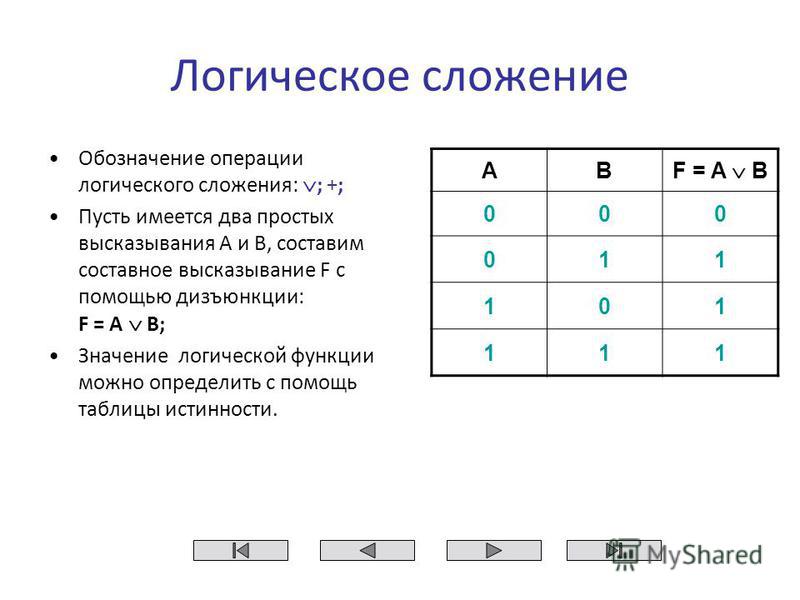
F = AvB&C, если А=1, В=0, С=1 (0).
F = (AvB) & (CvB), если А=0, В=1, С=0 (1).
F = ¬ (А&В&С), если А=0, В=0, С=1 (1).
F = ¬ (A&B&C) v (B & C v A), если А=1, В=1, С=0 (1).
F = B& Av B&A, если А=0, В=0 (0).
Сивова А.Ю., МОУ «Лицей №31» г. Саранск
Домашнее задание
№1
Составьте таблицы истинности и определите истинность
формулы:
1) F = ((Av B)→B)&( AvB).
2)F = ¬(AvB)≡( AvB).
F = ¬ ((А В) ≡ ( B →Ā)).
№2
Составьте логические схемы к следующим логическим
выражениям:
A) F = Bv(C& A) v (A&B).
B) F= ¬ (A&B) vC&D.
№3
Постройте логические выражения к логическим схемам:
A
B
A
B
&
&
&&
11
&&
C
C
&&
11
D
D
Сивова А.Ю., МОУ «Лицей №31» г. Саранск
&&
English Русский Правила
Таблица истинности логических операций — алгоритм построения
Используя таблицы истинности логических операций, можно точно определить, верна ли функция при определённых значениях.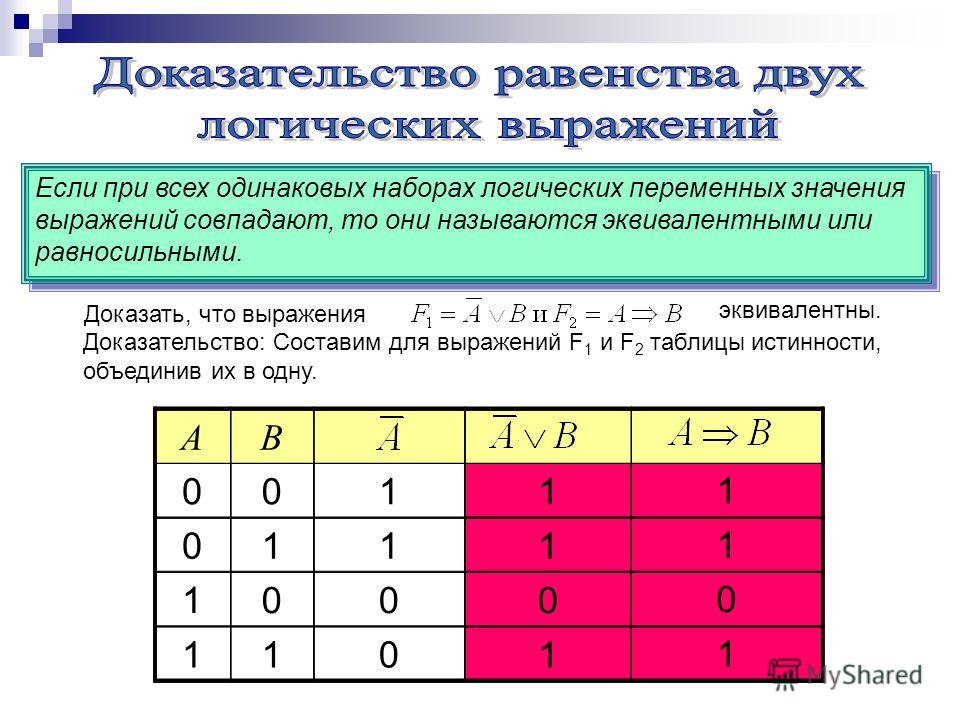 В перечень заносят всевозможные комбинации переменных появляющихся на входе и соответствующие им состояния на выходе. Чаще всего таблицы применяют при проектировании и анализе цифровых схем. При этом в интернете существуют сервисы, с помощью которых построить такого рода сводку не составит труда даже слабо разбирающемуся в этой сфере пользователю.
В перечень заносят всевозможные комбинации переменных появляющихся на входе и соответствующие им состояния на выходе. Чаще всего таблицы применяют при проектировании и анализе цифровых схем. При этом в интернете существуют сервисы, с помощью которых построить такого рода сводку не составит труда даже слабо разбирающемуся в этой сфере пользователю.
Содержание
- Определения и понятия
- Виды логических операций
- Аксиомы и законы
- Алгоритм построения
- Пример задания
- Вычисления онлайн
Определения и понятия
Под таблицей истинности понимают свод значений, которые может принять высказывание при сочетании различных входящих комбинаций. Другими словами, каждому набору функций или сигналам, присутствующим на входе чего-либо, соответствует строго определённые показатели на выходе. Все значения, являющиеся всевозможными высказываниями, называют логическими выражениями. Если в таблице последние столбцы логичных выражений идентичны, то рассматриваемый объект считается равносильным.
Любое выражение можно описать формулой, в которую будут включаться переменные, характеризующие состояния, и обозначающие функции знаки логических операций. Поэтому используя язык математики, в частности, алгебры, любое сложное высказывание можно разделить на несколько простых, а затем объединить логической связью.
Обычно значениями истинности описывают логическую функцию, у которой показатели параметров определяют верность. Раздел математики рассматривающий их на правдивость или ложность называется булевым. В 1854 году английский учёный Джордж Буль предложил метод, позволяющий проводить анализ классов и высказываний. Согласно ему, любое значение может принимать одно из двух состояний — истина или ложь.
Эти состояния принято обозначать арабскими цифрами один либо ноль или словами true и false. Это возможно из-за того, что для математики важна только истинность высказываний, а конкретное содержание второстепенно. Простые высказывания принято считать логическими переменными, а сложные — функциями логики.
Выражения для упрощения записи обозначают латинскими буквами A, B, C.
Применение двух цифр подчёркивает соответствие между двоичной системой счисления и математической логикой. В итоге с помощью последней стало удобным описывать работу цифровых схем радиоэлектронной аппаратуры, алгоритмы в программировании, проводить синтез и анализ результата выполнения операций.
Суждение о правильности построения таблиц истинности для логических выражений основано на учёте всех переменных и операций, последовательно выполняющихся в рассматриваемой функции. Обычно для начертания используют 2n+1 строк, где n обозначает количество входных переменных, и n+m столбцов, m — число значений на выходе.
Виды логических операций
В качестве наименьшей единицы измерения объёма данных принято считать бит. В него заносится одно из двух значений — ложь (0) или правда (1).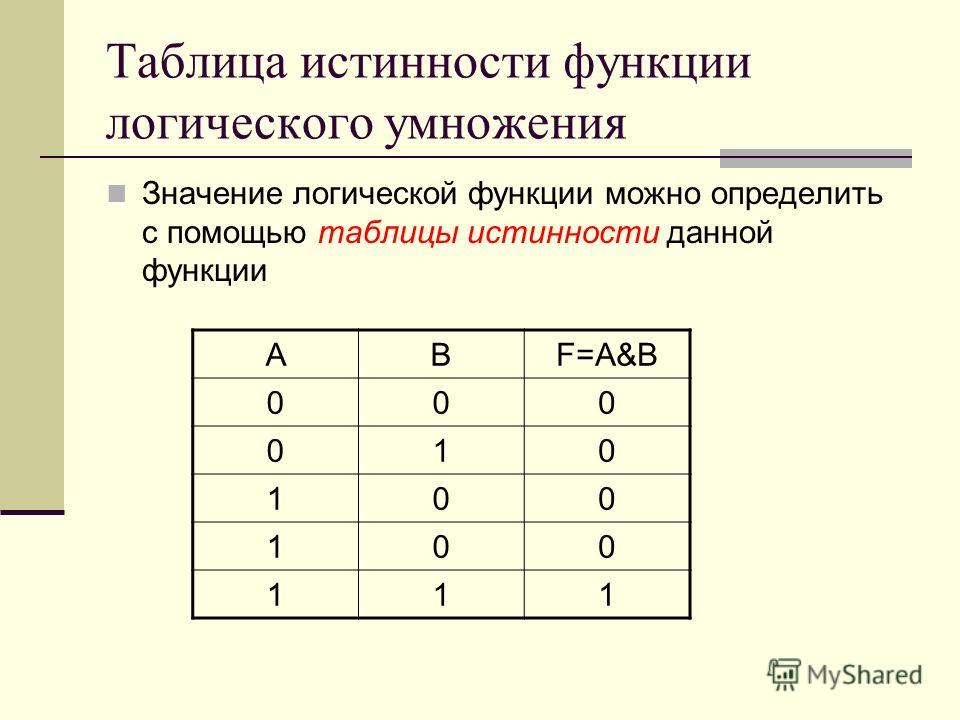 Каждая ячейка, соответствующая биту, находится лишь в одном из этих состояний. Существуют определённые операции, используемые для действий с ячейками:
Каждая ячейка, соответствующая биту, находится лишь в одном из этих состояний. Существуют определённые операции, используемые для действий с ячейками:

Эти операции являются основными элементами при составлении таблиц истинности и получения возможного результата. На основании их построена алгебра Буля. Некоторые элементы получаются путём объединения нескольких операций. Так, существует состояние: NAND (И-НЕ) и NOR (ИЛИ-НЕ). Первый элемент является инверсией операции «И», а второй — «ИЛИ». На основании рассмотренных операторов строится работа всех цифровых интегральных схем.
В информатике существует своя терминология, обозначающая то или иное логическое действие. Так, AND называют операцией конъюнкции, OR — дизъюнкции, XOR — сложение по модулю 2, NOT — отрицание. Задача инженера при анализе схем или алгоритма сводится к выполнению булевой арифметики и упрощению выражений. Для этого используют различные правила и положения не требующих доказательства.
Аксиомы и законы
Построение таблиц в удобной форме позволяет определить, когда определённое действие или высказывание принимает верное значение, а в каком случае нет. В верхней строчке записывают логическую форму высказывания, а в столбцах — истинные значения. Некоторые комбинации высказываний всегда будут истинными или ложными, независимо от содержания. Поэтому и были сформулированы следующие законы:
В верхней строчке записывают логическую форму высказывания, а в столбцах — истинные значения. Некоторые комбинации высказываний всегда будут истинными или ложными, независимо от содержания. Поэтому и были сформулированы следующие законы:
 То есть третьего не дано.
То есть третьего не дано.Эти три закона фундаментальны. Без их соблюдения сделать любое правильное утверждение невозможно.
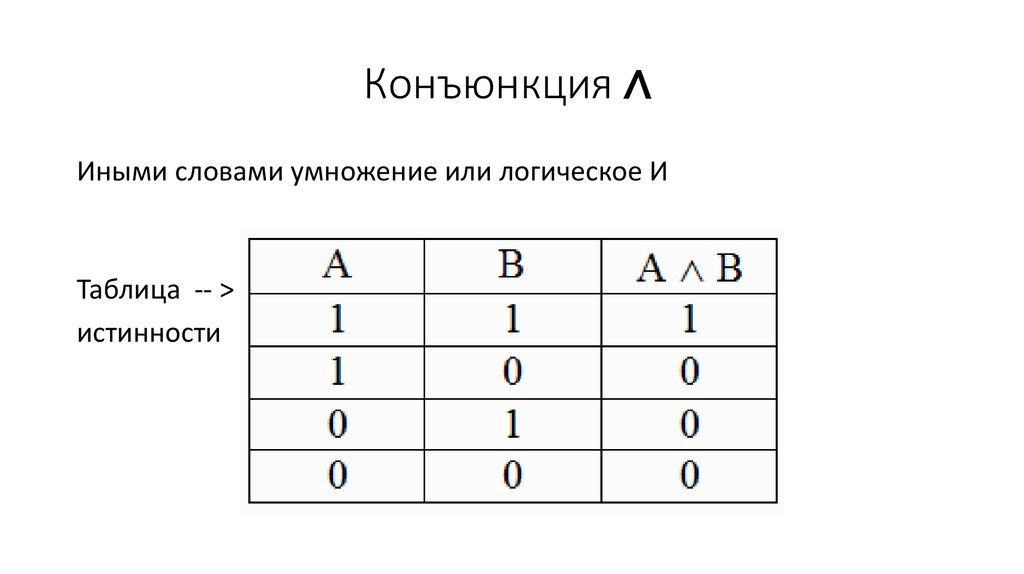
Для решения логических задач с помощью таблиц истинности используют различные формулы, соответствующие разного вида операциям. Одно из них логическое умножение (конъюнкция). В этом случае считается, что функция истинная лишь тогда, когда оба выражения являются верными: F = A & B. Другое логическое сложение (дизъюнкция). Оно гласит, что если оба выражения ложны, то и логическая функция будет неверной.
Кроме того, используется закон:
- инверсии (отрицания) — если логическое высказывание истинно, то отрицание его будет ложным выражением;
- импликации (следования) — для всегда истинного сложного логического выражения ложь будет тогда, когда из верности следует отрицание;
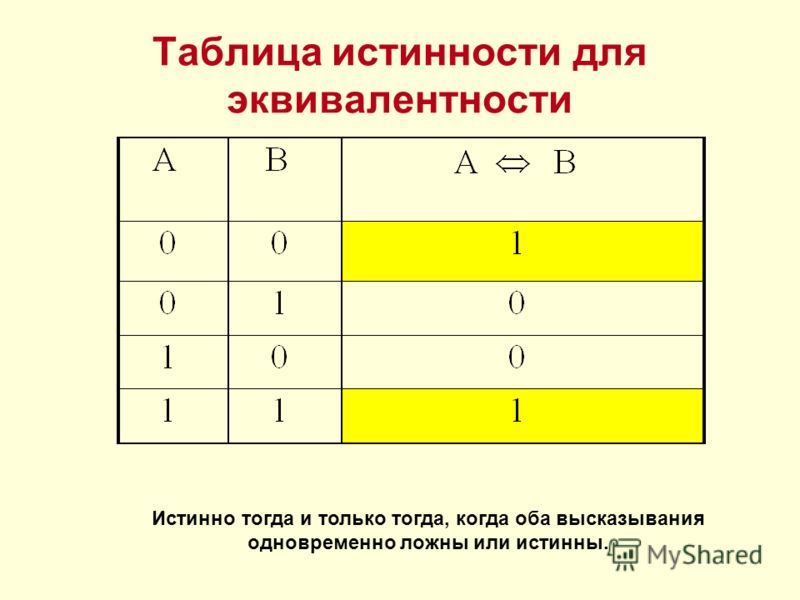
- эквивалентности (равнозначности) — выражение будет истинным лишь тогда, когда оба высказывания имеют одинаковое значение.

При построении таблиц нужно придерживаться установленного порядка выполнения упрощения операций. Вначале считают инверсию и конъюнкцию, а затем дизъюнкцию, импликацию и эквиваленцию. При изменении же порядка выполнения действий в описании логических операций используют скобки.
Алгоритм построения
Таблицы истинности показывают, какой вид может принять выражение при различных входящих в него значениях переменных. Для того чтобы их правильно построить и выполнить вычисление логического выражения нужно придерживаться установленного алгоритма. Построение таблиц выполняют в следующей последовательности:
- подсчитывают количество переменных n;
- вычисляют число строк для будущей таблицы используя формулу m = 2n+1;
- определяют число логических операций;
- устанавливают порядок выполнения операций в соответствии со скобками и приоритетами;
- строят таблицу с указанием столбцов и наборов значений, заданных логических операций;
- заполняют оставшиеся ячейки в таблице.

Для заполнения таблиц нужно упрощать выражения с учётом последовательности выполнения операций. При этом учитывать, что если значение какого-то из аргументов функции в соответствующей строке таблицы будет равное нулю, то записывать его нужно в виде отрицания.
Пример задания
Пусть необходимо построить таблицу для логического выражения F = (A → B) * (A + B). Эта формула состоит из двух логических переменных A и B и нескольких операций. Начинают построение с определения строк. Используя формулу 2n+1 для рассматриваемого примера можно установить, что их число будет: x = 22 + 1 = 5.
Теперь следует определить число столбцов. Для этого используется формула, в которой учитывается количество переменных и операций. Последние можно просто посчитать, сложив количество разных знаков, используемых в записи формулы. Но правильней сначала расставить порядок операций, а затем посчитать. Согласно порядку действия над операциями их нумерацию можно представить в следующей очерёдности:
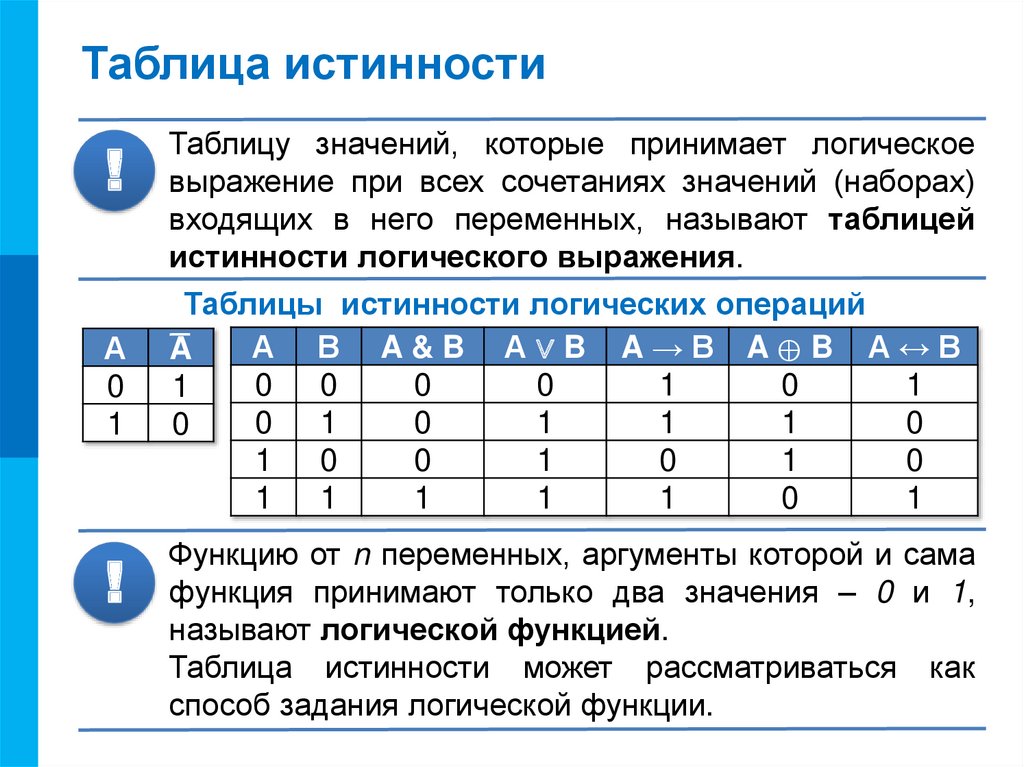
В итоге получится, что столбцов будет: Y = 2 + 5 = 7. Теперь нужно построить таблицу 7Х5. В шапку первого и второго столбца вписывают переменные, а затем операции над ними. Затем в строках, соответствующих A и B нужно записать всё, что с ними может произойти. В итоге останется только правильно посчитать последний столбец.
Для этого нужно использовать законы. Необходимо выполнить логическое умножение значений в скобках. Первой и второй строчке будет соответствовать операция произведения один на один, что в ответе даст единицу. Третьей и четвёртой — ноль на один, что в итоге даст ноль. Последний столбец является главным для рассматриваемой логической функции. По нему можно узнать значение логической функции для любых форм переменных A и B.
Это довольно простая задача, содержащая всего две переменных. Но в реальности, например, в программировании, их может быть намного больше.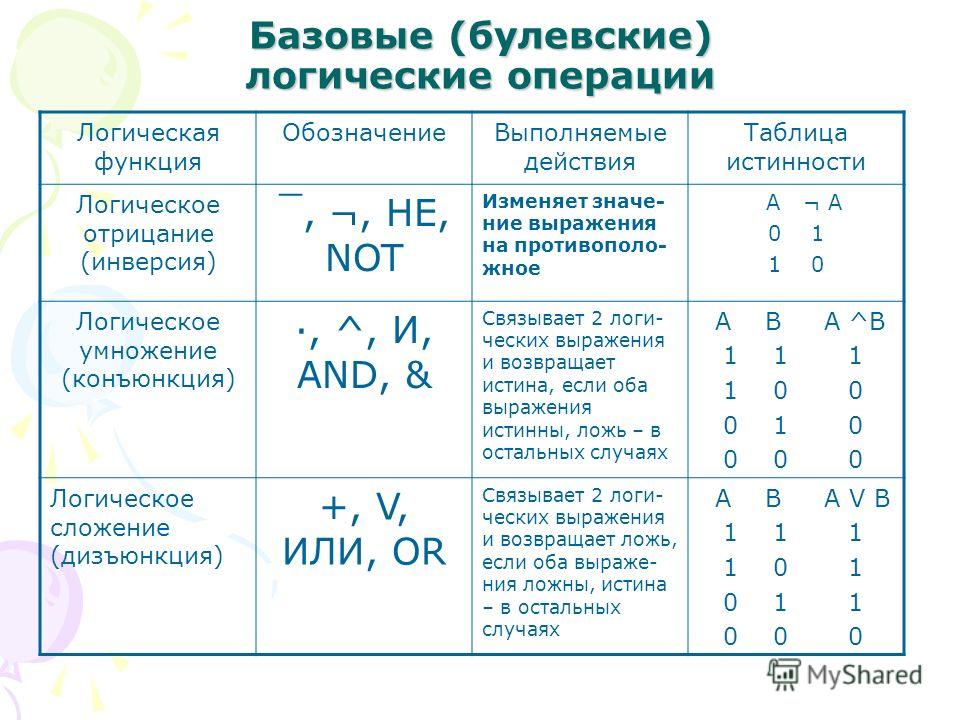 Решать такие задания методом перебора проблематично. Поэтому при решении сложных примеров функцию вначале пытаются упростить.
Решать такие задания методом перебора проблематично. Поэтому при решении сложных примеров функцию вначале пытаются упростить.
Например, заданно выражение (x + y + z) * (x + y). По сути, оно записано в совершенно нормальной конъюнктивной форме. Но для приведения его к этому виду нужно, чтобы во втором выражении стояла z. Для того чтобы её добавить необходимо обратить внимание на то, что внутри скобок стоит логическое сложение. Поэтому дописав к нему ноль, результат не изменится. Добавить ноль через z можно, как ноль умножить на НЕ z. В итоге получится выражение (x + y + z) * (x + y + z + z), для которого, используя алгоритм составить таблицу уже не так и сложно.
Вычисления онлайн
В интернете есть сервисы, автоматически строящие таблицы истинности. Такие сайты предлагают свои услуги бесплатно и доступны даже тем, кто слабо ориентируется в теме. С их помощью можно находить таблицы для довольно сложных выражений, решение которых требует скрупулёзности в расчёте. В основе онлайн-вычислений заложены принципы логических законов, поэтому за достоверность результата можно не переживать. Тем более расчёт занимает совсем небольшое количество времени.
В основе онлайн-вычислений заложены принципы логических законов, поэтому за достоверность результата можно не переживать. Тем более расчёт занимает совсем небольшое количество времени.
Для того чтобы воспользоваться сайтами-калькуляторами пользователю необходимо знать обозначение операций, иметь подключение к интернету и установленный веб-обозреватель, поддерживающий Flash-технологию. Регистрацию, указание личных данных сервисы, предлагающие такого рода услуги, не требуют.
Из различных порталов можно отметить три наиболее популярных калькулятора:
Эти сайты имеют интуитивно понятный интерфейс и что довольно полезно, на своих страницах содержат краткую теорию, используемую для составления таблиц истинности и даже примеры решений.
Предыдущая
ИнформатикаКак рисовать в Паскале АВС — команды, алгоритмы и примеры
Следующая
ИнформатикаРеляционные базы данных — определение, структура, примеры
 ru
ru1
Первый слайд презентации
Что такое таблица истинности? Приведите примеры
Изображение слайда
2
Слайд 2: Пример:
Изображение слайда
3
Слайд 3: Логические схемы и выражения
Раздел 9.1А: Архитектура компьютера суббота, 22 сентября 2018 г.
Изображение слайда
4
Слайд 4: Цели обучения
9.4.2.1 строить логические схемы и логические выражения Критерии оценивания Знать обозначения и определение логических операций Уметь составлять таблицу истинности и строить схему по предложенному выражению Составлять выражение и таблицу истинности исходя из логической схемы
Изображение слайда
5
Слайд 5
Цель обучения
9. 4.2.1 строить логические схемы и логические выражения
Критерий оценивания:
Знать обозначения и определение логических операций
Задание 1. (И) Используя поисковую систему найдите определение и обозначения логическим операциям.
Оценивание : — Самооценивание. Отмечаем в листах самооценивания
— Взаимооценивание. оценка другой группе через комментарий **+ пожелание
Дескриторы :
Определяет логический элемент и обозначение
Определяет таблицу истинности
Записывает определение логической операции
Определяет логический элемент и обозначение
Использует
— предметную лексику : дизъюнкция, конъюнкция и инверсия;
— фразу для диалога :
К логическим функциям относятся…
4.2.1 строить логические схемы и логические выражения
Критерий оценивания:
Знать обозначения и определение логических операций
Задание 1. (И) Используя поисковую систему найдите определение и обозначения логическим операциям.
Оценивание : — Самооценивание. Отмечаем в листах самооценивания
— Взаимооценивание. оценка другой группе через комментарий **+ пожелание
Дескриторы :
Определяет логический элемент и обозначение
Определяет таблицу истинности
Записывает определение логической операции
Определяет логический элемент и обозначение
Использует
— предметную лексику : дизъюнкция, конъюнкция и инверсия;
— фразу для диалога :
К логическим функциям относятся…
Изображение слайда
6
Слайд 6
6 Элемент « Дизъюнктор » « ИЛИ» ( OR) Элемент « Конъюктор » «И » ( AND) Элемент «Инвертор» « НЕ» ( NOT)
Изображение слайда
7
Слайд 7
Цель обучения
9. 4.2.1 строить логические схемы и логические выражения
Критерий оценивания:
Уметь составлять таблицу истинности и строить схему по предложенному выражению
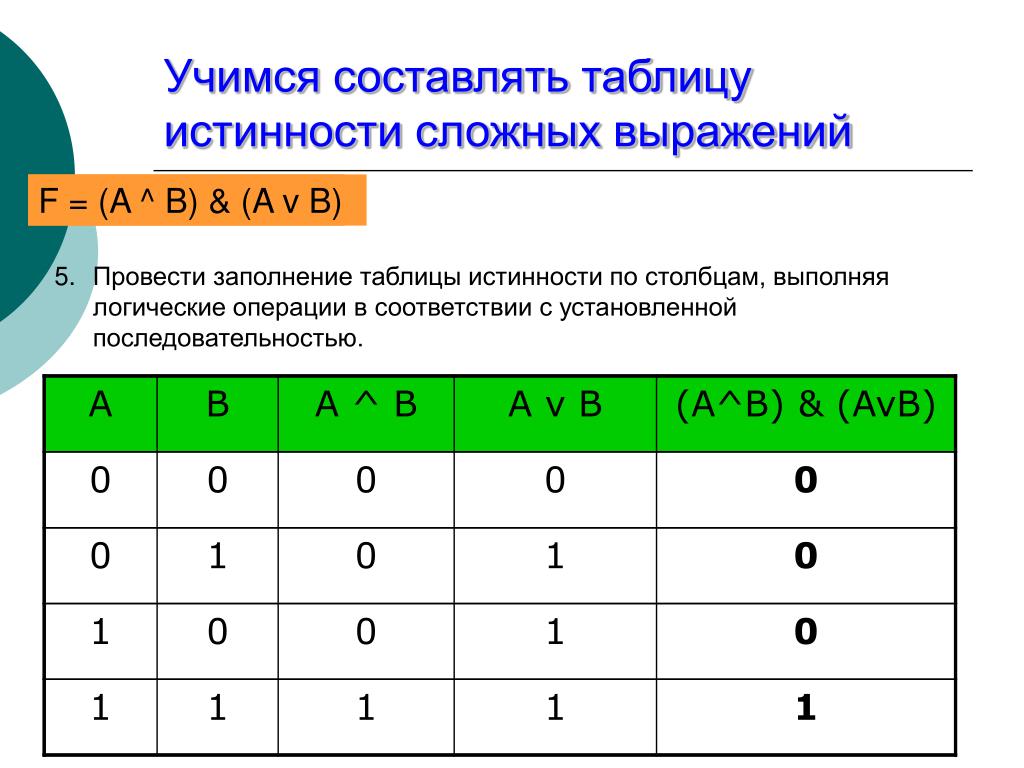
Задание 2. ( И,ф ) Построить таблицу истинности и логическую схему: (¬А v ¬ В) & С
Оценивание : — Самооценивание. Отмечаем в листах самооценивания
— Обратная связь учителя.
Дескриторы :
Правильно определил последовательность выполнения логических операции
Правильно заполнил таблицу истинности
Правильно построил схему
Проверил схему в онлайн симуляторе логических схем (www.logic.ly/ demo )
4.2.1 строить логические схемы и логические выражения
Критерий оценивания:
Уметь составлять таблицу истинности и строить схему по предложенному выражению
Задание 2. ( И,ф ) Построить таблицу истинности и логическую схему: (¬А v ¬ В) & С
Оценивание : — Самооценивание. Отмечаем в листах самооценивания
— Обратная связь учителя.
Дескриторы :
Правильно определил последовательность выполнения логических операции
Правильно заполнил таблицу истинности
Правильно построил схему
Проверил схему в онлайн симуляторе логических схем (www.logic.ly/ demo )
Изображение слайда
8
Слайд 8
Цель обучения
9.4.2.1 строить логические схемы и логические выражения
Критерий оценивания:
Составлять выражение и таблицу истинности исходя из логической схемы
Задание 3. ( И,ф ) По схеме напишите логическое выражение и постройте таблицу истинности.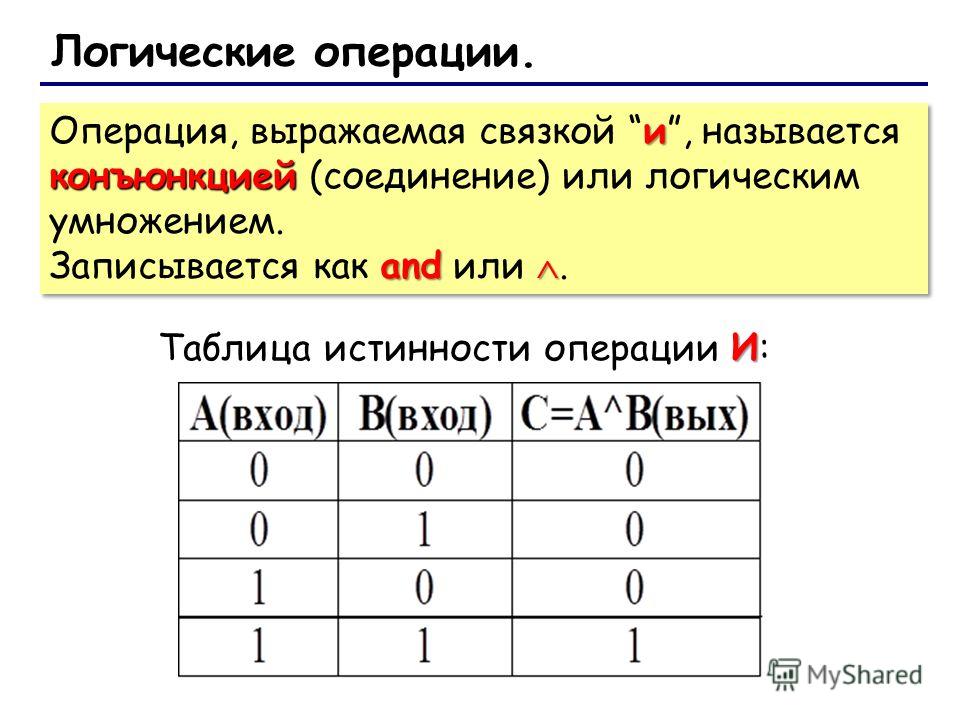 Оценивание : — Самооценивание. Отмечаем в листах самооценивания
— Обратная связь учителя.
Дескриторы :
Правильно записал логическое выражение
Правильно определил последовательность выполнения логических операции
Правильно заполнил таблицу истинности
Оценивание : — Самооценивание. Отмечаем в листах самооценивания
— Обратная связь учителя.
Дескриторы :
Правильно записал логическое выражение
Правильно определил последовательность выполнения логических операции
Правильно заполнил таблицу истинности
Изображение слайда
9
Слайд 9
Обозначьте своё мнение по изучению темы в свои индивидуальные листы
Изображение слайда
10
Слайд 10: Цели обучения
9.4.2.1 строить логические схемы и логические выражения Критерии оценивания Знать обозначения и определение логических операций Уметь составлять таблицу истинности и строить схему по предложенному выражению Составлять выражение и таблицу истинности исходя из логической схемы
Изображение слайда
11
Слайд 11
Изображение слайда12
Слайд 12
Изображение слайда
13
Слайд 13: Логические схемы и выражения
Раздел 9. 1А: Архитектура компьютера
суббота, 22 сентября 2018 г.
1А: Архитектура компьютера
суббота, 22 сентября 2018 г.
Изображение слайда
14
Слайд 14: Цели обучения
9.4.2.1 строить логические схемы и логические выражения Критерии оценивания Составлять выражение и таблицу истинности исходя из логической схемы
15
Слайд 15: Повторение тем
5 (мин)
Изображение слайда
16
Слайд 16: Знакомство с рубрикой
2 мин
Изображение слайда
17
Слайд 17: СОР «Архитектура компьютера»
20 мин
Изображение слайда
18
Слайд 18: (И) Поиграйте в игру Logic Gate Puzzler в онлайн режиме, составляя логические схемы и изучая логические операции https://goo.
 gl/iWsPqA
gl/iWsPqA
Изображение слайда
19
Слайд 19
Обозначьте своё мнение по изучению темы в свои индивидуальные листы
Изображение слайда
20
Слайд 20: Цели обучения
9.4.2.1 строить логические схемы и логические выражения Критерии оценивания Составлять выражение и таблицу истинности исходя из логической схемы
Изображение слайда
21
Последний слайд презентации: Что такое таблица истинности? Приведите примеры: Подведение итогов урока
Рефлексия
Изображение слайда
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Домашняя страница > Логика > Символика Логика > Логические связки | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
| Философия 103: Введение в логику Конъюнкция, отрицание и дизъюнкция Аннотация: Логические операции конъюнкции, отрицания и дизъюнкции (альтерации) обсуждаются относительно их табличных определений истинности.
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Присылайте исправления или предложения по адресу webmaster@philosophy. | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Аргументы | Язык | Заблуждения | Предложения | Силлогизмы | Перевод | Символический | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| . | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
ЛУЧШИЙ КАЛЬКУЛЯТОР ЛОГИЧЕСКОГО ОПЕРАТОРА? США 2022
Калькулятор логических операторов (LOC) — это онлайн-инструмент, который вычисляет логические операторы предложения. Его можно использовать для нахождения результата условных операторов и союзных предложений. Эта информация предоставляется вам, чтобы вы могли принимать более обоснованные решения и лучше понимать отношения между идеями в своем письме.
Мы хотим, чтобы вы могли сделать осознанный выбор в отношении того, что вы можете или не можете делать. Вы можете не соглашаться с выбором и методами, которые мы используем. Приносим искренние извинения за доставленные неудобства и будем работать с вами до тех пор, пока не достигнем удовлетворительного компромисса.
Вы можете связаться с нами в любой момент, когда будете готовы к диалогу, который намного продуктивнее спора. Мы надеемся, что каждый найдет это ценным ресурсом. Если вы обнаружите какие-либо проблемы, связанные с логикой и калькулятором . пожалуйста свяжитесь с нами.
(1) Если вы находитесь на начальной стадии планирования своего письма и еще не написали ни одного предложения, вы можете спросить себя, почему вы начинаете этот проект. Если ответ «научиться писать», то вы на правильном пути. Постоянной целью ВСЕХ писателей является рост и совершенствование своих навыков. Вы захотите вернуться к этой статье как можно скорее, чтобы внести коррективы там, где это необходимо.
(2) У писателей много вопросов. Если вы никогда раньше ничего не писали, то есть вероятность, что мы только знакомимся с вашими идеями. У нас есть способы сделать так, чтобы вы чувствовали себя более комфортно, чтобы вы не так нервничали по поводу письма, как сейчас. Мы используем различные методы, чтобы облегчить процесс начинающему писателю и помочь нам лучше узнать вас. Один из лучших способов — задавать вопросы, начинающиеся со слов «почему» и «что». Это называется активным залогом.
Статья по теме: Калькулятор гиперболы Easy Ways поможет вам добиться успеха в работе
(3) Задавая себе вопросы о процессе письма, вы не только поможете себе в долгосрочной перспективе, но и сможете писать и планировать все в однажды. Вы также можете задавать вопросы, чтобы упорядочить свой контент. Вот как вы тщательно выбираете слова. Вы можете использовать вопросы, чтобы написать черновой вариант своей статьи, а затем начать совершенствовать его на основе того, что вы узнали.
(4) Например, если вы пишете эссе о влиянии фильмов на нашу культуру, вы начнете писать с таких вопросов, как «Кто может повлиять на наши идеи?» и «где мы учимся этим идеям?» Опрос вашей аудитории также является еще одним важным аспектом. Вы захотите спросить себя, что их интересует, как вы можете удовлетворить их потребности и как лучше всего информировать их о вашей информации.
(5) Мы также хотим, чтобы вы использовали этот калькулятор как средство для получения отзывов обо всех ваших идеях, как связанных с темой, так и более личных идей. Мы постоянно получаем комментарии о том, что мы пишем, потому что никто не хочет быть единственным человеком, который думает, что контент достаточно хорош или не подходит для вашей аудитории.
Малоизвестные пути к ЛОГИЧЕСКОМУ ОПЕРАТОРУ КАЛЬКУЛЯТОР?Во многих случаях вам понадобится логический калькулятор
. Например, в компьютер вашего автомобиля будет встроен калькулятор, который автоматически сделает за вас математические расчеты. Это одна из причин, по которой в большинстве автомобилей есть простой калькулятор и почему он есть, например, в вашем телефоне. В настоящее время калькуляторы представляют собой универсальные машины, которые выполняют множество различных вычислений одновременно.
Это одна из причин, по которой в большинстве автомобилей есть простой калькулятор и почему он есть, например, в вашем телефоне. В настоящее время калькуляторы представляют собой универсальные машины, которые выполняют множество различных вычислений одновременно.
Калькуляторы могут использоваться как студентами, так и профессионалами практически во всех профессиях и ситуациях, связанных с математикой. Когда вам нужно сделать быстрые математические вычисления, калькулятор — ваш лучший друг.
Видите ли, не в любой ситуации: Вы хотите получить максимально точные результаты. Например, если вы занимаетесь финансовым планированием или подсчитываете свой банковский счет, вам нужен калькулятор, который может обрабатывать все это и многое другое. Возможно, вы захотите использовать его и для своей работы. Если это так, правильный калькулятор сделает все ваши расчеты намного проще и точнее. Многие калькуляторы могут принимать практически любую информацию, которую вы хотите ввести, и преобразовывать ее в числа. Это делает их очень полезными для решения арифметических задач. Вы даже можете использовать их, чтобы вернуть числам их первоначальную форму после их предварительного преобразования. Если вы ищете хороший калькулятор, вам следует обратить внимание на несколько вещей. К ним относятся количество кнопок на калькуляторе, тип устройств ввода и вывода и простота использования.
Это делает их очень полезными для решения арифметических задач. Вы даже можете использовать их, чтобы вернуть числам их первоначальную форму после их предварительного преобразования. Если вы ищете хороший калькулятор, вам следует обратить внимание на несколько вещей. К ним относятся количество кнопок на калькуляторе, тип устройств ввода и вывода и простота использования.
В письменной форме все дело в редактировании. Редактирование является такой же частью написания, как и написание статьи. На самом деле, вы не сможете написать первый черновик, пока не отредактируете статью много раз. И это редактирование просто означает больше, чем переформулирование предложений или добавление отсутствующих идей как таковых: это также означает выявление лучших частей вашей статьи, отбрасывая плохие и заставляя все ваши идеи работать вместе, а не бороться друг с другом.
Калькулятор логических операторов поможет вам ответить на любые ваши вопросы, используя логические операторы. Логические операторы можно использовать в комбинациях, чтобы помочь вам ответить на ваши вопросы. Отдельные логические операторы используются для управления данными, извлекаемыми из трех источников: полей (столбцов), записей (строк) и таблиц.
Логические операторы можно использовать в комбинациях, чтобы помочь вам ответить на ваши вопросы. Отдельные логические операторы используются для управления данными, извлекаемыми из трех источников: полей (столбцов), записей (строк) и таблиц.
Калькулятор также поможет вам в решении проблемы, познакомив вас с тем, как работают функции. Функции выполняют определенное действие над ячейкой или диапазоном ячеек на листе. Они могут работать с числами, текстом, датами или формулами и помогут вам получить именно тот результат, который вы хотите.
Логика, простые и составные утверждения, логические операции и таблицы истинности, условные утверждения и доказательства Экзаменационные уроки
СОДЕРЖАНИЕ
— Значение простых и составных утверждений.
– Логические операции и таблицы истинности.
— Условные заявления и косвенные доказательства.
ПРОСТЫЕ И СЛОЖНЫЕ ПРЕДЛОЖЕНИЯ
Предлог – это утверждение или предложение, которое либо истинно, либо ложно, но не то и другое одновременно. Мы будем использовать заглавные буквы английского алфавита, такие как A, B, C, D, P, Q, R, S, …, для обозначения простых утверждений или предлогов. Простое высказывание или предложение — это высказывание, не содержащее связок. Другими словами, предложение считается простым, если оно не может быть разбито на подпредложения. С другой стороны, сложное предложение состоит из двух или более предложений, соединенных связками. Этими связками являются и, или, если… то, тогда и только тогда, когда. Их также называют логическими операторами. В таблице ниже показаны логические операторы и их символы. 9
Мы будем использовать заглавные буквы английского алфавита, такие как A, B, C, D, P, Q, R, S, …, для обозначения простых утверждений или предлогов. Простое высказывание или предложение — это высказывание, не содержащее связок. Другими словами, предложение считается простым, если оно не может быть разбито на подпредложения. С другой стороны, сложное предложение состоит из двух или более предложений, соединенных связками. Этими связками являются и, или, если… то, тогда и только тогда, когда. Их также называют логическими операторами. В таблице ниже показаны логические операторы и их символы. 9
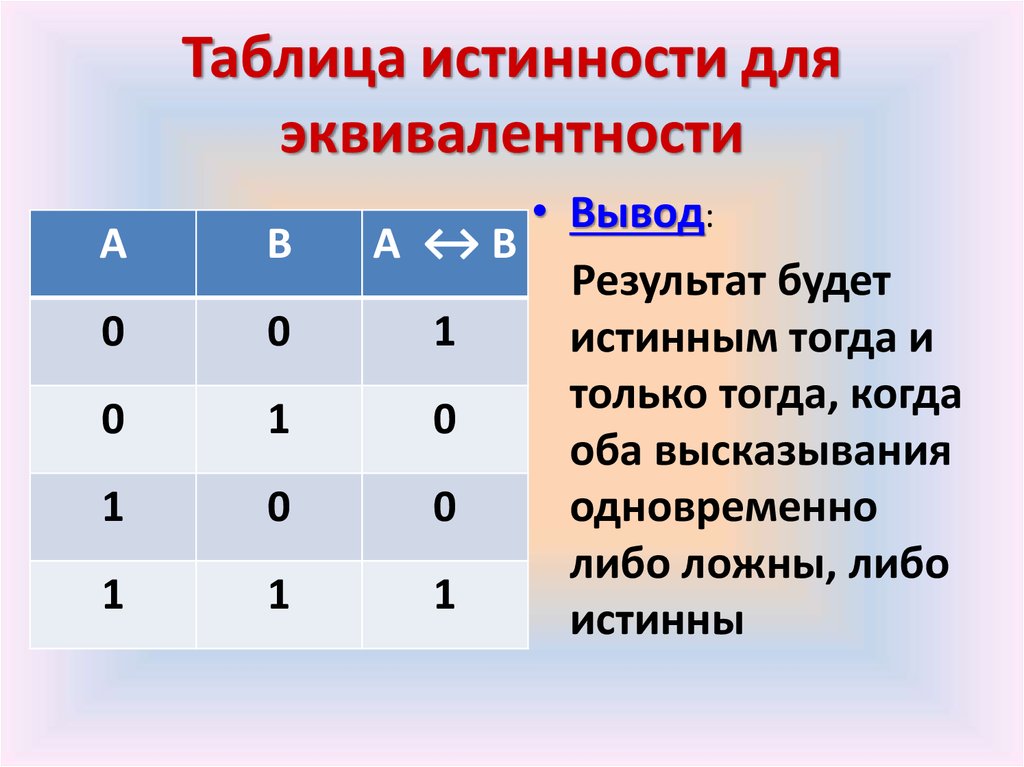 Q означает P и Q.
Q означает P и Q.Таблицы истинности
Истинность или ложность предложения есть его истинностное значение, т.е. Истинное предложение имеет значение истинности T, а ложное предложение имеет значение истинности F. Таблицы истинности для логических операторов приведены ниже.
Рисунок 2
| P | ~ P |
| T | F |
| F | T |
| F | T |
| I ITRAIN) I ITRAN) I ITRAVE) I ITRAVER) ITRAIN 7. Обратное, обратное и контрапозитивное — условные и биусловные операторы, логика, геометрияОбратное условного утверждения «если P, то Q» — это условное утверждение «если Q, то P», т. е. обращение P⇒ Q есть Q ⇒ P. Обратное утверждение Обратное условному утверждению «если P, то Q» является условным утверждением «если не P, то не Q». , т. е. обратное P ⇒ Q равно ∼P ⇒ ∼Q. Противоположное высказывание Обратным условному высказыванию «если P, то Q» является условное высказывание «если не Q, то не P». , то есть контрапозитив P ⇒ Q составляет ∼P, щула P Логические операции и таблицы истинности com=»» category=»» mathematics-olevel=»»> Tautology и Compladication 0 Tautology и Contradication 0 . составляющих его утверждений, это называется тавтологией . С другой стороны, когда предложение всегда ложно, оно называется противоречием . ЦЕПОЧНОЕ ПРАВИЛОЦепное правило гласит, что если X, Y и Z такие утверждения, что X ⇒ Y и Y ⇒ Z, то X ⇒ Z. цепочка утверждений может иметь столько звеньев ‘ по мере необходимости. Пример 5 является примером цепного правила. При использовании правила цепочки. Важно, чтобы стрелки импликации указывали в одном направлении. Например, не имеет большой ценности иметь что-то вроде X ⇒ Q ⇐ R, потому что из этого нельзя сделать никаких полезных выводов. Пример В следующем рассуждении определите, обязательно ли следует вывод из данных посылок. Все водители осторожны. (1 ST Premise) Осторожные люди — терпеливые (2 и предпосылка) Следовательно, все водители являются терпеливыми (заключение) , если D: люди, которые являются драйверами C: люди, которые являются осторожными P: водители C: : терпеливые люди , затем D ⇒ C (1 -я предпосылка) и Cth (2 nd ) , если D ⇒ C и C ⇒ P , затем D ⇒ P (цепное правило) помещение. УСЛОВНЫЕ ЗАЯВЛЕНИЯ И КОСВЕННЫЕ ДОКАЗАТЕЛЬСТВА. |

 Выражения для упрощения записи обозначают латинскими буквами A, B, C.
Выражения для упрощения записи обозначают латинскими буквами A, B, C.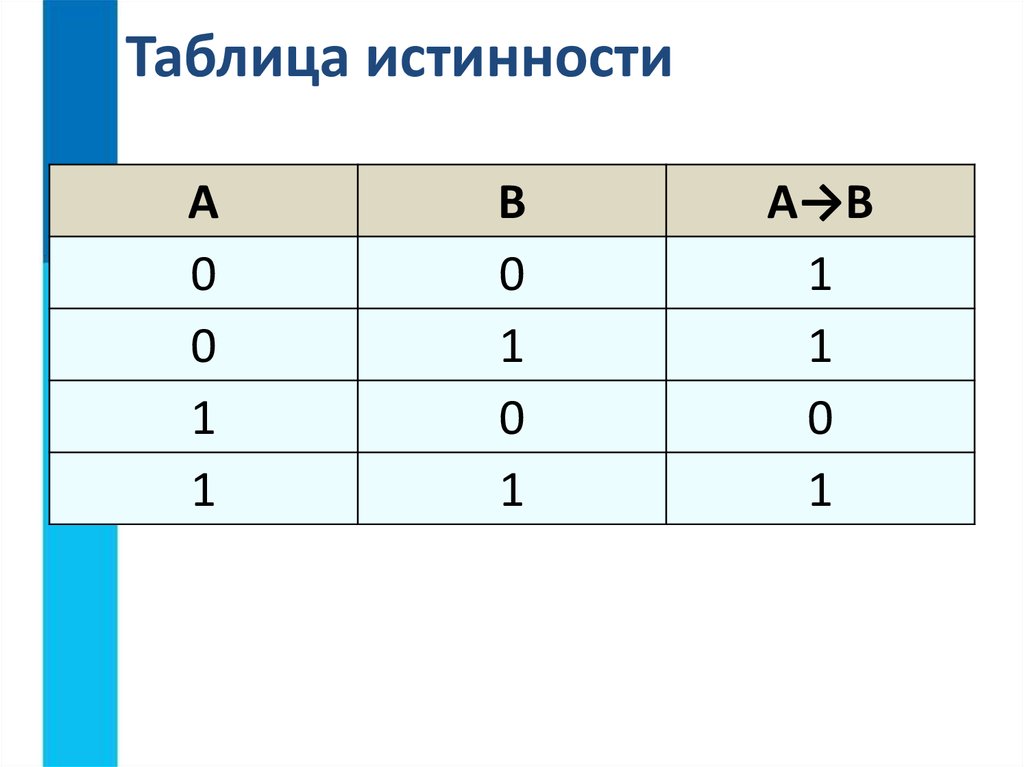
 lander.edu
lander.edu 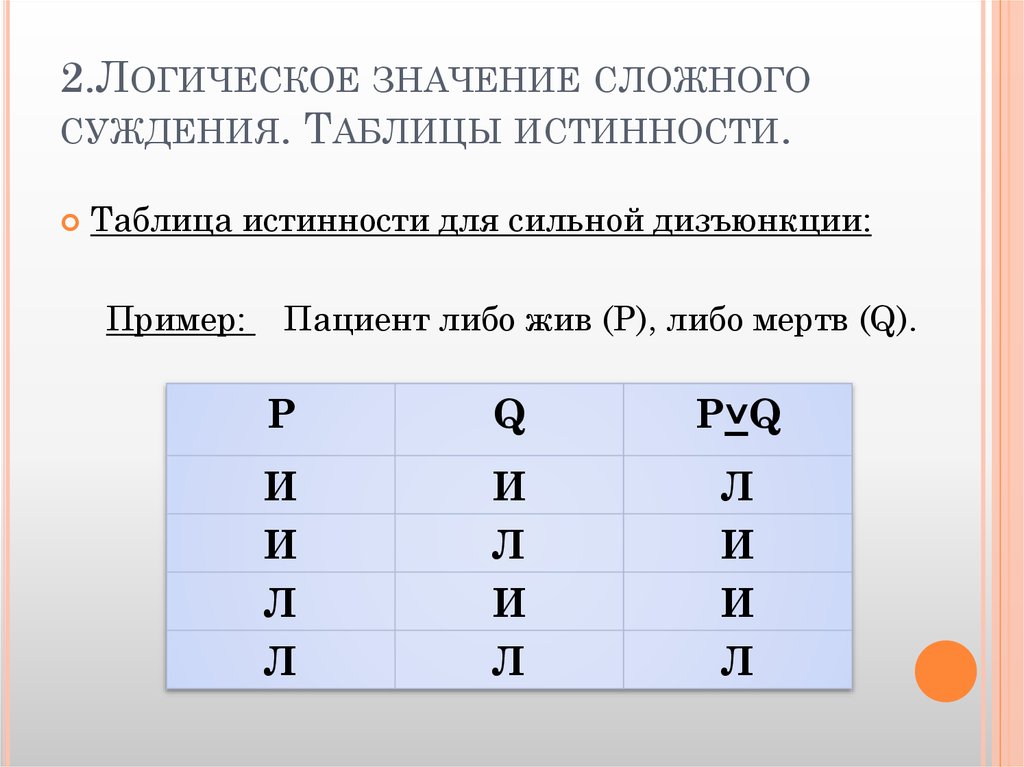
 Эти случаи могут быть
перечислены ниже в том, что называется таблица истинности .
Эти случаи могут быть
перечислены ниже в том, что называется таблица истинности .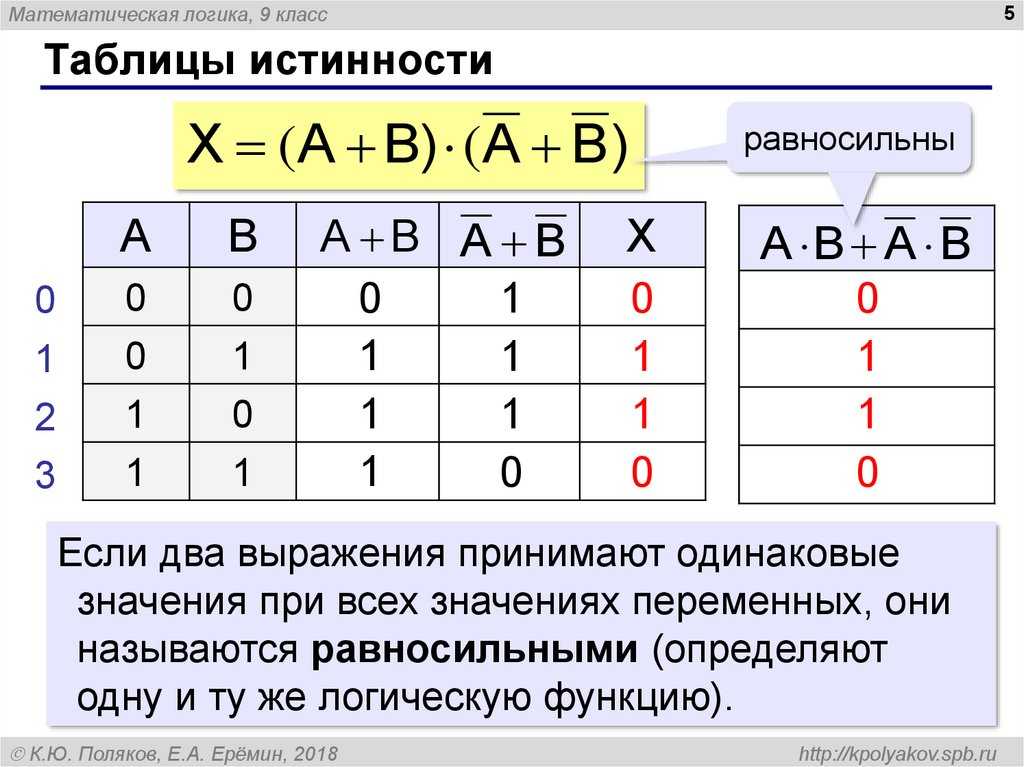 Его можно рассматривать как «минимальный
общий логический смысл» для соединенных утверждений.
Его можно рассматривать как «минимальный
общий логический смысл» для соединенных утверждений.
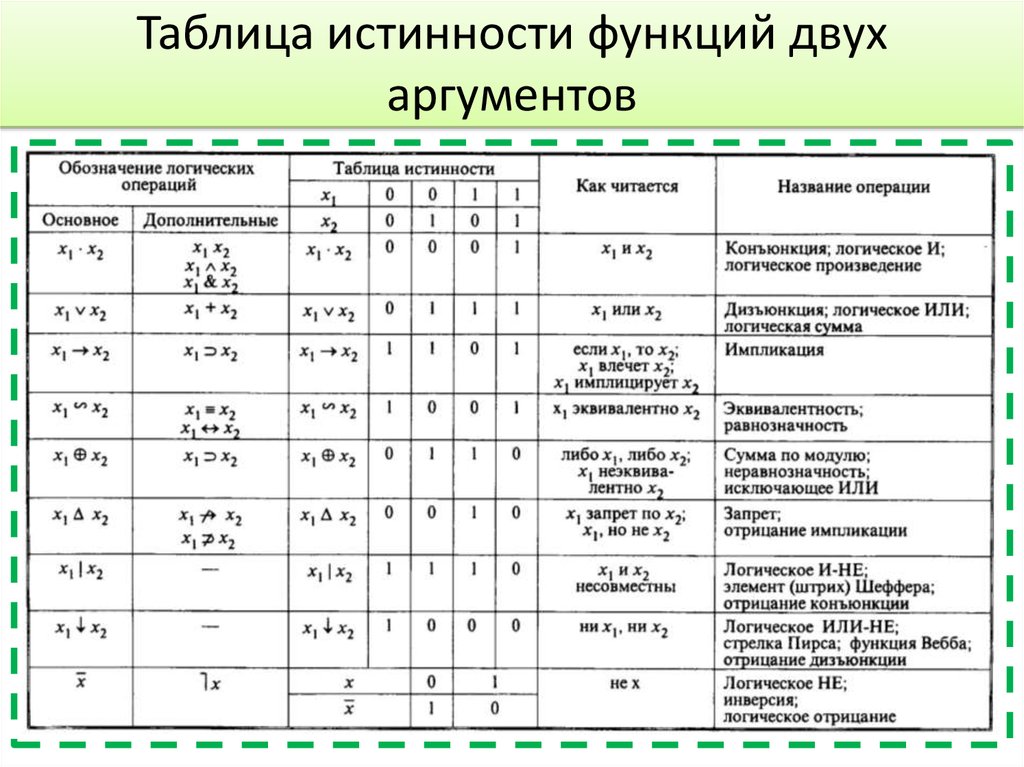 которые ложны, только если оба утверждения (дизъюнкты) ложны.
которые ложны, только если оба утверждения (дизъюнкты) ложны.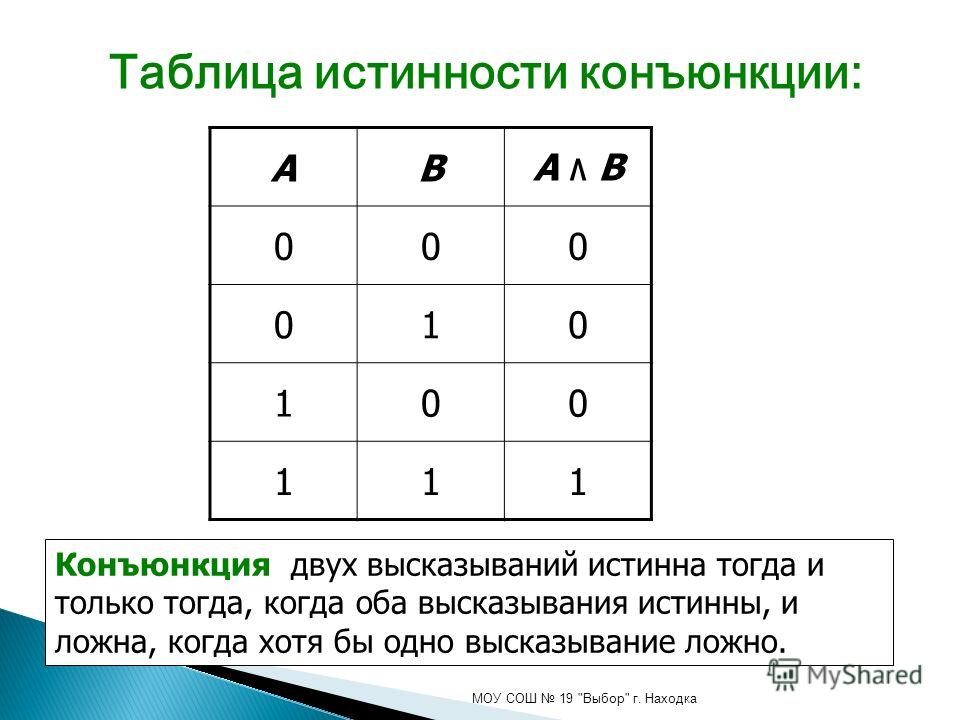 » Если в этом примере Джон не на
библиотека и Джон не учится, то истинность сложного утверждения
неверно:
» Если в этом примере Джон не на
библиотека и Джон не учится, то истинность сложного утверждения
неверно: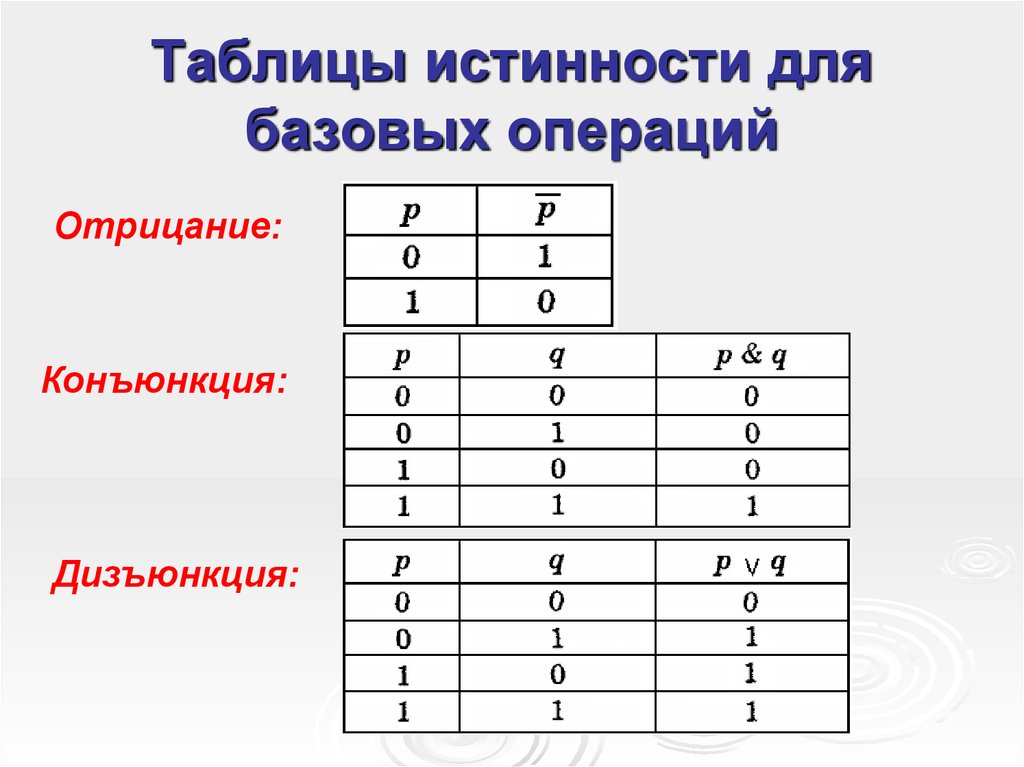
 lander.edu
lander.edu 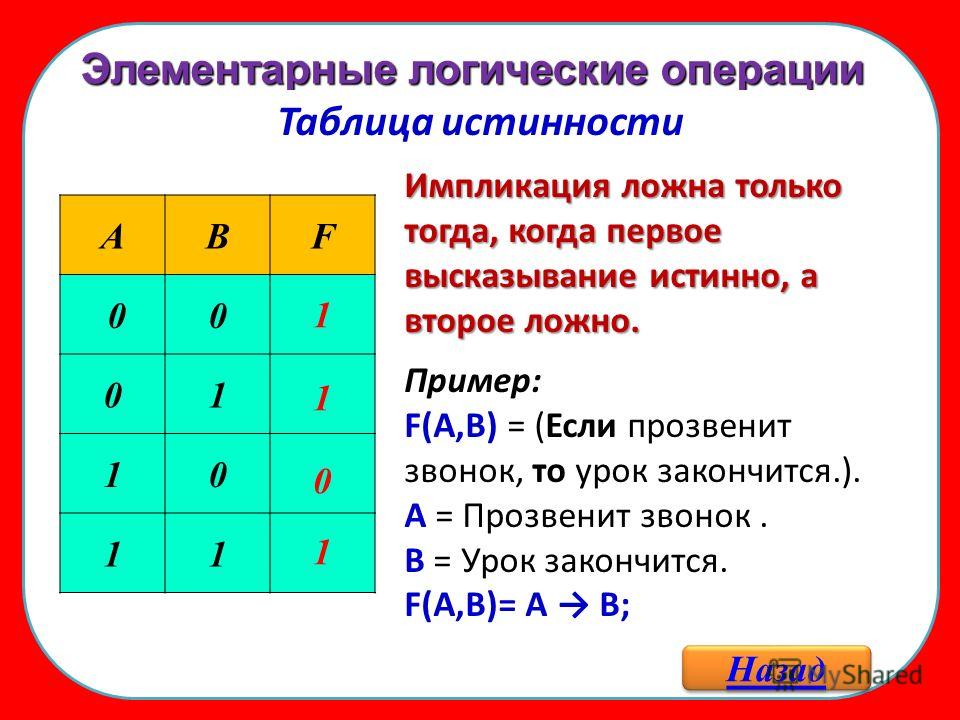 и если P ложно, то ~P истинно.
и если P ложно, то ~P истинно.
