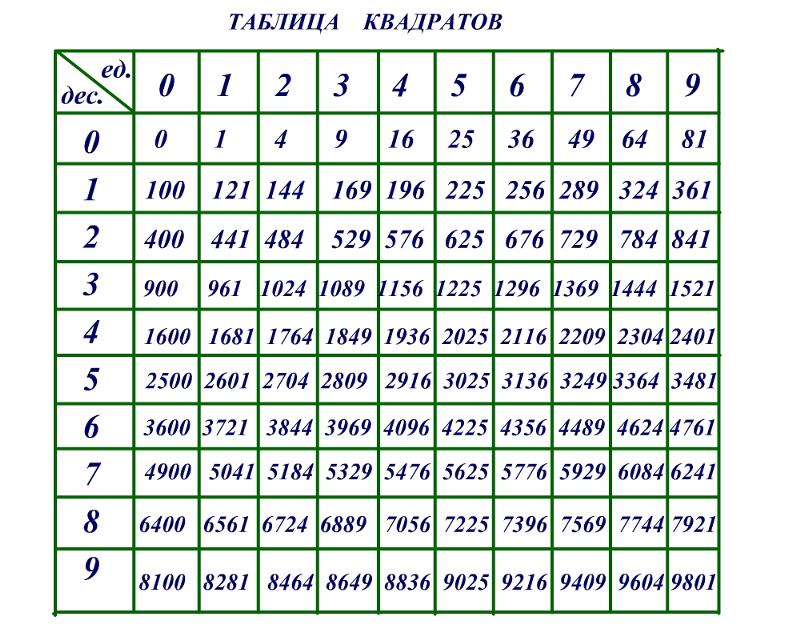
Таблица степеней от 1 до 10 по алгебре для 7 класса: распечатать в хорошем качестве
В начальной школе мы учили наизусть таблицу умножения, но давайте зайдем немного дальше и узнаем о таблице степеней от 1 до 10. Мы расскажем, как ей пользоваться и что с ее помощью можно сделать
Таблица степеней от 1 до 10 по алгебре. Фото: MART PRODUCTION, pixals.comНаталия Юмагулова Учитель математики
Содержание
- Как пользоваться
- Задачи
- Вопросы и ответы
Сложение, вычитание, деление и умножение — первые арифметические действия, которые ученики начинают изучать в школе. С погружением в познание математики учителя начинают знакомить школьников с возведением чисел в степень. Для простоты понимания этой темы математики разработали таблицу степеней. В статье расскажем, как применять ее на практике, но для начала вспомним немного теории.
Для простоты понимания этой темы математики разработали таблицу степеней. В статье расскажем, как применять ее на практике, но для начала вспомним немного теории.
Возведение числа в степень — произведение нескольких равных множителей. Есть и более простое определение — многократное умножение числа на себя: an, где a — основание, n — показатель степени.
Важно!
Возведение числа в степень — произведение нескольких равных множителей.
Рассмотрим пример:
32 = 3 × 3 = 9
3 — основание, 2 — показатель степени
Чтобы решить эту задачу, нам необходимо число 3 умножить само на себя 2 раза.
А вот другая задача — найдите значение выражения: 78. Здесь арифметическое действие становится довольно длительным. Мы не сомневаемся, что вы справитесь с умножением числа 7 самого на себя 8 раз, но с помощью таблицы степеней вы справитесь в один миг.
Как пользоваться таблицей степеней
Пользоваться таблицей степеней очень просто. Например, нам необходимо посчитать 78. В 1-м столбце находим число, которое нужно возвести в степень, — 7С. В 1-й строке ищем показатель степени — 8. Ответ смотрим на пересечении столбца и строки и получаем ответ: 78 = 5764801. Для удобства таблицу можно скачать и пользоваться ею при подготовке к ЕГЭ по математике.
Например, нам необходимо посчитать 78. В 1-м столбце находим число, которое нужно возвести в степень, — 7С. В 1-й строке ищем показатель степени — 8. Ответ смотрим на пересечении столбца и строки и получаем ответ: 78 = 5764801. Для удобства таблицу можно скачать и пользоваться ею при подготовке к ЕГЭ по математике.
Задачи с использованием таблицы степеней
Задача №1
Найдите значение выражения:
84 × 83
Упростим выражение, используя свойство умножения степеней, а затем с помощью таблицы получим ответ:
84 × 83 = 84+3 = 87 = 2097152
Задача №2
Найдите значение выражения:
493
Основание 49 заменим на основание 7, так как 49 = 72. Применим свойство возведения степени в степень и данные таблицы:
493 = (72)3 = 76 = 117649
Задача №3
Решите уравнение:
х5 = 59049
х5 = 95
х = 9
Ответ: х = 9
это интересно
Свойства степеней
Изучаем формулы, приводим примеры и доказательства
подробнее
Популярные вопросы и ответы
Почему таблицу степеней изучают на алгебре в 7-м классе?
Так как программа 7-го класса по алгебре включает в себя понятие степени и все, что с ним связано.
Зачем нужна таблица степеней?
Таблица степеней нужна для экономии времени при выполнении громоздких вычислений.
Где в повседневной жизни можно использовать таблицу степеней?
В информатике: если использовать таблицу степеней двойки, то перевод в десятичную систему счисления целых двоичных чисел будет значительно проще. Таблица степеней десяти используется для записи и вычислений больших величин, измерений, расстояний в химии, географии и физике. Например: площадь Земли равна 510 × 106 км2.
Таблица степеней по Алгебре (от 1 до 10; от 2 до 20)
Главная / Математика / Таблицы степеней по Алгебре
Таблица степеней от 1 до 10
| Xn | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 |
| 2 | 2 | 4 | 8 | 16 | 32 | 64 | 128 | 256 | 512 | 1024 |
| 3 | 3 | 9 | 27 | 81 | 243 | 729 | 2187 | 6561 | 19683 | 59049 |
| 4 | 4 | 16 | 64 | 256 | 1024 | 4096 | 16384 | 65536 | 262144 | 1048576 |
| 5 | 5 | 25 | 125 | 625 | 3125 | 15625 | 78125 | 390625 | 1953125 | 9765625 |
| 6 | 6 | 36 | 216 | 1296 | 7776 | 46656 | 279936 | 1679616 | 10077696 | 60466176 |
| 7 | 7 | 49 | 343 | 2401 | 16807 | 117649 | 823543 | 5764801 | 40353607 | 282475249 |
| 8 | 8 | 64 | 512 | 4096 | 32768 | 262144 | 2097152 | 16777216 | 134217728 | 1073741824 |
| 9 | 9 | 81 | 729 | 6561 | 59049 | 531441 | 4782969 | 43046721 | 387420489 | 3486784401 |
| 10 | 10 | 100 | 1000 | 10000 | 100000 | 1000000 | 10000000 | 100000000 | 1000000000 | 10000000000 |
Таблица степеней от 2 до 20
|
Xn |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
|
2 |
4 |
8 |
16 |
32 |
64 |
128 |
256 |
512 |
1 024 |
|
3 |
9 |
27 |
81 |
243 |
729 |
2 187 |
6 561 |
19 683 |
59 049 |
|
4 |
16 |
64 |
256 |
1 024 |
4 096 |
16 384 |
65 536 |
262 144 |
1 048 576 |
|
5 |
25 |
125 |
625 |
3 125 |
15 625 |
78 125 |
390 625 |
1 953 125 |
9 765 625 |
|
6 |
36 |
216 |
1 296 |
7 776 |
46 656 |
279 936 |
1 679 616 |
10 077 696 |
60 466 176 |
|
7 |
49 |
343 |
2 401 |
16 807 |
117 649 |
823 543 |
5 764 801 |
40 353 607 |
282 475 249 |
|
8 |
64 |
512 |
4 096 |
32 768 |
262 144 |
2 097 152 |
16 777 216 |
134 217 728 |
1 073 741 824 |
|
9 |
81 |
729 |
6 561 |
59 049 |
531 441 |
4 782 969 |
43 046 721 |
387 420 489 |
3 486 784 401 |
|
10 |
100 |
1 000 |
10 000 |
100 000 |
1 000 000 |
10 000 000 |
100 000 000 |
1 000 000 000 |
10 000 000 000 |
|
11 |
121 |
1 331 |
14 641 |
161 051 |
1 771 561 |
19 487 171 |
214 358 881 |
2 357 947 691 |
25 937 424 601 |
|
12 |
144 |
1 728 |
20 736 |
248 832 |
2 985 984 |
35 831 808 |
429 981 696 |
5 159 780 352 |
61 917 364 224 |
|
13 |
169 |
2 197 |
28 561 |
371 293 |
4 826 809 |
62 748 517 |
815 730 721 |
10 604 499 373 |
137 858 491 849 |
|
14 |
196 |
2 744 |
38 416 |
537 824 |
7 529 536 |
105 413 504 |
1 475 789 056 |
20 661 046 784 |
289 254 654 976 |
|
15 |
225 |
3 375 |
50 625 |
759 375 |
11 390 625 |
170 859 375 |
2 562 890 625 |
38 443 359 375 |
576 650 390 625 |
|
16 |
256 |
4 096 |
65 536 |
1 048 576 |
16 777 216 |
268 435 456 |
4 294 967 296 |
68 719 476 736 |
1 099 511 627 776 |
|
17 |
289 |
4 913 |
83 521 |
1 419 857 |
24 137 569 |
410 338 673 |
6 975 757 441 |
118 587 876 497 |
2 015 993 900 449 |
|
18 |
324 |
5 832 |
104 976 |
1 889 568 |
34 012 224 |
612 220 032 |
11 019 960 576 |
198 359 290 368 |
3 570 467 226 624 |
|
19 |
361 |
6 859 |
130 321 |
2 476 099 |
47 045 881 |
893 871 739 |
16 983 563 041 |
322 687 697 779 |
6 131 066 257 801 |
|
20 |
400 |
8 000 |
160 000 |
3 200 000 |
64 000 000 |
1 280 000 000 |
25 600 000 000 |
512 000 000 000 |
10 240 000 000 000 |
Администратор 39004 просмотра
Теги: степень, алгебра
Комментарии 2
0 Георгий #
17 января 2021 в 16:54
Спасибо большое!
Ответить
0 абдулох #
17 ноября 2022 в 07:58
норм
Ответить
Использование таблиц — эффективная стратегия обучения алгебре
Будучи учителями математики в старших классах, мы часто сталкиваемся с ситуациями, когда ученики не понимают, что они изучают. Они часто не понимают, как то, чему мы учим, связано с тем, что они узнали раньше, или даже почему это правда. Предвидя эти опасения, мы создаем на наших уроках возможности для учащихся использовать структуру (важный навык в математических стандартах Common Core) для связи с математическими идеями.
Они часто не понимают, как то, чему мы учим, связано с тем, что они узнали раньше, или даже почему это правда. Предвидя эти опасения, мы создаем на наших уроках возможности для учащихся использовать структуру (важный навык в математических стандартах Common Core) для связи с математическими идеями.
Мы регулярно используем таблицы или организационные схемы, чтобы помочь учащимся распознавать структуру и использовать ее для решения задач. Таблицы — особенно мощный инструмент для обучения алгебре, поскольку большинству студентов сложно освоить абстрактные обозначения, используемые в курсе. Таблицы помогают учащимся связать два набора информации (основная математическая задача) и организовать свое мышление. В этой статье мы опишем два эффективных способа использования таблиц в алгебре.
Модель площади
Методы умножения и деления чисел, которые обычно преподают в начальной школе («вертикальный» метод и деление в длинную), имеют несколько проблем. Во-первых, они не похожи друг на друга, хотя умножение и деление являются обратными операциями. Шаги в этих процедурах не имеют значения («сбить число», «перенести два», «переместиться на одно место»). И эти методы не укрепляют идею разрядности, которая является основной темой базовой математики.
Шаги в этих процедурах не имеют значения («сбить число», «перенести два», «переместиться на одно место»). И эти методы не укрепляют идею разрядности, которая является основной темой базовой математики.
Дальнейшие проблемы возникают в алгебре, когда учащиеся работают с многочленами, такими как x 2 + 4 x + 2, которые расширяют понятие разрядного значения. Хотя в алгебре можно использовать вертикальный метод и длинное деление, учащиеся также изучают сокращения, которые совсем не похожи на то, что они изучали раньше. К сожалению, такие упрощения побуждают учащихся думать, что математика — это всего лишь набор трюков.
Мы предпочитаем учить площадную модель умножения и деления, потому что она позволяет учащимся связать понятия, которые они изучили в начальной школе, с тем, что они узнают позже. Поскольку модель площади основана на идее, что площадь прямоугольника является произведением его длины и ширины, она связывает алгебру с геометрией, позволяя учащимся визуализировать алгебраический процесс. В таблице ниже модель площади сравнивается с более традиционными методами умножения и деления:
В таблице ниже модель площади сравнивается с более традиционными методами умножения и деления:
Предоставлено Бобсоном Вонгом и Ларисой Букаловой
Учащиеся более четко определяют математическую структуру с моделью площади. Это показывает им связь между умножением и делением, потому что учащимся даны разные части одного и того же прямоугольника, и им нужно найти то, чего не хватает. Кроме того, они видят, что умножение выражений с переменными аналогично умножению и делению чисел.
Мы также используем площадную модель для решения квадратных уравнений, переменная которых возведена во вторую степень. Большинство студентов используют устрашающую «квадратичную формулу» или метод под названием «заполнение квадрата», который имеет, казалось бы, произвольные шаги («взять половину среднего члена и возвести его в квадрат»). Напротив, модель площади показывает, почему заполнение квадрата носит такое название: учащиеся рисуют неполный квадрат, а затем находят число (в данном случае 9).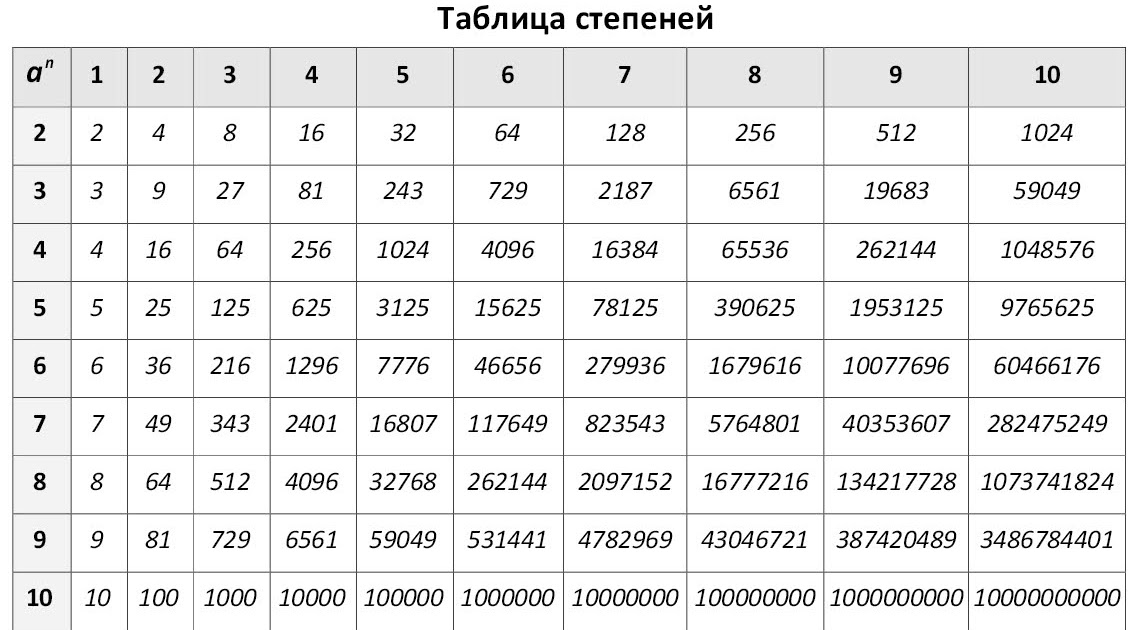 ), который завершает квадрат, как показано на следующей диаграмме:
), который завершает квадрат, как показано на следующей диаграмме:
Предоставлено Бобсоном Вонгом и Ларисой Букалов
Завершение квадрата затрагивает зрительную память учащихся. Это не только позволяет им легче запоминать шаги, но и помогает им понять почему этот процесс работает. Это укрепляет их математическое понимание.
Решение текстовых задач
Многим учащимся трудно понять, как преобразовать слова в математические символы, особенно в таких задачах, как эта: «У Хуаниты есть сумка, в которой только десять центов и пятицентовики. Количество пятаков на 5 меньше, чем удвоенное количество десятицентовиков. Общая стоимость монет в ее сумке составляет 1,9 доллара.5. Определить количество десятицентовиков и пятицентовиков в ее сумке».
Студенты могут прибегнуть к утомительному словесному описанию, которое объясняет каждую часть уравнения, необходимого для решения этой задачи. Напротив, написание таблицы позволяет учащимся легче и четче организовать свою информацию. Из последнего столбца таблицы они могут вывести уравнение 10 d + 5(2 d − 5) = 195, как показано здесь:
Из последнего столбца таблицы они могут вывести уравнение 10 d + 5(2 d − 5) = 195, как показано здесь:
Предоставлено Бобсоном Вонгом и Ларисой Букаловой
Одним из наших любимых применений таблиц является их использование для решения текстовых задач, связанных с вероятностью, таких как следующая: «На книжной полке в классе стоит 10 книг, каждая из которых имеет цвет (красный или зеленый) и переплет (твердый переплет). или нет). Шесть книг в твердом переплете, 7 в красном и 4 в красном и в твердом переплете. Учитель случайным образом выбирает одну книгу с полки. Найдите вероятность того, что книга будет в твердом переплете, если книга красного цвета».
Это можно решить, используя формулу условной вероятности, которая имеет загадочные символы, такие как Р ( А | Б ). Организовав данную информацию в таблицу, учащиеся находят вероятность, определяя соответствующие числа из таблицы:
Предоставлено Бобсоном Вонгом и Ларисой Букаловой
Создание таблицы демистифицирует процесс перевода слов в математические символы, что приносит пользу все студентов.
По мере того, как учащиеся привыкают к систематизации информации в виде таблиц, они улучшают свою способность выражать математические идеи. Поскольку таблицы могут быть включены во множество различных математических тем, они укрепляют предыдущие знания и повышают уверенность учащихся. Использование таблиц также укрепляет справедливость, делая сложные математические концепции более доступными.
1.2 Типы таблиц | Matrix Algebra Companion for Statistical Learning (matrix4sl)
Наиболее типичным форматом таблицы является формат отдельных лиц (строки) и переменных (столбцы). Однако компоновка индивидуальных переменных — не единственный тип настройки; существуют и другие типы таблиц, такие как таблицы непредвиденных обстоятельств, перекрестные таблицы, таблицы расстояний, а также таблицы подобия и близости. Итак, давайте рассмотрим несколько примеров различных прямоугольных форматов.
1.2.1 Неоднородные Таблица
Возможно, наиболее распространенным типом таблиц являются таблицы индивидуумов и переменных, в которых переменные представляют смешанную или разнородную информацию. Данные игрушек, представленные до сих пор, являются примером разнородной таблицы, включающей различные разновидности переменных, таких как имя, пол, рост и вес. Другими словами, Имя и Пол имеют строковые значения или категории, а Рост и Вес имеют числовые значения (представляющие количество).
Данные игрушек, представленные до сих пор, являются примером разнородной таблицы, включающей различные разновидности переменных, таких как имя, пол, рост и вес. Другими словами, Имя и Пол имеют строковые значения или категории, а Рост и Вес имеют числовые значения (представляющие количество).
Рисунок 1.6: Смешанные или разнородные переменные
Как вы видите, рост и вес уже выражены в числовых значениях, и вы можете выполнять над ними некоторые математические операции (например, применять арифметические и алгебраические операции). Напротив, Имя и Пол не кодируются в числовом виде, поэтому тип математических операций, которые вы можете выполнять с ними, очень ограничен. Чтобы использовать их информацию в более глубоком смысле, вам придется преобразовать категории мужчин и женщин с некоторым числовым кодированием.
1.2.2 Двоичная таблица
Другим распространенным типом таблицы является двоичная таблица. Как видно из названия, этот тип таблицы содержит переменные, которые могут принимать только два значения. Например, присутствие-отсутствие, женщина-мужчина, да-нет, успех-неудача, случай-контроль и т. д. В таблице ниже переменные представляют потребляемые напитки: пиво, вино, сок, кофе и чай. Каждая переменная принимает два возможных значения: да и нет , что указывает на то, употребляет ли человек определенный тип напитка.
Например, присутствие-отсутствие, женщина-мужчина, да-нет, успех-неудача, случай-контроль и т. д. В таблице ниже переменные представляют потребляемые напитки: пиво, вино, сок, кофе и чай. Каждая переменная принимает два возможных значения: да и нет , что указывает на то, употребляет ли человек определенный тип напитка.
Рисунок 1.7: Двоичная таблица (необработанные значения)
Хотя значения yes и no очень информативны, вам потребуется кодировать их численно, чтобы иметь возможность выполнять с ними статические или алгебраические операции. Возможно, наиболее естественным способом кодирования двоичных значений является использование нулей и единиц: «да» = 1, а «нет» = 0.
Рисунок 1.8: Двоичная таблица (числовые значения)
Другой возможной кодировкой может быть «да» = 1 и «нет» = -1. Или также с логическими значениями: «да» = ИСТИНА, а «нет» = ЛОЖЬ.
1.2.3 Таблица модальностей
Другой тип таблицы состоит из так называемых модальностей . Они могут исходить из переменных или вопросов в опросе о том, как часто вы используете/потребляете определенный продукт.
Они могут исходить из переменных или вопросов в опросе о том, как часто вы используете/потребляете определенный продукт.
Рисунок 1.9: Таблица модальностей (необработанные значения)
Для статистической обработки таблицы модальностей вам, скорее всего, придется преобразовать значения категорий (то есть модальностей) в числовое кодирование. Например, вы можете присвоить значения 1 = «никогда», 2 = «иногда» и 3 = «всегда».
Рисунок 1.10: Таблица модальностей (числовые значения)
1.2.4 Таблица предпочтений
Таблица предпочтений – это частный случай таблицы индивидуальных переменных, в которой переменные измеряются в некоторой шкале предпочтений. Например, мы можем измерить уровень предпочтения различных видов фруктовых соков по порядковой шкале от 1 = «совсем не нравится» до 5 = «очень нравится».
Рисунок 1.11: Таблица частот
1.2.5 Таблица частот
Как следует из названия, этот тип таблицы содержит частоты (т. е. числа), полученные в результате пересечения двух категориальных переменных.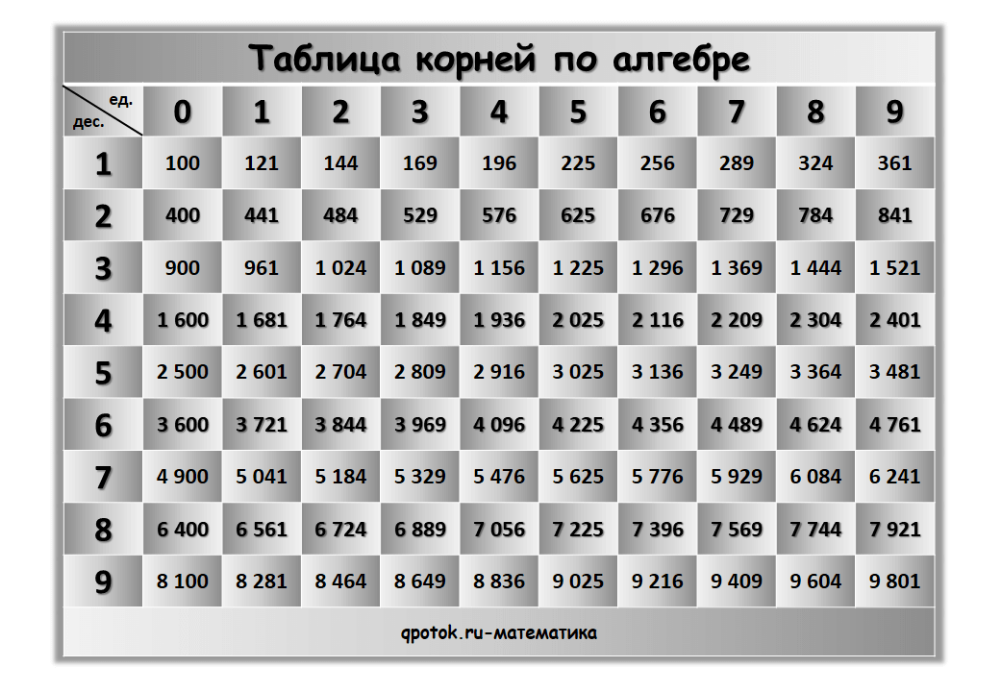 По этой причине для этого типа табличных данных вы также найдете название перекрестных таблиц. Другое распространенное название для этого типа таблиц — таблица непредвиденных обстоятельств .
По этой причине для этого типа табличных данных вы также найдете название перекрестных таблиц. Другое распространенное название для этого типа таблиц — таблица непредвиденных обстоятельств .
В приведенном ниже примере показана частотная таблица количества диалогов каждого персонажа в эпизоде (в оригинальной трилогии «Звездных войн»). Строки соответствуют категориям переменной Name, а столбцы — категориям переменной Episode.
Рисунок 1.12: Таблица частот
Значение в ячейке ij ( i -th строка, j -th столбец) показывает количество вхождений, которые разделяют категорию имени i и категорию эпизода j . Если вы добавите все записи, вы получите общее количество людей в каждой переменной.
Этот табличный формат на самом деле не является таблицей индивидуальных переменных. Несмотря на то, что в приведенном выше примере есть строки с именами трех человек, подобная таблица получается с двумя категориальными переменными.
1.2.6 Таблица расстояний
Еще одним интересным типом таблиц является таблица расстояний. В зависимости от того, с кем вы разговариваете, термин «расстояние» может использоваться в немного разных значениях. Некоторые авторы ссылаются на расстояние слова, передающее метрическое значение расстояния. Вместо этого другие авторы используют слово «расстояние», чтобы передать общую идею непохожести.
В общем, вы можете найти расстояний таблиц под двумя противоположными точками зрения: сходство и различие. В таблице ниже приведен пример таблицы подобия.
Рисунок 1.13: Таблица близости
1.2.7 Резюме
Для большинства методов статистического обучения требуются данные в формате таблицы с несколькими столбцами и строками.
Важно помнить о разнице между необработанной таблицей данных и чистой таблицей , закодированной числовым кодом.
Если не указано иное, в этой книге мы будем предполагать, что все переменные в матрице данных имеют числовые переменные.