Таблица чисел в двоичной системе счисления: Таблица соответствия десятеричного от 1 до 255 (decimal), двоичного (binary) и шестнадцатеричного (hexadecimal) представлений чисел. Шестнадцатиричная система счисления, двоичное счисление.

alexxlab / / Разное

Двоичная система счисления – таблица последовательности, примеры (8 класс, информатика)

4.7

Средняя оценка: 4.7

Всего получено оценок: 242.

4.7

Средняя оценка: 4.7

Всего получено оценок: 242.

Информация в компьютере обрабатывается в цифровом формате, в виде набора нулей и единиц, поэтому все числа переводятся в двоичный вид. Система счисления, в которой для обозначения чисел применяется всего два знака, называется двоичной. Метод представления чисел в двоичном формате изучается в курсе информатики 8 класса.

Двоичная система

Система счисления, которая в своем арсенале использует только две цифры, то есть имеющая основание два, называется двоичной или бинарной. В такой системе числа заменяются последовательностью нулей и единиц. Например, десятичное число 134 в двоичном формате выглядит как 10000110. Для того чтобы понять, как это работает, следует придерживаться правил перевода чисел из одной системы счисления в другую.

Рис. 1. Двоичная система счисления.

Перевод чисел из десятичной системы счисления в двоичную

Перевод целой части десятичного числа производится путем поочередного деления частного на основание двоичной системы, то есть на два. В остатке от деления останется либо ноль, либо единица. Эти остатки записываются, начиная с последнего частного в направлении слева направо. Это и будет двоичным представлением десятичного числа.

Рассмотрим примеры.

Для перевода десятичного числа 29 в двоичный формат:

Делят 29 на два, получают 14 и в остатке 1. Остаток следует запомнить.

Затем частное от деления, то есть число 14 снова делят на два, получено 7 и в остатке 0 (ноль).

Разделим 7 на два, получим частное 3 и остаток 1.

Три делят на два, получено в частном 1 и остаток 1.

Так как последнее частное 1 меньше основания системы счисления, то есть числа 2, то последовательное деление прекращают.

Затем записывают остатки, начиная с последнего частного, и получают последовательность чисел: 11101.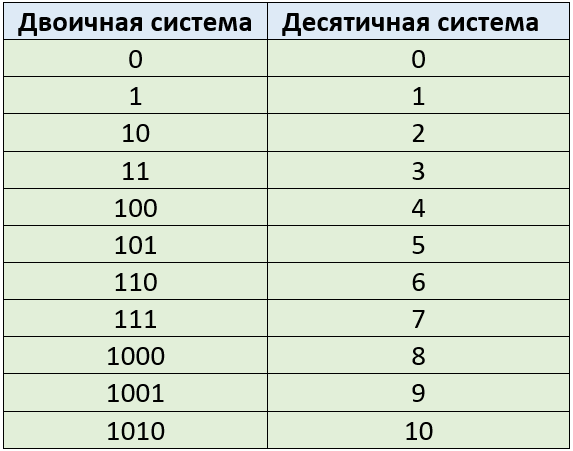

Таким образом, десятичное число 29 в двоичной системе счисления равно 11101.

Еще один пример: перевод числа 37 в двоичный формат.

37 / 2 = 18 (1)

18 / 2 = 9 (0)

9 / 2 = 4 (1)

4 / 2 = 2 (0)

2 / 2 = 1 (0)

Получен результат: 100101.

Если десятичные числа расположить последовательно и сопоставить с их двоичными эквивалентами, то можно увидеть некоторую закономерность.

Таблица двоичной системы счисления

0

0

8

1000

1

01

9

1001

2

10

10

1010

3

11

11

1011

4

100

12

1100

5

101

13

1101

6

110

14

1110

7

111

15

1111

Как видно из таблицы, после 11 в числовом ряду двоичных чисел идет число 100. Так как в двоичной системе счисления только два знака 0 и 1 для обозначения числа, то происходит сдвиг разрядной сетки влево. После двузначного числа 11 идет трехзначное число 100.

Таблицей двоичной системы удобно пользоваться для перевода только небольших десятичных чисел. Ее даже рекомендуется запомнить, как таблицу умножения в математике. Но ни в коем случае нельзя по таблице переводить отдельные цифры числа в десятичный формат. Это приведет к ошибке. Например, десятичное число 15 это не 1 и 101, (вместе 1101), а все-таки 1111.

Перевод двоичных чисел в десятичную систему счисления

Обратный перевод двоичного числа в десятичную систему производится также строго по правилу перевода.

Рис. 2. Портрет Г. В. Лейбница.

Сначала нумеруются разряды двоичного числа справа налево, начиная с нулевого, а затем каждая цифра двоичного числа умножается на основание двоичной системы, то есть на два, возведенной в степень соответствующего разряда. Полученные произведения суммируются, и получается десятичное число.

Например: двоичное число 1110001 в десятичной системе равно 113.

Нумеруем разряды числа, начиная с нуля: 1(6) 1(5) 1(4) 0(3) 0(2) 0(1) 1(0).

Каждую цифру двоичного числа умножаем на два в степени разряда и суммируем:

1*26 + 1*25 + 1*24 +0*23 + 0*22 + 0*21 + 1*20 = 64 + 32 + 16 + 0 + 0 + 0 +1 = 113

Следует помнить, что любое число в степени ноль равно единице.

Двоичная система счисления была описана Готфридом Вильгельмом Лейбницем в 18 веке. На это его вдохновили гексограммы из китайской книги Перемен, которые соответствовали двоичным числам от 0 до 111111.

Рис. 3. Гексаграммы книги перемен.

Что мы узнали?

Данные в ЭВМ представляются в двоичном формате. Двоичная система счисления оперирует для записи чисел только двумя символами 0 и 1. Перевод десятичных чисел в двоичную систему и обратно производится строго по правилам.

Тест по теме

Доска почёта

Чтобы попасть сюда — пройдите тест.

  • Альбина Авезова

    5/10

Оценка статьи

4.7

Средняя оценка: 4.7

Всего получено оценок: 242.

А какая ваша оценка?

Дистанционный репетитор — онлайн-репетиторы России и зарубежья

КАК ПРОХОДЯТ
ОНЛАЙН-ЗАНЯТИЯ?

Ученик и учитель видят и слышат
друг друга, совместно пишут на
виртуальной доске, не выходя из
дома!

КАК ВЫБРАТЬ репетитора

Выбрать репетитора самостоятельно

ИЛИ

Позвонить и Вам поможет специалист

8 (800) 333 58 91

* Звонок является бесплатным на территории РФ
** Время приема звонков с 10 до 22 по МСК

ПОДАТЬ ЗАЯВКУ

Россия +7Украина +380Австралия +61Белоруссия +375Великобритания +44Израиль +972Канада, США +1Китай +86Швейцария +41

Выбранные репетиторы

Заполните форму, и мы быстро и бесплатно подберем Вам дистанционного репетитора по Вашим пожеланиям.
Менеджер свяжется с Вами в течение 15 минут и порекомендует специалиста.

Отправляя форму, Вы принимаете Условия использования и даёте Согласие на обработку персональных данных

Вы также можете воспользоваться
расширенной формой подачи заявки

Как оплачивать и СКОЛЬКО ЭТО СТОИТ

от
800 до 5000 ₽

за 60 мин.

и зависит

ОТ ОПЫТА и
квалификации
репетитора

ОТ ПОСТАВЛЕННЫХ ЦЕЛЕЙ ОБУЧЕНИЯ
(например, подготовка к олимпиадам, ДВИ стоит дороже, чем подготовка к ЕГЭ)

ОТ ПРЕДМЕТА (например, услуги репетиторовиностранных языков дороже)

Оплата непосредственно репетитору, удобным для Вас способом

Почему я выбираю DisTTutor

БЫСТРЫЙ ПОДБОР
РЕПЕТИТОРА И
ИНДИВИДУАЛЬНЫЙ ПОДХОД

ОПТИМАЛЬНОЕ
СООТНОШЕНИЕ ЦЕНЫ И
КАЧЕСТВА

ПРОВЕРЕНЫ ДОКУМЕНТЫ ОБ ОБРАЗОВАНИИ У ВСЕХ РЕПЕТИТОРОВ

НАДЕЖНОСТЬ И ОПЫТ.
DisTTutor на рынке с 2008 года.

ПРОВЕДЕНИЕ БЕСПЛАТНОГО, ПРОБНОГО УРОКА

ЗАМЕНА РЕПЕТИТОРА, ЕСЛИ ЭТО НЕОБХОДИМО

376750 УЧЕНИКОВ ИЗ РАЗНЫХ СТРАН МИРА
уже сделали свой выбор

И вот, что УЧЕНИКИ ГОВОРЯТ
о наших репетиторах

Чулпан Равилевна Насырова

«

Я очень довольна репетитором по химии. Очень хороший подход к ученику,внятно объясняет. У меня появились сдвиги, стала получать хорошие оценки по химии. Очень хороший преподаватель. Всем , кто хочет изучать химию, советую только её !!!

«

Алина Крякина

Надежда Васильевна Токарева

«

Мы занимались с Надеждой Васильевной по математике 5 класса. Занятия проходили в удобное для обоих сторон время. Если необходимо было дополнительно позаниматься во внеурочное время, Надежда Васильевна всегда шла навстречу. Ей можно было позванить, чтобы просто задать вопрос по непонятной задачке из домашнего задания. Моя дочь существенно подняла свой уровень знаний по математике и начала демонстрировать хорошие оценки. Мы очень благодарны Надежде Васильевне за помощь в этом учебном году, надеемся на продолжение отношений осенью.

«

Эльмира Есеноманова

Ольга Александровна Мухаметзянова

«

Подготовку к ЕГЭ по русскому языку мой сын начал с 10 класса. Ольга Александровна грамотный педагог, пунктуальный, ответственный человек. Она всегда старается построить занятие так, чтобы оно прошло максимально плодотворно и интересно. Нас абсолютно все устраивает в работе педагога. Сотрудничество приносит отличные результаты, и мы его продолжаем. Спасибо.

«

Оксана Александровна

Наталья Борисовна Карасева

«

Мы восторге от репетитора. Наталья Борисовна грамотный педагог, она любит свою профессию, любит учеников. Занятия с сыном (2 класс), он находится на домашнем обучении, проходят по скайпу в комфортной обстановке. Репетитор умеет заинтересовать ребенка и выстраивает занятие с учетом его способностей, доступно объясняя предметы русский язык и математику. По результатам занятий можно сразу заметить повышение уровня успеваемости ученика. Наталья Борисовна хороший педагог, умеет быстро найти общий язык с ребенком, внимательная, легко передающая знания ученику. С большим удовольствием будем продолжать наши занятия, т.к. мы всем довольны.

«

Елена Васильевна


Клиентам

  • Репетиторы по математике
  • Репетиторы по русскому языку
  • Репетиторы по химии
  • Репетиторы по биологии
  • Репетиторы английского языка
  • Репетиторы немецкого языка

Репетиторам

  • Регистрация
  • Публичная оферта
  • Библиотека
  • Бан-лист репетиторов

Партнеры

  • ChemSchool
  • PREPY. RU
  • Class

Таблица преобразования десятичных и двоичных чисел — Исследование двоичных чисел

Автор: Rick Regan 30 июня 2009 г.

Вот таблица, которую вы можете использовать для преобразования небольших целых чисел — целых чисел от 0 до 255 — непосредственно между десятичными и двоичными числами (в качестве альтернативы использованию десятичного/двоичного преобразователя):

Целые числа от 0 до 255, в Двоичный
Декабрь Двоичный Декабрь Двоичный Декабрь Двоичный Декабрь Двоичный
0 0 64 1000000 128 10000000 192 11000000
1 1 65 1000001 129 10000001 193 11000001
2 10 66 1000010 130 10000010 194 11000010
3 11 67 1000011 131 10000011 195 11000011
4 100 68 1000100 132 10000100 196 11000100
5 101 69 1000101 133 10000101 197 11000101
6 110 70 1000110 134 10000110 198 11000110
7 111 71 1000111 135 10000111 199 11000111
8 1000 72 1001000 136 10001000 200 11001000
9 1001 73 1001001 137 10001001 201 11001001
10 1010 74 1001010 138 10001010 202 11001010
11 1011 75 1001011 139 10001011 203 11001011
12 1100 76 1001100 140 10001100 204 11001100
13 1101 77 1001101 141 10001101 205 11001101
14 1110 78 1001110 142 10001110 206 11001110
15 1111 79 1001111 143 10001111 207 11001111
16 10000 80 1010000 144 10010000 208 11010000
17 10001 81 1010001 145 10010001 209 11010001
18 10010 82 1010010 146 10010010 210 11010010
19 10011 83 1010011 147 10010011 211 11010011
20 10100 84 1010100 148 10010100 212 11010100
21 10101 85 1010101 149 10010101 213 11010101
22 10110 86 1010110 150 10010110 214 11010110
23 10111 87 1010111 151 10010111 215 11010111
24 11000 88 1011000 152 10011000 216 11011000
25 11001 89 1011001 153 10011001 217 11011001
26 11010 90 1011010 154 10011010 218 11011010
27 11011 91 1011011 155 10011011 219 11011011
28 11100 92 1011100 156 10011100 220 11011100
29 11101 93 1011101 157 10011101 221 11011101
30 11110 94 1011110 158 10011110 222 11011110
31 11111 95 1011111 159 10011111 223 11011111
32 100000 96 1100000 160 10100000 224 11100000
33 100001 97 1100001 161 10100001 225 11100001
34 100010 98 1100010 162 10100010 226 11100010
35 100011 99 1100011 163 10100011 227 11100011
36 100100 100 1100100 164 10100100 228 11100100
37 100101 101 1100101 165 10100101 229 11100101
38 100110 102 1100110 166 10100110 230 11100110
39 100111 103 1100111 167 10100111 231 11100111
40 101000 104 1101000 168 10101000 232 11101000
41 101001 105 1101001 169 10101001 233 11101001
42 101010 106 1101010 170 10101010 234 11101010
43 101011 107 1101011 171 10101011 235 11101011
44 101100 108 1101100 172 10101100 236 11101100
45 101101 109 1101101 173 10101101 237 11101101
46 101110 110 1101110 174 10101110 238 11101110
47 101111 111 1101111 175 10101111 239 11101111
48 110000 112 1110000 176 10110000 240 11110000
49 110001 113 1110001 177 10110001 241 11110001
50 110010 114 1110010 178 10110010 242 11110010
51 110011 115 1110011 179 10110011 243 11110011
52 110100 116 1110100 180 10110100 244 11110100
53 110101 117 1110101 181 10110101 245 11110101
54 110110 118 1110110 182 10110110 246 11110110
55 110111 119 1110111 183 10110111 247 11110111
56 111000 120 1111000 184 10111000 248 11111000
57 111001 121 1111001 185 10111001 249 11111001
58 111010 122 1111010 186 10111010 250 11111010
59 111011 123 1111011 187 10111011 251 11111011
60 111100 124 1111100 188 10111100 252 11111100
61 111101 125 1111101 189 10111101 253 11111101
62 111110 126 1111110 190 10111110 254 11111110
63 111111 127 1111111 191 10111111 255 11111111

Имеется четыре столбца по 64 записи в каждой, всего 256 записей.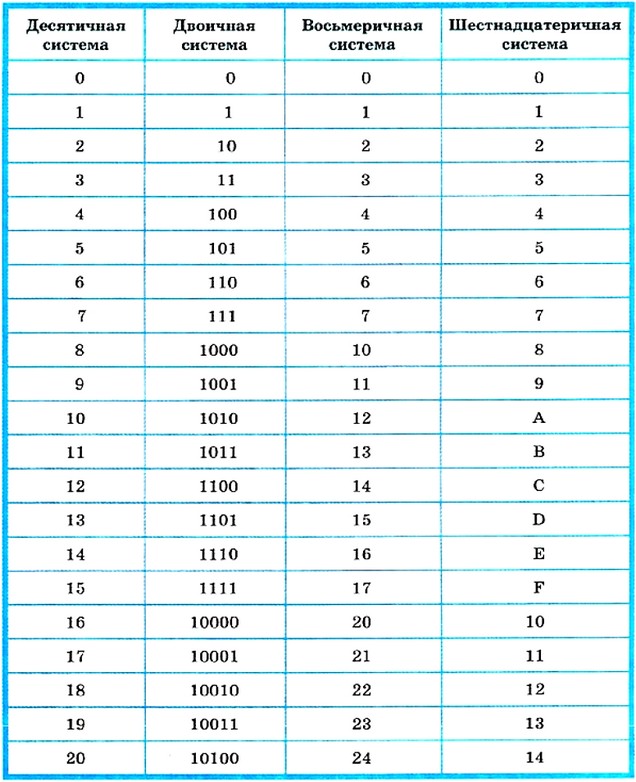

Если вы используете эти значения для хранения в компьютерном слове — например, в байте — не забудьте дополнить их начальными нулями, если это необходимо.

Категории Двоичные числа

Таблица / Список двоичных чисел ▶️ от 0 до 100

В ConvertBinary вы можете найти числа от 0 до 100 в их двоичном кодовом представлении.

Если вы хотите узнать двоичное представление любого десятичного числа до 7 цифр, воспользуйтесь конвертером десятичных чисел в двоичные.

ДЕСЯТИЧНЫЕ ЧИСЛА В ДВОИЧНОМ

90 013 9001 3 900 13 90 043 31 900 43 100110 900 43 41 9 0041 900 41 9 0041 91 001110 9004 3 81 9 0043 1011000 9001 3 900 41
Десятичное Двоичное
0 0
1 1
2 10
3 11
4 100
5 101
6 110
7 111
8 1000
9 1001
10 1010
11 1011
12 1100
13 1101 9 0044
14 1110
15 1111
16 10000
17 10001
18 10010
19 10011
20 10100 900 44
21 10101
22 10110
23 10111
2 4 11000
25 11001
26 11010
27 11011
28 11100
29 11101
30 11110
11111
32 100000
33 100001
34 10 0010
35 100011
36 100100
37 100101
38
39 100111
40 101000
101001
42 101010
43 101011
44 101100 9 0044
45 101101
46 101110
47 101111
48 110 000
49 110001
50 110010
51 110011
52 110100
53 110101
54 110110
55 110111
56 111000
57 111001
58 111010 90 044
59 111011
60 111100
61 111101
62 111110
63 111111
64 1000000
65 1000001
66 1000010
67 1000011
68 1000100
69 1000101
70 1000110
71 9 0044 1000111
72 1001000
73 1001001
74 1001010
75 1001011
79 1001111
80 1010000
1010001
82 1010010
83 1010011
84 1010100 9004 4
85 1010101
86 1010110
87 1010111
88
89 1011001
90 1011010
91 1011011
92 1011100
93 1011101
94 101111 0
95 1011111
96 1100000
97 1100001
98 9 0044 1100010
99 1100011
100 1100100

Ознакомьтесь с двоичным алфавитом слишком!

Вопросы и ответы о двоичных числах

🔟 Как вы читаете двоичные числа?

Чтобы прочитать двоичные числа и преобразовать их в десятичный эквивалент, у вас есть два варианта: вы можете либо использовать Конвертер двоичных чисел в десятичные на ConvertBinary. com, или вы можете сделать это вручную.

Короче говоря, чтобы преобразовать двоичные числа в десятичные числа, вы должны умножить каждую двоичную цифру на два в степени ее разряда справа налево, а затем сложить все результаты вместе. При вычислении разрядного номера самая правая цифра разрядного разряда имеет нулевое значение.

Так, например, если вы хотите преобразовать двоичное число 1010 в десятичное, вы начинаете с самого правого 0.

Давайте сделаем это с двоичным числом 1010:
0 × 2 0 = 0
1 × 2 1 = 2
0 × 2 2 = 0
1 × 2 3 = 8

9000 2 Добавьте 0+2+0+8, и вы получите десятичную дробь. 10.

🔟 Как считать до 10 в двоичном формате?

Чтобы считать в двоичном формате, вы начинаете с 0, затем переходите к 1. Затем добавляете еще одну цифру, как при десятичном счете, когда переходите от 9 к 10. Вы добавляете еще одну цифру, так что теперь у вас есть две цифры. . Итак, в двоичном формате вы переходите от 1 к 10, поскольку 1 — ваше последнее счетное число.

Итак, считая в двоичном виде, вы считаете так:

0
1
10
11
100
101
110
111
1000
1 001
1010

Вы можете найти десятичные числа от 0 до 100 (один сто) в таблице двоичных чисел на ConvertBinary.com

✏️ Как вы конвертируете десятичные числа в двоичные?

Чтобы преобразовать десятичные числа в их двоичные эквиваленты, у вас есть два варианта: вы можете использовать Конвертер десятичных чисел в двоичные на ConvertBinary.com, или вы можете сделать это вручную.

Если вы хотите научиться преобразовывать десятичные числа в двоичные вручную, вы можете прочитать это руководство или посмотреть соответствующий учебник.

🎓 Что представляют собой двоичные числа?

В математике и цифровой электронике двоичное число — это число, выраженное в системе счисления с основанием 2 или в двоичной системе счисления, в которой используются только два символа: обычно «0» (ноль) и «1» (единица).

No related posts.

Добавить комментарий

Ваш адрес email не будет опубликован. Обязательные поля помечены *