«Таблица умножения (квадрат Пифагора)» — Математика — Страна детей
Страна детей
- Точные науки
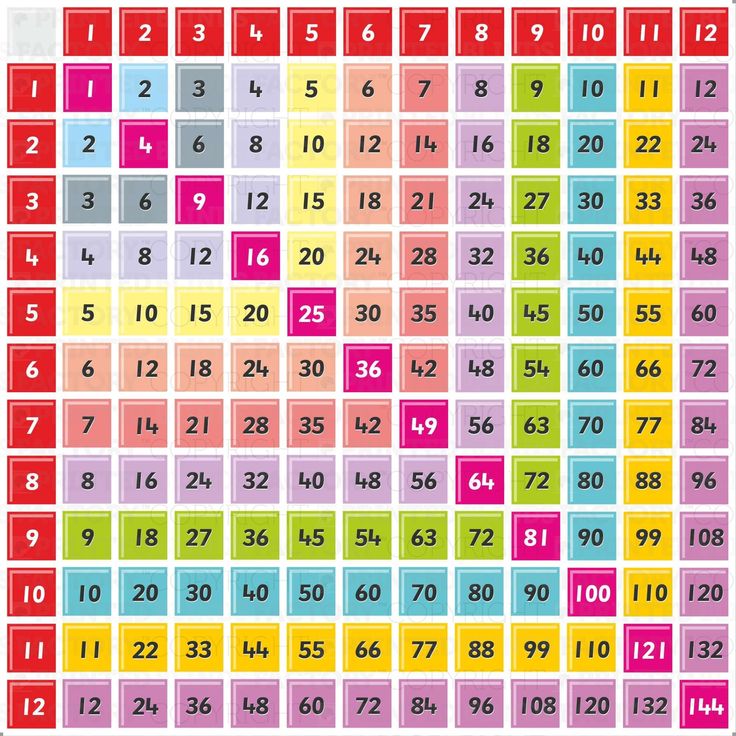
Для закрепления таблицы умножения рекомендуется использовать, таблицу Пифагора, которая хорошо развивает зрительную память.
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | |
|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 2 | 2 | 4 | 6 | 8 | 10 | 12 | 14 | 16 | 18 | 20 |
| 3 | 3 | 6 | 9 | 12 | 15 | 18 | 21 | 24 | 27 | 30 |
| 4 | 4 | 8 | 12 | 16 | 20 | 24 | 28 | 32 | 36 | 40 |
| 5 | 5 | 10 | 15 | 20 | 25 | 30 | 35 | 40 | 45 | 50 |
| 6 | 6 | 12 | 18 | 24 | 30 | 36 | 42 | 48 | 54 | 60 |
| 7 | 7 | 14 | 21 | 28 | 35 | 42 | 49 | 56 | 63 | 70 |
| 8 | 8 | 16 | 24 | 32 | 40 | 48 | 56 | 64 | 72 | 80 |
| 9 | 9 | 18 | 27 | 36 | 45 | 54 | 63 | 72 | 81 | 90 |
| 10 | 10 | 20 | 30 | 40 | 50 | 60 | 70 | 80 | 90 | 100 |
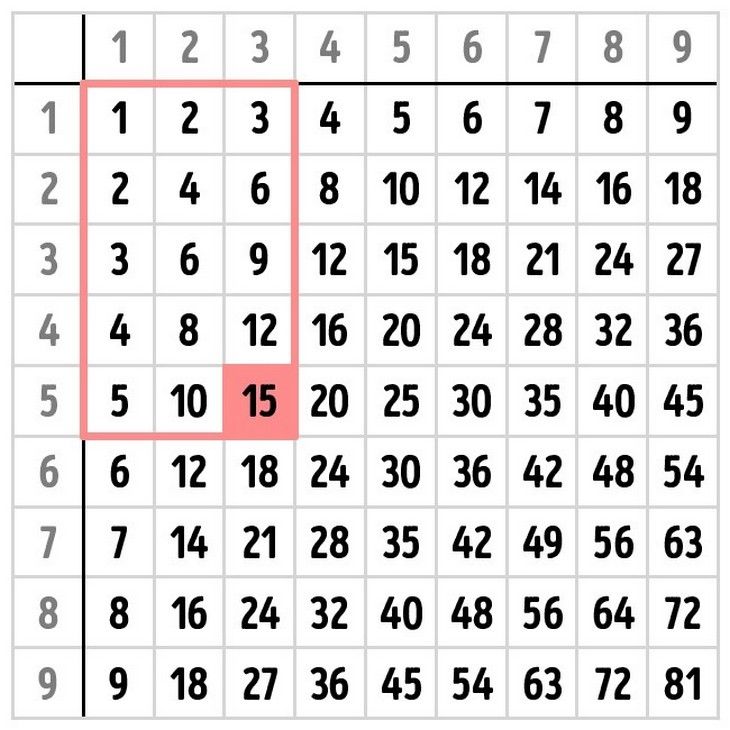
В таблице Пифагора по горизонтали и по вертикали расположены числа натурального ряда, а на пересечении столбцов и строк стоят их произведения. Диагональ таблицы образуют квадраты чисел. А если ткнуть в любое число и провести прямоугольник от начала таблицы до этого числа, то количество клеточек в прямоугольнике будет равняться выбранному числу.
Диагональ таблицы образуют квадраты чисел. А если ткнуть в любое число и провести прямоугольник от начала таблицы до этого числа, то количество клеточек в прямоугольнике будет равняться выбранному числу.
Почему квадрат пифагора лучше чем таблица представленная в столбцах:
- если таблица постоянно под рукой, волей-неволей начинаешь запоминать эти числа.
- запоминать гораздо проще чем примеры из столбцов.
- быстрее считывается закономерность.
- мозг не просто запоминает, а привыкает анализировать.
- помогает понять геометрию: площадь прямоугольника равна произведению его сторон.
Изображение для распечатывания:
69.98%
925 351Таблица умножения (квадрат Пифагора)
Таблица умножения Пифагора | Сайт о таблице умножения
Таблица умножения > Как быстро выучить таблицу умножения > Таблица умножения Пифагора
2018-02-11
Рубрика:
Как быстро выучить таблицу умножения
Автор:
Y.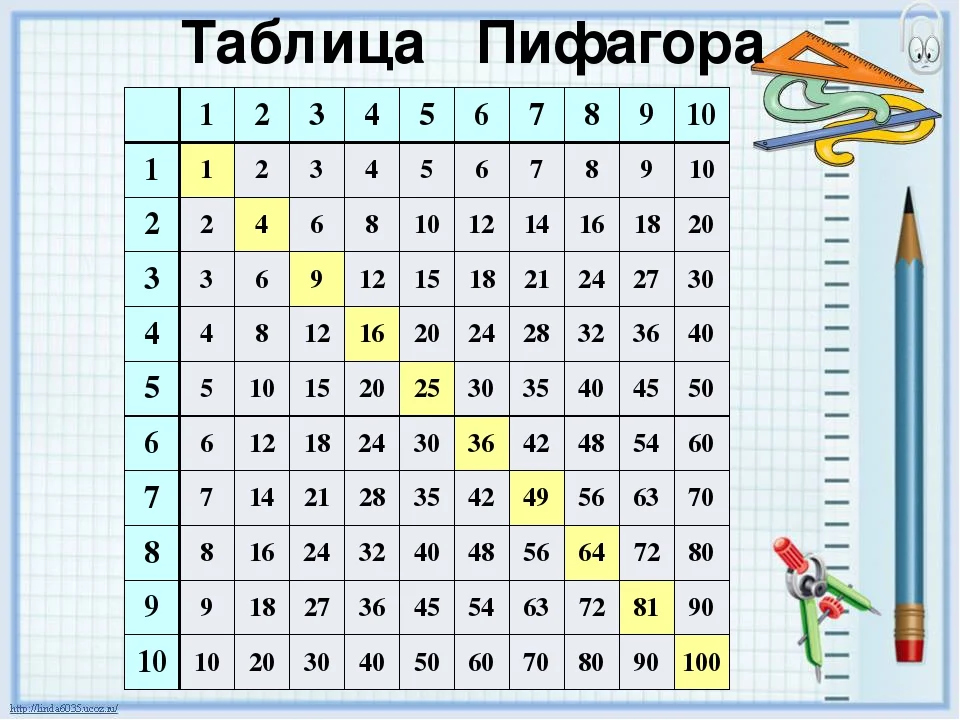 L.ERH
L.ERH
Таблица умножения Пифагора известна с древности. Ее создание, как следует из названия, приписывают древнегреческому философу и математику Пифагору и его ученикам.
Таблица Пифагора
Таблица умножения Пифагора представляет собой квадрат, на левой и верхней гранях которого расположены числа от 1 до 10, а ячейки содержат результат их перемножения. Размеры таблицы 1-10 не являются конечными, расширить таблицу можно до бесконечности.
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 10 | ||
| 1 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 2 | 2 | 4 | 6 | 8 | 10 | 12 | 14 | 16 | 18 | 20 |
| 3 | 3 | 6 | 9 | 12 | 15 | 18 | 21 | 24 | 27 | 30 |
| 4 | 4 | 8 | 12 | 16 | 20 | 24 | 28 | 32 | 36 | 40 |
| 5 | 5 | 10 | 15 | 20 | 25 | 30 | 35 | 40 | 45 | 50 |
| 6 | 6 | 12 | 18 | 24 | 30 | 36 | 42 | 48 | 54 | 60 |
| 7 | 7 | 14 | 21 | 28 | 35 | 42 | 49 | 56 | 63 | 70 |
| 8 | 8 | 16 | 24 | 32 | 40 | 48 | 56 | 64 | 72 | 80 |
| 9 | 9 | 18 | 27 | 36 | 45 | 54 | 63 | 72 | 81 | 90 |
| 10 | 10 | 20 | 30 | 40 | 50 | 60 | 70 | 80 | 90 | 100 |
На главной диагонали, выделенной серым цветом, расположены квадраты чисел, а произведение двух разных чисел находится на их пересечении.
В таблице Пифагора достаточно много закономерностей, на эту тему достаточно много информации в сети. Однако, большая часть данных закономерностей слишком сложна даже для взрослого человека, если рассматривать их практическое применение. Поэтому выделим всего 3 из них:
- Как упоминалось выше, по главной диагонали расположены квадраты чисел.
- Таблица симметрична.
- Каждый следующий столбец (строка) – это результат сложения предыдущего столбца (строки) на число в левой (верхней) грани квадрата.
С помощью этих свойств легче объяснить главный принцип умножения, что, по сути, это многократное сложение. В целом таблица Пифагора хороша в теоретическом плане на начальном этапе, но для практики ее лучше дополнить другими методами, например, логическим.
Плюсы метода
- Краткость. Таблица Пифагора куда меньше, чем таблица из столбцов.
- Наглядность. Из таблицы хорошо понятен принцип умножения и его свойства.

Минусы метода
- Не подходит для мысленного применения. Таблица хорошо и удобна, если видеть ее перед собой, но запомнить ее очень тяжело. Поэтому она не поможет при подготовке к сдаче умножения.
Статьи в тему:
- Как выучить таблицу умножения наизусть
- Таблица умножения на пальцах
- Логический способ изучения таблицы умножения
- Как выучить таблицу умножения игровой форме
Поделиться с друзьми:
Таблица умножения — Etsy.de
Etsy больше не поддерживает старые версии вашего веб-браузера, чтобы обеспечить безопасность пользовательских данных. Пожалуйста, обновите до последней версии.
Воспользуйтесь всеми преимуществами нашего сайта, включив JavaScript.
Найдите что-нибудь памятное, присоединяйтесь к сообществу, делающему добро.
( 1000+ релевантных результатов, с рекламой Продавцы, желающие расширить свой бизнес и привлечь больше заинтересованных покупателей, могут использовать рекламную платформу Etsy для продвижения своих товаров. Вы увидите результаты объявлений, основанные на таких факторах, как релевантность и сумма, которую продавцы платят за клик. Узнать больше. )
Степени таблицы умножения
Таблицы умножения восходят к вавилонянам более 4000 лет назад. Самые ранние десятичные примеры появились в Китае примерно в 300 г. до н.э., они были построены с использованием бамбуковых полосок и могли использоваться для умножения целых и полуцелых чисел до 99,5. Одним из самых ранних известных нам примеров является Таблица Пифагора , включенная Никомахом в его Введение в арифметику примерно в 100 г. н.э.
Самые ранние десятичные примеры появились в Китае примерно в 300 г. до н.э., они были построены с использованием бамбуковых полосок и могли использоваться для умножения целых и полуцелых чисел до 99,5. Одним из самых ранних известных нам примеров является Таблица Пифагора , включенная Никомахом в его Введение в арифметику примерно в 100 г. н.э.
Один из самых ранних примеров десятичной таблицы умножения, построенной из бамбуковых полосок, примерно 300 г. до н.э. в Китае
Сегодня в школе таблица умножения — это устройство, которое учащиеся используют для обучения умножению с помощью зубрежки и быстрых упражнений на запоминание. Хотя некоторые считают овладение таблицей умножения само по себе достижением, на самом деле это дает учащимся прочную основу для кладки математического кирпичика. Давайте окунемся в более глубокие воды и исследуем некоторые удивительные закономерности, раскрывающие силы, скрытые в таблице умножения.
Треугольники и квадраты
В море целых чисел красные числа на главной (с северо-запада на юго-восток) диагонали таблицы умножения явно равны 9.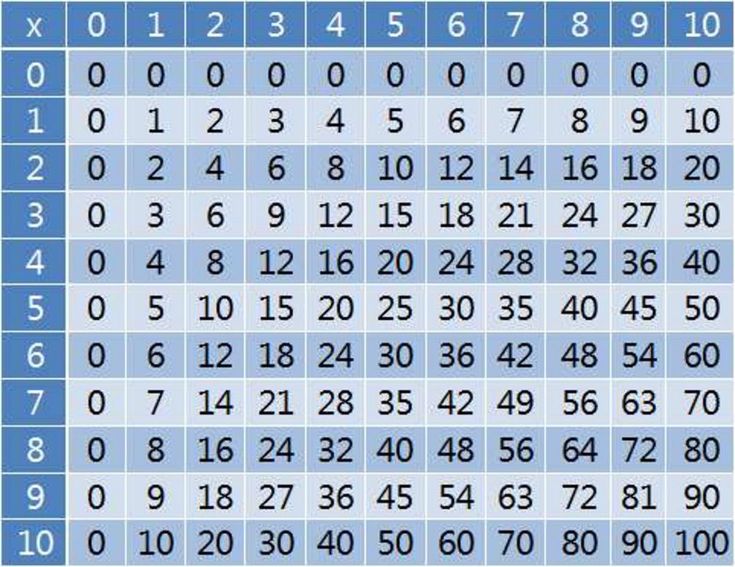 0138 квадратных чисел — счетные числа, возведенные в степень 2.
0138 квадратных чисел — счетные числа, возведенные в степень 2.
В статье Plus Треугольные числа авторы показали, что таблица умножения также дает нам треугольных чисел (числа, которые могут быть представлены набором точек, расположенных в виде равностороннего треугольника). Суммируя числа в каждой квадратной решетке, начиная с строки 1 и столбца 1, мы получаем треугольные числа в квадрате.
Суммируя числа в квадратных решетках, начиная с строки 1 и столбца 1, получаем треугольные числа в квадрате.
В таблице умножения можно найти не только треугольные числа, но и квадратные числа. В той же статье Plus мы видели, что когда кратные числа окрашены в синий цвет (см. ниже), сумма чисел в квадратной решетке, заключенной в эти синие кратные, также включает треугольное число. Сумма чисел в квадратной решетке равна , где и идентифицируют квадратную решетку, считая сверху и слева соответственно, и — треугольное число.
Мы видим, что суммы квадратных решеток, заключенных в синие кратные на главной (с северо-запада на юго-восток) диагонали (выделены желтым цветом внизу), также являются квадратными числами. В этом легко убедиться, взяв исходную формулу суммы из статьи и изменив ее. Мы будем использовать в формуле только потому, что вертикальное и горизонтальное положение одинаковы.
В этом легко убедиться, взяв исходную формулу суммы из статьи и изменив ее. Мы будем использовать в формуле только потому, что вертикальное и горизонтальное положение одинаковы.
Разделение квадратов
Если мы углубимся в другие образования квадратной решетки другого размера и географии в таблице умножения, мы сможем найти больше квадратных чисел. Квадратная решетка, которая опирается на главную (с северо-запада на юго-восток) диагональ, кажется, всегда генерирует соответствующее квадратное число на основе суммы общих меток столбца и строки. Сумма квадратной решетки, состоящей из одного квадрата из строки 2, столбца 2, равна . Числа в квадратной решетке на пересечении строк и столбцов 3 и 4 в сумме дают , а сумма чисел на пересечении строк и столбцов 5, 6 и 7 равна .
Таблица умножения с метками для строк, записанными слева, и метками для столбцов, написанными сверху.
Кажется, это справедливо даже в том случае, когда квадратная решетка строится путем пересечения непоследовательных строк и столбцов. Если мы возьмем пересечение строк и столбцов 1, 4 и 8, сумма (расщепленной) квадратной решетки равна .
Есть некоторое математическое понимание того, почему это работает с тремя целыми числами, выбранными из таблицы умножения для определения решетки, и мы можем придумать общую формулу, которая работает для любых трех чисел. В нашем примере выше сумма чисел в квадратной решетке:
И вообще
Сумма чисел в квадратной решетке, созданной путем пересечения одного и того же набора строк (, и ) с соответствующим набором столбцов (, и ), дает квадрат суммы меток строки/столбца .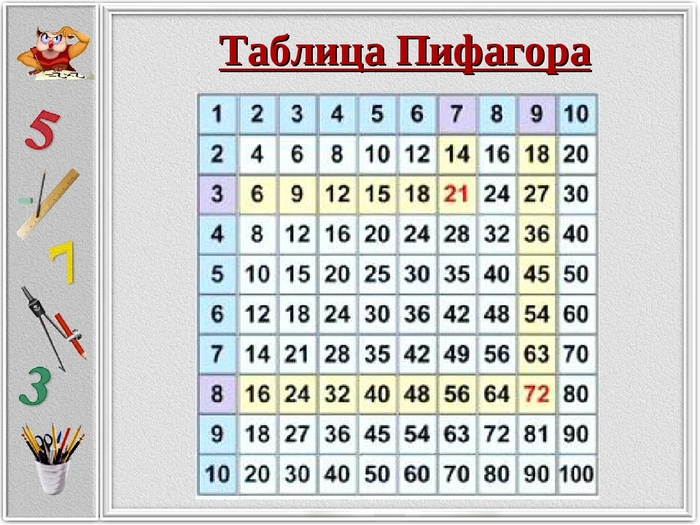 Может ли это распространяться на четыре числа, пять чисел и далее?
Может ли это распространяться на четыре числа, пять чисел и далее?
Квадраты из квадратов и квадраты из кубов
Благодаря этому знанию мы можем обнаружить некоторые необычные закономерности. Например, вы можете быстро показать (возможно, с помощью лего!), что сумма последовательных нечетных чисел (начиная с 1) равна квадрату. Давайте посмотрим на пересекающиеся строки, помеченные последовательными нечетными числами с соответствующими столбцами.
Сумма меток строк/столбцов будет квадратным числом, так как это сумма последовательных нечетных чисел, которые, как мы знаем, являются квадратами. И квадрат суммы меток строки/столбца будет квадратом квадрата числа: это число, возведенное в четвертую степень. Таким образом, мы можем собирать положительные целые числа, возведенные в 4-ю степень, из таблицы умножения, используя эту конкретную структуру решетки.
Сумма синих квадратов на пересечении последовательно пронумерованных строк и столбцов дает числа, возведенные в 4-ю степень.
Мы можем использовать еще один интересный результат: кубическое число (число, возведенное в степень 3) можно записать в виде суммы последовательных нечетных чисел. Например, , и . Итак, если мы выберем квадратные решетки, которые являются пересечением этих последовательных нечетных строк и столбцов, сумма чисел в этих квадратных решетках будет квадратом кубического числа, то есть числа, возведенного в степень 6. Зеленый квадраты ниже являются пересечением строк и столбцов 3 и 5, а их сумма равна . А желтые квадраты — это пересечения строк и столбцов 7, 9и 11, поэтому их сумма равна .
Учителя математики всегда ищут новые способы введения понятий умножения, показателей и алгебры. Если мы мыслим нестандартно, то обнаружим, что таблица умножения — это больше, чем просто средство для запоминания таблицы умножения. Если мы решим погрузиться глубоко в кристально голубые воды, мы обнаружим множество математических сокровищ на ее морском дне.
Дальнейшее чтение
Узнайте больше о Plus о треугольных числах и о том, где их можно найти в таблице умножения.