Таблицы по статистике с решением: Решение задач по статистике онлайн. Примеры решений

Содержание

Задачи по статистике с решениями и выводами. Решение задач по статистике на заказ. Онлайн-помощь

На этой странице выложено большое количество решенных задач по статистике — от простых до сложных, с запутанными условиями. Данные типовые примеры предназначены для самостоятельной работы студентов экономических и управленческих специальностей ВУЗов. Тематика охватывает весь курс общей теории статистики, основные разделы курса социально-экономической статистики и статистики предприятия. Решения содержат пояснения и выводы.

Задачи с решениями по математической статистике находятся в разделе сайта Теория вероятностей и математическая статистика

О платной помощи студентам с учебой можно почитать на странице Как заказать решение задач по статистике…

Кратко рассматривается статистическая сводка и группировка, виды группировок, а также формула Стерджесса. Приведен пример решения задачи на группировку статистической совокупности.

Рассматриваются абсолютные величины. Приведены примеры расчета рассматриваемых показателей.

Рассматриваются относительные показатели планового задания, выполнения плана, динамики и их взаимосвязь между собой. Приведены примеры расчета рассматриваемых относительных величин.

На странице рассмотрен расчет относительных показателей структуры (ОВС), координации (ОВК) и сравнения (ОВСр). Приведены примеры расчета рассматриваемых относительных величин.

На странице рассматриваются относительные показатели динамики (ОВД) и интенсивности (ОВИ). Приведены примеры расчета рассматриваемых относительных величин.

Решено несколько задач по статистике на использование средних величин.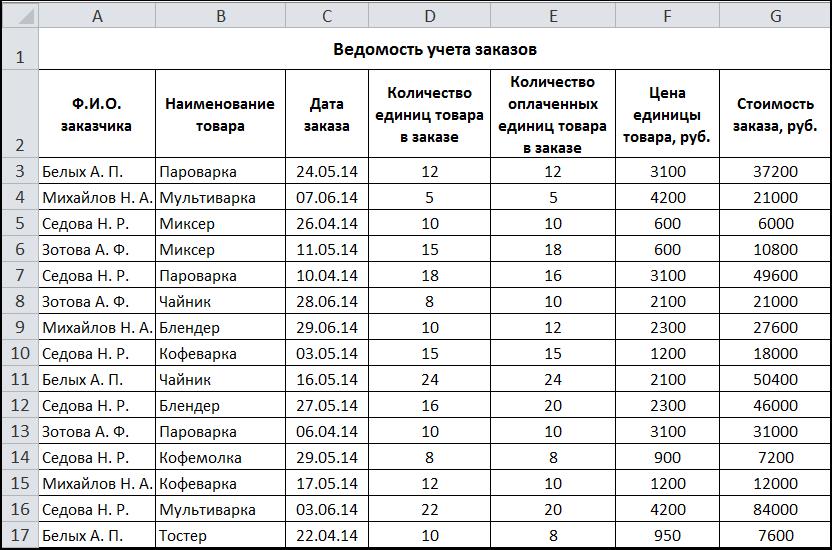

Рассматривается понятие средней хронологической величины в рядах динамики, виды средней хронологической. Приведены примеры расчета средней хронологической для моментных и интервальных рядов с равноотстоящими и неравноотстоящими интервалами.

Описание структурных средних дискретного и интервального рядов. На примерах решения задач показан расчет показателей — моды, медианы, квартилей, децилей.

Рассматривается подробно построение полигона и гистограммы частот и относительных частот — графиков статистического ряда распределения. Также затронута тема построения графиков накопленных частот — кумуляты и огивы с примерами задач.

В приведенной на странице задаче показано вычисление абсолютных и относительных показателей вариации интервального ряда — размах вариации, среднее линейное отклонение, дисперсия, коэффициент вариации, осцилляции, относительное линейное отклонение.

На странице рассмотрена задача на правило сложения дисперсий и сопутствующий расчет средней внутригрупповой и межгрупповой дисперсий.

Приведены необходимые теоретические сведения на тему показателей асимметрии и эксцесса, и образцы решения задач, где показан подробный расчет коэффициента асимметрии и эксцесса распределения.

Выборочное наблюдение

Рассматривается выборочное наблюдение и решена типовая задача на вычисление числовых характеристик выборки и интервалов для средней и доли бесповторной выборки.

В задаче, приведенной на странице, вычисляется несмещенная оценка дисперсии (исправленная выборочная дисперсия)

Страница содежит описание методов выборочного наблюдения, приведены формулы для расчета средней и предельной ошибок выборки. Изложены сведения по методам собственно-случайного отбора, механической выборки, типической (районированной) выборки, серийной выборки.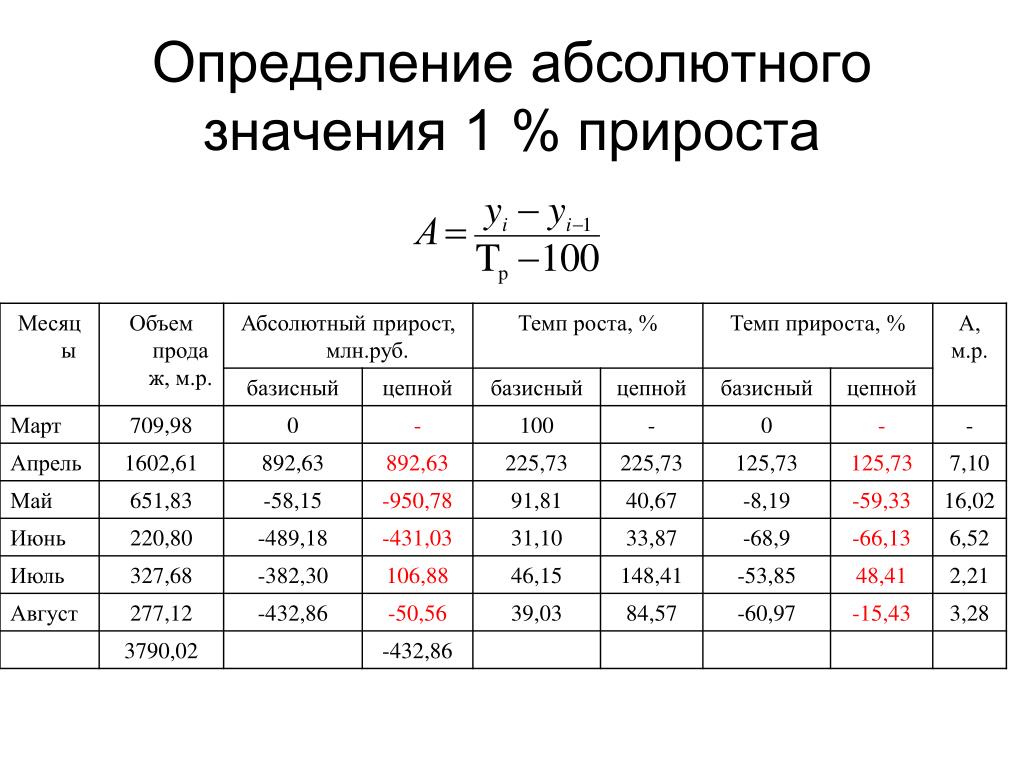 Привена таблица с формулами для определения численности выборки при различных методах отбора.

Коэффициент корреляции знаков Фехнера

Приведена краткая теория и рассмотрен пример решения задачи на расчет коэффициента корреляции знаков Фехнера.

Рассмотрены формула и смысл коэффициента линейной корреляции. Страница содержит типовой пример по расчету выборочного линейного коэффициента корреляции и проверке его значимости.

На странице даны образцы решения задач на построение парной линейной регрессии методом наименьших квадратов (МНК). Решение задач предваряют краткие теоретические сведения, где подробно рассматривается соответствующая система нормальных уравнений и следующие из нее формулы для нахождения параметров парной линейной регрессии.

Рассматриваются нелинейные уравнения парной регрессии — степенные, гиперболические, показательные и параболические.

Содержится краткая теория и пример решения задачи на ранговую корреляцию. Дано понятие ранговой корреляции, показан расчет коэффициента ранговой корреляции Спирмена.

На странице рассмотрено применение ранговой корреляции и коэффициента ранговой корреляции Кендалла в статистике. Приведена краткая теория, а также задача с примером расчета коэффициента Кендалла с проверкой гипотезы о его значимости.

Рассмотрено вычисление эмпирического корреляционного отношения и эмпирического коэффициента детерминации, на примере показан расчет внутригрупповой и межгрупповой дисперсии.

Дана краткая теория и на примере решения задачи показан расчет коэффициентов ассоциации и контингенции.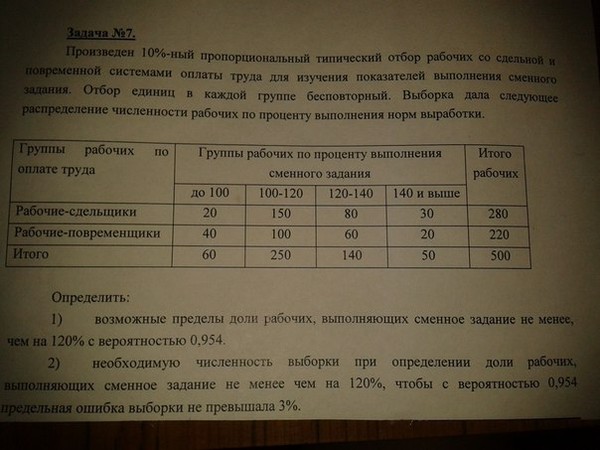

Страница содержит сведения по методам изучения взаимосвязей между качественными признаками с помощью коэффициентов взаимной сопряженности Чупрова и Пирсона.

На странице рассмотрены задачи на ряды динамики. Показано вычисление цепных, базисных и средних показателей динамики, а также недостающих уровней динамических рядов. Приведены формулы цепных, базисных и средних абсолютных приростов, темпов роста и темпов прироста.

Страница содержит последовательное и систематизированное изложение проверенных практикой методов обработки динамических рядов — метода скользящей средней и метода укрупнения интервалов.

Содержатся сведения по анализу рядов динамики — изучение тренда временного ряда с помощью аналитического выравнивания по прямой методом наименьших квадратов, построение точечного и интервального прогноза.

Представлены базовые методы индексного анализа. В решенных задачах рассчитаны индивидуальные и общие индексы цен, себестоимости, физического объема, стоимости товарооборота и затрат, а также показано разложение абсолютного прироста по факторам. Приведен расчет средних индексов — индексов цен и себестоимости переменного и постоянного составов, а также индекс структурных сдвигов. Показано разложение абсолютного прироста средней цены и себестоимости на факторы.

Приведен пример решения задачи на вычисление индексов цен Пааше, Ласпейреса, Фишера, а также индексов физического объема Ласпейреса и Пааше. Показана взаимосвязь между исчисленными индексами.

Изложена методика расчета календарного, табельного и максимально-возможного фондов рабочего времени, а также коэффициентов их использования. Содержатся сведения по составлению балансов рабочего времени на предприятии. Рассматриваются коэффициенты использования рабочего дня, рабочего периода, а также интегральный показатель использования рабочего времени.

Решена задача с вычислением уровня и динамики производительности труда. Рассчитаны индексы средней производительности труда — индекс переменного состава, постоянного состава и структурных сдвигов. Показано разложение на факторы прироста продукции, вычисление числа высвободившихся работников в связи с ростом производительности.

В представленной на странице задаче вычислены индексы средней заработной платы переменного состава, постоянного состава, структурных сдвигов, показано разложение на факторы изменения средней заработной платы и фонда заработной платы.

Страница содержит краткое описание показателей движения рабочей силы, также на примере показаны расчеты коэффициентов текучести кадров, оборота по приему и увольнению, общего оборота и постоянства кадров.

Рассмотрены основные показатели статистики основых фондов — полная и остаточная стоимость основных фондов, коэффициенты годности и износа, коэффициенты обновления и выбытия, показатели фондоотдачи и фондоемкости.

Страница содержит описание показателей естественного и механического движения населения. Рассмотрены общие коэффициенты рождаемости, смертности, механического движения, естественного и общего прироста населения.

Рассматриваются показатели статистики трудовых ресурсов — трудоспособное население, экономически активное население, коэффициенты замещения и воспроизводства трудовых ресурсов, коэффициент пенсионной нагрузки, коэффициент экономической активности населения, коэффициенты занятости и безработицы.

Краткое описание системы национальных счетов и основные показатели этой системы. Рассматривается пример решения задачи на составление консолидированных счетов СНС.

Приведены необходимые теоретические сведения и образцы решения задач для расчета валового внутреннего продукта (ВВП) тремя методами — производственным методом, распределительным методом и методом конечного использования.

На странице рассмотрены понятия номинальной и реальной стоимости ВВП — валового внутреннего продукта в текущих и постоянных ценах. Рассмотрена задача с применением индекса-дефлятора и индекса физической стоимости ВВП.

Приведена таблица значений функции Лапласа и образцы решения задач.

Приведена таблица критических точек t-критерия Стьюдента и образцы решения задач.

Приведена таблица критических точек распределения χ2 (хи-квадрат) критерия Пирсона и образцы решения задач.

Приведена таблица критических точек распределения F Фишера-Снедекора и образцы решения задач.

Большое количество типовых задач по статистике для самостоятельного решения с подсказками в виде ссылок на страницу решебника с похожими задачами, полностью решенными и оформленными.

Часть первая: 90 типовых задач по статистике
Часть вторая: 114 типовых задач по статистике
Часть третья: 123 типовые задачи по статистике

Задачи по статистике с решениями

Задачи по статистике с решениями и выводами

Задачи по статистике с решениями

На главную
Поиск
Задачи по банковскому делу с решениями и выводами
Контрольные по английскому (сочинения, ответы, деловая корреспонденция)
Лекции и контрольные по маркетингу
СВОТ-анализ. Примеры SWOT-анализа
Лекции по менеджменту
Тесты и контрольные по менеджменту организации
Лекции по БЖД Безопасности жизнедеятельности
Статьи по анализу ассортимента Оптимизации затрат
Контрольные по финансам, Финансовому менеджменту с решением
Разное
Миссия компании. Примеры миссий
Лекции и задачи с решениями
Бизнес-планирование. Примеры бизнес-планов
Контрольные и лекции по бухгалтерскому учету
Тестирование студентов в Вузах
Задачи по экономике предприятия с решениями
Студентам и аспирантам документы к защите
Информационные технологии в экономике
Предприятия. Примеры предприятий
Документоведение: пример оформления документов
Лекции по статистике
Задачи по статистике с решениями и выводами
Хостинг и Joomla
Аннотации
Правовые вопросы
Организация производства: курсовые, контрольные
Организация производства — Лекции
Лекции по экономике предприятия
Бизнес-планирование: оценка эффективности инвестиций
Идеи для бизнеса. Примеры бизнес-планов
Контрольные работы по стратегическому менеджменту
Документы для получения ученого звания доцента

Есть антитела? Но вы не обращались к врачу. Значит не болели
Метод анализа ассортимента МАРКОН. Сущность
Задача по экономике – Расчет критического объема продукции при маржинальном подходе
Внедрение сбалансированной системы показателей стратегического развития компании Пример
Задачи по статистике с решением — Средние величины
Примеры решенных задач – Расчет прибыли и себестоимости
SWOT-анализ (СВОТ-анализ) университета

Все права на материалы сайта принадлежат авторам. Копирование (полное или частичное) любых материалов сайта возможно только при указании ссылки на источник (администратор сайта).

Решения задач статистической таблицы

формула стандартизации. Кроме того, мы также научили вас основам чтения z-таблицы и тому, что такое z-таблица. В этом разделе мы больше сосредоточимся на использовании z-таблиц и их интерпретации , а также предложим пару практических задач для применения того, что вы узнали.

Что такое Z-оценка и Z-таблица?

Необработанные баллы — это немодифицированные точки данных, которые могут включать что угодно, от результатов тестов до роста. В статистике эти необработанные оценки стандартизированы, или преобразовал в z-оценку, чтобы сравнить их с остальным набором данных. Формула стандартизации такая же, как и формула z-показателя, что может объяснить, почему их также называют стандартными показателями.

Z-оценка показывает, на сколько стандартных отклонений отличается данное число от среднего. Z-показатели можно вставить в z-таблицу, чтобы также узнать, какие процента распределения ниже или выше этого z-показателя.

Распределение является стандартным нормальным распределением, поскольку мы стандартизируем данные. Z-таблицы можно использовать, чтобы дать процент от определенное распределение выше, ниже или между определенным интервалом распределения. Ниже вы найдете пошаговый пример нахождения z-показателя.

Лучшие репетиторы по математике

Поехали

Пример Z-счета

У вас есть следующие данные о весе в кампусе колледжа. Вы хотите иметь возможность сравнивать точки данных друг с другом, но не иметь стандартизированных данных. Однако у вас есть информация о среднем значении и стандартном отклонении.

Измерение	Значение
Среднее значение	73 кг
SD	12

Мы хотим знать, насколько типичен вес 95 кг находится в нашем наборе данных. В частности, мы хотим знать процента людей с весом выше и ниже 95 кг. Для этого мы должны сначала найти стандартную оценку 95.

Напомним, что интерпретировать z-значение легко, потому что оно выражает количество стандартных отклонений 95 кг на от среднего на . Напомним, что для стандартных нормальных распределений среднее значение равно 0, а стандартное отклонение равно 1. Причина, по которой среднее значение равно 0, заключается в том, что стандартизация среднего приводит к 0, как вы можете видеть ниже на нашем примере.

Это, конечно, имеет смысл, поскольку среднее значение 73 отличается от самого себя на 0 стандартных отклонений. Для того, чтобы найти процент веса выше и ниже 95 кг, мы можем использовать левосторонний z-стол. Имейте в виду, что есть как левая, так и правая хвостовые z-таблицы . Давайте начнем с определения 95 кг на стандартном нормальном распределении ниже.

Это служит иллюстрацией того, почему z-таблицы называются «правым хвостом» и «левым хвостом», как мы можем видеть на изображении выше, область справа выглядит как хвост.

Поскольку мы пытаемся найти площадь слева от 95 кг , нам нужно использовать левую хвостовую z-таблицу. На изображении ниже показано, как найти процент в z-таблице.

Получаем число 0,96638, что означает около 97% веса распределения ниже 95 кг с учетом среднего значения и стандартного отклонения. Если мы хотим узнать, какой процент набрал больше 97% , нам не обязательно использовать правую хвостовую z-таблицу.

Поскольку мы знаем, что вся площадь под кривой стандартной таблицы распределения равна 1, что связано с тем, что она представляет собой распределение вероятностей, мы знаем, что можем найти правильный процент сказки, взяв 1 минус процент остатка.

Здесь это даст нам

Что составляет около 3%. Это означает, что около 3% раздачи весит более 95 кг. Это имеет смысл, потому что, сложив вместе, процент того, что слева от 95 кг, и того, что справа от него , должно добавить к 100%.

Практические задачи

В этом разделе мы проверим то, что вы узнали, и попросим вас решить различные задачи, связанные с z-показателями и z-таблицами.

Проблема 1

Вы заинтересованы в изучении цен на мобильные телефоны в США. Недавно на рынке появилась новая модель телефона по цене около 1200 долларов США. Если средняя цена телефона в стране 1200?

9 0037 0,99534

Z	0	0,01
2	0,97725	0,97778
2.1	0,98214	0,98257
2,2	0,98610	0,98645
2,3	0,98928	0,98956
2,4	0,99180	0,99202
2,5	0,99379	0,99396
2,6	0,99547
2,7	0,99653	0,99664

9020 4

Задача 2

Ваш друг переживает из-за оценки, которую он получил за последний экзамен. Вы пытаетесь убедить его, что он на самом деле хорошо справлялся, несмотря на полученную оценку. Чтобы он почувствовал себя лучше, вы получили средний балл и стандартное отклонение экзамена от его учителя. Используйте таблицу и информацию ниже, чтобы вычислить , сколько людей набрали 9 баллов.0004 выше и ниже него.

Оценка друзей: 49 из 100 баллов
Средняя оценка: 15 040 0 0,01 0,02 0,03 0,04 0,05 0,06 0,07 0,08 3 0,99865 0,99869 0,99874 0,99878 9003 3.1 0,99903 0,99906 0,99910 0,99913 0,99916 0,99918 0,99921 0,99924 0,99926 9 0045 3. 2 0,99931 0,99934 0,99936 0,99938 0,99940 0,99942 0,99944 0,99946 0,99948
Задача 3
9000 2 Вас интересует аренда квартиры у пары районов. Чтобы сузить выборку, вы решаете взять среднюю цену для всех районов и стандартное отклонение этих цен. Ваш бюджет составляет от 600 до 800 фунтов в месяц. Учитывая, что средняя цена составляет 1200 фунтов, а стандартное отклонение равно 250, какой процент квартир находится в вашем ценовом диапазоне? Используйте z-таблицу ниже.
Z 0 0,01
1,6 0,94520 0,94630
…
2,4 0,99180 0,99202

Решения практических задач
Ниже приведены решения практических задач. Обязательно попробуйте решить эти задачи самостоятельно, прежде чем проверять свои ответы.
Решение Задача 1
Z-показатель находится из следующего:

Это означает, что примерно 99,7% телефонов дешевле новой модели. Это показано на изображении ниже.
Решение Задача 2
Z-показатель находится из следующего:

Это означает, что он набрал больше 99,9% класса и только 0,07% набрал выше него, как подсчитано ниже.

Решение задачи 3
Z-значения находятся из следующего:

0002 Это можно проиллюстрировать на изображении ниже.
Это означает, что проценты для каждого z-показателя составляют0005

Это означает, что только около 5% квартир доступны в вашем ценовом диапазоне.
Таблица статистики (Результаты)
- Обслуживание клиентов
- Опыт сотрудников
- Знакомство с брендом
- Опыт использования продукта
- Core XM
- Дизайн ХМ
Qtip: Доступна новая версия результатов. Чтобы подписаться на новые панели результатов, перейдите на вкладку Результаты и нажмите Попробовать сейчас .
О таблицах статистики
Таблицы статистики
помогают вам увидеть несколько сводных показателей для выбранного вами источника данных. Эта визуализация оценивает все ответы, собранные для вашего источника данных, и отображает вычисленные результаты, такие как среднее значение и стандартное отклонение.
Параметры настройки
Общие настройки см. на странице поддержки Обзор визуализаций. Ознакомьтесь с настройками, характерными для таблицы статистики.
Показать значения перекодирования
При выборе Показать значения перекодирования значения перекодирования будут отображаться рядом с каждым вариантом ответа.
Столбцы
Вы можете настроить информацию, включенную в вашу таблицу статистики. Установите флажок рядом с каждым элементом, который вы хотите включить.
- Минимум: Наименьшее собранное значение.
- Максимум: Наибольшее собранное значение.
- Среднее значение: Среднее значение всех собранных значений.
- Стандартное отклонение: Стандартное отклонение для всех собранных значений.
- Дисперсия: Дисперсия по всем собранным значениям.
- Всего ответов: Общее количество собранных ответов, вносящих вклад в статистику.
- Верхний ящик: Верхний ящик — это процент респондентов, попадающих в верхние части шкалы. Вы можете указать, сколько точек шкалы включено в это поле, введя текст в поле.
  Пример: Существует три группы NPS®. Если установить его равным 3, верхняя ячейка будет равна 100% респондентов, поскольку 100% респондентов ответили на вопросы. Но если вы измените значение верхнего поля на 1, оно будет смотреть только на промоутеров, а процент будет соответствовать проценту респондентов, которые были промоутерами.
- Нижняя ячейка: Нижняя ячейка — это процент респондентов, которые соответствуют нижним концам шкалы. Вы можете указать, сколько точек шкалы включено в это поле, введя текст в поле.
  Qtip: Верхнее и нижнее поле — это варианты только для вопросов со шкалой, таких как множественный выбор. Непрерывные переменные, такие как ползунки и ввод текста, не могут отображать верхнее и нижнее поле.
Qtip : на данный момент отчеты Qualtrics не могут отображать медиану.
Перемещение таблицы
Иногда в таблице может быть несколько измерений. Например, предположим, что у вас есть матричная таблица с утверждениями. Или у вас есть вопрос об удовлетворенности с множественным выбором, и вы применили разбивку по полу к визуализации.
В этом случае отображается параметр Транспонировать таблицу . Это позволяет вам переключать строки (утверждения или разбивки) и столбцы (какие статистические данные вы включили).
Если вы объединяете двумерный вопрос (например, матричную таблицу) с разбивкой, Транспонировать разбивки позволяет переключать разбивку с содержимым из источника данных.
Совместимость
Таблица статистики совместима только с переменными, которые могут иметь числовой формат.
- Один ответ Множественный выбор
- Net Promoter Score
- Матричная таблица с одним ответом
- Таблицы биполярной, ранговой, профильной, постоянной суммы и MaxDiff Matrix
- Ввод текста с числовой проверкой
- Поле формы с числовой проверкой
- Открытые текстовые поля в других вопросах, таких как Матричные таблицы ввода текста, столбцы ввода текста в столбцах «Рядом» и текстовые поля «Другое», которые имеют числовую проверку
- Бок о бок
  Qtip: Должны быть поля с несколькими вариантами ответов или поле ввода текста с числовой проверкой.
  No related posts.