App Store: Синус Косинус Тангенс
Описание
Здесь объясняется поведение основных функций синуса, косинуса и тангенса. Вы можете изменять амплитуду и частоту функции. Кроме того, вы можете ввести значение x или периодический шаг для нужного вам решения. Приложение показывает все важные вычисления, предоставляет информационное изображение и отображает график.
Поддерживаются десятичные и дробные числа, отрицательные значения и π. Решение показывается шаг за шагом. Все вычисления сохраняются в истории. Окончательным решением можно поделиться.
[ Содержание ]
— все важные величины для синуса, косинуса и тангенса
— область определения, область значений, длина периода, максимум, минимум, нули и полюса функций
— доказательство симметрии и периодического поведения функций
— результаты также вычисляются как π-значение
— графики для синуса, косинуса и тангенса
— функция истории для сохранения вводимых данных
— подробное решение
— поддерживаются отрицательные значения, десятичные числа, дроби и π
[ Использование ]
— имеются поля для ввода значений с помощью специальной клавиатуры
— нажмите кнопку с галочкой в правом нижнем углу, чтобы начать вычисления
— если значения отсутствуют, приложение будет использовать значения по умолчанию
— если значения неверны, соответствующее поле будет выделено красным цветом
— записи в истории можно удалять или сортировать
— если выбрать запись в истории, она будет автоматически загружена для расчета
— вся история может быть удалена нажатием одной кнопки
— решениями можно обмениваться
000Z» aria-label=»14 ноября 2022 г.»>14 нояб. 2022 г.
Версия 1.11
— Hindi and Indonesian translation added
Разработчик Flooki указал, что в соответствии с политикой конфиденциальности приложения данные могут обрабатываться так, как описано ниже. Подробные сведения доступны в политике конфиденциальности разработчика.
Данные, используемые для отслеживания информации
Следующие данные могут использоваться для отслеживания информации о пользователе в приложениях и на сайтах, принадлежащих другим компаниям:
- Геопозиция
- Идентификаторы
- Данные об использовании
- Диагностика
Связанные с пользователем данные
Может вестись сбор следующих данных, которые связаны с личностью пользователя:
- Геопозиция
- Идентификаторы
- Данные об использовании
- Диагностика
Не связанные с пользователем данные
Может вестись сбор следующих данных, которые не связаны с личностью пользователя:
Конфиденциальные данные могут использоваться по-разному в зависимости от вашего возраста, задействованных функций или других факторов. Подробнее
Подробнее
Информация
- Провайдер
- Glindemann, Sennoun, Langer GbR
- Размер
- 31,5 МБ
- Категория
- Образование
- Возраст
- 4+
- Copyright
- © 2022 Glindemann, Sennoun, Langer GbR
- Цена
- Бесплатно
- Сайт разработчика
- Поддержка приложения
- Политика конфиденциальности
Другие приложения этого разработчика
Вам может понравиться
Выражения — Геометрия
Графики: синус, косинус и тангенс
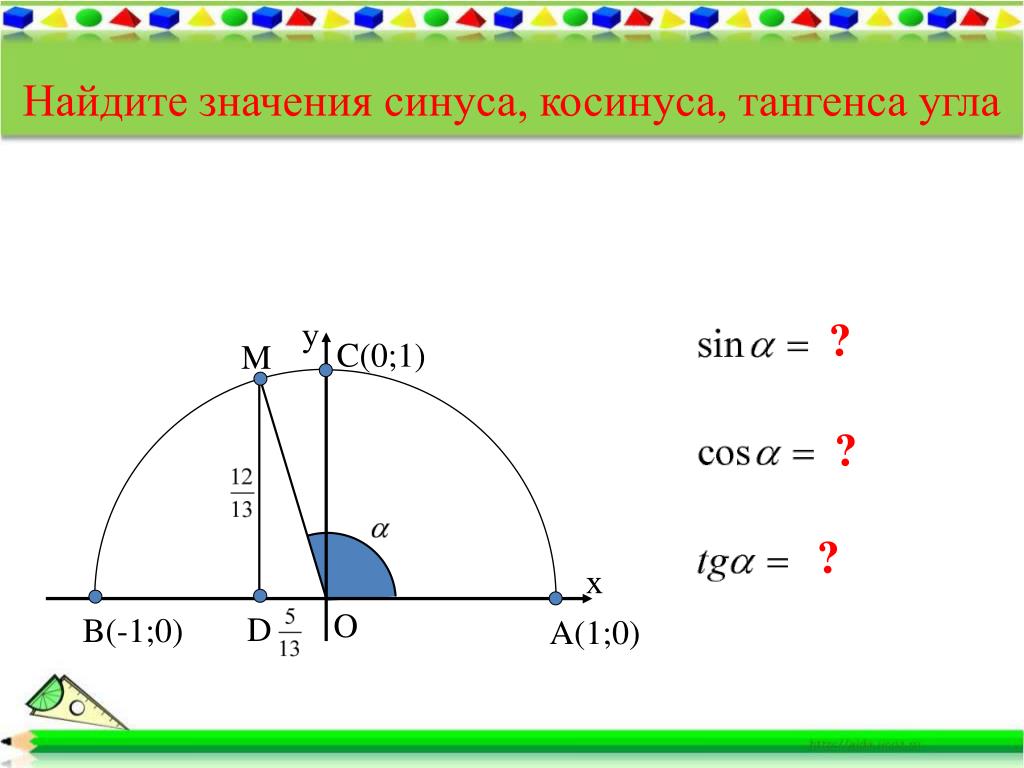
Возможно, вы заметили в предыдущем разделе некоторые определенные отношения между величиной угла и значениями его тригонометрической функции:
Для углов до 90° увеличение угла A также
увеличить длину противоположной стороны (при условии, что гипотенуза остается
то же самое, что показано здесь).
После поворота на 90° треугольник переворачивается горизонтально, и противоположная и соседняя стороны начнут соответственно уменьшаться или увеличиваться:
Итак, синус начинает убывать, а косинус начинает увеличивать. Они снова меняют направление после 180°, и снова после 270°. Наконец, после 360° весь рисунок повторяется, потому что они основаны на измерениях углов (которые являются периодическими), тригонометрических функции периодические.
Если бы вы построили график синусоидальных значений углов в диапазоне от нуля до 360 ° вы увидите катящуюся волну, также известную как «синусоида»:
. Косинус показывает аналогичную картину, 90 градусов от
фаза.
Tangent показывает совершенно другой график, потому что его результаты стремятся к бесконечности под углами около 90 и 270 градусов. На этих углах длина прилегающей стороны становится все меньше, а противоположная сторона приближается к длине гипотенузы треугольника. В результате значения тангенса начинают быстро приближаться к бесконечности. Потому что «бесконечность» не является допустимым возвращаемым значением, After Effects возвращает смехотворно большое значение для тангенса (90) или тангенса (270) – более 5 квадриллионов.
Вы заметите, что результаты касательной медленно меняются вокруг
углы 0 или 180 градусов, но быстро меняются при углах, близких к 90 или
270 градусов. Например, от нуля до 89 градусов тангенс увеличивается
с нуля до примерно 57,3; но в этой последней степени от 89 до 90,
тангенс увеличивается с 57,3 до примерно 5 квадриллионов.
Вы также заметите, что результаты тангенса являются прерывистыми — они переключаться с положительного на отрицательное сразу после пересечения 90 или 270 градусов. Это связано с тем, что соседняя сторона меняет направление в этих местах. углы.
Наконец, период касательной (диапазон, в котором она начинается для повторения значений) составляет всего 180°.
Интерактивная демонстрация
Вот простой проект, демонстрирующий, как тригонометрические функции относятся к углам. В проекте сплошной желтый кружок управляет вращением линиив дополнение к рисованию дуги, указывающей центральный угол, и противолежащие и прилежащие стороны соответствующего прямоугольного треугольника. Цифры в нижнем углу показывают размер центрального угла и результаты этих трех тригонометрических функций.
Нажмите здесь, чтобы загрузить
этот проект. (пользователи Windows нажимают
здесь.)
(пользователи Windows нажимают
здесь.)
Когда вы смотрите на этот проект и другие рисунки на этой странице вы должны заметить тесную связь между тригонометрическими функции и круги. На самом деле, в некоторых старых учебниках эти функции называются «круговые функции». Это потому, что множество всех прямоугольных треугольников с та же гипотенуза образует окружность, причем гипотенуза определяет ее радиус. Мы рассмотрим эту связь в следующем разделе.
, если у меня есть синус, косинус или тангенс, как мне найти опорный угол в градусах?
ТригонометрияКоллет Л.
спросил 28.08.16cos 0 = 1/2 как определить базовый угол в градусах
Подписаться І 4
Подробнее
Отчет
3 ответа от опытных наставников
Лучший Новейшие Самый старыйАвтор: Лучшие новыеСамые старые
Кеннет С. ответил 28.08.16
ответил 28.08.16
Репетитор
4,8 (62)
Я раскрываю тайны и секреты тригонометрии, и вам это понравится.
Смотрите таких репетиторов
Смотрите таких репетиторов
Так что это просто вопрос определения применимого квадранта.
Квадранты сини по косинусам
I + +
II + —
III — —
IV — +
Вы выясняете контрольный угол, рисуя заданный угол с его начальной в стандартное положение (направление на восток) и приземление конечной стороны, где это необходимо, после углового поворота против часовой стрелки на указанную величину.
Базовый угол, всегда положительный, представляет собой острый угол между конечной стороной и горизонтальной осью.
Например, исходный угол для 210 градусов равен 30 o , так что гипотенуза исходного треугольника равна единице (единичная окружность), а катеты исходного треугольника равны:
Вертикаль: -½, значение sin 210 0
По горизонтали: -½√3, значение cos 210 o
Голосовать за 1 Понизить
Подробнее
Отчет
Майкл Дж. ответил 28.08.16
Репетитор
5 (5)
Эффективный репетитор STEM средней школы и лидер CUNY по математике
См. таких репетиторов
Смотрите таких репетиторов
В дополнение к ответу Кеннета я хотел бы показать вам таблицу, которая объясняет, почему каждая тригонометрическая функция положительна и отрицательна в определенных квадрантах.
https://www.wyzant.com/resources/files/330953/trigonometric_functions_in_a_coordinate_system
Голосовать за 0 Понизить
Подробнее
Отчет
Марк М. ответил 28.08.16
Репетитор
5,0 (248)
Учитель математики — высококвалифицированный специалист NCLB
Об этом репетиторе ›
Об этом репетиторе ›
cos θ = 1/2
θ = π/3
Это одно из значений треугольника 30-60-90.
Заучить их все будет очень полезно.
Голосовать за 0 Понизить голос
Подробнее
Отчет
Все еще ищете помощи? Получите правильный ответ, быстро.