Повторяем и систематизируем школьный курс алгебры и начал анализа
Повторяем и систематизируем школьный курс алгебры и начал анализа
ОглавлениеПРЕДИСЛОВИЕГЛАВА I. § 1. НАТУРАЛЬНЫЕ ЧИСЛА И ДЕЙСТВИЯ НАД НИМИ § 2. СЛОЖЕНИЕ И ЗАКОНЫ СЛОЖЕНИЯ § 3.  ВЫЧИТАНИЕ ВЫЧИТАНИЕ§ 4. УМНОЖЕНИЕ И ЗАКОНЫ УМНОЖЕНИЯ § 6. ПРИЗНАКИ ДЕЛИМОСТИ ЧИСЕЛ § 7. ПОНЯТИЕ МНОЖЕСТВА § 8. ОПЕРАЦИИ НАД МНОЖЕСТВАМИ § 9. ВЗАИМНО ОДНОЗНАЧНОЕ СООТВЕТСТВИЕ § 10. ПРОСТЫЕ И СОСТАВНЫЕ ЧИСЛА § 11. НАИБОЛЬШИЙ ОБЩИЙ ДЕЛИТЕЛЬ § 12. НАИМЕНЬШЕЕ ОБЩЕЕ КРАТНОЕ Контрольные вопросы ГЛАВА II § 1. ОБЫКНОВЕННЫЕ ДРОБИ § 2. ПРАВИЛЬНЫЕ И НЕПРАВИЛЬНЫЕ ДРОБИ § 3. ОСНОВНОЕ СВОЙСТВО ДРОБИ § 4. СЛОЖЕНИЕ И ВЫЧИТАНИЕ ДРОБЕЙ § 5. УМНОЖЕНИЕ ДРОБЕЙ § 6. ДЕЛЕНИЕ ДРОБЕЙ § 7. ДЕСЯТИЧНЫЕ ДРОБИ § 8. ОБРАЩЕНИЕ ДЕСЯТИЧНОЙ ДРОБИ В ОБЫКНОВЕННУЮ И ОБЫКНОВЕННОЙ В ДЕСЯТИЧНУЮ. ПЕРИОДИЧЕСКИЕ ДРОБИ § 9. ОТНОШЕНИЕ. ПРОПОРЦИЯ § 10. СВОЙСТВА ПРОПОРЦИИ § 11. ПРОЦЕНТ. ОСНОВНЫЕ ЗАДАЧИ НА ПРОЦЕНТЫ § 12. ДЕЛЕНИЕ ЧИСЛА НА ЧАСТИ, ПРЯМО И ОБРАТНО ПРОПОРЦИОНАЛЬНЫЕ ДАННЫМ ЧИСЛАМ Контрольные вопросы ГЛАВА III § 1. КООРДИНАТНАЯ ПРЯМАЯ § 2. МНОЖЕСТВО ЦЕЛЫХ ЧИСЕЛ § 3. МНОЖЕСТВО РАЦИОНАЛЬНЫХ ЧИСЕЛ § 4. МОДУЛЬ ЧИСЛА § 5. 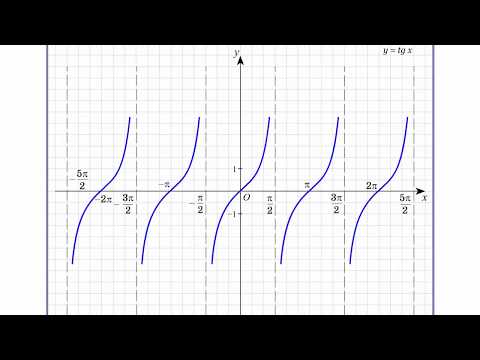 СРАВНЕНИЕ РАЦИОНАЛЬНЫХ ЧИСЕЛ СРАВНЕНИЕ РАЦИОНАЛЬНЫХ ЧИСЕЛ§ 6. СЛОЖЕНИЕ И ВЫЧИТАНИЕ РАЦИОНАЛЬНЫХ ЧИСЕЛ § 7. УМНОЖЕНИЕ И ДЕЛЕНИЕ РАЦИОНАЛЬНЫХ ЧИСЕЛ § 8. ВОЗВЕДЕНИЕ РАЦИОНАЛЬНЫХ ЧИСЕЛ В СТЕПЕНЬ С НАТУРАЛЬНЫМ ПОКАЗАТЕЛЕМ Контрольные вопросы ГЛАВА IV § 1. СВОЙСТВА СТЕПЕНИ С НАТУРАЛЬНЫМ ПОКАЗАТЕЛЕМ § 2. ЧИСЛОВЫЕ ВЫРАЖЕНИЯ § 3. ВЫРАЖЕНИЯ С ПЕРЕМЕННЫМИ § 4. ТОЖДЕСТВЕННО РАВНЫЕ ВЫРАЖЕНИЯ § 5. ОДНОЧЛЕНЫ § 6. МНОГОЧЛЕНЫ § 7. ПРЕОБРАЗОВАНИЕ СУММЫ И РАЗНОСТИ МНОГОЧЛЕНОВ § 8. УМНОЖЕНИЕ МНОГОЧЛЕНА НА ОДНОЧЛЕН И МНОГОЧЛЕНА НА МНОГОЧЛЕН § 9. РАЗЛОЖЕНИЕ МНОГОЧЛЕНА НА МНОЖИТЕЛИ СПОСОБОМ ВЫНЕСЕНИЯ ОБЩЕГО МНОЖИТЕЛЯ ЗА СКОБКИ § 10. РАЗЛОЖЕНИЕ МНОГОЧЛЕНА НА МНОЖИТЕЛИ СПОСОБОМ ГРУППИРОВКИ § 11. ФОРМУЛЫ СОКРАЩЕННОГО УМНОЖЕНИЯ Контрольные вопросы ГЛАВА V § 1. ДРОБЬ § 2. ЦЕЛЫЕ И ДРОБНЫЕ ВЫРАЖЕНИЯ § 3. ТОЖДЕСТВЕННОЕ ПРЕОБРАЗОВАНИЕ СУММЫ И РАЗНОСТИ ДВУХ ДРОБЕЙ § 4. ТОЖДЕСТВЕННОЕ ПРЕОБРАЗОВАНИЕ ПРОИЗВЕДЕНИЯ И ЧАСТНОГО ДВУХ ДРОБЕЙ Контрольные вопросы ГЛАВА VI § 1.  ПОНЯТИЕ ОБ ИРРАЦИОНАЛЬНОМ ЧИСЛЕ ПОНЯТИЕ ОБ ИРРАЦИОНАЛЬНОМ ЧИСЛЕ§ 2. РАЗВИТИЕ ПОНЯТИЯ О ЧИСЛЕ. МНОЖЕСТВО ДЕЙСТВИТЕЛЬНЫХ ЧИСЕЛ § 3. КОРЕНЬ СТЕПЕНИ ИЗ ДЕЙСТВИТЕЛЬНОГО ЧИСЛА § 4. АЛГОРИТМ ИЗВЛЕЧЕНИЯ КВАДРАТНОГО КОРНЯ ИЗ ЧИСЛА § 5. АРИФМЕТИЧЕСКИЕ ДЕЙСТВИЯ С ДЕЙСТВИТЕЛЬНЫМИ ЧИСЛАМИ § 6. ПРЕОБРАЗОВАНИЯ АРИФМЕТИЧЕСКИХ КОРНЕЙ § 7. СТЕПЕНЬ С ЦЕЛЫМ И ДРОБНЫМ ПОКАЗАТЕЛЕМ Контрольные вопросы ГЛАВА VII § 1. УРАВНЕНИЯ С ОДНОЙ ПЕРЕМЕННОЙ § 2. ПОНЯТИЕ О РАВНОСИЛЬНОСТИ УРАВНЕНИЙ § 3. СВОЙСТВА ЧИСЛОВЫХ РАВЕНСТВ И ТЕОРЕМЫ О РАВНОСИЛЬНОСТИ УРАВНЕНИЙ § 4. ЛИНЕЙНОЕ УРАВНЕНИЕ С ОДНОЙ ПЕРЕМЕННОЙ, СОДЕРЖАЩЕЕ ПАРАМЕТР Контрольные вопросы ГЛАВА VIII § 1. ПОНЯТИЕ ФУНКЦИИ § 2. СПОСОБЫ ЗАДАНИЯ ФУНКЦИИ § 3. МОНОТОННОСТЬ ФУНКЦИИ § 4. ЧЕТНЫЕ И НЕЧЕТНЫЕ ФУНКЦИИ СПРАВОЧНЫЙ МАТЕРИАЛ § 5. ПЕРИОДИЧЕСКИЕ ФУНКЦИИ § 6. ПРОМЕЖУТКИ ЗНАКОПОСТОЯНСТВА И КОРНИ ФУНКЦИИ Контрольные вопросы ГЛАВА IX § 1. ГЕОМЕТРИЧЕСКИЕ ПРЕОБРАЗОВАНИЯ ГРАФИКОВ ФУНКЦИЙ § 2. ЛИНЕЙНАЯ ФУНКЦИЯ И ЕЕ ГРАФИК § 3.  КВАДРАТИЧНАЯ ФУНКЦИЯ И ЕЕ ГРАФИК КВАДРАТИЧНАЯ ФУНКЦИЯ И ЕЕ ГРАФИК§ 4. ФУНКЦИЯ y=k/x И ЕЕ ГРАФИК § 5. ДРОБНО-ЛИНЕЙНАЯ ФУНКЦИЯ И ЕЕ ГРАФИК Контрольные вопросы ГЛАВА X § 1. КВАДРАТНЫЕ УРАВНЕНИЯ § 2. ТЕОРЕМА ВИЕТА § 3. ГРАФИЧЕСКИЙ СПОСОБ РЕШЕНИЯ КВАДРАТНЫХ УРАВНЕНИЙ § 4. УРАВНЕНИЕ СО МНОГИМИ ПЕРЕМЕННЫМИ § 5. СИСТЕМЫ УРАВНЕНИЙ Контрольные вопросы ГЛАВА XI § 1. НЕРАВЕНСТВА § 2. ОСНОВНЫЕ СВОЙСТВА НЕРАВЕНСТВ § 3. ДЕЙСТВИЯ С НЕРАВЕНСТВАМИ § 4. ДОКАЗАТЕЛЬСТВА НЕРАВЕНСТВ § 5. НЕРАВЕНСТВА, СОДЕРЖАЩИЕ ПЕРЕМЕННУЮ § 6. РЕШЕНИЕ ЛИНЕЙНЫХ И КВАДРАТНЫХ НЕРАВЕНСТВ Контрольные вопросы § 1. СИСТЕМЫ И СОВОКУПНОСТИ НЕРАВЕНСТВ § 2. НЕРАВЕНСТВА И СИСТЕМЫ НЕРАВЕНСТВ С ДВУМЯ ПЕРЕМЕННЫМИ § 3. РЕШЕНИЕ НЕРАВЕНСТВ, СОДЕРЖАЩИХ ПЕРЕМЕННУЮ ПОД ЗНАКОМ МОДУЛЯ § 4. РЕШЕНИЕ РАЦИОНАЛЬНЫХ НЕРАВЕНСТВ МЕТОДОМ ПРОМЕЖУТКОВ Контрольные вопросы ГЛАВА XIII § 1. ЧИСЛОВАЯ ПОСЛЕДОВАТЕЛЬНОСТЬ § 2. АРИФМЕТИЧЕСКАЯ ПРОГРЕССИЯ § 3. ГЕОМЕТРИЧЕСКАЯ ПРОГРЕССИЯ § 4. 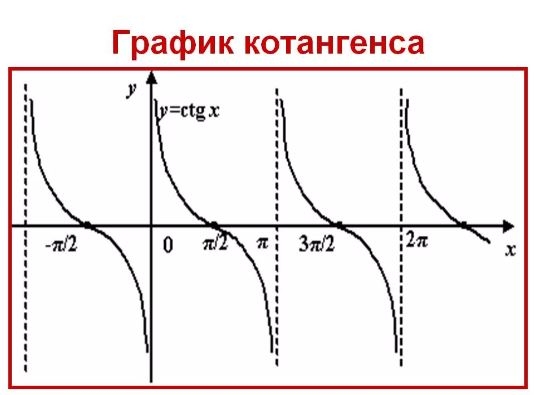 СУММА БЕСКОНЕЧНОЙ ГЕОМЕТРИЧЕСКОЙ ПРОГРЕССИИ ПРИ |q|Контрольные вопросы СУММА БЕСКОНЕЧНОЙ ГЕОМЕТРИЧЕСКОЙ ПРОГРЕССИИ ПРИ |q|Контрольные вопросыГЛАВА XIV § 1. ГРАДУСНОЕ ИЗМЕРЕНИЕ УГЛОВЫХ ВЕЛИЧИН § 2. РАДИАННОЕ ИЗМЕРЕНИЕ УГЛОВЫХ ВЕЛИЧИН § 3. СИНУС И КОСИНУС ЧИСЛОВОГО АРГУМЕНТА § 4. ТАНГЕНС И КОТАНГЕНС ЧИСЛОВОГО АРГУМЕНТА. СЕКАНС И КОСЕКАНС ЧИСЛА а § 5. ОСНОВНЫЕ ТРИГОНОМЕТРИЧЕСКИЕ ТОЖДЕСТВА § 6. ДОПОЛНИТЕЛЬНЫЕ СВОЙСТВА ТРИГОНОМЕТРИЧЕСКИХ ФУНКЦИЙ Контрольные вопросы ГЛАВА XV § 1. ФОРМУЛЫ ПРИВЕДЕНИЯ § 2. ФОРМУЛЫ СЛОЖЕНИЯ § 3. ФОРМУЛЫ ДВОЙНОГО УГЛА СПРАВОЧНЫЙ МАТЕРИАЛ § 4. ПРЕОБРАЗОВАНИЕ ПРОИЗВЕДЕНИЯ ТРИГОНОМЕТРИЧЕСКИХ ФУНКЦИЙ В СУММУ § 5. ФОРМУЛЫ СУММЫ И РАЗНОСТИ ОДНОИМЕННЫХ ТРИГОНОМЕТРИЧЕСКИХ ФУНКЦИЙ § 6. ТРИГОНОМЕТРИЧЕСКИЕ ФУНКЦИИ ПОЛОВИННОГО АРГУМЕНТА § 7. ВЫРАЖЕНИЕ ТРИГОНОМЕТРИЧЕСКИХ ФУНКЦИЙ ЧЕРЕЗ ТАНГЕНС ПОЛОВИННОГО АРГУМЕНТА Контрольные вопросы ГЛАВА XVI § 1. СВОЙСТВА ФУНКЦИИ y = sin(x) И ЕЕ ГРАФИК § 2. СВОЙСТВА ФУНКЦИ И у = cos(x) И ЕЕ ГРАФИК § 3. СВОЙСТВА ФУНКЦИ И у=tg(x) И ЕЕ ГРАФИК § 4. 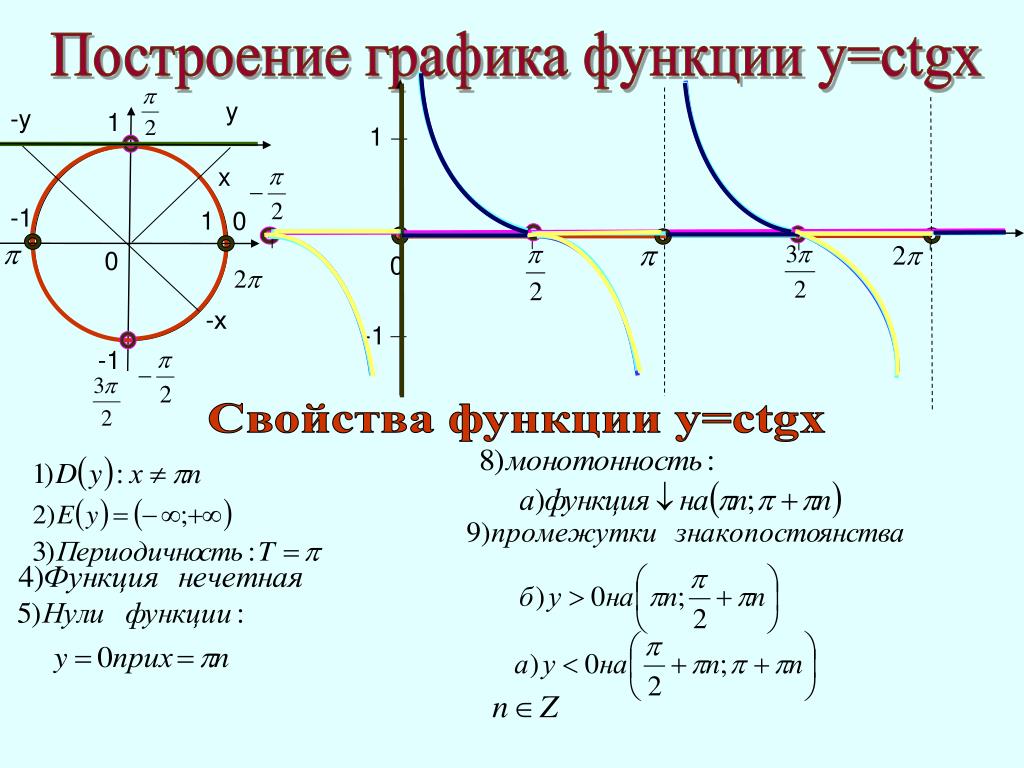 СВОЙСТВА ФУНКЦИ И y=ctg(x) И ЕЕ ГРАФИК СВОЙСТВА ФУНКЦИ И y=ctg(x) И ЕЕ ГРАФИК§ 5. НАХОЖДЕНИЕ ПЕРИОДОВ ТРИГОНОМЕТРИЧЕСКИХ ФУНКЦИЙ Контрольные вопросы ГЛАВА XVII § 1. АРКСИНУС И АРККОСИНУС § 2. АРКТАНГЕНС И АРККОТАНГЕНС Контрольные вопросы ГЛАВА XVIII § 1. РЕШЕНИЕ УРАВНЕНИЙ ВИДА cos(x)=а § 2. РЕШЕНИЕ УРАВНЕНИЙ ВИДА sin(x)=a § 3. РЕШЕНИЕ УРАВНЕНИЙ ВИДА tg(х)=а § 4. РЕШЕНИЕ ТРИГОНОМЕТРИЧЕСКИХ УРАВНЕНИЙ, ПРИВОДИМЫХ К КВАДРАТНОМУ § 6. ТРИГОНОМЕТРИЧЕСКИЕ УРАВНЕНИЯ, РЕШАЕМЫЕ С ПОМОЩЬЮ ФОРМУЛ СЛОЖЕНИЯ, ПОНИЖЕНИЯ СТЕПЕНИ § 7. РЕШЕНИЕ СИСТЕМ ТРИГОНОМЕТРИЧЕСКИХ УРАВНЕНИЙ Контрольные вопросы ГЛАВА XIX § 1. РЕШЕНИЕ ТРИГОНОМЕТРИЧЕСКИХ НЕРАВЕНСТВ ВИДА sin(х) > а, sin(х) § 2. РЕШЕНИЕ ТРИГОНОМЕТРИЧЕСКИХ НЕРАВЕНСТВ ВИДА cos(x) > a, cos(x) § 3. РЕШЕНИЕ ТРИГОНОМЕТРИЧЕСКИХ НЕРАВЕНСТВ ВИДА tg(х) > a, tg(х) § 4. РЕШЕНИЕ ТРИГОНОМЕТРИЧЕСКИХ НЕРАВЕНСТВ ГЛАВА XX § 1. ПРИРАЩЕНИЕ АРГУМЕНТА И ПРИРАЩЕНИЕ ФУНКЦИИ § 2. 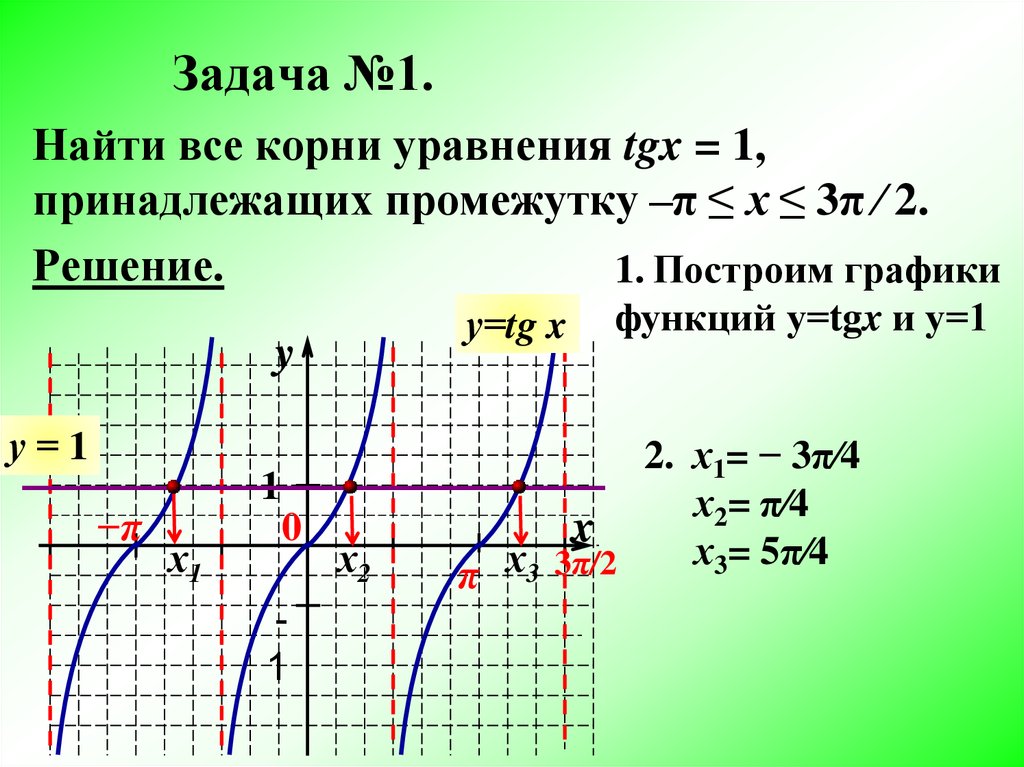 ПРЕДЕЛ ФУНКЦИИ ПРЕДЕЛ ФУНКЦИИ§ 3. НЕПРЕРЫВНОСТЬ ФУНКЦИИ § 4. ОПРЕДЕЛЕНИЕ ПРОИЗВОДНОЙ § 5. ПРОИЗВОДНАЯ СУММЫ, ПРОИЗВЕДЕНИЯ, ЧАСТНОГО § 6. ПРОИЗВОДНАЯ СТЕПЕННОЙ И СЛОЖНОЙ ФУНКЦИИ § 7. ПРОИЗВОДНЫЕ ТРИГОНОМЕТРИЧЕСКИХ ФУНКЦИЙ Контрольные вопросы ГЛАВА XXI § 1. ПРИМЕНЕНИЕ ПРОИЗВОДНОЙ К НАХОЖДЕНИЮ ПРОМЕЖУТКОВ МОНОТОННОСТИ ФУНКЦИИ § 2. КРИТИЧЕСКИЕ ТОЧКИ ФУНКЦИИ, ЕЕ МАКСИМУМЫ И МИНИМУМЫ § 3. ОБЩАЯ СХЕМА ИССЛЕДОВАНИЯ ФУНКЦИИ § 4. ЗАДАЧИ НА НАХОЖДЕНИЕ НАИМЕНЬШЕГО И НАИБОЛЬШЕГО ЗНАЧЕНИЯ ФУНКЦИИ Контрольные вопросы ГЛАВА XXII § 1. ФОРМУЛЫ ПРИБЛИЖЕННЫХ ВЫЧИСЛЕНИЙ СПРАВОЧНЫЙ МАТЕРИАЛ § 2. КАСАТЕЛЬНАЯ К ГРАФИКУ ФУНКЦИИ § 3. СКОРОСТЬ И УСКОРЕНИЕ В ДАННЫЙ МОМЕНТ ВРЕМЕНИ § 4. ГРАФИКИ ГАРМОНИЧЕСКИХ КОЛЕБАНИЙ Контрольные вопросы ГЛАВА XXIII § 1. ПОТЕРЯННЫЕ И ПОСТОРОННИЕ КОРНИ ПРИ РЕШЕНИИ УРАВНЕНИЙ (НА ПРИМЕРАХ) § 2. ПОСТОРОННИЕ КОРНИ ИРРАЦИОНАЛЬНОГО УРАВНЕНИЯ (НА ПРИМЕРАХ) § 3. РЕШЕНИЕ ИРРАЦИОНАЛЬНЫХ УРАВНЕНИЙ § 4. РЕШЕНИЕ ИРРАЦИОНАЛЬНЫХ НЕРАВЕНСТВ СПРАВОЧНЫЙ МАТЕРИАЛ Контрольные вопросы ГЛАВА XXIV § 1.  ПОКАЗАТЕЛЬНАЯ ФУНКЦИЯ, ЕЕ СВОЙСТВА И ГРАФИК ПОКАЗАТЕЛЬНАЯ ФУНКЦИЯ, ЕЕ СВОЙСТВА И ГРАФИК§ 3. ПОКАЗАТЕЛЬНЫЕ НЕРАВЕНСТВА § 4. СИСТЕМЫ ПОКАЗАТЕЛЬНЫХ УРАВНЕНИЙ И НЕРАВЕНСТВ Контрольные вопросы ГЛАВА XXV § 1. ОБРАТНАЯ ФУНКЦИЯ § 2. ПОНЯТИЕ ЛОГАРИФМА § 3. СВОЙСТВА ЛОГАРИФМОВ § 4. ЛОГАРИФМИЧЕСКАЯ ФУНКЦИЯ, ЕЕ СВОЙСТВА И ГРАФИК § 5. ТЕОРЕМЫ О ЛОГАРИФМЕ ПРОИЗВЕДЕНИЯ, ЧАСТНОГО И СТЕПЕНИ. ФОРМУЛА ПЕРЕХОДА К НОВОМУ ОСНОВАНИЮ § 6. ДЕСЯТИЧНЫЕ ЛОГАРИФМЫ И ИХ СВОЙСТВА § 7. ЛОГАРИФМИРОВАНИЕ И ПОТЕНЦИРОВАНИЕ Контрольные вопросы ГЛАВА XXVI § 1. ЛОГАРИФМИЧЕСКИЕ УРАВНЕНИЯ § 2. ЛОГАРИФМИЧЕСКИЕ НЕРАВЕНСТВА § 3. СИСТЕМЫ ЛОГАРИФМИЧЕСКИХ УРАВНЕНИЙ И НЕРАВЕНСТВ § 4. ПРОИЗВОДНЫЕ ЛОГАРИФМИЧЕСКОЙ И ПОКАЗАТЕЛЬНОЙ ФУНКЦИЙ. ЧИСЛО e Контрольные вопросы ГЛАВА XXVII § 1. ПОНЯТИЕ ПЕРВООБРАЗНОЙ ФУНКЦИИ § 2. ОСНОВНОЕ СВОЙСТВО ПЕРВООБРАЗНОЙ ФУНКЦИИ § 3. ТРИ ПРАВИЛА НАХОЖДЕНИЯ ПЕРВООБРАЗНЫХ § 4. КРИВОЛИНЕЙНАЯ ТРАПЕЦИЯ И ЕЕ ПЛОЩАДЬ Контрольные вопросы ГЛАВА XXVIII § 1.  ФОРМУЛА НЬЮТОНА—ЛЕЙБНИЦА ФОРМУЛА НЬЮТОНА—ЛЕЙБНИЦА§ 2. ОСНОВНЫЕ ПРАВИЛА ИНТЕГРИРОВАНИЯ § 3. ВЫЧИСЛЕНИЕ ПЛОЩАДЕЙ С ПОМОЩЬЮ ИНТЕГРАЛА § 4. МЕХАНИЧЕСКИЕ И ФИЗИЧЕСКИЕ ПРИЛОЖЕНИЯ ОПРЕДЕЛЕННОГО ИНТЕГРАЛА ПРИЛОЖЕНИЕ Введение 1. Задачи на движение 2. Задачи на совместную работу 3. Задачи на планирование 4. Задачи на зависимость между компонентами арифметических действий 5. Задачи на проценты 6. Задачи на смеси (сплавы) 7. Задачи на разбавление |
Дистанционный репетитор — онлайн-репетиторы России и зарубежья
КАК ПРОХОДЯТ
ОНЛАЙН-ЗАНЯТИЯ?
Ученик и учитель видят и слышат
друг друга, совместно пишут на
виртуальной доске, не выходя из
дома!
КАК ВЫБРАТЬ репетитора
Выбрать репетитора самостоятельно
ИЛИ
Позвонить и Вам поможет специалист
8 (800) 333 58 91
** Время приема звонков с 10 до 22 по МСК
ПОДАТЬ ЗАЯВКУ
Россия +7Украина +380Австралия +61Белоруссия +375Великобритания +44Израиль +972Канада, США +1Китай +86Швейцария +41
Выбранные репетиторы
Заполните форму, и мы быстро и бесплатно подберем Вам дистанционного репетитора по Вашим пожеланиям.
Менеджер свяжется с Вами в течение 15 минут и порекомендует специалиста.
Отправляя форму, Вы принимаете Условия использования и даёте Согласие на обработку персональных данных
Вы также можете воспользоваться
расширенной формой подачи заявки
Как оплачивать и СКОЛЬКО ЭТО СТОИТ
от
800 до 5000 ₽
за 60 мин.
и зависит
ОТ ОПЫТА и
квалификации
репетитора
ОТ ПОСТАВЛЕННЫХ ЦЕЛЕЙ ОБУЧЕНИЯ
(например, подготовка к олимпиадам, ДВИ стоит дороже, чем подготовка к ЕГЭ)
ОТ ПРЕДМЕТА (например, услуги репетиторовиностранных языков дороже)
Оплата непосредственно репетитору, удобным для Вас способом
Почему я выбираю DisTTutor
БЫСТРЫЙ ПОДБОР
РЕПЕТИТОРА И
ИНДИВИДУАЛЬНЫЙ ПОДХОД
ОПТИМАЛЬНОЕ
СООТНОШЕНИЕ ЦЕНЫ И
КАЧЕСТВА
ПРОВЕРЕНЫ ДОКУМЕНТЫ ОБ ОБРАЗОВАНИИ У ВСЕХ РЕПЕТИТОРОВ
НАДЕЖНОСТЬ И ОПЫТ.
DisTTutor на рынке с 2008 года.
ПРОВЕДЕНИЕ БЕСПЛАТНОГО, ПРОБНОГО УРОКА
ЗАМЕНА РЕПЕТИТОРА, ЕСЛИ ЭТО НЕОБХОДИМО
376356 УЧЕНИКОВ ИЗ РАЗНЫХ СТРАН МИРА
уже сделали свой выбор
И вот, что УЧЕНИКИ ГОВОРЯТ
о наших репетиторах
Владимир Александрович Кузьмин
«
Тренинг у Кузьмина В. А. проходил в экстремальных условиях. Мой модем совершенно не держал соединение. За время часового тренинга связь прерывалась практически постоянно. Ясно, что в таких условиях чрезвычайно непросто чему-то учить.
Однако Владимир Александрович проявил удивительную выдержку и терпение. Неоднократно он перезванивал мне на сотовый телефон, чтобы дать пояснения или комментарии.
Ценой больших усилий нам удалось рассмотреть три программы: ConceptDraw MINDMAP Professional Ru, GeoGebra и Ultra Flash Video FLV Converter. Владимир Александрович открыл мне курс на платформе dist-tutor.info и научил подключать и настраивать Виртуальный кабинет, порекомендовав изучать возможности этого ресурса, чтобы постепенно уходить от использования Skype. В итоге, занятие мне очень понравилось! Спокойное объяснение материала, дружелюбный настрой, подбадривание дистанционного ученика даже в самых непростых ситуациях — вот далеко не полный перечень качеств Владимира Александровича как дистанционного педагога. Мне следует учиться у такого замечательного репетитора!
В итоге, занятие мне очень понравилось! Спокойное объяснение материала, дружелюбный настрой, подбадривание дистанционного ученика даже в самых непростых ситуациях — вот далеко не полный перечень качеств Владимира Александровича как дистанционного педагога. Мне следует учиться у такого замечательного репетитора!
«
Вячеслав Юрьевич Матыкин
Чулпан Равилевна Насырова
«
Я очень довольна репетитором по химии. Очень хороший подход к ученику,внятно объясняет. У меня появились сдвиги, стала получать хорошие оценки по химии. Очень хороший преподаватель. Всем , кто хочет изучать химию, советую только её !!!
«
Алина Крякина
Надежда Васильевна Токарева
«
Мы занимались с Надеждой Васильевной по математике 5 класса. Занятия проходили в удобное для обоих сторон время. Если необходимо было дополнительно позаниматься во внеурочное время, Надежда Васильевна всегда шла навстречу. Ей можно было позванить, чтобы просто задать вопрос по непонятной задачке из домашнего задания. Моя дочь существенно подняла свой уровень знаний по математике и начала демонстрировать хорошие оценки. Мы очень благодарны Надежде Васильевне за помощь в этом учебном году, надеемся на продолжение отношений осенью.
Моя дочь существенно подняла свой уровень знаний по математике и начала демонстрировать хорошие оценки. Мы очень благодарны Надежде Васильевне за помощь в этом учебном году, надеемся на продолжение отношений осенью.
«
Эльмира Есеноманова
Ольга Александровна Мухаметзянова
«
Подготовку к ЕГЭ по русскому языку мой сын начал с 10 класса. Ольга Александровна грамотный педагог, пунктуальный, ответственный человек. Она всегда старается построить занятие так, чтобы оно прошло максимально плодотворно и интересно. Нас абсолютно все устраивает в работе педагога. Сотрудничество приносит отличные результаты, и мы его продолжаем. Спасибо.
«
Оксана Александровна
Клиентам
- Репетиторы по математике
- Репетиторы по русскому языку
- Репетиторы по химии
- Репетиторы по биологии
- Репетиторы английского языка
- Репетиторы немецкого языка
Репетиторам
- Регистрация
- Публичная оферта
- Библиотека
- Бан-лист репетиторов
Партнеры
- ChemSchool
-
PREPY.
 RU
RU
- Class
Графики функций тангенса и котангенса
Графики функций тангенса и котангенсаВведение
Задачи: Определить свойства функции тангенса и котангенса; построить тангенс и котангенсные функции.
Занятие 1 для учащихся — построение графика y = tanx
I. Во-первых, давайте установим и осмотрим стол координат некоторых точек, которые будут удовлетворять уравнение y = tanx.
1. Откройте электронную таблицу Excel. Метка столбца A «координаты x» и столбец B «координаты y». Установите оба столбца для округления до 4 знаков после запятой.
2. Заполните координаты x в столбце A. в диапазоне от -2p до 2p с шагом p/4. Помните, что x представляет угловую меру — мы используя радианы в качестве наших единиц.
3. Заполните координаты y в столбце B. используя уравнение, y = tanx.
Что вы заметили в значениях в эта колонка? Что означает #####? Можете ли вы предсказать, что график будет выглядеть?
II. Графики в графическом калькуляторе.
1. График y = tanx от -2p до 2p.
2. Объясните, что означают вертикальные линии на график представляет.
3. Какова продолжительность одного периода у = Танкс?
4. У касательных графов есть «амплитуда?» Почему или почему нет?
III. Проверь себя.
Нарисуйте (от руки!) что график y = tanx будет выглядеть, учитывая следующие ограничения домена. Будьте внимательны к тому, где график пересекает ось X, где точки перегиба и асимптоты.
а) 2 от 4 до
б) -4 р до 0
в) -3 р /2 до р/2
Ключ учителя для задания для учащихся 1
И.
2. В ячейке A2 введите «=-2*pi()». В ячейке A3 введите «=A2+pi()/ 4». Перетащите, чтобы заполнить до строки 18.
3. В ячейке B2 введите «=tan(A2)». Перетащите, чтобы заполнить строку 18.
Вот пример таблицы:
| -6,2832 | 0 |
| -5,4978 | 1 |
| -4,7124 | ##### |
| -3,9270 | -1 |
| -3,1416 | 0 |
| -2,3562 | 1 |
| -1,5708 | ##### |
| -0,7854 | -1 |
| 0 | 0 |
| 0,7854 | 1 |
1. 5708 5708 | ##### |
| 2,3562 | -1 |
| 3.1416 | 0 |
| 3,9270 | 1 |
| 4,7124 | ##### |
| 5,4978 | -1 |
| 6.2832 | 0 |
Ответы: значения в столбце координат Y повторить. ##### означает «неопределенный».
II.
1. Вот пример графика:
2. Вертикальные линии – асимптоты график.
3. Одна точка = с.
4. Нет. Касательные графики всегда продолжаются по вертикали. направления, поэтому они не могут иметь «высоту».
III.
а)
б)
в)
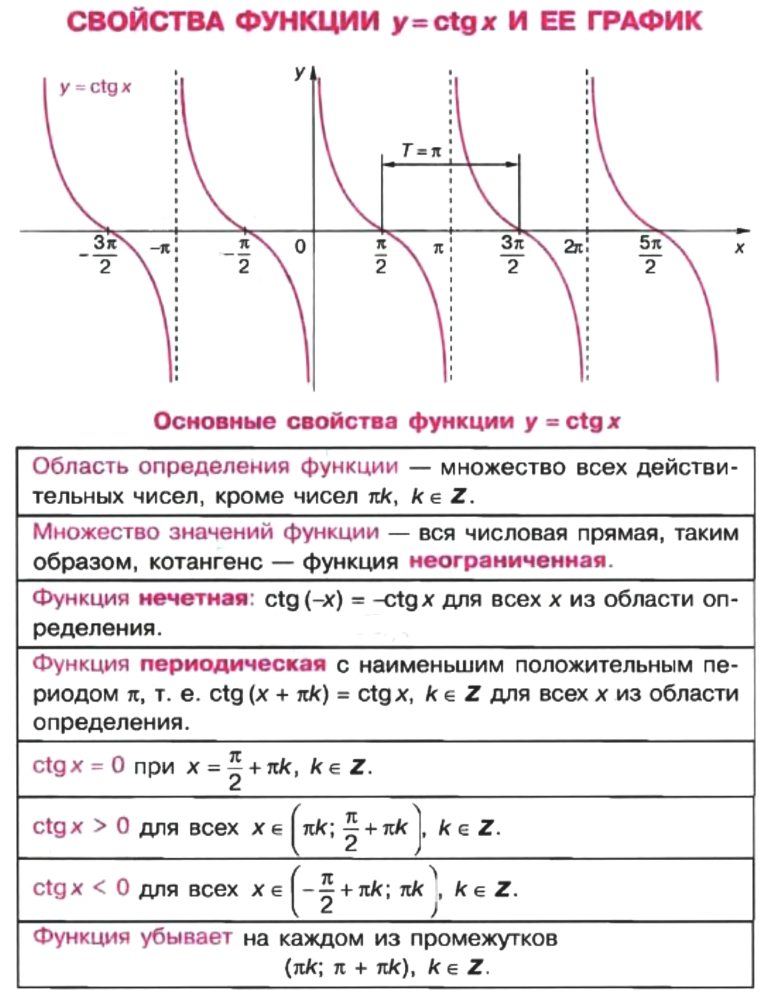
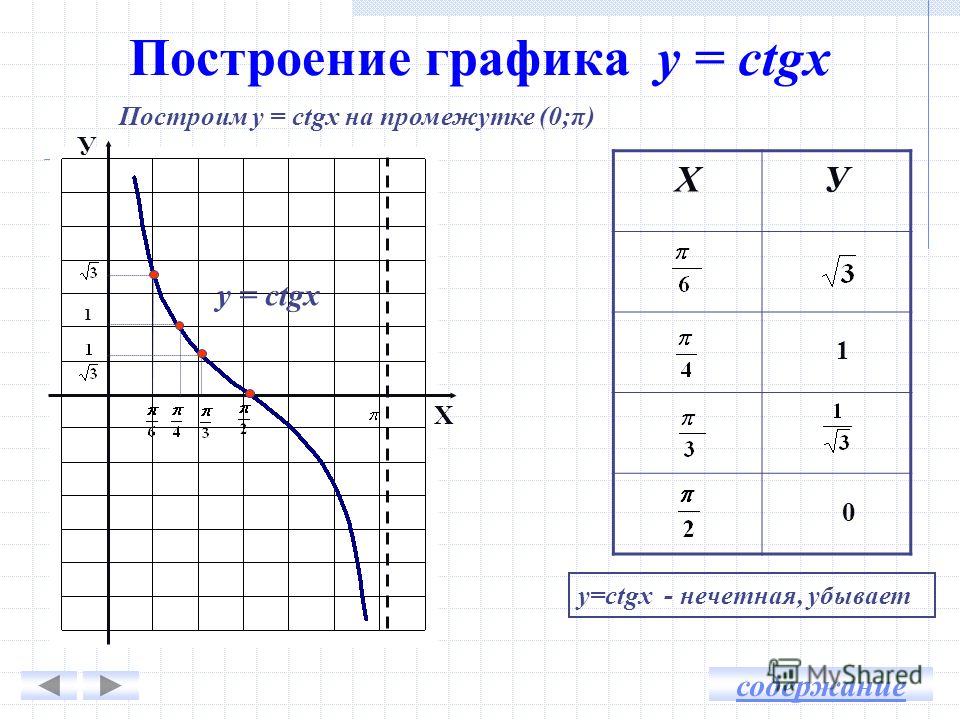
Учебное задание 2 — Графики y = cotx
I.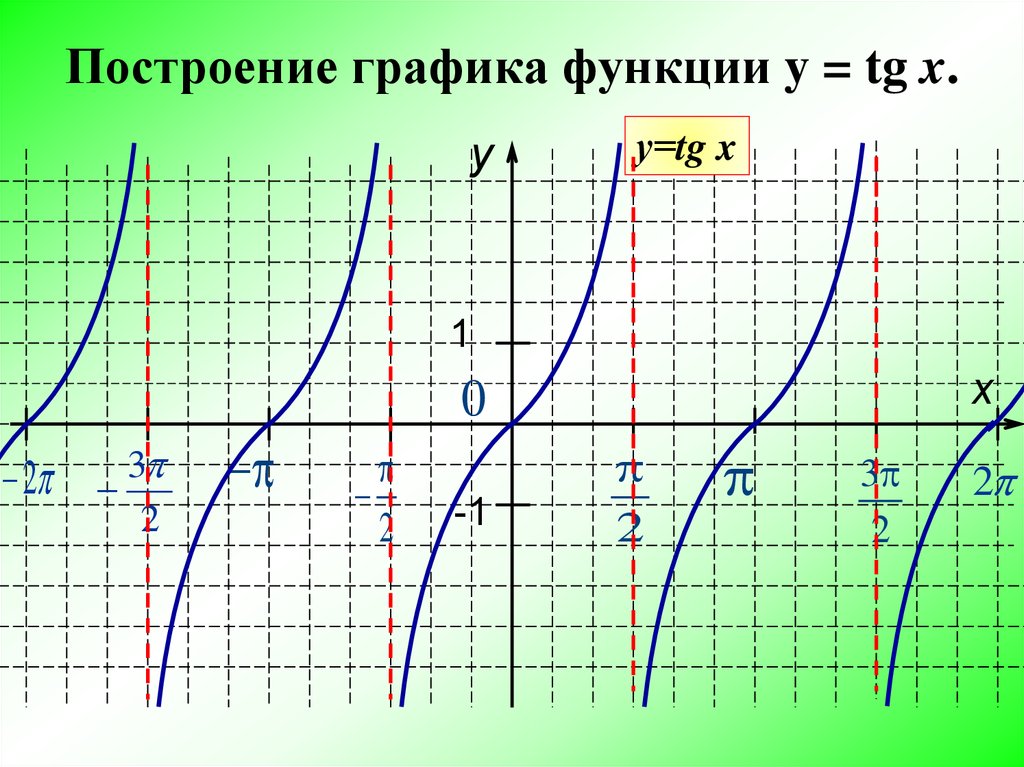 Во-первых, давайте установим и осмотрим стол
координат некоторых точек, которые будут удовлетворять
уравнение y = cotx.
Во-первых, давайте установим и осмотрим стол
координат некоторых точек, которые будут удовлетворять
уравнение y = cotx.
1. Откройте электронную таблицу Excel. Метка столбца A «координаты x» и столбец B «координаты y». Установите оба столбца для округления до 4 знаков после запятой.
2. Заполните координаты x в столбце A. в диапазоне от -2p до 2p с шагом p/4. Помните, что x представляет угловую меру — мы используя радианы в качестве наших единиц.
3. Заполните координаты y в столбце B. используя уравнение, y = cotx. Помните, что cotx обратный tanx.
Что вы заметили в значениях в эта колонка? Что означает #####? Можете ли вы предсказать, что график будет выглядеть?
Как координаты y в этой таблице относятся к координатам y в таблице для y = tanx?
II. Графики в графическом калькуляторе.
1. График y = cotx от -2p до 2p.
2.
Объясните, что означают вертикальные линии на график представляет.
3. Какова продолжительность одного периода у = коткс?
4. Имеют ли графики котангенса «амплитуду»? Почему или почему нет?
5. Как этот график относится к графику у = tanx?
III. Проверь себя.
Нарисуйте (от руки!) что график y = cotx будет выглядеть с учетом следующих ограничений домена. Будьте внимательны к тому, где график пересекает ось X, где точки перегиба и асимптоты.
а) 2 от 4 до
б) -4 р до 0
в) -3 р /2 до р/2
Ключ учителя для задания для учащихся 2
И.
2. В ячейке A2 введите «=-2*pi()». В ячейке A3 введите «=A2+pi()/ 4». Перетащите, чтобы заполнить до 18 ряда.
3. В ячейке B2 введите «=1/(tan(A2))». Перетащите, чтобы заполнить строку 18.
Вот пример таблицы:
x-координаты y-координаты -6,2832 ##### -5,4978 1 -4,7124 0 -3,9270 -1 -3,1416 ##### -2,3562 1 -1,5708 0 -0,7854 -1 0 ##### 0,7854 1 1,5708 0 2,3562 -1 3. 1416
##### 3,9270 1 4,7124 0 5,4978 -1 6.2832 ##### Ответы: значения в столбце координат Y повторить. ##### означает «неопределенный».
Координаты Y в этой таблице просто обратные координаты y в таблице для y = tanx.
II.
1. Вот пример графика:
2. Вертикальные линии – асимптоты график.
3. Одна точка = с.
4. Нет. Графики котангенсов продолжаются вечно по вертикали. направления, поэтому они не могут иметь «высоту».
5. Х-пересечения графика y = tanx становятся асимптотами на графике y = cotx. Асимптоты график y = tanx становится x-пересечением в графике y = cotx.
Точки с координатами y, равными 1 и -1, имеют одинаковые значения. x-координаты соответственно в графиках как y = tanx, так и у = коткс. По сути, графики «смотрят» в противоположные стороны. — y = tanx вправо и y = cotx влево.
III.
а)
б)
в)
Задание для учащихся 3. Графическое изображение вариантов y = tanx и y = коткс
I. Использование графического калькулятора,
1. Графики y = tanx и y = 2tanx на одном и том же координатная плоскость (но в другом цвете).
2. Тогда график y = cotx и y = -0,5cotx на той же координатной плоскости (но в разных цветах).
Изучите больше графиков этой формы, если найдете необходимо уметь ответить на следующие вопросы.
Ответьте на следующие вопросы об уравнениях в формах y = Atanx и y = Acotx:
а) Что происходит с графиком y = tanx и y = cotx, когда A > 1?
б) Что происходит, когда 0 < A < 1?
в) Когда -1 < А < 0?
d) Что делать, когда A = -1?
д) А когда А < -1?
II.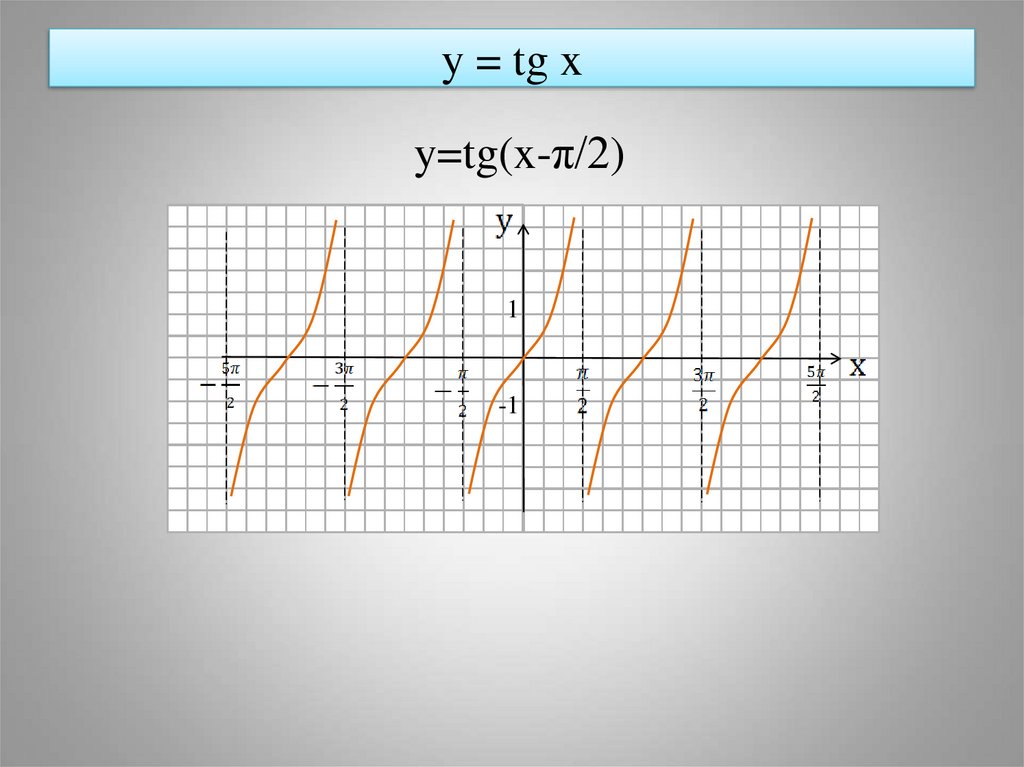 Использование графического калькулятора,
Использование графического калькулятора,
1. График y = tanx и y = tan2x на одном и том же координатная плоскость (но в другом цвете).
2. Тогда граф y = cotx и y = cot0.5x на той же координатной плоскости (но в разных цветах).
Изучите больше графиков этой формы, если найдете необходимо уметь ответить на следующие вопросы.
Ответьте на следующие вопросы об уравнениях в формах y = tanBx и y = cotBx:
а) Что происходит с графиками y = tanx и y = cotx, когда B > 1?
б) Что происходит, когда 0 < B < 1?
в) Когда -1 < В < 0?
d) Что делать, когда B = -1?
д) А когда В < -1?
е) Как определить период функция, основанная на ее уравнении?
III. Использование графического калькулятора,
1. график y = tanx и y = tan(x — p/2) на одном и том же координатная плоскость (но в другом цвете).
2. Тогда граф y = cotx и y = cot(x + p/4) на той же координатная плоскость (но в другом цвете).
Изучите больше графиков этой формы, если найдете необходимо уметь ответить на следующие вопросы.
Ответьте на следующие вопросы об уравнениях в формах y = tan(x + C) и y = cot(x + C):
а) Что происходит с графиком y = tanx и y = cotx, когда C положителен?
б) Что делать, если C отрицательно?
IV. Использование графического калькулятора,
1. График y = tanx и y = tanx + 2 на той же координатной плоскости (но в разных цветах).
2. Тогда граф y = cotx и y = cotx — 1 на той же координатной плоскости (но в разных цветах).
Изучите больше графиков этой формы, если найдете необходимо уметь ответить на следующие вопросы.
Ответьте на следующие вопросы об уравнениях в формах y = tanx + D и y = cotx + D:
а) Что происходит с графиками y = tanx и y = cotx, когда D положителен?
б) Что делать, если D отрицательно?
Ключ учителя для задания для учащихся 3
(Примечание: все графики y = tanx выделены зеленым цветом, а их парные графики выделены красным цветом; все графы y = cotx бирюзовые, а их парные графы фиолетовые)
I.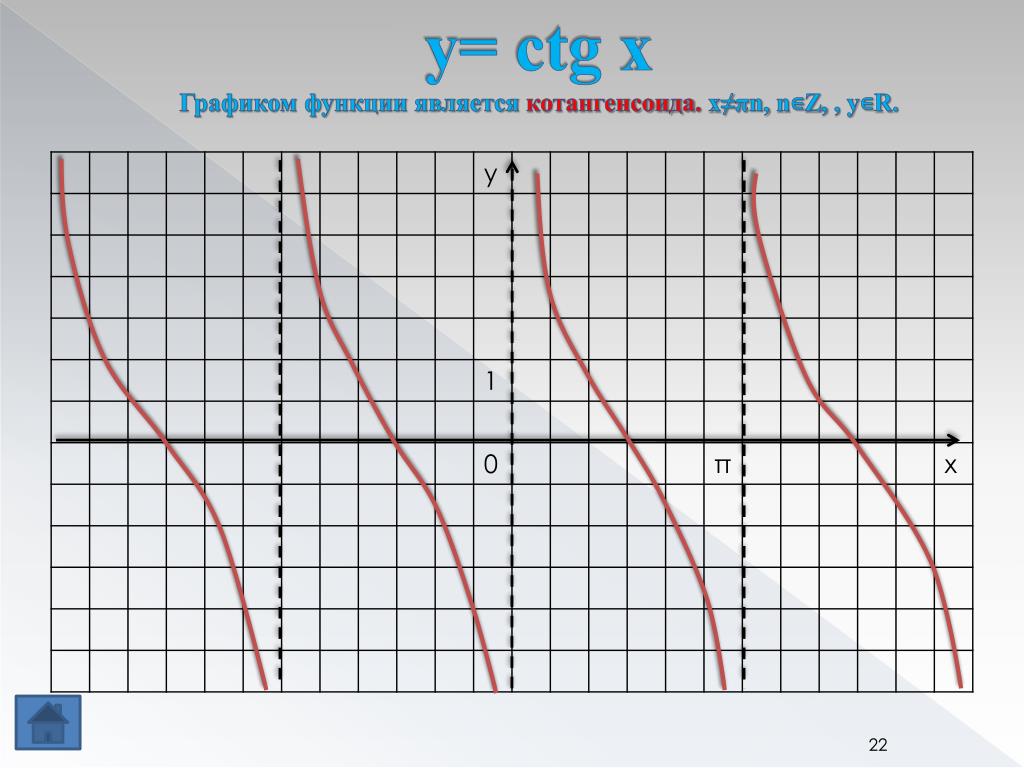 Вот несколько примеров графиков:
Вот несколько примеров графиков:
1.
2.
а) Графики «растягиваются» от ось х.
б) Графики «сжимаются» в сторону ось х.
c) Графики «переворачиваются» вокруг оси X и «сжиматься» по оси x.
d) Графики «переворачиваются» вокруг оси x.
e) Графики «переворачиваются» вокруг оси X и «растянуть» от оси x.
II. Вот несколько примеров графиков:
1.
2.
а) Графики «сжимаются» по горизонтали.
б) Графики «вытянуты» по горизонтали.
c) Графики «переворачиваются» вокруг оси X и «растянуть» по горизонтали.
d) Графики «переворачиваются» вокруг оси x.
e) Графики «переворачиваются» вокруг оси X и «выжать» по горизонтали.
f) Период = p / | Б |
III. Вот несколько примеров графиков:
1.
2.
а) График смещается на C единиц влево.
б) График смещается на C единиц вправо.
IV. Вот несколько примеров графиков:
1.
2.
а) График перемещается на D единиц вверх.
б) График смещается на D единиц вниз.
Студенческая практика
1. Определить вертикальное растяжение/сжатие,
период, фазовый сдвиг и вертикальный сдвиг каждой функции.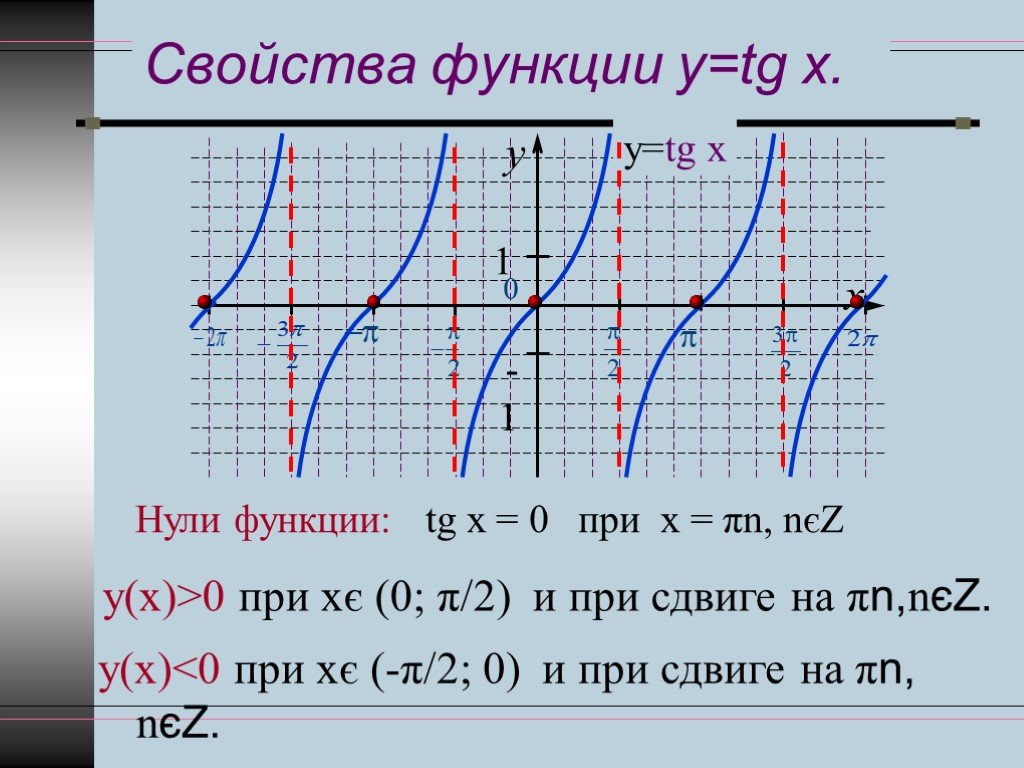
а) у = тангенс2(х + р) + 3
б) у = 5кот(х + 2п/3)
в) у = cot3(x — p) — 5
г) у = 3tan4x + 1
2. Постройте график каждой функции на интервале [-2p, 2p] (не забудьте график по этапам, если необходимо).
а) у = 2котх -3
б) у = тангенс (х — р)
в) у = тангенс (х + р/2) +1
г) у = 4cot2x
Ключ учителя для студенческой практики
1.
а) нет, pd = p/2, ps = p слева, vs = 3 вверх
б) ст. протяжка = 5, пд = п, пс = 2п/3 влево, изн = 0
c) нет, pd = p/3, ps = p справа, vs = 5 вниз
г) ст. растяжка = 3, пд = п/4, пд = 0, вс = 1 ип
2.
а)
93 6 Решить для ? cos(x)=1/2 7 Найти х sin(x)=-1/2 8 Преобразование градусов в радианы 225 9 Решить для ? cos(x)=(квадратный корень из 2)/2 10 Найти х cos(x)=(квадратный корень из 3)/2 11 Найти х sin(x)=(квадратный корень из 3)/2 92=9 14 Преобразование градусов в радианы 120 градусов 15 Преобразование градусов в радианы 180 16 Найти точное значение желтовато-коричневый(195) 92-4 38 Найти точное значение грех(255) 39 Оценить лог база 27 из 36 40 Преобразовать из радианов в градусы 2 шт.

 RU
RU
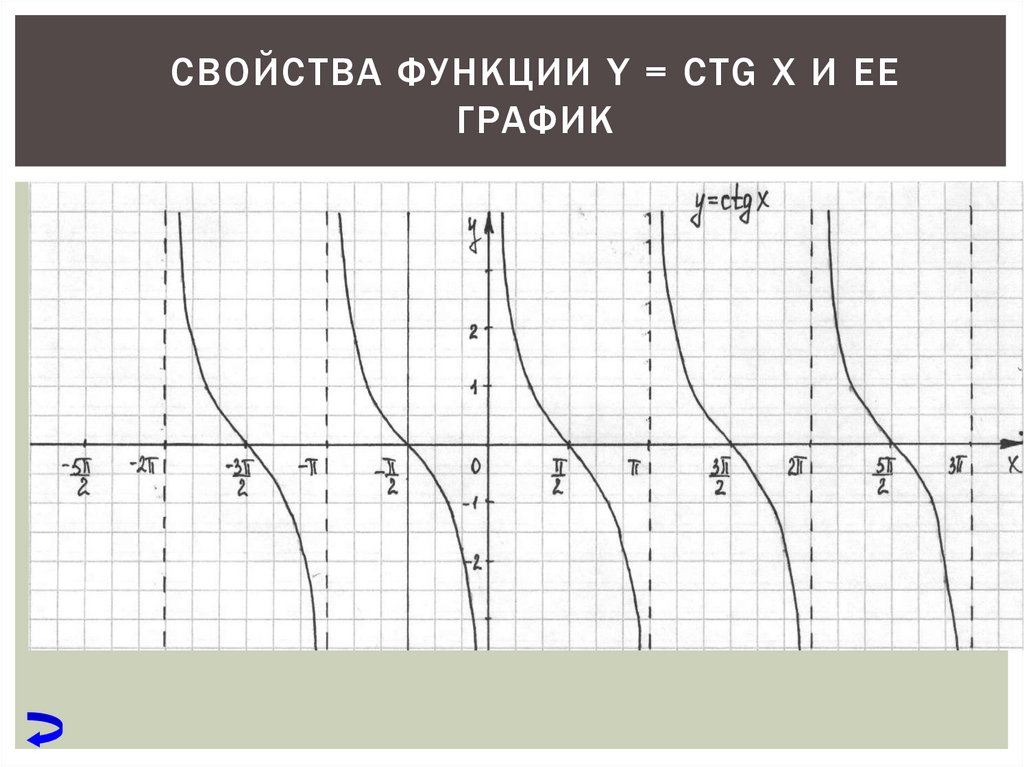
 Объясните, что означают вертикальные линии на
график представляет.
Объясните, что означают вертикальные линии на
график представляет. 
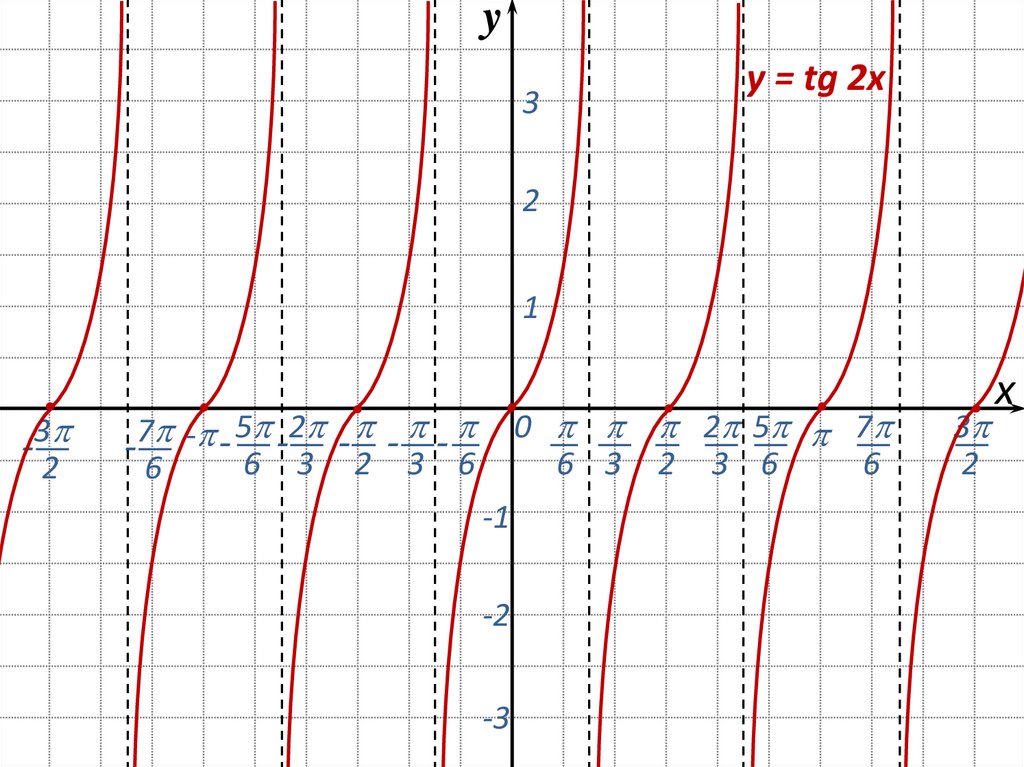 1416
1416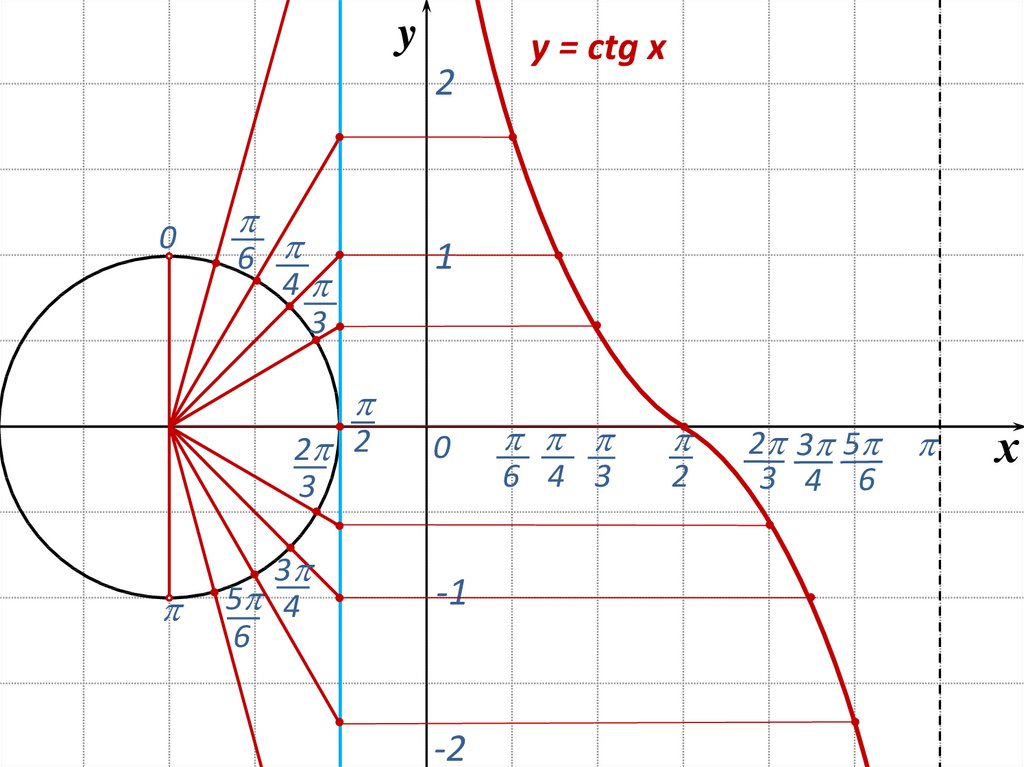 Точки с координатами y, равными 1 и -1, имеют одинаковые значения.
x-координаты соответственно в графиках как y = tanx, так и
у = коткс. По сути, графики «смотрят» в противоположные стороны.
— y = tanx вправо и y = cotx влево.
Точки с координатами y, равными 1 и -1, имеют одинаковые значения.
x-координаты соответственно в графиках как y = tanx, так и
у = коткс. По сути, графики «смотрят» в противоположные стороны.
— y = tanx вправо и y = cotx влево.