Примеры решенных задач по физике на тему «Свободное движение тела, брошенного под углом к горизонту»
Ниже размещены условия задач и отсканированные решения. Если вам нужно решить задачу на эту тему, вы можете найти здесь похожее условие и решить свою по аналогии. Загрузка страницы может занять некоторое время в связи с большим количеством рисунков. Если Вам понадобится решение задач или онлайн помощь по физике- обращайтесь, будем рады помочь.
Принцип решения этих задач заключается в разложении скорости свободно падающего тела на две составляющие — горизонтальную и вертикальную. Горизонтальная составляющая скорости постоянна, вертикальное движение происходит с ускорением свободного падения g=9.8 м/с2. Также может применяться закон сохранения механической энергии, согласно которому сумма потенциальной и кинетической энерги тела в данном случае постоянна.
Материальная точка брошена под углом к горизонту с начальной скоростью 15 м/с. Начальная кинетическая энергия в 3 раза больше кинетической энергии точки в верхней точке траектории. На какую высоту поднималась точка?
На какую высоту поднималась точка?
Тело брошено под углом 40 градусов к горизонту с начальной скоростью 10 м/с. Найти расстояние, которое пролетит тело до падения, высоту подъема в верхней точке траектории и время в полете.
Тело брошено с башни высотой H вниз, под углом α к горизонту, с начальной скоростью v. Найти расстояние от башни до места падения тела.
Тело массой 0,5 кг брошено с поверхност Земли под углом 30 градусов к горизонту, с начальной скоростью 10 м/с. Найти потенциальную и кинетическую энергии тела через 0,4 с.
Материальная точка брошена вверх с поверхности Земли под углом к горизонту с начальной скоростью 10 м/с. Определить скорость точки на высоте 3 м.
Тело брошено вверх с поверхности Земли под углом 60 градусов с начальной скоростью 10 м/с. Найти расстояние до точки падения, скорость тела в точке падения и время в полете.
Тело брошено вверх под углом к горизонту с начальной скоростю 20 м/с.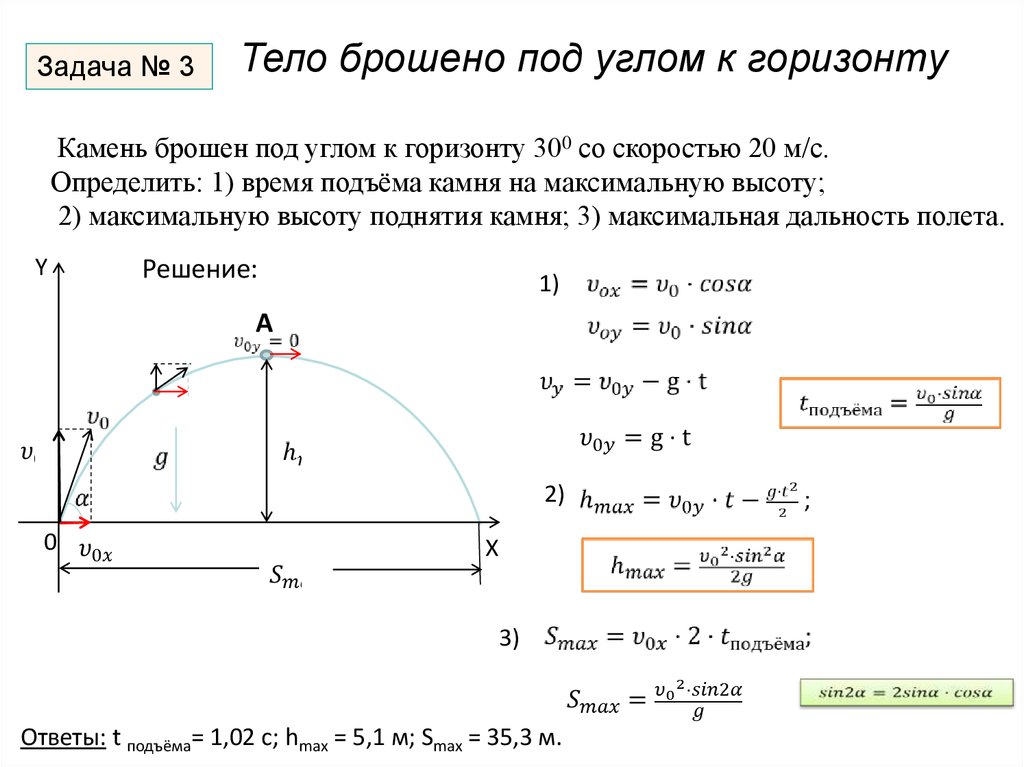 Расстояние до точки падения в 4 раза больше максимальной высоты подъема. Найти угол, под которым брошено тело.
Расстояние до точки падения в 4 раза больше максимальной высоты подъема. Найти угол, под которым брошено тело.
Тело брошено с высоты 5 м под углом 30 градусов к горизонту с начальной скоростью 22 м/с. Найти дальность полета тела и время полета тела.
Тело брошено с поверхности Земли под углом к горизонту с начальной скоростью 30 м/с. Найти тангенциальное и нормальное ускорения тела через 1с после броска.
Тело брошено с поверхности Зесли под углом 30 градусов к горизонту с начальной скоростью 14,7 м/с. Найти тангенциальное и нормальное ускорения тела через 1,25с после броска.
Тело брошено под углом 60 градусов к горизонту с начальной скоростью 20 м/с. Через какое время угол между скоростью и горизонтом станет равным 45 градусов?
Мяч, брошенный в спортзале под углом к горизонту, с начальной скоростью 20 м/с, в верхней точке траектории коснулся потолка на высоте 8м и упал на некотором расстоянии от места броска. Найти это расстояние и угол, под которым брошено тело.
Тело, брошеное с поверхности Земли под углом к горизонту, упало через 2,2с. Найти максимальную высоту подъема тела.
Камень брошен под углом 30 градусов к горизонту. На некоторой высоте камень побывал дважды — через время 1с и 3 с после броска. Найти эту высоту и начальную скорость камня.
Камень брошен под углом 30 градусов к горизонту с начальной скоростью 10 м/с. Найти расстояние от точки бросания до камня через 4 с.
Снаряд выпущен в момент, когда самолет пролетает над орудием, под углом к горизонту с начальной скоростью 500 м/с. Снаряд поразил самолет на высоте 3,5 км через 10с после выстрела. Какова скорость самолета?
Ядро массой 5 кг брошено с поверхности Земли под углом 60 градусов к горизонту. На разгон гири потрачена энергия 500Дж. Определить дальность полета и время в полете.
Тело брошено с высоты 100м вниз под углом 30 градусов к горизонту с начальной скоростью 5 м/с. Найти дальность полета тела.
Тело массой 200г, брошеное с поверхности Земли под углом к горизонту, упало на расстоянии 5м через время 1,2с. Найти работу по броску тела.
Ниже предлагаем вам посмотреть видеоуроки по данной теме:
| ||||||||||||
| Специальный поиск | ||||||||||||
|
Физика Теория вероятностей и мат. статистика Гидравлика Теор. механика Прикладн. механика Химия Электроника Витамины для ума |
Главная Поиск по сайту Формулы Все задачи Помощь Контакты Билеты |
|||||||||||
тело брошено под углом Задача 13099 Тело брошено под углом α = 45° к горизонту со скоростью v0 = 15 м/с Используя закон сохранения энергии, определите скорость v тела в высшей точке его траектории.
Задача 19915 Тело брошено под углом 45° к горизонту. Определить наибольшую высоту подъема и дальность полета, если начальная скорость тела v0 = 20 м/с.
Задача 20257 На какую наибольшую высоту h поднимется тело, брошенное под углом α к горизонту, если время полета тела равно t = 2 с.
Задача 11027 Тело брошено под углом α = 30° к горизонту. Найти тангенциальное аτ и нормальное аn ускорения в начальный момент движения.
Задача 13651 Тело, брошенное под углом α = 60° к горизонту (см. рис.), через время τ = 4 с после начала движения имело вертикальную составляющую скорости v y = 10 м/с. Требуется: 1) написать кинематические уравнения движения тела; 2) вывести уравнение траектории тела; 3) определить дальность L полета тела; 4) найти максимальную высоту Нmax подъема.
Задача 15246 Тело брошено под углом 60° к горизонту с начальной скоростью 20 м/с. Определить координаты точек на траектории тела, в которых нормальное ускорение равно тангенциальному.
Задача 20366 Тело брошено под углом α = 30° к горизонту. За время Δt = 5 с полета модуль изменения импульса тела равен Δр = 200 кг·м/с. Сопротивление воздуха не учитывать. Масса этого тела равна … кг.
Задача 22037 Тело бросают под углом 30° к горизонту с начальной скоростью 14 м/с. На расстоянии 11 м от точки бросания тело упруго ударяется о вертикальную стенку. На каком расстоянии от стенки оно упадет на землю?
Задача 23422 Тело, брошенное под углом α = 60° к горизонту, через время t = 4,0 с после начала движения имело вертикальную проекцию скорости ау = 9,8 м/с.
Задача 23604 Тело, брошенное под углом α к горизонту, пролетает за первые 3 с движения расстояние 25 м. Определить угол α, под которым бросили тело, модуль вектора начальной скорости, если наибольшая высота поднятия тела 26,8 м?
Задача 23669 Два тела брошены под углами α1 и α2 к горизонту из одной точки. Каково отношение сообщенных им начальных скоростей, если они упали на землю в одном и том же месте?
Задача 24147 Тело брошено под углом α = 30° к горизонту со скоростью v0 = 20 м/с с высоты Н = 10 м. Требуется: 1) написать кинематические уравнения движения; 2) вывести уравнение траектории; 3) найти время полета τ до высоты h = 5 м; 4) определить по модулю и направлению скорость v тела на высоте h.
| ||||||||||||
Вопрос
Вопрос
A2Z-ДВИЖЕНИЕ В ДВУХ ИЗМЕРЕНИЯХ-Снаряд с высоты и движущейся рамы
19 видеоРЕКЛАМА
Ab Padhai karo bina ads ke
3
3 9 киси ад ки рукаават ке! Обновлено: 27-06-2022
Текст Решение
Ответ
Правильный ответ d g=10 мс−2
Для горизонтального движения R=ucosθt
t=Rucosθ=17,310cos30∘=17,3×210×√3=17,3×210×1,73=2s
Для вертикального движения h=usinθt=12gt2
=10sin30∘×2−12× 10×22
=10−20=−10м.
Высота башни =10м.
Ответить
Пошаговое решение, разработанное экспертами, чтобы помочь вам в решении вопросов и получении отличных оценок на экзаменах.
Похожие видео
Мяч брошен из точки на уровне со скоростью u и на горизонтальном расстоянии r от вершины башни высотой h.
На каком горизонтальном расстоянии x от подножия башни мяч коснется земли?
11296763
Мяч брошен с вершины башни с начальной скоростью 10 м/с под углом 30∘ над горизонтом. Он попадает в землю на расстоянии 17,3 м от основания башни. Высота башни (g=10 м/с2) будет равна
14798229
Объект брошен в сторону башни, которая находится на расстоянии 50 м по горизонтали с начальной скоростью 10 м/с и образует угол 30° с горизонтальный. Объект попадает в башню на определенной высоте. Высота от основания башни, где объект попадает в башню, составляет (Примите, g = 10 мс-2)
18246944
Мяч брошен вертикально вниз со скоростью 20 м/с с вершины башни. Через некоторое время он ударяется о землю со скоростью 80 м/с. Высота башни: (g= 10 мг2)
359388329
Мяч брошен вертикально вверх с вершины башни со скоростью 10 м/с. Если мяч упадет на землю через 5 секунд, высота башни будет равна? (используйте g=10 м/с2)
460907944
Тело брошено горизонтально с вершины башни высотой 5 м. (-2) )
(-2) )
510428095
Мяч брошен с вершины башни высотой 67 м со скоростью 24,4 мс−1 на высоте 30∘ над горизонталью. Каково расстояние от подножия башни до точки падения мяча на землю?
576404089
Текст Решение
С вершины башни высотой 5 м горизонтально брошено тело. Он касается земли на расстоянии 10 м от подножия башни. Тогда начальная скорость тела
576404523 9(-2))
643395127
Текстовое решение
Компоненты начальной скорости
Уже было сказано и подробно обсуждено, что горизонтальное и вертикальное движения снаряда не зависят друг от друга.
горизонтальная скорость снаряда не влияет на то, как далеко (или как быстро) падает снаряд
вертикально . Перпендикулярные составляющие движения не зависят друг от друга. Таким образом, анализ движения снаряда требует, чтобы две составляющие движения анализировались независимо друг от друга, стараясь не смешивать информацию о горизонтальном движении с информацией о вертикальном движении.
То есть, если анализировать движение для определения вертикального смещения, можно использовать кинематические уравнения с параметрами вертикального движения (начальная вертикальная скорость, конечная вертикальная скорость, вертикальное ускорение), а не с параметрами горизонтального движения (начальная горизонтальная скорость, конечная горизонтальная скорость, горизонтальное ускорение). Именно по этой причине одним из начальных шагов задачи о движении снаряда является определение составляющих начальной скорости.
Определение компонентов вектора скорости Ранее в этом разделе обсуждался метод векторного разрешения. Векторное разрешение — это метод взятия одного вектора под углом и разделения его на две перпендикулярные части. Две части вектора называются компонентами и описывают влияние этого вектора в одном направлении. Если снаряд пущен под углом к горизонту, то начальная скорость снаряда имеет как горизонтальную, так и вертикальную составляющие.
Горизонтальная составляющая скорости ( v x ) описывает влияние скорости на перемещение снаряда по горизонтали. Компонент вертикальной скорости ( v y ) описывает влияние скорости на перемещение снаряда по вертикали. Таким образом, анализ задач о движении снаряда начинается с использования обсуждавшихся ранее тригонометрических методов для определения горизонтальной и вертикальной составляющих начальной скорости. Рассмотрим снаряд, запущенный с начальной скоростью 50 м/с под углом 60 градусов к горизонту. Такой снаряд начинает свое движение с горизонтальной скоростью 25 м/с и вертикальной скоростью 43 м/с. Они известны как горизонтальная и вертикальная составляющие начальной скорости. Эти числовые значения были определены путем построения эскиза вектора скорости с заданным направлением, а затем с использованием тригонометрических функций для определения сторон скорость треугольник. Эскиз показан справа, а использование тригонометрических функций для определения величин показано ниже. (При необходимости просмотрите этот метод на предыдущей странице этого раздела.)
(При необходимости просмотрите этот метод на предыдущей странице этого раздела.)
Все проблемы с векторным разрешением могут быть решены аналогичным образом. В качестве проверки вашего понимания используйте тригонометрические функции для определения горизонтальной и вертикальной составляющих следующих значений начальной скорости. Когда закончите, нажмите кнопку, чтобы проверить свои ответы.
Практика A: Воздушный шар с водой запускается со скоростью 40 м/с под углом 60 градусов к горизонтали.
Практика B: Мотоциклист-каскадер, едущий со скоростью 70 миль в час, прыгает с трапа под углом 35 градусов к горизонтали.
Практика C: Прыжок с трамплина прыгает со скоростью 10 м/с под углом 80 градусов к горизонту.
Попробуйте еще! Нужно больше практики? Используйте приведенный ниже виджет Компоненты скорости для снаряда , чтобы решить некоторые дополнительные задачи. Введите любую величину скорости и угол относительно горизонтали. Используйте свой калькулятор, чтобы определить значения v x и v y . Затем нажмите Кнопка Отправить , чтобы проверить свои ответы.
Введите любую величину скорости и угол относительно горизонтали. Используйте свой калькулятор, чтобы определить значения v x и v y . Затем нажмите Кнопка Отправить , чтобы проверить свои ответы.
Как упоминалось выше, смысл разложения вектора начальной скорости на две его составляющие заключается в использовании значений этих двух составляющих для анализа движения снаряда и определения таких параметров, как горизонтальное смещение, вертикальное смещение, конечная вертикальная скорость, время достижения пика траектории, время падения на землю и т. д. Этот процесс продемонстрирован на оставшейся части этой страницы. Начнем с определения времени.
Определение времени полета Время вертикального подъема снаряда до пика (а также время падения с пика) зависит от параметров вертикального движения. Процесс вертикального подъема на вершину траектории представляет собой вертикальное движение и, таким образом, зависит от начальной вертикальной скорости и вертикального ускорения (g = 9,8 м/с/с, вниз). Процесс определения времени подъема на пик — простой процесс, при условии, что вы хорошо понимаете концепцию ускорения. При первом введении было сказано, что ускорение — это скорость, с которой изменяется скорость объекта. Значение ускорения указывает величину изменения скорости за данный интервал времени. Сказать, что снаряд имеет вертикальное ускорение -90,8 м/с/с означает, что вертикальная скорость изменяется на 9,8 м/с (в направлении — или вниз) каждую секунду. Например, если снаряд движется вверх со скоростью 39,2 м/с в 0 секунд, то его скорость будет 29,4 м/с через 1 секунду, 19,6 м/с через 2 секунды, 9,8 м/с через 3 секунды, и 0 м/с через 4 секунды. Такому снаряду с начальной вертикальной скоростью 39,2 м/с потребуется 4 секунды, чтобы достичь пика, где его вертикальная скорость равна 0 м/с. Имея это в виду, становится очевидным, что время, за которое снаряд достигает своего пика, зависит от деления вертикальной составляющей начальной скорости (v
Процесс определения времени подъема на пик — простой процесс, при условии, что вы хорошо понимаете концепцию ускорения. При первом введении было сказано, что ускорение — это скорость, с которой изменяется скорость объекта. Значение ускорения указывает величину изменения скорости за данный интервал времени. Сказать, что снаряд имеет вертикальное ускорение -90,8 м/с/с означает, что вертикальная скорость изменяется на 9,8 м/с (в направлении — или вниз) каждую секунду. Например, если снаряд движется вверх со скоростью 39,2 м/с в 0 секунд, то его скорость будет 29,4 м/с через 1 секунду, 19,6 м/с через 2 секунды, 9,8 м/с через 3 секунды, и 0 м/с через 4 секунды. Такому снаряду с начальной вертикальной скоростью 39,2 м/с потребуется 4 секунды, чтобы достичь пика, где его вертикальная скорость равна 0 м/с. Имея это в виду, становится очевидным, что время, за которое снаряд достигает своего пика, зависит от деления вертикальной составляющей начальной скорости (v iy ) ускорением свободного падения.
Зная время подъема на вершину траектории, можно определить общее время полета. Для снаряда, приземлившегося на той же высоте, на которой он стартовал, общее время полета в два раза превышает время подъема на пик. Вспомним из последнего раздела Урока 2, что траектория снаряда симметрична относительно вершины. То есть, если подъем на вершину занимает 4 секунды, то и падение с вершины займет 4 секунды; общее время полета 8 секунд. Время полета снаряда вдвое превышает время подъема на пик.
Определение горизонтального смещения Горизонтальное смещение снаряда зависит от горизонтальной составляющей начальной скорости. Как обсуждалось в предыдущей части этого урока, горизонтальное перемещение снаряда можно определить с помощью уравнения
x = v ix • t скорость 20 м/с, то горизонтальное перемещение 160 метров (20 м/с • 8 с). Если снаряд имеет время полета 8 секунд и горизонтальную скорость 34 м/с, то снаряд имеет горизонтальное перемещение 272 метра (34 м/с • 8 с). Горизонтальное смещение зависит от единственного горизонтального параметра, существующего для снарядов, — горизонтальной скорости ( v ix ).
Если снаряд имеет время полета 8 секунд и горизонтальную скорость 34 м/с, то снаряд имеет горизонтальное перемещение 272 метра (34 м/с • 8 с). Горизонтальное смещение зависит от единственного горизонтального параметра, существующего для снарядов, — горизонтальной скорости ( v ix ).
Определение высоты пика Негоризонтально запущенный снаряд с начальной вертикальной скоростью 39,2 м/с достигнет пика за 4 секунды. Процесс подъема на пик является вертикальным движением и опять-таки зависит от параметров вертикального движения (начальной вертикальной скорости и вертикального ускорения). Высота снаряда в этом пиковом положении может быть определена с помощью уравнения
y = v iy • t + 0,5 • g • t 2 где v iy — начальная вертикальная скорость в м/с, g — ускорение силы тяжести 9,8 м/с/с), а t — время в секундах, необходимое для достижения пика. Это уравнение может быть успешно использовано для определения вертикального смещения снаряда на первой половине его траектории (т. Е. Высота пика) при условии, что алгебра выполнена правильно и заданные переменные заменены правильными значениями. Особое внимание следует уделить тому факту, что t в уравнении представляет собой время до пика, а g имеет отрицательное значение -9,8 м/с/с.
Это уравнение может быть успешно использовано для определения вертикального смещения снаряда на первой половине его траектории (т. Е. Высота пика) при условии, что алгебра выполнена правильно и заданные переменные заменены правильными значениями. Особое внимание следует уделить тому факту, что t в уравнении представляет собой время до пика, а g имеет отрицательное значение -9,8 м/с/с.
Мы хотели бы предложить … Иногда недостаточно просто прочитать об этом. Вы должны взаимодействовать с ним! И это именно то, что вы делаете, когда используете один из интерактивов The Physics Classroom. Мы хотели бы предложить вам совместить чтение этой страницы с использованием нашего симулятора движения снарядов. Вы можете найти его в разделе Physics Interactives на нашем сайте. Симулятор позволяет исследовать концепции движения снаряда в интерактивном режиме. Измените высоту, измените угол, измените скорость и запустите снаряд.
Посетите: Симулятор движения снаряда
Проверьте свое понимание Ответьте на следующие вопросы и нажмите кнопку, чтобы увидеть ответы.
1. Аарон Эйгин разлагает векторы скорости на горизонтальную и вертикальную составляющие. В каждом случае оцените, правильные или неправильные диаграммы Аарона. Если неверно, объясните проблему или внесите поправку.
2. Используйте тригонометрические функции, чтобы разделить следующие векторы скорости на горизонтальную и вертикальную составляющие. Затем используйте кинематические уравнения для расчета других параметров движения. Будьте осторожны с уравнениями; руководствоваться принципом, что «перпендикулярные составляющие движения независимы друг от друга».
3.
Для горизонтального движения R=ucosθt
t=Rucosθ=17,310cos30∘=17,3×210×√3=17,3×210×1,73=2s
Для вертикального движения h=usinθt=12gt2
=10sin30∘×2−12× 10×22
=10−20=−10м.
Высота башни =10м.

На каком горизонтальном расстоянии x от подножия башни мяч коснется земли?
 (-2) )
(-2) )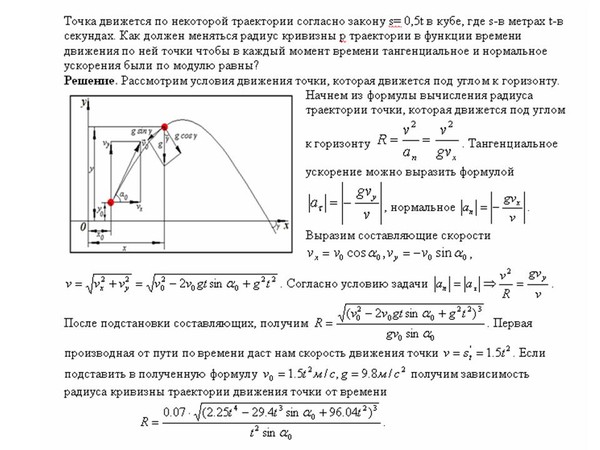

 (При необходимости просмотрите этот метод на предыдущей странице этого раздела.)
(При необходимости просмотрите этот метод на предыдущей странице этого раздела.)
Практика B: Мотоциклист-каскадер, едущий со скоростью 70 миль в час, прыгает с трапа под углом 35 градусов к горизонтали.
Практика C: Прыжок с трамплина прыгает со скоростью 10 м/с под углом 80 градусов к горизонту.
 Введите любую величину скорости и угол относительно горизонтали. Используйте свой калькулятор, чтобы определить значения v x и v y . Затем нажмите Кнопка Отправить , чтобы проверить свои ответы.
Введите любую величину скорости и угол относительно горизонтали. Используйте свой калькулятор, чтобы определить значения v x и v y . Затем нажмите Кнопка Отправить , чтобы проверить свои ответы. Процесс определения времени подъема на пик — простой процесс, при условии, что вы хорошо понимаете концепцию ускорения. При первом введении было сказано, что ускорение — это скорость, с которой изменяется скорость объекта. Значение ускорения указывает величину изменения скорости за данный интервал времени. Сказать, что снаряд имеет вертикальное ускорение -90,8 м/с/с означает, что вертикальная скорость изменяется на 9,8 м/с (в направлении — или вниз) каждую секунду. Например, если снаряд движется вверх со скоростью 39,2 м/с в 0 секунд, то его скорость будет 29,4 м/с через 1 секунду, 19,6 м/с через 2 секунды, 9,8 м/с через 3 секунды, и 0 м/с через 4 секунды. Такому снаряду с начальной вертикальной скоростью 39,2 м/с потребуется 4 секунды, чтобы достичь пика, где его вертикальная скорость равна 0 м/с. Имея это в виду, становится очевидным, что время, за которое снаряд достигает своего пика, зависит от деления вертикальной составляющей начальной скорости (v
Процесс определения времени подъема на пик — простой процесс, при условии, что вы хорошо понимаете концепцию ускорения. При первом введении было сказано, что ускорение — это скорость, с которой изменяется скорость объекта. Значение ускорения указывает величину изменения скорости за данный интервал времени. Сказать, что снаряд имеет вертикальное ускорение -90,8 м/с/с означает, что вертикальная скорость изменяется на 9,8 м/с (в направлении — или вниз) каждую секунду. Например, если снаряд движется вверх со скоростью 39,2 м/с в 0 секунд, то его скорость будет 29,4 м/с через 1 секунду, 19,6 м/с через 2 секунды, 9,8 м/с через 3 секунды, и 0 м/с через 4 секунды. Такому снаряду с начальной вертикальной скоростью 39,2 м/с потребуется 4 секунды, чтобы достичь пика, где его вертикальная скорость равна 0 м/с. Имея это в виду, становится очевидным, что время, за которое снаряд достигает своего пика, зависит от деления вертикальной составляющей начальной скорости (v 
 Если снаряд имеет время полета 8 секунд и горизонтальную скорость 34 м/с, то снаряд имеет горизонтальное перемещение 272 метра (34 м/с • 8 с). Горизонтальное смещение зависит от единственного горизонтального параметра, существующего для снарядов, — горизонтальной скорости ( v ix ).
Если снаряд имеет время полета 8 секунд и горизонтальную скорость 34 м/с, то снаряд имеет горизонтальное перемещение 272 метра (34 м/с • 8 с). Горизонтальное смещение зависит от единственного горизонтального параметра, существующего для снарядов, — горизонтальной скорости ( v ix ). Это уравнение может быть успешно использовано для определения вертикального смещения снаряда на первой половине его траектории (т. Е. Высота пика) при условии, что алгебра выполнена правильно и заданные переменные заменены правильными значениями. Особое внимание следует уделить тому факту, что t в уравнении представляет собой время до пика, а g имеет отрицательное значение -9,8 м/с/с.
Это уравнение может быть успешно использовано для определения вертикального смещения снаряда на первой половине его траектории (т. Е. Высота пика) при условии, что алгебра выполнена правильно и заданные переменные заменены правильными значениями. Особое внимание следует уделить тому факту, что t в уравнении представляет собой время до пика, а g имеет отрицательное значение -9,8 м/с/с.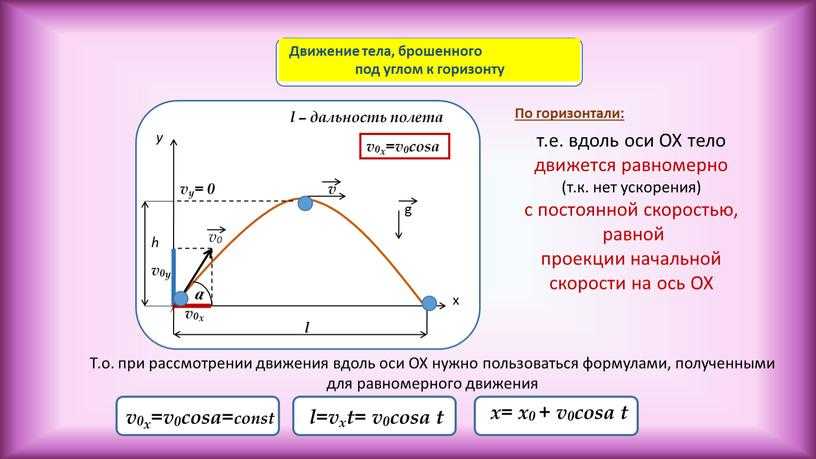
Посетите: Симулятор движения снаряда



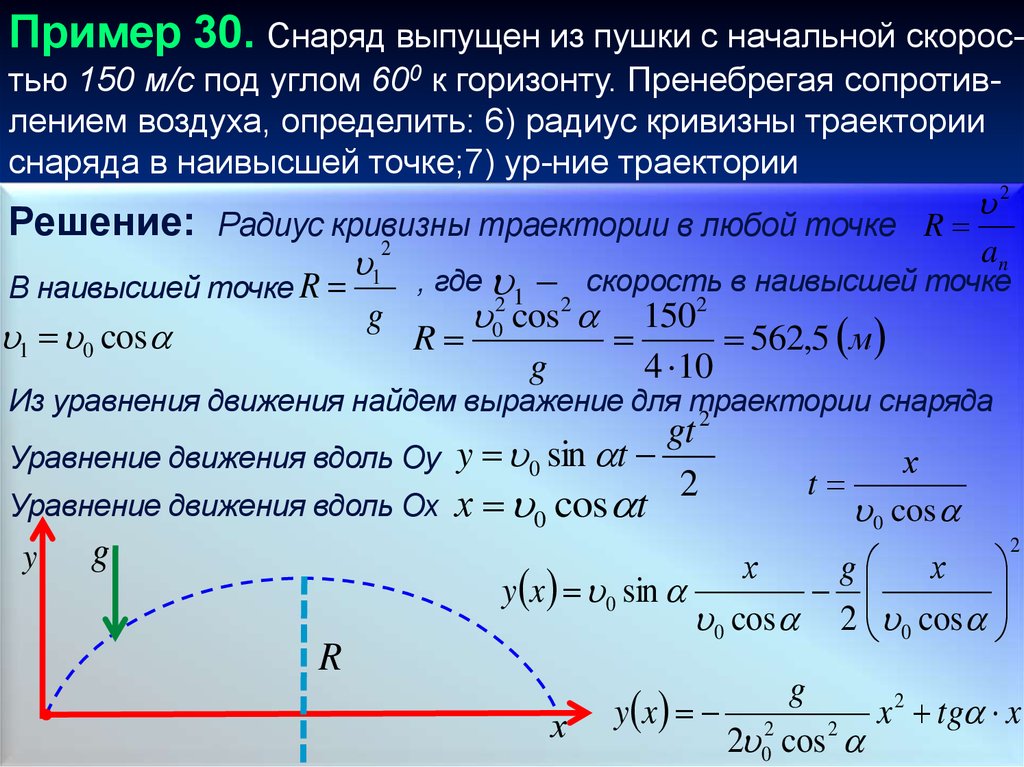 Тело рассматривать как материальную точку и принять g = 10 м/с2.
Тело рассматривать как материальную точку и принять g = 10 м/с2. Найти расстояние S между местом бросания и местом падения.
Найти расстояние S между местом бросания и местом падения.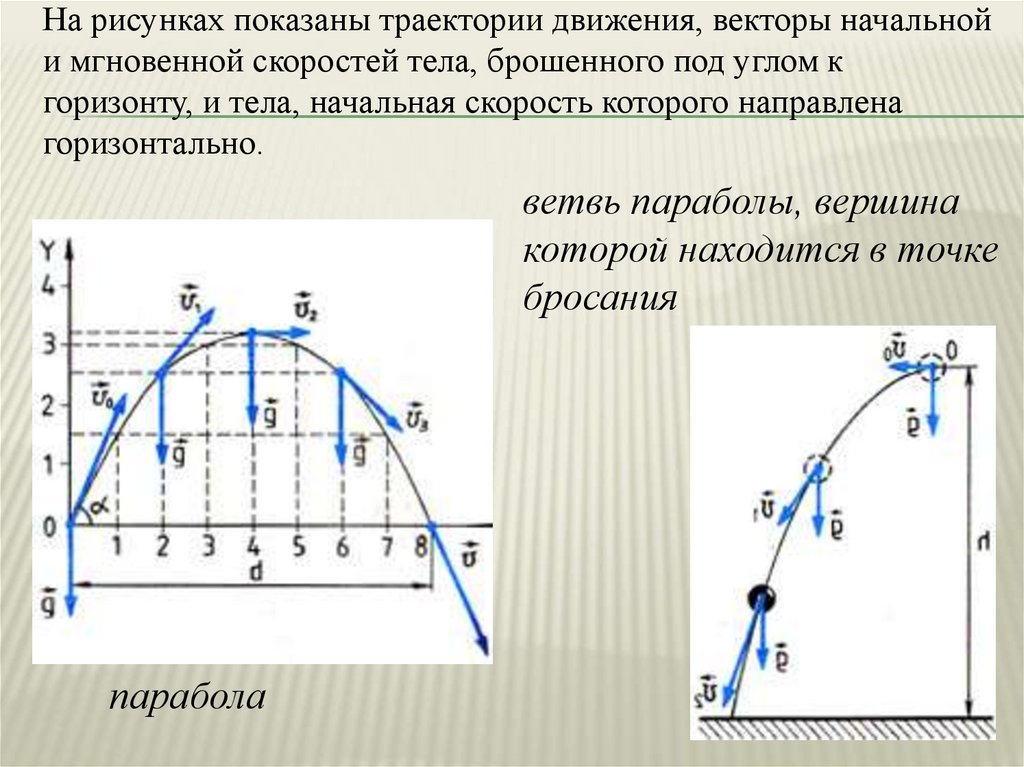 Тело рассматривать как материальную точку и принять g = 10 м/с2.
Тело рассматривать как материальную точку и принять g = 10 м/с2.