Теорема о площади треугольника. Теорема синусов. Теорема косинусов 9 класс онлайн-подготовка на Ростелеком Лицей |
Тема 31.
Терема о площади треугольника. Теорема синусов. Теорема косинусов.
Теорема
Площадь треугольника равна половине произведения двух его сторон на синус угла между ними.
Доказательство
Пусть в треугольнике АВС
АВ=c, ВС=a, СА=b
S — площадь треугольника.
Докажем, что S=12absinC
Введем систему координат с началом в точке C так, чтобы точка В лежала на положительной полуоси Cx, а точка А имела положительную ординату. Площадь данного треугольника можно вычислить по формуле S=12ah, где h — высота треугольника. Но h равна ординате точки А, то есть h = b sin C. Следовательно, S=12absinC
Следовательно, S=12absinC
Теорема
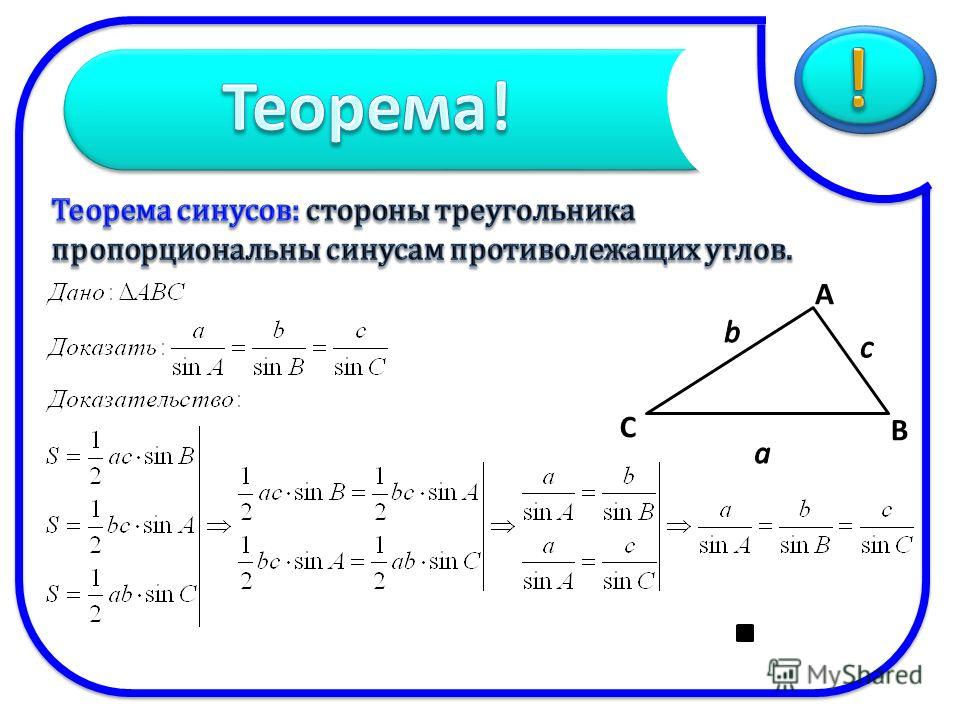
Стороны треугольника пропорциональны синусам противолежащих углов.
Доказательство
Пусть в треугольнике АВС
АВ = c, ВС = a, СА = b
Докажем, что
asinA=bsinB=csinC
По теореме о площади треугольника
S=12absinC,S=12bcsinA, S=12acsinB
Из первых двух равенств получим
12absinC = 12bcsinA, откуда
asinA=csinC
Аналогично, asinA=bsinB
Итак, asinA=bsinB=csinC
Заметим, что отношение стороны треугольника к синусу противолежащего угла равно диаметру описанной окружности. Следовательно, для любого треугольника АВС со сторонами АВ = с, ВС = а, СА = bимеют место равенства
asinA=bsinB=csinC=2R
где R — радиус описанной окружности.
Теорема
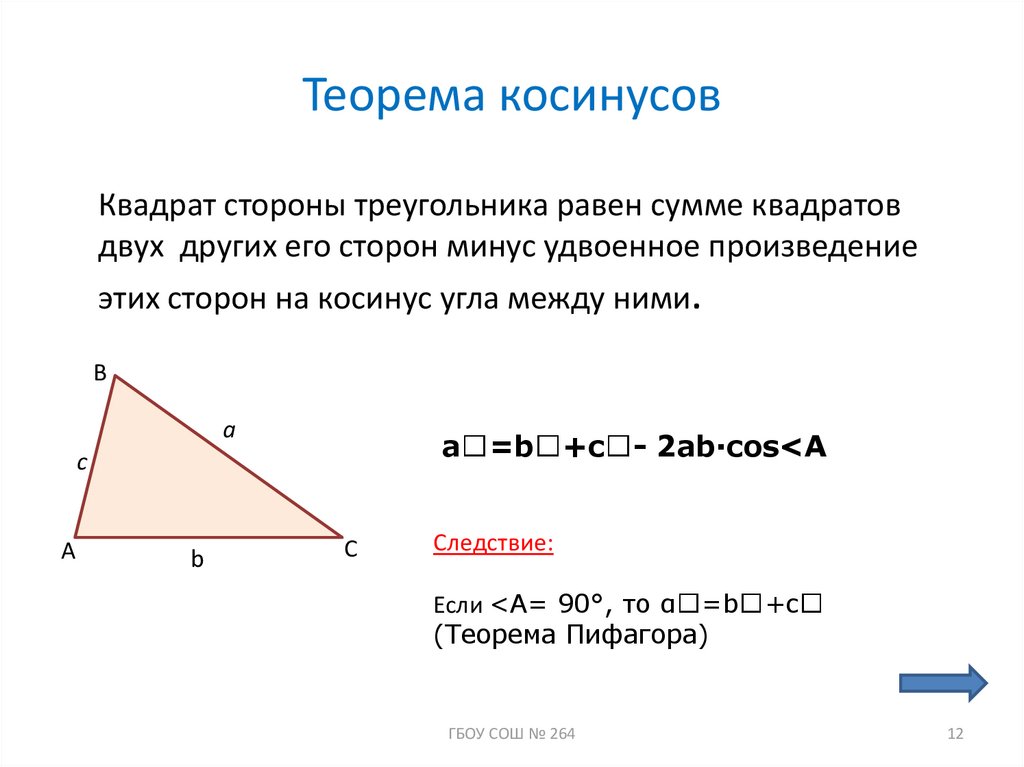
Квадрат стороны треугольника равен сумме квадратов других сторон минус удвоенное произведение этих сторон на косинус угла между ними.
Доказательство
Пусть в треугольнике АВС
АВ = c, ВС = a, СА = b
Докажем, например, что
a2 = b2 + c2 — 2bc cos A
Введем систему координат с началом в точке A так, как показано на рисунке. Тогда точка В имеет координаты (c;0), а точка С имеет координаты b cos
BC2=a2=bcosA-c2+b2sin2A
a2=b2cos2A+b2sin2A-2bccosA+c2
a2=b2cos2A+sin2A-2bccosA+c2
a2=b2+c2-2bccosA
Найти площадь ∆ABC, если BC = 3 см, AB=182 см, ∠B = 45°.
По теореме о площади треугольника
S=12BC∙AB∙sinB
S=12∙3∙182∙sin45°
S=12∙3∙182∙22
S = 27 см2
Ответ: 27 см2
Теорема синусов. Теорема косинусов
При решении прямоугольных треугольников используются только основные тригонометрические функции. Для решения же косоугольных треугольников потребуется знание зависимостей между сторонами и тригонометрическими функциями углов косоугольных треугольников, известные как теоремы синусов, косинусов и тангенсов. К выводу этих теорем мы и переходим.
В дальнейшем мы будем пользоваться следующими обозначениями: a, b и c — стороны треугольника; А, В и С — противолежащие им углы; S — площадь; 2р — периметр; R — радиус описанного круга; r — радиус вписанного круга; hа, lа и mа — высота, биссектриса и медиана, соответствующие стороне а.
Теорема синусов
Теорема. Во всяком треугольнике стороны пропорциональны синусам противолежащих углов:
$$ \frac{a}{sinA} = \frac{b}{sinB} = \frac{c}{sinC} $$
Доказательство. Опишем круг около данного треугольника ABC. Пусть R — радиус этого круга. Возьмём одну из вершин треугольника, например А; через одну из других вершин, например через В, проведём диаметр ВА описанного круга. Вспомогательный треугольник АВС прямоугольный, так как вписанный угол АСВ опирается на диаметр. Из вспомогательного треугольника найдём:
а = 2Rsin A.
Если угол А острый, то А = А, так как вписанные углы A и A опираются на одну и ту же дугу.
Если угол А тупой, то угол А острый, измеряющийся половиной дуги ВАС:
$$ A = \frac{1}{2}\smile BAC = \frac{1}{2}(2\pi-\smile BAC) = \pi — \frac{\smile BAC}{2} = \pi-A $$
Итак, или A= А, или A =\(\pi\) — A, в обоих случаях sin A = sin A, а потому
а = 2R sin A. (1)
(1)
Если угол Aпрямой, то а = 2R, sin A= 1 и равенство (1) также справедливо.
Аналогичные равенства найдём и для прочих углов В и С. Итак,
а =2R sin A; b =2R sin В; с = 2R sin С, откуда
$$ \frac{a}{sinA} = \frac{b}{sinB} = \frac{c}{sinC} = 2R $$
Следствие. Отношение стороны треугольника к синусу противолежащего угла равно диаметру круга, описанного около треугольника.
Теорема косинусов
Теорема. Квадрат стороны треугольника равен сумме квадратов двух других его сторон минус удвоенное произведение этих сторон на косинус угла между ними:
а2 =b2 + с2 — 2bccosА
b2 =c2 + a2 — 2cacosB
c2 =a2 + b2 — 2abcosC
Доказательство. Докажем первое равенство.
Докажем первое равенство.
Случай 1. Угол A острый.
Пусть ВН — высота, опущенная из вершины В ; из геометрии известно, что
а2 = b2 + с2—2b · АН. (1)
Из прямоугольного треугольника АВН найдём
АН = с cos А; подставив в формулу (1), получим доказываемое равенство.
Случай 2. Угол A тупой.
В этом случае а2 = b2 + с2 +2b · АН. (2)
Из треугольника АВН найдём:
АН = с cos∠BAH = с cos(\(\pi\) — A) = — с cosA.
Подставив в формулу (2), получим доказываемое равенство.
Случай 3. Угол А прямой.
В этом случае (по теореме Пифагора):
а2 = b2 + с2= b2 + с2 — 2bccosА
(так как cos А = 0).
Итак, во всех случаях
а2 = b2 + с2 — 2bccosА
Как работают синус, косинус и тангенс?
МАТЕМАТИКА — Геометрия
Задумывались ли вы когда-нибудь.
 ..
..- Что такое тригонометрия?
- Что такое синус, косинус и тангенс?
- Как найти синус, косинус и тангенс?
Теги:
Просмотреть все теги
- Математика,
- Геометрия,
- Тригонометрия,
- Функция,
- Синус,
- Косинус,
- Тангенс,
- Треугольник,
- Прямоугольный треугольник,
- Формула,
- Угол,
- Гипотенуза
Сегодняшнее чудо дня было вдохновлено Саем. Sai Wonders , “ Как работают синус, косинус и тангенс? «Спасибо, что ДУМАЕТЕ вместе с нами, Сай!
Sai Wonders , “ Как работают синус, косинус и тангенс? «Спасибо, что ДУМАЕТЕ вместе с нами, Сай!
Многие из наших чудесных друзей уже знают о теореме Пифагора. Возможно, они читали о треугольнике Паскаля. Они могут даже знать другие типы треугольников. Сегодня нас интересует еще одна тема, связанная с треугольниками. О чем мы говорим? Синус, косинус и тангенс, конечно!
Что такое синус, косинус и тангенс? Это три основные функции в тригонометрии. Возможно, вы уже слышали о них на уроках математики. Тригонометрия связана с геометрией и другими разделами математики. Это может помочь нам лучше понять связи между сторонами и углами прямоугольников.
Синус, косинус и тангенс важны для изучения прямоугольных треугольников. Вы когда-нибудь видели такой треугольник? Если да, то вы знаете, что один из трех его углов всегда равен 90° (прямой угол). Два других угла могут иметь любые измерения, если сумма всех трех углов составляет 180°.
Как математики находят синус, косинус и тангенс? Начнем с одного из непрямых углов прямоугольного треугольника. Обычно они обозначают этот угол как тета (Θ). Затем они обозначают три стороны треугольника.
Сторона треугольника, расположенная непосредственно напротив прямого угла, называется гипотенузой. Это самая длинная сторона треугольника. Сторона напротив теты называется «противоположной». Это довольно легко запомнить — это на противоположной стороне от тета-угла! Наконец, сторона, которая касается теты, но не является гипотенузой, называется «прилегающей».
Правильное обозначение сторон очень важно при нахождении синуса, косинуса и тангенса. Это потому, что у каждого есть формула, которая делит длину одной стороны на длину другой. Вот формулы для нахождения каждой из этих функций:
Синус Θ = Противоположный ÷ Гипотенуза
Косинус Θ = Прилегающий ÷ Гипотенуза
Тангенс Θ = Op место ÷ соседние
На первый взгляд, эти формулы могут показаться трудными для запоминания.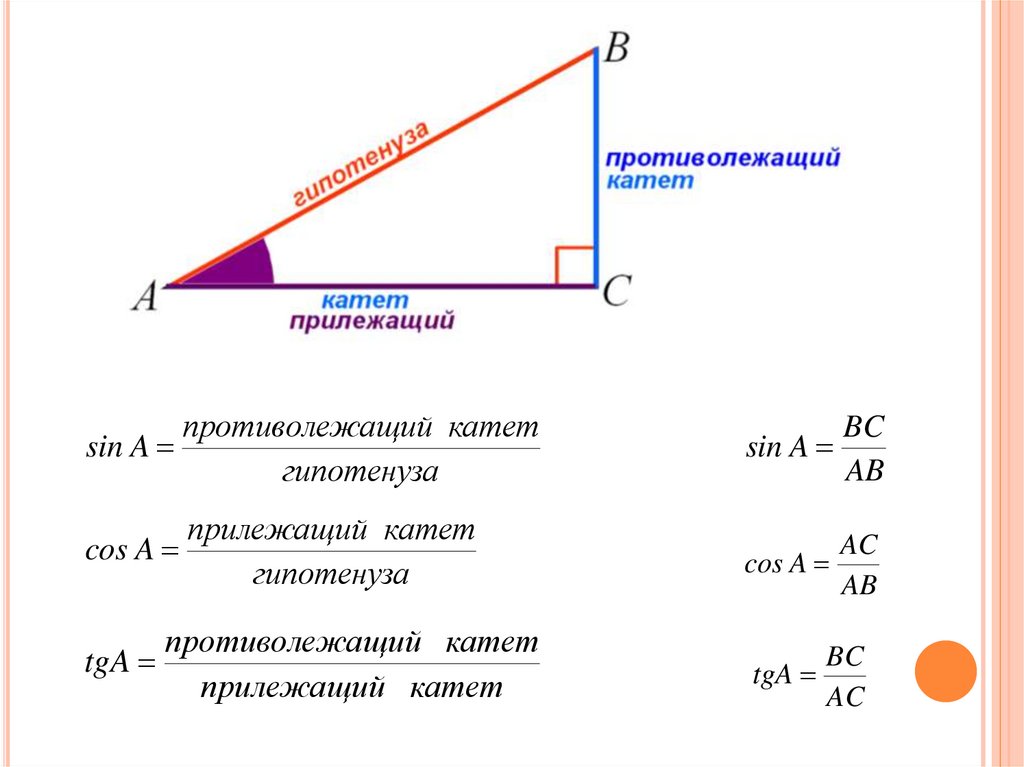 Тем не менее, запоминание полезной мнемоники может помочь. При нахождении синуса, косинуса и тангенса просто помните SOHCATOA (sō-kŭ-tō-ŭ). В этом примере S, C и T обозначают синус, косинус и тангенс. O, A и H обозначают противоположность, смежность и гипотенузу.
Тем не менее, запоминание полезной мнемоники может помочь. При нахождении синуса, косинуса и тангенса просто помните SOHCATOA (sō-kŭ-tō-ŭ). В этом примере S, C и T обозначают синус, косинус и тангенс. O, A и H обозначают противоположность, смежность и гипотенузу.
Запомнив SOHCATOA, вы сможете правильно писать формулы для синуса, косинуса и тангенса. Затем просто введите правильные числа, и все готово! Чтобы найти эти функции, нужно запомнить формулы и использовать правильные измерения сторон. Многие люди считают полезным пометить треугольник перед тем, как начать.
Можете ли вы найти синус, косинус и тангенс угла? Мы уверены, что вы можете! Однако поначалу новые математические темы могут быть трудными. С практикой и помощью учителя или друга мы знаем, что скоро вы многое узнаете о тригонометрии!
Common Core, Научные стандарты следующего поколения и Национальный совет по социальным исследованиям. »> Стандарты: CCSS.MATH.HSF.TF.A.2, CCRA.R.1, CCRA.R.2, CCRA.R.4, CCRA.R.10, CCRA.L.1, CCRA.L.2, CCRA .L.3, CCRA.L.6, CCRA.W.2, CCRA.W.4, CCRA.W.9, CCRA.W.10, CCRA.SL.1, CCRA.SL.2
»> Стандарты: CCSS.MATH.HSF.TF.A.2, CCRA.R.1, CCRA.R.2, CCRA.R.4, CCRA.R.10, CCRA.L.1, CCRA.L.2, CCRA .L.3, CCRA.L.6, CCRA.W.2, CCRA.W.4, CCRA.W.9, CCRA.W.10, CCRA.SL.1, CCRA.SL.2
Интересно, что дальше?
Сегодняшнее чудо дня обычно выходит только ночью.
Попробуйте
Готовы продолжать учиться? Проверьте действия ниже с помощью друга или члена семьи!
- Узнайте больше о синусе, косинусе и тангенсе, а также посмотрите полезные диаграммы на веб-сайте Math Is Fun. Помогло ли это вам глубже понять эти функции? Обобщите то, что вы узнали сегодня, для друга или члена семьи.
- Теперь, когда у вас есть мнемоника, которая поможет вам запомнить формулы синуса, косинуса и тангенса, сделайте плакат, который поможет другим запомнить. Используйте мнемонику SOHCAHTOA и включите любые изображения или диаграммы, которые, по вашему мнению, помогут вашим друзьям или членам семьи научиться находить эти функции.
 Не забудьте также указать правильные формулы!
Не забудьте также указать правильные формулы! - Чувствуете себя лукавым? Узнайте больше о геометрических фигурах и проявите творческий подход, создавая свои собственные! Вы можете попробовать сделать некоторые фигуры самостоятельно или следовать этому видео, чтобы научиться создавать трехмерные фигуры, используя только бумагу и ножницы. Убедитесь, что взрослый помогает вам, и получайте удовольствие, создавая свои фигуры.
Wonder Sources
- https://www.khanacademy.org/math/geometry-home/right-triangles-topic/intro-to-the-trig-ratios-geo/v/basic-trigonometry
- https ://www.mathsisfun.com/sine-cosine-tangent.html
- https://www.livescience.com/51026-what-is-trigonometry.html
- https://learnersdictionary.com/
Ты понял?
Проверьте свои знанияWonder Words
- ответвления
- углы
- этикетка
- функций
- формулы
- измерений
- тригонометрия
- геометрия
- математиков
Примите участие в конкурсе Wonder Word
Оцените это чудо
Поделись этим чудом
×ПОЛУЧАЙТЕ СВОЕ ЧУДО ЕЖЕДНЕВНО
Подпишитесь на Wonderopolis и получайте Wonder of the Day® по электронной почте или SMS
Присоединяйтесь к Buzz
Не пропустите наши специальные предложения, подарки и рекламные акции. Узнай первым!
Узнай первым!
Поделитесь со всем миром
Расскажите всем о Вандополисе и его чудесах.
Поделиться Wonderopolis
Wonderopolis Widget
Хотите делиться информацией о Wonderopolis® каждый день? Хотите добавить немного чуда на свой сайт? Помогите распространить чудо семейного обучения вместе.
Добавить виджет
Ты понял!
ПродолжитьНе совсем!
Попробуйте еще раз
коэффициентов синуса, косинуса и тангенса. – Бизнес/Техническая математика
5. Тригонометрия
Ожидается, что к концу этого раздела вы сможете
- Находить недостающую сторону прямоугольного треугольника, используя отношения синуса, косинуса или тангенса
- Найдите недостающий угол прямоугольного треугольника, используя отношения синуса, косинуса или тангенса
- Решение приложений с помощью тригонометрии прямого угла
Теперь, когда мы знаем основы алгебры и геометрии, связанные с прямоугольным треугольником, мы можем приступить к изучению тригонометрии. Многие реальные жизненные задачи можно представить и решить с помощью прямоугольной тригонометрии.
Многие реальные жизненные задачи можно представить и решить с помощью прямоугольной тригонометрии.
Мы знаем, что любой прямоугольный треугольник имеет три стороны и прямой угол. Сторона, противолежащая прямому углу, называется гипотенузой. Два других угла прямоугольного треугольника — острые углы (с мерой меньше 90 градусов). Один из этих углов мы называем опорным углом, и мы используем θ (тета) для его представления.
Гипотенуза всегда является наибольшей стороной прямоугольного треугольника. Две другие стороны называются противоположной стороной и смежной стороной. Названия этих сторон зависят от того, какой из двух острых углов используется в качестве опорного угла.
Рисунок 1.В прямоугольном треугольнике каждая сторона помечена строчной буквой, соответствующей прописной букве противоположной вершины.
Назовите стороны треугольника и найдите гипотенузу, противоположную и прилежащую.
Решение
Мы пометили стороны строчными буквами, чтобы они совпадали с прописными буквами противоположной вершины.
с — гипотенуза
а противоположна
b — смежна
Назовите стороны треугольника и найдите гипотенузу, противолежащую и прилежащую.
Показать ответy — гипотенуза
z противоположно
х рядом
Тригонометрические отношения — это отношения сторон прямоугольного треугольника. Для любого прямоугольного треугольника мы можем определить три основных тригонометрических соотношения: синус, косинус и тангенс.
Давайте обратимся к рисунку 1 и определим три основных тригонометрических отношения как:
- синус θ =
- косинус θ =
- тангенс θ =
Где θ — мера опорного угла, измеренная в градусах.
Очень часто мы используем сокращения для синуса, косинуса и тангенса.
- sin θ =
- , потому что θ =
- тангенс θ =
Некоторые помнят определение тригонометрических соотношений как SOH CAH TOA.
Давайте воспользуемся примером из примера 1, чтобы найти три соотношения.
Для данного треугольника найти отношение синуса, косинуса и тангенса.
Решение
sin θ =
cos θ =
tan θ =
Для данного треугольника найти отношение синуса косинуса и тангенса.
Показать ответsin θ =
потому что θ =
тангенс θ =
В примере 2 опорные углы могут быть или . Используя определение тригонометрических отношений, мы можем написать sinE = , cosE = и tanE = .
При расчетах мы обычно округляем отношения до четырех знаков после запятой, а в конце наш окончательный ответ — до одного знака после запятой, если не указано иное.
Для данного треугольника найти отношения синуса, косинуса и тангенса. При необходимости округлить до четырех знаков после запятой.
Решение
У нас есть два возможных опорных угла: R и S.
Используя определения, тригонометрические соотношения для угла R составляют:
- sin R= = 0,8
- , потому что R= = 0,6
- тангенс R= = 1,3333…
Используя определения, тригонометрические соотношения для угла S:
- sin S = = 0,6
- cos S = = 0,8
- тангенс S = = 0,75
Для данного треугольника найти отношения синуса, косинуса и тангенса.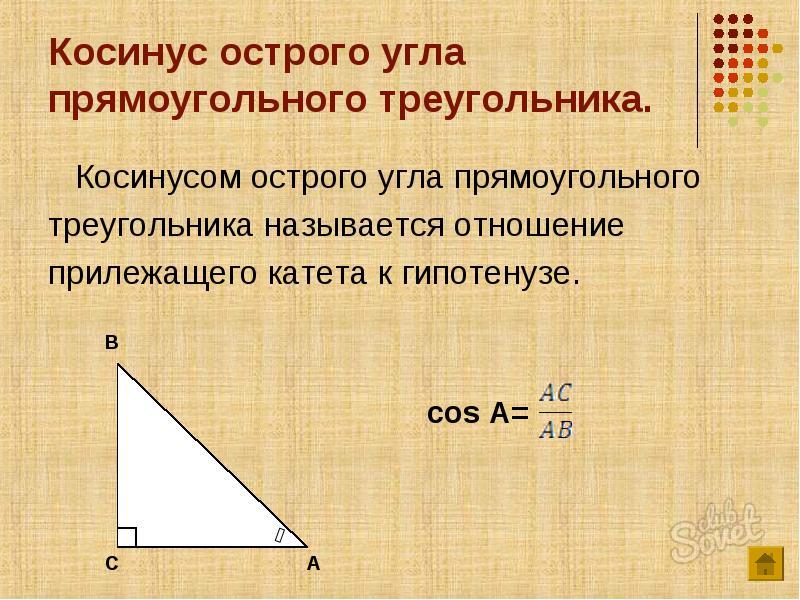 При необходимости округлить до четырех знаков после запятой.
При необходимости округлить до четырех знаков после запятой.
- sin F = = 0,8
- cos F = =0,6
- тангенс F = = 1,3333…
- sin D = = 0,6
- cos D = = 0,8
- тангенс D = = 0,75
Теперь воспользуемся научным калькулятором, чтобы найти тригонометрические отношения. Сможете ли вы найти кнопки sin, cos и tan на своем калькуляторе? Чтобы найти тригонометрические соотношения, убедитесь, что ваш калькулятор находится в режиме градусов.
С помощью калькулятора найдите тригонометрические соотношения. При необходимости округлить до 4 знаков после запятой.
a) sin 30°
b) cos 45°
c) tan 60°
Решение
Убедитесь, что ваш калькулятор находится в режиме Градусов.
а) С помощью калькулятора найдите, что sin 30° = 0,5
б) С помощью калькулятора найдите, что cos 45° = 0,7071 Округлив до 4 знаков после запятой.
c) С помощью калькулятора найдите тангенс 60° = 1,7321.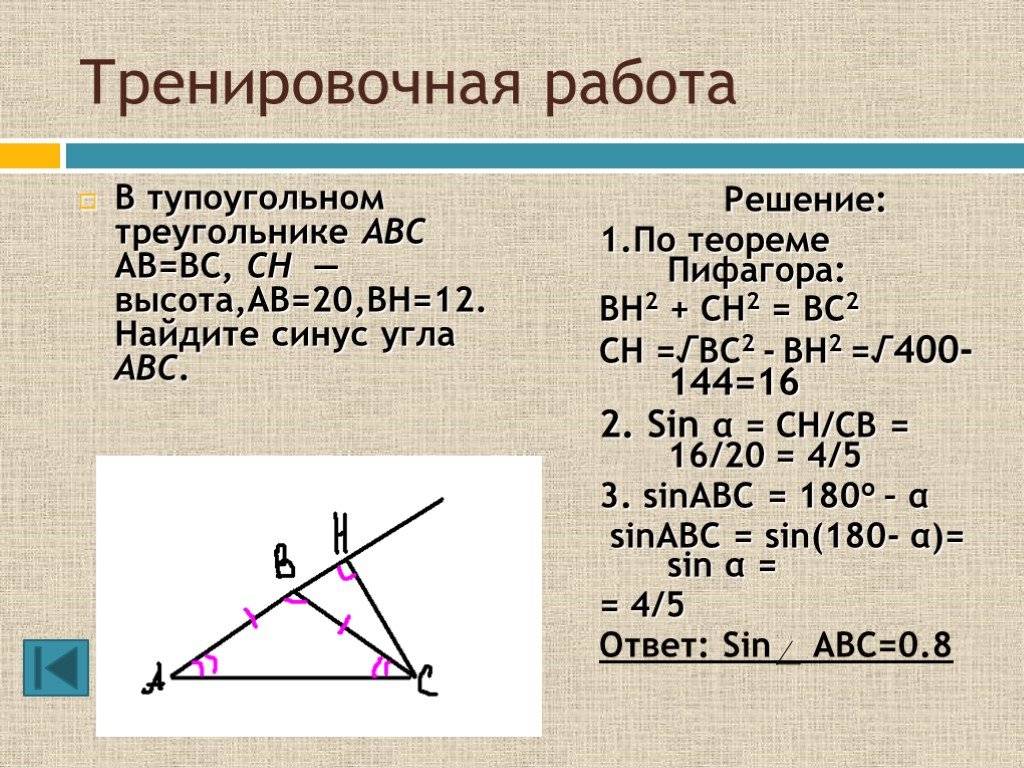 Округлите до 4 знаков после запятой.
Округлите до 4 знаков после запятой.
Найдите тригонометрические соотношения. При необходимости округлить до 4 знаков после запятой.
a) sin 60°
b) cos 30°
c) tan 45°
Показать ответa) sin 60° = 0,8660
б) cos 30° = 0,8660
в) тангенс 45° = 1
В этом разделе вы будете использовать тригонометрические отношения для решения задач прямоугольного треугольника. Мы адаптируем нашу стратегию решения задач для приложений тригонометрии. Кроме того, поскольку в этих задачах будет фигурировать прямоугольный треугольник, будет полезно нарисовать его (если рисунок не предоставлен) и пометить его заданной информацией. Мы включим это в первый шаг стратегии решения задач для тригонометрических приложений. .
- Прочтите задачу и убедитесь, что все слова и идеи понятны. Нарисуйте прямоугольный треугольник и обозначьте данные части.
- Определите , что мы ищем.

- Метка того, что мы ищем, выбрав переменную для ее представления.
- Найдите требуемое тригонометрическое отношение.
- Решите отношение, используя хорошие методы алгебры.
- Проверьте ответ, подставив его обратно в соотношение на шаге 4 и убедившись, что он имеет смысл в контексте задачи.
- Ответьте на вопрос полным предложением.
В следующих нескольких примерах, зная меру одного острого угла и длину одной стороны прямоугольного треугольника, мы решим прямоугольный треугольник относительно недостающих сторон.
Найти недостающие стороны. Округлите окончательный ответ до двух знаков после запятой
Решение
1. Прочтите задачу и убедитесь, что все слова и идеи понятны. Нарисуйте прямоугольный треугольник и обозначьте указанные части. 904:00 Нарисуйте прямоугольный треугольник и обозначьте указанные части. 904:00 | Дается чертеж. Угол Y — это наш опорный угол, y — противоположная сторона, z — смежная сторона, а x = 14 — гипотенуза. | |
| 2. Определите , что мы ищем. | а) противоположная сторона | б) смежная сторона |
| 3. Пометьте то, что мы ищем, выбрав переменную для ее представления. | г=? | г=? |
| 4. Найдите искомое тригонометрическое соотношение. 904:00 | sin 35° = | cos 35° = |
| 5. Решите отношение , используя хорошие методы алгебры. | 14 sin 35° = у 8.03 = у | 14 cos 35° = z 11,47 = z |
| 6. Проверьте ответ в задаче и убедитесь, что он имеет смысл. | 0,57 8,03 14 0,57 = 0,57 | 0,82 11,47 14 0,82 = 0,82 |
7. Ответьте на вопрос полным предложением. Ответьте на вопрос полным предложением. | Противоположная сторона 8.03 | Прилегающая сторона 11.47 |
Найти недостающие стороны. Округлите окончательный ответ до одного знака после запятой.
Показать ответа = 20,2
б = 16,4
Найдите гипотенузу. Округлите окончательный ответ до одного знака после запятой.
Решение
| 1. Прочтите задачу и убедитесь, что все слова и идеи понятны. Нарисуйте прямоугольный треугольник и обозначьте указанные части. 904:00 | Дается чертеж. Угол S – это исходный угол, s – противоположная сторона, r = 4 – прилежащая сторона, а p – гипотенуза 90 400. |
| 2. Определите , что мы ищем. | гипотенуза |
| 3. Пометьте то, что мы ищем, выбрав переменную для ее представления. | р=? |
4. Найдите искомое тригонометрическое соотношение. | cos 32° = |
| 5. Решите отношение, используя хорошие методы алгебры. | 0,8480 = р = 4,7170 Округление долей до 4 знаков после запятой |
| 6. Проверьте ответ в задаче и убедитесь, что он имеет смысл. | 0,8480 0,8480 = 0,8480 |
| 7. Ответьте на вопрос полным предложением. | Гипотенуза равна 4,7. Округлите мой окончательный ответ до одного знака после запятой. |
Найдите гипотенузу. Округлите окончательный ответ до одного знака после запятой.
Показать ответp = 22,7
Иногда у нас есть прямоугольный треугольник с данными только сторонами. Как найти недостающие углы? Чтобы найти недостающие углы, мы используем обратные тригонометрические отношения. Обратные кнопки sin -1 , cos -1 и tan -1 находятся на вашем научном калькуляторе.
Найдите углы. Округлите окончательный ответ до одного знака после запятой.
a) sin A = 0,5
b) cos B = 0,9735
c) tan C = 2,89358
Решение
Воспользуйтесь калькулятором и нажмите 2-ю FUN CTION, а затем нажмите SIN, COS или TAN. ключ
a) A = sin -1 0,5
= 30°
b) B = cos -1 0,9735
= 13,2° ed до одного знака после запятой
c) C = tan -1 2,89358
= 70,9° Округлено до одного десятичного знака
Найдите углы. Округлите окончательный ответ до одного знака после запятой.
a) sin X = 1
b) cos Y = 0,375
c) tan Z = 1,676767
Показать ответa) = 90°
б) = 68°
в) = 59,2°
В приведенном ниже примере у нас есть прямоугольный треугольник с двумя заданными сторонами. У нас отсутствуют острые углы. Давайте посмотрим, каковы шаги, чтобы найти недостающие углы.
Найдите пропавший . Округлите окончательный ответ до одного знака после запятой.
Округлите окончательный ответ до одного знака после запятой.
Решение
| 1. Прочтите задачу и убедитесь, что все слова и идеи понятны. Нарисуйте прямоугольный треугольник и обозначьте указанные части. | Дается чертеж. Угол T — это наш исходный угол, t = 7 — противоположная сторона, s — смежная сторона, а r = 11 — гипотенуза | .
| 2. Определите , что мы ищем. | угол T |
| 3. Пометьте то, что мы ищем, выбрав переменную для ее представления. 904:00 | =? |
| 4. Найдите искомое тригонометрическое соотношение. | sin T = |
| 5. Решите отношение , используя хорошие методы алгебры. | sin T = 0,6364 Т = sin -1 0,6364 = 39,5239° |
6. Проверьте ответ в задаче и убедитесь, что он имеет смысл. | sin 39,5239° 0,6364 0,6364 = 0,6364 |
| 7. Ответьте на вопрос полным предложением. | Недостающий угол T равен 39,5°. |
Найдите недостающий угол X. Округлите окончательный ответ до одного знака после запятой.
Показать ответ20.1°
Найдите недостающий угол A. Округлите окончательный ответ до одного десятичного знака.
Решение
| 1. Прочтите задачу и убедитесь, что все слова и идеи понятны. Нарисуйте прямоугольный треугольник и обозначьте указанные части. 904:00 | Дается чертеж. Угол A — это наш исходный угол, a = 9 — противолежащая сторона, c = 5 — прилежащая сторона, а b — гипотенуза 90 400. |
| 2. Определите , что мы ищем. | угол А |
| 3. Пометьте то, что мы ищем, выбрав переменную для ее представления. | =? |
4. Найдите искомое тригонометрическое соотношение. Найдите искомое тригонометрическое соотношение. | тангенс А = |
| 5. Решите отношение , используя хорошие методы алгебры. | тангенс А = 1,8 А = тангенс -1 1,8 = 60,9° |
| 6. Проверьте ответ в задаче и убедитесь, что он имеет смысл. | тангенс 60,9° 1,8 1,8 = 1,8 |
| 7. Ответьте на вопрос полным предложением. | Недостающий угол A равен 60,9°. |
Найдите недостающий угол C. Округлите окончательный ответ до одного знака после запятой.
Показать ответ29.1°
Из предыдущего раздела мы знаем, что любой треугольник имеет три стороны и три внутренних угла. В прямоугольном треугольнике, когда известны все шесть частей треугольника, мы говорим, что прямоугольный треугольник решен.
Решите прямоугольный треугольник. Округлите окончательный ответ до одного знака после запятой.
Решение
Поскольку сумма углов в любом треугольнике равна 180°, величину угла B можно легко вычислить.
= 180° − 90° − 42°
= 48°
| 1. Прочтите задачу и убедитесь, что все слова и идеи поняты. Нарисуйте прямоугольный треугольник и обозначьте данные части. | Дается чертеж. Угол A — это исходный угол, a = 8 — противолежащая сторона, b — прилежащая сторона, а c — гипотенуза. | |
| 2. Определите , что мы ищем. | а) соседняя сторона | б) гипотенуза 904:00 |
| 3. Пометьте то, что мы ищем, выбрав переменную для ее представления. | б = ? | с = ? |
| 4. Найдите искомое тригонометрическое соотношение. | тангенс 42° = | sin 42° = |
5. Решите отношение , используя хорошие методы алгебры. | 0,9004 = 0,9004 б = 8 б = 8,8849 | 0,6691 = 0,6691 с = 8 с = 11,9563 |
| 6. Проверьте ответ в задаче и убедитесь, что он имеет смысл. | тангенс 42° 0,9 = 0,9 | sin 42° 0,6691 = 0,6691 |
| 7. Ответьте на вопрос полным предложением. | Смежная сторона равна 8,9. Округляется до одного десятичного знака. | Гипотенуза равна 12 |
Мы решили прямоугольный треугольник
= 42°
= 48°
= 90°
a = 8
b = 8,9
c = 12
Решите прямоугольный треугольник. Округлите окончательный ответ до одного знака после запятой.
= 21°
= 69°
= 90°
Показать ответa = 6
б = 15,6
с = 16,7
Решите прямоугольный треугольник. Округлить до двух знаков после запятой.
Решение
1. Прочтите задачу и убедитесь, что все слова и идеи понятны. Нарисуйте прямоугольный треугольник и обозначьте указанные части. 904:00 Прочтите задачу и убедитесь, что все слова и идеи понятны. Нарисуйте прямоугольный треугольник и обозначьте указанные части. 904:00 | Дается чертеж. Пусть угол D — наш опорный угол, d = 4 — противолежащая сторона, f — прилежащая сторона, а e = 9 — гипотенуза | .|
| 2. Определите , что мы ищем. | а) уголок D | б) смежный |
| 3. Пометьте то, что мы ищем, выбрав переменную для ее представления. | =? | е = ? |
| 4. Найдите искомое тригонометрическое соотношение. 904:00 | sin D = | 4 2 + f 2 = 9 2 |
| 5. Решите отношение , используя хорошие методы алгебры. | sin D = 0,4444 Д = sin -1 0,4444 = 26,3850° | 16 + f 2 = 81 ф 2 = 81 – 16 ф 2 = 65 f = квадратный корень из 65 f = 8,06 |
6. Проверка ответ в задаче и убедившись, что это имеет смысл. Проверка ответ в задаче и убедившись, что это имеет смысл. | sin 26,3850° 0,4444 = 0,4444 | 4 2 + 8,06 2 9 2 81 = 81 |
| 7. Ответьте на вопрос полным предложением. | Недостающий угол D равен 26,39°. | Прилежащая сторона равна 8,06 Округлено до двух знаков после запятой |
Недостающий угол F = 180° – 90° – 26,39° = 63,64°
Решили прямоугольный треугольник
= 26,39°
= 90°
= 63,61°
d = 4
e = 9
f = 8,06
Решите прямоугольный треугольник. Округлить до одного десятичного знака.
= 29,3°
= 90°
= 60,7°
Показать ответd = 29,4
е = 18,4
f = 60,6
В предыдущих примерах мы смогли найти недостающие стороны и недостающие углы прямоугольного треугольника. Теперь давайте воспользуемся тригонометрическими отношениями для решения задач из реальной жизни.
Многие применения тригонометрических соотношений связаны с пониманием угла подъема или угла наклона.
Угол возвышения — это угол между горизонтальной линией (землей) и линией визирования наблюдателя.
Угол наклона — это угол между горизонтальной линией (параллельной земле) и линией обзора наблюдателя.
Джеймс стоит в 31 метре от базы Harbour Center в Ванкувере. Он смотрит на вершину здания под углом 78°. Какова высота Harbour Centre?
Решение
| 1. Прочтите задачу и убедитесь, что все слова и идеи понятны. Нарисуйте прямоугольный треугольник и обозначьте указанные части. | Угол X — это исходный угол, x — противоположная сторона, y = 31 м — прилежащая сторона, а z — гипотенуза. |
| 2. Определите , что мы ищем. | Противоположная сторона |
3. Этикетка то, что мы ищем, выбрав переменную для ее представления. | х=? |
| 4. Найдите искомое тригонометрическое соотношение. | тангенс 78° = |
| 5. Решите отношение , используя хорошие методы алгебры. | 4,7046 = х = 145,8426 |
| 6. Проверьте ответ в задаче и убедитесь, что он имеет смысл. | 4,7046 4,7046 = 4,7046 904:00 |
| 7. Ответьте на вопрос полным предложением. | Центр гавани составляет 145,8426 метра или округляется до 146 метров. |
Марта стоит в 23 метрах от основания самого высокого многоквартирного дома в Принс-Джордже и смотрит на крышу здания под углом 62°. Насколько высокое здание?
Показать ответ43,3 метра
Томас стоит на вершине здания высотой 45 метров и смотрит на свою подругу, стоящую на земле в 22 метрах от основания здания. Что такое угол депрессии?
Решение
1. Прочтите задачу и убедитесь, что все слова и идеи понятны. Нарисуйте прямоугольный треугольник и обозначьте указанные части. Прочтите задачу и убедитесь, что все слова и идеи понятны. Нарисуйте прямоугольный треугольник и обозначьте указанные части. | Угол Y – это исходный угол, y = 45 м – противолежащая сторона, z = 22 м – прилежащая сторона, а x – гипотенуза |
| 2. Определите , что мы ищем. | угол Y |
| 3. Этикетка то, что мы ищем, выбрав переменную для ее представления. | =? |
| 4. Найдите искомое тригонометрическое соотношение. | тангенс Y = |
| 5. Решите отношение , используя хорошие методы алгебры. | тангенс Y = 2,0455 Y = желто-коричневый – №2.0455 = 63,9470° |
| 6. Проверьте ответ в задаче и убедитесь, что он имеет смысл. 904:00 | загар 63,9470° 2,0455 2,0455 = 2,0455 |
7. Ответьте на вопрос полным предложением. Ответьте на вопрос полным предложением. | Угол наклона составляет 63,9470° или 64° с округлением до одного десятичного знака. |
Хемант стоит на вершине скалы на высоте 250 футов над землей и смотрит на своего друга, стоящего на земле в 40 футах от основания скалы. Что такое угол депрессии?
Показать ответ80,9°
- Три основных тригонометрических отношения: (Где θ — мера опорного угла, измеренная в градусах.)
- синус θ =
- косинус θ =
- тангенс θ =
- Стратегия решения проблем для приложений тригонометрии
- Прочтите задачу и убедитесь, что все слова и идеи понятны. Нарисуйте прямоугольный треугольник и обозначьте указанные части.
- Определите , что мы ищем.
- Метка того, что мы ищем, выбрав переменную для ее представления.

- Найдите требуемое тригонометрическое отношение.
- Решите отношение, используя хорошие методы алгебры.
- Проверьте ответ, подставив его обратно в отношение, найденное на шаге 5, и убедившись, что оно имеет смысл в контексте задачи.
- Ответьте на вопрос полным предложением.
Обозначьте стороны треугольника.
| 1 | 2. |
- Если исходный угол в вопросе 1 равен B, найдите смежный угол ?
- Если исходный угол в вопросе 2 равен Z, найти противоположный угол?
Обозначьте стороны треугольника и найдите гипотенузу, противолежащую и прилежащую.
| 5. | 6. |
Используйте свой калькулятор, чтобы найти данные отношения. При необходимости округлить до четырех знаков после запятой:
При необходимости округлить до четырех знаков после запятой:
Для заданных треугольников найдите синус, косинус и тангенс θ.
| 11. | 12. |
| 13. | 14. |
Для данных треугольников найдите недостающую сторону. Округлите его до одного десятичного знака.
| 15. Найдите гипотенузу. | 16. Найдите b, если a = 6. |
| 17. Найдите противоположное. | 18. Найдите соседнее. |
Найдите недостающие стороны данных треугольников. Округлите его до одного десятичного знака.
| 19. | 20. |
Решите треугольники. Округлить до одного десятичного знака.
21. | 22. |
| 23. | 24. |
- Ким стоит в 75 метрах от низа дерева и смотрит на верхушку дерева под углом 48°. Насколько высокое дерево?
- Дерево отбрасывает тень длиной 6 метров, когда угол подъема к солнцу составляет 52°. Насколько высокое дерево?
- Лестница высотой 15 футов прислонена к дому и образует с землей угол 45°. На каком расстоянии основание лестницы от дома?
- Роксана запускает воздушного змея и выпустила веревку длиной 100 футов. Угол возвышения с землей 38°. Как высоко ее воздушный змей над землей?
- Марта запускает воздушного змея и выпустила 28 метров веревки. Если воздушный змей находится на высоте 10 метров над землей, каков угол возвышения?
- Самолет взлетает с земли под углом 25°. Если самолет пролетел 200 км, на какой высоте он находится над землей?
| 1. | 3. |

 Не забудьте также указать правильные формулы!
Не забудьте также указать правильные формулы!
