2°. Точка С — середина отрезка АВ, точка D — середина отрезка АС… 7 класс Зив геометрия ГДЗ. Контрольные работы. Вариант 2. К-1. – Рамблер/класс
2°. Точка С — середина отрезка АВ, точка D — середина отрезка АС… 7 класс Зив геометрия ГДЗ. Контрольные работы. Вариант 2. К-1. – Рамблер/классИнтересные вопросы
Школа
Подскажите, как бороться с грубым отношением одноклассников к моему ребенку?
Новости
Поделитесь, сколько вы потратили на подготовку ребенка к учебному году?
Школа
Объясните, это правда, что родители теперь будут информироваться о снижении успеваемости в школе?
Школа
Когда в 2018 году намечено проведение основного периода ЕГЭ?
Новости
Будет ли как-то улучшаться система проверки и организации итоговых сочинений?
Вузы
Подскажите, почему закрыли прием в Московский институт телевидения и радиовещания «Останкино»?
2°.
Точка С — середина отрезка АВ,
BD= 15,3см. Найдите длину отрез-
ка АС. Ответ выразите в миллиметрах.
ответы
ответ
ваш ответ
Можно ввести 4000 cимволов
отправить
дежурный
Нажимая кнопку «отправить», вы принимаете условия пользовательского соглашения
похожие темы
Экскурсии
Мякишев Г.Я.
Досуг
Химия
похожие вопросы 5
Докажите, что треугольники подобны. Вопросы и задачи 64, Геометрия, 10-11 класс, Атанасян Л.С.
Привет. Запуталась при решении, нужна помощь знатоков!!!
Три прямые, проходящие через одну точку и не лежащие в одной (Подробнее…)
ГДЗГеометрия11 класс10 классАтанасян Л.С.
Самостоятельная работа 19. Вариант 2. № 2 ГДЗ Геометрия 9 класс Зив Б.
Используя параллельный перенос, докажите, что углы при основании равнобедренной трапеции равны между собой.
ГДЗЭкзаменыГеометрия9 классЗив Б. Г.
ГДЗ Тема 21 Физика 7-9 класс А.В.Перышкин Задание №476 Изобразите силы, действующие на тело.
Привет всем! Нужен ваш совет, как отвечать…
Изобразите силы, действующие на тело, когда оно плавает на поверхности жидкости. (Подробнее…)
ГДЗФизикаПерышкин А.В.Школа7 класс
9. Определите ряд, в котором в обоих словах пропущена одна и та же буква. ЕГЭ-2017 Русский язык Цыбулько И. П. ГДЗ. Вариант 12.
9.
Определите ряд, в котором в обоих словах пропущена одна и та же буква. Выпишите
эти слова, вставив пропущенную букву. (Подробнее…)
ГДЗРусский языкЕГЭЦыбулько И.П.
11. Выпишите слово, в котором на месте пропуска пишется буква Е. Русский язык ЕГЭ-2017 Цыбулько И.
П. ГДЗ. Вариант 12.
11.
Выпишите слово, в котором на месте пропуска пишется буква Е.
произнос., шь (Подробнее…)
ГДЗЕГЭРусский языкЦыбулько И.П.
Отрезок. Длина и середина отрезка. Сравнение отрезков
- Длина отрезка
- Равные отрезки
- Сравнение отрезков
- Середина отрезка
Отрезок — это часть прямой, ограниченная двумя точками, лежащими на этой прямой. Точки, определяющие границы отрезка, называются концами отрезка.
Отрезок обозначается двумя большими латинскими буквами, поставленными при его концах: отрезок AB или BA.
Длина отрезка
Длина отрезка — это расстояние между концами отрезка. Любой отрезок имеет длину, бо́льшую нуля:
Измерение длины отрезка осуществляется путём сравнения данного отрезка с длиной единичного отрезка. Единичный отрезок — это отрезок, длина которого принимается за единицу.
Следовательно:
длина отрезка – это положительное число, показывающее, сколько раз единичный отрезок и его части укладываются в данном отрезке.
Чаще всего используются единичные отрезки равные 1 мм, 1 см, 1 дм, 1 м или 1 км. Измерить длину отрезка можно линейкой или любым другим прибором для измерения длины:
AB = 6 см.
Свойства длин отрезков:
- Основное свойство длины отрезка: если точка делит отрезок на два отрезка, длина всего отрезка равна сумме длин этих двух отрезков.
- Длины равных отрезков равны.
- Любой отрезок имеет определённую длину, большую нуля.
Равные отрезки
Равные отрезки — это отрезки, имеющие одинаковую длину. Если наложить равные отрезки друг на друга, то их концы совпадут.
Пример. Возьмём два отрезка CD и LM:
Если расположить отрезки параллельно друг над другом так, чтобы точка C была над точкой L, то станет видно, что точка D располагается над точкой М:
Значит длины отрезков равны, следовательно CD = LM.
Сравнение отрезков
Сравнить два отрезка — это значит определить, равны они, или один больше другого.
Сравнить два отрезка можно, отложив на прямой оба отрезка из одной точки в одну и туже сторону. Для этого можно воспользоваться циркулем.
Чтобы отложить на прямой отрезок равный данному, сначала помещают ножки циркуля так, чтобы острия их концов упирались в концы отрезка, а затем, не изменяя раствора циркуля, переносят его так, чтобы оба его конца находились на прямой.
При сравнении двух отрезков возможно получение одного из представленных результатов: отрезки будут равны, первый отрезок будет больше второго или первый отрезок будет меньше второго.
Пример. Если отложить на прямой от любой точки, например C, в одну сторону два отрезка CA и CB и точка A окажется между точками C и B, то отрезок CA меньше отрезка CB (или CB больше отрезка CA):
CA < CB или CB > CA.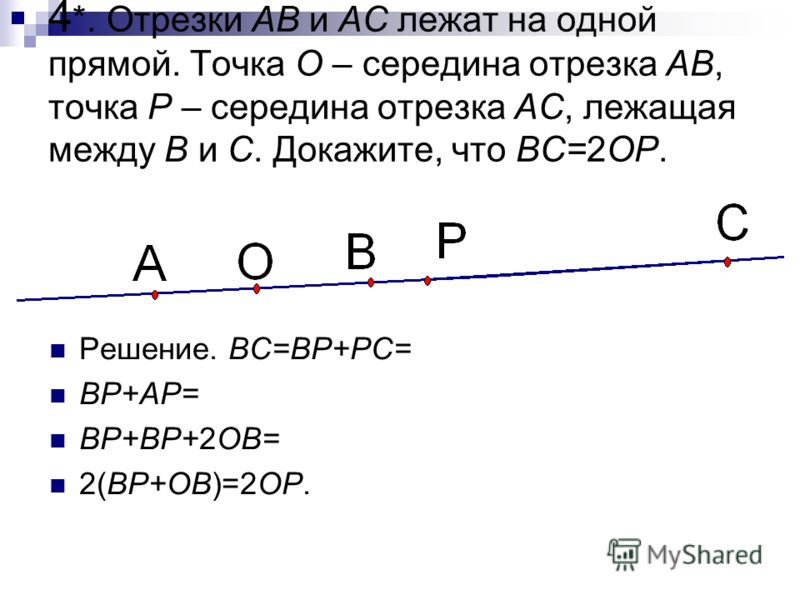
Если точка B окажется между точками C и A, то отрезок CA больше отрезка CB (или CB меньше отрезка CA):
CA > CB или CB < CA.
Если точки A и B совпадут, то отрезки CA и CB равны:
CA = CB.
Если при наложении отрезков оба их конца совмещаются, значит отрезки равны.
При сравнении отрезков путём измерения их длин больше будет тот отрезок, у которого больше длина.
Пример. Сравнить длину отрезков AB и AC.
Так как отрезок AB имеет большую длину, чем отрезок AC, то
AB > AC.
Так как отрезки AB и AC имеют одинаковую длину, то
AB = AC.
Если при измерении отрезков их длины равны, то и отрезки равны.
Середина отрезка
Середина отрезка — это точка, делящая отрезок на две равные части.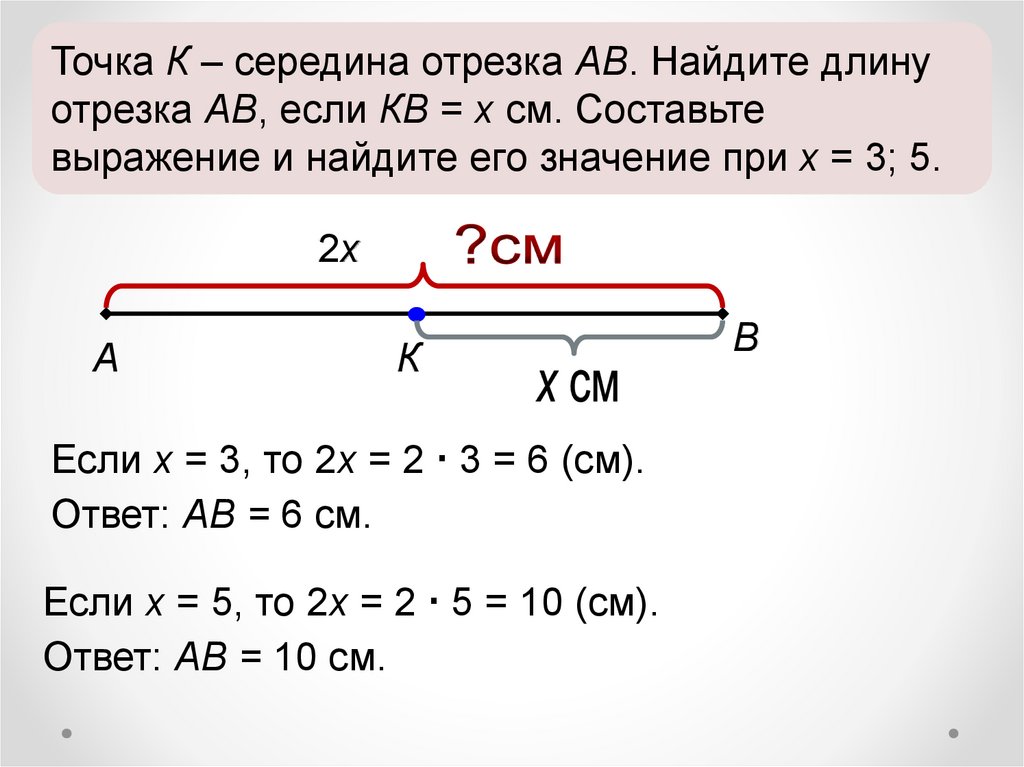
Формула средней точки — ACT Math
Все ресурсы ACT Math
14 диагностических тестов 767 практических тестов Вопрос дня Карточки Learn by Concept
← Предыдущая 1 2 Следующая →
ACT Math Help » Алгебра » Координатная плоскость » Линии » Midpoint Formula
В стандартной координатной плоскости (x,y) середина линии XY равна (12, – 3) и точка X находится в (3, 4). Каковы координаты точки Y ?
Возможные ответы:
(7,5, 0,5)
(9, — 7)
(9, 7)
( — 4, 11)
(21, — 10 10. )
Правильный ответ:
(21, – 10)
Объяснение:
Чтобы добраться из середины (12, – 3) в точку (3,4), мы проходим – 9 единиц в направлении x и 7 единиц в направлении y.
Чтобы найти другую точку, мы проходим ту же величину в противоположном направлении от средней точки, 9 единиц по оси x и – 7 единиц по оси y до точки (21, – 10).
Сообщить об ошибке
Середина отрезка . Если одна конечная точка отрезка равна , то какая другая конечная точка?
Возможные ответы:
Правильный ответ:
Объяснение:
Для решения этой задачи можно использовать формулу средней точки, где средняя точка — это среднее значение двух координат.
Даны середина и одна конечная точка. Подставьте эти значения в формулу.
Найдите переменные, чтобы найти координаты второй конечной точки.
Конечные координаты другой конечной точки .
Сообщить об ошибке
Предположим, что середина отрезка равна Каковы конечные точки отрезка?
Возможные ответы:
Правильный ответ:
Объяснение:
Середина отрезка находится по формуле .
Середина задается как Проходя через варианты ответов, только баллы и дают правильную середину .
Сообщить об ошибке
Какова середина сегмента
между и ?
Возможные ответы:
Правильный ответ:
Объяснение:
Какова середина отрезка
между и ?
Чтобы найти эту среднюю точку, вы должны сначала вычислить две конечные точки. Таким образом, замените:
Тогда, для:
Таким образом, два рассматриваемых пункта:
и
Средняя точка двух точек:
Таким образом, для наших данных, это:
или
Сообщить об ошибке
Если это середина и другой точки, что это за другая точка?
Возможные ответы:
Правильный ответ:
Объяснение:
Напомним, что значения средней точки и являются средним значением значений и двух рассматриваемых точек.
и
. Решим каждое уравнение соответственно:
Для умножим обе части на:
Таким образом,
То же самое и с другим уравнением:
5
, поэтому
Таким образом, наша точка
Сообщить об ошибке
Если является серединой и другой точки, что это за другая точка?
Возможные ответы:
Правильный ответ:
Объяснение:
Если является серединой и еще одной точки, что это за другая точка?
Напомним, что значения средней точки и являются средним значением значений и двух рассматриваемых точек. Таким образом, если мы назовем другую точку, мы знаем, что:
и
Решите каждое уравнение соответственно:
Для умножьте обе части на и затем вычтите из обеих частей:
Таким образом,
Для , умножьте обе стороны на 2, а затем вычтите 10 из обеих сторон:
Таким образом,
Таким образом, наша точка равна
Сообщить об ошибке
Какова координата точки на полпути между (-2, -4) и (6, 4)?
Возможные ответы:
(0,2)
(2,0)
(3,1)
(2,2)
Правильный ответ:
(2) ,0)
Объяснение:
Формула средней точки:
Сообщить об ошибке
Какова середина MN между точками M(2, 6) и N (8, 4)?
Возможные ответы:
(3, 5)
(5, 2)
(5, 5)
(3, 1)
(2, 1)
Правильный ответ:
(5, 5)
Объяснение:
Формула средней точки равна .
Сложите значения x вместе и разделите их на 2, и сделайте то же самое для значений y.
x: (2 + 8) / 2 = 10 / 2 = 5
y: (6 + 4) / 2 = 10 / 2 = 5
Середина MN равна (5,5).
Сообщить об ошибке
В стандартной координатной плоскости какова середина отрезка, идущего из точки (3, 5) в точку (7, 9)?
Возможные ответы:
(6,6)
(10,14)
(5, 7)
(–2, –2)
(7, 5)
05 9: Правильный ответ
(5, 7)
Объяснение:
Формула средней точки . Простой способ запомнить это состоит в том, что для нахождения средней точки просто нужно найти среднее значение двух координат x и среднее значение двух координат y. В этом случае две координаты x равны 3 и 7, а две координаты y равны 5 и 9. Если мы подставим эти значения в формулу средней точки, мы получим (3 + 7/2), (5 + 9) /2, что равно (5, 7). Если вы получили (–2, –2), возможно, вы вычли свои координаты x и y вместо сложения.
Если вы получили (10,14), возможно, вы забыли разделить свои координаты x и y на 2. Если вы получили (6,6), возможно, вы нашли среднее значение x 1 и y 2 и x 2 и y 1 вместо того, чтобы хранить вместе координаты x и координаты y. Если вы получили (7, 5), возможно, вы поменяли местами координаты x и y.
Сообщить об ошибке
Найти середину отрезка с концами (–1, 4) и (3, 6).
Возможные ответы:
(1, 5)
(5, 1)
(4, 5)
(3, 2)
Правильный ответ:
(1, 5)
Объяснение:
Формула для средней точки = (x 1 + x 2 )/2, (y 1 + y 2 )/2. Подставляя две координаты x и две координаты y от конечных точек, мы получаем (–1 + 3)/2.
(4 + 6)/2 или (1, 5) в качестве средней точки.
Сообщить об ошибке
← Назад 1 2 Далее →
Уведомление об авторских правах
Все ресурсы ACT Math
14 Диагностические тесты 767 практических тестов Вопрос дня Карточки Учитесь по концепции
Средняя точка Определение и значение | Dictionary.com
- Основные определения
- Викторина
- Связанный контент
- Примеры
- Британский
Показывает уровень сложности слова.
или середина
[ середина ]
/ ˈmɪdˌpɔɪnt /
Сохранить это слово!
См. синонимы для средней точки на сайте Thesaurus.com
Показывает уровень оценки в зависимости от сложности слова.
сущ.
точка в середине или около середины, или равноудаленная от обоих концов, как у линии: середина границы.
Момент времени на полпути между началом и концом процесса, события или ситуации: середина переговоров.
Геометрия. точка на отрезке прямой или дуги, равноудаленная при измерении вдоль прямой или дуги от обеих конечных точек.
Статистика. медиана (определ. 3).
Астрология. точка на дуге, равноудаленная от двух планет: считается чувствительной точкой и используется в гороскопических интерпретациях.
ВИКТОРИНА
МОЖЕТЕ ЛИ ВЫ ОТВЕЧАТЬ НА ЭТИ ОБЫЧНЫЕ ГРАММАТИЧЕСКИЕ СПОРЫ?
Есть грамматические дебаты, которые никогда не умирают; и те, которые выделены в вопросах этой викторины, наверняка снова всех разозлят. Знаете ли вы, как отвечать на вопросы, которые вызывают самые ожесточенные споры по грамматике?
Вопрос 1 из 7
Какое предложение верно?
Начало средней точки
13:25–75; Средний английский.
См. mid-, point
Слова рядом с midpoint
полуночное солнце, полдень, срединно-океанический хребет, середина прочь, середина, середина, середина, мидраш, средняя жила, середина, середина подъема
Dictionary.com Unabridged На основе Random House Unabridged Dictionary, © Random House, Inc., 2023
Слова, относящиеся к средней точке
ось, яблочко, центральность, центриоль, центр, ядро, cynosure, сущность, фокус, суть, сердце, очаг, ступица , внутри, внутри, ядро, основной поток, костный мозг, медиана, середина
Как использовать среднюю точку в предложении
Губернатор Вирджинии говорит, что поддерживает легализацию марихуаны Пятница — это «день перехода», традиционно середина сессии, когда каждая палата должна завершить работу над своим собственным законодательством и обратиться к законопроектам, подготовленным другой палатой.
Генеральная ассамблея Вирджинии готовится к историческим голосованиям за легализацию марихуаны и отмену смертной казни|Грегори С.
Шнайдер, Лаура Воззелла|4 февраля 2021 г.|Washington PostЭто делает среднюю точку точкой решетки, и, как мы заметили выше, поэтому он соответствует вершине треугольника в кувыркающемся пространстве.
Кривая геометрия круговых бросков|Патрик Хоннер|13 января 2021 г.|Журнал Quanta
В разгар регулярного сезона это явно не проблема для Флориды и Траска, которые бросили на 1815 ярдов, 22 тачдауна и три перехвата в пяти играх.
Победители и проигравшие в студенческом футболе недели 10: Флорида снова веселая, а Джорджия закончилась|Патрик Стивенс|8 ноября 2020 г.|Washington Post
Затем он нашел среднюю точку этой пары точек и определил ее x и y координаты.
Новая геометрическая перспектива разрушает старую проблему о прямоугольниках|Кевин Хартнетт|25 июня 2020 г.|Журнал Quanta
Шнайдер, Лаура Воззелла|4 февраля 2021 г.|Washington PostВо-первых, помните, что прямоугольник можно представить как две пары точек, которые имеют общую среднюю точку и являются равными расстояние друг от друга.
Новая геометрическая перспектива дает трещину в старой задаче о прямоугольниках|Кевин Хартнетт|25 июня 2020 г.|Журнал Quanta
Но чем шире основание в средней точке, тем стабильнее поездка — независимо от того, сколько нагромождений в крайних точках.
Центрист сходит с ума|Марк Маккиннон|13 октября 2010 г.|DAILY BEAST
Спинной плавник небольшой, расположен за серединой спины и имеет различную форму от серповидной до треугольной.
Киты, дельфины и морские свиньи западной части Северной Атлантики|Стивен Лезервуд
Примерно здесь, я бы сказал, в середине этого здания.
Комиссия Уоррена (2 из 26): Слушания Том. II (из 15)|Президентская комиссия по делу об убийстве президента Кеннеди
Чуть меньше трети расстояния до средней точки за более чем половину времени.
Out Around Rigel|Robert H. Wilson
К тому времени, когда середина была пройдена, я жил в своего рода сне наяву; или, скорее, состояние сомнамбулизма.
