Вместе с этим калькулятором также используют следующие:
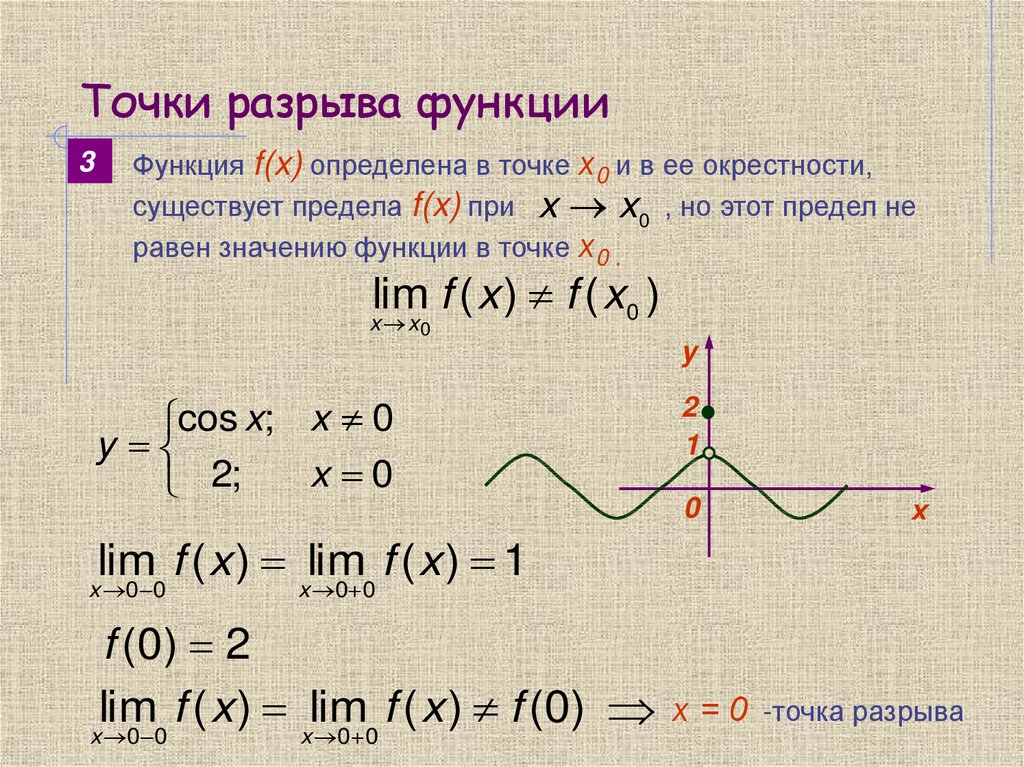
Точки разрыва функции
Решение пределов:
Построение графика функции методом дифференциального исчисления
Экстремум функции двух переменных
Вычисление интегралов
см. также Вычисление приближенно с помощью дифференциала
Определение. Функция y=f(x) называется дифференцируемой в точке x0, если ее приращение в этой точке можно представить в виде ∆y=A∆x + α(∆x)∆x, где A – константа, а α(∆x) – бесконечно малая при ∆x → 0.
Требование дифференцируемости функции в точке эквивалентно существованию производной в этой точке, причем A=f’(x0).
Пусть f(x) дифференцируема в точке x0 и f ‘(x0)≠0, тогда ∆y=f’(x0)∆x + α∆x, где α= α(∆x) →0 при ∆x→0.
то есть ∆y~f’(x0)∆x. Следовательно, f’(x0)∆x представляет собой главную и вместе с тем линейную относительно ∆x часть приращения ∆y (линейная – значит содержащая ∆x в первой степени). Это слагаемое называют дифференциалом функции y=f(x) в точке x0 и обозначают dy(x0) или df(x0). Итак, для произвольных значений x
dy=f′(x)∆x. (1)
Полагают dx=∆x, тогда
dy=f′(x)dx. (2)
Пример. Найти производные и дифференциалы данных функций.
а) y=4tg2x
Решение:
дифференциал:
б)
Решение:
дифференциал:
y=arcsin2(lnx)
Решение:
дифференциал:
г)
Решение:
=
дифференциал:
Пример.
Для функции y=x3 найти выражение для ∆y и dy при некоторых значениях x и ∆x.
Решение. ∆y = (x+∆x)3 – x3 = x3 + 3x2∆x +3x∆x2 + ∆x3 – x3 = 3x2∆x+3x∆x2+∆x3; dy=3x2∆x (взяли главную линейную относительно ∆x часть ∆y). В данном случае α(∆x)∆x = 3x∆x2 + ∆x3.
Построение графика функции методом дифференциального исчисления
Существует способ построения графика функции, основанный на аналитическом исследовании функции. Исследование проводится по следующей примерной схеме:1) выяснение области определения функции;
2) решается вопрос о четности или нечетности функции;
4) находят точки пересечения кривой с осями координат;
5) находят точки разрыва функции и определяют их характер;
6) проводят исследования на экстремум, находят экстремальные значения функции;
7) ищутся точки перегиба и интервалы выпуклости и вогнутости кривой;
8) отыскание асимптот кривой;
9) полученные результаты наносят на чертеж и получают график исследуемой функции.
(2/3)
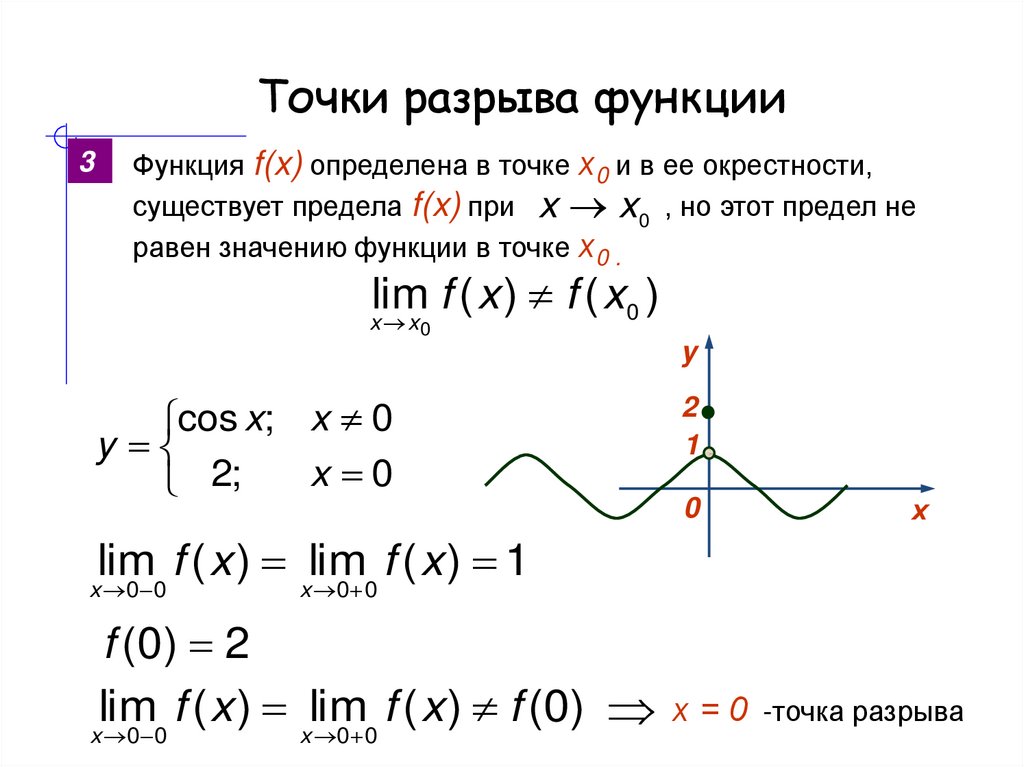
Пример №1. Провести полное исследование функции и построить ее график.
1) Функция определена всюду, кроме точек .
2) Функция нечетная, так как f(-x) = -f(x), и, следовательно, ее график симметричен относительно начала координат. Поэтому ограничимся исследованием только для 0 ≤ x ≤ +∞.
3) Функция не периодическая.
4) Так как y=0 только при x=0, то пересечение с осями координат происходит только в начале координат.
5) Функция имеет разрыв второго рода в точке , причем , . Попутно отметим, что прямая – вертикальная асимптота.
6) Находим и приравниваем ее к нулю: , откуда x1 = -3, x2 = 0, x3 = 3. На экстремум надо исследовать только точку x=3 (точку x2=0 не исследуем, так как она является граничной точкой промежутка [0, +∞)).
В окрестности точки x3=3 имеет: y’>0 при x<3 и y ’<0 при x>3, следовательно, в точке x3 функция имеет максимум, ymax(3)=-9/2.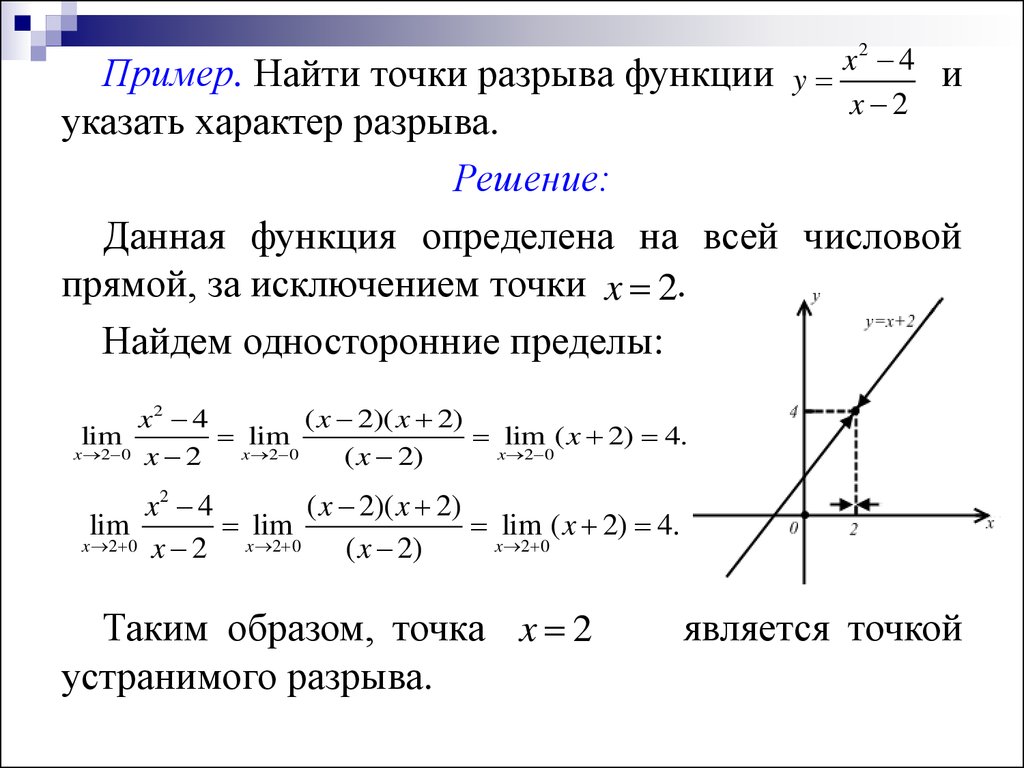
Для проверки правильности нахождения минимального и максимального значения.
7) Находим . Видим, что y’’=0 только при x=0, при этом y”<0 при x<0 и y”>0 при x>0, следовательно, в точке (0,0) кривая имеет перегиб. Иногда направление вогнутости может измениться при переходе через разрыв кривой, поэтому следует выяснить знак y” и около точек разрыва функции. В нашем случае y”>0 на промежутке (0, ) и y”<0 на (, +∞), следовательно, на (0, ) кривая вогнута и выпукла на (, ∞).
8) Выясним вопрос об асимптотах.
Наличие вертикальной асимптоты установлено выше. Ищем горизонтальные: , следовательно, горизонтальных асимптот нет.
Найдем наклонные асимптоты: , , следовательно, y=-x – наклонная двусторонняя асимптота.
9) Теперь, используя полученные данные, строим чертеж:
Пример №2.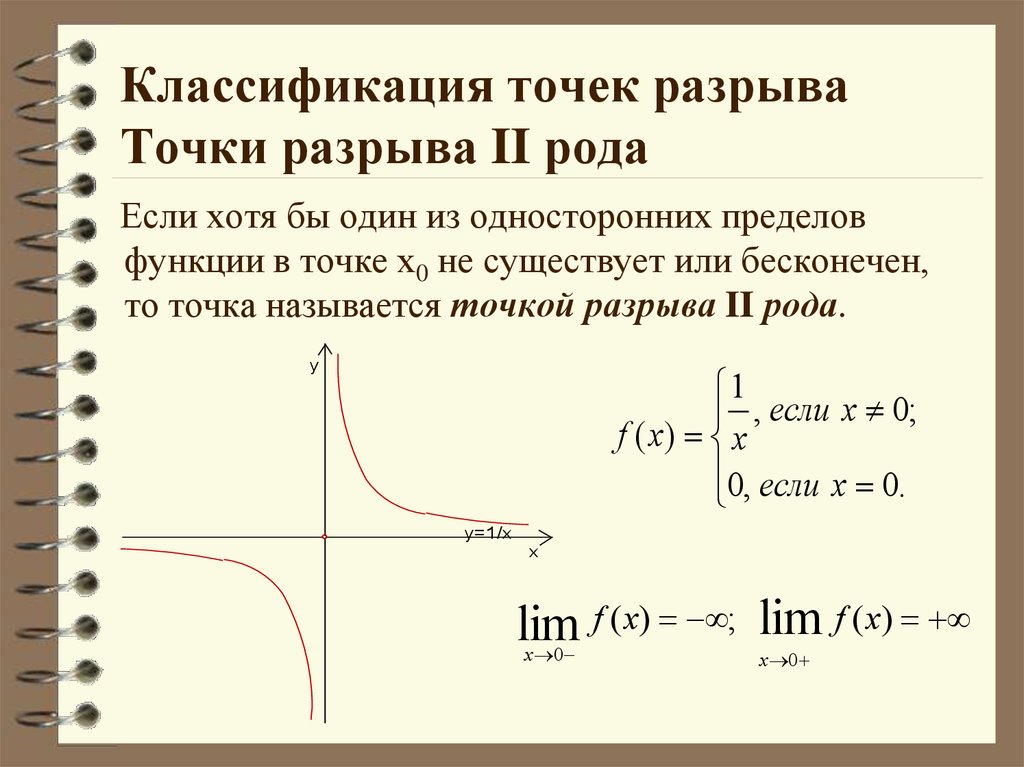
Решение.
1. Область определения функции D(y) = (-∞;0)U(0;∞).
2. Функция не является четной или нечетной.
3. Найдем точки пересечения графика с осью ОХ; имеем
; .
4. Точки разрыва x=0, причем ; следовательно, x=0 является вертикальной асимптотой графика.
Найдем наклонные асимптоты:
;
.
Наклонная асимптота имеет уравнение
y=x.
5. Найдем экстремум функции и интервалы возрастания и убывания. Имеем . Существует единственная критическая точка x=2. В промежутках x∈(-∞ ;0)∪(2; +∞) y’>0, следовательно, функция возрастает; в промежутке x∈(0;2) y'<0, функция убывает. Далее, находим ; y»(2)>0, следовательно, x=2 – точка минимума ymin=3.
6. Найдем интервалы выпуклости и вогнутости кривой и точки ее перегиба. Так как y’’>0 (x≠0), то график функции всюду вогнут. Точек перегиба кривая не имеет.
Строим график функции.
Калькулятор точки безубыточности
— MathCracker.com
Финансы Решатели
Инструкции: Используйте этот калькулятор точки безубыточности для расчета точки безубыточности (\(BEP\)), указав фиксированную стоимость (\(FC\)), переменную стоимость единицы продукции (\(VC\)) и цену продажи. (\(П\)):
Фиксированная стоимость \((FC)\) =
Переменная стоимость за единицу \((VC)\) =
Цена продажи \((P)\) =
Подробнее о калькуляторе безубыточности, чтобы лучше понять, как им пользоваться.
Сначала начнем с определения безубыточности: Точка безубыточности — это объем производства, при котором прибыль будет равна нулю.
Прежде всего, что такое точка останова?
В финансах точка разрыва наступает тогда, когда выручка равняется затратам, поэтому компания «безубыточна» (именно здесь наступает «прорыв»). от).
Обычно точка останова измеряется либо в единицах, либо в долларах. Так, например, вы находите количество единиц, которые необходимо, чтобы выручка покрывала расходы. Вы также можете найти стоимость продаж в долларах, необходимую для безубыточности.
Как рассчитать точку безубыточности?
Расчет довольно прост.
Вам нужно использовать следующую формулу:
\[ BEP = \displaystyle \frac{FC}{P — VC} \]
Часто, когда дело доходит до концепции точки безубыточности в бухгалтерском учете, вместо точки безубыточности рассматриваются продажи за наличные, связанные с уровнем продаж в точке безубыточности.
Обратите внимание на формулу цены безубыточности, что знаменатель имеет \(P — VC\). Так что же происходит, когда \(P = VC\)? В этом случае точка безубыточности равна бесконечности, и в этом случае вывод состоит в том, что, когда цена равна переменным затратам на единицу, точка безубыточности отсутствует.
Что такое анализ безубыточности?
Идея безубыточности в реальной жизни заключается в том, что я не проигрываю и не выигрываю.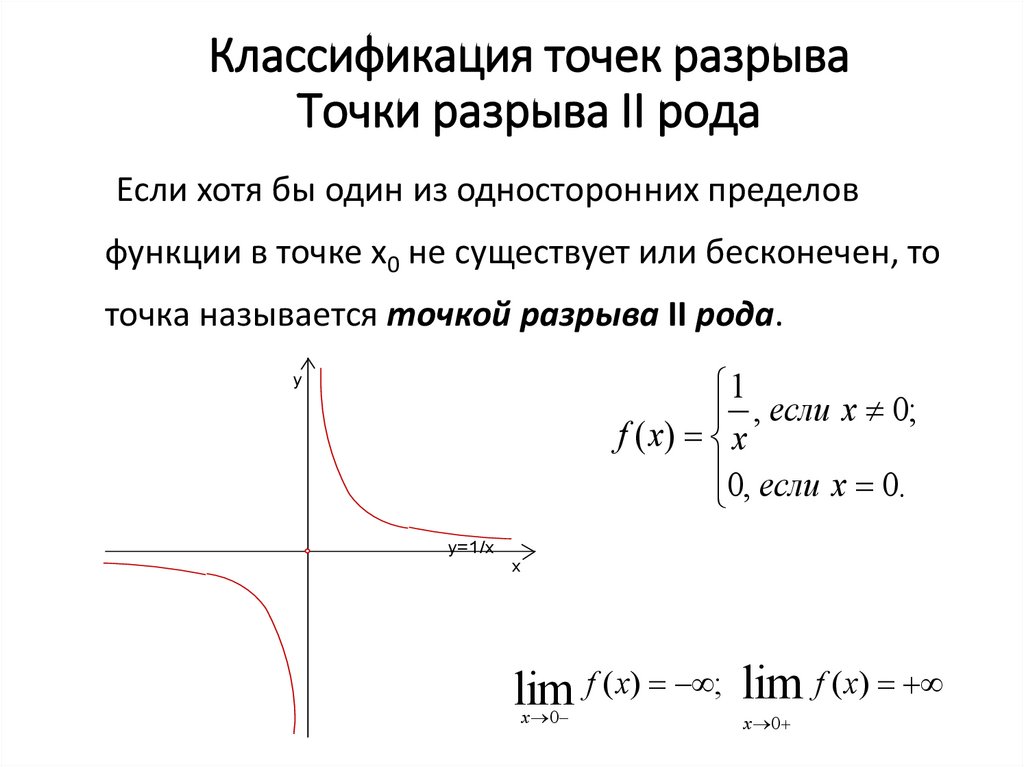
И именно в этом заключается идея анализа безубыточности: вам нужно определить, сколько единиц продукции вам нужно произвести, чтобы ваша прибыль была равна нулю, так что не проигрывайте и не выигрывайте, вы просто безубыточны.
Таким образом, точка безубыточности соответствует количеству единиц, которые вам нужно продать, чтобы выйти на уровень безубыточности. Если вы продаете меньше, чем это, вы получаете убыток, а если вы продаете больше, вы получаете прибыль.
Пример точки безубыточности
Предположим, вы владеете фирмой с фиксированными затратами в размере 10 000 долларов США (включая аренду, интернет и т. д.). Вы продаете виджет, производство которого обходится вам в 1,25 доллара, и вы можете продать его за 2,50 доллара. Какова будет ваша точка безубыточности?
В этом случае постоянные затраты равны \(FC = 10 000\), переменные затраты на единицу продукции равны \(VC = 1,25\), а цена продажи равна \(P = 2,50\).
Нам нужно подставить эти числа в следующую формулу:
\[ \text{Точка безубыточности} = \displaystyle \frac{FC}{P — VC} = \displaystyle \frac{10,000}{2,50 — 1,25} = \displaystyle \frac{10,000}{1,25} = 8,000 \text {единицы измерения} \]
Следовательно, чтобы выйти в безубыток, вам нужно будет продать 8000 единиц. Если вы продадите менее 8000 единиц, вы есть убыток, и если вы продадите более 8000 единиц, вы получите положительную прибыль.
Другие связанные финансовые калькуляторы
Другие финансовые калькуляторы, которые могут вас заинтересовать, это
калькулятор чистой приведенной стоимости
и калькулятор внутренней нормы прибыли.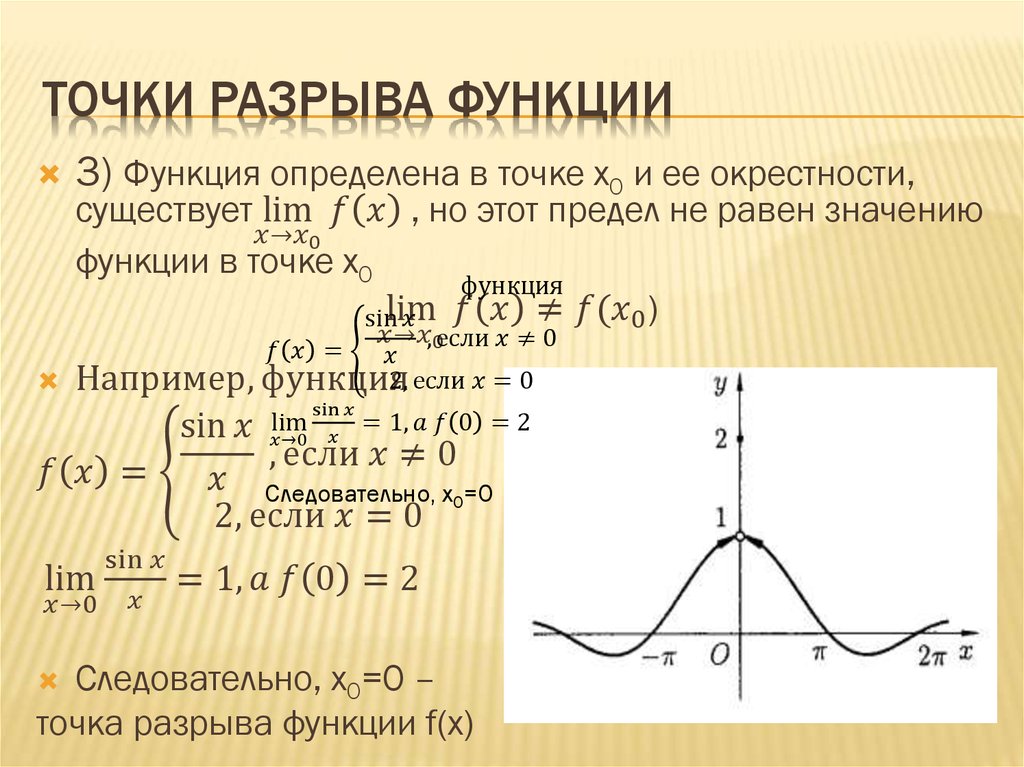
Базовый финансовый пакет Калькулятор точки безубыточности Калькулятор безубыточности Финансовый калькулятор Финансовый решатель
точка безубыточности | анализ безубыточности | Калькулятор
Единица измерения Цена
Фиксированная стоимость
Переменная стоимость за единицу
Цена за единицу
Тип BEP:
Фиксированная стоимость:
Что такое анализ безубыточности?Формула расчета безубыточности
Единица измерения
Точка безубыточности (ед.) = Фиксированная стоимость / (Цена за единицу — Переменная стоимость за единицу)
Цена
Точка безубыточности (цена) = Итого Переменная стоимость + Постоянная стоимость / Количество единиц
Анализ безубыточности — это процесс определения точки безубыточности организации.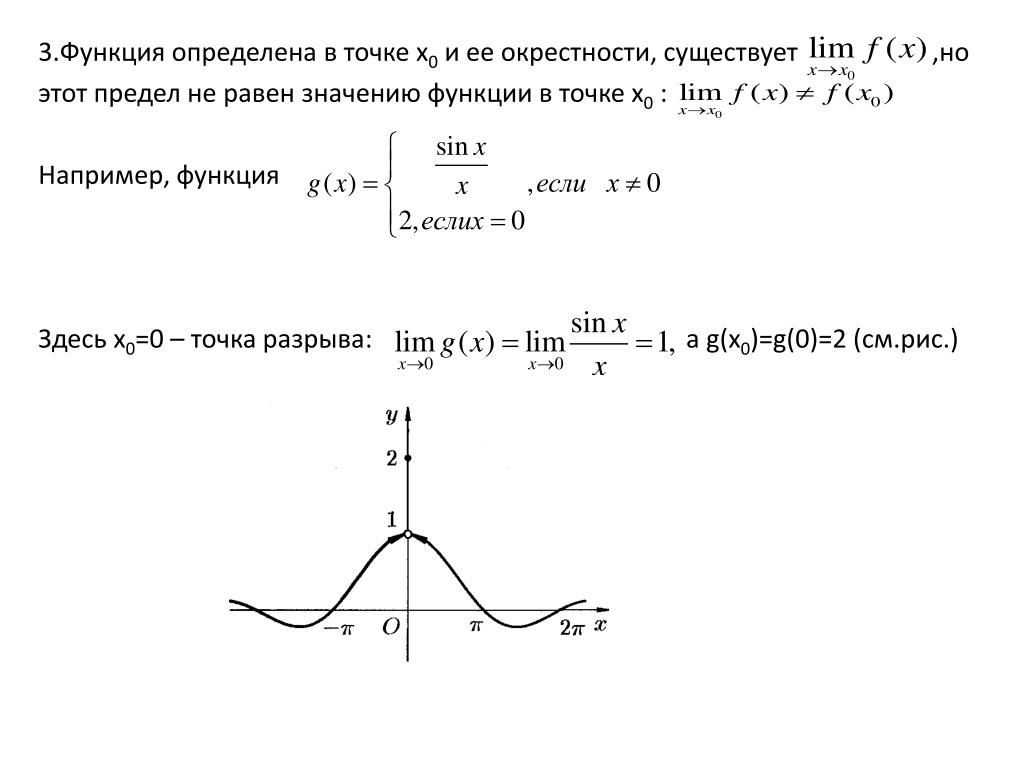
Это требует учета постоянных затрат, переменных затрат, цены за единицу и количества единиц. Анализ безубыточности помогает, когда:
Вы хотите определить количество единиц, которое вам нужно продать, чтобы достичь точки безубыточности
Например, когда вы запускаете новый ассортимент товаров, вам нужно знать, какое минимальное количество единиц вам нужно продать, чтобы возместить ваши постоянные и переменные затраты.
Вы знаете количество товаров, которые вам нужно продать, но хотите выбрать правильную цену для вашего продукта
Например, вы установили цель по количеству единиц, которые вы хотите продать к концу квартала, но нахожу это немного запутанным, чтобы установить правильную цену за пункт
Что такое фиксированная стоимость? Постоянные затраты — это затраты, которые несет организация при производстве или продаже товара и не зависят от уровня производства или количества проданных единиц. Некоторые распространенные примеры постоянных затрат включают арендную плату, страховые взносы и заработную плату.
Вы можете видеть, что все эти затраты не меняются, даже если вы увеличиваете производство или увеличиваете продажи в определенном месяце.
Чтобы узнать больше о постоянных затратах, Загрузите наш шаблон Excel
Что такое переменные затраты?Переменные затраты — это затраты, которые напрямую связаны с уровнем производства или количеством единиц, проданных на рынке. Переменные затраты рассчитываются на единицу продукции, поэтому, если вы производите или продаете больше единиц, переменные затраты будут увеличиваться. Некоторыми распространенными примерами переменных затрат являются комиссионные с продаж, расходы на доставку и временная заработная плата.
Чтобы узнать больше о переменных затратах, Загрузите наш шаблон Excel
Как точка безубыточности может помочь вашему бизнесу?
Точка безубыточности — отличный показатель и важный инструмент, который помогает вашему бизнесу во многих отношениях.
Вот три главных преимущества точки безубыточности в управлении вашим бизнесом:
Осуществимость
Важно изучить осуществимость любого проекта или новой линейки продуктов, которую вы планируете запустить. С помощью анализа безубыточности вы можете определить время и цену, при которых ваш бизнес станет прибыльным. Это поможет вам спланировать ряд действий, необходимых для достижения этой точки, установить время выполнения ваших задач и придерживаться временной шкалы.
Анализ
Колебания в бизнесе — обычный сценарий. Внешние обстоятельства, такие как торговые соглашения и изменения политического климата, влияют на ваши продажи. Это может привести к росту ваших переменных или постоянных затрат. В таких случаях анализ безубыточности поможет вам принять решение о новых ценах на вашу продукцию. Точка безубыточности дает вам четкое представление о том, сколько времени потребуется вашему бизнесу, чтобы возместить любые убытки и снова стать безубыточным после изменения бизнес-прогноза.