Транспортная задача линейного программирования: Транспортная задача линейного программирования / Хабр

Транспортная задача | это… Что такое Транспортная задача?

Транспортная задача (задача Монжа — Канторовича) — математическая задача линейного программирования специального вида о поиске оптимального распределения однородных объектов из аккумулятора к приемникам с минимизацией затрат на перемещение.^[1][2] Для простоты понимания рассматривается как задача об оптимальном плане перевозок грузов из пунктов отправления в пункты потребления, с минимальными затратами на перевозки. Транспортная задача является по теории сложности вычислений NP-сложной и входит в класс сложности NP. Когда суммарный объём предложений (грузов, имеющихся в пунктах отправления) не равен общему объёму спроса на товары (грузы), запрашиваемые пунктами потребления, транспортная задача называется несбалансированной (открытой).

Содержание 1 Постановка задачи 2 История поиска методов решения 3 Методы решения 3. 1 Итерационное улучшение плана перевозок 3.1.1 Нахождение опорного плана 3.1.1.1 Метод северо-западного угла (диагональный) 3.1.1.2 Метод наименьшего элемента 3.1.2 Итерации 3.2 Решение с помощью теории графов 4 Обобщения 4.1 Транспортная задача в сетевой постановке 4.2 Транспортная задача с ограничениями пропускной способности 4.3 Многопродуктовая Транспортная задача 5 Примечания 6 Ссылки

Постановка задачи

Транспортная задача (классическая) — задача об оптимальном плане перевозок однородного продукта из однородных пунктов наличия в однородные пункты потребления на однородных транспортных средствах (предопределённом количестве) со статичными данными и линеарном подходе (это основные условия задачи).

Для классической транспортной задачи выделяют два типа задач: критерий стоимости (достижение минимума затрат на перевозку) или расстояний и критерий времени (затрачивается минимум времени на перевозку).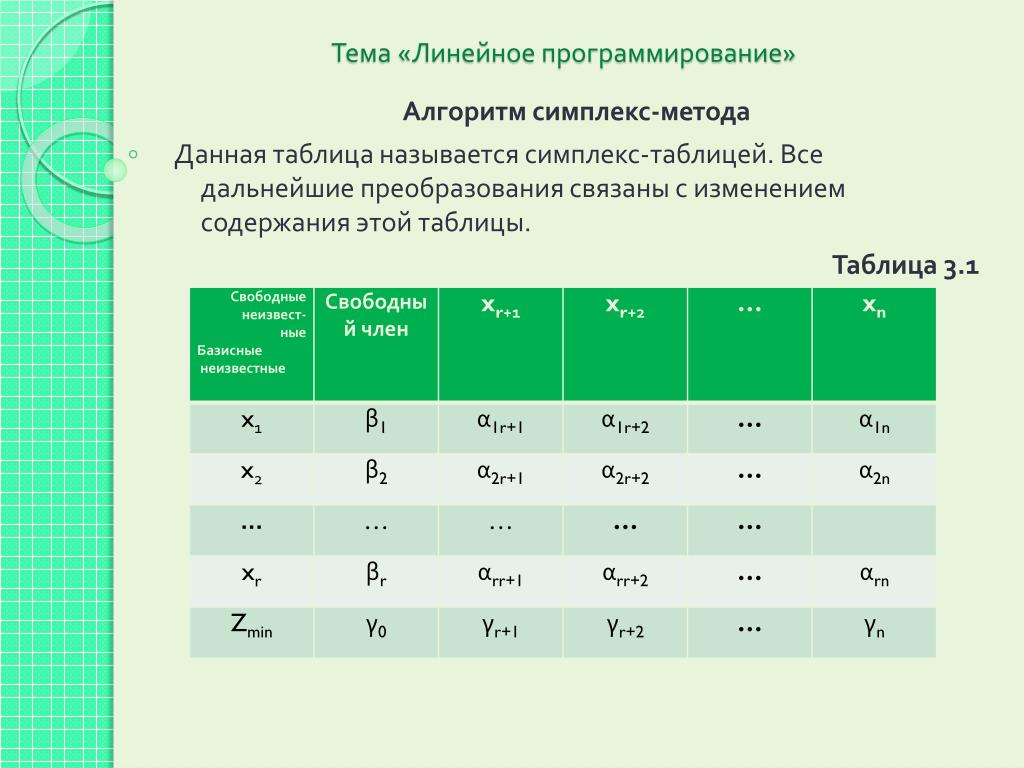 Под названием транспортная задача ,определяется широкий круг задач с единой математической моделью, эти задачи относятся к задачам линейного программирования и могут быть решены оптимальным методом. Однако, спец.метод решения транспортной задачи позволяет существенно упростить её решение, поскольку транспортная задача разрабатывалась для минимизации стоимости перевозок.

История поиска методов решения

Проблема была впервые формализована французским математиком Гаспаром Монжем в 1781 году^[3]. Основное продвижение было сделано на полях во время Великой Отечественной войны советским математиком и экономистом Леонидом Канторовичем^[4]. Поэтому иногда эта проблема называется транспортной задачей Монжа — Канторовича.

Методы решения

Классическую транспортную задачу можно решить симплекс-методом, но в силу ряда особенностей её можно решить проще (для задач малой размерности).

Условия задачи располагают в таблице, вписывая в ячейки количество перевозимого груза из в груза , а в маленькие клетки — соответствующие тарифы .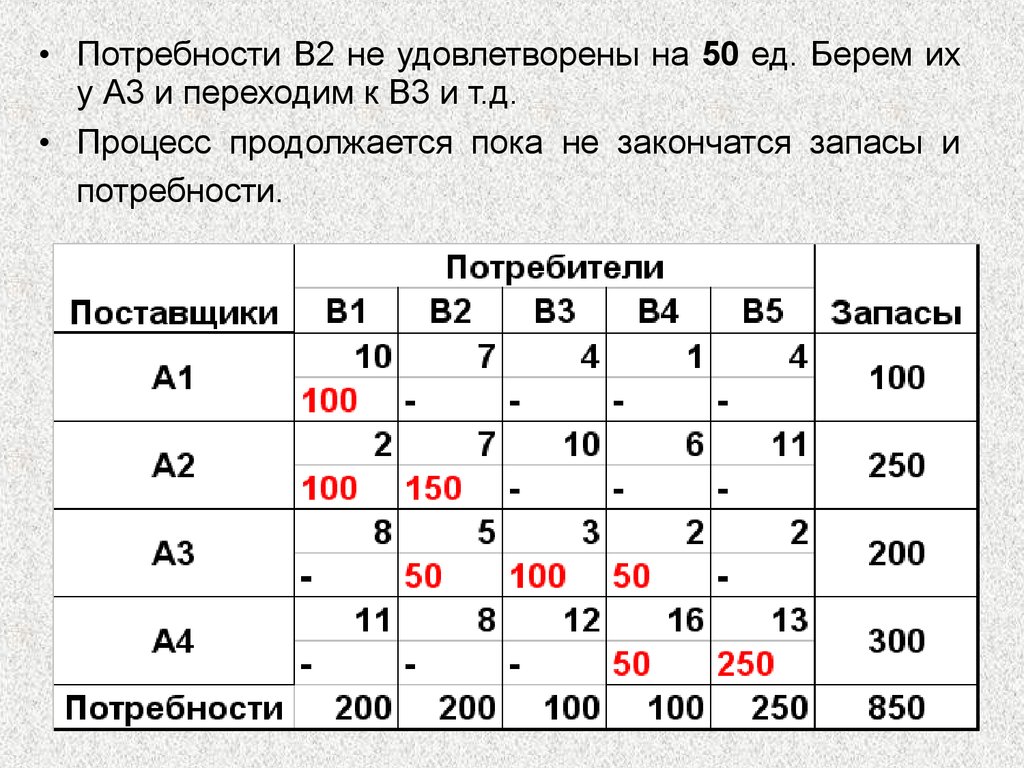

Итерационное улучшение плана перевозок

Нахождение опорного плана

Требуется определить опорный план и путём последовательных операций найти оптимальное решение. Опорный план можно найти следующими методами: «северо-западного угла», «наименьшего элемента», двойного предпочтения и аппроксимации Фогеля.

Метод северо-западного угла (диагональный)

На каждом этапе максимально возможным числом заполняют левую верхнюю клетку оставшейся части таблицы. Заполнение таким образом, что полностью выносится груз из или полностью удовлетворяется потребность .

Метод наименьшего элемента

Одним из способов решения задачи является метод минимального (наименьшего) элемента. Его суть заключается в сведении к минимуму побочных перераспределений товаров между потребителями.

Алгоритм:

1. Из таблицы стоимостей выбирают наименьшую стоимость и в клетку, которая ей соответствует, вписывают большее из чисел.
2. Проверяются строки поставщиков на наличии строки с израсходованными запасами и столбцы потребителей на наличие столбца, потребности которого полностью удовлетворены.
   Такие столбцы и строки далее не рассматриваются.
3. Если не все потребители удовлетворены и не все поставщики израсходовали товары, возврат к п. 1, в противном случае задача решена.

Итерации

После нахождения опорного плана перевозок, нужно применить один из алгоритмов его улучшения, приближения к оптимальному.

• Метод падающего камня (нем.)
• Метод потенциалов.

Решение с помощью теории графов

Рассматривается двудольный граф, в котором пункты производства находятся в верхней доле, а пункты потребления — в нижней. Пункты производства и потребления попарно соединяются рёбрами бесконечной пропускной способности и цены за единицу потока .

К верхней доле искусственно присоединяется исток. Пропускная способность рёбер из истока в каждый пункт производства равна запасу продукта в этом пункте. Цена за единицу потока у этих рёбер равна 0.

Аналогично к нижней доле присоединяется сток. Пропускная способность рёбер из каждого пункта потребления в сток равна потребности в продукте в этом пункте. Цена за единицу потока у этих рёбер тоже равна 0.

Дальше решается задача нахождения максимального потока минимальной стоимости (mincost maxflow). Её решение аналогично нахождению максимального потока в алгоритме Форда — Фалкерсона. Только вместо кратчайшего дополняющего потока ищется самый дешёвый. Соответственно, в этой подзадаче используется не поиск в ширину, а алгоритм Беллмана — Форда. При возврате потока стоимость считается отрицательной.

Алгоритм «mincost maxflow» можно запускать и сразу — без нахождения опорного плана. Но в этом случае процесс решения будет несколько более долгим. Выполнение алгоритма «mincost maxflow» происходит не более чем за операций. ( — количество рёбер,  — количество вершин.) При случайно подобраных данных обычно требуется гораздо меньше — порядка операций.

При решении несбалансированной транспортной задачи применяют приём, позволяющий сделать ее сбалансированной. Для этого вводят фиктивные пункты назначения или отправления. Выполнение баланса транспортной задачи необходимо для того, чтобы иметь возможность применить алгоритм решения, построенный на использовании транспортных таблиц.

Обобщения

Транспортная задача в сетевой постановке

В этом варианте пункты не делятся на пунктов отправления и пункты потребления, все пункты равноправны, но производство задается положительным числом, а потребление — отрицательным. Перевозки осуществляются по заданной сети, в которой дуги могут соединять любые пункты (включая производитель -> производитель, потребитель -> потребитель). Задача решается слегка измененным методом потенциалов, практически тем же, что и классическая постановка.

Транспортная задача с ограничениями пропускной способности

Вариант транспортной задачи в сетевой постановке, в котором задается максимальная пропускная способность некоторых дуг. Задача решается слегка усложненным методом потенциалов.

Многопродуктовая Транспортная задача

Вариант транспортной задачи, в которой присутствует несколько продуктов (пункты могут производить/потреблять несколько продуктов). Для некоторых дуг задается ограничение на пропускную способность (без этого ограничения задача распадается на отдельные задачи по продуктам). Задача решается симплекс-методом (используется разложение Данцига-Вулфа, в качестве подзадач используются однопродуктовые транспортные задачи)

Примечания

1. ↑ А. В. Кузнецов, Н. И. Холод, Л. С. Костевич. Руководство к решению задач по математическому программированию. — Минск: Высшая школа, 1978. — С. 110.
2. ↑ Словарь по кибернетике / Под редакцией академика В. С. Михалевича. — 2-е. — Киев: Главная редакция Украинской Советской Энциклопедии имени М. П. Бажана, 1989. — 751 с. — (С48). — 50 000 экз. — ISBN 5-88500-008-5
3. ↑ Monge G. Mémoire sur la théorie des déblais et de remblais. Histoire de l’Académie Royale des Sciences de Paris, avec les Mémoires de Mathématique et de Physique pour la même année, pages 666—704, 1781.
4. ↑ Kantorovich L. On the translocation of masses // C. R. (Doklady) Acad. Sci. URSS (N. S.), 37:199-201, 1942.

Ссылки

• Транспортная задача
• Алгоритмы нахождения максимального потока
• http://kb.mista.ru/article.php?id=859 Решение транспортной задачи в 1С:Предприятие 8.2

Транспортная задача. Метод потенциалов и метод минимального элемента. Решение задач и контрольных работ по линейному программированию онлайн

Краткая теория

---

Cимплекс-метод решения задачи линейного программирования является универсальным и применим для решения любых таких задач. Однако существуют некоторые частные типы задач линейного программирования, которые, в силу некоторых особенностей своей структуры, допускают решение более простыми методами. К ним относится, в частности, так называемая транспортная задача.

Классическая транспортная задача линейного программирования формулируется следующим образом:

Имеется  пунктов отправления: , в которых сосредоточены запасы какого-то однородного товара (груза) в количестве соответственно  единиц.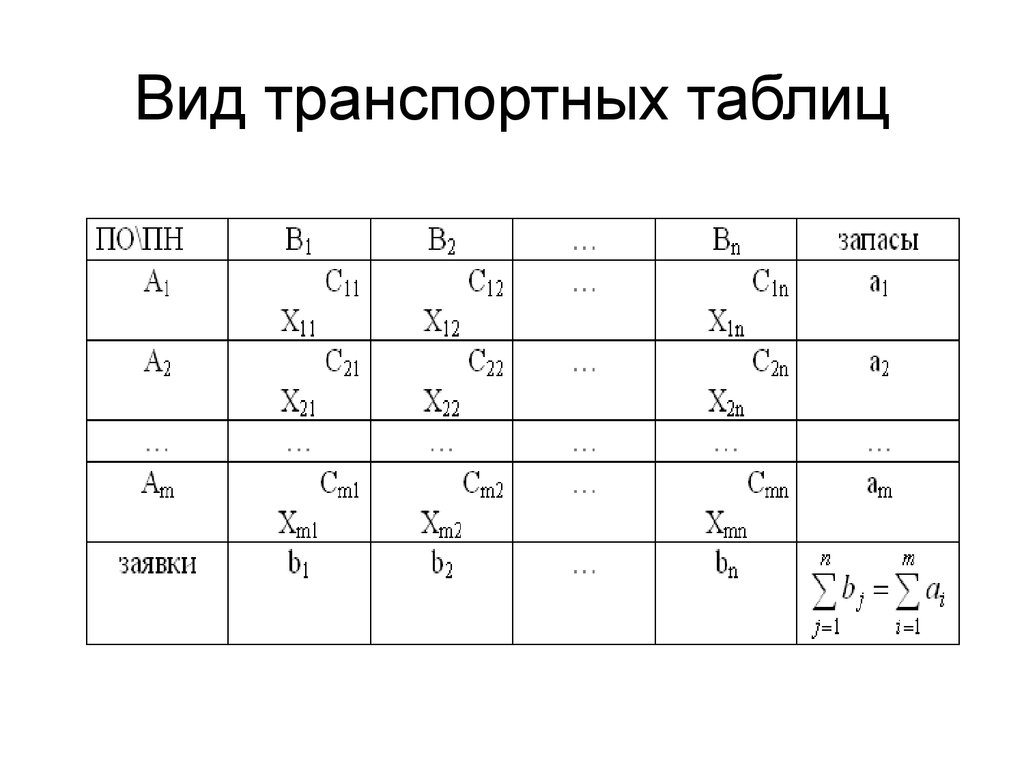 Кроме того имеется  пунктов назначения: , подавших заявки соответственно на  единиц товара.

Предполагается, что сумма всех заявок равна сумме всех запасов:

Известная стоимость  перевозки единицы товара от каждого пункта отправления  до каждого пункта назначения . Таблица (матрица) стоимостей перевозки  задана:

Требуется составить такой план перевозок, при котором все заявки были выполнены, и при этом общая стоимость всех перевозок была минимальна.

При такой постановке задачи показателем эффективности плана перевозок является стоимость, поэтому поставленную задачу точнее называют транспортной задачей по критерию стоимости.

Дадим этой задаче математическую формулировку. Обозначим  — количество груза, отправляемого из i-го пункта отправления  и j-й пукнта назначения    Неотрицательные переменные  (число которых, очевидно, равно ) должны удовлетворять следующим условиям:

1. Суммарное количество груза, направляемое из каждого пункта отправления во все пункты назначения, должно быть равно запасу груза в данном пункте. Это даст дам  условий-равенств:

2. Суммарное количество груза, доставляемое в каждый пункт назначения изо всех пунктов отправления, должно быть равно заявке, поданной данным пунктом. Это даст  условий-равенств:

Суммарная стоимость всех перевозок, то есть сумма величин , умноженных на соответствующие стоимости  должна быть минимальной:

Перед нами типичная задача линейного программирования с ограничениями-равенствами.

Как и всякую другую задачу линейного программирования, ее можно было бы решить симплекс-методом, но данная задача имеет некоторые особенности, позволяющие решить ее более просто.

Условимся о терминологии. Значения  количества единиц груза, направляемых из пункта  в пункт  будем называть перевозками.

Любую совокупность значений  будем называть планом перевозок или просто планом.

План  будем называть допустимым, если он удовлетворяет условиям системы равенств (так называемым «балансовым условиям»): все заявки удовлетворены, все запасы исчерпаны.

Допустимый план будем называть опорным, если в нем отличны от нуля не более  базисных перевозок , а остальные перевозки равны нулю.

План  будем называть оптимальным, если он, среди всех допустимых планов, приводит к наименьшей стоимости всех перевозок.

Основные этапы решения транспортной задачи будут такими:

I этап.  Нахождение начального опорного плана .

II этап. Выделение из небазисных переменных вводимой в базис переменной (метод потенциалов). Если все небазисные переменные удовлетворяют условию оптимальности, то следует закончить вычисления; в противном случае — перейти к III этапу.

III этап. Выбор выводимой из базиса переменной (используя условия допустимости) из числа переменных текущего базиса; затем нахождение нового опорного решения и возвращение ко II этапу.

Пример решения задачи

---

В трех пунктах отправления  имеется однородный груз в количестве  соответственно. Этот груз нужно доставить пяти заказчикам . Потребности в грузе в каждом пункте  известны и равны  соответственно. Известны также тарифы перевозки  — стоимость перевозки единицы груза из пункта  в пункт . Нужно найти такой план перевозок, при котором весь груз из пунктов потребления будет вывезен, потребности всех заказчиков будут удовлетворены, и при этом общая стоимость перевозки всего груза будет наименьшей. Данные в таблице,  в клетках которой проставлены элементы матрицы тарифов ; в последнем столбце таблицы указаны значения величин , в последней строке - значения величин .

 

Заказчики Пункты
	4	9	2	5	3	23
	4	6	2	1	8	25
	6	2	3	4	5	17
	14	10	16	10	15

Требуется:

• Составить математическую модель задачи.
• Найти оптимальное решение транспортной задачи методом потенциалов.

На сайте можно заказать решение контрольной или самостоятельной работы, домашнего задания, отдельных задач. Для этого вам нужно только связаться со мной:

ВКонтакте
WhatsApp
Telegram

Мгновенная связь в любое время и на любом этапе заказа. Общение без посредников. Удобная и быстрая оплата переводом на карту СберБанка. Опыт работы более 25 лет.

Подробное решение в электронном виде (docx, pdf) получите точно в срок или раньше.

Решение

Математическая модель задачи

Обозначим через  количество груза, перевозимого от  поставщика  потребителю. Тогда общая стоимость перевозок равна:

Ограничения для поставщиков:

Ограничения для потребителей:

Объем суммарных поставок любого поставщика к потребителю не может быть отрицательным числом, поэтому справедливы ограничения:   

Полученную задачу можно решить симплекс-методом, так как это классическая ЗЛП, однако относительная простота систем уравнений дает возможность использовать метод решения более простой.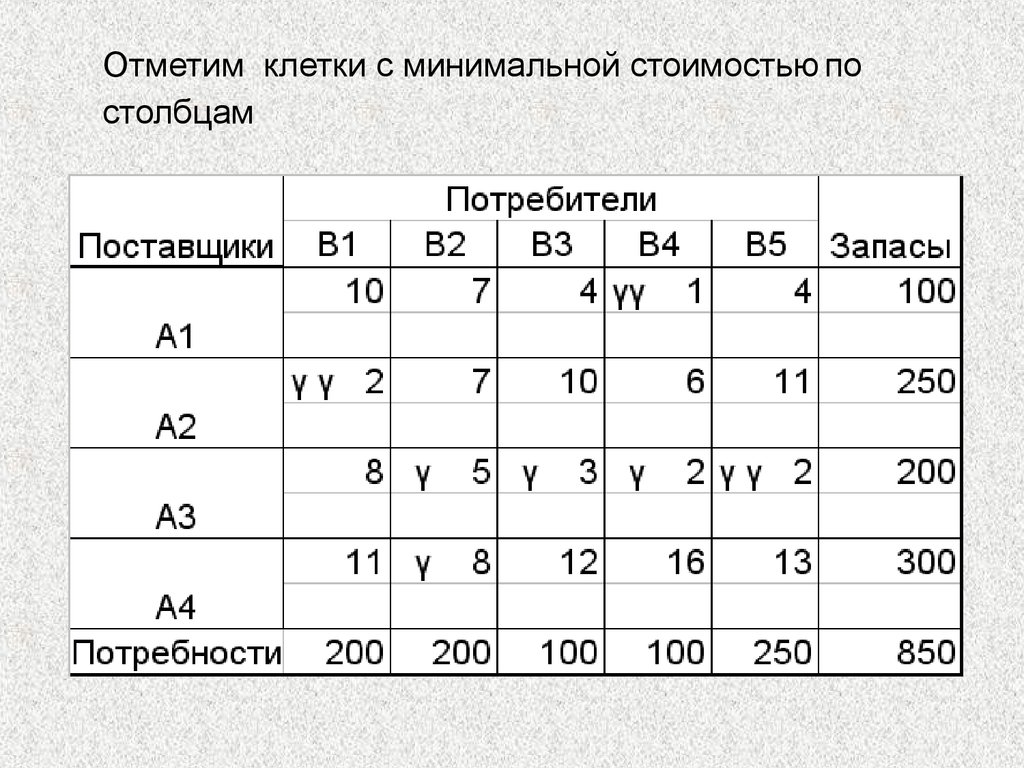 Особенности систем следующие:

коэффициенты при неизвестных во всех уравнениях равны 1;
1. каждая переменная встречается только в двух уравнениях; система уравнений транспортной задачи симметричная относительно всех переменных ;матрица, составленная из коэффициентов при переменных  состоит из единиц и нулей, причем каждый столбец матрицы содержит два элемента, равных 1, а остальные 0.

Проверка задачи на закрытость модели

Стандартная транспортная задача разрешима только в том случае, когда выполняется условие баланса:

В нашем случае:

Модель транспортной задачи закрытая.

Нахождение начального опорного плана и метод потенциалов

Заполняем таблицу по правилу минимального элемента .

Просматривая таблицу замечаем, что наименьшие затраты соответствуют маршруту , поэтому в клетку помещаем .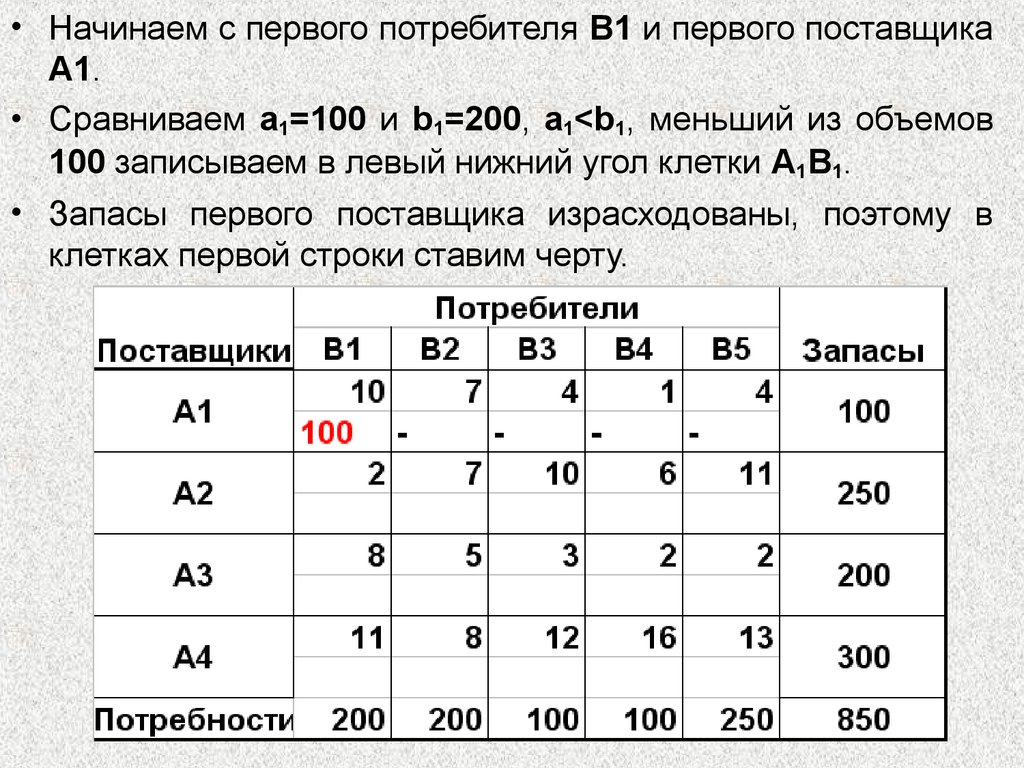 В этом случае 4-й столбец в расчет не принимается. Просматриваем оставшиеся таблицы клетки. Наименьший тариф имеет клетка

Далее действуя по аналогичной схеме:

 

 Решать задачу будем методом потенциалов. Число занятых клеток должно быть . Потенциал 1-й строки принимаем равным нулю. После этого мы можем вычислить остальные потенциалы (если известны потенциал и тариф занятой клетки, то из соотношения v + u =c легко определить неизвестный потенциал).

Найдем оценки свободных клеток по формуле: 

S ( 1, 1)= 4-( 0-1)=  5	S ( 1, 2)= 9-( 0+ 0)=  9
S ( 1, 4)= 5-( 0-4)=  9	S ( 2, 2)= 6-( 5+ 0)=  1
S ( 2, 3)= 2-( 5+ 2)= -5	S ( 3, 1)= 6-( 2-1)=  5
S ( 3, 3)= 3-( 2+ 2)= -1	S ( 3, 4)= 4-( 2-4)=  6

Для клетки ( 2, 3) с минимальной отрицательной оценкой строим цикл.

Перемещаем груз, равный 1 из вершин, помеченных минусом к вершинам цикла, помеченным плюсом.

Вычисляем потенциалы:

Найдем оценки свободных клеток по формуле

S ( 1, 1)= 4-( 0+ 4)=  0	S ( 1, 2)= 9-( 0+ 0)=  9
S ( 1, 4)= 5-( 0+ 1)=  4	S ( 2, 2)= 6-( 0+ 0)=  6
S ( 2, 5)= 8-( 0+ 3)=  5	S ( 3, 1)= 6-( 2+ 4)=  0
S ( 3, 3)= 3-( 2+ 2)= -1	S ( 3, 4)= 4-( 2+ 1)=  1

 

Для клетки ( 3, 3) с минимальной отрицательной оценкой строим цикл.

Перемещаем груз, равный 7 из вершин, помеченных минусом к вершинам цикла, помеченным плюсом.

Вычисляем потенциалы:

Найдем оценки свободных клеток по формуле

S ( 1, 1)= 4-( 0+ 4)=  0	S ( 1, 2)= 9-( 0+ 1)=  8
S ( 1, 4)= 5-( 0+ 1)=  4	S ( 2, 2)= 6-( 0+ 1)=  5
S ( 2, 5)= 8-( 0+ 3)=  5	S ( 3, 1)= 6-( 1+ 4)=  1
S ( 3, 4)= 4-( 1+ 1)=  2	S ( 3, 5)= 5-( 1+ 3)=  1

Оценки свободных клеток не отрицательны, следовательно, полученный план является оптимальным:

Ответ

Пункт      поставляет 8 единиц груза в пункт   и 15 единиц груза в пункт  

Пункт   поставляет 14 единиц груза в пункт  , 1 единицу груза в пункт  и 10 единиц груза в пункт

Пункт      поставляет 10 единиц груза в пункт   и 7 единиц груза в пункт  

Минимальные транспортные издержки оптимального плана:

Решение транспортной задачи с помощью линейного программирования | by Soham Shinde

Когда я прошел курс «Транспортные задачи с использованием Excel», я узнал о транспортной задаче. Я подумал, что эту концепцию нужно разделить в моем блоге, так как она немного сбивает с толку. Я буду объяснять, что означает транспортировка, с помощью диаграмм, чтобы каждый из вас мог понять эту концепцию.

Транспортная задача:

Чтобы понять транспортную задачу, необходимо понять значение линейного программирования. Потому что транспортные задачи будут использовать линейное программирование.

Линейное программирование в транспортной отрасли в основном определяет, сколько товаров перевозится из пункта отправления в пункт назначения с соблюдением баланса между спросом и предложением. Кроме того, он принимает во внимание, что общая стоимость транспортировки должна быть минимизирована. Когда спрос и предложение равны, это называется сбалансированной задачей . Когда спрос и предложение не равны, мы преобразуем их в сбалансированную задачу, добавляя строку или столбец.

В линейном программировании есть три важных термина,

1. Целевая функция : Это говорит нам, какова цель проблемы. Например, минимизация затрат на транспортировку товара.
2. Ограничения : Это уравнения, определяющие ограничение каждой переменной. Например, мы не можем отгружать клиентам больше, чем мощность завода. Таким образом, предложение должно быть равно спросу. Это одно ограничение. Задачи линейного программирования могут не иметь ограничений или иметь более одного ограничения.
3. Переменные решения : Это переменные, которые мы хотим найти. По сути, в транспортных задачах переменными решения будут такие, какое количество продукта мы должны отправить из источника (завода) в пункт назначения (покупателям), чтобы свести к минимуму.

Теперь давайте разберемся, как проанализировать проблему в Excel. В транспортной цепочке поставок мы должны убедиться, что весь спрос был удовлетворен заводом-изготовителем. В этом типе проблем мы удовлетворяем спрос, используя прямую транспортировку от источника к месту назначения. Источником может быть завод-изготовитель или фабрика, распределительный центр, компания, поставщик и т. д. Пунктом назначения может быть заказчик, другой завод, конечный пользователь и т. д.

Транспортная модель в Excel:

Построение модели с целевой функцией

На приведенном выше рисунке я разработал матрицу затрат ( синих ячеек ), которая показывает тарифы на транспортировку мешков с рисом от фабрик до клиентов. . Желтая ячейка дает минимальную стоимость доставки после запуска решателя. Это мы увидим в следующем разделе. Теперь давайте посмотрим, как разработать проблему.

Целевая функция: (желтая ячейка)

В этой задаче мы хотим минимизировать стоимость доставки.

Ограничения:

Эта задача имеет 2 ограничения, одно для предложения, а другое для спроса. Таким образом, у нас есть 2 ограничения. Во-первых, ограничение состоит в том, что количество мешков, поступающих к каждому покупателю, равно поставке с завода. т. е. D10:G10 равно D11:G11 , а H7:H9 равно I7:I9. Эта проблема является сбалансированной, потому что предложение равно спросу, как вы можете видеть в 9.0005 J15 и J16 .

Переменная решения (зеленые ячейки):

Переменные решения в этой задаче — это количество мешков, отгруженных с каждой фабрики каждому покупателю. Мы должны выбрать ячеек D7:G9 в файле Excel. Они указывают ячейки, которые являются переменными решения.

Запуск Решателя Excel (линейное программирование):

Когда мы запускаем Решатель, Решатель дает удовлетворительное решение, в котором говорится, что все ограничения удовлетворены. В решении указано, что мы можем отправить 17 мешков риса с фабрики 3 покупателю 1. Кроме того, 10 мешков риса с фабрики 1 покупателю 2. Точно так же я называю отгруженные количества, указанные в матрице выше.

В желтой ячейке указана оптимальная стоимость доставки мешков с рисом. $ 1980$ это МИНИМАЛЬНАЯ СТОИМОСТЬ доставки.

Таким образом, мы моделируем задачу о транспортировке и находим минимальную стоимость доставки, удовлетворяющую всем ограничениям. Это помогает нам узнать, какое точное количество товаров необходимо доставить из источника в пункт назначения.

Спасибо, что читаете этот блог!

Сохам С. Шинде

ВАЖНОЕ ПРИМЕЧАНИЕ:
Надеюсь, вам понравится эта история. Пожалуйста, следуйте за мной для получения дополнительной информации. Имейте в виду, что это мои мысли, и любой, кто копирует этот контент, будет сообщен мной и заблокирован мной. Кроме того, за использование этой истории будут приняты соответствующие юридические меры.

Решение транспортной задачи с помощью линейного программирования на Python — Компьютерщик машинного обучения

10 февраля 2022 г. 30 апреля 2022 г. Авинаш Навлани Линейное программирование, методы оптимизации, PuLP, python, транспортная задача

Узнайте, как использовать Python PuLP для решения транспортных задач с помощью линейного программирования.

В этом уроке мы расширим кругозор задач линейного программирования. Мы обсудим транспортную проблему. Он предлагает различные приложения, связанные с оптимальной транспортировкой товаров. Транспортная модель — это в основном модель минимизации.

Транспортная задача относится к типу задач линейного программирования. В этом типе задач основной целью является транспортировка товаров со складов-источников в различные места назначения с минимальными затратами. Чтобы решить такие проблемы, у нас должны быть объемы спроса, объемы поставок и стоимость доставки из источника и пункта назначения. Имеется m источников или пунктов отправления и n пунктов назначения, каждый из которых представлен узлом. Ребра представляют собой маршруты, соединяющие источники и пункты назначения.

В этом руководстве мы рассмотрим следующие темы:

Транспортная задача

Транспортные модели имеют дело с особым типом задачи линейного программирования, целью которой является минимизация стоимости. Здесь у нас есть однородный товар, который необходимо переместить из разных мест происхождения или фабрик в разные пункты назначения или склады.

Типы транспортных задач

• Сбалансированная Транспортная задача :  В задаче такого типа общие потребности и предложения равны.
• Несбалансированный Транспортная проблема : В этом типе проблемы общие запасы и потребности не равны.

Методы решения транспортной задачи:

1. Метод северо-западного угла
2. Метод наименьших затрат
3. Метод приближения Фогеля (VAM)

9000 2 Давайте рассмотрим один пример ниже. Компания связалась с тремя складами, чтобы предоставить сырье для своих 3 проектов.

Склад	Снабжение Вместимость
А	30 0
B	600
C	600

Стол подачи

9 0164

Проект	Спрос Мощность
1	150
2	450
3	900

Таблица спроса

Из	Проект-1	Проект-2	Проект-3
Склад-А	5	1	9
Склад-Б	4	2	8 90 169
Склад- c	8	7	2

Матрица затрат

Это информация, необходимая для решения проблемы.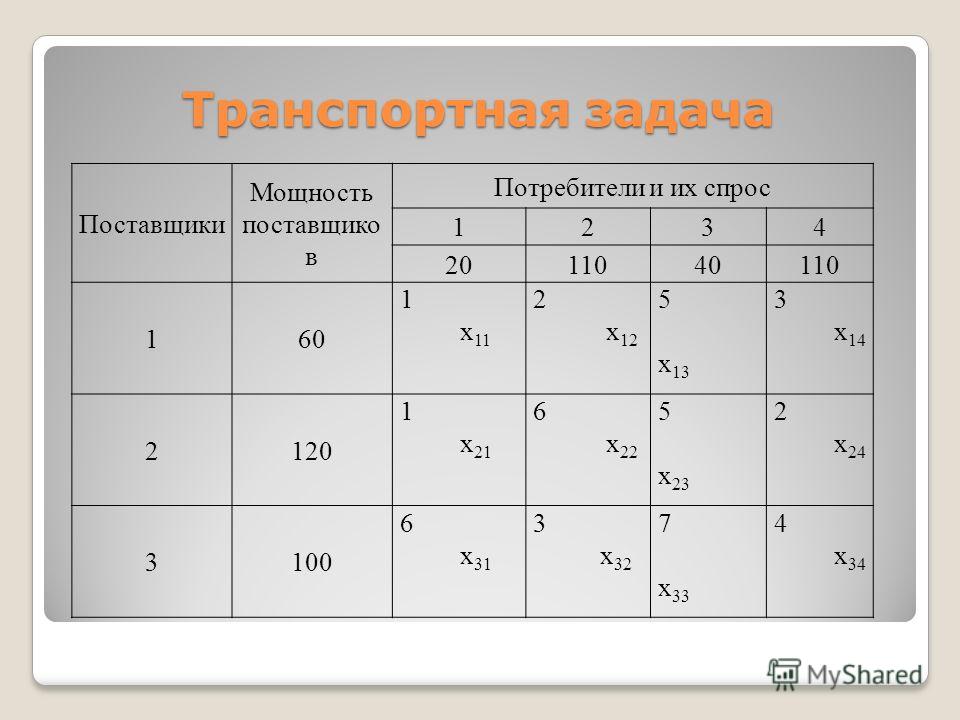 Следующим шагом является организация информации в решаемую транспортную задачу.

Формулировка задачи

Давайте сначала сформулируем задачу. во-первых, мы определяем склад и его запасы, проект и его потребности, а также матрицу затрат.

 # Создает список всех узлов снабжения
склады = ["А", "Б", "С"]
# Создает словарь для количества единиц снабжения для каждого узла снабжения
поставка = {"A": 300, "B": 600, "C": 600}
# Создает список всех узлов спроса
проекты = ["1", "2", "3"]
# Создает словарь для количества единиц спроса для каждого узла спроса
спрос = {
    «1»: 150,
    «2»: 450,
    «3»: 900,
}
# Создает список затрат каждого пути транспортировки
затраты = [ # проектов
    [5,1,9], # склады А
    [4,2,8], # Б
    [8,7,2]#С
]
# Данные о затратах помещаются в словарь
затраты = makeDict([склады, проекты], затраты, 0) 

Инициализация модели LP

На этом этапе мы импортируем все классы и функции модуля целлюлозы и создадим задачу минимизации LP с использованием класса LpProblem.

 # Импорт функций модуля моделирования PuLP
от импорта целлюлозы *
# Создает переменную 'prob' для хранения данных о проблеме
prob = LpProblem("Проблема поставки материалов", LpMinimize) 

Определить переменную решения

На этом шаге мы определим переменные решения. В нашей задаче у нас есть различные переменные Route. Давайте создадим их с помощью класса LpVariable.dicts() . LpVariable.dicts()  используется с пониманием списков Python. LpVariable.dicts()  принимает следующие четыре значения:

• Во-первых, префикс имени того, что представляет эта переменная.
• Во-вторых, это список всех переменных.
• В-третьих, это нижняя граница этой переменной.
• Четвертая переменная — верхняя граница.
• Четвертый по сути тип данных (дискретные или непрерывные). Варианты для четвертого параметра: LpContinuous или LpInteger .

Давайте сначала создадим маршрут списка для маршрута между складом и сайтом проекта и создадим переменные решения, используя метод LpVariable. dicts().

 # Создает список кортежей, содержащих все возможные маршруты транспорта
Маршруты = [(w, b) для w на складах для b в проектах]
# Создается словарь с именем 'Vars', содержащий переменные, на которые ссылаются (маршруты)
vars = LpVariable.dicts("Маршрут", (склады, проекты), 0, Нет, LpInteger) 

Определение целевой функции

На этом этапе мы определим минимальную целевую функцию, добавив ее к объекту LpProblem . lpSum(vector) используется здесь для определения нескольких линейных выражений. Он также использовал понимание списка для добавления нескольких переменных.

 # Минимальная целевая функция сначала добавляется к 'prob'
проблема += (
    lpSum([vars[w][b] * cost[w][b] for (w, b) в Routes]),
    "Сумма_из_транспортных_затрат",
) 

В этом коде мы суммировали значения списка двух переменных (полный рабочий день и неполный рабочий день) аддитивным способом.

Определение ограничений

Здесь мы добавляем два типа ограничений: максимальные ограничения предложения и минимальные ограничения спроса. Мы добавили 4 ограничения, определенные в задаче, добавив их в объект LpProblem .

 # Максимальные ограничения поставок добавляются в prob для каждого узла снабжения (складов)
для ж на складах:
    проблема += (
        lpSum([vars[w][b] для b в проектах]) <= поставка[w],
        "Sum_of_Products_out_of_warehouses_%s" % w,
    )
# Минимальные ограничения спроса добавляются в prob для каждого узла спроса (проекта)
для b в проектах:
    проблема += (
        lpSum([vars[w][b] для w на складах]) >= спрос[b],
        "Sum_of_Products_into_projects%s" % b,
    ) 

Модель решения

На этом этапе мы решим задачу LP, вызвав методsolve(). Мы можем напечатать окончательное значение, используя следующий цикл for.

 # Проблема решена с помощью решения PuLP.
проблема.решить()
# Вывести оптимизированное значение переменных
для v в prob.variables():
    print(v.name, "=", v.varValue)
    
# Значение оптимизированной целевой функции выводится на экран
print("Значение целевой функции = ", value(prob. objective)) 

  Вывод: 
Маршрут_A_1 = 0,0
Маршрут_A_2 = 300,0
Маршрут_A_3 = 0,0
Маршрут_B_1 = 150,0
Маршрут_B_2 = 150,0
Маршрут_B_3 = 300,0
Маршрут_C_1 = 0,0
Маршрут_C_2 = 0,0
Маршрут_C_3 = 600,0
Значение целевой функции = 4800,0 

Из приведенных выше результатов мы можем сделать вывод, что Склад-А поставляет 300 единиц для Проекта -2. Warehouse-B поставляет 150, 150 и 300 на соответствующие проектные площадки. И, наконец, Склад-С поставляет 600 единиц Проекту-3.

Резюме

В этой статье мы узнали о проблемах транспорта, формулировании проблем и реализации с использованием библиотеки Python PuLp. Мы решили транспортную задачу, используя задачу линейного программирования на Python. Конечно, это всего лишь простой пример, мы можем добавить к нему больше ограничений и сделать его более сложным. В следующих статьях мы напишем больше о различных проблемах оптимизации, таких как проблема перегрузки, проблема назначения, проблема сбалансированного питания.