Формула бинома Ньютона. Свойства биноминальных коэффициентов. Треугольник Паскаля. | Презентация к уроку по алгебре (10, 11 класс):
Слайд 2
НЬЮТОН — английский математик, механик, астроном и физик, создатель классической механики. Разработал дифференциальное и интегральное исчисления. Открыл дисперсию света, исследовал интерференцию и дифракцию, развивал корпускулярную теорию света. Построил зеркальный телескоп. Сформулировал основные законы классической механики. Открыл закон всемирного тяготения, создал теорию движения небесных тел, создав основы небесной механики. 1643-1727 г.г.
Слайд 3
создание условий для усвоения студентами основных понятий комбинаторики, задач на перебор вариантов, формулы бинома Ньютона с использованием треугольника Паскаля; выработать навыки решения ключевых задач; показать применение теоретического материала при решении задач; способствовать развитию памяти, внимания, логического мышления; воспитание культуры интеллектуального труда; способствовать развитию интереса к учебному предмету.
Слайд 4
Бином Ньютона. «Би»-удвоение, раздвоение … «Ном»(фран . nombre) – номер, нумерация. «Бином» -»два числа»
Слайд 5
Степени суммы двух чисел:
Слайд 6
В теории многочленов часто двучлены называют биномами .
Слайд 7
Биномиальная формула Ньютона.
Слайд 8
Степени суммы двух чисел:
Слайд 9
Правило Паскаля:
Слайд 10
Треугольник Паскаля
Слайд 11
Треугольник Паскаля чаще встречается в виде значений коэффициентов бинома Ньютона для натуральных n:
Слайд 12
Боковые стороны треугольника Паскаля состоят из единиц. Внутри треугольника Паскаля стоят числа, получающиеся сложением двух соответствующих чисел над ним. Например, значение десять (выделено красным) получено как сумма четверки и шестерки (выделены голубым). Это правило справедливо для всех внутренних чисел, составляющих треугольник Паскаля, и объясняется свойствами коэффициентов бинома Ньютона.
Слайд 13
1 1 1 1 2 1 1 3 3 1 1 4 6 4 1 1 5 10 10 5 1 1 6 15 20 15 6 1 1 7 21 35 35 21 7 1 Биномиальные коэффициенты легко находить с помощью треугольника Паскаля
Слайд 14
ПАСКАЛЬ -французский математик, физик, религиозный философ и писатель. Работы по арифметике, теории чисел, алгебре, геометрии, теории вероятностей. В 1641г. сконструировал суммирующую машину . 1623-1662 г.г.
Работы по арифметике, теории чисел, алгебре, геометрии, теории вероятностей. В 1641г. сконструировал суммирующую машину . 1623-1662 г.г.
Слайд 15
0 1 2 3 4 5 6 7 8 9 10 0 1 1 1 1 2 1 2 1 3 1 3 3 1 4 1 4 6 4 1 5 1 5 10 10 5 1 6 1 6 15 20 15 6 1 7 1 7 21 35 35 21 7 1 8 1 8 28 56 70 56 28 8 1 9 1 9 36 84 126 126 84 36 9 1 10 1 10 45 120 210 252 210 120 45 10 1
Слайд 16
Биноминальные коэффициенты:
Слайд 17
Биноминальные коэффициенты:
Слайд 18
Число слагаемых на 1 больше степени бинома. Коэффициенты находятся по треугольнику Паскаля. Коэффициенты симметричны. Если в скобке знак минус, то знаки + и – чередуются. Сумма степеней каждого слагаемого равна степени бинома.
Слайд 19
Записать разложение бинома:
Доклад на тему «Бином Ньютона и треугольник Паскаля»
?Previous Entry | Next Entry
Бином Ньютона — формула для разложения на отдельные слагаемые целой неотрицательной степени суммы двух переменных, имеющая вид
где — биноминальные коэффициенты, — неотрицательное целое число.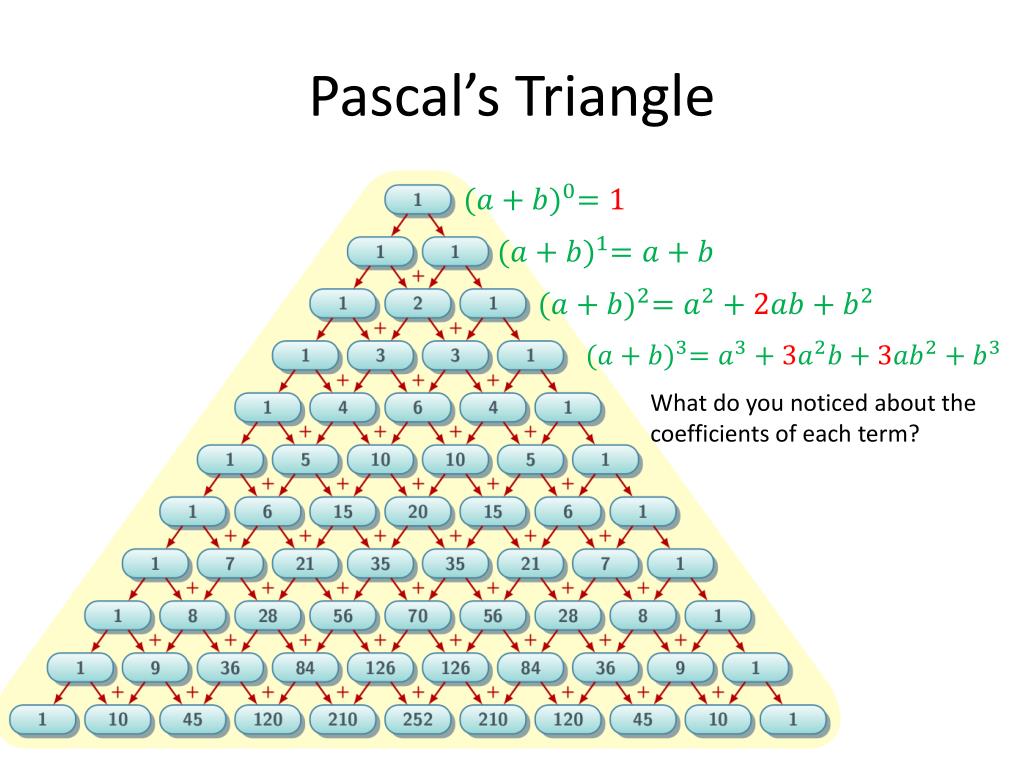
Это формула, представляющая выражение ( a + b ) n при положительном целом n в виде многочлена:
Заметим, что сумма показателей степеней для a и b постоянна и равна n.
Числа называются биномиальными коэффициентами.
Их можно вычислить, применяя только сложение, если пользоваться следующей схемой. В верхней строке пишем две единицы. Все последующие строки начинаются и заканчиваются единицей. Промежуточные числа в этих строках получаются суммированием соседних чисел из предыдущей строки. Эта схема называется
Первая строка в этой таблице содержит биномиальные коэффициенты для n = 1; вторая — для n = 2; третья — для n = 3 и т.д. Поэтому, если необходимо, например, разложить выражение:
( a + b )7 ,
мы можем получить результат моментально, используя таблицу:
Свойства биномиальных коэффициентов.
1. Сумма коэффициентов разложения ( a + b ) n равна 2 n .
Для доказательства достаточно положить a = b = 1. Тогда в правой части разложения бинома Ньютона мы будем иметь сумму биномиальных коэффициентов, а слева:
2. Коэффициенты членов, равноудалённых от концов разложения, равны.
Это свойство следует из соотношения:
3. Сумма коэффициентов чётных членов разложения равна сумме коэффициентов нечётных членов разложения; каждая из них равна
Для доказательства воспользуемся биномом: Здесь чётные члены имеют знак « + » , а нечётные — « — ». Так как в результате разложения получается 0, то следовательно, суммы их биномиальных коэффициентов равны между собой, поэтому каждая из них равна: что и требовалось доказать.
| January 2014 | ||||||
| S | M | T | W | T | F | S |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | |||
| 5 | 6 | 7 | 8 | 9 | 10 | 11 |
| 12 | 13 | 14 | 15 | 16 | 17 | 18 |
| 19 | 20 | 21 | 22 | 23 | 24 | 25 |
| 26 | 27 | 28 | 29 | 30 | 31 | |
Powered by LiveJournal.com
{n-1}$.Другой очевидной особенностью треугольника Паскаля является симметрия: каждая строка одинаково читается вперед и назад. То есть имеем:
Теорема 1.3.3 $\ds {n\выберите i}={n\выберите n-i}$.
Доказательство. Это довольно легко увидеть комбинаторно: каждое $i$-подмножество
$n$-множество связано с $(n-i)$-подмножеством.
Другой поразительной особенностью треугольника Паскаля является то, что элементы по ряду строго возрастают к середине ряда, а затем строго убывает. Поскольку мы уже знаем, что строки симметричный, первая часть этого подразумевает вторую.
Теорема 1.3.4 Для $1\le i\le \lfloor{n\over 2}\rfloor$, $\ds {n\choose i}>{n\выбрать i-1}$.
Доказательство. Это по индукции; базовый случай очевиден с первых нескольких ряды. Писать $$\выравнивание{ {n\выбрать i}&={n-1\выбрать i-1}+{n-1\выбрать i}\cr {n\выбрать i-1}&={n-1\выбрать i-2}+{n-1\выбрать i-1}\cr }$$ При условии, что $1\le i\le \lfloor{n-1\over 2}\rfloor$, мы знаем по индукционная гипотеза о том, что $${n-1\выбрать i}>
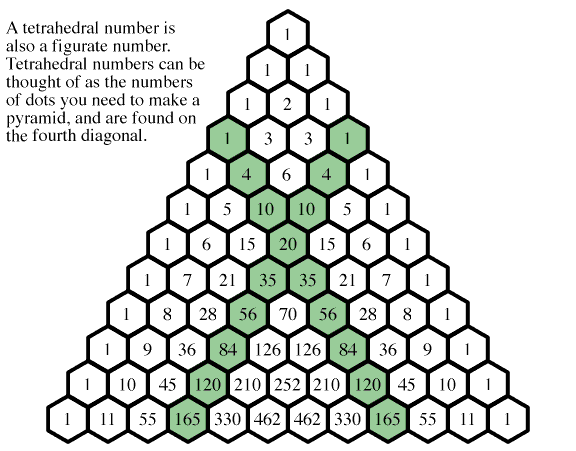 $$
При условии, что $1\le i-1\le \lfloor{n-1\over 2}\rfloor$ или
эквивалентно $2\le i\le \lfloor{n-1\over 2}\rfloor+1$, мы знаем, что
$${n-1\выбрать i-1}>{n-1\выбрать i-2}.$$
Следовательно, если $2\le i\le \lfloor{n-1\over 2}\rfloor$,
$${n\выбрать i}>{n\выбрать i-1}.$$
Остается проверить два особых случая: $i=1$ и для четного $n$
$i=\lfloor{n-1\более 2}\rfloor+1=\lfloor{n\более 2}\rfloor$.
Они оставлены в качестве упражнения.
$\qed$
9n {k\выбрать i} = {n+1\выбрать i+1}$
для $n\ge 0$ и $i\ge 0$; то есть,
объясните, почему левая часть считается так же, как и правая
сторона.
$$
При условии, что $1\le i-1\le \lfloor{n-1\over 2}\rfloor$ или
эквивалентно $2\le i\le \lfloor{n-1\over 2}\rfloor+1$, мы знаем, что
$${n-1\выбрать i-1}>{n-1\выбрать i-2}.$$
Следовательно, если $2\le i\le \lfloor{n-1\over 2}\rfloor$,
$${n\выбрать i}>{n\выбрать i-1}.$$
Остается проверить два особых случая: $i=1$ и для четного $n$
$i=\lfloor{n-1\более 2}\rfloor+1=\lfloor{n\более 2}\rfloor$.
Они оставлены в качестве упражнения.
$\qed$
9n {k\выбрать i} = {n+1\выбрать i+1}$
для $n\ge 0$ и $i\ge 0$; то есть,
объясните, почему левая часть считается так же, как и правая
сторона.Пример 1.3.4 Используйте комбинаторный аргумент, чтобы докажите, что ${k \выберите 2} + {n-k \выберите 2}+k(n-k) = {n \выберите 2}$.
Пример 1.3.5
Используйте комбинаторный аргумент, чтобы докажите, что ${2n\choose n}$ четно. Пример 1.3.6 Предположим, что $A$ — непустое конечное множество.
Докажите, что $A$ имеет столько же четных подмножеств, сколько и нечетных. подмножества.
9k {m\выберите i}{n\выберите k-i}={m+n\выберите k}.$$
Перепишите это тождество в более простой форме, если $m=n$, и
когда $k=m=n$.
подмножества.
9k {m\выберите i}{n\выберите k-i}={m+n\выберите k}.$$
Перепишите это тождество в более простой форме, если $m=n$, и
когда $k=m=n$.
Пример 1.3.15 Завершите доказательство теоремы 1.3.4.
Пример 1.3.16 Дайте альтернативное доказательство теоремы 1.3.4. характеризуя те $i$, для которых ${n\choose i}/{n\choose i-1} > 1$.
Пример 1.3.17 Когда ${n\выбрать i}/{n\выбрать i-1}$ максимум? Когда ${n\выберите i}/{n\выберите i-1}=2$?
Пример 1.3.18 Когда ${n\выбрать i}-{n\выбрать i-1}$ максимум?
Пример 1.3.19 Доска Galton
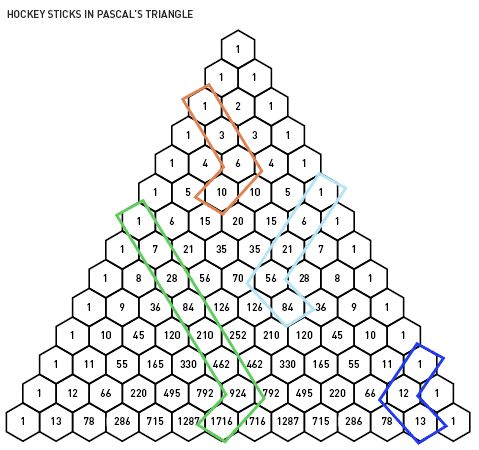 Если мы пронумеруем ящики
от 0 до $n$, сколько путей может пройти мяч, чтобы оказаться в ячейке $k$?
Если мы пронумеруем ящики
от 0 до $n$, сколько путей может пройти мяч, чтобы оказаться в ячейке $k$?Это можно интерпретировать с точки зрения вероятности, что и было намерением сэра Фрэнсиса Гальтона, когда он его проектировал. Каждый путь одинаково вероятно, будет взято мячом. Если выпало много шаров, количество шаров в ячейке $k$ соответствует вероятности попадания в эту мусорное ведро Чем больше путей заканчивается в ячейке, тем выше вероятность. Когда выпадает очень большое количество шаров, шары будет аппроксимировать кривую нормального распределения, известную из вероятность и статистика.
Есть анимация процесса https://www.randomservices.org/random/apps/GaltonBoardExperiment.html. Когда-то была очень хорошая физическая реализация на Тихоокеанский научный центр в Сиэтле.
Биномиальные коэффициенты в треугольнике Паскаля
Математические слова: Биномиальные коэффициенты в треугольнике Паскаля
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||

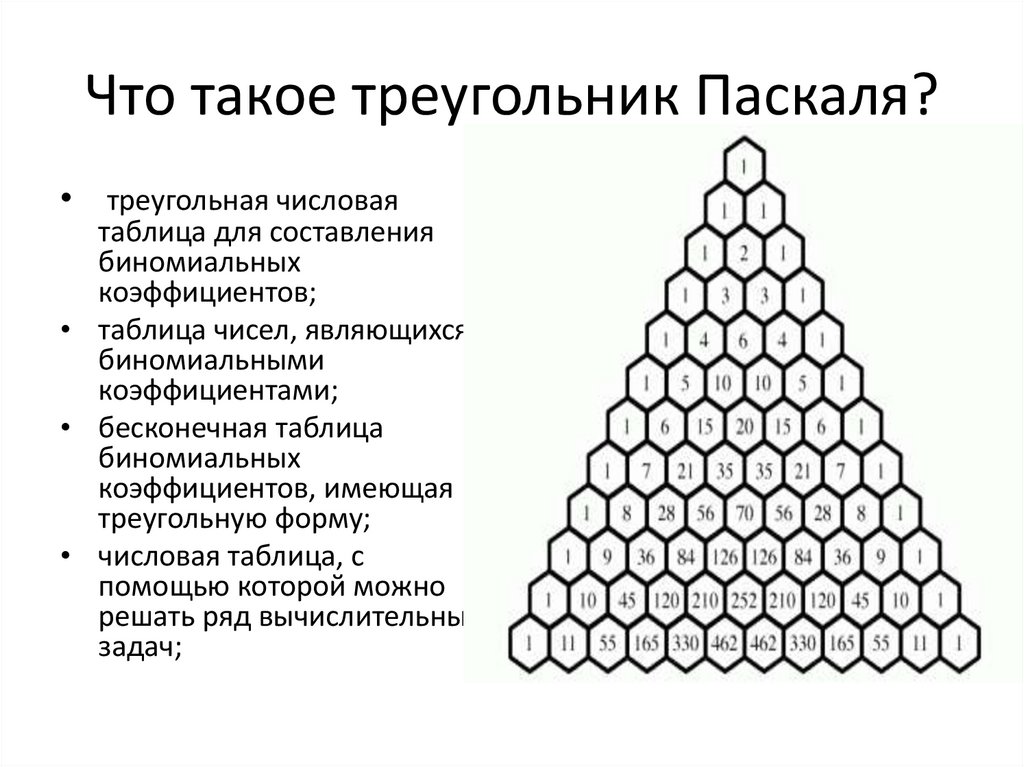 Каждое обозначение
читается вслух « n выбрать r «.
Каждое обозначение
читается вслух « n выбрать r «.