определение, формула и доказательство, способы применения
Основная формула треугольника Паскаля
В рамках курса алгебры знакомство с теорией вероятности начинается с изучения комбинаторики — науке о комбинациях и сочетаниях элементов внутри множества.
Предположим, имеется множество, состоящее из n элементов. Из множества необходимо выбрать k элементов без учета их порядка. Такое сочетание принято обозначать Cnk. Формула для нахождения сочетания Cnk имеет вид:
Формула 1Cnk=n!k!·(n-k)!
Существует простой метод упорядочить запись чисел Cnk — треугольник Паскаля, названный так в честь французского ученого XVII века — Блеза Паскаля. Фактически треугольник был описан задолго до жизни Б. Паскаля, но именно он представил самое полное описание треугольника в своем труде «Трактат об арифметическом треугольнике». Поэтому такую форму записи и назвали в его честь.
Дадим определение треугольнику Паскаля.
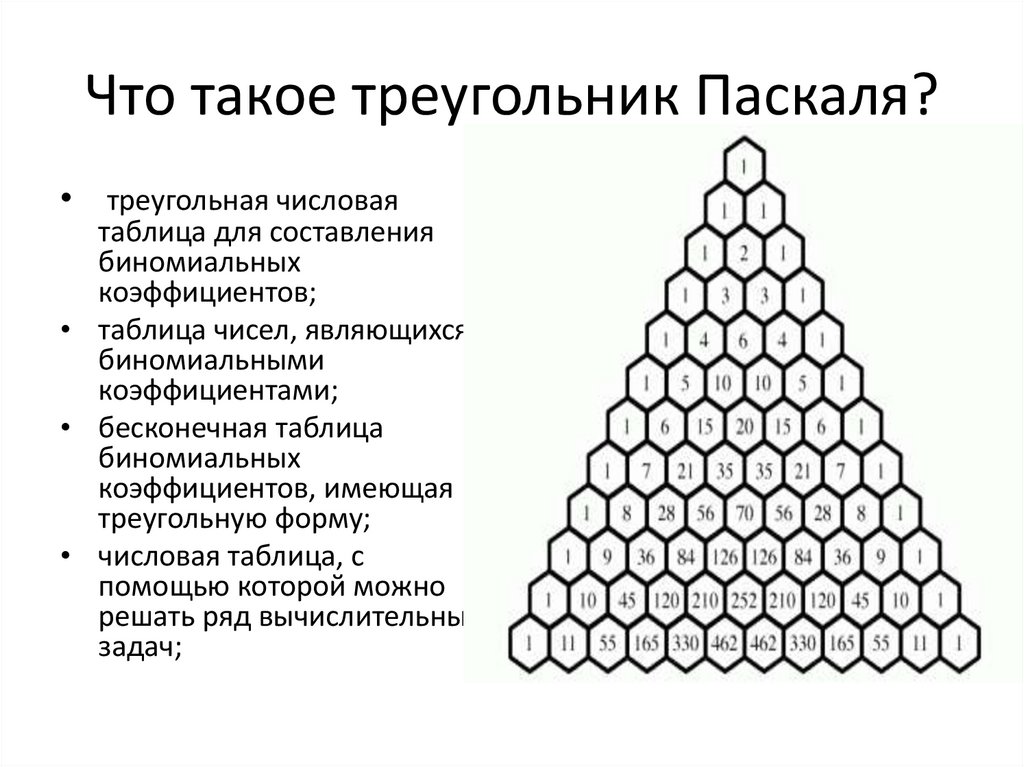
ОпределениеТреугольник Паскаля — форма записи биномиальных коэффициентов в виде бесконечной треугольной таблицы. Элементы массива обозначаются Cnk, где n — номер строки, k — порядковый номер элемента в строке. Нумерацию строк начинают с нулевой, при этом нулевая строка — это вершина, то есть число 1. Нумерацию чисел в строке также начинают с нуля и с левого края.
Элементы массива обозначаются Cnk, где n — номер строки, k — порядковый номер элемента в строке. Нумерацию строк начинают с нулевой, при этом нулевая строка — это вершина, то есть число 1. Нумерацию чисел в строке также начинают с нуля и с левого края.
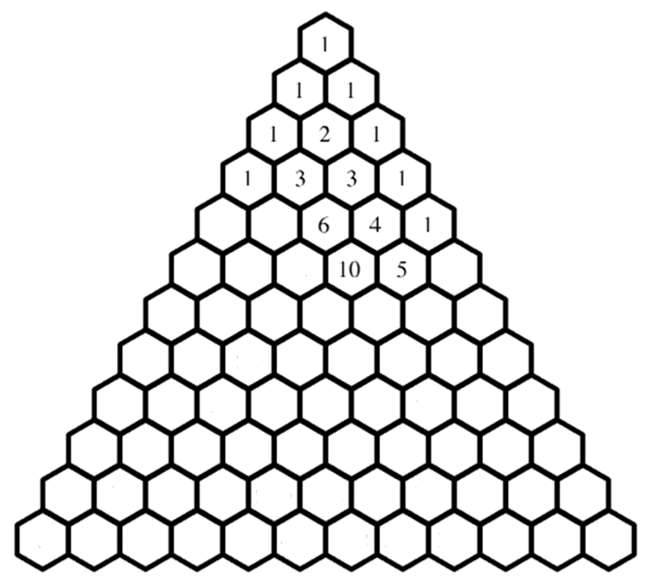
Приведем алгоритм построения треугольника:
- в вершине массива и на боковых сторонах помещают число 1;
- затем в каждую строку, начиная с левой стороны, помещают число, равное сумме двух стоящих наверху элементов.
Основная формула для расчета каждого числа в треугольнике имеет вид:
Формула 2Cnk=Cn-1k-Cn-1k-1
Приведем пример использования треугольника в решении задач комбинаторики.
Пример 1Сколько существует вариантов выбора 3 шаров из бочки, если общее количество шаров в ней 8.
Решение. По условию нам не важен порядок выбора шаров. В треугольнике находим элемент, который находится на пересечении 3-ей диагонали и 8-ой строки.
Получим, что существует 56 вариантов выбора.
Отличительные черты треугольника Паскаля
Треугольник Паскаля имеет ряд отличительных особенностей:
- в вершине и на боковых сторонах располагаются единицы;
- строки симметричны относительно вертикальной оси;
- диагональ, идущая сразу после единичной боковой стороны, содержит только натуральные числа.
 Утверждение справедливо как для диагонали правой стороны, так и левой стороны. Чтобы доказать это, достаточно обратиться к свойству симметричности строк;
Утверждение справедливо как для диагонали правой стороны, так и левой стороны. Чтобы доказать это, достаточно обратиться к свойству симметричности строк; - если треугольник выравнять по левому краю, то сумма чисел, расположенных на диагоналях, равна числу Фибоначчи. Диагонали направляют слева направо и снизу вверх.
Последовательность Фибоначчи — последовательность чисел, в которой каждый элемент является суммой двух предыдущих.
Закономерности треугольника Паскаля
Интересны числовые закономерности, которые можно наблюдать в треугольнике:
- Возведем каждый элемент n-ой строки в квадрат, а потом найдем их сумму. Тогда полученная сумма равна элементу, который находится в центре строки с номером 2n.
- Сумма чисел в n-ой строке больше суммы чисел в предыдущей в два раза.
- Если первая после единичных ребер диагональ представляет собой последовательность натуральных чисел, то следующая за ней диагональ – последовательность треугольных чисел.
 После диагонали идет диагональ тетраэдральных чисел и так далее. Треугольные числа показывают, какое количество шаров одинакового диаметра нужно, чтобы построить равносторонний треугольник, тетраэдральные — количество шаров для построения правильного тетраэдра.
После диагонали идет диагональ тетраэдральных чисел и так далее. Треугольные числа показывают, какое количество шаров одинакового диаметра нужно, чтобы построить равносторонний треугольник, тетраэдральные — количество шаров для построения правильного тетраэдра.
Свойства треугольника Паскаля и их применение в решении задач
Треугольник Паскаля имеет важное практическое применение. Рассмотрим свойства треугольника и приведем примеры задач, где используется треугольник Паскаля.
Свойство 1Степень числа 2. Сумма элементов n-ой строки равна 2n. То есть по треугольнику Паскаля можно вычислять степень числа 2.
Пример 2Не используя операции умножения и возведения в степень, найдите значение выражения 27-4.
Решение. По условию операции умножения и возведения в степень запрещены. Тогда воспользуемся треугольником Паскаля. Находим 7-ую строку и суммируем ее элементы: 1+7+21+35+35+21+7+1=128. Получим, что значение выражения равно 124.
Свойство 2Степень числа 11. Если числа в n-ой строке записать по порядку в виде одного числа, то получим значение 11n. Это утверждение справедливо для всех n, однако, чтобы получить значение 11n для n≥5 необходимо перенести десятки на предыдущий элемент.
Если числа в n-ой строке записать по порядку в виде одного числа, то получим значение 11n. Это утверждение справедливо для всех n, однако, чтобы получить значение 11n для n≥5 необходимо перенести десятки на предыдущий элемент.
Не используя операции возведения в степень и умножения, вычислить, какое число должно получится в результате 117-5.
Решение. Воспользуемся треугольником Паскаля, выпишем 7-ую строку: 1 7 21 35 35 21 7 1. Так как n≥5, необходимо править строку и переносить попадающиеся десятки на предыдущий элемент.
Тогда 117-5=19487166.
Свойство 3Элементы в строках треугольника являются коэффициентами разложения бинома Ньютона.
Формула 3(a+b)n=an+Cn1an-1b+Cn2an-2b2+…+Cnkan-kbk+…+Cnn-1abn-1+bn
Примечание 2Биномом называют сумму или разность одночленов. Само слово «бином» дословно переводится как «две части».
В качестве доказательства этого свойства выпишем в строки разложение (a+b)n, где n меняется от 0 до 3.
Коэффициенты при множителях a и b совпадают с числами треугольника Паскаля в соответствующей строке.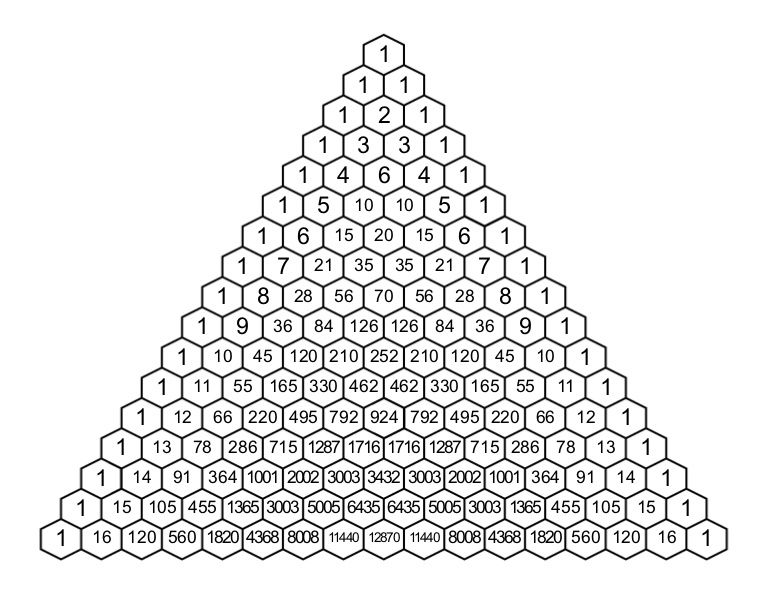
Выполнить разложение (x+y)6.
Решение. Элементы 6-ой строки будут коэффициентами при x и y: 1; 6; 15; 20; 15; 6; 1. Показатели степени получим из формулы для бинома Ньютона. Получим:
(x+y)6=x6+6x5y+15x4y2+20x3y3+15x2y4+6xy5+y6
Треугольник Паскаля — формула, свойства, правило построения фигуры
Основная формула
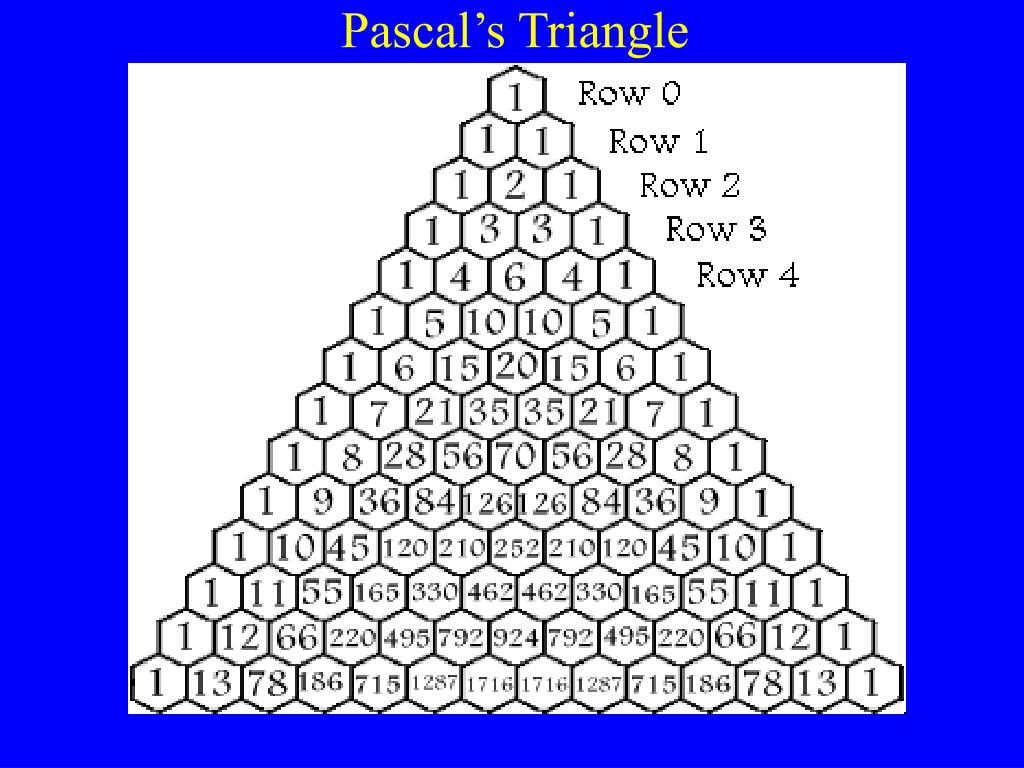
Строки треугольника обычно нумеруются, начиная со строки n = 0 в верхней части. Записи в каждой строке целочисленные и нумеруются слева, начиная с k = 0, обычно располагаются в шахматном порядке относительно чисел в соседних строчках. Построить фигуру можно следующим образом:
- В центре верхней части листа ставится цифра «1».
- В следующем ряду — две единицы слева и справа от центра (получается треугольная форма).
- В каждой последующей строке ряд будет начинаться и заканчиваться числом «1». Внутренние члены вычисляются путём суммирования двух цифр над ним.

Запись в n строке и k столбце паскалевской фигуры обозначается (n k). Например, уникальная ненулевая запись в самой верхней строке (0 0) = 1. С помощью этого конструкция предыдущего абзаца может быть записана следующим образом, образуя формулу треугольника Паскаля (n k) = (n — 1 k-1) + (n — 1 k), для любого неотрицательного целого числа n и любого целого числа k от 0 до n включительно. Трёхмерная версия называется пирамидой или тетраэдром, а общие — симплексами.
История открытия
Паскаль ввёл в действие многие ранее недостаточно проверенные способы использования чисел треугольника, и он подробно описал их в, пожалуй, самом раннем из известных математических трактатов, специально посвящённых этому вопросу, в труде об арифметике Traité du triangle (1665). За столетия до того обсуждение чисел возникло в контексте индийских исследований комбинаторики и биномиальных чисел, а у греков были работы по «фигурным числам».
Из более поздних источников видно, что биномиальные коэффициенты и аддитивная формула для их генерации были известны ещё до II века до нашей эры по работам Пингала. К сожалению, бо́льшая часть трудов была утеряна. Варахамихира около 505 года дал чёткое описание аддитивной формулы, а более подробное объяснение того же правила было дано Халаюдхой (около 975 года). Он также объяснил неясные ссылки на Меру-прастаара, лестницы у горы Меру, дав первое сохранившееся определение расположению этих чисел, представленных в виде треугольника.
Примерно в 850 году джайнский математик Махавира вывел другую формулу для биномиальных коэффициентов, используя умножение, эквивалентное современной формуле. В 1068 году Бхаттотпала во время своей исследовательской деятельности вычислил четыре столбца первых шестнадцати строк. Он был первым признанным математиком, который уравнял аддитивные и мультипликативные формулы для этих чисел.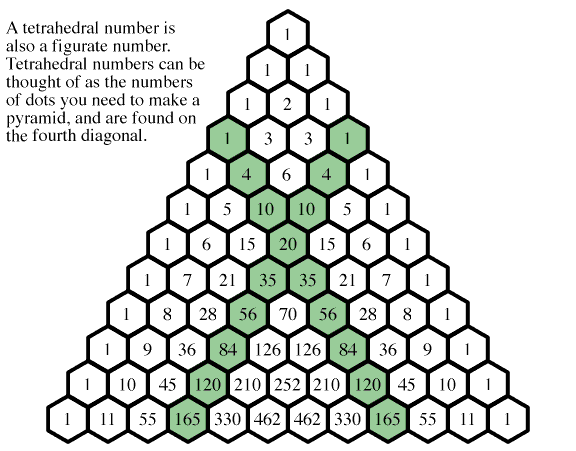
Примерно в то же время персидский учёный Аль-Караджи (953–1029) написал книгу (на данный момент утраченную), в которой содержалось первое описание треугольника Паскаля. Позднее работа была переписана персидским поэтом, астрономом и математиком Омаром Хайямом (1048–1131). Таким образом, в Иране фигура упоминается как треугольник Хайяма.
Известно несколько теорем, связанных с этой темой, включая биномы. Хайям использовал метод нахождения n-x корней, основанный на биномиальном разложении и, следовательно, на одноимённых коэффициентах. Треугольник был известен в Китае в начале XI века благодаря работе китайского математика Цзя Сианя (1010–1070). В XIII веке Ян Хуэй (1238–1298) представил этот способ, и поэтому в Китае он до сих пор называется треугольником Ян Хуэя.
На западе биномиальные коэффициенты были рассчитаны Жерсонидом в начале XIV века, он использовал мультипликативную формулу. Петрус Апиан (1495–1552) опубликовал полный треугольник на обложке своей книги примерно в 1527 году.
В Италии паскалевский треугольник зовут другим именем, в честь итальянского алгебраиста Никколо Фонтана Тарталья (1500–1577). Вообще, современное имя фигура приобрела благодаря Пьеру Раймонду до Монтрмору (1708), который назвал треугольник «Таблица Паскаля для сочетаний» (дословно: Таблица мистера Паскаля для комбинаций) и Абрахамом Муавром (1730).
Отличительные черты
Треугольник Паскаля и его свойства — тема довольно обширная. Главное, в нём содержится множество моделей чисел.
- Сумма элементов одной строки в два раза больше суммы строки, предшествующей ей. Например, строка 0 (самая верхняя) имеет значение 1, строчка 1–2, а 2 имеет значение 4 и т.
 д. Это потому что каждый элемент в строке производит два элемента в следующем ряду: один слева и один справа. Сумма элементов строки n равна 2 n.
д. Это потому что каждый элемент в строке производит два элемента в следующем ряду: один слева и один справа. Сумма элементов строки n равна 2 n. - Принимая произведение элементов в каждой строке, последовательность продуктов можно связать с основанием натурального логарифма.
- В треугольнике Паскаля через бесконечный ряд Нилаканты можно найти число Пи.
- Значение строки, если каждая запись считается десятичным знаком (имеется в виду, что числа больше 9 переносятся соответственно), является степенью 11 (11n для строки n). Таким образом, в строке 2 ⟨1, 2, 1⟩ становится 112, равно как ⟨1, 5, 10, 10, 5, 1⟩ в строке пять становится (после переноса) 161, 051, что составляет 11 5. Это свойство объясняется установкой x = 10 в биномиальном разложении (x + 1) n и корректировкой значений в десятичной системе.
- Некоторые числа в треугольнике Паскаля соотносятся с числами в треугольнике Лозанича.

- Сумма квадратов элементов строки n равна среднему элементу строки 2 n. Например, 1 2 + 4 2 + 6 2 + 4 2 + 1 2 = 70.
- В любой строчке n, где n является чётным, средний член за вычетом члена в двух точках слева равен каталонскому числу (n / 2 + 1).
- В строчке р, где р представляет собой простое число, все члены в этой строке, за исключением 1s, являются кратными р.
- Чётность. Для измерения нечётных терминов в строке n необходимо преобразовать n в двоичную форму. Пусть x будет числом 1s в двоичном представлении. Тогда количество нечётных членов будет 2 х. Эти числа являются значениями в последовательности Гулда.
- Каждая запись в строке 2 n-1, n ≥ 0, является нечётной.
- Полярность. Когда элементы строки треугольника Паскаля складываются и вычитаются вместе последовательно, каждая строка со средним числом, означающим строки с нечётным числом целых чисел, даёт 0 в качестве результата.

Диагонали треугольника содержат фигурные числа симплексов. Например:
- Идущие вдоль левого и правого краёв диагонали содержат только 1.
- Рядом с рёбрами диагонали содержат натуральные числа по порядку.
- Двигаясь внутрь, следующая пара содержит треугольные числа по порядку.
- Следующая пара — тетраэдрические, а следующая пара — числа пятиугольника.
Существуют простые алгоритмы для вычисления всех элементов в строке или диагонали без вычисления других элементов или факториалов.
Общие свойства
Образец, полученный путём раскраски только нечётных чисел, очень похож на фрактал, называемый треугольником Серпинского. Это сходство становится всё более точным, так как рассматривается больше строк в пределе, когда число рядов приближается к бесконечности, получающийся в результате шаблон представляет собой фигуру, предполагающую фиксированный периметр. В целом числа могут быть окрашены по-разному в зависимости от того, являются ли они кратными 3, 4 и т. д.
В целом числа могут быть окрашены по-разному в зависимости от того, являются ли они кратными 3, 4 и т. д.
В треугольной части сетки количество кратчайших путей от заданного до верхнего угла треугольника является соответствующей записью в паскалевском треугольнике. На треугольной игровой доске Плинко это распределение должно давать вероятности выигрыша различных призов. Если строки треугольника выровнены по левому краю, диагональные полосы суммируются с числами Фибоначчи.
Благодаря простому построению факториалами можно дать очень простое представление фигуры Паскаля в терминах экспоненциальной матрицы: треугольник — это экспонента матрицы, которая имеет последовательность 1, 2, 3, 4… на её субдиагонали, а все другие точки — 0.
Количество элементов симплексов фигуры можно использовать в качестве справочной таблицы для количества элементов (рёбра и углы) в многогранниках (треугольник, тетраэдр, квадрат и куб).
Шаблон, созданный элементарным клеточным автоматом с использованием правила 60, является в точности паскалевским треугольником с биномиальными коэффициентами, приведёнными по модулю 2.
Секреты треугольника
Конечно, сейчас большинство расчётов для решения задач не в классе можно сделать с помощью онлайн-калькулятора. Как пользоваться треугольником Паскаля и для чего он нужен, обычно рассказывают в школьном курсе математики. Однако его применение может быть гораздо шире, чем принято думать.
Начать следует со скрытых последовательностей. Первые два столбца фигуры не слишком интересны — это только цифры и натуральные числа. Следующий столбец — треугольные числа. Можно думать о них, как о серии точек, необходимых для создания групп треугольников разных размеров.
Точно так же четвёртый столбец — это тетраэдрические числа или треугольные пирамидальные. Как следует из их названия, они представляют собой раскладку точек, необходимых для создания пирамид с треугольными основаниями.
Столбцы строят таким образом, чтобы описывать «симплексы», которые являются просто экстраполяциями идеи тетраэдра в произвольные измерения. Следующий столбец — это 5-симплексные числа, затем 6-симплексные числа и так далее.
Полномочия двойки
Если суммировать каждую строку, получатся степени основания 2 начиная с 2⁰ = 1. Если изобразить это в таблице, то получится следующее:
| 1 | ||||||||||||||
| 1 | + | 1 | = | 2 | ||||||||||
| 1 | + | 2 | + | 1 | = | 4 | ||||||||
| 1 | + | 3 | + | 3 | + | 1 | = | 8 | ||||||
| 1 | + | 4 | + | 6 | + | 4 | + | 1 | = | 16 | ||||
| 1 | + | 5 | + | 10 | + | 10 | + | 5 | + | 1 | = | 32 | ||
| 1 | + | 6 | + | 15 | + | 20 | + | 15 | + | 6 | + | 1 | = | 64 |
Суммирование строк показывает силы базы 2.
Силы одиннадцати
Треугольник также показывает силы основания 11. Всё, что нужно сделать, это сложить числа в каждом ряду вместе. Как показывает исследовательский опыт, этого достаточно только для первых пяти строк. Сложности начинаются, когда записи состоят из двузначных чисел. Например:
| 1 | = | 11° |
| 11 | = | 11¹ |
| 121 | = | 11² |
| 1331 | = | 11³ |
Оказывается, всё, что нужно сделать — перенести десятки на одно число слева.
Совершенные квадраты
Если утверждать, что 4² — это 6 + 10 = 16, то можно найти идеальные квадраты натуральных чисел в столбце 2, суммируя число справа с числом ниже. Например:
Например:
- 2² → 1 + 3 = 4
- 3² → 3 + 6
- 4² → 6 + 10 = 16 и так далее.
Комбинаторные варианты
Чтобы раскрыть скрытую последовательность Фибоначчи, которая на первый взгляд может отсутствовать, нужно суммировать диагонали лево-выровненного паскалевского треугольника. Первые 7 чисел в последовательности Фибоначчи: 1, 1, 2, 3, 5, 8, 13… найдены. Используя исходную ориентацию, следует заштриховать все нечётные числа, и получится изображение, похожее на знаменитый фрактальный треугольник Серпинского.
Возможно, самое интересное соотношение, найденное в треугольнике — это то, как можно использовать его для поиска комбинаторных чисел, поскольку его первые шесть строк написаны с помощью комбинаторной записи. Поэтому, если нужно рассчитать 4, стоит выбрать 2, затем максимально внимательно посмотреть на пятую строку, третью запись (поскольку счёт с нуля), и будет найден ответ.

Действия с биномами
Например, есть бином (x + y), и стоит задача повысить его до степени, такой как 2 или 3. Обычно нужно пройти долгий процесс умножения (x + y)² = (x + y)(x + y) и т. д. Если воспользоваться треугольником, решение будет найдено гораздо быстрее. К примеру, нужно расширить (x + y)³. Поскольку следует повышать (x + y) до третьей степени, то необходимо использовать значения в четвёртом ряду фигуры Паскаля (в качестве коэффициентов расширения). Затем заполнить значения x и y. Получится следующее: 1 x³ + 3 x²y + 3 xy² + 1 y³. Степень каждого члена соответствует степени, до которой возводится (x + y).
В виде более удобной формулы этот процесс представлен в теореме бинома. Как известно, всё лучше разбирать на примерах. Итак — (2x – 3)³. Пусть x будет первым слагаемым, а y — вторым. Тогда x = 2x, y = –3, n = 3 и k — целые числа от 0 до n = 3, в этом случае k = {0, 1, 2, 3}. Следует внести эти значения в формулу. Затем заполнить значения для k, которое имеет 4 разные версии, их нужно сложить вместе. Лучше упростить условия с показателями от нуля до единицы.
Следует внести эти значения в формулу. Затем заполнить значения для k, которое имеет 4 разные версии, их нужно сложить вместе. Лучше упростить условия с показателями от нуля до единицы.
Как известно, комбинаторные числа взяты из треугольника, поэтому можно просто найти четвёртую строку и подставить в значения 1, 3, 3, 1 соответственно, используя соответствующие цифры Паскаля 1, 3, 3, 1. Последнее — необходимо завершить умножение и упрощение, в итоге должно получиться: 8 x³ — 36 x² + 54x — 27. С помощью этой теоремы можно расширить любой бином до любой степени, не тратя время на умножение.
Биномиальное распределение описывает распределение вероятностей на основе экспериментов, которые можно разделить на группы с двумя возможными исходами. Самый классический пример этого — бросание монеты. Например, есть задача выбросить «решку» — успех с вероятностью p. Тогда выпадение «орла» является случаем «неудачи» и имеет вероятность дополнения 1 – p.
Тогда выпадение «орла» является случаем «неудачи» и имеет вероятность дополнения 1 – p.
Если спроектировать этот эксперимент с тремя испытаниями, с условием, что нужно узнать вероятность выпадения «решки», можно использовать функцию вероятности массы (pmf) для биномиального распределения, где n — это количество испытаний, а k — это число успехов. Предполагаемая вероятность удачи — 0,5 (р = 0,5). Самое время обратиться к треугольнику, используя комбинаторные числа: 1, 3, 3, 1. Вероятность получить ноль или три «решки» составляет 12,5%, в то время как переворот монеты один или два раза на сторону «орла» — 37,5%. Вот так математика может применяться в жизни.
Треугольник Паскаля — свойства, приложения и примеры
Треугольник Паскаля — один из интересных числовых шаблонов в математике. Это треугольный массив, построенный суммированием соседних элементов в предыдущих строках .
Треугольник Паскаля назван в честь французского математика 17 века, Блеза Паскаля (1623–1662), хотя другие математики изучали его за столетия до него в Индия, Персия, Китай, Германия и Италия . Паскаль изобрел множество ранее неизвестных способов использования чисел треугольника, которые он подробно описал в самом раннем известном математическом трактате, специально посвященном треугольнику, в его Traité du треугольник арифметики (1654; опубликовано 1665).
Построение треугольника ПаскаляЧтобы построить треугольник, начните с «1» вверху. В следующем ряду напишите две единицы, образуя треугольник. В каждой последующей строке начинайте и заканчивайте с 1 и вычисляйте каждый внутренний член на 9.0003 суммируя два числа над ним .
Повторяя этот процесс, мы получим треугольник Паскаля. Это бесконечный треугольник .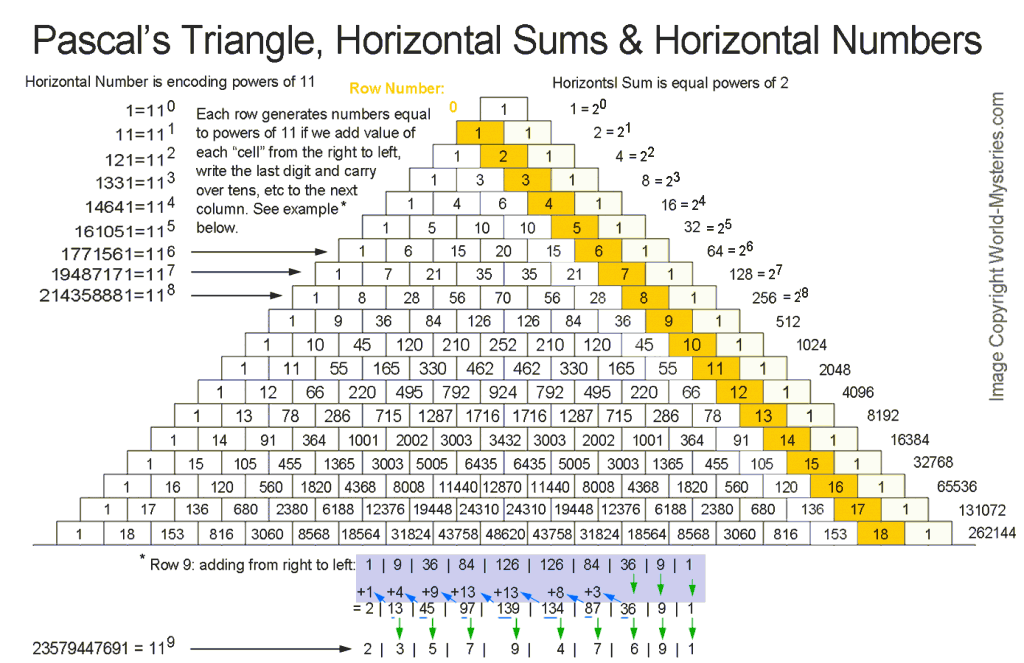
- Каждое число r равно сумме двух чисел над ним .
- Треугольник симметричен .
- Диагонали, идущие вдоль левого и правого краев, содержат только единицы. Диагонали рядом с диагоналями ребер содержат натуральные числа по порядку. Следующая диагональ 9.0003 треугольные числа . Точно так же следующие диагонали — это тетраэдрических числа или треугольные пирамидальные числа.
- Сумма диагоналей выровненного по левому краю треугольника Паскаля образует последовательность Фибоначчи
- Суммы строк дают степени числа 2 .
- Каждая строка содержит цифры степеней числа 11 .

- Начните с любого числа в треугольнике и двигайтесь вниз по диагонали. Затем измените направление по диагонали для последнего числа. Это последнее число является суммой всех остальных чисел по диагонали, оно известно как Шаблон хоккейной клюшки .
- Каталонские цифры можно найти, взяв многоугольники и найдя, сколькими способами их можно разбить на треугольники. Эти числа находятся в треугольнике Паскаля, начиная с 3-й строки посередине и вычитая соседнее число. (Catalan numbers are 1, 1, 2, 5, 14, 42, 132, 429, 1430, 4862, 16796, 58786, 208012, 742900, 2674440, 9694845, 35357670, 129644790, 477638700, 1767263190, 6564120420, 24466267020)
- Если заштриховать все четные числа, получится фрактал .
 Это также рекурсия треугольника Серпинского .
Это также рекурсия треугольника Серпинского .
Теперь давайте посмотрим на применение треугольника Паскаля.
Биномиальное разложениеТреугольник Паскалей определяет коэффициенты , возникающие при биномиальном разложении.
Предположим, у вас есть бином ( x + y ) и вы хотите возвести его в степень 2 или 3.
Например, :
Давайте расширим (x+y)³. Поскольку мы возводим (x+y) в 3-ю степень , используйте значения в четвертой строке Паскалей в качестве коэффициентов вашего разложения. Затем заполните условия x и y, как показано ниже.
Треугольник Паскаля может указать нам путь как могут сочетаться орел и решка . Это дает вероятность любой комбинации.
Это дает вероятность любой комбинации.
Например:
Если H обозначает орел, а T обозначает решку, то при 4-кратном подбрасывании монеты возможны следующие комбинации: HTHT, HTTH,THHT, THTH
Таким образом, наблюдаемая закономерность 1,4,6,4,1. (Ряд в треугольнике Паскаля) 9{n}_{k} = {n \choose k} = \frac{n!}{k!(n – k)!}\)
Но это формула записи ячейки в треугольнике Паскаля как Что ж. Итак, мы можем просто найти эту конкретную запись в треугольнике и найти ее.
Примечание: Для этого нумерация первой строки и первой записи в строке должна начинаться с 0.
Например: (Для нахождения значения комбинации)
Предположим, что в баскетбольной команде 11 игроков и хочет знать, сколько существует способов выбора 8. 94
\)
Вопрос 2. В треугольнике Паскаля каждая запись представляет собой сумму двух записей над ней.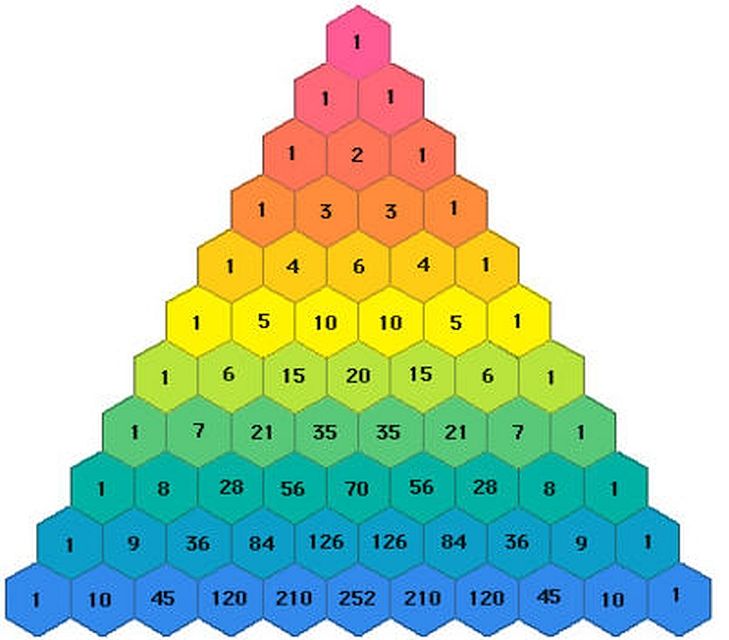 В какой строке треугольника находятся три последовательных элемента в соотношении 3:4:5?
В какой строке треугольника находятся три последовательных элемента в соотношении 3:4:5?
Решение: Назовите строку x и число с крайней левой стороны t.
Назовите первый член отношения \(N\), который равен \(N = {x \выберите t}\).
Следующий член равен \(N * \frac{x – t}{t + 1}\),
и последний член равен \(N * \frac{(x – t) * (x – t – 1)}{(t + 1) * (t + 2)}\).
Поскольку у нас есть отношение
\(N : N * \frac{x – t}{t + 1} : N * \frac{(x – t) * (x – t – 1)}{(t + 1) * (t + 2)} = 3 : 4 : 5\).
Итак, \(\frac{x – t}{t + 1} = \frac{4}{3}\) и \(\frac{(x – t) * (x – t – 1)}{ (t + 1) * (t + 2)} = \frac{5}{3}\).
Решите уравнение, чтобы получить t = 26 и x = 69
Часто задаваемые вопросыКакое правило треугольника Паскаля?
Треугольник Паскаля — это бесконечный равносторонний треугольник чисел, которые следуют правилу сложения двух чисел выше, чтобы получить число ниже. Две стороны — «все единицы», а поскольку треугольник бесконечен, у него нет «нижней стороны».
Две стороны — «все единицы», а поскольку треугольник бесконечен, у него нет «нижней стороны».
Какова цель треугольника Паскаля?
Треугольник Паскаля имеет множество применений в математике и статистике, в том числе помогает вычислять комбинации.
Почему его называют треугольником Паскаля?
Треугольник Паскаля назван в честь Блеза Паскаля, французского математика, который использовал треугольник в своих исследованиях по теории вероятностей в 17 веке. Блез Паскаль на самом деле не «открыл» треугольник, названный в его честь, хотя на самом деле его изучали во всем мире в течение тысяч лет.
Свойства треугольника Паскаля | Живая наука
Живая наука поддерживается своей аудиторией. Когда вы покупаете по ссылкам на нашем сайте, мы можем получать партнерскую комиссию. Вот почему вы можете доверять нам.
Треугольник Паскаля — это бесконечный равносторонний треугольник чисел, которые следуют правилу сложения двух чисел выше, чтобы получить число ниже. Две стороны — «все единицы», а поскольку треугольник бесконечен, у него нет «нижней стороны».
Он назван в честь Блеза Паскаля, французского математика 17-го века, который использовал треугольник в своих исследованиях по теории вероятностей. Тем не менее, он изучался во всем мире на протяжении тысячелетий, особенно в древней Индии и средневековом Китае, а также во времена Золотого века ислама и Возрождения, которые начались в Италии, а затем распространились по Европе.
Какой бы простой ни была эта модель, она удивительным образом связана со многими областями математики, включая алгебру, теорию чисел, вероятность, комбинаторику (математику счетных конфигураций) и фракталы. В колонке «Голоса экспертов» для Live Science за 2013 год Майкл Роуз, математик, обучающийся в Университете Ньюкасла, описал многие закономерности, скрытые в треугольнике Паскаля. В этой статье мы подробно остановимся на свойствах высшей математики.
В колонке «Голоса экспертов» для Live Science за 2013 год Майкл Роуз, математик, обучающийся в Университете Ньюкасла, описал многие закономерности, скрытые в треугольнике Паскаля. В этой статье мы подробно остановимся на свойствах высшей математики.
Комбинации
Треугольник Паскаля возникает естественным путем при изучении комбинаторики. Например, представьте, что вы выбираете три цвета из набора маркеров, состоящего из пяти цветов. Порядок выбора цветов не имеет значения для выбора того, что использовать на плакате, но имеет значение для выбора одного цвета для Алисы, Боба и Кэрол. Количество возможных конфигураций представлено и рассчитано следующим образом:
- По одному цвету для Алисы, Боба и Кэрол: случай, подобный этому, где заказ делает дело называется перестановкой . Для случая с пятью вариантами, когда будут выбраны и упорядочены три, это количество возможных перестановок выражается как 5P3 и рассчитывается как 5!/(5-3)!.
 Оператор «!» называется факториалом, что означает умножение всех меньших целых чисел на единицу (например, 5! = 5 × 4 × 3 × 2 × 1). Выражение для 5P3 упрощается до 5!/2! = 5 × 4 × 3 = 60
Оператор «!» называется факториалом, что означает умножение всех меньших целых чисел на единицу (например, 5! = 5 × 4 × 3 × 2 × 1). Выражение для 5P3 упрощается до 5!/2! = 5 × 4 × 3 = 60 - Три цвета для одного плаката: такой случай, когда заказ не соответствует дело называется комбинацией . Количество возможных комбинаций всегда будет частью количества возможных перестановок. Для случая с пятью вариантами, когда будут выбраны три, это выражается как 5C3 и рассчитывается как 5!/[3! (5-3)!] = 5!/(3! × 2!) = 5 × 4 × 3 / (3 × 2 × 1) = 10
Этот второй случай важен для треугольника Паскаля, поскольку значения могут вычисляется следующим образом:
Числа треугольника Паскаля соответствуют количеству возможных комбинаций (nCr), когда приходится выбирать r-количество объектов из n-количества доступных вариантов. (Изображение предоставлено Робертом Дж. Кулманом) Из процесса создания треугольника Паскаля мы видим, что любое число может быть получено путем сложения двух указанных выше чисел. Математически это выражается как n C r = n-1 C r-1 + n-1 C r — это соотношение отмечалось различными учеными-математиками на протяжении всей истории.
Математически это выражается как n C r = n-1 C r-1 + n-1 C r — это соотношение отмечалось различными учеными-математиками на протяжении всей истории.
Биномиальная теорема
Биномиальный термин — это слово, используемое в алгебре, которое примерно означает «две вещи, сложенные вместе». Биномиальная теорема относится к шаблону коэффициентов (чисел, которые появляются перед переменными), которые появляются, когда двучлен умножается сам на себя определенное количество раз. Математически это записывается как (x + y) n . Треугольник Паскаля можно использовать для определения расширенного набора коэффициентов. Первые несколько расширенных полиномов приведены ниже.
Проведите по экрану для горизонтальной прокрутки
| n | (x + y)n | Расширенный многочлен | Pascal’s Triangle | |||||||||
| 0 | (x + y)0 | 1 | 1 | |||||||||
| 1 | (x + y)1 | 1x + 1y | 1,1 | |||||||||
| 2 | (x + y) 2 | 1×2 + 2xy + 1y2 | 1,2,1 | |||||||||
| 3 | (x + y) 3 | 1×3 + 3x2y + 3x2y + 3x2y + 3x2y + 3x2y + 3x2y + 3x2y + 3x2y + 3x2y + 3x2y + 3x2y + 3x2y + 3x2y + 3×217 + 3x2y + 3x2y + 3×217 + | + | + | + | + | + | + | + | + | + | (x + y). 3,1 3,1 |
| 4 | (x + y)4 | 1×4 + 4x3y + 6x2y2 + 4xy3 + 1y4 | 1,4,6,4,1 | |||||||||
| 5 | (x + y)5 | 1×5 + 5x4y + 10x3y2 + 10x2y3 + 5xy4 + 1y5 | 1,1,5,17 1,1,5,17||||||||||
| ↓ | ↓ | ↓ | ↓ |
Использование номинации и суммирования. В союмиациях. В соответствии с надписью. (Изображение предоставлено Робертом Дж. Кулманом)
Биномиальное распределение
Для вероятностного процесса с двумя результатами (например, подбрасывание монеты) последовательность результатов определяется тем, что математики и статистики называют биномиальное распределение . Это также относится к треугольнику Паскаля.
Например, для трех подбрасываний монеты существует 2 × 2 × 2 = 8 возможных последовательностей орел/решка. При сортировке по группам «сколько головок (3, 2, 1 или 0)» каждая группа заполняется последовательностями 1, 3, 3 и 1 соответственно. Обратите внимание, как это соответствует третьей строке треугольника Паскаля. Доказано, что эта тенденция сохраняется для любого количества подбрасываний монеты и всех строк треугольника.
При сортировке по группам «сколько головок (3, 2, 1 или 0)» каждая группа заполняется последовательностями 1, 3, 3 и 1 соответственно. Обратите внимание, как это соответствует третьей строке треугольника Паскаля. Доказано, что эта тенденция сохраняется для любого количества подбрасываний монеты и всех строк треугольника.
Проведите по экрану для горизонтальной прокрутки
| Coin flips | Possible sequences of heads (H) or tails (T) | Pascal’s Triangle |
| 1 | H T | 1 1 |
| 2 | HH HT TH TT | 1 2 1 |
| 3 | HHH HHT HTH THH HTT THT TTH TTT | 1 3 3 1 |
| 4 | HHHH HHHT HHTH HTHH THHH HHTT HTHT HTTH THHT THTH TTHH HTTT THTT TTHT TTTH TTTT | 1 4 6 4 1 |
| ↓ | ↓ | ↓ |
Согласно Джорджу Е. П. Вставка в «Статистика для экспериментаторов (открывается в новой вкладке)» (Wiley, 1978) для большого количества подбрасываний монеты (примерно более 20) биномиальное распределение является разумным приближением к нормальному распределению, фундаментальной «кривой колокола». распределение, используемое в качестве основы в статистическом анализе. Это приближение значительно упрощает статистический анализ многих явлений.
П. Вставка в «Статистика для экспериментаторов (открывается в новой вкладке)» (Wiley, 1978) для большого количества подбрасываний монеты (примерно более 20) биномиальное распределение является разумным приближением к нормальному распределению, фундаментальной «кривой колокола». распределение, используемое в качестве основы в статистическом анализе. Это приближение значительно упрощает статистический анализ многих явлений.
Физический пример такого приближения можно увидеть в бобовой машине, устройстве, которое случайным образом сортирует шары по корзинам в зависимости от того, как они падают на треугольное расположение колышков. Поскольку мяч, ударяясь о колышек, имеет одинаковую вероятность упасть влево или вправо, вероятность того, что мяч приземлится полностью влево (или вправо) после прохождения определенного количества рядов колышек, точно соответствует вероятности попасть во все орел (или решка) от одного и того же количества подбрасываний монеты. После того, как достаточное количество мячей собралось за треугольником с n рядов колышков, отношения количества шаров в каждом ящике, скорее всего, соответствуют n th ряду треугольника Паскаля.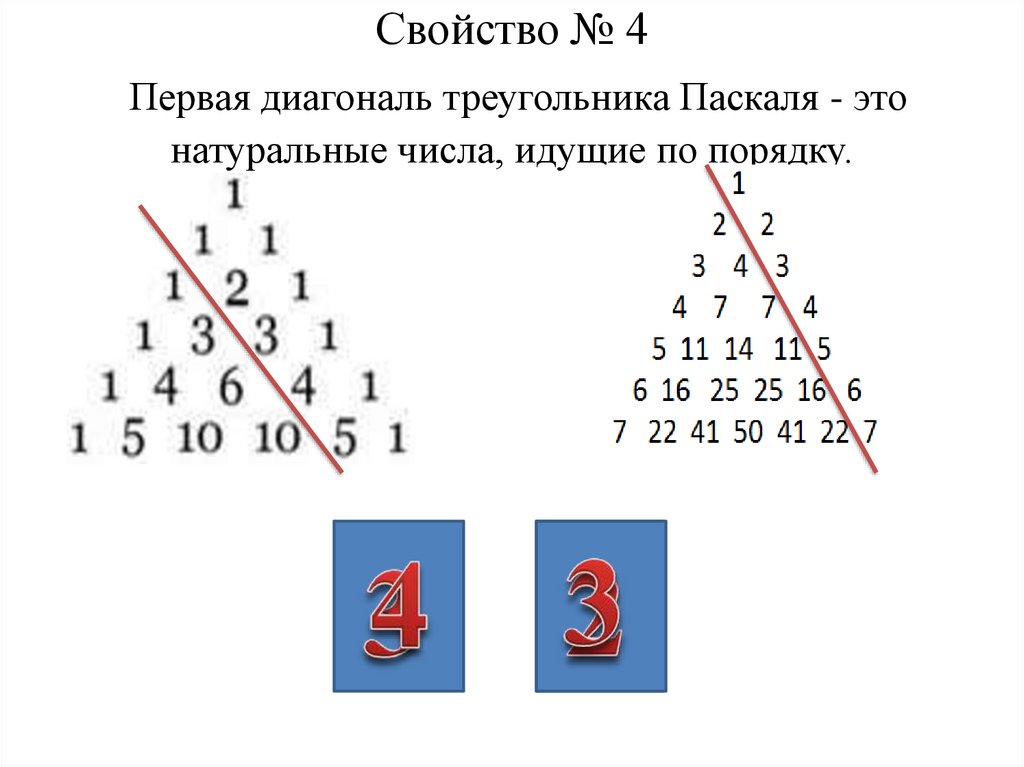
Последовательность Фибоначчи
Треугольник Паскаля также тесно связан с теорией чисел. Наиболее очевидная связь — с последовательностью Фибоначчи. Складывание чисел треугольника Паскаля по некоторой диагонали дает числа последовательности.
Суммы вдоль определенной диагонали треугольника Паскаля дают последовательность Фибоначчи. (Изображение предоставлено Робертом Дж. Кулманом)Фракталы
Раскрашивание чисел треугольника Паскаля в соответствии с их делимостью дает интересное разнообразие фракталов. В частности, раскраска всех чисел, делящихся на два (все четные числа), дает треугольник Серпинского. По данным Wolfram MathWorld, эти узоры появились в итальянском искусстве с 13 века.
Для треугольника Паскаля раскраска чисел, делящихся на определенное количество, дает фрактал. Подобно треугольнику Паскаля, эти закономерности продолжаются до бесконечности. (Изображение предоставлено Робертом Дж. Кулманом)Дополнительные ресурсы
Дополнительную информацию о треугольнике Паскаля см.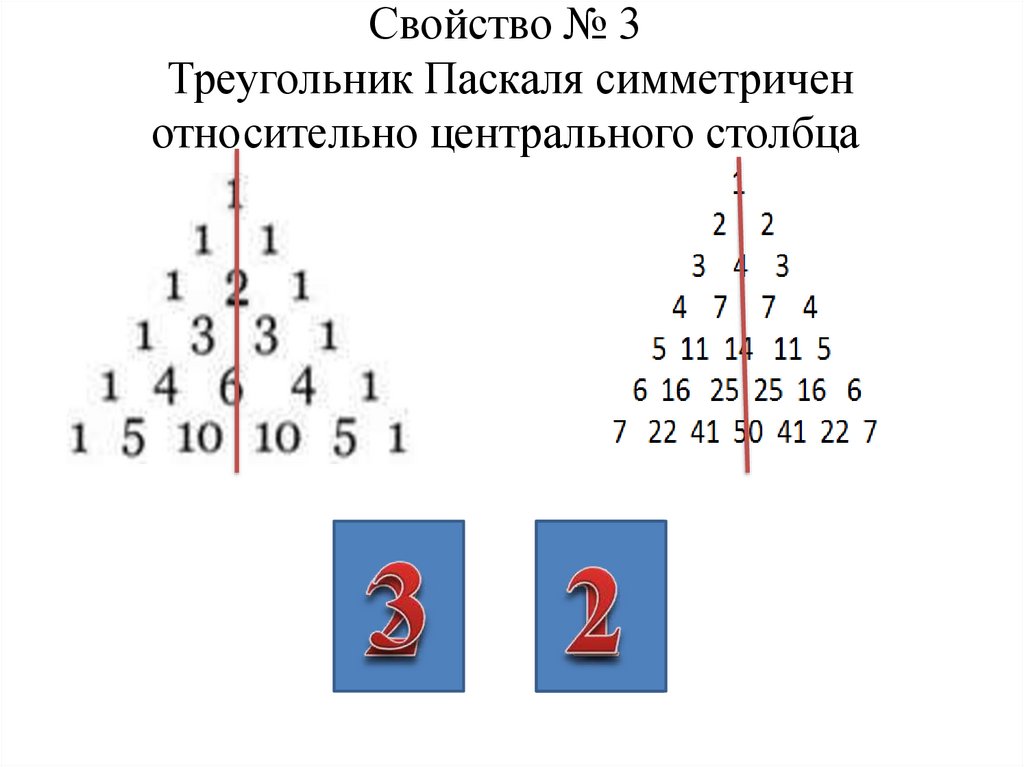

 Утверждение справедливо как для диагонали правой стороны, так и левой стороны. Чтобы доказать это, достаточно обратиться к свойству симметричности строк;
Утверждение справедливо как для диагонали правой стороны, так и левой стороны. Чтобы доказать это, достаточно обратиться к свойству симметричности строк; После диагонали идет диагональ тетраэдральных чисел и так далее. Треугольные числа показывают, какое количество шаров одинакового диаметра нужно, чтобы построить равносторонний треугольник, тетраэдральные — количество шаров для построения правильного тетраэдра.
После диагонали идет диагональ тетраэдральных чисел и так далее. Треугольные числа показывают, какое количество шаров одинакового диаметра нужно, чтобы построить равносторонний треугольник, тетраэдральные — количество шаров для построения правильного тетраэдра.
 д. Это потому что каждый элемент в строке производит два элемента в следующем ряду: один слева и один справа. Сумма элементов строки n равна 2 n.
д. Это потому что каждый элемент в строке производит два элемента в следующем ряду: один слева и один справа. Сумма элементов строки n равна 2 n.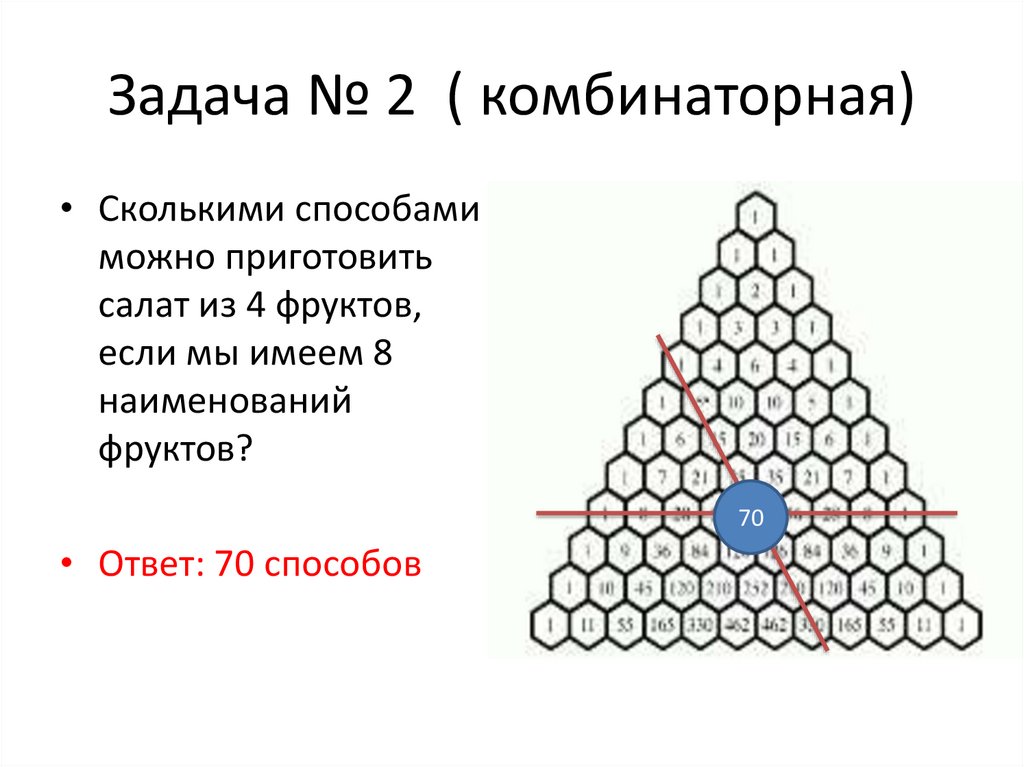


 Это также рекурсия треугольника Серпинского .
Это также рекурсия треугольника Серпинского .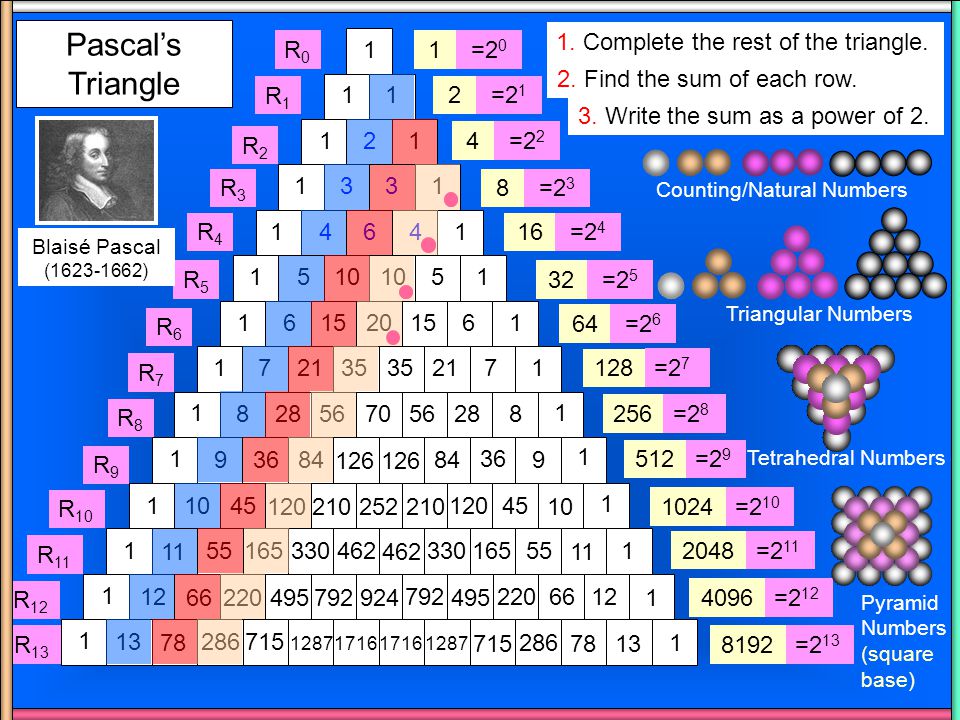 Оператор «!» называется факториалом, что означает умножение всех меньших целых чисел на единицу (например, 5! = 5 × 4 × 3 × 2 × 1). Выражение для 5P3 упрощается до 5!/2! = 5 × 4 × 3 = 60
Оператор «!» называется факториалом, что означает умножение всех меньших целых чисел на единицу (например, 5! = 5 × 4 × 3 × 2 × 1). Выражение для 5P3 упрощается до 5!/2! = 5 × 4 × 3 = 60