Треугольник плюс треугольник равно: Круг плюс квадрат равно 5 Квадрат плюс треугольник равно 5 Квадрат плюс квадрат равно 6…

Задача на смекалку про квадрат, круг и треугольник

У моей подруги сын учится в начальной школе. Бывает, вечером отдыхаешь, ничего не подозревая, а тут звонит возмущенная подруга. «Нет, ну ты послушай, какие задания они детям дают!» И дальше следует длинная тирада о том, что учебники для детей кто-то разрабатывает в пьяном угаре и тому подобное. Иногда я действительно соглашаюсь с этим. Но недавно подруга позвонила с очередным заданием. Это была довольно интересная задача на смекалку. Поэтому хочу поделиться и с тобой. Сможешь ли ты справиться с заданием, которое дают детям в начальной школе? Вот и проверим.

© Depositphotos

Задача на смекалку

Подруга сразу обсудила задачу в родительском чате. Многие, как и она, были возмущены. Они посчитали, что детям явно такое не под силу. Оказалось, что и некоторым взрослым тоже. Итак, давай уже перейдем ближе к делу. Посмотри на картинку в самом верху. У нас есть три геометрические фигуры: круг, треугольник и квадрат. Они якобы имеют вес, который дан во всяких вариациях. Круг и квадрат весят 10 кг, круг и треугольник — 20 кг, а треугольник и квадрат — 24 кг.

© Depositphotos

Задача состоит в том, чтобы выяснить, сколько же вместе весят круг, квадрат и треугольник. Подумай хорошенько. Решить задание можно даже в уме, но можно и упростить себе задачу и провести нехитрые подсчеты на листике. Правильный ответ раскрою в конце статьи. Листай дальше, если хочешь себя проверить.

© Depositphotos

Спешу сообщить также, что мы в редакции регулярно ищем для тебя что-то интересненькое, что помогает держать мозг в тонусе. Все эти задания, головоломки, тесты и прочее собраны в рубрике «Прокачай мозг». Делись с друзьями ссылкой — и вы сможете устраивать самые настоящие битвы умов.

© Depositphotos

Правильный ответ на задачу

Круг, треугольник и квадрат вместе весят 27 кг. Как же получить это значение? Как я уже говорила, можно быстренько прикинуть всё в уме, предполагая разные варианты числовых значений фигур.

Но всё же гораздо быстрее будет подойти к решению с рациональной стороны.

© Depositphotos

Итак, сложим все фигуры вместе — 10 + 20 + 24 = 54. У нас есть 2 круга, 2 квадрата и 2 треугольника: 2 (круг + квадрат + треугольник) = 54. Чтобы узнать сумму в скобках, делим 54 на 2. Получаем 27. Всё, оказывается, было очень просто.

© Depositphotos

А ты справился с заданием? Каким способом решал? Делись с нами в комментариях.

Поделиться

Екатерина Кукиб

Редактор, который не пишет статьи, а просто общается с читателем как с хорошим другом. Главные ориентиры в жизни — свобода и безбарьерность. Катя любит людей и их истории, которые собирает для своей собственной, чтобы потом рассказать ее миру. Любимая книга — «Искусство любить» Эриха Фромма.

Элементарная математика

Сканави М. И. Элементарная математика. 2-е изд., перераб. и доп., М.: 1974г. — 592с. Книга представляет собой повторительный курс элементарной математики и рассчитана на тех, кто хочет пополнить, укрепить и систематизировать свои знания. Как и в первом издании, содержание ориентировано на программы вступительных экзаменов в технические вузы и, в особенности, на программы подготовительных отделений при высших учебных заведениях, для учащихся которых, как мы надеемся, книга окажется полезной. (Книга включает в себя Ч1 — Арифметика, алгебра и элементарные функции и Ч2 — Геометрия. Каждый раздел включает в себя теоретическую часть и большое количество задач с решениями.) Оглавление ВВЕДЕНИЕ Часть первая. АРИФМЕТИКА, АЛГЕБРА И ЭЛЕМЕНТАРНЫЕ ФУНКЦИИ Глава I. ДЕЙСТВИТЕЛЬНЫЕ И КОМПЛЕКСНЫЕ ЧИСЛА 2. Простые и составные числа. Признаки делимости. 3. Наибольший общий делитель и наименьшее общее кратное. 4. Целые числа. Рациональные числа. 5. Десятичные дроби. Представление рациональных чисел десятичными дробями. 6. Иррациональные числа. Действительные числа. 7. Действия с приближенными числами. 8. Числовая ось. Координаты точки на плоскости. § 2. Степени и корни 9. Степени с натуральными показателями. 10. Степени с целыми показателями. 11. Корни. 12. Степени с рациональными показателями. Степени с действительными показателями. 13. Алгоритм извлечения квадратного корня. § 3. Комплексные числа 14. Основные понятия и определения. 15. Рациональные действия с комплексными числами. 16. Геометрическое изображение комплексных чисел. Тригонометрическая форма комплексного числа. 17. Действия с комплексными числами, заданными в тригонометрической форме. Формула Муавра. 18. Извлечение корня из комплексного числа. Глава II. ТОЖДЕСТВЕННЫЕ ПРЕОБРАЗОВАНИЯ 19. Алгебраические выражения. Одночлены и многочлены. 20. Формулы сокращенного умножения. n. 41. Обратная пропорциональная зависимость. Степенная функция с рациональным показателем степени. 42. Показательная функция. 43. Логарифмическая функция. § 3. Преобразование графиков 44. Параллельный сдвиг графика. 45. График квадратного трех члена. 46. График дробно-линейной функции. 47. Преобразование симметрии. Сжатие и растяжение графика. 48. Построение графиков функций. 49. Сложение графиков. § 4. Некоторые сведения о рациональных функциях 50. Целые и дробные рациональные функции. Деление многочленов. 51. Схема Горнера. Теорема Безу. 52. Нули многочлена. Разложение многочлена на множители. Глава V. УРАВНЕНИЯ 53. Уравнение. Корни уравнения. 54. Равносильные уравнения. 55. Системы уравнений. 56. Графическое решение уравнений. §. 2. Алгебраические уравнения с одной неизвестной 57. Число и кратность корней. 58. Уравнения первой степени (линейные уравнения). 59. Уравнения второй степени (квадратные уравнения). 60. Формулы Виета. Разложение квадратного трехчлена на множители. 61. Исследование квадратного уравнения. 62. Уравнения высших степеней. Целые корни. 63. Двучленные уравнения. 64. Уравнения, сводящиеся к квадратным. 65. Возвратные уравнения. § 3. Системы алгебраических уравнений 66. Линейные системы. 67. Определители второго порядка. Исследование линейных систем двух уравнений с двумя неизвестными. 68. Системы, состоящие из уравнения второй степени и линейного уравнения. 69. Примеры систем двух уравнений второй степени. Системы уравнений высших степеней. § 4. Иррациональные, показательные и логарифмические уравнения 70. Иррациональные уравнения. 71. Показательные уравнения. 72. Логарифмические уравнения. 73. Разные уравнения. Системы уравнений. Глава VI. НЕРАВЕНСТВА 74. Свойства неравенств. Действия над неравенствами. 75. Алгебраические неравенства. § 2. Решение неравенств 76. Множество решений неравенства. Равносильные неравенства. 77. Графическое решение неравенств. 79. Квадратные неравенства. 80. Неравенства высших степеней. Неравенства, содержащие дробные рациональные функции от х. 81. Иррациональные, показательные и логарифмические неравенства. 82. Неравенства с двумя неизвестными. Глава VII. ПОСЛЕДОВАТЕЛЬНОСТИ 83. Числовая последовательность. 84. Предел числовой последовательности. 85. Бесконечно малые. Правила предельного перехода. § 2. Арифметическая прогрессия 86. Арифметическая прогрессия. Формула общего члена. 87. Свойства арифметической прогрессии. 88. Формула для суммы n членов арифметической прогрессии. § 3. Геометрическая прогрессия 89. Геометрическая прогрессия. Формула общего члена. 90. Свойства геометрической прогрессии. 91. Формулы для суммы n членов геометрической прогрессии. 92. Бесконечно убывающая геометрическая прогрессия. Глава VIII. ТРИГОНОМЕТРИЧЕСКИЕ ФУНКЦИИ УГЛА (ДУГИ) 93. Вектор, проекция вектора. 94. Положительные углы и дуги, меньшие 360°. 95. Углы и дуги, большие 360°. 96. Отрицательные углы. Сложение и вычитание углов. § 2. Тригонометрические функции произвольного угла 97. Определение основных тригонометрических функций. 98. Изменение основных тригонометрических функций при изменении угла от 0 до 2pi. § 3. Соотношения между тригонометрическими функциями одного и того же угла 99. Основные тригонометрические тождества. 100. Вычисление значений тригонометрических функций по значению одной из них. 101. Значения тригонометрических функций некоторых углов. § 4. Четность, нечетность и периодичность тригонометрических функций 102. Четность и нечетность. 103. Понятие периодической функции. 104. Периодичность тригонометрических функций. § 5. Формулы приведения 105. Зависимость между тригонометрическими функциями дополнительных углов. 106. Формулы приведения. Глава IX. ТРИГОНОМЕТРИЧЕСКИЕ ФУНКЦИИ ЧИСЛОВОГО АРГУМЕНТА И ИХ ГРАФИКИ § 1. Тригонометрические функции числового аргумента 108. Области определения и области изменения значений тригонометрических функций. 109. Некоторые неравенства и их следствия. § 2. Графики тригонометрических функций 110. Первоначальные сведения о таблицах тригонометрических функций. 111. Основные графики. 112. Примеры построения графиков некоторых других тригонометрических функций. 113. Дальнейшие примеры построения графиков функций. Глава X. ПРЕОБРАЗОВАНИЕ ТРИГОНОМЕТРИЧЕСКИХ ВЫРАЖЕНИЙ 114. Расстояние между двумя точками на плоскости. 115. Косинус суммы и разности двух аргументов. 116. Синус суммы и разности двух аргументов. 117. Тангенс суммы и разности двух аргументов. 118. О формулах сложения для нескольких аргументов. § 2. Формулы для двойного и половинного аргумента. Выражение sin na и cos na через степени sin a и cos a 119. Тригонометрические функции двойного аргумента. 120. Выражение sin na и cos na через степени sin a и cos a при натуральном числе n. 121. Тригонометрические функции половинного аргумента. 122. Выражение основных тригонометрических функций аргумента а через tg(a/2). § 3. Преобразование в сумму выражений вида sina•cosb, cosa•cosb и sinа•sinb § 4. Преобразование в произведение сумм вида § 5. Преобразование некоторых выражений в произведения с помощью введения вспомогательного аргумента 127. Преобразование в произведение выражения a•sina + b•cosa. 128. Преобразование в произведение выражений a•sina+b и a•cosa+b 129. Преобразование в произведение выражения a•tga+b. Глава XI. ОБРАТНЫЕ ТРИГОНОМЕТРИЧЕСКИЕ ФУНКЦИИ И ИХ ГРАФИКИ 130. Функция у = arcsin x (арксинус). 131. Функция y = arccos x (арккосинус). 132. Функция y = arctg x (арктангенс). 133. Функция y = arcctg x (арккотангенс). 134. Пример. § 2. Операции над обратными тригонометрическими функциями 135. Тригонометрические операции. 136. Операции сложения (вычитания). § 3. Обратные тригонометрические операции над тригонометрическими функциями 137. Функция у = arcsin (sin x). 138. Функция y = arctg (tg x). Глава XII. ТРИГОНОМЕТРИЧЕСКИЕ УРАВНЕНИЯ И НЕРАВЕНСТВА 139. Уравнение sin х = а. 140. Уравнение cos х = a. 141. Уравнение tg x = a. 142. Уравнение ctg x = a. 143. Некоторые дополнения. § 2. Способ приведения к одной функции одного и того же аргумента 145. Некоторые типы уравнений, приводящихся к уравнениям относительно функции одного аргумента. 146. Способ разложения на множители. 147. Решение рациональных тригонометрических уравнений с помощью универсальной тригонометрической подстановки tg(x/2) = t. § 3. Некоторые частные приемы решения тригонометрических уравнений и систем 148. Введение вспомогательного аргумента. 149. Преобразование произведения в сумму или разность. 150. Переход к функциям удвоенного аргумента. 151. Решение уравнения типа… 152. Применение подстановок sinx ± соsx = y. § 4. Решение тригонометрических неравенств 154. Простейшие тригонометрические неравенства. 155. Примеры тригонометрических неравенств, сводящихся к простейшим. Часть вторая. ГЕОМЕТРИЯ 156. Точка. Прямая. Луч. Отрезок. 157. Плоскость. Фигуры и тела. 160. Равенство фигур. Движение. 161. Равенство тел. § 2. Измерение геометрических величин 162. Сложение отрезков. Длина отрезка. 163. Общая мера двух отрезков. 164. Сравнительная длина отрезков и ломаных. 165. Измерение углов. 166. Радианная мера угла. 167. Измерение площадей. 168. Площадь прямоугольника. Объем прямоугольного параллелепипеда. Глава XIV. ПЕРПЕНДИКУЛЯРНЫЕ И ПАРАЛЛЕЛЬНЫЕ ПРЯМЫЕ. ЗАДАЧИ НА ПОСТРОЕНИЕ 169. Перпендикуляр и наклонные. 170. Свойство перпендикуляра, проведенного к отрезку в его середине. 171. Параллельные прямые. 172. Углы, образованные двумя параллельными прямыми и секущей. 173. Углы с параллельными или перпендикулярными сторонами. § 2. Геометрические места точек. Окружность 174. Геометрическое место точек. 175. Свойство биссектрисы угла. 176. Окружность. 177. Взаимное расположение прямой и окружности. Касательная и секущая. 178. Хорда и диаметр. Сектор и сегмент. 179. Взаимное расположение двух окружностей. § 3. Основные задачи на построение 181. Деление отрезка пополам. Построение перпендикуляров. 182. Построение углов. 183. Другие задачи на построение. Глава XV. ТРЕУГОЛЬНИКИ, ЧЕТЫРЕХУГОЛЬНИКИ 184. Стороны и углы треугольника. 185. Биссектрисы треугольника. Вписанная окружность. 186. Оси симметрии сторон треугольника. Описанная окружность. 187. Медианы и выcоты треугольника. 188. Равенство треугольников. 189. Построение треугольников. 190. Равнобедренные треугольники. 191. Прямоугольные треугольники. § 2. Параллелограммы 192. Четырехугольники. 193. Параллелограмм и его свойства. 194. Прямоугольник. § 3. Трапеция 196. Трапеция. 197. Средняя линия треугольника. 198. Средняя линия трапеции. 199. Деление отрезка на равные части. § 4. Площади треугольников и четырехугольников 200. Площадь параллелограмма. 201. Площадь треугольника. 202. Площадь трапеции. Глава XVI. ПОДОБИЕ ГЕОМЕТРИЧЕСКИХ ФИГУР 203. Пропорциональные отрезки. 204. Свойства биссектрис внутреннего и внешнего углов треугольника. § 2. Подобное преобразование фигур (гомотетия) 205. Определение гомотетичных фигур. 206. Свойства преобразования подобия. § 3. Общее подобное соответствие фигур 207. Подобные фигуры. 208. Периметры и площади подобных треугольников. 209. Применение подобия к решению задач на построение. Глава XVII. МЕТРИЧЕСКИЕ СООТНОШЕНИЯ В ТРЕУГОЛЬНИКЕ И КРУГЕ 210. Углы с вершиной на окружности. 211. Углы с вершиной внутри и вне круга. 212. Угол, под которым виден данный отрезок. 213. Четырехугольники, вписанные в окружность. 214. Пропорциональные отрезки в круге. 215. Задачи на построение. § 2. Метрические соотношения в треугольнике 216. Пропорциональные отрезки в прямоугольном треугольнике. Теорема Пифагора. 218. Теорема синусов. Формула Герона. 217. Квадрат стороны, лежащей против острого или тупого утла и треугольнике. Теорема косинусов. 218. Теорема синусов. Формула Герона. 219. Радиусы вписанной и описанной окружностей. § 3. Решение треугольников 220. Таблицы функций. 221. Решение треугольников. Сводка основных формул. 222. Решение прямоугольных треугольников. 223. Решение косоугольных треугольников. Глава XVIII. ПРАВИЛЬНЫЕ МНОГОУГОЛЬНИКИ. ДЛИНА окружности И ПЛОЩАДЬ КРУГА 224. Выпуклые многоугольники. 225. Правильные многоугольники. 226. Соотношения между стороной, радиусом и апофемой. 227. Периметр и площадь правильного n-угольника. 228. Удвоение числа сторон правильного многоугольника. § 2. Длина окружности. Площадь круга и его частей 229. Длина окружности. 230. Площадь круга и его частей. Глава XIX. ПРЯМЫЕ И ПЛОСКОСТИ В ПРОСТРАНСТВЕ 231. Взаимное расположение двух прямых в пространстве. 232. Взаимное расположение прямой линии и плоскости. 233. Взаимное расположение двух плоскостей. 234. Свойства параллельных прямых и плоскостей. 235. Построения в стереометрии. § 2. Перпендикулярность прямых и плоскостей 236. Перпендикуляр к плоскости. 237. Перпендикуляр и наклонные. 238. Угол между прямой и плоскостью. 239. Связь между перпендикулярностью и параллельностью прямых и плоскостей. 240. Общий перпендикуляр двух скрещивающихся прямых. § 3. Двугранные и многогранные углы 241. Двугранный угол. 242. Взаимно перпендикулярные плоскости. 243. Трехгранные углы. 244. Многогранные углы. § 4. Многогранники 245. Многогранники. 246. Правильные многогранники. Глава XX. МНОГОГРАННИКИ И КРУГЛЫЕ ТЕЛА 247. Цилиндры и призмы. 248. Параллелепипеды. 249. Объемы призм и цилиндров. 250. Площадь боковой поверхности призмы. 251. Площадь поверхности цилиндра. § 2. Пирамида. Конус 252. Свойства пирамиды и конуса. 253. Объем пирамиды и конуса. 254. Площадь боковой поверхности правильной пирамиды и конуса. 255. Усеченный конус и усеченная пирамида. § 3. Шаровая поверхность. Шар 256. Шар и шаровая поверхность. 257. Объем шара и его частей. 258. Площадь поверхности шара и ее частей. 259. Понятие телесного угла. Ответы к упражнениям Приложения

Круг Треугольник Квадрат Уравнение Загадка

Сложность Популярность

Сможете ли вы решить приведенную ниже головоломку, найдя значение треугольника?

Посмотреть ответ Отправить ответы

категория : МАТЕМАТИКА | УРАВНЕНИЕ

Предложения

Сложность Популярность

Перед выходом на работу инспектор Монтальбано подрался с женой. Вернувшись с работы, он обнаружил, что в доме находится полиция, а его жена только что убила грабителя.
Полиция сообщила, что она убила грабителя в целях самообороны. Она рассказала мужу историю о том, что услышала звонок в дверь и подумала, что это я, и как только она открыла дверь, грабитель прыгнул в нее, и она так испугалась, что сразу же убила грабителя ножом. Инспектор Монтальбано попросил полицию арестовать ее жену за заговор с целью убийства. Почему?

Посмотреть ответ Обсудить

категория : ЛОГИКА | ТАЙНА

Сложность Популярность

Старик в деревне чувствует, что его конец близок. Он звонит своим двум сыновьям, чтобы обсудить землю, которой он владеет, и другую собственность. Он велит им устроить скачки на лошадях до границы города. Тот, у кого медленнее лошадь, получит все имущество.

Оба они бродят туда-сюда безрезультатно, так как никто не заправляется, чтобы добраться до границы. Затем они посещают мудреца деревни и просят у него совета. Мудрецы говорят им что-то, слушая, что они вскакивают на лошадей и мчатся так быстро, как только могут, до границы города.

Что сказал им мудрец?

Посмотреть ответ Обсудить

категория : ЛОГИКА

Сложность Популярность

Стойка для носков Prinka содержит 11 розовых носков, 12 красных носков, 13 оранжевых носков, 14 белых носков и 15 коричневых носков.
сколько носков она должна вытащить в темноте, чтобы быть уверенной, что она найдет подходящую пару?

Посмотреть ответ Обсудить

категория : ЛОГИКА

Сложность Популярность

Перед вами два стакана. Один из стаканов полон кока-колы, а другой стакан полон лимонада. Вы берете ложку колы и смешиваете ее со стаканом лимонада. Теперь в стакане для лимонада есть смесь колы и лимонада. Вы берете ложку этой смеси и смешиваете ее в стакане кока-колы.

Что вы думаете? — В стакане с колой больше лимонада или в стакане с лимонадом больше кока-колы?

Посмотреть ответ Обсудить

категория : ЛОГИКА | ПУТЕШЕСТВИЯ | ГРАЖДАНСКАЯ СЛУЖБА

Сложность Популярность

Мы самые популярные охотники мира.
Мы боремся с адом.
Убиваем криминальных вампиров.
Убиваем демонов.
Мы всегда делаем это вместе, потому что мы братья.

Кто мы?

Посмотреть ответ Обсудить

Сложность Популярность

На данной картинке вы можете найти несколько чисел. Теперь вам нужно заполнить каждый квадрат сетки таким образом, чтобы каждая строка и каждый столбец содержали цифры от 1 до 6. Еще одна вещь, о которой следует помнить, это то, что в соединенных квадратах должно быть одно и то же число.

Принимаете ли вы сложную задачу?

Посмотреть ответ Обсудить

категория : ЛОГИКА | КАРТИНА

Сложность Популярность

Адам — ​​один из финалистов чемпионата IQ. В качестве финального испытания ему выдаются два песочных часа. Один из них может измерять одиннадцать минут, а другой — тринадцать минут.
Его просят отмерить ровно пятнадцать минут с помощью этих двух песочных часов. Как он это сделает?

Посмотреть ответ Обсудить

категория : ЛОГИКА | МЕРА

Сложность Популярность

Время 12:21 является палиндромом, поскольку оно одинаково читается как вперед, так и назад.
Что такое Самый короткий интервал между двумя временами-палиндромами?

пример => 11:11 и 12:21 имеют интервал 1 час 10 минут.

Посмотреть ответ Обсудить

категория : ЛОГИКА

Сложность Популярность

Завершить пирамиду моей замены? с правильным номером.
1
1 1
2 1
1 2 1 1
1 1 1 2 2 1
? ? ? ? ? ?
? ? ? ? ? ? ? ?

Посмотреть ответ Обсудить

категория : ЛОГИКА | РЯД

Сложность Популярность

На гоночной трассе три машины. Трасса сделана в форме идеального круга и достаточно широка, чтобы по ней одновременно могли проехать несколько автомобилей. Автомобиль, который лидирует, едет со скоростью 55 миль в час, а самый медленный автомобиль едет со скоростью 45 миль в час. Автомобиль, который находится посередине этих двух скоростей, едет между ними. На данный момент можно сказать, что расстояние между самым быстрым автомобилем и средним автомобилем равно x миль, и такое же расстояние между средним автомобилем и самым медленным автомобилем. Кроме того, x не равен 0 или 1.

Машина продолжает движение до тех пор, пока первая машина не догонит самую медленную машину, после чего все машины останавливаются. В данном случае, думаете ли вы, что в какой-то момент расстояние между любыми двумя парами снова станет x миль?

Посмотреть ответ Обсудить

категория : ЛОГИКА | ОБМАНЫВАТЬ | МАТЕМАТИКА

Теги

• ЛОГИКА
• МАТЕМАТИКА
• ЮМОР
• ТАЙНА
• РЯД
• ЗАГАДКА
• ШИФРОВЫЙ
• ГРАЖДАНСКАЯ СЛУЖБА
• ОБМАНЫВАТЬ
• ВРЕМЯ И РАССТОЯНИЕ
• ИСТОРИЯ
• УРАВНЕНИЕ
• ВЕРОЯТНОСТЬ
• ЧТО Я
• КАРТИНА
• НАУКА
• ПУТЕШЕСТВИЯ
• РЕБУС
• АКБАР И БИРБАЛ
• МЕРА
• КВАДРАТНЫЙ СЧЕТ
• СЧЕТ ТРЕУГОЛЬНИКОВ
• ЗАЯВЛЕНИЯ
• спички
• НЕЧЕТНЫЙ ОДИН ИЗ
• СИТУАЦИЯ

Последние головоломки

Теорема Пифагора – формула, доказательство, примеры

Теорема Пифагора , также называемая теоремой Пифагора, объясняет взаимосвязь между тремя сторонами прямоугольного треугольника. По теореме Пифагора квадрат гипотенузы равен сумме квадратов двух других сторон треугольника. Давайте узнаем больше о теореме Пифагора, формуле теоремы Пифагора и доказательстве теоремы Пифагора вместе с примерами.

1.	Что такое Теорема Пифагора?
2.	История теоремы Пифагора
3.	Теорема Пифагора Формула
4.	Доказательство теоремы Пифагора
5.	Теорема Пифагора Треугольники
6.	Теорема Пифагора Квадраты
7.	Приложения теоремы Пифагора
8.	Часто задаваемые вопросы по теореме Пифагора

Что такое теорема Пифагора?

Теорема Пифагора утверждает, что если треугольник прямоугольный, то квадрат гипотенузы равен сумме квадратов двух других сторон. Обратите внимание на следующий треугольник ABC, в котором имеем ВС ² = АВ ² + АС ² . Здесь АВ — основание, АС — высота (высота), ВС — гипотенуза. Следует отметить, что гипотенуза является наибольшей стороной прямоугольного треугольника.

Уравнение теоремы Пифагора

Уравнение теоремы Пифагора выражается следующим образом: две другие ноги. Следовательно, любой треугольник с одним углом, равным 90 градусов дает треугольник Пифагора, и уравнение Пифагора может быть применено к треугольнику.

История теоремы Пифагора

Теорема Пифагора была введена греческим математиком Пифагором Самосским. Он был древнегреческим философом, который сформировал группу математиков, которые религиозно работали над числами и жили как монахи. Хотя эту теорему ввел Пифагор, есть свидетельства того, что она существовала и в других цивилизациях за 1000 лет до рождения Пифагора. Самые старые известные свидетельства встречаются между 20 и 16 веками до нашей эры в старовавилонский период.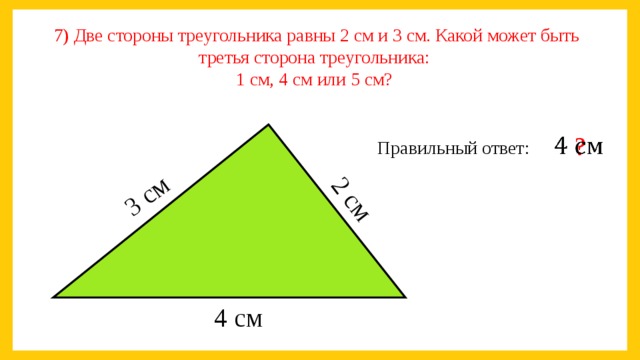

Теорема Пифагора Формула

Формула теоремы Пифагора утверждает, что в прямоугольном треугольнике ABC квадрат гипотенузы равен сумме квадратов двух других катетов. Если АВ и АС — стороны, а ВС — гипотенуза треугольника, то: ВС ² = АВ ² + АС ² ​. В этом случае АВ — основание, АС — высота или высота, а ВС — гипотенуза.

Другой способ понять формулу теоремы Пифагора — использовать следующий рисунок, который показывает, что площадь квадрата, образованного самой длинной стороной прямоугольного треугольника (гипотенузой), равна сумме площадей квадратов, образованных две другие стороны прямоугольного треугольника.

В прямоугольном треугольнике формула теоремы Пифагора выражается как: треугольник

‘a’ и ‘b’ — две другие ноги.

Доказательство теоремы Пифагора

Теорему Пифагора можно доказать разными способами. Одними из наиболее распространенных и широко используемых методов являются алгебраический метод и метод подобных треугольников. Давайте посмотрим на оба этих метода по отдельности, чтобы понять доказательство этой теоремы.

Доказательство теоремы Пифагора Формула с использованием алгебраического метода

Доказательство теоремы Пифагора может быть получено с использованием алгебраического метода. Например, давайте использовать значения a, b и c, как показано на следующем рисунке, и выполнить шаги, указанные ниже:

• Шаг 1: Этот метод также известен как «доказательство перестановкой». Возьмем 4 конгруэнтных прямоугольных треугольника со сторонами «а» и «b» и гипотенузой «с». Расположите их так, чтобы гипотенузы всех треугольников образовывали наклонный квадрат. Видно, что в квадрате PQRS длина сторон равна «a + b». Четыре прямоугольных треугольника имеют основание «b», высоту «a» и гипотенузу «c».
• Шаг 2: 4 треугольника образуют внутренний квадрат WXYZ, как показано, с четырьмя сторонами «с».
• Шаг 3: Площадь квадрата WXYZ при расположении четырех треугольников равна c ² .
• Шаг 4: Площадь квадрата PQRS со стороной (a + b) = площадь 4 треугольников + площадь квадрата WXYZ со стороной «c». Это означает (a + b) ² = [4 × 1/2 × (a × b)] + c ² . Это приводит к a ² + b ² + 2ab = 2ab + c ² . Следовательно, a ² + b ² = c ² . Таким образом, формула теоремы Пифагора доказана.

Формула теоремы Пифагора Доказательство с использованием подобных треугольников

Два треугольника называются подобными, если их соответствующие углы имеют одинаковую меру и их соответствующие стороны находятся в одном и том же отношении. Кроме того, если углы имеют одинаковую меру, то, используя закон синусов, мы можем сказать, что соответствующие стороны также будут в том же отношении. Следовательно, соответствующие углы в подобных треугольниках приводят нас к равным отношениям длин сторон.

Формула вывода теоремы Пифагора

Рассмотрим прямоугольный треугольник ABC с прямым углом в точке B. Проведите перпендикуляр BD, пересекающий AC в точке D. А (общий)

∠ADB = ∠ABC (оба угла прямые)

Таким образом, △ABD ∼ △ACB (по критерию подобия AA)

Аналогично можно доказать △BCD ∼ △ACB.

Таким образом, △ABD ∼ △ACB, Следовательно, AD/AB = AB/AC. Мы можем сказать, что AD × AC = AB ² .

Аналогично, △BCD ∼ △ACB. Следовательно, CD/BC = BC/AC. Мы также можем сказать, что CD × AC = BC ² .

Сложив эти 2 уравнения, мы получим AB ² + BC ² = (AD × AC) + (CD × AC)

AB ² + BC ² =AC(AD +DC)

3

3

3

AB ² + BC ² = AC ²

Отсюда доказано.

Теорема Пифагора Треугольники

Прямоугольные треугольники подчиняются правилу теоремы Пифагора и называются треугольниками по теореме Пифагора. Три стороны такого треугольника в совокупности называются тройками Пифагора. Все треугольники по теореме Пифагора следуют теореме Пифагора, которая гласит, что квадрат гипотенузы равен сумме двух сторон прямоугольного треугольника. Это можно выразить как c ² = а ² + б ² ; где «с» — гипотенуза, а «а» и «b» — катеты треугольника.

Теорема Пифагора Квадраты

Согласно теореме Пифагора, площадь квадрата, построенного на гипотенузе прямоугольного треугольника, равна сумме площадей квадратов, построенных на двух других сторонах. Эти квадраты известны как квадраты Пифагора.

приложений теоремы Пифагора

Применение теоремы Пифагора можно увидеть в нашей повседневной жизни. Вот некоторые из приложений теоремы Пифагора.

• Инженерные и строительные отрасли

Большинство архитекторов используют технику теоремы Пифагора для нахождения неизвестных размеров. Когда известна длина или ширина, очень легко вычислить диаметр конкретного сектора. Он в основном используется в двух измерениях в инженерных областях.

• Распознавание лиц в камерах наблюдения

Функция распознавания лиц в камерах безопасности использует концепцию теоремы Пифагора, то есть расстояние между камерой безопасности и местоположением человека отмечается и хорошо проецируется через объектив с использованием концепции.

• Изделия из дерева и дизайн интерьера

Концепция Пифагора применяется в дизайне интерьеров и архитектуре домов и зданий.

• Навигация

Люди, путешествующие по морю, используют эту технику, чтобы найти кратчайшее расстояние и маршрут, чтобы добраться до нужных им мест.

☛ Статьи по теме

• Формулы прямоугольного треугольника
• Теорема о катете гипотенузы
• Подобные треугольники
• Теорема Пифагора Рабочие листы

Часто задаваемые вопросы по теореме Пифагора

Что такое теорема Пифагора в математике?

Теорема Пифагора утверждает, что в прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов двух других сторон. Эта теорема может быть выражена как c ² = a ² + b ² ; где «с» — гипотенуза, а «а» и «b» — катеты треугольника. Эти треугольники также известны как треугольники теоремы Пифагора.

Что такое обратная теорема Пифагора?

Обратная теорема Пифагора: если сумма квадратов любых двух сторон треугольника равна квадрату третьей (наибольшей) стороны, то треугольник называется прямоугольным.

В чем польза формулы теоремы Пифагора?

Теорема Пифагора работает только для прямоугольных треугольников. Когда известны любые два значения, мы можем применить теорему Пифагора и вычислить неизвестные стороны треугольника. Есть и другие реальные приложения теоремы Пифагора, например, в области навигации, инженерии и архитектуры.

Какая польза от теоремы Пифагора?

Теорема Пифагора используется в различных областях. Ниже приведены некоторые из его применений.

• Архитектура, строительство и судоходство.
• Для вычисления расстояния между точками на плоскости.
• Для расчета периметра, площади поверхности, объема геометрических фигур и т. д.

Можно ли применить формулу теоремы Пифагора к любому треугольнику?

Нет, теорему Пифагора можно применить только к прямоугольному треугольнику, поскольку теорема Пифагора выражает отношение между сторонами треугольника, где квадрат двух катетов равен квадрату третьей стороны, которая является гипотенузой. .

Как вычислить теорему Пифагора?

Теорему Пифагора можно использовать для нахождения неизвестной стороны прямоугольного треугольника. Например, если два катета прямоугольного треугольника равны 4 единицам и 6 единицам, то гипотенузу (третью сторону) можно рассчитать по формуле c ² = а ² + б ² ; где «с» — гипотенуза, а «а» и «b» — два катета. Подставляя значения в формулу, c ² = a ² + b ² = c ² = 4 ² + 6 ² = 16 + 36 = √52 = 7,2 единицы.

Что такое формула теоремы Пифагора?

Формула теоремы Пифагора выражается как Гипотенуза ² = Основание ² + Высота ² . Это также пишется как c ² = а ² + б ² ; где «с» — гипотенуза, а «а» и «b» — катеты прямоугольного треугольника. Используя формулу теоремы Пифагора, можно вычислить любую неизвестную сторону прямого угла, если известны две другие стороны.

Почему важна теорема Пифагора?

Теорема Пифагора важна, потому что она помогает вычислить неизвестную сторону прямоугольного треугольника. У него есть и другие реальные приложения в области архитектуры и инженерии, навигации и так далее.

Как теорема Пифагора используется в навигации?

Теорема Пифагора широко используется в аэронавигации и судовой навигации. Теорема Пифагора дает возможность штурману корабля рассчитать расстояние до точки в океане, например, если расстояние между двумя точками задано как 600 км к северу и 800 км к западу, требуемое расстояние можно рассчитать с помощью Пифагора. теорема.

Когда используется теорема Пифагора?

Теорема Пифагора используется, когда известны любые две стороны прямоугольного треугольника и необходимо вычислить третью сторону.