Треугольник с двумя равными сторонами: Ошибка 403 — доступ запрещён

Пространство треугольников (окончание)

Алексей Панов, Дмитрий Ал. Панов, Пётр Панов
«Квантик» №3, 2021

Начало в «Квантике» № 1 и № 2, 2021.

А теперь двинемся к границам и полюсам Треугольного Мира. При этом постоянно будем следить за треугольниками, мимо которых проходим.

Равнобедренные треугольники

Особое место в Треугольном Мире занимают равнобедренные треугольники, нанизанные на его экваторы как позвонки (рис. 12).

Определение. Равнобедренный треугольник — это треугольник с двумя равными сторонами (рис. 11).

Теорема. В равнобедренном треугольнике против равных сторон лежат равные углы. Если в треугольнике два угла равны, то против них лежат равные стороны и треугольник равнобедренный.

В направлении границы

Что происходит с нарисованными на карте треугольниками по мере приближения к границе (движение вдоль первой стрелки на рисунке 12)?

Ответ очевиден: они сплющиваются и на самой границе превращаются в отрезок с отмеченной на нём точкой — в сплюснутый треугольник (рис.  13).

Для сплюснутого треугольника неравенство треугольника превращается в равенство. В нём большая сторона равна сумме двух других: a = b + c.

Углы равны, равны ли стороны?

С теоремой о равнобедренном треугольнике на границе Треугольного Мира нас ждёт сюрприз. Наверное, вы догадались, что у сплюснутого треугольника на рисунке 13 один угол (зелёный) равен 180°, а остальные два — по 0°. Но против этих двух равных нулевых углов лежат две неравные стороны b ≠ c.

Выходит, вторая часть теоремы неверна? К счастью, математики давно разработали нужную теорию — анализ бесконечно малых. На нашем маршруте мы шли мимо треугольников, у которых можно отметить свои синий и красный углы. При подходе к границе и синие, и красные углы постепенно «превращаются» в нулевые, но делают это не одинаково. Вычислив в каждом треугольнике отношение синего угла к красному, мы увидим: пока эти углы ещё не стали нулями, но уже практически «бесконечно малы», их отношение не отличить от b/c. С этой точки зрения, условно будем считать, что в сплюснутом треугольнике синий и красный углы относятся друг к другу как b/c.

Так бесконечно малые спасают теорему о равнобедренном треугольнике: нулевые углы (рис. 13) не равны друг другу с точки зрения их отношения! Они будут равными лишь для равнобедренного сплюснутого треугольника, где \( a = \frac{1}{2} \), \( b = \frac{1}{4} \), \( c = \frac{1}{4} \).

Но продолжим наш маршрут.

К полюсу вдоль границы

По мере приближения к Красному полюсу (вдоль второй стрелки) длины сторон a и b выравниваются, сторона c уменьшается, а две вершины сплюснутого треугольника (зелёная и синяя) сближаются (рис. 12). В итоге полюс предстаёт перед нами равнобедренным треугольником со сторонами \( a = \frac{1}{2} \), \( b = \frac{1}{2} \), c = 0.

Угол между a и b равен 0°. А два других угла?

Тайна красного полюса

Мы зашли в Красный полюс вдоль границы Треугольного Мира. Все треугольники, мимо которых мы проходили, были сплюснутыми и все имели углы 0°, 180° и 0°. Менялись только длины их сторон. С этой точки зрения углы полюсного сплюснутого треугольника (рис. 14) тоже должны быть 180°, 0° и 0°.

Но если входить в Красный полюс вдоль экватора, то у полюсного треугольника стороны будут те же самые \( \frac{1}{2} \), \( \frac{1}{2} \), 0, а вот углы будут 90°, 90° и 0°. Тот же треугольник с углами 90°, 90° и 0° мы получим, входя в полюс вдоль меридиана, соответствующего 90°.

И вообще, входя вдоль меридиана, отвечающего углу α°, мы увидим на полюсе треугольник со сторонами \( \frac{1}{2} \), \( \frac{1}{2} \), 0 и углами α°, 180° − α°, 0°. Значит, мы не можем приписать двум нашим углам какие-то определённые значения, а получаем на Красном полюсе целое семейство сплюснутых треугольников (рис. 15). И то же самое — на остальных полюсах.

На полюсе: стороны равны, углы нет

Итак, Красный полюс вмещает целое семейство треугольников с равными сторонами \( a = b = \frac{1}{2} \), углы против которых не равны между собой. И неверна первая часть теоремы о равнобедренном треугольнике.

В этот раз мы спасём теорему, применив другой математический трюк: превратим её в определение.

Определение. Треугольник — равнобедренный, если в нём есть две равные стороны и два равных угла, причём равные углы лежат против равных сторон, а равные стороны — против равных углов.

Замечание. Среди сплюснутых треугольников есть два типа равнобедренных — с двумя углами 0° и с двумя углами 90°. Равнобедренные треугольники второго типа расположены в полюсах Треугольного Мира.

Наше путешествие завершено, но история Треугольного Мира на этом не заканчивается.

Послесловие: треугольный мир II

Треугольный Мир возник благодаря нескольким измерениям внутри правильного треугольника.

Предлагаем вам провести новую серию измерений. Нарисуйте любой треугольник. Измерьте транспортиром его углы α, β, γ и вычислите их сумму α + β + γ. Сделайте пять экспериментов, рисуя каждый раз новый треугольник, и заполните журнал измерений. Вы получите удивительный результат! Попробуйте на его основе построить новый Треугольный Мир II.

Художник Мария Усеинова

Равнобедренный прямоугольный треугольник – площадь, длина основания, свойства

4.1

Средняя оценка: 4.1

Всего получено оценок: 74.

4.1

Средняя оценка: 4.1

Всего получено оценок: 74.

И равнобедренный, и прямоугольный треугольник достаточно привычны любому, кто знаком с геометрией. Сочетание этих признаков встречается довольно редко и плохо поддается визуальному восприятию. Не всегда можно представить полный набор свойств такого треугольника, поэтому поговорим о нем более подробно.

Материал подготовлен совместно с учителем высшей категории Харитоненко Натальей Владимировной.

Опыт работы учителем математики — более 33 лет.

Определение

Равнобедренный треугольник – это треугольник, боковые стороны которого равны. Прямоугольный треугольник содержит в себе прямой угол. Значит равнобедренный прямоугольный треугольник – это прямоугольный треугольник, катеты которого равны.

Гипотенуза прямоугольного треугольника всегда больше катета. Это следует из теоремы о соотношениях сторон и углов треугольника. Значит, в прямоугольном треугольнике только гипотенуза может быть основанием, а величина гипотенузы будет соответствовать длине основания.

Рис. 1. Равнобедренный прямоугольный треугольник

Свойства

Поговорим подробнее о свойствах и формулах. Не совсем ясно, как будут проходить высоты в таком треугольнике, все привыкли пользоваться свойством, которое говорит о том, что в равнобедренном треугольнике высота, проведенная к основанию, совпадает с медианой и биссектрисой.

В равнобедренном прямоугольном треугольнике такая высота всегда будет направлена из прямого угла к гипотенузе. А две другие высоты будут совпадать с катетами.

Рис. 2. Высота прямоугольного равнобедренного треугольника

Если к гипотенузе прямоугольного равнобедренного треугольника провести высоту, то она разделит треугольник на два, равных между собой, равнобедренных прямоугольных треугольника.

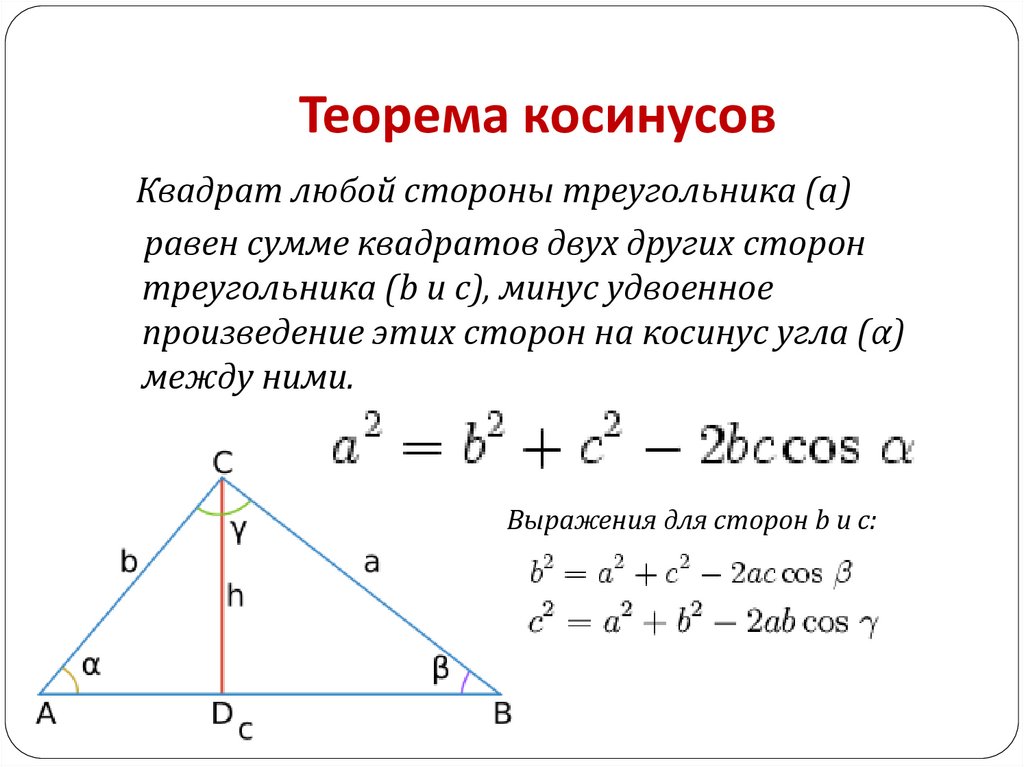
Теорема Пифагора для равнобедренного треугольника выглядит немного упрощенной:

Квадрат гипотенузы равен удвоенному квадрату катета. Это значительно упрощает решение.

Вообще, любые задачи, связанные с прямоугольными равнобедренными треугольниками, решаются очень просто. Любого значения достаточно, чтобы определить все остальное. Значения любого из катетов достаточно, чтобы определить гипотенузу через упрощенную теорему Пифагора, а затем найти периметр и площадь прямоугольного равнобедренного треугольника.

Через гипотенузу можно найти катет и через тригонометрическую функцию, так как все углы прямоугольного равнобедренного треугольника заранее известны: один угол 90 градусов и два по 45.

Рис. 3. Углы прямоугольного равнобедренного треугольника

Разберем подробно, почему известны все углы. В любом прямоугольном треугольнике сумма острых углов равна 90 градусам. Это следует из общей суммы углов в треугольнике, которая всегда равна 180 градусам.

При этом углы при основании равнобедренного треугольника, а в нашем случае это всегда гипотенуза, всегда равны.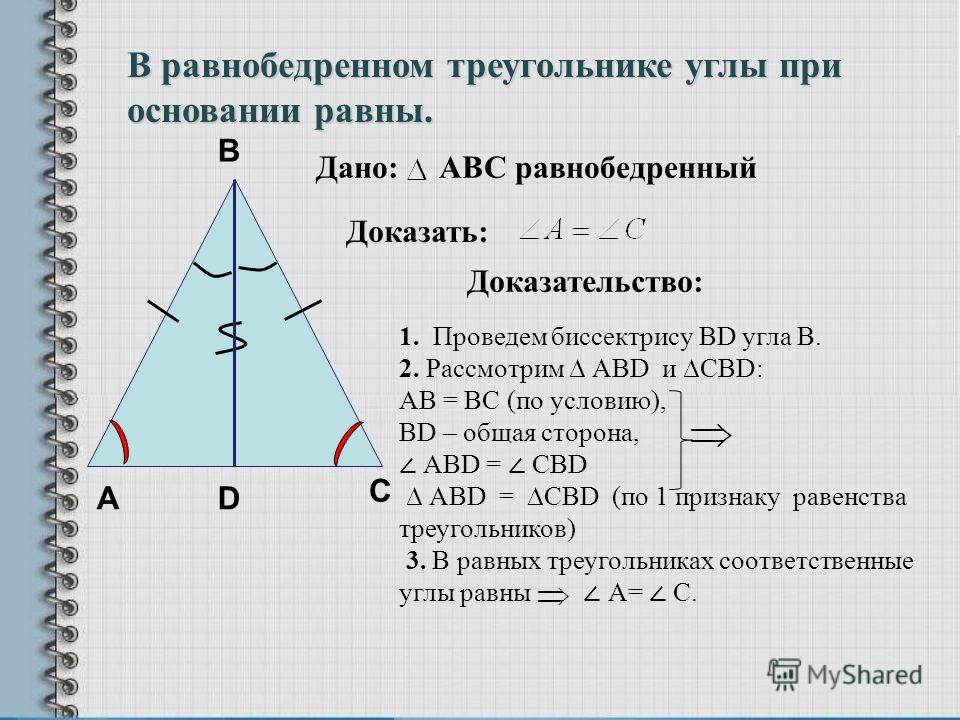

Значит, чтобы найти каждый из острых углов при гипотенузе, нужно их сумму, т.е. 90 градусов, разделить пополам. Получается, что каждый из углов при гипотенузе прямоугольного равнобедренного треугольника будет равен 45 градусам.

Можно рассмотреть это свойство и с другой стороны: если сумма двух углов треугольника равняется 90 градусам и эти углы равны между собой, то этот треугольник является равнобедренным и прямоугольным.

Из этого же свойства вытекает равенство синусов и косинусов острых углов прямоугольного равнобедренного треугольника между собой, а также равенство их тангенсов и котангенсов.

То есть, синус любого острого угла прямоугольного равнобедренного треугольника равен косинусу любого острого угла данного треугольника и равен $${\sqrt{2}\over2}$$. Тангенс любого острого угла прямоугольного равнобедренного треугольника равен котангенсу любого острого угла данного треугольника и равен 1.

Что мы узнали?

Мы подробно поговорили о всех взаимосвязях свойств прямоугольного и равнобедренного треугольника.

А также о том, как эти связи проявляются в равнобедренном прямоугольном треугольнике. Разобрали в подробностях, почему любые задачи на нахождение параметров прямоугольного равнобедренного треугольника легко решаются и выделили основную и единственную проблему в решениях таких задач: трудность визуального восприятия.

Тест по теме

Доска почёта

Чтобы попасть сюда — пройдите тест.

Пока никого нет. Будьте первым!

Оценка статьи

4.1

Средняя оценка: 4.1

Всего получено оценок: 74.

---

А какая ваша оценка?

Равнобедренный треугольник — определение, углы, свойства, примеры

Что такое равнобедренный треугольник?

Треугольник с двумя сторонами равной длины является равнобедренным треугольником.

Примеры равнобедренного треугольника:

Неравнобедренный треугольник:

Примеры равнобедренного треугольника в реальной жизни:

Многие вещи в мире имеют форму равнобедренного треугольника. Некоторые популярные примеры этих треугольников в реальной жизни:

Родственные игры

Части равнобедренного треугольника

 Части равнобедренного треугольника

1. Катеты: Две равные стороны равнобедренного треугольника называются катетами. В треугольнике ABC (данном выше) AB и AC являются двумя катетами равнобедренного треугольника.

2. Основание: Основанием равнобедренного треугольника является третья и неравная сторона. В треугольнике АВС основание равнобедренного треугольника ВС.

3. Угол при вершине: «Угол при вершине» — это угол, образованный двумя равными сторонами равнобедренного треугольника. ∠BAC — угол при вершине равнобедренного треугольника.

4. Углы при основании: «Углы при основании» — это углы, которые опираются на основание равнобедренного треугольника. ∠ABC и ∠ACB — два угла при основании равнобедренного треугольника.

Похожие рабочие листы

Свойства равнобедренного треугольника

Вот список некоторых свойств равнобедренных треугольников:

• В равнобедренном треугольнике, если две стороны равны, то углы, противоположные двум сторонам, соответствуют друг другу и также всегда равны.

В приведенном выше равнобедренном треугольнике два угла ∠B и ∠C, лежащие напротив равных сторон AB и AC, равны друг другу.

• Равнобедренный треугольник имеет три острых угла, то есть углы меньше 90°.
• Сумма трех углов равнобедренного треугольника всегда равна 180°.

Типы равнобедренных треугольников

 Как правило, равнобедренные треугольники подразделяются на три различных типа:

• Равнобедренный остроугольный треугольник: Равнобедренный остроугольный треугольник – это треугольник, в котором все три угла меньше 90°, и по крайней мере два его угла равны по измерению. Одним из примеров углов равнобедренного остроугольного треугольника являются 50 °, 50 ° и 80 °.

• Равнобедренный прямоугольный треугольник: Ниже приведен пример прямоугольного треугольника с двумя катетами (и соответствующими им углами) равной величины.

• Равнобедренный тупоугольный треугольник: Равнобедренный тупоугольный треугольник — это треугольник, в котором один из трех углов тупой (лежит между 90° и 180°), а два других острых угла равны по измерению. Один пример углов равнобедренного тупого треугольника составляет 30 °, 30 ° и 120 °.

Площадь и периметр равнобедренного треугольника

• Площадь равнобедренного треугольника находится по следующей формуле:

Площадь (A) = ½ × основание (b) × высота (h)

• Периметр равнобедренного треугольника находится по формуле:

Периметр (P) = 2a + основание (b)

Здесь «a» относится к длине равных сторон равнобедренного треугольника, а «b» относится к длине третьей неравной стороны.

Решенные примеры

Пример 1

Какова высота равнобедренного треугольника с площадью 12 кв.см и основанием 6см?

Решение:

Площадь равнобедренного треугольника = ½ x основание x высота

т.е. 12 = ½ x 6 x высота

т.е. 12 = 3 x высота

т.е. 0007

Что равен периметру равнобедренного треугольника, если равные стороны равны a см каждая, а неравная сторона равна b см?

Решение:

Периметр равнобедренного треугольника = сумма его сторон

Периметр равнобедренного треугольника = (a + a + b) см, т. е. (2a + b) см

Пример 3

Найти периметр равнобедренного треугольника, если основание равно 16 см, а равные стороны по 24 см каждая.

Решение: 

Формула периметра равнобедренного треугольника, P = 2a + b

Здесь a (стороны) = 24 см и b (основание) = 16 см

Следовательно, периметр равнобедренного треугольника P = 2(24) + 16 = 64 см.

Следовательно, периметр равен 64 см.

Игры с треугольниками

С SplashLearn есть несколько игр о треугольниках, которые дети могут попробовать. Давайте рассмотрим некоторые из них:

• Определение типов треугольников : В этой игре ваш ребенок будет определять различные типы треугольников. Они будут использовать данные атрибуты, чтобы определить правильный треугольник и изучить характеристики треугольника. Учащиеся выбирают правильный ответ из предложенных.
• Classify Triangles : Игра предлагает вашему ребенку отточить свои навыки, решая ряд задач, связанных с двумерными фигурами, чтобы определить различные типы треугольников. Учащиеся будут анализировать стороны треугольника и измерения углов и классифицировать каждую из них в соответствующей категории.

Другие игры

• Классифицируй треугольники и прямоугольники как замкнутые фигуры :   Эта игра поможет детям классифицировать различные типы фигур и поможет их запомнить. Это поможет вашему ребенку быстрее и легче распознавать различные формы.
• Сортировка фигур по имени : Это будет веселая игра, в конце которой ваш ребенок узнает все о различных формах! Игра включает в себя сортировку фигур по их именам, и таким образом ваш юный математик получит больше практики с концепциями 2D-форм. Эта игра подтолкнет вашего ребенка к мастерству, развивая при этом общие математические способности.

Ученикам также может быть сложно запомнить свойства равнобедренных треугольников. Но именно здесь вам потребуется много терпения при обучении вашего ребенка. Позвольте вашему ребенку сиять ярко с SplashLearn .

---

Практические задачи на равнобедренные треугольники

1

Какова высота равнобедренного треугольника с площадью 10 кв. см и основанием 5 см?

10 см

5 см

2 см

4 см

Правильный ответ: 4 см т. е. высота = 4 см

2

В ΔABC, если ∠A = ∠B, то

AC ≠ BC

AC = BC

AB = AC

AB = BC

Правильный ответ: AC = BC
Стороны, противоположные равным углам, также равны. ∠A = ∠B, BC противоположен ∠A, а AC противоположен углу B. Следовательно, AC = BC в ΔABC.

3

Какова площадь равнобедренного треугольника, указанного ниже?

21 см ²

45 см ²

90 см ²

180 см ²

0196 2
Площадь равнобедренного треугольника = ½ x основание x высота = ½ x 15 см x 6 см = 45 см ²

---

Часто задаваемые вопросы

Как узнать, является ли треугольник равнобедренным?

Треугольник называется равнобедренным, если две его стороны равны. Возьмем треугольник, у которого три стороны АВ, ВС и СА. Если хоть одно из этих утверждений верно — AB = BC, BC = CA или CA = AB, — то треугольник равнобедренный.

Может ли прямоугольный треугольник быть равнобедренным?

Да, прямоугольный или прямоугольный треугольник может быть равнобедренным. В равнобедренном прямоугольном треугольнике 1 прямой угол и 2 других угла равны.

Сможете ли вы найти все углы равнобедренного треугольника, если знаете один из равных углов?

Да, если мы знаем два равных угла, то мы можем легко вычесть их сумму из 180°, так как сумма всех углов треугольника равна 180°.

Какими свойствами обладает равнобедренный треугольник?

• Имеет две стороны одинаковой длины.
• Углы, противолежащие равным сторонам, также равны по размеру.

Треугольники — равносторонние, равнобедренные и разносторонние

c2ZWPA3kduw

		Треугольник имеет три стороны и три угла
		Сумма трех углов всегда равна 180°

Равносторонний, равнобедренный и разносторонний

Треугольникам даны три специальных названия, которые говорят, сколько сторон (или углов) равны.

Могут быть 3 , 2 или нет равные стороны/углы:

	Равносторонний треугольник Три равных стороны Три равных угла , всегда 60°
	Равнобедренный треугольник Две равные стороны Два равных уголка
	Разносторонний треугольник № равносторонние № равнополочные уголки

Как запомнить? В алфавитном порядке идут 3, 2, нет:

• Равносторонний : «равный» -поперечный (боковой означает сторону), поэтому у них все равные стороны
• Равнобедренный : означает «равные ноги», и у нас две ноги , верно? Также i SOS celes имеет два равных «S ides», соединенных стороной « O dd».
• Scalene : означает «нечетный» или «нечетный», поэтому нет равных сторон.

Какой угол?

Треугольники также могут иметь имена, которые говорят вам, что тип уголка внутри :

	Остроугольный треугольник Все углы меньше 90°
	Прямоугольный треугольник Имеет прямой угол (90°)
	Тупоугольный треугольник Имеет угол более 90°

Объединение имен

Иногда у треугольника может быть два имени, например:

Прямоугольный равнобедренный треугольник Имеет прямой угол (90°), а также два равных угла Угадайте, какие углы равны?

Поиграй с этим.

..

Попробуйте перетащить точки и сделать разные треугольники:

геометрия/изображения/triangle.js?mode=тип

Вы также можете поиграть с интерактивным треугольником.

Уголки

Сумма трех внутренних углов всегда составляет 180°

геометрия/изображения/triangle.js?mode=angles

Периметр

Периметр — это расстояние вокруг края треугольника: просто сложите три стороны:

геометрия/изображения/triangle.js?mode=perim

Район

 

Площадь равна половине основания, умноженному на высоту .

• «b» — расстояние по базе
• «h» — высота (измеряется под прямым углом к ​​основанию)

Площадь = ½ × ширина × высота

Формула работает для всех треугольников.

Примечание: формулу проще записать так: bh/2

Пример: Какова площадь этого треугольника?

(Примечание: 12 — это высота , а не длина левой стороны)

 

Высота = h = 12

Основание = b = 20

Площадь = ½ × b × h = ½ × 20 × 12 = 120

Основание может быть любой стороной.