Тригонометрические функции свойства: Тригонометрические функции (свойства, графики)

Содержание

Тригонометрические функции, их свойства и графики. Лекция 10-1

1. Тригонометрические функции, их свойства и графики. Периодичность тригонометрических функций. Понятие обратной функции, ее

свойства.
Учебник Мордкович А.Г.
§§ 7-9, 16, 20
ОПРЕДЕЛЕНИЕ 1. Пусть X и Y – числовые множества. Если задано правило,
по которому каждому элементу х из множества Х ставится в соответствие
единственный элемент y из множества Y, то говорят, что на множестве Х
задана функция y= f(x).
Переменную х называют независимой переменной или
аргументом, переменную у – зависимой переменной.
Множество Х, т.е. множество всех значений, которые может принимать
независимая переменная, называют областью определения функции и
обозначают D(f).
Множество Y, т.е. множество всех значений, которые может принимать
зависимая переменная, называют областью значений функции и
обозначают E(y).
D(f)
X
E(f)
x
Y
y
ОПРЕДЕЛЕНИЕ 2. Функция y = f(x) называется четной, если ее область
определения симметрична относительно 0 и для любого значения х из
области определения выполняется равенство f(- x) = f(x).

Функция y = f(x) называется нечетной, если ее область
определения симметрична относительно 0 и для любого значения х из
области определения выполняется равенство f(- x) = — f(x)
График четной функции симметричен относительно оси Оу.
График нечетной функции симметричен относительно начала координат,
т.е. относительно точки (0; 0).
Верно и обратное: если график функции симметричен относительно оси
Оу, то функция четная,
если график симметричен относительно начала координат,
то функция нечетная.
ОПРЕДЕЛЕНИЕ 3. Функция y = f(x) называется возрастающей на
промежутке Р, принадлежащим области определения функции, если
для любых значений аргумента х1 и х2 из промежутка Р, таких, что х1 < х2
выполняется неравенство f(х1) < f(х2 ).
Функция y = f(x) называется убывающей на промежутке Р,
принадлежащим области определения функции, если для любых
значений аргумента х1 и х2 из промежутка Р, таких, что х1 < х2
выполняется неравенство f(х1) > f(х2 ).

Функция y = f(x) называется неубывающей на промежутке Р,
принадлежащим области определения функции, если для любых
значений аргумента х1 и х2 из промежутка Р, таких, что х1 < х2
выполняется неравенство f(х1) ≤ f(х2 ).
Функция y = f(x) называется невозрастающей на промежутке Р,
принадлежащим области определения функции, если для любых
значений аргумента х1 и х2 из промежутка Р, таких, что х1 < х2
выполняется неравенство f(х1) ≥ f(х2 ).
Функция называется возрастающей, если она возрастает на всей
области определения. Функция называется убывающей, если она
убывает на всей области определения.
ОПРЕДЕЛЕНИЕ 4. Функция y = f(x) называется
ограниченной снизу, если существует число m, такое, что
f(x) ≥ m для всех значений аргумента х из области
определения функции.
Функция y = f(x) называется ограниченной сверху, если
существует число М, такое, что f(x) ≤ М для всех значений
аргумента х из области определения функции.

Если функция ограничена и сверху, и снизу, то ее называют
ограниченной
ОПРЕДЕЛЕНИЕ 5. Нули функции – это значения аргумента, при которых
Функция обращается в 0.
На графике это абсциссы точек пересечения с осью Ох.
Определение. Говорят, что функция у = f (x) имеет период Т,
если для любого х ϵ D(f) числа х + Т и х – Т также принадлежат
D(f) и при этом выполняется равенство
f(x – T) = f( x) = f(x + T)
Определение. Функцию, имеющую отличный от нуля период Т,
называют периодической.
Если функция имеет период Т, то любое число кратное Т
(т.е. число вида кТ, к ϵ Z) также является ее периодом.
Наименьший положительный период называют основным
периодом
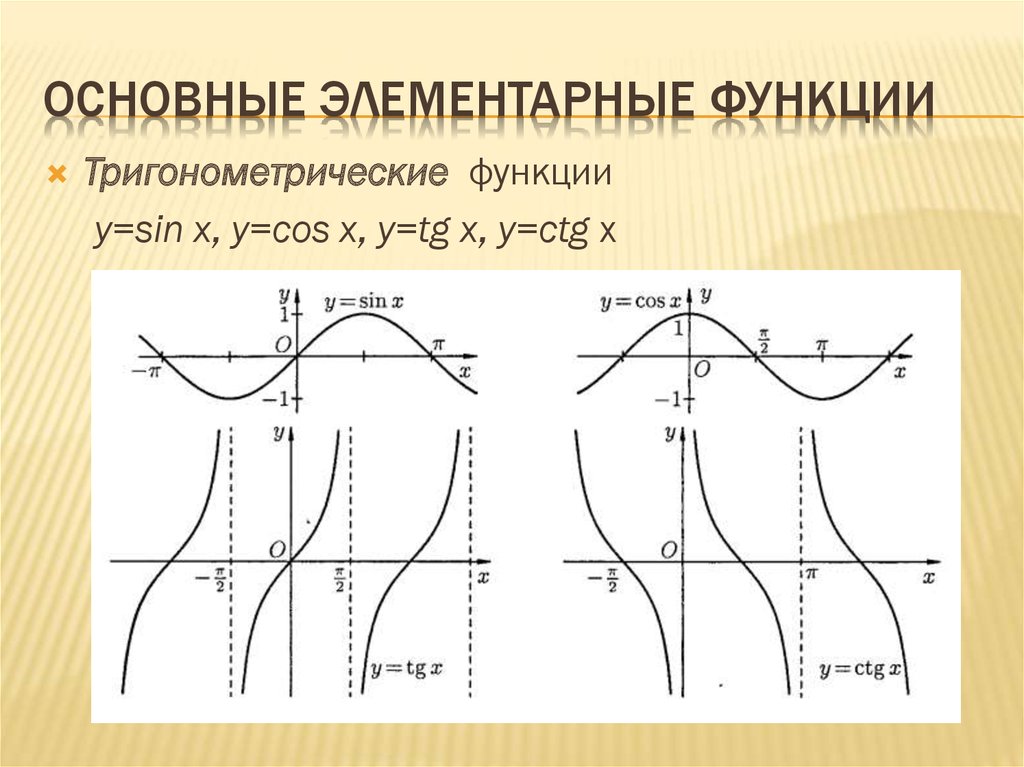
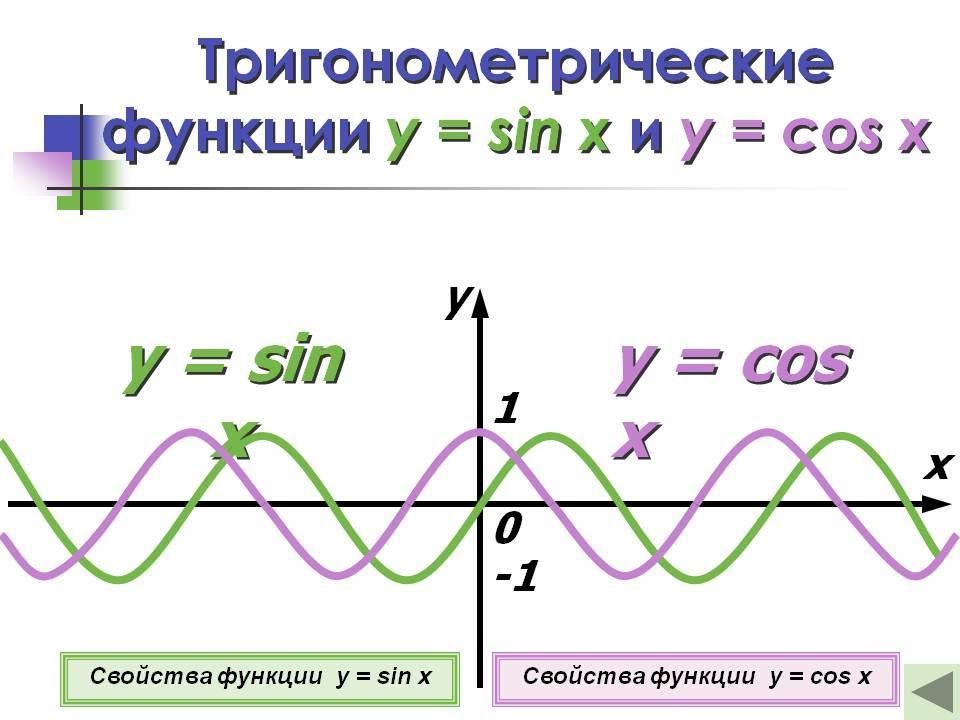
Функция y = sin x, ее свойства и
график
1. D(sin) = ( — ∞; + ∞)
2. Функция у = sin x нечетная: sin( х) sin х
3. Нули функции
x k , k Z
4. Функция периодическая, основной период 2π
5. Функция возрастает на любом отрезке
2 2 k ; 2 2 k , k Z
вида
и убывает на любом отрезке вида
3
2
k
;
2
k
, k Z
2
2
6.

Функция ограничена снизу и сверху
1 sin х 1
7. Наименьшее значение yнаим. 1
достигается при
х
2
2 k , k Z
Наибольшее значение унаиб. 1
достигается при
х
2
2 k , k Z
8. Функция y = sin x — непрерывная функция
9. Область значений
Е(sin)=[-1; 1]
Функция y = cos x, ее свойства и
график
cos х sin(
2
x)
1. D(cos) = ( — ∞; + ∞)
2. Функция у = cos x четная cos( х) cos x
3. Нули функции
x
2
k , k Z
4. Функция периодическая.
Основной период равен 2π.
5. Функция возрастает на любом отрезке
вида 2 k; 2 2 k , k Z
и убывает на любом отрезке вида
0 2 k; 2 k , k Z
6. Функция ограничена снизу и сверху
1 cos х 1
7. Наименьшее значение
достигается при
yнаим. 1
х 2 k , k Z
Наибольшее значение унаиб. 1
достигается при
х 2 k , k Z
8. Функция y = cos x — непрерывная функция
9. Область значений функции y = cos x:
Е(cos)=[-1; 1]

21.

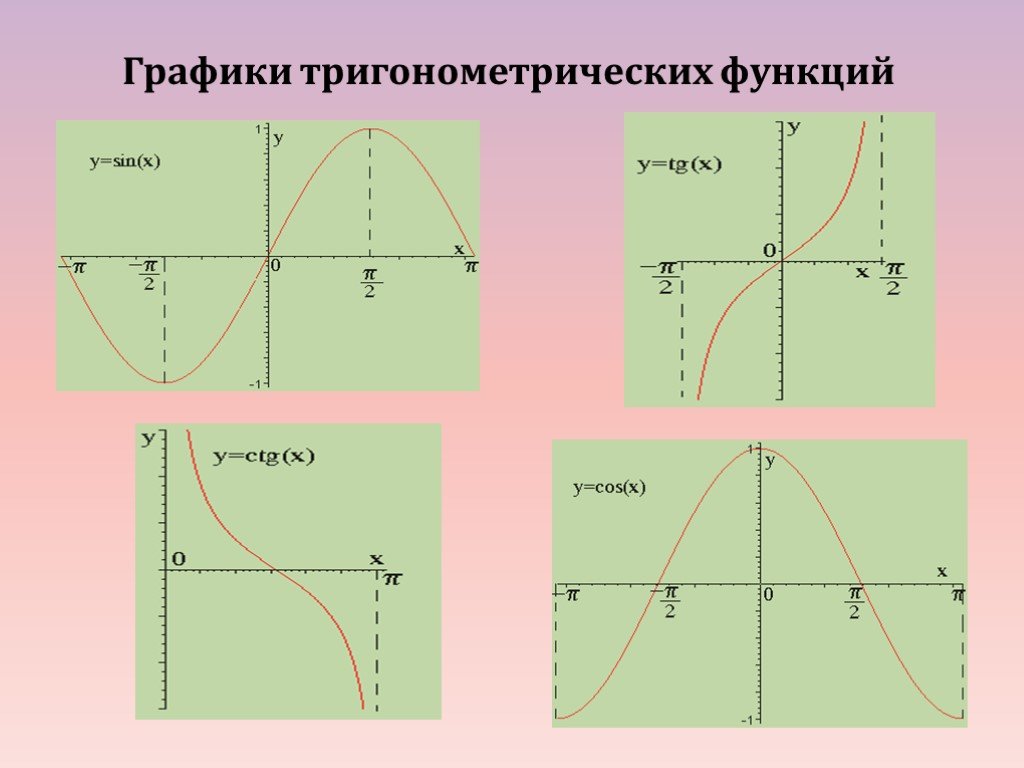
Функции y = tg x, y = ctg x, их свойства и графикиСвойства функции y = tg x
1. D(tg): x k , k Z
2
2. Функция у = tg x нечетная. График
симметричен относительно начала координат
tg ( х) tg x
3. Функция у = tg x периодическая.
Основной период равен π
tg ( x ) tg x tg ( x )
4. Нули функции
x k , k Z
5. Функция возрастает на любом интервале
вида
k ; k , k Z
2
2
6. Функция y = tg x не ограничена ни снизу,
ни сверху
7. Функция y = tg x не имеет ни
наибольшего, ни наименьшего значения
8. Функция y = tg x – непрерывна на любом
интервале вида k ; k , k Z
2
2
Прямые x
k , k Z
2
являются вертикальными асимптотами
9. Область значений функции y = tg x:
Е(tg) = (-∞; +∞)
Свойства функции y = ctg x
1. D(ctg):
x k , k Z
2. Функция у = ctg x нечетная.
сtg ( х) сtg x
3. Функция у = ctg x периодическая.
Основной период равен π
сtg ( x ) сtg x сtg ( x )
4.

Нули функции
x
2
k , k Z
5. Функция убывает на любом интервале
вида
k; k , k Z
6. Функция y = сtg x не ограничена ни снизу,
ни сверху
7. Функция y = сtg x не имеет ни
наибольшего, ни наименьшего значения
8. Функция y = сtg x – непрерывна на любом
k; k , k Z
интервале вида
Прямые
x k , k Z
являются вертикальными асимптотами
9. Область значений функции y = сtg x:
Е(сtg) = (-∞; +∞)
сtgx tg ( x )
2
Определение. Функцию у = f (x) называют обратимой на
множестве Х, если любое свое значение она принимает только в
одной точке множества Х (т.е. разным значениям аргумента
соответствуют разные значения функции)
Теорема. Если функция y = f (x) монотонна на множестве Х,
то она обратима на Х.
Определение. Пусть обратимая функция y = f (x) определена на
множестве Х и Е(f) = Y. Поставим в соответствие каждому у ϵ Y
то единственное значение х, при котором f( x ) = y. Тогда получим
Функцию, которая определена на Y, а Х – область значений
функции.

Эту функцию называют обратной к функции y = f (х ) и
обозначают y = f -1(x).
Теорема. Если функция = f(x) возрастает (убывает) на множестве
Х, а Y – область значений функции, то обратная функция
возрастает (убывает ) на Y.

Обратные тригонометрические функции, их свойства и графики

Лазарь Людмила Павловна

Разделы: Математика

Занятие №1

Определение обратных тригонометрических функций их свойства и графики.

Цель: дать понятие обратных тригонометрических функций, рассмотреть свойства этих функция и построение графиков обратных тригонометрических функций.

I. История развития тригонометрии.

Тригонометрия в своем развитии прошла две стадии. Первой стадией положены начала в античном мире; в связи с запросами астрономии возникает учение о взаимной связи круговых дуг и их хорд и составляются таблицы хорд через каждые полградуса до 180

0 в трудах александрийских ученых Гиппарха (IIв.до н.э.) и Птолемея (II в. до н. э.) В дальнейшем потребности географии, геодезии, военного дела способствовали развитию зачатков нового предмета, заложенного Гиппархом и Птолемеем. Особенно усиленно шло развитие тригонометрии в средневековое время, в первую очередь в Индии Узбекистане, Азербайджане. Творения ученых этого периода привели к выделению нового самостоятельного предмета в Азербайджане Насирэддином Туси (1201- 1274) в его “Трактате о полном четырехстороннике”, а позднее в 1595 году в Европе в трудах Варфоломея Питискуса “ Тригонометрия, или краткий обзорный трактат о решении треугольников”.
Итак, на первой стадии тригонометрия сложилась как теория, вычислительного приема решения треугольников и фигур, сводимых к ним, причем решения проводились с помощью таблиц синусов и тангенсов, основой для вычисления которых служили теоремы Пифагора и Птолимея.
Вторая стадия, начало которой положено в трудах Франсуа Виетта (1540-1630), полностью раскрывается в школе академика Леонарда Эйлера (1707-1783), когда создается аналитическая теория тригонометрических
( круговых) функций. Начиная с XVII в., тригонометрические функции начали применять к решению уравнений, задач механики, оптики, электричества, радиотехники, для описания колебательных процессов, распространения волн, движения различных механизмов, для изучения переменного электрического тока и т.д. Поэтому тригонометрические функции всесторонне и глубоко исследовались и приобрели важное значение для всей математики.

Название обратной тригонометрической функции образуется от названия соответствующей ей тригонометрической функции добавлением приставки “арк-” (от лат. arc — дуга). Это связано с тем, что геометрически значение обратной тригонометрической функции можно связать с длиной дуги единичной окружности (или углом, стягивающим эту дугу), соответствующей тому или иному отрезку.
Продолжение статьи
Презентация
12.05.2011
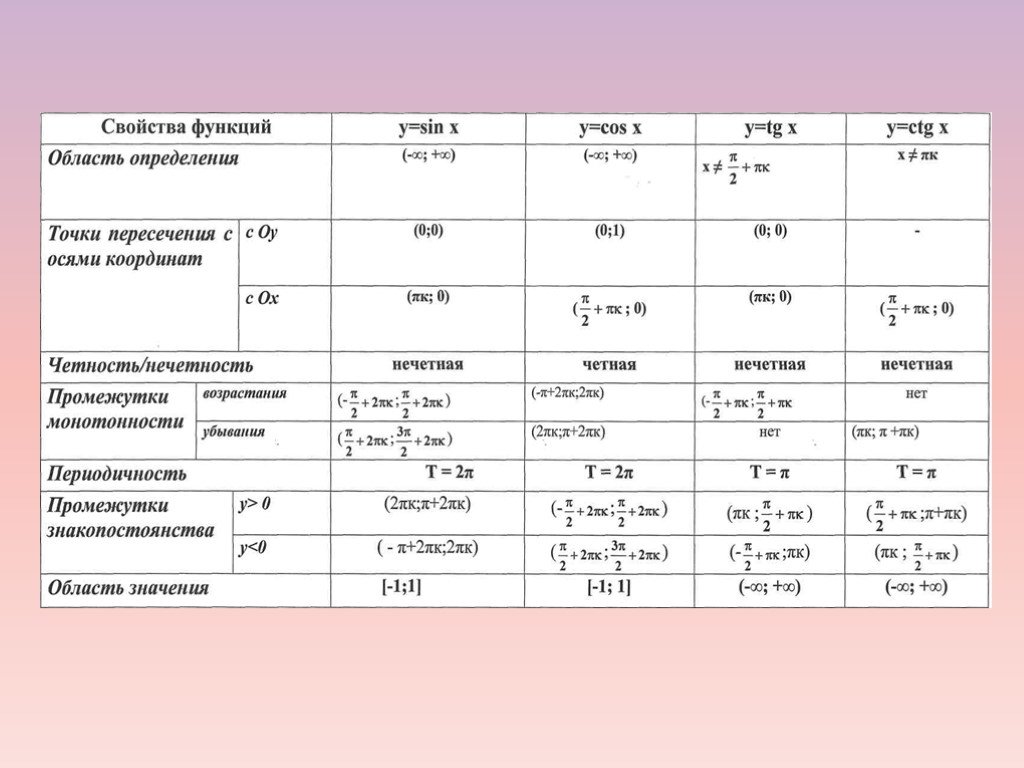
Тригонометрические функции и их свойства
Wolfram Community »
Язык Wolfram »
Демонстрации »
Подключенные устройства »

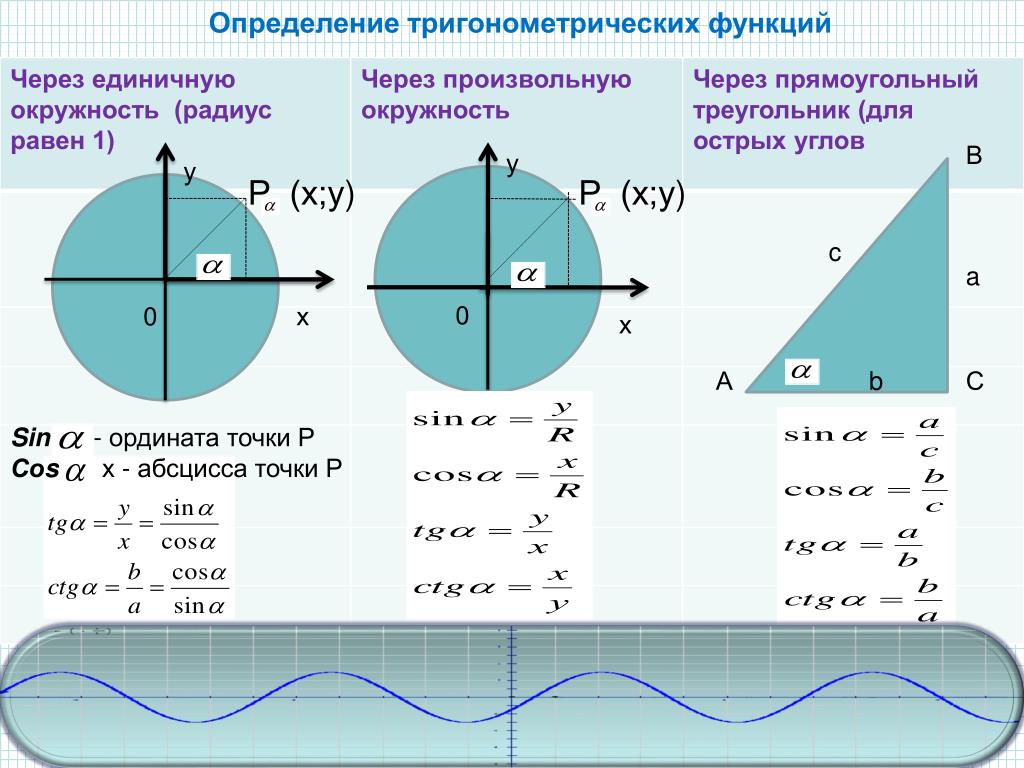
Тригонометрические функции
Круговые функции в сложных формах
.
sin x | cos x | коричневый x | сек x | csc x | детская кроватка x

Формулы тригонометрических функций
Основные отношения
Примеры:
Расширения серии
Примеры:
Сумма и разность углов
Примеры:
Половинный, двойной, многоугольный
Примеры:
Полномочия функций
Примеры:
Комбинация функций
Примеры:
Соотношения с гиперболическими функциями
Примеры:
Обратные тригонометрические функции

.
sin x | arcsin x | арккос x | арктан x | арксек x | арксск x | арккот x
.
Основные отношения
Примеры:
Соотношения с обратными гиперболическими функциями
Примеры: Основные значения

Чтобы определить однозначных функций
Идентификация алгебраических свойств, чаще всего используемых при решении идентификаторов
: Мэри Джейн Стерлинг и
Обновлен: 03-26-2016
71: 03-26-2016
77771: 03-26-2016
777771: 03-26-2016
777.
771: 03-26-2016
701:
7: .0037
Тригонометрия для чайников
Исследуйте книгу Купить на Amazon
Решение тождеств является почти обрядом посвящения для тех, кто изучает тригонометрию. Перспектива решения тождеств, а затем и упрощения триггерных выражений в исчислении, проходит гораздо легче, если у вас есть под рукой некоторые алгебраические инструменты. Имея план действий, вы добьетесь успеха быстрее и эффективнее и получите желаемый продукт.
При решении тождества вы вносите некоторые триггерные замены (базовые тождества, такие как sin ² x + cos ² x = 1), но вся ваша работа основана на алгебраических правилах и методах. Вот алгебраические свойства, которые чаще всего встречаются при работе с тождествами:
Коммутативное свойство сложения и умножения: 2 sin x + sin y + sin x = 2 sin x
+ sin x + sin x8 + 8 y 06 и 06
Вы можете изменить порядок членов или факторов, чтобы сделать объединение членов более удобным.
Ассоциативное свойство сложения и умножения: 2 sin x + (sin x + sin y ) = (2 sin x + sin x ) и
Перегруппировав термины или факторы, вы можете добавить или умножить термины, которые объединяются.
Распределительное свойство умножения на сложение: sin x (1 – csc x ) = sin x – sin x csc х . Распределительное свойство очень полезно, особенно когда вы понимаете, что один из продуктов оказывается функцией, умноженной на обратную.
Свойство симметрии:
также пишется
Выполнение триггера двух сторон может сделать более удобным в работе или при решении уравнения.

Свойство умножения уравнений: Если
, тогда 2 sin x = 1. Вы можете умножить обе части уравнения на одно и то же число (только не на 0). При решении тригонометрического уравнения у вас есть много скрытых возможностей умножить каждую часть уравнения на 0 или разделить (умножить на обратную величину) на 0. Тригонометрические функции синуса, косинуса, тангенса и котангенса равны 0 для многих мер угла. Просто примите во внимание эти угловые меры при определении решения уравнения (другими словами, выбросьте их).
Squaring a binomial: (sin x + cos x ) ² = sin ² x + 2 sin x cos x + cos ² x . Одна из наиболее частых ошибок, обнаруживаемых при возведении бинома в квадрат, — забывание среднего члена. Возведение биномов в квадрат особенно полезно в тригонометрии, потому что оно имеет тенденцию создавать термины, которые являются частью одного из пифагорейских тождеств.

Factoring (greatest common factor): sin ² x tan ² x – tan ² x = tan ² x (sin ² x – 1 ). Когда два или более термина имеют общий фактор, деление каждого термина на этот фактор создает одно или несколько рабочих выражений. Только не забудьте разделить всех членов на множитель и сохранить правильные знаки. При делении на отрицательный множитель все знаки меняются местами.
Факторинг (разность квадратов): сек ² x – 1 = (сек x – 1)(сек x + 1). Все тождества Пифагора имеют в своих уравнениях три квадрата членов. Это дает много возможностей учитывать разность квадратов. Вы смотрите вперед, чтобы увидеть, что может быть разделено на следующем шаге. Другие методы факторинга используются реже, но не стесняйтесь обращаться к своей алгебре, чтобы выкопать что-то, не упомянутое здесь.

Эта статья взята из книги:
Тригонометрия для чайников,
Об авторе книги:
Мэри Джейн Стерлинг — автор книги Алгебра I для чайников и многих других книг для чайников 90.
No related posts.