Урок 10. Тригонометрические функции. Тригонометрические уравнения и их системы. Теория 11 класс онлайн-подготовка на
Подготовка к ЕГЭ по математике
Эксперимент
Урок 10. Тригонометрические функции. Тригонометрические уравнения и их системы.
Теория
Конспект урока
Тригонометрические функции и их свойства
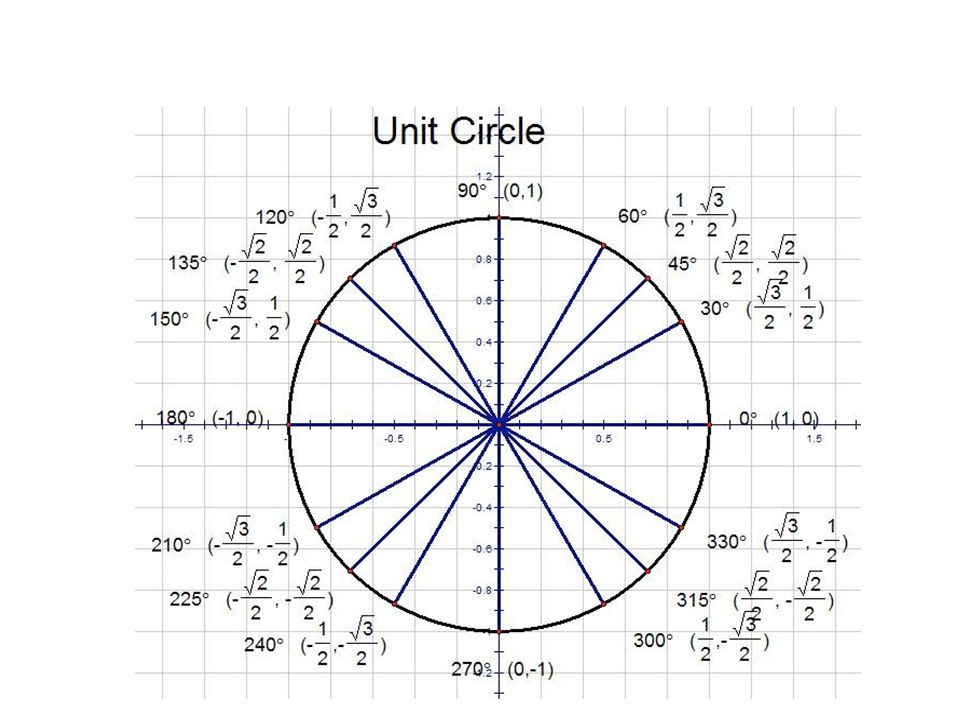
Мы с вами уже многократно применяли термин «тригонометрическая функция». Еще на первом уроке этой темы мы определили их с помощью прямоугольного треугольника и единичной тригонометрической окружности. Используя такие способы задания тригонометрических функций, мы уже можем сделать вывод, что для них одному значению аргумента (или угла) соответствует строго одно значение функции, т.е. мы вправе называть синус, косинус, тангенс и котангенс именно функциями.
На этом уроке самое время попробовать абстрагироваться от рассмотренных ранее способов вычисления значений тригонометрических функций. Сегодня мы перейдем к привычному алгебраическому подходу работы с функциями, мы рассмотрим их свойства и изобразим графики.
Что касается свойств тригонометрических функций, то особое внимание следует обратить на:
— область определения и область значений, т.к. для синуса и косинуса есть ограничения по области значений, а для тангенса и котангенса ограничения по области определения;
— периодичность всех тригонометрических функций, т.к. мы уже отмечали наличие наименьшего ненулевого аргумента, добавление которого не меняет значение функции. Такой аргумент называют периодом функции и обозначают буквой . Для синуса/косинуса и тангенса/котангенса эти периоды различны.
Функция синус и ее график
Рассмотрим функцию:
Основные свойства этой функции:
1) Область определения ;
2) Область значений ;
3) Функция нечетная ;
4) Функция не является монотонной на всей своей области определения;
5) Функция периодична с периодом .
Построим график функции . При этом удобно начинать построение с изображения области, которая ограничивает график сверху числом 1 и снизу числом , что связано с областью значений функции. Кроме того, для построения полезно помнить значения синусов нескольких основных табличных углов, например, что Это позволит построить первую полную «волну» графика и потом перерисовывать ее вправо и влево, пользуясь тем, что картинка будет повторяться со смещением на период, т.е. на .
Функция косинус и ее график
Теперь рассмотрим функцию:
Основные свойства этой функции:
1) Область определения ;
2) Область значений ;
3) Функция четная Из этого следует симметричность графика функции относительно оси ординат;
4) Функция не является монотонной на всей своей области определения;
5) Функция периодична с периодом .
Построим график функции . Как и при построении синуса удобно начинать с изображения области, которая ограничивает график сверху числом 1 и снизу числом , что связано с областью значений функции.
Также нанесем на график координаты нескольких точек, для чего необходимо помнить значения косинусов нескольких основных табличных углов, например, что С помощью этих точек мы можем построить первую полную «волну» графика и потом перерисовывать ее вправо и влево, пользуясь тем, что картинка будет повторяться со смещением на период, т.е. на .
Функция тангенс и ее график
Перейдем к функции:
Основные свойства этой функции:
1) Область определения кроме , где . Мы уже указывали в предыдущих уроках, что не существует. Это утверждение можно обобщить, учитывая период тангенса;
2) Область значений , т.е. значения тангенса не ограничены;
3) Функция нечетная ;
4) Функция монотонно возрастает в пределах своих так называемых веток тангенса, которые мы сейчас увидим на рисунке;
5) Функция периодична с периодом
Построим график функции . При этом удобно начинать построение с изображения вертикальных асимптот графика в точках, которые не входят в область определения, т.
е. и т.д. Далее изображаем ветки тангенса внутри каждой из образованных асимптотами полосок, прижимая их к левой асимптоте и к правой. При этом не забываем, что каждая ветка монотонно возрастает. Все ветки изображаем одинаково, т.к. функция имеет период, равный . Это видно по тому, что каждая ветка получается смещением соседней на вдоль оси абсцисс.
Функция котангенс и ее график
И завершаем рассмотрением функции:
Основные свойства этой функции:
1) Область определения кроме , где . По таблице значений тригонометрических функций мы уже знаем, что не существует. Это утверждение можно обобщить, учитывая период котангенса;
2) Область значений , т.е. значения котангенса не ограничены;
3) Функция нечетная ;
4) Функция монотонно убывает в пределах своих веток, которые похожи на ветки тангенса;
5) Функция периодична с периодом
Построим график функции . При этом, как и для тангенса, удобно начинать построение с изображения вертикальных асимптот графика в точках, которые не входят в область определения, т.
е. и т.д. Далее изображаем ветки котангенса внутри каждой из образованных асимптотами полосок, прижимая их к левой асимптоте и к правой. В этом случае учитываем, что каждая ветка монотонно убывает. Все ветки аналогично тангенсу изображаем одинаково, т.к. функция имеет период, равный .
Вычисление периодов тригонометрических функций со сложным аргументом
Отдельно следует отметить тот факт, что у тригонометрических функций со сложным аргументом может быть нестандартный период. Речь идет о функциях вида:
У них период равен . И о функциях:
У них период равен .
Как видим, для вычисления нового периода стандартный период просто делится на множитель при аргументе. От остальных видоизменений функции он не зависит.
Подробнее разобраться и понять, откуда берутся эти формулы, вы сможете в уроке про построение и преобразование графиков функций.
Тригонометрические уравнения и методы их решения
Мы подошли к одной из самых главных частей темы «Тригонометрия», которую мы посвятим решению тригонометрических уравнений.
Умение решать такие уравнения важно, например, при описании колебательных процессов в физике. Представим, что вы на спортивной машине проехали несколько кругов на картинге, определить сколько времени вы уже участвуете в гонке в зависимости от положения машины на трассе поможет решение тригонометрического уравнения.
Запишем простейшее тригонометрическое уравнение:
Решением такого уравнения являются аргументы, синус которых равен . Но мы уже знаем, что из-за периодичности синуса таких аргументов существует бесконечное множество. Таким образом, решением этого уравнения будут и т.п. То же самое относится и к решению любого другого простейшего тригонометрического уравнения, их будет бесконечное количество.
Тригонометрические уравнения делятся на несколько основных типов. Отдельно следует остановиться на простейших, т.к. все остальные к ним сводятся. Таких уравнений четыре (по количеству основных тригонометрических функций). Для них известны общие решения, их необходимо запомнить.
Простейшие тригонометрические уравнения и их общие решения выглядят следующим образом:
1)
2)
3)
4)
Обратите внимание, что на значения синуса и косинуса необходимо учитывать известные нам ограничения. Если, например, , то уравнение не имеет решений и применять указанную формулу не следует.
Кроме того, указанные формулы корней содержат параметр в виде произвольного целого числа . В школьной программе это единственный случай, когда решение уравнения без параметра содержит в себе параметр. Это произвольное целое число показывает, что можно выписать бесконечное количество корней любого из указанных уравнений просто подставляя вместо по очереди все целые числа.
Ознакомиться с подробным получением указанных формул вы можете, повторив главу «Тригонометрические уравнения» в программе алгебры 10 класса.
Отдельно необходимо обратить внимание на решение частных случаев простейших уравнений с синусом и косинусом. Эти уравнения имеют вид:
и
.
К ним не следует применять формулы нахождения общих решений. Такие уравнения удобнее всего решаются с использованием тригонометрической окружности, что дает более простой результат, чем формулы общих решений.
Например, решением уравнения является . Попробуйте сами получить этот ответ и решить остальные указанные уравнения.
Кроме указанного наиболее часто встречающегося типа тригонометрических уравнений существуют еще несколько стандартных. Перечислим их с учетом тех, которые мы уже указали:
1) Простейшие, например, ;
2) Частные случаи простейших уравнений, например, ;
3) Уравнения со сложным аргументом, например, ;
4) Уравнения, сводящиеся к простейшим путем вынесения общего множителя, например, ;
5) Уравнения, сводящиеся к простейшим путем преобразования тригонометрических функций, например, ;
6) Уравнения, сводящиеся к простейшим с помощью замены, например, ;
7) Однородные уравнения, например, ;
8) Уравнения, которые решаются с использованием свойств функций, например, .
Пусть вас не пугает, что в этом уравнении две переменные, оно при этом решается;
А также уравнения, которые решаются с использованием различных методов.
Системы тригонометрических уравнений и методы их решения
Кроме решения тригонометрических уравнений необходимо уметь решать и их системы.
Наиболее часто встречаются системы следующих типов:
1) В которых одно из уравнений степенное, например, ;
2) Системы из простейших тригонометрических уравнений, например, .
На сегодняшнем уроке мы рассмотрели основные тригонометрические функции, их свойства и графики. А также познакомились с общими формулами решения простейших тригонометрических уравнений, указали основные типы таких уравнений и их систем.
В практической части урока мы разберем методы решения тригонометрических уравнений и их систем.
Вставка 1. Решение частных случаев простейших тригонометрических уравнений.
Как мы уже говорили в основной части урока частные случаи тригонометрических уравнений с синусом и косинусом вида:
и
имеют более простые решения, чем дают формулы общих решений.
Для этого используется тригонометрическая окружность. Разберем метод их решения на примере уравнения .
Изобразим на тригонометрической окружности точку, в которой значение косинуса равно нулю, оно же является координатой по оси абсцисс. Как видим, таких точек две. Наша задача указать чему равен угол, который соответствует этим точкам на окружности.
Начинаем отсчет от положительного направления оси абсцисс (оси косинусов) и при откладывании угла попадаем в первую изображенную точку, т.е. одним из решений будет это значение угла. Но нас же еще устраивает угол, который соответствует второй точке. Как попасть в нее?
Для этого необходимо к уже отложенному углу добавить развернутый угол .
Если выписать первые три полученных нами корня уравнения, то можно увидеть закономерность:
, , , …и выписать формулу для всех корней:
Как видим, эта формула действительно выглядит проще общего решения уравнения с косинусом, хотя бы потому, что в ней отсутствует «». Однако это не значит, что общая формула даст неверное решение.
Аналогично можно получить решения для всех остальных указанных частных случаев тригонометрических уравнений.
Полезные ссылки:
1) Алгебра 9 класс: «Функция y=sinx, её свойства и график»
2) Алгебра 9 класс: «Функция y=cosx. Её свойства и график»
3) Алгебра 9 класс: «Функция y=cos t, её свойства и график»
4) Алгебра 9 класс: «Простейшие тригонометрические уравнения и сопутствующие задачи»
5) Алгебра 9 класс: «Элементы теории тригонометрических функций.
Функция y=sinx»
6) Алгебра 9 класс: «Элементы теории тригонометрических функций. Функция y=cosx»
7) Алгебра 10 класс: «Функция y=sinx, ее основные свойства и график»
8) Алгебра 10 класс: «Функция y=sinx, её свойства, график и типовые задачи»
9) Алгебра 10 класс: «Функция y=cos t, её основные свойства и график»
10) Алгебра 10 класс: «Функция y=cos t, её свойства, график и типовые задачи»
11) Алгебра 10 класс: «Периодичность функций y=sin t, y=cos t»
12) Алгебра 10 класс: «Как построить график функции y=m*f(x), если известен график функции y=f(x)»
13) Алгебра 10 класс: «Как построить график функции y=f(kx), если известен график функции y=f(x)»
14) Алгебра 10 класс: «Как построить график функции y=f(kx), если известен график функции y=f(x). Примеры построения»
15) Алгебра 10 класс: «График гармонического колебания»
16) Алгебра 10 класс: «Функция y=tgx, ее свойства и график»
17) Алгебра 10 класс: «Функция y=сtgx, ее свойства и график»
18) Алгебра 10 класс: «Первые представления о решении тригонометрических уравнений»
19) Алгебра 10 класс: «Простейшие тригонометрические уравнения»
|
|
|
переменные и
функции Числовые функции — это соответствие между элементами двух множеств, при котором каждому элементу одного множества (переменной, или аргументу) ставится в соответствие не более одного элемента другого множества (значение функции) |
|
периодические
функции Периодическая функция — для которой выполнено условие f(x)=f(x+Т)=f(x-Т).  Число Т
называют периодом функции. |
|
радианы и
градусы Измерение угла: если окружность покрыть равномерной сеткой от 0 до 2π (или от 0 до 360°), то любой угол можно измерить в радианах (долях 2π) или градусах. Радианная мера угла α = (π/180)⋅(α в °). Очевидно: α = α ± 2π = α ± 360° |
|
сумма углов
треугольника и
многоугольника Сумма углов любого треугольника α1+α2+α3 равна π = 180°, сумма углов многоугольника (N-угольника) равна π⋅(N-2) = 180°⋅(N-2).  |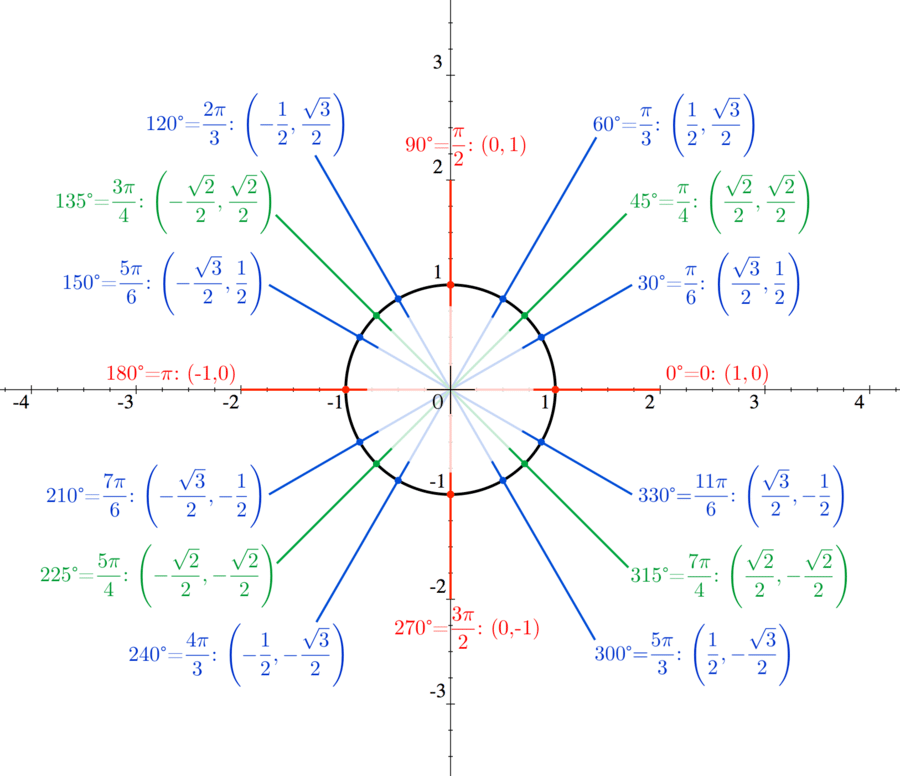
|
прямоугольный
треугольник Это треугольник, один из углов которого равен 90° = π/2. Стороны x, y при прямом угле называются катетами, а третья сторона — это гипотенуза |
|
теорема
Пифагора Прямоугольный треугольник задает простое соотношение между его сторонами: сумма квадратов длин катетов x, y равна квадрату длины гипотенузы: x² + y² = z² |
|
sin и cos, tg
и ctg Для острого угла α прямоугольного треугольника можно определить синус, как отношение противолежащего к углу катета y к гипотенузе z: sin(α) = y/z, косинус — как отношение прилежащего катета x к гипотенузе: cos(α) = x/z, тангенс и котангенс — как отношение катетов: tg(α) = y/x = sin(α)/cos(α) ctg(α) = x/y = 1/tg(α) |
|
теорема
синусов Для любого треугольника со сторонами х1, х2 и х3 и противолежащими им углами α1, α2 и α3 справедливо: x1/sin(α1) = x2/sin(α2) = x3/sin(α3) = 2R, где R — это радиус окружности, описанной вокруг треугольника |
|
теорема
косинусов Для любого треугольника со сторонами a,b,c и углом α между сторонами b,c справедливо: a² = b² + c² — 2⋅b⋅c⋅cos(α).  Следствие:
теорему Пифагора, при α=90°. |
|
единичная
окружность Это окружность радиусом R=1. По точкам (x,y) на ней удобно отсчитывать углы и определять тригонометрические функции (в том числе, для α < 0 и α > π/2). В частности, синус sin(α) = y, косинус cos(α) = x, тангенс tg(α) = y/x, котангенс ctg(α) = x/y, секанс sec(α) = 1/cos(α) = 1/x, косеканс csc(α) = 1/sin(α) = 1/y. |
|
тригонометрические
функции: свойства Некоторые свойства тригонометрических функций: все они периодические sin(x)=sin(x+2π), четные cos(-x)=cos(x) или нечетные sin(-x)=-sin(x), tg(-x)=-tg(x) |
|
тригонометрические
тождества и формулы Основное тригонометрическое тождество: sin²(x)+cos²(x)=1, формулы приведения sin(k⋅π/2-x)=cos(x), tg(π/2+x)=-ctg(x) и т.  п.,
формулы сложения, двойного
угла, половинного угла,
преобразование суммы
тригонометрических функций в
произведение и т.д. |
|
arcsin,
arccos, arctg Обратные тригонометрические функции (круговые функции, аркфункции) — математические функции, являющиеся обратными к тригонометрическим функциям. Арксинус — это угол, синус которого равен х, т.е. если sin(α) = х, то арксинус arcsin(х) = α. Аналогично, арккосинус arccos(х) = α, если cos(α) = x и арктангенс arctg(х) = α, если tg(α) = x.  Причем arcsin определяет
-π/2 ≤ α ≤ π/2, а arccos для
0 ≤ α ≤ π. Очевидно:
arcsin(-х) = -arcsin(х),
arccos(-х) = π — arccos(х). |
|
гармонические
колебания Гармонический закон колебаний — это y(t) = A⋅cos(ω⋅t+φ) или y(t) = A⋅sin(ω⋅t+φ) = A⋅cos(ω⋅t+φ-π/2). Параметры A, ω, φ — это амплитуда, круговая частота и начальная фаза колебаний. Период колебаний равен Т = 2π/ω. |
|
Анна Малкова:
тригонометрия Курс по тригонометрии от А. Малковой: четные и
нечетные функции,
периодичность, градусы и
радианы, тригонометрические
тождества, синус, косинус,
тангенс, уравнения и
неравенства |
Контрольная работа по теме «Тригонометрия». Алгебра 10 класс
Главная / Старшие классы / Алгебра
Скачать
52.73 КБ, 1165413.pdf Автор: Волкова Наталья Евгеньевна, 5 Сен 2015
Контрольная работа по теме «Тригонометрия» в 10 вариантах.. Алгебра 10 класс. В работу включены задания на проверку знания основных тригонометрических формул и умений решать тригонометрические уравнения.
Автор: Волкова Наталья Евгеньевна
Похожие материалы
| Тип | Название материала | Автор | Опубликован |
|---|---|---|---|
| документ | Контрольная работа по теме «Тригонометрия». Алгебра 10 класс | Волкова Наталья Евгеньевна | 5 Сен 2015 |
| документ | Контрольная работа по математике 10 класс.Тема » Тригонометрия» | Аксёнова Светлана Валерьевна | 22 Янв 2016 |
| документ | Контрольная работа по алгебре по теме «Тригонометрия» | Волкова Наталья Евгеньевна | 1 Апр 2015 |
| документ | контрольная работа по теме «тригонометрия» | Богданенко Елена Николаевна | 21 Мар 2015 |
| документ | Контрольная работа по теме «Комбинаторика», 10 класс | Чехлова Ольга Юрьевна | 21 Мар 2015 |
| документ | Итоговый тест за 1 полугодие по теме «Тригонометрия».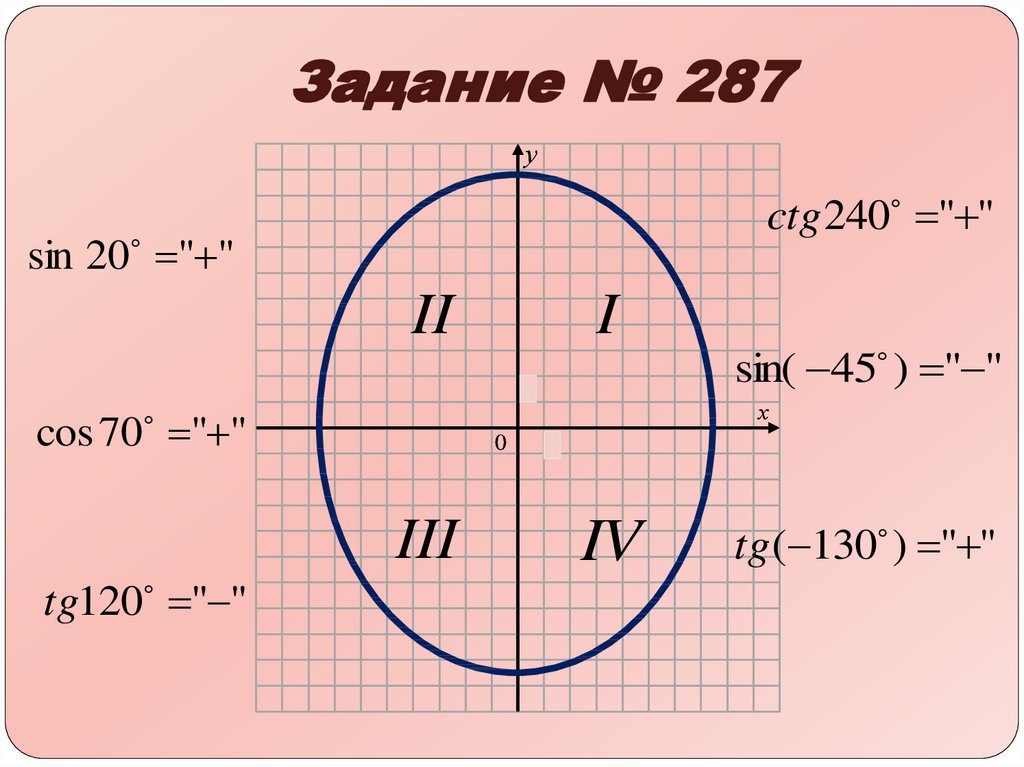 Алгебра и начала анализа 10 класс | Ермилова Нина Павловна | 1 Апр 2015 |
| документ | Контрольная работа по теме «Производная» в формате ЕГЭ алгебра 10 класс | Волкова Наталья Евгеньевна | 1 Апр 2015 |
| документ | Контрольная работа по алгебре и началам анализа по теме: «Логарифмическая функция», 10 класс | Кочухова Ирина Михайловна | 8 Фев 2016 |
| документ | Контрольная работа по теме: Тригонометрические функции 10 класс | Гончаренко Людмила Владимировна | 1 Апр 2015 |
| документ | Контрольная работа по теме «Тригонометрические уравнения», 10 класс | Кандыба Светлана Борисовна | 4 Апр 2015 |
| документ | Контрольная работа по теме «Степень с действительным показателем», 10 класс | Харчев Владимир Алексеевич | 4 Апр 2015 |
| документ | Разноуровневая контрольная работа по теме: » Применение непрерывности и производной. Касательная к графику функции «. 10 класс | Куликова Елена Георгиевна | 7 Мая 2015 |
| документ | Контрольная работа №2 по теме «Вычисления с многозначными часлами» 5 класс учебник Мордкович. Контрольная работа №2 Контрольная работа №2 Контрольная работа №2 Контрольная работа №2 Контрольная работа №3 Контрольная работа №3 Контрольная работа | Лыгина Ольга Владимировна | 21 Мар 2015 |
| документ | 10 класс. Контрольная работа по теме «Кинематика» | Семушина Наталья Геннадиевна | 21 Мар 2015 |
| документ | Контрольная работа по теме «Углеводороды» 10 класс | Олюхова Марина Геннадьевна | 20 Мар 2015 |
| документ | Контрольная работа по теме «Углеводороды» 10 класс | Жулина Надежда Павловна | 20 Мар 2015 |
| документ | Контрольная работа по теме» Динамика» 10 класс | Фёдорова Лариса Михайловна | 7 Апр 2015 |
| документ | Контрольная работа по теме «Кинематика» (10 класс) | Литовко Ирина Владимировна | 2 Мар 2016 |
| документ | Урок математики в 5 классе школы VIII вида по теме: «Контрольная работа № 10 по теме «Обыкновенные дроби»» | Покидышева Ирина Ивановна | 21 Мар 2015 |
| документ | Контрольная работа по теме «Интеграл», 11 класс | Чехлова Ольга Юрьевна | 21 Мар 2015 |
| документ | Контрольная работа 6 класс по теме «Пропорция» | Бурдюгова Светлана Викторовна | 31 Мар 2015 |
| разное | Контрольная работа по теме «Производная» 11 класс | Хожулина Елена Валентиновна | 1 Апр 2015 |
| документ | Контрольная работа: «Тригонометрия» | Федорчук Вера Ивановна | 1 Апр 2015 |
| разное | обобщающий урок в 10 классе по теме «Тригонометрия» | Юртайкина Елена Анатольевна | 6 Апр 2015 |
| документ | Алгебра 10 класс Тема «Тригонометрия. Аркфункции» | Григорьева Ольга Васильевна | 15 Окт 2015 |
| документ | Контрольная работа 10 класс по теме Производная в формате ЕГЭ. | Елена Геннадьевна Соколова | 18 Сен 2015 |
| разное | Контрольная работа по теме «Геометрические фигуры» | Узенкова Алла Николаевна | 31 Мар 2015 |
| документ | Контрольная работа » Производная» 10 класс | Пилюгина Наталья Анатольевна | 21 Мар 2015 |
| документ | Контрольная работа 10 класс «Производная» | Пилюгина Наталья Анатольевна | 21 Мар 2015 |
| документ | Тематический тест-зачет «Тригонометрия», 10 класс | Зудина Наталия Ивановна | 31 Мар 2015 |
| презентация | Презентация «Тригонометрия 10 класс» | Горина Татьяна Евгеньевна | 5 Апр 2015 |
| документ | Контрольная работа по физике 10 класс по теме «Механика» (за 1 полугодие) | Лапатин Алексей Леонидович | 21 Мар 2015 |
| документ | Контрольная работа по физике 10 класс по теме «Кинематика» | Лапатин Алексей Леонидович | 21 Мар 2015 |
| документ | Контрольная работа по географии 10 класс по теме :» Население мира» | Федорова Марина Викторовна | 21 Мар 2015 |
| документ | Контрольная работа по физике 10 класс по теме «Электростатика» | Казорина Оксана Васильевна | 14 Фев 2016 |
| документ | Контрольная работа по физике 10 класс по теме «Основы МКТ» | Казорина Оксана Васильевна | 14 Фев 2016 |
| документ | Контрольная работа по алгебре на повторение, 10 класс | Россамахина Ирина Юрьевна | 21 Мар 2015 |
| документ | Входная контрольная работа по математике 10 класс | Криворот Людмила Павловна | 31 Мар 2015 |
| документ | Входная контрольная работа по математике 10 класс | Марченко Марина Владимировна | 31 Мар 2015 |
| документ | Итоговая контрольная работа по алгебре 10 класс | Голик Людмила Александровна | 4 Ноя 2015 |
Обзор алгебраических триггеров
Показать мобильное уведомление Показать все примечания Скрыть все примечания
Уведомление для мобильных устройств
Похоже, вы используете устройство с «узкой» шириной экрана ( т.
е. вы наверное на мобильном телефоне). Из-за характера математики на этом сайте лучше всего просматривать в ландшафтном режиме. Если ваше устройство не находится в ландшафтном режиме, многие уравнения будут отображаться сбоку вашего устройства (должна быть возможность прокрутки, чтобы увидеть их), а некоторые пункты меню будут обрезаны из-за узкой ширины экрана.
Этот обзор изначально был написан для моего класса исчисления I, но он должен быть доступен для всех, кому нужен обзор по некоторым темам базовой алгебры и триггеров. Обзор содержит случайные комментарии о том, как тема будет/может быть использована в классе исчисления. Если вы не на уроке математики, вы можете игнорировать эти комментарии. Я не освещаю все темы, которые вы могли бы увидеть на типичном уроке алгебры или тригонометрии, я в основном рассмотрел те, которые, по моему мнению, были бы наиболее полезны для студента на уроке исчисления, хотя я включил пару, которые на самом деле не являются важными. требуется для урока исчисления.
Эти дополнительные темы были включены просто потому, что они время от времени возникают, и мне захотелось их включить. Есть также, по всей вероятности, несколько тем по алгебре/триггерам, которые время от времени возникают в
класс исчисления, который я не включил.
Поскольку этот обзор изначально был написан для моих студентов, изучающих математический анализ, для проверки их навыков алгебры и/или тригонометрии, он обычно представляет собой набор задач. Решение первой задачи в наборе содержит подробную информацию о том, как решить конкретный тип задачи. Остальные решения также достаточно подробны и могут содержать дополнительную необходимую информацию, которой не было в первой задаче, но они, вероятно, не будут содержать явных инструкций или причин для выполнения определенного шага в процессе решения. При написании решений я намеревался сделать их достаточно подробными, чтобы кто-то, кому нужно изучить конкретную тему, мог выбрать тему из решений проблем. Я надеюсь, что у меня это получилось.
Так зачем я вообще это написал?
Способность заниматься базовой алгеброй абсолютно необходима для успешной сдачи урока по математическому анализу. По мере прохождения курса по математическому анализу вы увидите, что почти каждая задача по математическому анализу требует достаточного количества алгебры. На самом деле, во многих математических задачах 90% или более проблем приходится на алгебру.
Таким образом, хотя вы можете понимать основные концепции исчисления, если вы не можете заниматься алгеброй, вы не сможете решать задачи. Если вы не справитесь с этими задачами, вам будет очень трудно пройти курс.
Точно так же вы обнаружите, что многие темы в классе исчисления требуют от вас знания основ тригонометрии. В некоторых задачах вам будет предложено работать с триггерными функциями, вычислять тригонометрические функции и решать тригонометрические уравнения. Без способности выполнять базовые триггеры вам будет трудно решать эти задачи.
Хорошие навыки алгебры и триггера также потребуются в исчислении II или исчислении III.
Итак, если у вас нет хороших навыков алгебры или тригонометрии, вам будет очень сложно пройти эту последовательность курсов.
Большая часть следующего набора задач иллюстрирует виды алгебры и триггерных навыков, которые вам понадобятся для успешного завершения любого курса исчисления здесь, в Университете Ламара. Алгебра и тригонометрия в этих задачах делятся на три категории:
- Легче, чем типичная задача исчисления,
- похож на типичную задачу исчисления, а
- сложнее, чем типичная задача исчисления.
К какой категории относится каждая проблема, зависит от вашего инструктора. В моем курсе исчисления вы обнаружите, что большинство этих задач относятся к первым двум категориям.
В зависимости от вашего преподавателя последние несколько разделов (функции обратного триггера через решение логарифмических уравнений) могут быть в той или иной степени изучены на вашем курсе. Тем не менее, даже если ваш инструктор преподает этот материал, вы сочтете полезным пройтись по этим разделам.
В своем курсе я трачу первые пару дней на изучение основ экспоненциальных и логарифмических функций, так как я обычно использую их на регулярной основе.
Этот набор задач предназначен не для того, чтобы обескуражить вас, а для того, чтобы убедиться, что у вас есть знания, необходимые для прохождения этого курса. Если у вас возникли проблемы с материалом на этом рабочем листе (особенно с разделами «Экспоненты — Решение триггерных уравнений»), вы обнаружите, что у вас также возникнут большие проблемы с прохождением курса исчисления.
Имейте в виду, что этот набор задач НЕ предназначен для замены курса алгебры или тригонометрии. Как я уже упоминал, я не освещаю все темы, которые обычно рассматриваются в курсах алгебры или триггеров. Большинство затронутых здесь тем — это те, которые я считаю важными темами, которые вы ДОЛЖНЫ изучить, чтобы успешно пройти курс исчисления (в частности, мой курс исчисления). Вы можете обнаружить, что существуют другие навыки алгебры или триггера, которые также необходимы для успешного прохождения этого курса, но не рассматриваются в этом обзоре. Вы также можете обнаружить, что вашему инструктору не потребуются все навыки, перечисленные в этом обзоре.
Вот краткий список и краткое объяснение каждой темы, затронутой в этом обзоре.
Алгебра
Экспоненты — краткий обзор основных свойств экспоненты.
Абсолютное значение — Пара быстрых задач, чтобы напомнить вам, как работает абсолютное значение.
Радикалы – Обзор радикалов и некоторых их свойств.
Рационализация. Обзор темы, которая не всегда хорошо освещается на уроках алгебры, но иногда требуется на уроках исчисления.
Функции – Обозначение функций и оценка функций.
Умножение полиномов — пара задач на умножение полиномов, иллюстрирующих распространенные ошибки в классе исчисления.
Факторинг – некоторые базовые факторы факторинга.
Упрощение рациональных выражений. Способность упрощать рациональные выражения может быть жизненно важной в некоторых задачах исчисления.
Графики и обычные графики — вот некоторые общие функции и способы их построения.
Функции включают параболы, окружности, эллипсы и гиперболы.
Решение уравнений, часть I – Решение уравнений с одной переменной, включая квадратичные формулы.
Решение уравнений, часть II – Решение уравнений с несколькими переменными.
Решение систем уравнений – Решение систем уравнений и некоторые интерпретации решения.
Решение неравенств – Решение полиномиальных и рациональных неравенств.
Уравнения и неравенства с абсолютными значениями – Решение уравнений и неравенств, включающих абсолютные значения.
Тригонометрия
Оценка триггерной функции — как использовать единичный круг для нахождения значения триггерной функции при некоторых основных углах.
Графики триггерных функций — графики триггерных функций и некоторые интересные свойства, которые можно увидеть на графиках.
Формулы триггеров — некоторые важные формулы триггеров, которые вы найдете полезными в курсе исчисления.
Решение триггерных уравнений – Методы решения уравнений, включающих триггерные функции.
Обратные функции запуска — основы обратных функций запуска.
Экспоненты и логарифмы
Основные экспоненциальные функции — экспоненциальные функции, оценка экспоненциальных функций и некоторые основные свойства.
Основные функции логарифмирования — функции логарифмирования, вычисление логарифмов.
Свойства логарифма — они достаточно важны, чтобы заслужить отдельный раздел.
Упрощение логарифмов — основы упрощения логарифмов.
Решение показательных уравнений – методы решения уравнений, содержащих показательные функции.
Решение логарифмических уравнений – Методы решения уравнений, содержащих логарифмические функции.
Algebra and Trigonometry — 1st Edition
Select country/regionUnited States of AmericaUnited KingdomAfghanistanÅland IslandsAlbaniaAlgeriaAmerican SamoaAndorraAngolaAnguillaAntigua and BarbudaArgentinaArmeniaArubaAustraliaAustriaAzerbaijanBahamasBahrainBangladeshBarbadosBelgiumBelizeBeninBermudaBhutanBoliviaBonaire, Sint Eustatius and SabaBosnia and HerzegovinaBotswanaBrazilBritish Indian Ocean TerritoryBritish Virgin IslandsBruneiBulgariaBurkina FasoBurundiCambodiaCameroonCanadaCanary IslandsCape VerdeCayman IslandsCentral African RepublicChadChileChinaChristmas IslandCocos (Keeling) IslandsColombiaComorosCongoCook IslandsCosta RicaCroatiaCubaCuraçaoCyprusCzech RepublicDemocratic Republic of КонгоДанияДжибутиДоминикаДоминиканская РеспубликаЭквадорЕгипетСальвадорЭкваториальная ГвинеяЭритреяЭстонияЭфиопияФолклендские (Мальвинские) островаФарерские островаФедеративные Штаты МикронезияФиджиФинляндияФранцияФранцузская ГвианаФранцузская ПолинезияГабонГамбияГрузияГерманияГанаГибралтарГрецияG reenlandGrenadaGuadeloupeGuamGuatemalaGuernseyGuineaGuinea-BissauGuyanaHaitiHondurasHong KongHungaryIcelandIndiaIndonesiaIranIraqIrelandIsle of ManIsraelItalyJamaicaJapanJerseyJordanKazakhstanKenyaKiribatiKuwaitKyrgyzstanLaoLatviaLesothoLiberiaLibyaLiechtensteinLuxembourgMacaoMacedoniaMadagascarMalawiMalaysiaMaldivesMaliMaltaMarshall IslandsMartiniqueMauritaniaMauritiusMayotteMexicoMoldovaMonacoMongoliaMontenegroMontserratMoroccoMozambiqueMyanmarNamibiaNepalNetherlandsNew CaledoniaNew ZealandNicaraguaNigerNiueNorfolk IslandNorth KoreaNorthern Mariana IslandsNorwayOmanPakistanPalauPanamaPapua New GuineaParaguayPeruPhilippinesPitcairnPolandPortugalPuerto RicoQatarRéunionRomaniaRwandaSaint BarthélemySaint HelenaSaint Kitts and NevisSaint LuciaSaint Martin (French part)Saint Pierre and MiquelonSaint Vincent and the GrenadinesSamoaSan MarinoSao Tome and PrincipeSaudi ArabiaSenegalSerbiaSeychellesSierra LeoneSingaporeSint Maarten (Dutch part)SlovakiaSloveniaSolomon IslandsSomaliaSouth Africa South Georgia and the South Sandwich IslandsSouth KoreaSouth SudanSpainSri LankaSudanSurinameSvalbard and Jan MayenSwazilandSwedenSwitzerlandSyriaTaiwanTajikistanTanzaniaThailandTimor LesteTogoTokelauTongaTrinidad and TobagoTunisiaTurkeyTurkmenistanTurks and Caicos IslandsTuvaluUgandaUkraineUnited Arab EmiratesUruguayUS Virgin IslandsUzbekistanVanuatuVatican CityVenezuelaVietnamWallis and FutunaWestern SaharaYemenZambiaZimbabwe
Варианты покупкиЭлектронная книга $72,95
Налог с продаж будет рассчитан при оформлении заказа
Бесплатная доставка по всему миру
Нет минимального заказа
Описание
Алгебра и тригонометрия представляет основы алгебры с некоторыми приложениями и тригонометрией.
Акцент делается на практических навыках, решении проблем и вычислительных методах. Охватываемые темы варьируются от уравнений и неравенств до функций и графиков, полиномиальных и рациональных функций, а также экспонент и логарифмов. Также рассматриваются тригонометрические функции и комплексные числа. Эта книга, состоящая из 11 глав, начинается с обсуждения основ алгебры, каждая тема объяснена, проиллюстрирована и сопровождается обширным набором упражнений. Подчеркивается правильное использование алгебраических обозначений и практических манипулятивных навыков, таких как разложение на множители, использование показателей степени и радикалов и упрощение рациональных выражений, а также наиболее распространенные ошибки в алгебре. Затем читатель знакомится с решением линейных, квадратных и других типов уравнений и систем уравнений, а также с решением неравенств. В последующих главах рассматриваются самые основные функции: полиномиальная, рациональная, экспоненциальная, логарифмическая и тригонометрическая.
Также представлены тригонометрия и обратные тригонометрические функции и тождества. Книга завершается обзором последовательностей, перестановок, комбинаций и биномиальной теоремы. Эта монография будет полезным ресурсом для студентов бакалавриата, изучающих математику и алгебру.
СОДЕРЖАНИЕ
-
ПРЕДИСЛОВИЕ
1 Основная алгебра
1. Характер алгебры
2. Алгебраическая нотация
3. Правила алгебры
4. 4. и Rationals
5. Интегральные экспоненты
6. 6. и Rationers
5.
6. Радикалы
7. Рациональные показатели
8. Многочлены
9. Многочлены от нескольких переменных
10. Факторинг
11. Рациональные выражения
12. Распространенные ошибки в алгебре
Тесты
2 Уравнения и неравенства
и 1. Уравнения0047 2. Линейные уравнения
3. Квадратные уравнения
4. Другие типы уравнений
5. Приложения
6. Порядок
7. Абсолютные значения
8. Неравенства
Тесты
3 Функции и графики
17 Координаты в координатах 29047
3.
Функции
4. Построение функций
5. Линейные функции
6. Квадратичные функции
7. Советы по построению графиков
Тесты
4 Полиномиальные и рациональные функции
1. Введение
2. Графики многочленов
3. Графики факторизованных полиномов
4. Рациональные функции
5. Графики рациональных функций
6. Факторизованные рациональные функции
Тесты
5 Экспоненты и логарифмы
1. Экспоненциальные функции
2. Логарифмические функции 4.047
3. Точность и округление
5. Таблицы и интерполяция
6. Логарифмические вычисления (дополнительно)
7. Вычисления с помощью небольшого калькулятора (дополнительно)
8. Приложения
9. Бизнес-приложения (дополнительно)
Тесты
6 Тригонометрические функции
1. Введение
2. Расстояния и углы
3. Синус и косинус
4. Другие тригонометрические функции
5. Графики синуса и косинуса
6. Графики других функций
Тождества Тесты
7 Обратные функции
1. Основные тождества
2. Законы сложения
3. Дополнительные тождества
4. Обратные функции
5. Приложения
Тесты
8 Тригонометрия
1. Прямоугольные треугольники
2. Косоугольные треугольники
3. Численное решение
4. Приложения к геометрии
5. Векторы (необязательно)
6. Длина и внутреннее произведение (необязательно)
Тесты
9 разделов алгебры
1. Деление многочленов
2. Нули многочленов
3. Частные дроби
4. Системы линейных уравнений
5. Определители
Тесты
10 комплексных чисел
1. Комплексная арифметика
2. Комплексная плоскость
3. Нули многочленов
4. Теорема де Муавра и корни из единицы
Тесты
0047 11 Дискретная алгебра
1. Последовательности
2. Перестановки и комбинации
3. Биномиальная теорема
4. Суммирование
5. Математическая индукция
Тесты
Ответы на упражнения с нечетными номерами
-Place Antilogarithms
3.
Функции 
Основные тождества 