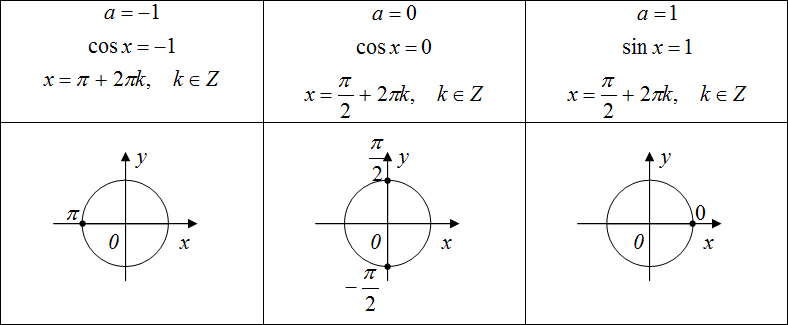Простейшие тригонометрические уравнения формулы частные случаи. Как решать тригонометрические уравнения
Соблюдение Вашей конфиденциальности важно для нас. По этой причине, мы разработали Политику Конфиденциальности, которая описывает, как мы используем и храним Вашу информацию. Пожалуйста, ознакомьтесь с нашими правилами соблюдения конфиденциальности и сообщите нам, если у вас возникнут какие-либо вопросы.
Сбор и использование персональной информации
Под персональной информацией понимаются данные, которые могут быть использованы для идентификации определенного лица либо связи с ним.
От вас может быть запрошено предоставление вашей персональной информации в любой момент, когда вы связываетесь с нами.
Ниже приведены некоторые примеры типов персональной информации, которую мы можем собирать, и как мы можем использовать такую информацию.
Какую персональную информацию мы собираем:
- Когда вы оставляете заявку на сайте, мы можем собирать различную информацию, включая ваши имя, номер телефона, адрес электронной почты и т.
 д.
д.
Как мы используем вашу персональную информацию:
- Собираемая нами персональная информация позволяет нам связываться с вами и сообщать об уникальных предложениях, акциях и других мероприятиях и ближайших событиях.
- Время от времени, мы можем использовать вашу персональную информацию для отправки важных уведомлений и сообщений.
- Мы также можем использовать персональную информацию для внутренних целей, таких как проведения аудита, анализа данных и различных исследований в целях улучшения услуг предоставляемых нами и предоставления Вам рекомендаций относительно наших услуг.
- Если вы принимаете участие в розыгрыше призов, конкурсе или сходном стимулирующем мероприятии, мы можем использовать предоставляемую вами информацию для управления такими программами.
Раскрытие информации третьим лицам
Мы не раскрываем полученную от Вас информацию третьим лицам.
Исключения:
- В случае если необходимо — в соответствии с законом, судебным порядком, в судебном разбирательстве, и/или на основании публичных запросов или запросов от государственных органов на территории РФ — раскрыть вашу персональную информацию.
 Мы также можем раскрывать информацию о вас если мы определим, что такое раскрытие необходимо или уместно в целях безопасности, поддержания правопорядка, или иных общественно важных случаях.
Мы также можем раскрывать информацию о вас если мы определим, что такое раскрытие необходимо или уместно в целях безопасности, поддержания правопорядка, или иных общественно важных случаях. - В случае реорганизации, слияния или продажи мы можем передать собираемую нами персональную информацию соответствующему третьему лицу – правопреемнику.
Защита персональной информации
Мы предпринимаем меры предосторожности — включая административные, технические и физические — для защиты вашей персональной информации от утраты, кражи, и недобросовестного использования, а также от несанкционированного доступа, раскрытия, изменения и уничтожения.
Соблюдение вашей конфиденциальности на уровне компании
Для того чтобы убедиться, что ваша персональная информация находится в безопасности, мы доводим нормы соблюдения конфиденциальности и безопасности до наших сотрудников, и строго следим за исполнением мер соблюдения конфиденциальности.
Требует знания основных формул тригонометрии — сумму квадратов синуса и косинуса, выражение тангенса через синус и косинус и другие. Для тех, кто их забыл или не знает рекомендуем прочитать статью » «.
Для тех, кто их забыл или не знает рекомендуем прочитать статью » «.
Итак, основные тригонометрические формулы мы знаем, пришло время использовать их на практике. Решение тригонометрических уравнений
Исходя из самого названия видно, что тригонометрическое уравнение – это уравнение, в котором неизвестное находится под знаком тригонометрической функции.
Существуют так называемые простейшие тригонометрические уравнения. Вот как они выглядят: sinх = а, cos x = a, tg x = a. Рассмотрим, как решить такие тригонометрические уравнения , для наглядности будем использовать уже знакомый тригонометрический круг.
sinх = а
cos x = a
tg x = a
cot x = a
Любое тригонометрическое уравнение решается в два этапа: приводим уравнение к простейшему виду и далее решаем его, как простейшее тригонометрическое уравнение.
Существует 7 основных методов, с помощью которых решаются тригонометрические уравнения.
Метод замены переменной и подстановки
Решение тригонометрических уравнений через разложение на множители
Приведение к однородному уравнению
Решение уравнений, через переход к половинному углу
Введение вспомогательного угла
Решить уравнение 2cos 2 (x + /6) – 3sin( /3 – x) +1 = 0
Используя формулы приведения получим:
2cos 2 (x + /6) – 3cos(x + /6) +1 = 0
Заменим cos(x + /6) на y для упрощения и получаем обычное квадратное уравнение:
2y 2 – 3y + 1 + 0
Корни которого y 1 = 1, y 2 = 1/2
Теперь идем в обратном порядке
Подставляем найденные значения y и получаем два варианта ответа:
Как решить уравнение sin x + cos x = 1 ?
Перенесем все влево, чтобы справа остался 0:
sin x + cos x – 1 = 0
Воспользуемся вышерассмотренными тождествами для упрощения уравнения:
sin x — 2 sin 2 (x/2) = 0
Делаем разложение на множители:
2sin(x/2) * cos(x/2) — 2 sin 2 (x/2) = 0
2sin(x/2) * = 0
Получаем два уравнения
Уравнение является однородным относительно синуса и косинуса, если все его члены относительно синуса и косинуса одной и той же степени одного и того же угла. Для решения однородного уравнения, поступают следующим образом:
Для решения однородного уравнения, поступают следующим образом:
а) переносят все его члены в левую часть;
б) выносят все общие множители за скобки;
в) приравнивают все множители и скобки к 0;
г) в скобках получено однородное уравнение меньшей степени, его в свою очередь делят на синус или косинус в старшей степени;
д) решают полученное уравнение относительно tg.
Решить уравнение 3sin 2 x + 4 sin x cos x + 5 cos 2 x = 2
Воспользуемся формулой sin 2 x + cos 2 x = 1 и избавимся от открытой двойки справа:
3sin 2 x + 4 sin x cos x + 5 cos x = 2sin 2 x + 2cos 2 x
sin 2 x + 4 sin x cos x + 3 cos 2 x = 0
Делим на cos x:
tg 2 x + 4 tg x + 3 = 0
Заменяем tg x на y и получаем квадратное уравнение:
y 2 + 4y +3 = 0, корни которого y 1 =1, y 2 = 3
Отсюда находим два решения исходного уравнения:
x 2 = arctg 3 + k
Решить уравнение 3sin x – 5cos x = 7
Переходим к x/2:
6sin(x/2) * cos(x/2) – 5cos 2 (x/2) + 5sin 2 (x/2) = 7sin 2 (x/2) + 7cos 2 (x/2)
Пререносим все влево:
2sin 2 (x/2) – 6sin(x/2) * cos(x/2) + 12cos 2 (x/2) = 0
Делим на cos(x/2):
tg 2 (x/2) – 3tg(x/2) + 6 = 0
Для рассмотрения возьмем уравнение вида: a sin x + b cos x = c ,
где a, b, c – некоторые произвольные коэффициенты, а x – неизвестное.
Обе части уравнения разделим на :
Теперь коэффициенты уравнения согласно тригонометрическим формулам обладают свойствами sin и cos, а именно: их модуль не более 1 и сумма квадратов = 1. Обозначим их соответственно как cos и sin , где – это и есть так называемый вспомогательный угол. Тогда уравнение примет вид:
cos * sin x + sin * cos x = С
или sin(x + ) = C
Решением этого простейшего тригонометрического уравнения будет
х = (-1) k * arcsin С — + k, где
Следует отметить, что обозначения cos и sin взаимозаменяемые.
Решить уравнение sin 3x – cos 3x = 1
В этом уравнении коэффициенты:
а = , b = -1, поэтому делим обе части на = 2
Соотношения между основными тригонометрическими функциями – синусом, косинусом, тангенсом и котангенсом — задаются  Одни формулы связывают тригонометрические функции одинакового угла, другие – функции кратного угла, третьи – позволяют понизить степень, четвертые – выразить все функции через тангенс половинного угла, и т.д.
Одни формулы связывают тригонометрические функции одинакового угла, другие – функции кратного угла, третьи – позволяют понизить степень, четвертые – выразить все функции через тангенс половинного угла, и т.д.
В этой статье мы по порядку перечислим все основные тригонометрические формулы, которых достаточно для решения подавляющего большинства задач тригонометрии. Для удобства запоминания и использования будем группировать их по назначению, и заносить в таблицы.
Навигация по странице.
Основные тригонометрические тождества
Основные тригонометрические тождества задают связь между синусом, косинусом, тангенсом и котангенсом одного угла. Они вытекают из определения синуса, косинуса, тангенса и котангенса, а также понятия единичной окружности . Они позволяют выразить одну тригонометрическую функцию через любую другую.
Подробное описание этих формул тригонометрии, их вывод и примеры применения смотрите в статье .
Формулы приведения
Формулы приведения следуют из свойств синуса, косинуса, тангенса и котангенса , то есть, они отражают свойство периодичности тригонометрических функций, свойство симметричности, а также свойство сдвига на данный угол. Эти тригонометрические формулы позволяют от работы с произвольными углами переходить к работе с углами в пределах от нуля до 90
градусов.
Эти тригонометрические формулы позволяют от работы с произвольными углами переходить к работе с углами в пределах от нуля до 90
градусов.
Обоснование этих формул, мнемоническое правило для их запоминания и примеры их применения можно изучить в статье .
Формулы сложения
Тригонометрические формулы сложения показывают, как тригонометрические функции суммы или разности двух углов выражаются через тригонометрические функции этих углов. Эти формулы служат базой для вывода следующих ниже тригонометрических формул.
Формулы двойного, тройного и т.д. угла
Формулы двойного, тройного и т.д. угла (их еще называют формулами кратного угла) показывают, как тригонометрические функции двойных, тройных и т.д. углов () выражаются через тригонометрические функции одинарного угла . Их вывод базируется на формулах сложения.
Более детальная информация собрана в статье формулы двойного, тройного и т.д. угла .
Формулы половинного угла
Формулы половинного угла показывают, как тригонометрические функции половинного угла выражаются через косинус целого угла . Эти тригонометрические формулы следуют из формул двойного угла.
Эти тригонометрические формулы следуют из формул двойного угла.
Их вывод и примеры применения можно посмотреть в статье .
Формулы понижения степени
Тригонометрические формулы понижения степени призваны содействовать переходу от натуральных степеней тригонометрических функций к синусам и косинусам в первой степени, но кратных углов. Иными словами, они позволяют понижать степени тригонометрических функций до первой.
Формулы суммы и разности тригонометрических функций
Основное предназначение формул суммы и разности тригонометрических функций заключается в переходе к произведению функций, что очень полезно при упрощении тригонометрических выражений. Указанные формулы также широко используются при решении тригонометрических уравнений, так как позволяют раскладывать на множители сумму и разность синусов и косинусов.
Формулы произведения синусов, косинусов и синуса на косинус
Переход от произведения тригонометрических функций к сумме или разности осуществляется посредством формул произведения синусов, косинусов и синуса на косинус .
Универсальная тригонометрическая подстановка
Обзор основных формул тригонометрии завершаем формулами, выражающими тригонометрические функции через тангенс половинного угла. Такая замена получила название универсальной тригонометрической подстановки . Ее удобство заключается в том, что все тригонометрические функции выражаются через тангенс половинного угла рационально без корней.
Список литературы.
- Алгебра: Учеб. для 9 кл. сред. шк./Ю. Н. Макарычев, Н. Г. Миндюк, К. И. Нешков, С. Б. Суворова; Под ред. С. А. Теляковского.- М.: Просвещение, 1990.- 272 с.: ил.- ISBN 5-09-002727-7
- Башмаков М. И. Алгебра и начала анализа: Учеб. для 10-11 кл. сред. шк. — 3-е изд. — М.: Просвещение, 1993. — 351 с.: ил. — ISBN 5-09-004617-4.
- Алгебра и начала анализа: Учеб. для 10-11 кл. общеобразоват. учреждений / А. Н. Колмогоров, А. М. Абрамов, Ю. П. Дудницын и др.; Под ред. А. Н. Колмогорова.- 14-е изд.- М.: Просвещение, 2004.
 — 384 с.: ил.- ISBN 5-09-013651-3.
— 384 с.: ил.- ISBN 5-09-013651-3. - Гусев В. А., Мордкович А. Г. Математика (пособие для поступающих в техникумы): Учеб. пособие.- М.; Высш. шк., 1984.-351 с., ил.
Copyright by cleverstudents
Все права защищены.
Охраняется законом об авторском праве. Ни одну часть сайта , включая внутренние материалы и внешнее оформление, нельзя воспроизводить в какой-либо форме или использовать без предварительного письменного разрешения правообладателя.
Тригонометрические уравнения.
Простейшие тригонометрические уравнения.
Методы решения тригонометрических уравнений.
Тригонометрические уравнения. Уравнение, содержащее неизвестное под знаком тригонометрической функции, называется тригонометрическим .
Простейшие тригонометрические уравнения.
Методы решения
тригонометрических уравнений. Решение тригонометрического уравнения
состоит из двух этапов: преобразование уравнения для получения его
простейшего
вида (см.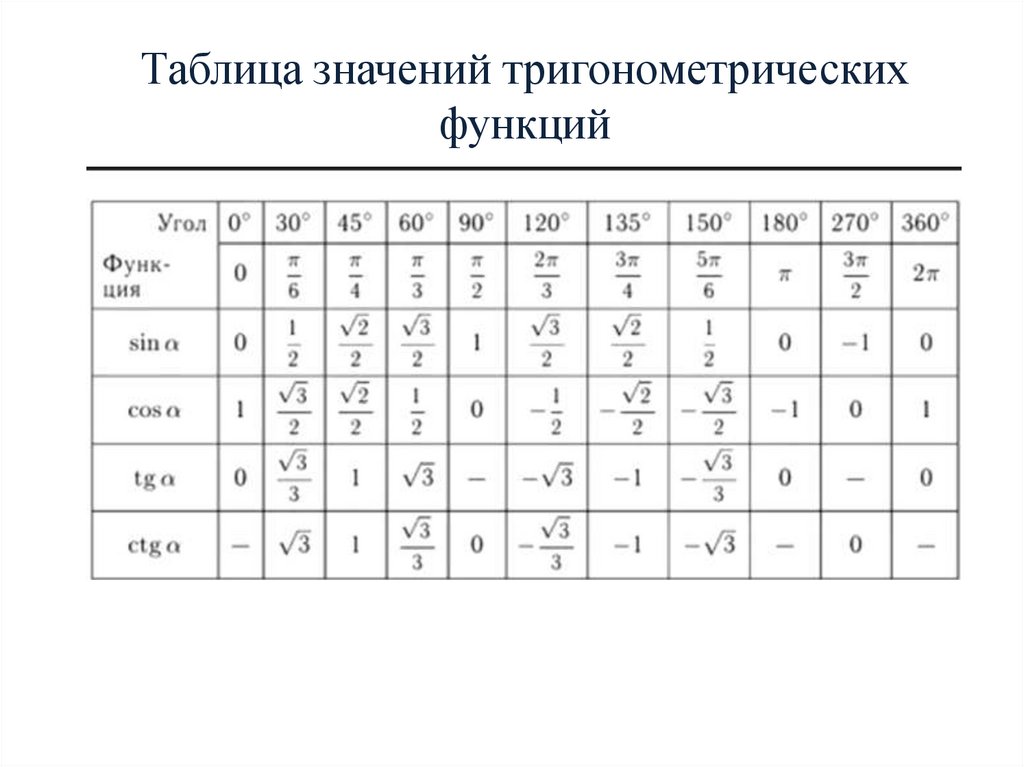 выше
)
и решение полученного простейшего
тригонометрического уравнения.
Существует семь
основных методов решения
тригонометрических уравнений.
выше
)
и решение полученного простейшего
тригонометрического уравнения.
Существует семь
основных методов решения
тригонометрических уравнений.
1. Алгебраический метод. Этот метод нам хорошо известен из алгебры
(метод замены переменной и подстановки).
2. Разложение на множители. Этот метод рассмотрим на примерах.
П р и м е р 1. Решить уравнение: sin x + cos x = 1 .
Р е ш е н и е. Перенесём все члены уравнения влево:
Sin x + cos x – 1 = 0 ,
Преобразуем и разложим на множители выражение в
Левой части уравнения:
П р и м е р 2. Решить уравнение: cos 2 x + sin x · cos x = 1.
Р е ш е н и е. cos 2 x + sin x · cos x – sin 2 x – cos 2 x = 0 ,
Sin x · cos x – sin 2 x = 0 ,
Sin x · (cos x – sin x ) = 0 ,
П р и м е р 3. Решить уравнение:
cos
2 x –
cos
8 x +
cos
6 x = 1.
Решить уравнение:
cos
2 x –
cos
8 x +
cos
6 x = 1.
Р е ш е н и е. cos 2 x + cos 6 x = 1 + cos 8 x ,
2 cos 4x cos 2x = 2 cos ² 4x ,
Cos 4x · (cos 2x – cos 4x ) = 0 ,
Cos 4x · 2 sin 3x · sin x = 0 ,
1). cos 4x = 0 , 2). sin 3x = 0 , 3). sin x = 0 ,
| 3. | Приведение к однородному уравнению. Уравнение называется однородным от носительно sin и cos , если все его члены одной и той же степени относительно sin и cos одного и того же угла . Чтобы решить однородное уравнение, надо: а ) перенести все его члены в левую часть; б ) вынести все общие множители за скобки; в ) приравнять все множители и скобки нулю; г ) скобки, приравненные нулю, дают однородное уравнение меньшей степени, которое следует разделить на cos (или sin ) в старшей степени; д ) решить полученное
алгебраическое уравнение относительно tan . П р и м е р. Решить уравнение: 3 sin 2 x + 4 sin x · cos x + 5 cos 2 x = 2. Р е ш е н и е. 3sin 2 x + 4 sin x · cos x + 5 cos 2 x = 2sin 2 x + 2cos 2 x , Sin 2 x + 4 sin x · cos x + 3 cos 2 x = 0 , Tan 2 x + 4 tan x + 3 = 0 , отсюда y 2 + 4y +3 = 0 , Корни этого уравнения: y 1 = — 1, y 2 = — 3, отсюда 1) tan x = –1, 2) tan x = –3, |
4. Переход к половинному углу. Рассмотрим этот метод на примере:
П р и м е р. Решить уравнение: 3 sin x – 5 cos x = 7.
Р е ш е н и е. 6 sin (x / 2) · cos (x / 2) – 5 cos ² (x / 2) + 5 sin ² (x / 2) =
7 sin ² (x / 2) + 7 cos ² (x / 2) ,
2 sin ² (x / 2) – 6 sin (x / 2) · cos (x / 2) + 12 cos ² (x / 2) = 0 ,
tan ² (x / 2) – 3 tan (x / 2) + 6 = 0 ,
. . . . . . . . . .
. . . . . . . . .
5. Введение вспомогательного угла. Рассмотрим уравнение вида :
a sin x + b cos x = c ,
Где a , b , c – коэффициенты; x – неизвестное.
Теперь коэффициенты уравнения обладают свойствами синуса и косинуса , а именно : модуль ( абсолютное значение ) каждого
|
Заглавная страница
КАТЕГОРИИ: Археология ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрации Техника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ? Влияние общества на человека Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. |
Стр 1 из 2Следующая ⇒ Простейшие тригонометрические уравнения Простейшими называются уравнения sinx=a,cosx=a,tgx=a,ctgx=asinx=a,cosx=a,tgx=a,ctgx=a, где xx — угол, который нужно найти, aa — любое число. Запишем для каждого из них формулы корней. 1. Уравнение sinx=asinx=a. При |a|>1|a|>1 не имеет решений. При |a|≤1|a|≤1 имеет бесконечное число решений. Формула корней: x=(−1)narcsina+πn,n∈Zx=(-1)narcsina+πn,n∈Z Таблица арксинусов 2. Уравнение cosx=acosx=a При |a|>1|a|>1 — как и в случае с синусом, решений среди действительных чисел не имеет. При |a|≤1|a|≤1 имеет бесконечное множество решений. Формула корней: x=±arccosa+2πn,n∈Zx=±arccosa+2πn,n∈Z Таблица арккосинусов Частные случаи для синуса и косинуса в графиках. 3. Уравнение tgx=atgx=a Имеет бесконечное множество решений при любых значениях aa. Формула корней: x=arctga+πn,n∈Zx=arctga+πn,n∈Z Таблица арктангенсов 4. Уравнение ctgx=actgx=a Также имеет бесконечное множество решений при любых значениях aa. Формула корней: x=artga+πn,n∈Zx=artga+πn,n∈Z Таблица арккотангенсов Формулы корней тригонометрических уравнений в таблице Для синуса: Для косинуса: Для тангенса и котангенса: Формулы решения уравнений, содержащих обратные тригонометрические функции: Методы решения тригонометрических уравнений Решение любого тригонометрического уравнения состоит из двух этапов:
Рассмотрим на примерах основные методы решения. Алгебраический метод. В этом методе делается замена переменной и ее подстановка в равенство. Пример. Решить уравнение: 2cos2(x+π6)−3sin(π3—x)+1=02cos2(x+π6)-3sin(π3—x)+1=0 Решение. Используя формулы приведения, имеем: 2cos2(x+π6)−3cos(x+π6)+1=02cos2(x+π6)-3cos(x+π6)+1=0, делаем замену: cos(x+π6)=ycos(x+π6)=y, тогда 2y2−3y+1=02y2-3y+1=0, находим корни: y1=1,y2=12y1=1,y2=12, откуда следуют два случая: 1. cos(x+π6)=1cos(x+π6)=1, x+π6=2πnx+π6=2πn, x1=−π6+2πnx1=-π6+2πn. 2. cos(x+π6)=12cos(x+π6)=12, x+π6=±arccos12+2πnx+π6=±arccos12+2πn, x2=±π3−π6+2πnx2=±π3-π6+2πn. Ответ: x1=−π6+2πnx1=-π6+2πn, x2=±π3−π6+2πnx2=±π3-π6+2πn. Разложение на множители. Пример. Решить уравнение: sinx+cosx=1sinx+cosx=1. Решение. Перенесем влево все члены равенства: sinx+cosx−1=0sinx+cosx-1=0. Используя формулы двойного угла, преобразуем и разложим на множители левую часть: sinx—2sin2 x2=0sinx—2sin2 x2=0, 2sin x2cos x2−2sin2 x2=02sin x2cos x2-2sin2 x2=0, 2sin x2(cos x2−sin x2)=02sin x2(cos x2-sin x2)=0,
Ответ: x1=2πnx1=2πn, x2=π2+2πnx2=π2+2πn. Переход к половинному углу Пример. Решить уравнение: 11sinx—2cosx=1011sinx—2cosx=10. Решение. Применим формулы двойного угла, в результате: 22sin(x2)cos(x2)−22sin(x2)cos(x2)- 2cos2x2+2sin2x2=2cos2x2+2sin2x2= 10sin2x2+10cos2x210sin2x2+10cos2x2 4tg2x2—11tgx2+6=04tg2x2—11tgx2+6=0 Применив описанный выше алгебраический метод, получим:
Ответ. x1=2arctg2+2πn,n∈Zx1=2arctg2+2πn,n∈Z, x2=arctg34+2πnx2=arctg34+2πn, n∈Zn∈Z. Алгебраический метод. В этом методе делается замена переменной и ее подстановка в равенство. Пример. Решить уравнение: 2cos2(x+π6)−3sin(π3—x)+1=02cos2(x+π6)-3sin(π3—x)+1=0 Решение. Используя формулы приведения, имеем: 2cos2(x+π6)−3cos(x+π6)+1=02cos2(x+π6)-3cos(x+π6)+1=0, делаем замену: cos(x+π6)=ycos(x+π6)=y, тогда 2y2−3y+1=02y2-3y+1=0, находим корни: y1=1,y2=12y1=1,y2=12, откуда следуют два случая: 1. 2. cos(x+π6)=12cos(x+π6)=12, x+π6=±arccos12+2πnx+π6=±arccos12+2πn, x2=±π3−π6+2πnx2=±π3-π6+2πn. Ответ: x1=−π6+2πnx1=-π6+2πn, x2=±π3−π6+2πnx2=±π3-π6+2πn. Разложение на множители. Пример. Решить уравнение: sinx+cosx=1sinx+cosx=1. Решение. Перенесем влево все члены равенства: sinx+cosx−1=0sinx+cosx-1=0. Используя формулы двойного угла, преобразуем и разложим на множители левую часть: sinx—2sin2 x2=0sinx—2sin2 x2=0, 2sin x2cos x2−2sin2 x2=02sin x2cos x2-2sin2 x2=0, 2sin x2(cos x2−sin x2)=02sin x2(cos x2-sin x2)=0, 1. sin x2=0sin x2=0, x2=πnx2=πn, x1=2πnx1=2πn. 2. cos x2−sin x2=0cos x2-sin x2=0, tg x2=1tg x2=1, x2=arctg1+πnx2=arctg1+πn, x2=π4+πnx2=π4+πn, x2=π2+2πnx2=π2+2πn. Ответ: x1=2πnx1=2πn, x2=π2+2πnx2=π2+2πn. Переход к половинному углу Пример. Решить уравнение: 11sinx—2cosx=1011sinx—2cosx=10. Решение. Применим формулы двойного угла, в результате: 22sin(x2)cos(x2)−22sin(x2)cos(x2)- 2cos2x2+2sin2x2=2cos2x2+2sin2x2= 10sin2x2+10cos2x210sin2x2+10cos2x2 4tg2x2—11tgx2+6=04tg2x2—11tgx2+6=0 Применив описанный выше алгебраический метод, получим: 1. 2. tgx2=34tgx2=34, x2=arctg34+2πnx2=arctg34+2πn, n∈Zn∈Z. Ответ. x1=2arctg2+2πn,n∈Zx1=2arctg2+2πn,n∈Z, x2=arctg34+2πnx2=arctg34+2πn, n∈Zn∈Z. Простейшие тригонометрические уравнения Простейшими называются уравнения sinx=a,cosx=a,tgx=a,ctgx=asinx=a,cosx=a,tgx=a,ctgx=a, где xx — угол, который нужно найти, aa — любое число. Запишем для каждого из них формулы корней. 1. Уравнение sinx=asinx=a. При |a|>1|a|>1 не имеет решений. При |a|≤1|a|≤1 имеет бесконечное число решений. Формула корней: x=(−1)narcsina+πn,n∈Zx=(-1)narcsina+πn,n∈Z Таблица арксинусов 2. Уравнение cosx=acosx=a При |a|>1|a|>1 — как и в случае с синусом, решений среди действительных чисел не имеет. При |a|≤1|a|≤1 имеет бесконечное множество решений. Формула корней: x=±arccosa+2πn,n∈Zx=±arccosa+2πn,n∈Z Таблица арккосинусов Частные случаи для синуса и косинуса в графиках. 3. Уравнение tgx=atgx=a Имеет бесконечное множество решений при любых значениях aa. Формула корней: x=arctga+πn,n∈Zx=arctga+πn,n∈Z Таблица арктангенсов 4. Уравнение ctgx=actgx=a Также имеет бесконечное множество решений при любых значениях aa. Формула корней: x=artga+πn,n∈Zx=artga+πn,n∈Z Таблица арккотангенсов 12Следующая ⇒ Читайте также: Коммуникативные барьеры и пути их преодоления Рынок недвижимости. Сущность недвижимости Решение задач с использованием генеалогического метода История происхождения и развития детской игры |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2021-04-20; просмотров: 302; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia. 2. Уравнение `cos x=a` При `|a|>1` — как и в случае с синусом, решений среди действительных чисел не имеет. При `|a| \leq 1` имеет бесконечное множество решений. Формула корней: `x=\pm arccos a + 2\pi n, n \in Z` Частные случаи для синуса и косинуса в графиках. 3. Уравнение `tg x=a` Имеет бесконечное множество решений при любых значениях `a`. Формула корней: `x=arctg a + \pi n, n \in Z` 4. Уравнение `ctg x=a` Также имеет бесконечное множество решений при любых значениях `a`. Формула корней: `x=arcctg a + \pi n, n \in Z` Формулы корней тригонометрических уравнений в таблицеДля синуса: Методы решения тригонометрических уравненийРешение любого тригонометрического уравнения состоит из двух этапов:
Тригонометрия прямоугольного треугольника
Прямоугольный треугольник имеет один угол измерения 90°. Хотите узнать больше? Пройдите онлайн-курс Precalculus.
Кроме того, изучение геометрии показывает, что подобные треугольники (где треугольник A подобен треугольнику B, если с помощью некоторой серии перемещений, вращений, отражений и расширений, A может быть преобразован в новый треугольник, конгруэнтный с Б). Свойство подобных треугольников состоит в том, что все их внутренние углы равны, и, следовательно, длины их соответствующих сторон пропорциональны. Некоторые подобные треугольники показаны ниже. Применяя свойства, упомянутые выше, A 1 , A 2 и A 3 пропорциональны (как и H 1 , H 2 и H 3 , 90, а также 1 , О 2 и О 3 ).
Это соотношение применимо к любым двум подобным треугольникам, независимо от того, являются ли они прямоугольными. Кроме того, для любых двух подобных треугольников отношение двух сторон одного треугольника, таким образом, такое же, как отношение двух соответствующих сторон другого треугольника. Например,
Наконец, обратите внимание, что эти соотношения меняются с углом θ Вопрос является численным значением уровня этих сторон. ? Ответ находится в тригонометрических функциях. Давайте снова посмотрим на обычный прямоугольный треугольник с углом θ. Обозначим гипотенузу прямоугольного треугольника H; сторона, противоположная углу θ — это O, а сторона, примыкающая к θ , — это A.
Теперь мы хотим определить функцию с точки зрения каждая пара сторон: O и H, A и H, O и A. Эти функции представляют собой синус , косинус , тангенс и , соответственно угла θ. Для краткости эти функции часто записываются как sin, cos и tan. Ниже приведены отношения этих функций к сторонам прямоугольного треугольника.
Один из способов запомнить эти функции и их отношения к сторонам прямоугольного треугольника — мнемоника на.
В отличие от таких функций, как полиномы, мы обычно не можем вычислить десятичное значение для заданного угла без использования калькулятора или таблицы значений. Однако в некоторых особых случаях мы можем вычислить значения. Чем больше вы используете триггерные функции, тем лучше вы будете знакомиться с этими особыми случаями; однако мы не будем здесь на них сосредотачиваться.
Использование калькулятора в тригонометрии
Хотя таблицы тригонометрических значений доступны в Интернете и в некоторых технических книгах, большинство функций тригонометрического калькулятора сегодня могут вычислять значения, используя значения. Например, если вы используете Windows, встроенный инструмент калькулятора предлагает эту возможность при использовании в «научном» режиме.
Обратите внимание на кнопки «sin», «cos» и «tan» в левой части инструмента. Чтобы использовать эти функции в этом случае, введите значение угла, затем щелкните триггерную функцию. Например, если вы введете 90, а затем нажмите «sin», результат будет 1. Убедитесь, что ваш калькулятор находится в режиме градусов, если вы используете градусы в качестве единицы измерения угла; мы обсудим другую такую единицу, радианы, позже. Однако сейчас мы будем придерживаться исключительно степеней.
Практическая задача: Используйте калькулятор для вычисления приблизительного десятичного значения для каждого приведенного ниже триггерного выражения. Округление неточных десятичных знаков до трех знаков.
а. грех 45° б. cos 0° с. тангенс –10° д. sin 90°
Решение: В каждом случае, используя калькулятор в режиме градусов, введите угол и вычислите триггерную функцию. Возможно, вам придется обратиться к руководству пользователя вашего калькулятора, так как для разных устройств требуются разные процедуры. В любом случае результаты представлены ниже.
а. 0,707 б. 1 в. –0,176 д. 1 Обратные тригонометрические функции Это косеканс (csc), секанс (sec) и котангенс (cot), которые являются не чем иным, как обратными функциями синуса, косинуса и тангенса соответственно.
Не все научные калькуляторы имеют кнопки для этих взаимных функций, но вы можете просто рассчитать соответствующую функцию TRIG, а затем взять его повторную обработку.
Практическая задача: Используйте калькулятор для вычисления приблизительного десятичного значения для каждого приведенного ниже триггерного выражения. Округление неточных десятичных знаков до трех знаков.
а. кроватка 45° б. csc 30° с. сек 45° д. sin 60°
Решение: Опять же, в каждом случае, используя калькулятор в режиме градусов, введите угол и вычислите обратную триггерную функцию. Возможно, вам придется сначала вычислить соответствующую стандартную триггерную функцию, а затем взять ее обратную.
а. б.
с. д. 0,866
Использование триггерных функций
Пока наше изучение триггерных функций выглядит как академическое упражнение. Тем не менее, эти функции бесценны при расчете параметров треугольников, когда предоставляется только некоторая информация. Ниже приведены несколько примеров использования триггерных функций для вычисления неизвестных длин сторон треугольников. Практическая задача:Вычислите длину гипотенузы прямоугольного треугольника.
Решение: Мы хотим вычислить длину гипотенузы (стороны, противоположной прямому углу), учитывая угол 40° и длину смежной стороны 10 единиц. Глядя на наши тригонометрические функции, обратите внимание, что косинус связывает смежную сторону ( A ) и гипотенузу ( H ) с мерой угла.
Подставьте известные значения.
С помощью калькулятора вычислите значение косинуса, затем примените простую алгебру, чтобы найти H. Практическая задача: Равнобедренный треугольник, показанный ниже, имеет высоту 5 дюймов. Какова длина его основания? Решение: Во-первых, обратите внимание, что отрезок, определяющий высоту равнобедренного треугольника, подобного этому, делит треугольник на два конгруэнтных прямоугольных треугольника: угол помечен как x. Итак, мы знаем длину стороны, противоположной углу, и хотим найти длину прилежащей стороны. Это означает, что нам нужно использовать функцию касательной.
Основой треугольника Isocles составляет 2 x, или около 24,75 дюйма. Здесь мы увидели пример того, как тригонометрию можно использовать даже в задачах, не связанных напрямую с прямоугольными треугольниками.
Объяснение урока: Простые тригонометрические уравненияВ этом объяснении мы узнаем, как находить меры угла по заданным значениям интервала и функции. Тригонометрическое уравнение — это уравнение, которое включает по крайней мере одно из следующего: тригонометрическую функцию, такую как синус, косинус или тангенс; обратная тригонометрическая функция, такая как косеканс, секанс или котангенс; или инверсия любого из них. Некоторые из более простых примеров таких уравнений можно решить без использования калькулятора; однако для большинства из них было бы утомительно пытаться запомнить конкретные значения тригонометрической функции. В этих случаях мы используем обратную функцию наряду со знанием симметрии и периодичности их графиков для вычисления дополнительных решений. Прежде чем мы продемонстрируем, как использовать симметрию графика тригонометрической функции для нахождения всех решений в заданном интервале, мы сначала напомним точные значения синуса, косинуса и тангенса ряда специальных углов. Рассмотрим прямоугольный равнобедренный треугольник с двумя сторонами длиной 1 см, как показано на рисунке. Используя теорему Пифагора, мы можем вычислить длину гипотенузы как √1+1=√2см. Затем, используя тригонометрическое соглашение для обозначения сторон относительно угла в верхней части диаграммы, мы можем вычислить точное значение sin(45)∘. синоффипсин𝜃=45=1√2=√22,∘ Используя этот равнобедренный треугольник и приведенный ниже равносторонний треугольник, вы сможете получить следующие точные значения синуса, косинуса и тангенса (как показано в таблице). Точные значения для заданных значений 𝜃 следующие.
Важно, чтобы мы могли вспомнить эти точные значения, не чувствуя необходимости тянуться к калькулятору, и поэтому нам нужно время, чтобы ознакомиться с приведенными таблицами. В первом примере мы покажем, как использовать симметрию графика синуса вместе с таблицей точных значений, чтобы найти все решения простого тригонометрического уравнения. Пример 1. Определение общего решения тригонометрического уравненияКаково общее решение sin𝜃=√22? ОтветЧтобы найти общее решение тригонометрического уравнения, мы начинаем с поиска частного решения. В этом случае может помочь таблица точных тригонометрических величин. Для угла 𝜃, выраженного в радианах, точные значения функции синуса следующие.
We observe that sin𝜋4=√22, so 𝜃=𝜋4 is частное решение уравнения sin𝜃=√22. Чтобы найти другие решения, мы нарисуем график 𝑦=𝜃sin, как показано на следующем рисунке. Решения sin𝜃=√22 находятся добавлением к диаграмме линии 𝑦=√22. Поскольку синусоида имеет симметрию относительно 𝜋2 в интервале 0≤𝜃≤𝜋, второе решение находится вычитанием 𝜋4 из 𝜋: 𝜋−𝜋4=3𝜋4. Помните, функция синуса является периодической с периодом 2𝜋 радиан, поэтому дальнейшие решения можно найти, добавляя или вычитая 2𝜋 радиан из конкретных решений. Другими словами, решение 𝜋4+2𝑛𝜋, 3𝜋4+2𝑛𝜋, для целых значений 𝑛. В качестве альтернативы, это может быть представлено с помощью обозначения множества как 𝜋4+2𝑛𝜋, 3𝜋4+2𝑛𝜋, где 𝑛∈ℤ. В предыдущем примере мы продемонстрировали, как интерпретировать симметрию графика синуса, чтобы найти все решения уравнения. Другим мощным инструментом, который можно использовать для расширения области определения функции синуса, является единичный круг. Помните, что это круг с центром в начале координат и радиусом в 1 единицу. Чтобы использовать единичную окружность для определения синуса 90 575 любого угла 90 576 𝜃, мы начинаем в точке (1,0) и движемся по окружности в направлении против часовой стрелки, пока угол, который образуется между этой точкой, началом , а положительная 𝑥-ось равна 𝜃. Обратите внимание, что значение 𝑦-координаты положительно как в 1-м, так и во 2-м квадрантах; следовательно, значение sin𝜃 также будет положительным в этих квадрантах. Кроме того, поскольку единичный круг обладает отражательной симметрией относительно оси 𝑦, мы можем видеть, что sinsin𝜃=(180−𝜃). Продолжая двигаться по окружности единичной окружности, мы можем увидеть, что sinsin𝜃=(360+𝜃) для всех значений 𝜃. Эти результаты можно обобщить следующим образом. Практическое руководство. Поиск решений простых уравнений с использованием функции синусаЕсли 𝜃=𝜃 является решением уравнения sin𝜃=𝑐, для некоторой константы 𝑐∈[−1,1], второе решение определяется выражением 𝜃=180−𝜃. Тогда множество всех решений sin𝜃=𝑐 равно 𝜃=𝜃+2𝑛𝜋𝜃=𝜋−𝜃+2𝑛𝜋,𝑛∈ℤ.и где Если 𝜃 измеряется в градусах, решения 𝜃=𝜃+360𝑛𝜃=180−𝜃+360𝑛,𝑛∈ℤ.andwhere Хотя нам может показаться склонным запоминать эти формулы, на практике гораздо эффективнее набросать график функции синуса или единичный круг, чтобы помочь нам вывести множество решений уравнения, включающего функцию синуса. Пример 2. Поиск решений тригонометрического уравнения в заданном диапазонеНайдите набор значений, удовлетворяющих 4𝜃−1=0sin, где 90≤𝜃≤360∘∘. ОтветЧтобы решить это простое тригонометрическое уравнение, мы начнем с перестановки, чтобы сделать функцию синуса предметом: 4𝜃−1=04𝜃=1𝜃=14.sinsinsin Необходимо соблюдать осторожность на следующем этапе вычислений. Мы должны взять как положительные, так и отрицательные квадратные корни из 14. Это приведет к созданию пары уравнений с точки зрения греха𝜃: синорсинсинорсин𝜃=14𝜃=-14,𝜃=12𝜃=-12. Обратите внимание, что мы могли бы также разложить выражение 4𝜃−1sin на множители как (2𝜃−1)(2𝜃+1)sinsin, а затем решить уравнение (2𝜃−1)(2𝜃+1)=0sinsin, чтобы получить то же самое результат. Далее, чтобы решить первое уравнение, мы вспоминаем точные значения sin𝜃, где 𝜃 измеряется в градусах, следующим образом.
Следовательно, решением уравнения sin𝜃=12 является 𝜃=30∘. Обратите внимание, что это выходит за пределы указанного интервала 90≤𝜃≤360∘∘, поэтому мы будем учитывать симметрию единичного круга, чтобы найти дальнейшие решения. Мы видим, что единственным решением в заданном интервале является 𝜃=180−30=150∘. Теперь мы решим второе уравнение, снова используя симметрию единичного круга. Поскольку sin𝜃=𝑦 для всех 𝜃, а значение 𝑦 отрицательно в 3-м и 4-м квадрантах, мы добавляем здесь прямоугольные треугольники, как показано. Следовательно, следующие два решения равны 𝜃=180+30=210∘ и 𝜃=360−30=330∘. На этом этапе мы могли бы захотеть найти дополнительные решения, добавив к ним целые числа, кратные 360∘, но это привело бы к значениям, выходящим за пределы требуемого интервала. Набор значений, удовлетворяющих 4𝜃−1=0sin, где 90≤𝜃≤360∘∘, равен {150,210,330}.∘∘∘ В предыдущем примере мы продемонстрировали, как использовать симметрию единичного круга с информацией о точных значениях для решения тригнометрических уравнений, где 𝜃 не является острым углом. Если бы мы выбрали этот метод, нам пришлось бы рассматривать области единичного круга, где 𝜃0∘, и применять правила симметрии и периодичности как обычно. В нашем следующем примере мы рассмотрим, как использовать симметрию графика функции косинуса для решения тригнометрического уравнения. Пример 3. Решение тригонометрического уравнения со смещенным углом в заданном диапазонеНайдите множество значений, удовлетворяющих условию cos(𝜃−105)=−12, где 0𝜃360∘∘. ОтветЧтобы найти решения тригонометрического уравнения в заданном интервале, мы начинаем с поиска конкретного решения. В этом случае может помочь таблица точных тригонометрических величин. Сначала мы переопределим аргумент функции, положив 𝛼=𝜃−105 таким образом, что косанд𝛼=−12𝜃=𝛼+105. Изменение интервала действия наших решений путем добавления
105∘ дает
−105𝛼255∘∘.
Мы видим, что cos𝛼=12; однако в таблице нет таких значений 𝛼, что cos𝛼=−12. Нарисовав график функции косинуса и линии 𝑦=12 и 𝑦=-12, мы можем найти соответствующее значение 𝛼. Граф имеет вращательную симметрию между 0≤𝛼≤180∘∘ около (90,0)∘, поэтому первое решение cos𝛼=−12 есть 𝛼=180−60=120.∘ Используя симметрию кривой, следующее решение 𝛼=180+60=240.∘ По-видимому, есть еще одно решение, полученное с помощью 𝛼=120+360=480∘; однако это вне интервала 105𝛼465∘∘. Следовательно, решения cos𝛼=−12 равны 𝛼=120∘ и 𝛼=240∘. Поскольку мы определили 𝜃=𝛼+105, решения cos(𝜃−105)=−12 равны 𝜃=120+105=225𝜃=240+105=345,∘∘и Следовательно, множество решений
{225 345}. Обратите внимание, что альтернативный метод нахождения частного решения cos𝛼=−12 заключается в использовании функции арккосинуса, такой что 𝛼=−12=120.cos∘ На этом этапе оставшиеся шаги по поиску других решений такие же. Помните, мы также можем использовать симметрию единичного круга для достижения того же результата. Точно так же, как значение 𝑦-координаты точки пересечения конечной стороны угла с единичной окружностью говорит нам значение sin𝜃, значение 𝑥-координаты говорит нам значение cos𝜃. Поскольку значение 𝑥-координаты положительно в 1-м и 4-м квадрантах, в силу симметрии единичного круга coscos𝜃=(360−𝜃). Используя симметрию единичной окружности и периодичность функции косинуса, мы можем привести формулы для общего решения уравнений с участием этой функции. Практическое руководство. Решение простых уравнений с использованием функции косинуса Если 𝜃=𝜃 является решением уравнения cos𝜃=𝑐 для некоторой константы 𝑐∈[−1,1], второе решение определяется выражением 𝜃=360 −𝜃. Если 𝜃 измеряется в градусах, решения 𝜃=𝜃+360𝑛𝜃=360−𝜃+360𝑛,𝑛∈ℤ.andwhere В предыдущем примере мы показали, как решить тригонометрическое уравнение, в котором аргумент тригонометрической функции каким-то образом преобразован. В таких случаях мы начинаем с переопределения аргумента и изменения интервала, на котором мы решаем, что позволяет нам использовать симметрию стандартных тригонометрических кривых, прежде чем окончательно решить полученные уравнения в 𝜃. Как правило, это более разумный путь, чем попытки применить преобразования к кривым тригонометрических функций. Это кратко изложено ниже. Практическое руководство. Решение простого тригонометрического уравнения с преобразованным аргументомСейчас мы продемонстрируем, как использовать эту технику для решения уравнения с тройным углом. Пример 4. Решение тригонометрического уравнения с тройным углом в заданном диапазонеНайдите множество значений, удовлетворяющих условию sin3𝑥=1, где 0≤𝑥≤2𝜋. ОтветЧтобы решить sin3𝑥=1, мы начнем с переопределения аргумента. Положив 𝜃=3𝑥, так что 𝑥=𝜃3, уравнение принимает вид sin𝜃=1, где 0≤𝜃3≤2𝜋. Чтобы упростить этот интервал, мы умножаем на 3, чтобы получить 0≤𝜃≤6𝜋. Теперь мы можем решить уравнение sin𝜃=1 на этом новом интервале. Для угла 𝜃, заданного в радианах, точные значения функции синуса следующие.
Hence, a solution к уравнению sin𝜃=1 равно 𝜃=𝜋2. Мы видим, что решения встречаются каждые 2𝜋 радиан, поэтому наши дополнительные решения равны 𝜃=5𝜋2 и 𝜃=9𝜋2. Следовательно, множество решений sin𝜃=1 на требуемом интервале равно 𝜋2,5𝜋2,9𝜋2. Поскольку 𝑥=𝜃3, мы можем найти множество решений sin3𝑥=1, разделив каждое из этих значений на 3. Тогда множество решений равно 𝜋6,5𝜋6,3𝜋2. Сейчас мы продемонстрируем, как применить этот процесс для решения уравнений, включающих функцию тангенса. Пример 5. Решение тригонометрического уравнения со смещенным двойным углом в заданном диапазонеНайдите множество значений, удовлетворяющих tan2𝑥+𝜋5=−1, где 0≤𝑥≤2𝜋. Ответ Чтобы решить это уравнение, мы начнем с переопределения аргумента, что позволит нам использовать симметрию функции тангенса. Пусть 𝜃=2𝑥+𝜋5, поэтому tan𝜃=−1 на 𝜋5≤𝜃≤21𝜋5. Затем мы можем использовать таблицу точных значений и знания о периодичности функции тангенса для решения этого нового уравнения. Помните, что для 𝜃, измеренного в радианах, точные значения tan𝜃 следующие.
Мы видим, что tan𝜋4=1, поэтому давайте воспользуемся этим, чтобы найти значение 𝜃, где tan𝜃=−1. График 𝑦=𝜃tan нарисован на интервале 0≤𝜃≤21𝜋5 ниже. Мы видим, что график функции тангенса имеет вращательную симметрию относительно (𝑛𝜋,0), где 𝑛∈ℤ. Следовательно, первое решение tan𝜃=−1 равно 𝜃=𝜋−𝜋4=3𝜋4. Точно так же, поскольку функция является периодической с периодом 𝜋 радиан, остальные решения находятся путем добавления к этому значению множителей 𝜋: 𝜃=3𝜋4+𝜋=7𝜋4,𝜃=3𝜋4+2𝜋=11𝜋4,𝜃=3𝜋4+3𝜋=15𝜋4. Теперь у нас есть четыре решения tan𝜃=−1 на требуемом интервале. Аналогичным образом оставшиеся значения 𝑥 равны 31𝜋40, 51𝜋40 и 71𝜋40. Следовательно, набор значений, удовлетворяющих tan2𝑥+𝜋5=−1, где 0≤𝑥≤2𝜋, равен 11𝜋40,31𝜋40,51𝜋40,71𝜋40. В предыдущем примере мы рассмотрели периодичность функции тангенса. Как мы сделали для функций синуса и косинуса, мы можем привести общие решения уравнений, включающих эту функцию. Практическое руководство. Решение простых уравнений с использованием функции тангенсаЕсли 𝜃=𝜃 является решением уравнения tan𝜃=𝑐, для некоторой константы 𝑐∈ℝ множество всех решений уравнения tan𝜃=𝑐 равно 𝜃=𝜃+𝑛𝜋,𝑛∈ℤ.где Если 𝜃 измеряется в градусах, решение 𝜃=𝜃+180𝑛,𝑛∈ℤ.где До сих пор мы рассматривали только «стандартные» тригонометрические функции: синус, косинус и тангенс. Важно понимать, что процесс выполняется для обратных функций: косеканса, секанса и котангенса. Пример 6. Нахождение общего решения обратного тригонометрического уравненияНайдите общее решение уравнения sec𝜃=−√2. ОтветНапомним, что функция секанса является обратной функцией косинуса. Другими словами, секко𝜃≡1𝜃. Следовательно, уравнение sec𝜃=−√2 можно переписать как 1𝜃=-√2𝜃=-1√2=-√22.coscos Мы знаем, что для угла 𝜃, измеренного в радианах, применяются следующие точные значения функции косинуса.
While we observe the value cos𝜋4 равно √22, для −√22 нет значения. Вместо этого мы нарисуем график 𝑦=𝜃cos, чтобы вывести соответствующие решения. Граф имеет вращательную симметрию между 0≤𝛼≤180∘∘ относительно 𝜋2,0, поэтому первое решение cos𝜃=−√22 есть
𝜃=𝜋−𝜋4=3𝜋4. Аналогично, следующее решение дается выражением 𝜃=3𝜋2−𝜋4=5𝜋4. Поскольку функция косинуса является периодической с периодом 2𝜋 радиан, дальнейшие решения находятся путем добавления целых кратных к любому из этих решений. Например, мы могли бы найти другое решение, вычитая 2𝜋 из 5𝜋4: 𝜃=5𝜋4−2𝜋=−3𝜋4. Другими словами, общее решение sec𝜃=−√2 есть 3𝜋4+2𝜋𝑛,5𝜋4+2𝜋𝑛,𝑛∈ℤ.где Альтернативно, где интервал или его общее решение. Сейчас мы повторим ключевые понятия. Ключевые моментыВведение в тригонометриюДобро пожаловать на введение в тригонометрию . Эта веб-книга знакомит учащихся средних и старших классов с тригонометрией с использованием системы углов в градусах и геометрии треугольника. Это первая книга из трех частей: .ВведениеТригонометрия – это наука о треугольниках и углах. Первоначально этот предмет был вдохновлен астрономией, навигацией и геометрией и с тех пор получил широкое применение в математике, физике и информатике. Эта книга знакомит с тригонометрией с использованием системы градусных углов и базовой геометрии. УголкиTODO: дикий угол интерактивный Примечание: Иллюстрация выше является интерактивной, т. е. синие контрольные точки можно перетаскивать. Эти интерактивы появляются на этом веб-сайте. градусов Система градусных углов делит полный оборот на единицы, называемые градусами. В системе координат TODO: показать угловую систему градусов, ориентированную по оси — с нулем вверху. Измерение угловТипы уголковОстрый угол Острый угол определяется как угол, меньший перпендикулярного угла. Тупой угол Угол больше 90 градусов. Перпендикулярный угол Перпендикулярный угол равен четверти полного оборота. TODO: возможно, заменить приведенную выше таблицу с эскизами и определениями Треугольник Треугольник — это трехсторонний многоугольник. Фигура имеет три вершины, соответствующие углам, образованным сторонами фигуры. Существуют различные способы построения треугольника. Треугольник имени можно разбить на префикс «три», означающий три, и «угол». Форма проста, универсальна и, если присмотреться, имеет много общего с кругами. Остроугольный треугольникТупоугольный треугольникПрямоугольный треугольникПрямоугольный треугольник является частным случаем общего треугольника, где один из углов равен . TODO: показать разные случаи деления треугольников Специальные треугольникиЕсть два особых прямоугольных треугольника, свойства которых полезны и проявляются во многих местах: прямоугольный треугольник 45 45 90 и прямоугольный треугольник 30 60 90. Поскольку углы треугольников делят полный оборот поровну, их геометрия появляется во многих особых случаях. TODO: Почему треугольник 30-60-90 появляется в такой простой форме? 45-45-90 естественным образом следует из деления квадрата на диагональ. Теорема ПифагораУникальное свойство прямоугольного треугольника определяется теоремой Пифагора, которая связывает квадраты сторон вместе. Это можно визуализировать, нарисовав квадратную площадь каждой стороны рядом с прямоугольным треугольником. Триггер. ФункцииТригонометрические функции возвращают отношения сторон прямоугольного треугольника, если в качестве входных данных задан угол прямоугольного треугольника. Исторически сложилось так, что до появления калькуляторов и компьютеров углы, соответствующие отношениям, хранились в таблице. Ниже показаны прямоугольные определения тригонометрических функций.
Мнемоника «SoaCaoToa» — это мнемоника, которую можно использовать для запоминания различных соотношений, возвращаемых функцией. СинусУчитывая угол прямоугольного треугольника, функция синуса возвращает отношение его противоположной стороны к гипотенузе. КосинусДля заданного угла прямоугольного треугольника функция косинуса возвращает отношение прилежащего к гипотенузе. КасательнаяПри заданном угле прямоугольного треугольника функция тангенса возвращает отношение противоположного угла к прилежащему. Таблица соотношенийВ то время как калькуляторы повсюду и легко доступны в современной математике, исторически таблицы использовались для поиска соотношений, соответствующих углу. Именно поэтому тригонометрические функции также называют тригонометрические соотношения . Общие коэффициенты
Trig IdentitiesТригонометрические тождества представляют собой набор полезных уравнений, которые можно использовать для преобразования математических выражений и управления ими. Они представляют собой комбинацию различных теорем и наблюдений, относящихся к треугольникам. Однако для краткости в этой книге рассматриваются только две группы идентичностей. Сумма двух углов и разность двух углов. Сумма двух угловСумма двух углов выражает тригонометрические отношения синуса и косинуса через отношения отдельных углов. Эти тождества можно визуально выразить как «доказательство без слов», как показано на рисунке ниже. Чтобы получить это доказательство, см. эту страницу. Разность двух углов Разность двух углов выражает тригонометрические отношения синуса и косинуса через отношения отдельных углов. |

 д.
д. Мы также можем раскрывать информацию о вас если мы определим, что такое раскрытие необходимо или уместно в целях безопасности, поддержания правопорядка, или иных общественно важных случаях.
Мы также можем раскрывать информацию о вас если мы определим, что такое раскрытие необходимо или уместно в целях безопасности, поддержания правопорядка, или иных общественно важных случаях. — 384 с.: ил.- ISBN 5-09-013651-3.
— 384 с.: ил.- ISBN 5-09-013651-3.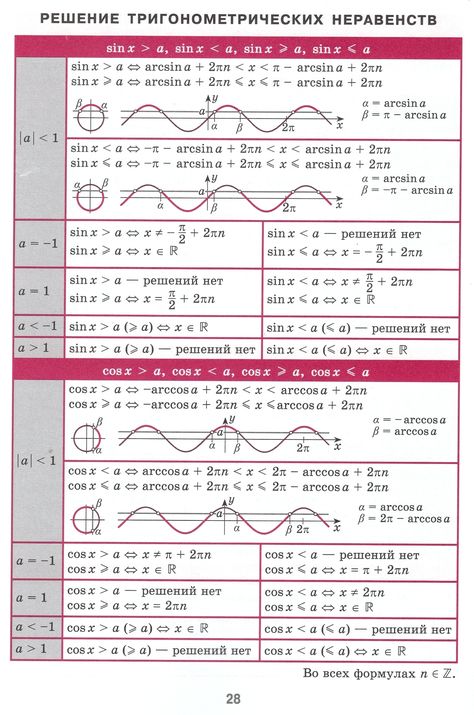

 Определение реакций опор и моментов защемления
Определение реакций опор и моментов защемления
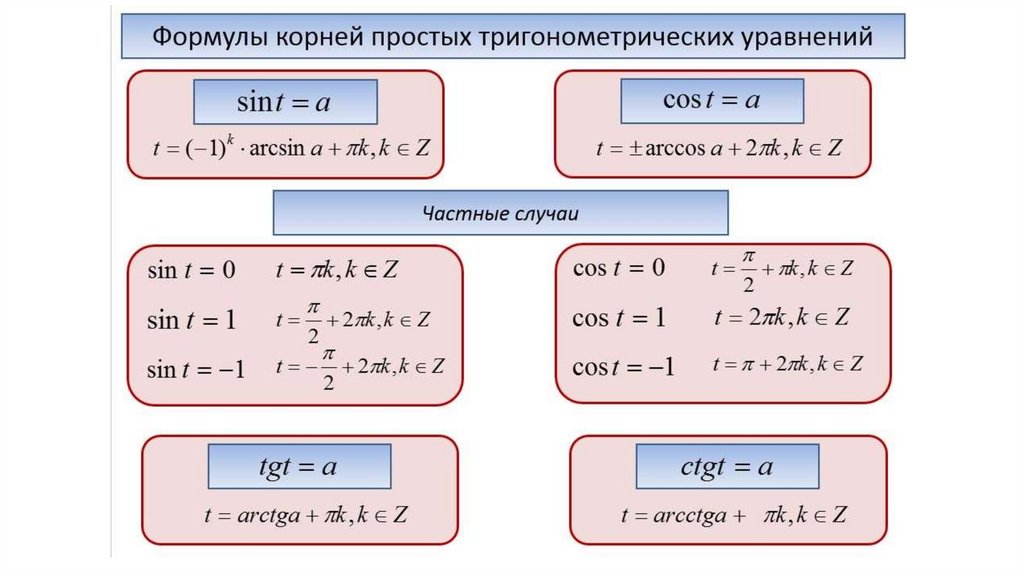


 cos(x+π6)=1cos(x+π6)=1, x+π6=2πnx+π6=2πn, x1=−π6+2πnx1=-π6+2πn.
cos(x+π6)=1cos(x+π6)=1, x+π6=2πnx+π6=2πn, x1=−π6+2πnx1=-π6+2πn. tgx2=2tgx2=2, x1=2arctg2+2πnx1=2arctg2+2πn, n∈Zn∈Z,
tgx2=2tgx2=2, x1=2arctg2+2πnx1=2arctg2+2πn, n∈Zn∈Z,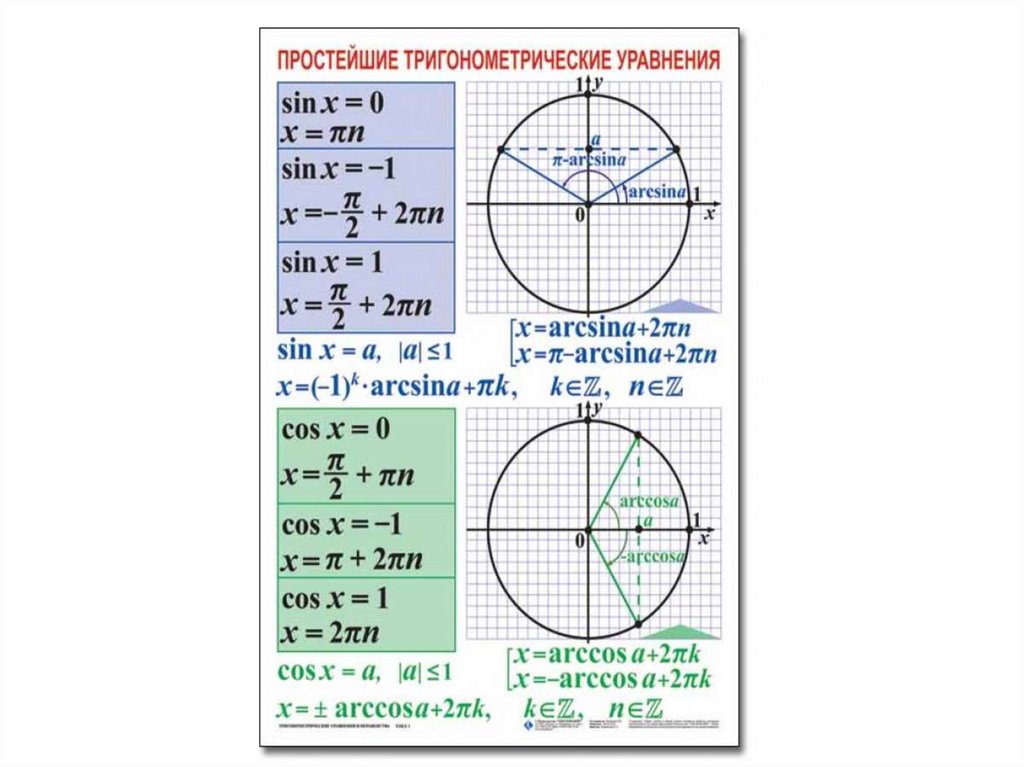
 n arcsin a + \pi n, n \in Z`
n arcsin a + \pi n, n \in Z` 2 x=0`, `sin x(1-sin x)=0`. Тогда `sin x=0` или `1-sin x=0`.
2 x=0`, `sin x(1-sin x)=0`. Тогда `sin x=0` или `1-sin x=0`. выше
)
и решение полученного простейшего
тригонометрического уравнения.
Существует семь
основных методов решения тригонометрических уравнений.
выше
)
и решение полученного простейшего
тригонометрического уравнения.
Существует семь
основных методов решения тригонометрических уравнений. 

 . . . . . . . . .
. . . . . . . . .




 Для любого треугольника сумма внутренних углов равна 180°. Ниже приведен пример прямоугольного треугольника, где маленький «квадрат» указывает на правую сторону (90°) угол. Один угол обозначен θ; другой угол равен 90° – θ .
Для любого треугольника сумма внутренних углов равна 180°. Ниже приведен пример прямоугольного треугольника, где маленький «квадрат» указывает на правую сторону (90°) угол. Один угол обозначен θ; другой угол равен 90° – θ .  Итак, глядя только на первые два треугольника, мы можем написать следующее выражение:
Итак, глядя только на первые два треугольника, мы можем написать следующее выражение: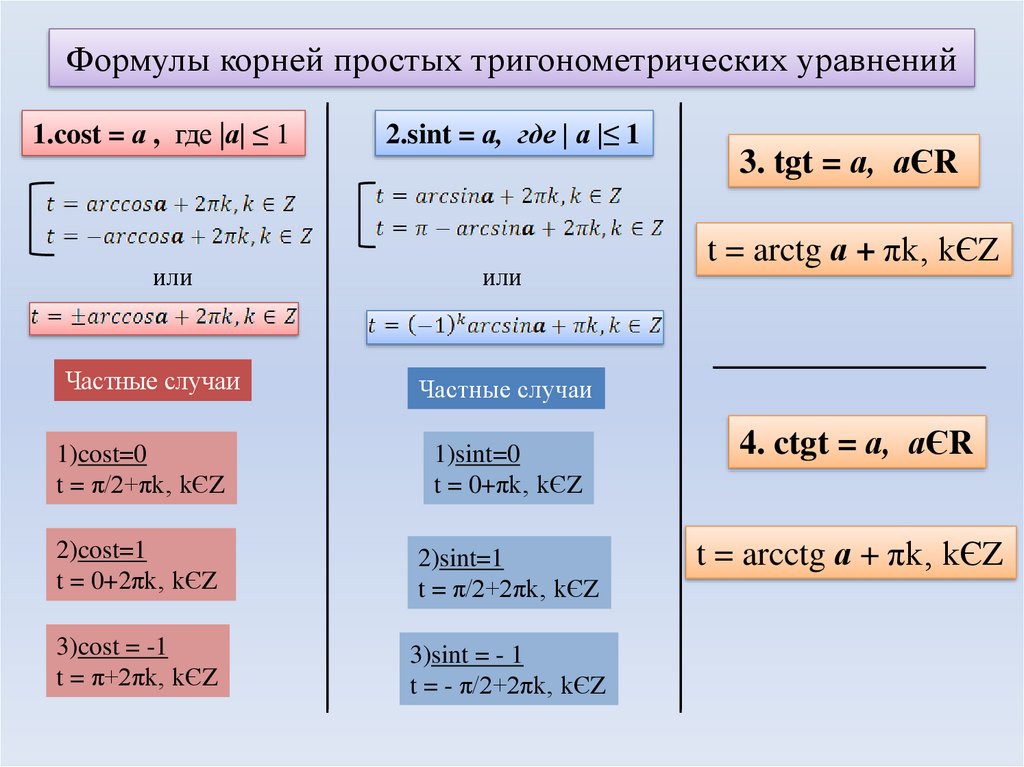 (Рисунок ниже не обязательно выполнен в масштабе.)
(Рисунок ниже не обязательно выполнен в масштабе.)
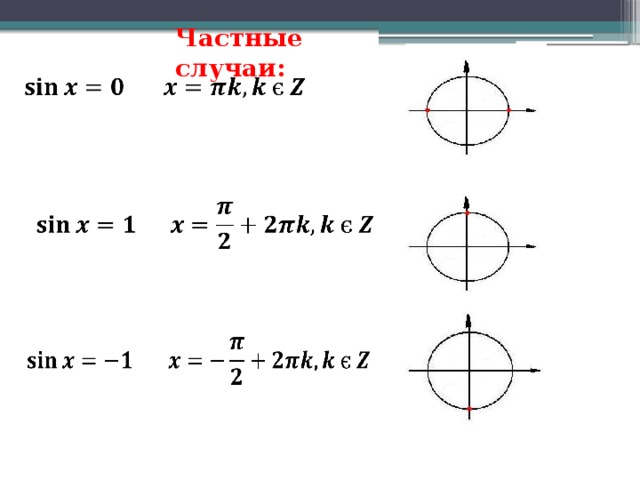
 Эти функции определены ниже — обратите внимание, что мы снова ссылаемся на стороны O, A и H одного и того же прямоугольного треугольника.
Эти функции определены ниже — обратите внимание, что мы снова ссылаемся на стороны O, A и H одного и того же прямоугольного треугольника.




 Значения 𝜃 в точках пересечения этой линии с синусоидой являются решениями уравнения.
Значения 𝜃 в точках пересечения этой линии с синусоидой являются решениями уравнения. Тогда, если эта точка имеет координаты (𝑥,𝑦), sin𝜃 равен значению 𝑦.
Тогда, если эта точка имеет координаты (𝑥,𝑦), sin𝜃 равен значению 𝑦. Давайте продемонстрируем это на нашем следующем примере.
Давайте продемонстрируем это на нашем следующем примере. 0477
0477 Стоит отметить, что для решения второго уравнения sin𝜃=−12 мы могли бы в качестве альтернативы использовать функцию обратного синуса и калькулятор, чтобы найти
𝜃=−12=−30.sin∘
Стоит отметить, что для решения второго уравнения sin𝜃=−12 мы могли бы в качестве альтернативы использовать функцию обратного синуса и калькулятор, чтобы найти
𝜃=−12=−30.sin∘ Тогда точные значения cos𝛼, где 𝛼 измеряется в градусах, следующие.
Тогда точные значения cos𝛼, где 𝛼 измеряется в градусах, следующие. ∘∘
∘∘ Тогда множество всех решений cos𝜃=𝑐 есть
𝜃=𝜃+2𝑛𝜋𝜃=2𝜋−𝜃+2𝑛𝜋,𝑛∈ℤ.и где
Тогда множество всех решений cos𝜃=𝑐 есть
𝜃=𝜃+2𝑛𝜋𝜃=2𝜋−𝜃+2𝑛𝜋,𝑛∈ℤ.и где
 Чтобы найти дальнейшие решения, нарисуем график 𝑦=𝜃sin на интервале 0≤𝜃≤6𝜋, помня, что функция синуса является периодической с периодом 2𝜋 радиан.
Чтобы найти дальнейшие решения, нарисуем график 𝑦=𝜃sin на интервале 0≤𝜃≤6𝜋, помня, что функция синуса является периодической с периодом 2𝜋 радиан.
 Поскольку мы определили 𝜃=2𝑥+𝜋5, мы можем найти значение 𝑥, установив 𝜃=2𝑥+𝜋5 в каждом случае и найдя 𝑥. В случае первого значения 𝜃 это дает
2𝑥+𝜋5=3𝜋42𝑥=11𝜋20𝑥=11𝜋40.
Поскольку мы определили 𝜃=2𝑥+𝜋5, мы можем найти значение 𝑥, установив 𝜃=2𝑥+𝜋5 в каждом случае и найдя 𝑥. В случае первого значения 𝜃 это дает
2𝑥+𝜋5=3𝜋42𝑥=11𝜋20𝑥=11𝜋40. Мы продемонстрируем это на следующем примере.
Мы продемонстрируем это на следующем примере.


 Например, треугольник, показанный в интерактивном ниже, образован тремя точками. Синие контрольные точки можно перетаскивать, чтобы изменить форму треугольника.
Например, треугольник, показанный в интерактивном ниже, образован тремя точками. Синие контрольные точки можно перетаскивать, чтобы изменить форму треугольника. Приводит ли построение шестиугольника к простой форме этого особого треугольника?
Приводит ли построение шестиугольника к простой форме этого особого треугольника?
 000
000  000
000  430
430