Функция корень из х (y = √x) её свойства и график, примеры
График и свойства функции $y = \sqrt{x}$
Составим таблицу для расчёта значений функции $y = \sqrt{x}$.
x | 0 | 0,25 | 1 | 2,25 | 4 | 6,25 | 9 | 12,25 | 16 |
$y = \sqrt{x}$ | 0 | 0,5 | 1 | 1,5 | 2 | 2,25 | 3 | 3,5 | 4 |
Отметим полученные точки на координатной плоскости и соединим их кривой:
Свойства функции $y = \sqrt{x}$
1. Область определения $x \in [0;+\infty)$ — все неотрицательные действительные числа.
2. Область значений $y \in [0;+\infty)$ — все неотрицательные действительные числа.
3. Наименьшее значение функции y = 0 при x = 0.
2 $
$ 0,17 \gt 0,16 \Rightarrow \sqrt{0,17} \gt 0,4 $
$ в) \sqrt{0,7} и-1 $
$ \sqrt{0,7} \gt 0 \gt -1 \Rightarrow \sqrt{0,7} \gt -1 $
$ г) \sqrt{2,3} и \sqrt{2 \frac{1}{3}} $
$ 2 \frac{1}{3} = 2,333… = 2,(3) \gt 2,3 $
$ 2,3 \lt 2,(3) \Rightarrow \sqrt{2,3} \lt \sqrt{2 \frac{1}{3}} $
Пример 3. Расположите числа в порядке возрастания:
$ а) \sqrt{0,4}; \frac{1}{3}; \sqrt{\frac{2}{9}}; \sqrt{3 \frac{1}{3}}; 1,8 $
Возведем весь ряд чисел в квадрат: $ 0,4; \frac{1}{9}; \frac{2}{9};3 \frac{1}{3};3,24 $
Расположим по возрастанию: $\frac{1}{9};\frac{2}{9};0,4;3,24; \sqrt{3 \frac{1}{3}}$
Опять вернёмся к корням:
$$ \frac{1}{3}; \sqrt{\frac{2}{9}}; \sqrt{0,4}; 1,8; \sqrt{3 \frac{1}{3}} $$
$ б) 0,7;-1; \sqrt{0,2};-0,5;\sqrt{0,25} $
(!) Уберем из ряда отрицательные числа: -1;-0,5
Оставшиеся числа возведём в квадрат: 0,49;0,2;0,25
Вернёмся к корням из оставшихся чисел: $\sqrt{0,2}; \sqrt{0,25}; 0,7$
Расположим всё по возрастанию:
$$ -1;-0,5; \sqrt{0,2}; \sqrt{0,25};0,7 $$
Пример 4.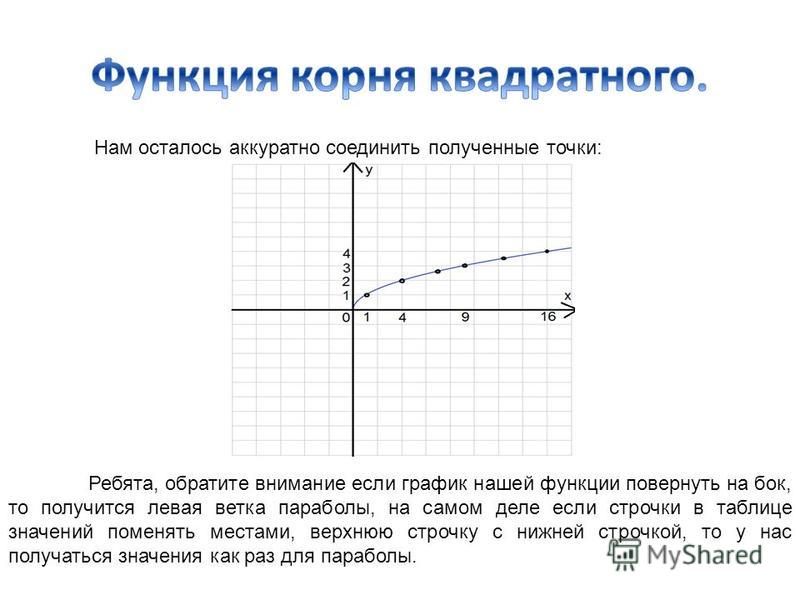
Решите уравнение графически:
а)
$ \sqrt{x} — \frac{8}{x} = 0 $
$ \sqrt{x} = \frac{8}{x} $
Чертим два графика:
$y = \sqrt{x} и y = \frac{8}{x}$
Ответ: x = 4
б)
$x+ \sqrt{x} = 2$
$ \sqrt{x} = -x+2 $
Чертим два графика:
$y = \sqrt{x} и y = -x+2$
Ответ: x = 1
в*)
$ \sqrt{|2x-1|} = 1 $
Область определения:
$x \in \Bbb R$, выражение под корнем всегда неотрицательно.
$ \sqrt{|2x-1|} = 1 \iff |2x-1| = 1 $
Чертим два графика:
$y = |2x-1| и y = 1$
Ответ: x = 1
г*)
$ \sqrt{|2x-1|} = \sqrt{2-x} $
Область определения: $x \le 2$
$ \sqrt{|2x-1|} = \sqrt{2-x} $
$ \iff {\left\{ \begin{array}{c} |2x-1| = \sqrt{2-x} \\ x \le 2 \end{array} \right.}$
Чертим два графика:
и выбираем корни слева от 2.
Ответ: $ x_1 = -1, x_2 = 1 $
Арифметический квадратный корень 8 класс онлайн-подготовка на Ростелеком Лицей
Арифметический квадратный корень
Пусть известно, что площадь квадрата равна 64 см2.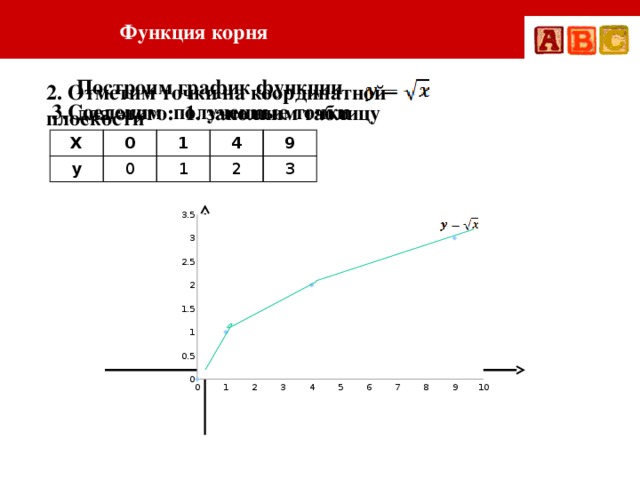
Чему равна длина стороны этого квадрата?
Обозначим длину стороны за х см.
Тогда выражение для площади S = х·х = х2 (см2).
Получим уравнение х2 = 64.
У этого уравнения два корня – х1 = 8 и х2 = -8.
Но длина стороны квадрата не может быть отрицательным числом, поэтому условию задачи удовлетворяет только х1.
Квадратным корнем из числа а называют число, квадрат которого равен а.
То есть квадратными корнями из 64 являются числа 8 и -8.
Число 8 – неотрицательный корень из 64, другими словами – арифметический.
Арифметическим квадратным корнем из числа а называется такое неотрицательное число, квадрат которого равен а.
Арифметический квадратный корень из числа а обозначают a. Знак √ называют знаком арифметического квадратного корня или знаком радикала. Выражение, стоящее под знаком корня, называют подкоренным выражением.
Запись a читают как «квадратный корень из а», слово «арифметический» при этом опускают.
Приведем примеры нахождения (еще говорят извлечения) арифметических квадратных корней.
4=2, так как 2 – неотрицательное и 22= 4.
1,21=1,1, так как 1,1 – число неотрицательное и 1,12 = 1,21.
0=0, так как 0 число неотрицательное и 02= 0.
В общем случае
При а<0 выражение a не имеет смысла.
Арифметический квадратный корень из отрицательных чисел не существует.
Например, -16 не имеет смысла, т. к. нет такого действительного числа a, которое в квадрате равно отрицательному числу: a2=-16.
При любом а, при котором выражение a имеет смысл, верно равенство (a)2=a.
Чтобы найти квадратный корень из числа, необходимо хорошо знать квадраты чисел.
Часто используемые квадраты целых чисел:
12 = 1
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
|
1 |
4 |
9 |
16 |
25 |
36 |
49 |
64 |
81 |
100 |
|
11 |
12 |
13 |
14 |
|
16 |
17 |
18 |
19 |
20 |
25 |
|
121 |
144 |
169 |
196 |
225 |
256 |
289 |
324 |
361 |
400 |
625 |
Значит, 81=9; 121=11 и т.
д.
Обрати внимание!
1=1; 0=0.
Если подкоренное число — десятичная дробь, то необходимо обращать внимание на количество цифр после запятой:
0,09=0,3, так как 0,32 = 0,3·0,3 = 0,09
0,0016=0,04.
Если подкоренное число заканчивается нулями, то необходимо обращать внимание на их количество:
400=20; 121000=1100.
2)=квадратный корень из 2, который не равен x+yПодписаться І 4
Подробнее
Отчет
3 ответа от опытных наставников
Лучший Новейшие Самый старыйАвтор: Лучшие новыеСамые старые
Парвиз Ф. ответил 18.03.14
Репетитор
92 ) = X + Y = 4 +3 =7
Учащиеся должны помнить, что они могут умножать и делить радикалы. но не может добавить или вычесть.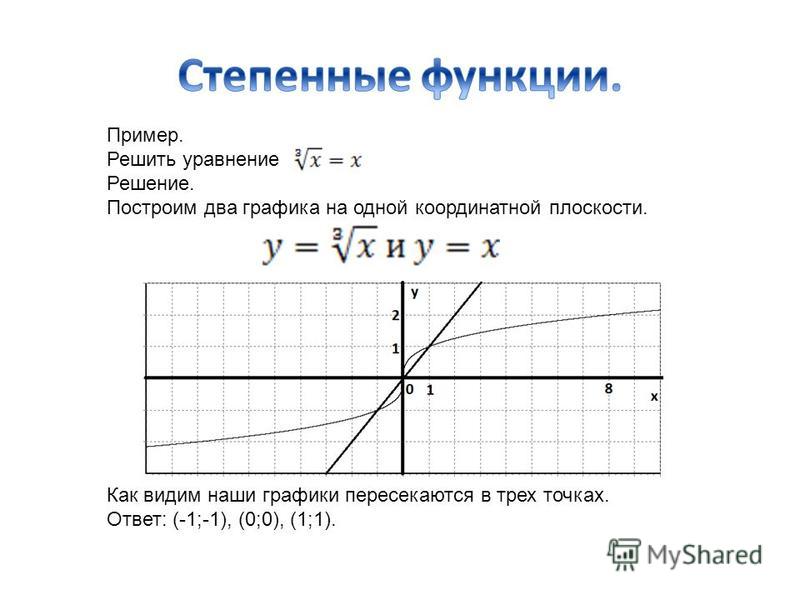
Голосовать за 0 голос против
Подробнее
Отчет
Стив С. ответил 18.03.14
Репетитор 92) ≠ х+у.
Голосовать за 0 голос против
Подробнее
Отчет
Эбенезер О. ответил 17.03.14
Репетитор
4.6 (13)
Выпускник аэрокосмической инженерии и управления воздушным движением для общего редактора. Репетиторство
Посмотреть таких репетиторов
Смотрите таких репетиторов
Итак, вам дано; √[(x 2 +y 2 )=4]
мы разобьем их на отдельные компоненты;
√x 2 + √y 2 = √4
Квадраты отменяют квадратные корни, и вы найдете квадратный корень 4
x + y = 2x + y = 2
Итак, вы правы.
Голосовать за 0 голос против
Подробнее
Отчет
Все еще ищете помощь? Получите правильный ответ, быстро.
Задайте вопрос бесплатно
Получите бесплатный ответ на быстрый вопрос.
Ответы на большинство вопросов в течение 4 часов.
ИЛИ
Д18
#1
Судя по всему, нет.
Не домашняя работа — просто провести некоторое время, возясь с математикой и пытаясь решить это в моем старом, скрюченном, иссохшем мозгу.
График y=sqrt(x) представляет собой лежащую на боку полупараболу – только положительные числа. 92 = x, и вы знаете, что такое x, вы можете сузить то, что такое y, только до двух возможностей. Например, если x = 4, вы знаете только, что либо y = 2, либо y = -2.
Джон_Мейс
#4
Я просто хочу сказать, что я абсолютно люблю эту песню и эту конкретную строчку в ней! Я тоже постоянно им пользуюсь!
Д18
#5
Спасибо за ответы.
Это кажется странно асимметричным, но это так!
И Джон Мейс: пой, брат!
Тадлоу_Боинк
#6
TonySinclair и leahcim дали хорошие и простые ответы. Я просто добавлю, что это не уникально для уравнения x = y[sup]2[/sup]; существует множество примеров отношений между x и y, где существует более одного возможного значения y для заданного x, так что вы не можете найти y = функцию от x. Студенты, изучающие алгебру, узнают о «тесте на вертикальную линию»: если любая вертикальная линия может касаться графика уравнения более чем в одной точке, у вас возникает такая же ситуация, как здесь: у вас есть более одного y для одного и того же x, поэтому вы не можете записать у как функцию от х.
ZenBeam
#7
Это зависит от того, определяется ли «sqrt(x)» как означающий либо квадратный корень, либо главный квадратный корень.
Согласно Википедии,
В математике квадратный корень из числа a — это число y такое, что y2 = a, другими словами, число y, квадрат которого (результат умножения числа на себя, или y × y) равен a.
[…]
Хотя главный квадратный корень положительного числа является лишь одним из двух его квадратных корней, обозначение «квадратный корень» часто используется для обозначения главного квадратного корня.
Если вы просто скажете «sqrt(x)» без каких-либо уточнений, это двусмысленно, что вы имеете в виду.
ультрафильтр
#8
Нет, довольно однозначно главный.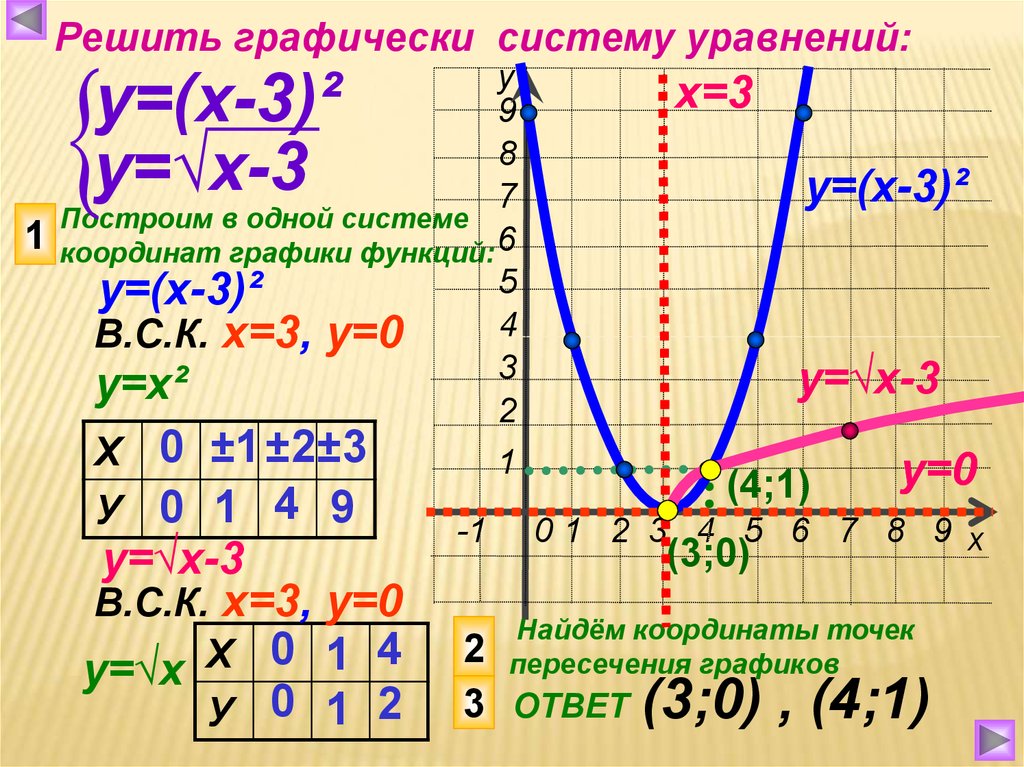
Существуют ли какие-либо сложные математические задачи, в которых «формулировка» вопроса одним способом, преобразование его в другой, а затем обратное преобразование создает логический абсурд?
дракои
#10
Когда я учился в школе, мы научились использовать маркеры абсолютного значения при решении подобных уравнений.
92 = x, вы действительно хотели бы преобразовать его в |y| = sqrt(x), чтобы не потерять половину возможных результатов. Потому что |-5| = 5, вы сохраняете тот же график с кривой как выше, так и ниже оси xНикто больше не упомянул об этом, так что, возможно, это просто мой учитель сделал это замечание.
Джарагон
#11
дракои:
Когда я учился в школе, мы научились использовать маркеры абсолютного значения при решении подобных уравнений. 92 = x, вы действительно хотели бы преобразовать его в |y| = sqrt(x), чтобы не потерять половину возможных результатов. Потому что |-5| = 5, вы сохраняете тот же график с кривой как выше, так и ниже оси x
Никто больше об этом не упоминал, так что, возможно, это просто мой учитель.
Это правда, но вы больше не работаете с функциями, если вы это сделаете. Большая часть причин, по которым мы предполагаем, что y=sqrt(x) берет положительный квадратный корень, заключается в том, что оба результата не являются функцией. |y|=sqrt(x) (или даже |y|=x) приводит к той же «проблеме». 92=25
И отвечает на вопрос +/- 5. Он не прав?
Да. Возведение в квадрат обеих частей уравнения может привести к посторонним решениям, которые не применимы к исходному уравнению, как показывает ваш пример.
y=5 имеет только одно решение, но (y)[sup]2[/sup] = (5)[sup]2[/sup] имеет два, одно из которых не относится к первому уравнению, потому что -5 а 5 — разные числа, которые «становятся» равными, когда их возводят в квадрат.
Вот более сложный пример того, как возведение в квадрат обеих частей уравнения может привести к посторонним решениям. Если вам нужны дополнительные примеры, некоторые из них есть в этом PDF-файле.
Тадлоу_Боинк
№13
ZenBeam:
Это зависит от того, определен ли «sqrt(x)» как означающий либо квадратный корень, либо главный квадратный корень.
Согласно Википедии,
Если вы просто скажете «sqrt(x)» без каких-либо уточнений, это двусмысленно, что вы имеете в виду.
2=25 92=x означает ли, что нас интересует только положительный корень?
2=25 92=x означает ли, что нас интересует только положительный корень?Да, Джонни ошибается. Чтобы использовать еще более вопиющий пример, предположим, что у Джонни есть проблема:
y = sqrt(25)
И он решает умножить обе части уравнения на ноль, чтобы получить:
0*y = 0
Тогда Джонни поворачивается и говорит: «Это уравнение верно для любого y, поэтому y — любое действительное число».
Это нечто тонкое, что часто упускается из виду на первых курсах алгебры. Когда вы решаете уравнение, многократно применяя функции к обеим частям, вы рассуждаете о переменных, участвующих в уравнении. Абстрактно вы рассуждаете (совершенно справедливо): 92 = 25 подразумевает y = 5.
Конечно, чтобы замутить воду, вы можете сделать второй вывод, если f является обратимым . (Фактически обратимые определяются как «функции, для которых можно сделать такой вывод»).
К сожалению, поскольку большинство функций, используемых в элементарной алгебре для решения уравнений (например, u -> u — b или u -> a * u), оказались обратимыми, учителя склонны замалчивать это требование до тех пор, пока вредные привычки не исчезнут.
уже сформировался.
дропзона
№15
Джон_Мейс:
Я просто хочу сказать, что я очень люблю эту песню…
Разве это не песня Чикаго? Нет, я помню — это было ЕСЛИ Y = 25 ИЛИ 624, ТО GOSUB что-то.
Сенегоид
№16
Когда я впервые взял Алгебру I в 9В 1965 году, когда мы учились в 1-м классе, нам определенно вдалбливали такие вещи, но я и я думаю, что в то время это постоянно сбивало с толку большую часть класса.
Прежде всего, несмотря на все уже опубликованные противоречивые замечания: Да, здесь ЕСТЬ элемент чистого произвольного соглашения: обозначение sqrt(x) или √ равно , несколько произвольно определяемому для обозначения только положительного квадратного корня.
Таким образом, утверждение: y = √25 может означать ТОЛЬКО положительный корень, просто потому, что мы все согласились, что символ √ означает именно это.
Тем не менее, факт остается фактом: учитывая утверждение: y[sup]2[/sup] = 25, вы можете подставить y = 5 или y = -5, и это сработает. В этой формулировке искусственное ограничение отсутствует.
То же самое относится и к функции абсолютного значения, которая также всегда вызывала путаницу.
Соглашение дает нам возможность указать, какие именно квадратные корни нам нужны. Если мы просто хотим поговорить о положительном, или главном, корне, нотация √x позволяет нам это сделать.
Если мы хотим поговорить об отрицательном корне, то для этого у нас есть запись -√x.
И, если мы на самом деле хотим говорить об ОБОИХ корнях (что мы иногда и делаем), мы с большой радостью и ликованием отмечаем, что для этого у нас есть запись ±√x! Таким образом, условные обозначения дают нам возможность говорить именно то, что мы имеем в виду, и иметь в виду именно то, что мы говорим!
На уровне начальных классов алгебры это, пожалуй, лучше всего видно в квадратичной формуле , что дает нам оба решения общего квадратного уравнения a x [sup]2[/sup] + b x + c = 0 как:
y = ( -b ± √(b[sup]2[/ sup] — 4ac)) / 2a
Вы увидите много того же, только еще хуже, с тригонометрическими функциями и их «обратными».
Сенегоид
# 17
зона сброса:
Разве это не песня Чикаго? Нет, я помню — это было ЕСЛИ Y = 25 ИЛИ 624, ТО GOSUB что-то.
Кажется, он говорит о песне из «Порги и Бесс»?
ОП, ты говоришь или не говоришь о песне из «Порги и Бесс»?
Сенегоид
# 18
Когда возникают подобные вещи, я обычно говорю:
Если вы запутались, это означает, что вы, вероятно, внимательно слушаете.
Если вы НЕ запутались, это означает, что вы, вероятно, не обращаете внимания.
лиацим
# 19
Сенегоид:
Да, здесь ЕСТЬ элемент чистого произвольного соглашения: обозначение sqrt(x) или √ несколько произвольно определено для обозначения только положительного квадратного корня.
Важно уяснить, что произвол необходим потому что было бы невозможно иметь функцию из 92 = x, функция sqrt должна выбирать и возвращать только один из них, чтобы быть действительной функцией от R до R .
Человеческое тщеславие о том, что положительные числа предпочтительнее отрицательных, облегчает выбор, но базовая математика требует, чтобы выбор был сделан.
Д18