|
Будем вращать радиус-вектор если вектор OM, начиная от положения OA, сделав n полных оборотов против часовой стрелки, повернулся еще на угол в градусов в том же направлении. Таким образом, при вращении подвижного радиус-вектора OM против часовой стрелки получаются положительные углы, а при вращении по часовой стрелке – отрицательные углы. |
Тригонометрия в жизни — Тригонометрия
ТРИГОНОМЕТРИЯ В НАШЕЙ ЖИЗНИ
Многие
задаются вопросами: зачем нужна тригонометрия? Как она используется в нашем
мире? С чем может быть связана тригонометрия? И вот ответы на эти вопросы. Тригонометрия
или тригонометрические функции используются в астрономии (особенно для расчётов положения небесных объектов), когда требуется сферическая тригонометрия, в морской и воздушной навигации, в теории музыки, в акустике, в оптике, в анализе финансовых рынков, в электронике, в теории вероятности, в статистике, в биологии, в медицинской визуализации ,например, компьютерной томографии и ультразвук, в аптеках, в химии, в теории чисел, в сейсмологии, в метеорологии, в океанографии, во многих физических науках, в межевании и геодезии, в архитектуре, в фонетике, в экономике, в электротехнике, в машиностроении, в гражданском строительстве, в компьютерной графике, в картографии, в кристаллографии, в разработке игр и многих других
областях.
Геодезия
Часто с синусами и косинусами приходится сталкиваться геодезистам. Они имеют специальные инструменты для точного измерения углов. При помощи синусов и косинусов углы можно превратить в длины или координаты точек на земной поверхности.
Древняя астрономия
Зачатки тригонометрии можно найти в математических рукописях Древнего Египта, Вавилона и Древнего Китая. 56-я задача из папируса Ринда (II тысячелетие до н. э.) предлагает найти наклон пирамиды, высота которой равна 250 локтей, а длина стороны основания — 360 локтей.
Дальнейшее развитие
тригонометрии связано с именем астронома Аристарха Самосского (III век
до н. э.). В его трактате «О величинах и расстояниях Солнца и Луны»
ставилась задача об определении расстояний до небесных тел; эта задача
требовала вычисления отношения сторон прямоугольного треугольника при
известном значении одного из углов. Аристарх рассматривал прямоугольный
треугольник, образованный Солнцем, Луной и Землёй во время квадратуры. Ему требовалось вычислить
величину гипотенузы (расстояние от Земли до Солнца) через катет (расстояние от
Земли до Луны) при известном значении прилежащего угла (87°), что эквивалентно
вычислению значения
Ему требовалось вычислить
величину гипотенузы (расстояние от Земли до Солнца) через катет (расстояние от
Земли до Луны) при известном значении прилежащего угла (87°), что эквивалентно
вычислению значения
Несколько десятилетий спустя Клавдий Птоломей в своих трудах «География», «Аналемма» и «Планисферий» даёт подробное изложение тригонометрических приложений к картографии, астрономии и механике. Среди прочего, описана стереографическая проекция, исследованы несколько практических задач, например: определить высоту и азимут небесного светила по его склонению и часовому углу. С точки зрения тригонометрии, это значит, что надо найти сторону сферического треугольника по другим двум сторонам и противолежащему углу.
В общем, можно сказать, что тригонометрия использовалась для:
·
точного определения времени суток;
· вычисления
будущего расположения небесных светил, моментов их восхода и заката, затмений Солнца и Луны;
·
нахождения географических координат текущего
места;
·
вычисления расстояния между городами с известными географическими координатами.
Гномон— древнейший астрономический инструмент, вертикальный предмет (стела, колонна, шест),
позволяющий по наименьшей
длине его тени (в полдень) определить угловую
высоту солнца.
Так, под котангенсом понималась длина тени от вертикального гномонавысотой 12 (иногда 7) единиц; первоначально эти понятия использовались для расчёта солнечных часов. Тангенсом называлась тень от горизонтального гномона. Косекансом и секансом назывались гипотенузы соответствующих прямоугольных треугольников (отрезки AO на рисунке слева)
Архитектура
Широко используется тригонометрия в строительстве, а особенно в архитектуре. Большинство композиционных решений и построений
рисунков проходило именно с помощью геометрии. Но теоретические данные мало что значат. Хочу привести пример на построение одной скульптуры французского мастера Золотого века искусства.
Пропорциональное соотношение в построении статуи было идеально. Однако при
поднятии статуи на высокий пьедестал, она смотрелась уродливой. Скульптором не
было учтено, что в перспективе к горизонту уменьшаются многие детали и при
взгляде снизу вверх уже не создается впечатления ее идеальности. Велось
Скульптором не
было учтено, что в перспективе к горизонту уменьшаются многие детали и при
взгляде снизу вверх уже не создается впечатления ее идеальности. Велось
множество расчетов, чтобы фигура с большой высоты смотрелась пропорционально. В основном они были основаны на методе визирования, то есть приблизительного измерения, на глаз. Однако коэффициент разности тех или иных пропорций позволили сделать фигуру более приближенной к идеалу. Таким образом, зная примерное расстояние от статуи до точки зрения, а именно от верха статуи до глаз человека и высоту статуи, можно рассчитать синус угла падения взгляда с помощью таблицы (тоже самое мы можем сделать и с нижней точкой зрения), тем самым найдем точку зрения
Ситуация меняется , так как статую поднимают на высоту, поэтому
расстояние от верхушки статуи до глаз человека увеличивается, следовательно и
синус угла падения увеличивается. Сравнив изменения расстояния от верхушки статуи до
земли в первом и во втором случаи, можно найти коэффициент пропорциональности. Впоследствии мы получим чертеж, а потом скульптуру, при поднятии которой
зрительно фигура будет приближена к идеалу
Впоследствии мы получим чертеж, а потом скульптуру, при поднятии которой
зрительно фигура будет приближена к идеалу
Медицина и биология.
Модель боритмов можно построить с помощью тригонометрических функций.
Для построения модели биоритмов необходимо ввести дату рождения человека, дату
отсчета (день, месяц, год) и длительность прогноза (кол-во дней).
Формула
сердца. В
результате исследования, проведенного студентом иранского университета Шираз Вахидом-Резой Аббаси, медики
впервые получили возможность упорядочить информацию, относящуюся к
электрической активности сердца или, другими словами, электрокардиографии. Формула
представляет собой комплексное алгебраически-тригонометрическое равенство,
состоящее из 8 выражений, 32 коэффициентов и 33 основных параметров, включая
несколько дополнительных для расчетов в случаях аритмии. Как утверждают медики,
эта формула в значительной степени облегчает процесс описания основных
параметров деятельности сердца, ускоряя, тем самым, постановку диагноза и
начало собственно лечения.
Также тригонометрия помогает нашему мозгу определять расстояния до объектов.
Американские ученые утверждают, что мозг оценивает расстояние до объектов, измеряя угол между плоскостью земли и плоскостью зрения. Строго говоря, идея «измерения углов» не является новой. Еще художники Древнего Китая рисовали удаленные объекты выше в поле зрения, несколько пренебрегая законами перспективы. Сформулировал теорию определения расстояния по оценке углов арабский ученый XI века Альхазен. После долгого забвения в середине прошлого столетия идею реанимировал психолог Джеймс
Гибсон (James Gibson), строивший свои выводы на основе опыта работы с пилотами военной авиации. Однако после того о теории
вновь позабыли.
Движение рыб в воде происходит по закону синуса или косинуса, если зафиксировать точку на хвосте, а потом рассмотреть траекторию движения. При плавании тело рыбы принимает форму
кривой,
которая напоминает график функции y=tgx.
Измерительные работы
Тригонометрией пользуются при измерение расстояния между точек на местности. Предположим, что нам надо найти расстояние d от пункта А до недоступного пункта «дерево». На местности можно выбрать точку
d B и измерим длину с отрезка АВ. Затем измерим, например
с помощью астролябии, углы A и B. Эти данные, т.е. c, a и b
позволяют решить треугольник АВС и найти искомое
расстояние d=AC.
Сначала находим угол С sinC:
С=180-а-b, sinC=sin(180-a-b)=sin(a+b)
Затем с помощью теоремы синусов находим d.
| | Адрес этой страницы (вложенность) в справочнике dpva.ru: главная страница / / Техническая информация / / Математический справочник / / Тригонометрические функции, формулы и графики. sin, cos, tg, ctg….Значения тригонометрических функций. Формулы приведения тригонометрических функций. Тригонометрические тождества. / / Углы 15°,18°,22,5°,36°,54°,67,5°,72°,(π/12,π/10,π/8,π/5,π,3π/10,3π/8, 2π/5). Синусы, косинусы, тангенсы и котангенсы. Значения тригонометрических функций нестандартных углов. Поделиться:
| ||||||
| Если Вы не обнаружили себя в списке поставщиков, заметили ошибку, или у Вас есть дополнительные численные данные для коллег по теме, сообщите , пожалуйста. Вложите в письмо ссылку на страницу с ошибкой, пожалуйста. | |||||||
| Коды баннеров проекта DPVA.ru Начинка: KJR Publisiers Консультации и техническая | Проект является некоммерческим. Информация, представленная на сайте, не является официальной и предоставлена только в целях ознакомления. Владельцы сайта www.dpva.ru не несут никакой ответственности за риски, связанные с использованием информации, полученной с этого интернет-ресурса.
Free xml sitemap generator Владельцы сайта www.dpva.ru не несут никакой ответственности за риски, связанные с использованием информации, полученной с этого интернет-ресурса.
Free xml sitemap generator | ||||||
Отсчёт углов на тригонометрическом круге. Положительные и отрицательные углы. Распределение углов по четвертям
В прошлом уроке мы с вами успешно освоили (или повторили — кому как) ключевые понятия всей тригонометрии. Это тригонометрический круг, угол на круге, синус и косинус этого угла, а также освоили знаки тригонометрических функций по четвертям. Освоили подробно. На пальцах, можно сказать.
Но этого пока мало. Для успешного практического применения всех этих простых понятий нам необходим ещё один полезный навык. А именно — правильная работа с углами в тригонометрии. Без этого умения в тригонометрии — никак. Даже в самых примитивных примерах. Почему? Да потому, что угол — ключевая действующая фигура во всей тригонометрии! Нет, не тригонометрические функции, не синус с косинусом, не тангенс с котангенсом а именно сам угол. Нет угла — нету и тригонометрических функций, да…
Даже в самых примитивных примерах. Почему? Да потому, что угол — ключевая действующая фигура во всей тригонометрии! Нет, не тригонометрические функции, не синус с косинусом, не тангенс с котангенсом а именно сам угол. Нет угла — нету и тригонометрических функций, да…
Как правильно работать с углами на круге? Для этого нам надо железно усвоить два пункта.
1) Как отсчитываются углы на круге?
2) В чём они считаются (измеряются)?
Ответ на первый вопрос — и есть тема сегодняшнего урока. С первым вопросом мы детально разберёмся прямо здесь и сейчас. Ответ на второй вопрос здесь не дам. Ибо достаточно развёрнутый он. Как и сам второй вопрос очень скользкий, да.) Вдаваться в подробности пока не буду. Это — тема следующего отдельного урока.
Приступим?
Как отсчитываются углы на круге? Положительные и отрицательные углы.
У прочитавших название параграфа, возможно, уже волосы встали дыбом. Как так?! Отрицательные углы? Разве такое вообще возможно?
Как так?! Отрицательные углы? Разве такое вообще возможно?
К отрицательным числам мы с вами уже попривыкли. На числовой оси их изображать умеем: справа от нуля положительные, слева от нуля отрицательные. Да и на градусник за окном поглядываем периодически. Особенно зимой, в мороз.) И денежки на телефоне в «минус» (т.е. долг) иногда уходят. Это всё знакомо.
А что же с углами? Оказывается, отрицательные углы в математике тоже бывают! Всё зависит от того, как отсчитывать этот самый угол… нет, не на числовой прямой, а на числовой окружности! То бишь, на круге. Круг — вот он, аналог числовой прямой в тригонометрии!
Итак, как же отсчитываются углы на круге? Ничего не поделать, придётся нам для начала этот самый круг нарисовать.
Я нарисую вот такую красивую картинку:
Она очень похожа на картинки из прошлого урока. Есть оси, есть окружность, есть угол. Но есть и новая информация.
Во-первых, я добавил номера четвертей (или квадрантов). Напоминаю, что четверти всегда нумеруются против часовой стрелки.
Также я добавил циферки 0°, 90°, 180°, 270° и 360° на осях. Вот это уже поинтереснее.) Что это за циферки? Правильно! Это значения углов, отсчитанные от нашей неподвижной стороны, которые попадают на координатные оси. Вспоминаем, что неподвижная сторона угла у нас всегда крепко-накрепко привязана к положительной полуоси ОХ. И любой угол в тригонометрии отсчитывается именно от этой полуоси. Это базовое начало отсчёта углов надо держать в голове железно. А оси — они же под прямым углом пересекаются, верно? Вот и прибавляем по 90° в каждой четверти.
И ещё добавлена красная стрелочка. С плюсом. Красная — это специально, чтобы в глаза бросалась. И в память хорошенько врезалась. Ибо это надо запомнить надёжно.) Что же означает эта стрелочка?
Так вот оказывается, если наш угол мы будем крутить по стрелочке с плюсом (против часовой стрелки, по ходу нумерации четвертей), то угол будет считаться положительным! В качестве примера на рисунке показан угол +45°. Кстати, обратите внимание, что осевые углы 0°, 90°, 180°, 270° и 360° также отмотаны именно в плюс! По красной стрелочке.
Кстати, обратите внимание, что осевые углы 0°, 90°, 180°, 270° и 360° также отмотаны именно в плюс! По красной стрелочке.
А теперь посмотрим на другую картинку:
Здесь почти всё то же самое. Только углы на осях пронумерованы в обратную сторону. По часовой стрелке. И имеют знак «минус».) Ещё нарисована синяя стрелочка. Также с минусом. Эта стрелочка — направление отрицательного отсчёта углов на круге. Она нам показывает, что, если мы будем откладывать наш угол по ходу часовой стрелки, то угол будет считаться отрицательным. Для примера я показал угол -45°.
Кстати, прошу заметить, что нумерация четвертей никогда не меняется! Неважно, в плюс или в минус мы мотаем углы. Всегда строго против часовой стрелки.)
Запоминаем:
1. Начало отсчёта углов — от положительной полуоси ОХ. По часам — «минус», против часов — «плюс».
2. Нумерация четвертей всегда против часовой стрелки вне зависимости от направления исчисления углов.
Нумерация четвертей всегда против часовой стрелки вне зависимости от направления исчисления углов.
Кстати говоря, подписывать углы на осях 0°, 90°, 180°, 270°, 360°, каждый раз рисуя круг — вовсе не обязаловка. Это чисто для понимания сути сделано. Но эти циферки обязательно должны присутствовать в вашей голове при решении любой задачи по тригонометрии. Почему? Да потому, что эти элементарные знания дают ответы на очень многие другие вопросы во всей тригонометрии! Самый главный вопрос — в какую четверть попадает интересующий нас угол? Хотите верьте, хотите нет, но правильный ответ на этот вопрос решает львиную долю всех остальных проблем с тригонометрией. Этим важным занятием (распределением углов по четвертям) мы займёмся в этом же уроке, но чуть позже.
Величины углов, лежащих на осях координат (0°, 90°, 180°, 270° и 360°), надо запомнить! Запомнить накрепко, до автоматизма. Причём как в плюс, так и в минус.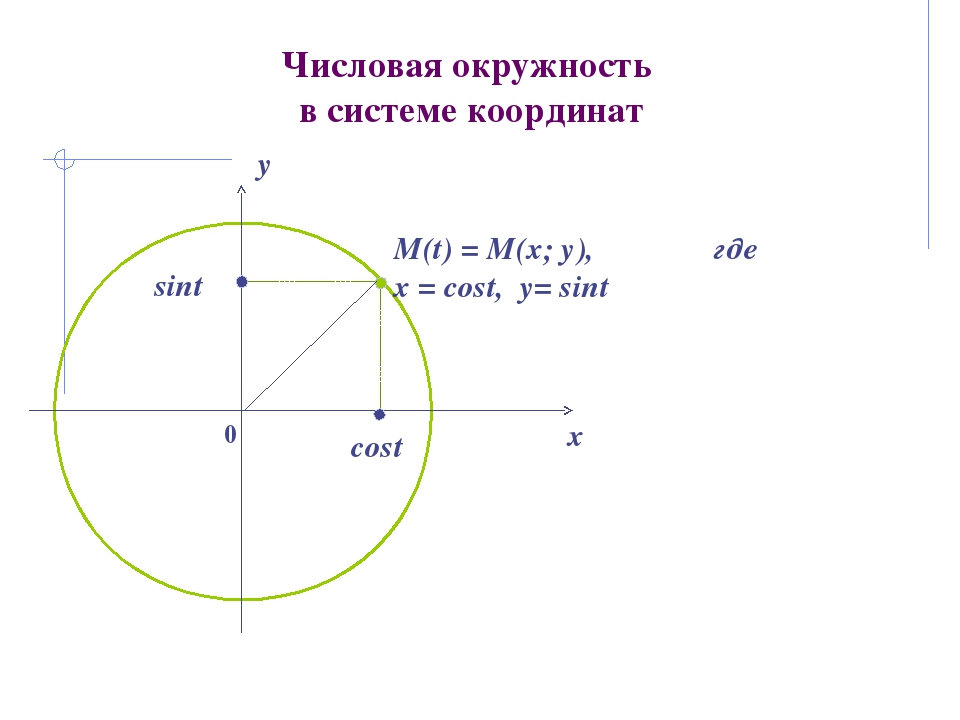
А вот с этого момента начинаются первые сюрпризы. И вместе с ними и каверзные вопросы в мой адрес, да…) А что будет, если отрицательный угол на круге совпадёт с положительным? Выходит, что одну и ту же точку на круге можно обозначить как положительным углом, так и отрицательным???
Совершенно верно! Так и есть.) Например, положительный угол +270° занимает на круге то же самое положение, что и отрицательный угол -90°. Или, например, положительный угол +45° на круге займёт то же самое положение, что и отрицательный угол -315°.
Смотрим на очередной рисунок и всё видим:
Точно так же положительный угол +150° попадёт туда же, куда и отрицательный угол -210°, положительный угол +230° — туда же, куда и отрицательный угол -130°. И так далее…
И что теперь делать? Как именно считать углы, если можно и так и сяк? Как правильно?
Ответ: по-всякому правильно! Ни одно из двух направлений отсчёта углов математика не запрещает. А выбор конкретного направления зависит исключительно от задания. Если в задании ничего не сказано прямым текстом про знак угла (типа «определите наибольший отрицательный угол» и т.п.), то работаем с наиболее удобными нам углами.
А выбор конкретного направления зависит исключительно от задания. Если в задании ничего не сказано прямым текстом про знак угла (типа «определите наибольший отрицательный угол» и т.п.), то работаем с наиболее удобными нам углами.
Конечно, например, в таких крутых темах, как тригонометрические уравнения и неравенства направление исчисления углов может колоссально влиять на ответ. И в соответствующих темах мы эти подводные камни рассмотрим.
Запоминаем:
Любую точку на круге можно обозначить как положительным, так и отрицательным углом. Любым! Каким хотим.
А теперь призадумаемся вот над чем. Мы выяснили, что угол 45° в точности совпадает с углом -315°? Как же я узнал про эти самые 315°? Не догадываетесь? Да! Через полный оборот.) В 360°. У нас есть угол 45°. Сколько не хватает до полного оборота? Отнимаем 45° от 360° — вот и получаем 315°. Мотаем в отрицательную сторону — и получаем угол -315°.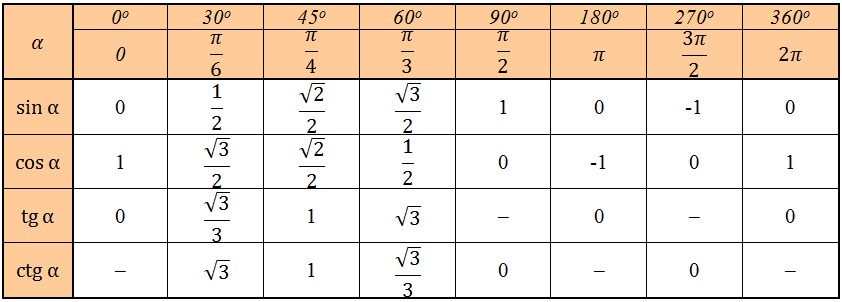 Всё равно непонятно? Тогда смотрим на картинку выше ещё раз.
Всё равно непонятно? Тогда смотрим на картинку выше ещё раз.
И так надо поступать всегда при переводе положительных углов в отрицательные (и наоборот) — рисуем круг, отмечаем примерно заданный угол, считаем, сколько градусов не хватает до полного оборота, и мотаем получившуюся разность в противоположную сторону. И всё.)
Чем ещё интересны углы, занимающие на круге одно и то же положение, как вы думаете? А тем, что у таких углов совершенно одинаковые синус, косинус, тангенс и котангенс! Всегда!
Например:
sin45° = sin(-315°)
cos120° = cos(-240°)
tg249° = tg(-111°)
ctg333° = ctg(-27°)
И так далее и тому подобное. В общем, вы поняли… Кстати, прошу заметить, что углы в этих парочках различны. Зато тригонометрические функции у них — одинаковы! Идея ясна?
А вот это уже крайне важно! Зачем? Да всё за тем же!) Для упрощения выражений. Ибо упрощение выражений — ключевая процедура успешного решения любых заданий по математике. И по тригонометрии в том числе.
Ибо упрощение выражений — ключевая процедура успешного решения любых заданий по математике. И по тригонометрии в том числе.
Итак, с общим правилом отсчёта углов на круге разобрались. Ну а коли мы тут заикнулись про полные обороты, про четверти, то пора бы уже покрутить и порисовать эти самые углы. Порисуем?)
Начнём пока с положительных углов. Они попроще в рисовании будут.
Рисуем углы в пределах одного оборота (между 0° и 360°).
Нарисуем, например, угол 60°. Тут всё просто, никаких заморочек. Рисуем координатные оси, круг. Можно прямо от руки, безо всякого циркуля и линейки. Рисуем схематично: у нас не черчение с вами. Никаких ГОСТов соблюдать не надо, не накажут.)
Можно (для себя) отметить значения углов на осях и указать стрелочку в направлении против часов. Ведь мы же в плюс откладывать собираемся?) Можно этого и не делать, но в голове держать всяко надо.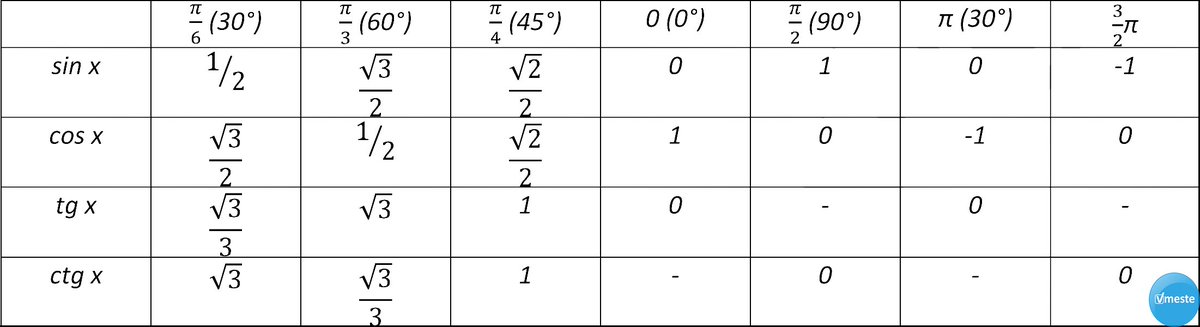
И теперь проводим вторую (подвижную) сторону угла. В какой четверти? В первой, разумеется! Ибо 60 градусов — это строго между 0° и 90°. Вот и рисуем в первой четверти. Под углом примерно 60 градусов к неподвижной стороне. Как отсчитать примерно 60 градусов без транспортира? Легко! 60° — это две трети от прямого угла! Делим мысленно первую чертвертинку круга на три части, забираем себе две трети. И рисуем… Сколько у нас там по факту получится (если приложить транспортир и померить) — 55 градусов или же 64 — неважно! Важно, что всё равно где-то около 60°.
Получаем картинку:
Вот и всё. И инструментов не понадобилось. Развиваем глазомер! В задачах по геометрии пригодится.) Этот неказистый рисунок бывает незаменим, когда надо нацарапать круг и угол на скорую руку, не особо задумываясь о красоте. Но при этом нацарапать правильно, без ошибок, со всей необходимой информацией. Например, как вспомогательное средство при решении тригонометрических уравнений и неравенств.
Например, как вспомогательное средство при решении тригонометрических уравнений и неравенств.
Нарисуем теперь угол, например, 265°. Прикидываем, где он может располагаться? Ну, ясное дело, что не в первой четверти и даже не во второй: они на 90 и на 180 градусов оканчиваются. Можно сообразить, что 265° — это 180° плюс ещё 85°. То есть, к отрицательной полуоси ОХ (там, где 180°) надо добавить примерно 85°. Или, что ещё проще, догадаться, что 265° не дотягивает до отрицательной полуоси OY (там, где 270°) каких-то несчастных 5°. Одним словом, в третьей четверти будет этот угол. Очень близко к отрицательной полуоси OY, к 270 градусам, но всё-таки в третьей!
Рисуем:
Повторюсь, абсолютная точность здесь не требуется. Пускай в реальности этот угол получился, скажем 263 градуса. Но на самый главный вопрос (какая четверть?) мы ответили безошибочно. Почему этот вопрос самый главный? Да потому, что любая работа с углом в тригонометрии (неважно, будем мы рисовать этот угол или не будем) начинается с ответа именно на этот вопрос! Всегда. Если этот вопрос проигнорировать или пробовать на него ответить мысленно, то ошибки почти неизбежны, да… Оно вам надо?
Если этот вопрос проигнорировать или пробовать на него ответить мысленно, то ошибки почти неизбежны, да… Оно вам надо?
Запоминаем:
Любая работа с углом (в том числе и рисование этого самого угла на круге) всегда начинается с определения четверти, в которую попадает этот угол.
Теперь, я надеюсь, вы уже безошибочно изобразите углы, например, 182°, 88°, 280°. В правильных четвертях. В третьей, первой и четвёртой, если что…)
Четвёртая четверть заканчивается углом 360°. Это один полный оборот. Ясен перец, что этот угол занимает на круге то же самое положение, что и 0° (т.е. начало отсчёта). Но углы на этом не заканчиваются, да…
Что делать с углами, большими 360°?
«А такие разве бывают?» — спросите вы. Бывают, ещё как! Бывает, например, угол 444°. А бывает, скажем, угол 1000°. Всякие углы бывают.) Просто визуально такие экзотические углы воспринимаются чуть сложнее, чем привычные нам углы в пределах одного оборота. Но рисовать и просчитывать такие углы тоже надо уметь, да.
Но рисовать и просчитывать такие углы тоже надо уметь, да.
Для правильного рисования таких углов на круге необходимо всё то же самое — выяснить, в какую четверть попадает интересующий нас угол. Здесь умение безошибочно определять четверть куда более важно, чем для углов от 0° до 360°! Сама процедура определения четверти усложняется всего одним шагом. Каким, скоро увидите.
Итак, например, нам надо выяснить, в какую четверть попадает угол 444°. Начинаем крутить. Куда? В плюс, разумеется! Угол-то нам дали положительный! +444°. Крутим, крутим… Крутанули на один оборот — дошли до 360°.
Ну и крутим себе дальше!
Сколько там осталось до 444°? Считаем оставшийся хвостик:
444°-360° = 84°.
Итак, 444° — это один полный оборот (360°) плюс ещё 84°. Очевидно, это первая четверть. Итак, угол 444° попадает в первую четверть. Полдела сделано.
Осталось теперь изобразить этот угол. Как? Очень просто! Делаем один полный оборот по красной (плюсовой) стрелке и добавляем ещё 84°.
Как? Очень просто! Делаем один полный оборот по красной (плюсовой) стрелке и добавляем ещё 84°.
Вот так:
Здесь я уж не стал загромождать рисунок — подписывать четверти, рисовать углы на осях. Это всё добро уже давно в голове быть должно.)
Зато я «улиткой» или спиралькой показал, как именно складывается угол 444° из углов 360° и 84°. Пунктирная красная линия — это один полный оборот. К которому дополнительно прикручиваются 84° (сплошная линия). Кстати, обратите внимание, что, если этот самый полный оборот отбросить, то это никак не повлияет на положение нашего угла!
А вот это важно! Положение угла 444° полностью совпадает с положением угла 84°. Никаких чудес нет, так уж получается.)
А можно ли отбросить не один полный оборот, а два или больше?
А почему — нет? Если угол здоровенный, то не просто можно, а даже нужно! Угол-то не изменится! Точнее, сам-то угол по величине, конечно же, изменится. А вот его положение на круге — никак нет!) На то они и полные обороты, что сколько экземпляров ни добавляй, сколько ни убавляй, всё равно будешь в одну и ту же точку попадать. Приятно, правда?
А вот его положение на круге — никак нет!) На то они и полные обороты, что сколько экземпляров ни добавляй, сколько ни убавляй, всё равно будешь в одну и ту же точку попадать. Приятно, правда?
Запоминаем:
Если к углу прибавить (отнять) любое целое число полных оборотов, положение исходного угла на круге НЕ изменится!
Например:
В какую четверть попадает угол 1000°?
Никаких проблем! Считаем, сколько полных оборотов сидит в тысяче градусов. Один оборот — это 360°, ещё один — уже 720°, третий — 1080°… Стоп! Перебор! Значит, в угле 1000° сидит два полных оборота. Выбрасываем их из 1000° и считаем остаток:
1000° — 2·360° = 280°
Значит, положение угла 1000° на круге то же самое, что и у угла 280°. С которым работать уже гораздо приятнее.) И куда же попадает этот угол? В четвёртую четверть он попадает: 270° (отрицательная полуось OY) плюс ещё десяточка.
Рисуем:
Здесь я уже не рисовал пунктирной спиралькой два полных оборота: уж больно длинная она получается. Просто нарисовал оставшийся хвостик от нуля, отбросив все лишние обороты. Как будто бы их и не было вовсе.)
И ещё раз. По-хорошему, углы 444° и 84°, а также 1000° и 280° — разные. Но для синуса, косинуса, тангенса и котангенса эти углы — одинаковые!
Как вы видите, для того чтобы работать с углами, большими 360°, надо определить, сколько полных оборотов сидит в заданном большом угле. Это и есть тот самый дополнительный шаг, который обязательно надо предварительно проделывать при работе с такими углами. Ничего сложного, правда?
Отбрасывание полных оборотов, конечно, занятие приятное.) Но на практике при работе с совсем уж кошмарными углами случаются и затруднения.
Например:
В какую четверть попадает угол 31240° ?
И что же, будем много-много раз прибавлять по 360 градусов? Можно, если не горит особо. Но мы же не только складывать можем.) Ещё и делить умеем!
Но мы же не только складывать можем.) Ещё и делить умеем!
Вот и поделим наш большущий угол на 360 градусов!
Этим действием мы как раз и узнаем, сколько полных оборотов запрятано в наших 31240 градусах. Можно уголком поделить, можно (шепну на ушко :)) на калькуляторе.)
Получим 31240:360 = 86,777777….
То, что число получилось дробным — не страшно. Нас же только целые обороты интересуют! Стало быть, до конца делить и не надо.)
Итак, в нашем лохматом угле сидит аж 86 полных оборотов. Ужас…
В градусах это будет 86·360° = 30960°
Вот так. Именно столько градусов можно безболезненно выкинуть из заданного угла 31240°. Останется:
31240° — 30960° = 280°
Всё! Положение угла 31240° полностью идентифицировано! Там же, где и 280°. Т.е. четвёртая четверть.) Кажется, мы уже изображали этот угол ранее? Когда угол 1000° рисовали?) Там мы тоже на 280 градусов вышли. Совпадение.)
Совпадение.)
Итак, мораль сей басни такова:
Если нам задан страшный здоровенный угол, то:
1. Определяем, сколько полных оборотов сидит в этом угле. Для этого делим исходный угол на 360 и отбрасываем дробную часть.
2. Считаем, сколько градусов в полученном количестве оборотов. Для этого умножаем число оборотов на 360.
3. Отнимаем эти обороты от исходного угла и работаем с привычным углом в пределах от 0° до 360°.
Как работать с отрицательными углами?
Не вопрос! Точно так же, как и с положительными, только с одним единственным отличием. Каким? Да! Крутить углы надо в обратную сторону, в минус! По ходу часовой стрелки.)
Нарисуем, например, угол -200°. Сначала всё как обычно для положительных углов — оси, круг. Ещё синюю стрелочку с минусом изобразим да углы на осях по-другому подпишем.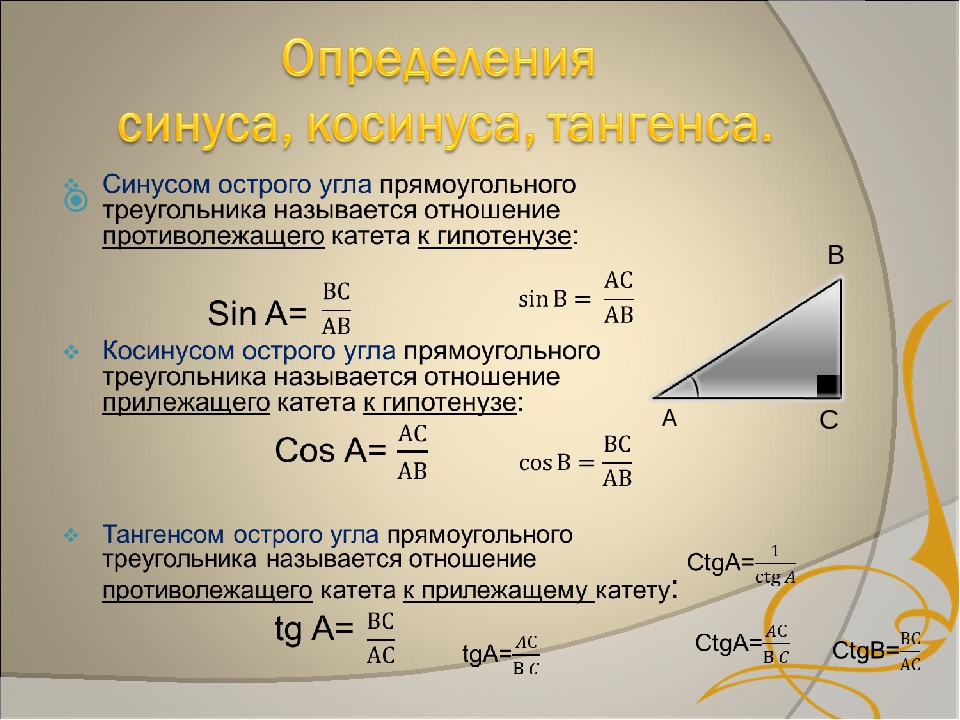 Их, естественно, также придётся отсчитывать в отрицательном направлении. Это будут всё те же самые углы, шагающие через 90°, но отсчитанные в обратную сторону, в минус: 0°, -90°, -180°, -270°, -360°.
Их, естественно, также придётся отсчитывать в отрицательном направлении. Это будут всё те же самые углы, шагающие через 90°, но отсчитанные в обратную сторону, в минус: 0°, -90°, -180°, -270°, -360°.
Картинка станет вот такой:
При работе с отрицательными углами часто возникает чувство лёгкого недоумения. Как так?! Получается, что одна и та же ось — это одновременно, скажем, и +90° и -270°? Неее, что-то тут нечисто…
Да всё чисто и прозрачно! Мы ведь же уже в курсе, что любую точку на круге можно обозвать как положительным углом, так и отрицательным! Совершенно любую. В том числе и на какой-то из координатных осей. В нашем случае нам нужно отрицательное исчисление углов. Вот и отщёлкиваем в минус все углы.)
Теперь нарисовать правильно угол -200° никакого труда не составляет. Это -180° и минус ещё 20°. Начинаем мотать от нуля в минус: четвёртую четверть пролетаем, третью тоже мимо, доходим до -180°. Куда мотать оставшуюся двадцатку? Да всё туда же! По часам.) Итого угол -200° попадает во вторую четверть.
Куда мотать оставшуюся двадцатку? Да всё туда же! По часам.) Итого угол -200° попадает во вторую четверть.
Теперь вы понимаете, насколько важно железно помнить углы на осях координат?
Углы на осях координат (0°, 90°, 180°, 270°, 360°) надо помнить именно для того, чтобы безошибочно определять четверть, куда попадает угол!
А если угол большой, с несколькими полными оборотами? Ничего страшного! Какая разница, куда эти самые полные обороты крутить — в плюс или в минус? Точка-то на круге не изменит своего положения!
Например:
В какую четверть попадает угол -2000°?
Всё то же самое! Для начала считаем, сколько полных оборотов сидит в этом злом угле. Чтобы не косячить в знаках, оставим минус пока в покое и просто поделим 2000 на 360. Получим 5 с хвостиком. Хвостик нас пока не волнует, его чуть позже сосчитаем, когда рисовать угол будем. Считаем пять полных оборотов в градусах:
5·360° = 1800°
Воот. Именно столько лишних градусов можно смело выкинуть из нашего угла без ущерба для здоровья.
Именно столько лишних градусов можно смело выкинуть из нашего угла без ущерба для здоровья.
Считаем оставшийся хвостик:
2000° — 1800° = 200°
А вот теперь можно и про минус вспомнить.) Куда будем мотать хвостик 200°? В минус, конечно же! Нам же отрицательный угол задан.)
-2000° = -1800° — 200°
Вот и рисуем угол -200°, только уже без лишних оборотов. Только что его рисовали, но, так уж и быть, накалякаю ещё разок. От руки.
Ясен перец, что и заданный угол -2000°, так же как и -200°, попадает во вторую четверть.
Итак, мотаем себе на кру… пардон… на ус:
Если задан очень большой отрицательный угол, то первая часть работы с ним (поиск числа полных оборотов и их отбрасывание) та же самая, что и при работе с положительным углом. Знак «минус» на данном этапе решения не играет никакой роли. Учитывается знак лишь в самом конце, при работе с углом, оставшимся после удаления полных оборотов.
Как видите, рисовать отрицательные углы на круге ничуть не сложнее, чем положительные.
Всё то же самое, только в другую сторону! По часам!
А вот теперь — самое интересное! Мы рассмотрели положительные углы, отрицательные углы, большие углы, маленькие — полный ассортимент. Также мы выяснили, что любую точку на круге можно обозвать положительным и отрицательным углом, отбрасывали полные обороты… Нету никаких мыслей? Должно отложиться…
Да! Какую точку на круге ни возьми, ей будет соответствовать бесконечное множество углов! Больших и не очень, положительных и отрицательных — всяких! И разница между этими углами будет составлять целое число полных оборотов. Всегда! Так уж тригонометрический круг устроен, да…) Именно поэтому обратная задача — найти угол по известным синусу/косинусу/тангенсу/котангенсу — решается неоднозначно.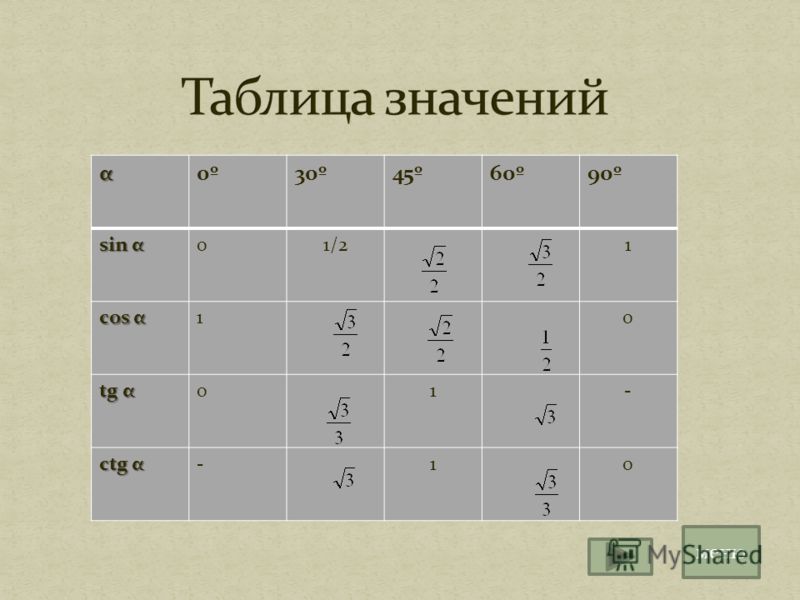 И куда сложнее. В отличие от прямой задачи — по заданному углу найти весь набор его тригонометрических функций. И в более серьёзных темах тригонометрии (арки, тригонометрические уравнения и неравенства) мы с этой фишкой будем сталкиваться постоянно. Привыкаем.)
И куда сложнее. В отличие от прямой задачи — по заданному углу найти весь набор его тригонометрических функций. И в более серьёзных темах тригонометрии (арки, тригонометрические уравнения и неравенства) мы с этой фишкой будем сталкиваться постоянно. Привыкаем.)
Итак, будем считать, что самые-самые азы работы с углами на круге мы с вами освоили. Можно и на вопросы поотвечать. Самостоятельно.)
1. В какую четверть попадает угол -345°?
2. В какую четверть попадает угол 666°?
3. В какую четверть попадает угол 5555°?
4. В какую четверть попадает угол -3700°?
Всё хорошо? Поехали дальше.
5. Какой знак имеет cos999°?
6. Какой знак имеет ctg999°?
И это получилось? Прекрасно! Есть проблемы? Тогда вам сюда.
Ответы:
1. 1
2. 4
4
3. 2
4. 3
5. «+»
6. «-«
В этот раз ответы выданы по порядку в нарушение традиций. Ибо четвертей всего четыре, а знаков так и вовсе два. Особо не разбежишься…)
В следующем уроке мы с вами поговорим про радианы, про загадочное число «пи», научимся легко и просто переводить радианы в градусы и обратно. И с удивлением обнаружим, что даже этих простых знаний и навыков нам будет уже вполне достаточно для успешного решения многих нетривиальных задачек по тригонометрии!
Math.ru
Израиль Моисеевич Гельфанд, Сергей Михайлович Львовский, Андрей Леонович ТоомМ., МЦНМО, 2002. 199 с.
ISBN ISBN 5-94057-050-X; Тираж 10000 экз.
| |||||||||||
Эта книга, написанная группой авторов под руководством одного из крупнейших математиков 20 века академика И.
 М.Гельфанда, призвана опровергнуть расхожее мнение о тригонометрии как скучном и непонятном разделе школьного курса математики. Читателю предлагается взглянуть на знакомый предмет по-новому. Изложение, сопровождающееся большим количеством задач, начинается ?с нуля? и доходит до материала, выходящего довольно далеко за рамки школьной программы; тригонометрические формулы иллюстрируются примерами из физики и геометрии.
М.Гельфанда, призвана опровергнуть расхожее мнение о тригонометрии как скучном и непонятном разделе школьного курса математики. Читателю предлагается взглянуть на знакомый предмет по-новому. Изложение, сопровождающееся большим количеством задач, начинается ?с нуля? и доходит до материала, выходящего довольно далеко за рамки школьной программы; тригонометрические формулы иллюстрируются примерами из физики и геометрии.Отдельная глава посвящена типичным приемам решения тригонометрических задач, предлагаемых на вступительных экзаменах в высшие учебные заведения.
Книга будет незаменимым помощником для школьников старших классов, преподавателей, родителей и всех, интересующихся математикой.
Содержание
1. Первое знакомство с тригонометрией
? 1. Как измерить крутизну
1.1. Синус
1.2. Измерение углов
? 2. Тангенс
? 3. Косинус
? 4. Малые углы
2. Начальные свойства тригонометрических функций
Начальные свойства тригонометрических функций
? 5. Часы, или современный взгляд на тригонометрию
5.1. Часы и процессы
5.2. Скорость
? 6. Определение тригонометрических функций
6.1. Ось тангенсов
6.2. Знаки тригонометрических функций
? 7. Простейшие формулы
? 8. Периоды тригонометрических функций
? 9. Формулы приведения
? 10. Простейшие тригонометрические уравнения
? 11. Графики синуса и косинуса
? 12. Графики тангенса и котангенса
? 13. Чему равно sin x + cos x?
3. Решение треугольников
? 14. Теорема косинусов
? 15. Вокруг площади треугольника
? 16. Теорема синусов
4. Формулы сложения и их следствия
? 17. Векторы
17.1. Направленные отрезки и векторы
17.2. Сложение векторов
17. 3. Вычитание и умножение на число
3. Вычитание и умножение на число
17.4. О векторах в физике
? 18. Скалярное произведение
? 19. Тригонометрические формулы сложения
? 20. Формула вспомогательного угла, или сложение колебаний равной частоты
? 21. Двойные, тройные и половинные углы
? 22. Преобразование произведения в сумму и суммы в произведение
? 23. Производные тригонометрических функций
5. Тригонометрия для абитуриентов
? 24. Как решать тригонометрические уравнения
? 25. Отбор чисел на тригонометрическом круге
? 26. Как решать тригонометрические неравенства
? 27. Задачи на повторение
6. Комплексные числа
? 28. Что такое комплексные числа
? 29. Модуль и аргумент комплексного числа
? 30. Показательная функция и формула Эйлера
Ответы и указания к некоторым задачам
Предметный указатель
| |||||||||||
Тригонометрия
ТРИГОНОМЕТРИЯ – раздел математики, изучающий тригонометрические функции и их применение в решении задач, главным образом геометрических. Слово «тригонометрия» дословно с греческого языка переводится как «треугольник+измерение»..
Задачи тригонометрии
Основная задача тригонометрии – решение треугольников, то есть нахождение неизвестных величин треугольника через известные его величины. Любую геометрическую задача можно свести к решению с помощью треугольников, поэтому тригонометрия применима и в планиметрии (изучении плоских геометрических фигур), и в стереометрии (изучении пространственных геометрических фигур).Любая тригонометрическая величина есть функция угла (изменяется с изменением угла), поэтому и появилось название «тригонометрические функции».
Тригонометрические функции – функции угла: синус (sin), косинус (cos), тангенс (tg), котангенс (ctg), секанс (sec) и косеканс (cosec).
Обратные тригонометрические функции, или круговые функции, — арксинус (arcsin), арккосинус (arccos), арктангенс (arctg) и арккотангенс (arcctg).
Прямые функции угла используют, когда по угла находят функцию, а обратные – когда по функции находят угол.
История тригонометрииРешение треугольников было долгое время одним из разделов астрономии. Но зачатки науки можно найти в математических рукописях Древнего Египта, Китая и Вавилона. Считается, что измерение углов в градусах, минутах и секундах пришло к нам от вавилонских математиков.
Способы решения сферических треугольников впервые были письменно изложены греческим астрономом Гиппархом в середины II века до н.э.
Решения треугольников Гиппархом и Птолемеем (создателем геоцентрической системы мира, господствовавшей до Коперника) не знали синусов, косинусов и тангенсов. Линии синусов и косинусов начали использовать индийские астрономы (IV-V в.в.). В дальнейшем тригонометрия развивалась арабоязычными учеными (Муххамед из Буджана, Насир эд-Дина из Туса).
Линии синусов и косинусов начали использовать индийские астрономы (IV-V в.в.). В дальнейшем тригонометрия развивалась арабоязычными учеными (Муххамед из Буджана, Насир эд-Дина из Туса).
Европейцы познакомились с тригонометрией в XII в. Выдающийся немецкий астроном Региомонтан составил таблицы синусов с точностью до седьмой значащей цифры с интервалом 1´.
Термин «тригонометрия» впервые появился в 1595 г. как название книги немецкого математика Бартоломеуса Питискуса (1561—1613).
Буквенные обозначения появились в тригонометрии лишь в середине XVIII в., ввели х русский академик Эйлер, именно он придал тригонометрии такой вид, который присущ ей до сих пор. Он же ввел и обратные тригонометрические функция.
См. также полезные материалы по тригонометрии: Содержание главы:
Периметр и площадь прямоугольника | Описание курса | Синус
Единичная окружность в тригонометрии
Единичная окружность в тригонометрии
Все процессы тригонометрии изучают на единичной окружности. Сейчас узнаем, какую окружность называют единичной и дадим определение.
Сейчас узнаем, какую окружность называют единичной и дадим определение.
Единичная окружность — это окружность с центром в начале прямоугольной декартовой системы координат и радиусом, равным единице.
Прямоугольная система координат — прямолинейная система координат с взаимно перпендикулярными осями на плоскости или в пространстве. Наиболее простая и поэтому часто используемая система координат.
Радиус — отрезок, который соединяет центр окружности с любой точкой, лежащей на окружности, а также длина этого отрезка. Радиус составляет половину диаметра.
Единичную окружность с установленным соответствием между действительными числами и точками окружности называют числовой окружностью.
Поясним, как единичная окружность связана с тригонометрией.
В тригонометрии мы постоянно сталкиваемся с углами поворота. А углы поворота связаны с вращением по окружности.
Угол поворота — это угол, который образован положительным направлением оси OX и лучом OA.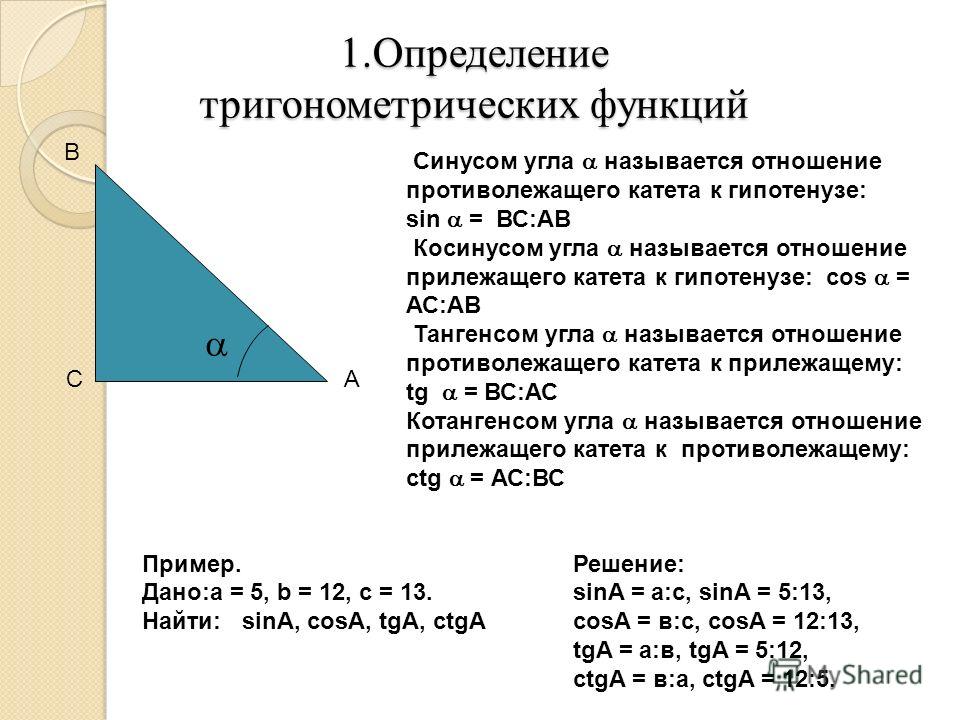
Величины углов поворота не зависят от радиуса окружности, по которой происходит вращение, поэтому удобно работать именно с окружностью единичного радиуса. Это позволяет избавиться от коэффициентов при математическом описании. Вот и все объяснение полезности единичной тригонометрической окружности.
Все углы, которые принадлежат одному семейству, дают одинаковые абсолютные значения тригонометрических функций, но эти значения могут различаться по знаку. Вот как:
- Если угол находится в первом квадранте, все тригонометрические функции имеют положительные значения.
- Для угла во втором квадранте все функции, за исключением sin и cos, отрицательны.
- В третьем квадранте значения всех функций, кроме tg и ctg, меньше нуля.
- В четвертом квадранте все функции, за исключением cos и sec, имеют отрицательные значения.
Градусная мера окружности равна 360°. Чтобы решать задачи быстро, важно запомнить, где находятся углы 0°; 90°; 180°; 270°; 360°. Единичная окружность с градусами выглядит так:
Единичная окружность с градусами выглядит так:
Радиан — одна из мер для определения величины угла.
Один радиан — это величина угла между двумя радиусами, проведенными так, что длина дуги между ними равна величине радиуса.
Число радиан для полной окружности — 360 градусов.
Длина окружности равна 2πr, что превышает длину радиуса в 2π раза.
Поскольку по определению 1 радиан — это угол между концами дуги, длина которой равна радиусу, в полной окружности заключен угол, равный 2π радиан.
Потренируемся переводить радианы в градусы. В полной окружности содержится 2π радиан, или 360 градусов. Таким образом:
- 2π радиан = 360°
- 1 радиан = (360/2π) градусов
- 1 радиан = (180/π) градусов
- 360° = 2π радиан
- 1° = (2π/360) радиан
- 1° = (π/180) радиан
Кстати, определение синуса, косинуса, тангенса и котангенса в тригонометрии дается через координаты точек на единичной окружности. 2 = 1
2 = 1
При помощи этого уравнения, вместе с определениями синуса и косинуса, можно записать основное тригонометрическое тождество:
Для чего использовать единичную окружность
- определить синус, косинус, тангенс и котангенс угла
- найти значения тригонометрических функций для некоторых значений числового и углового аргумента
- вывести основные формулы тригонометрии
- вывести формулы приведения
- найти области определения и области значений тригонометрических функций
- определить периодичность тригонометрических функций
- определить четность и нечетность тригонометрических функций
- определить промежутки возрастания и убывания тригонометрических функций
- определить промежутки знакопостоянства тригонометрических функций
- применить радианное измерение углов
- найти значения обратных тригонометрических функций
- решить простейшие тригонометрические уравнения
- решить простейшие неравенства.

Чтобы ребенок еще лучше учился в школе, запишите его на уроки математики в современную школу Skysmart. Наши преподаватели понятно объяснят что угодно — от дробей до синусов — и ответят на вопросы, которые бывает неловко задать перед всем классом. А еще помогут догнать сверстников и справиться со сложной контрольной.
Вместо скучных параграфов ребенка ждут интерактивные упражнения с мгновенной автоматической проверкой и онлайн-доска, где можно рисовать и чертить вместе с преподавателем. Приходите на бесплатный вводный урок и попробуйте сами!
Сводка тригонометрических формул
Сводка тригонометрических формулЭти формулы относятся к длине и площади определенных кругов или треугольников. На следующей странице вы найдете личности. Идентичности не относятся к конкретным геометрическим фигурам, но верны для всех углов.
Формулы дуг и секторов окружностей
Вы можете легко найти как длину дуги, так и площадь сектора для угла θ в окружности радиуса r .
| Длина дуги. Длина дуги равна радиусу r, в умноженному на угол θ , где угол измеряется в радианах. Чтобы преобразовать градусы в радианы, умножьте количество градусов на π /180. | |
| Площадь сектора. Площадь сектора равна половине квадрата радиуса, умноженного на угол, где, опять же, угол измеряется в радианах. |
Формулы для прямоугольных треугольников
Наиболее важные формулы для тригонометрии — формулы для прямоугольного треугольника.Если θ — один из острых углов в треугольнике, то синус тэты — это отношение противоположной стороны к гипотенузе, косинус — это отношение соседней стороны к гипотенузе, а тангенс — это отношение сторона, противоположная соседней стороне.
Эти три формулы известны мнемоническим языком SohCahToa. Помимо этого, существует очень важная формула Пифагора, которая гласит, что квадрат гипотенузы равен сумме квадратов двух других сторон.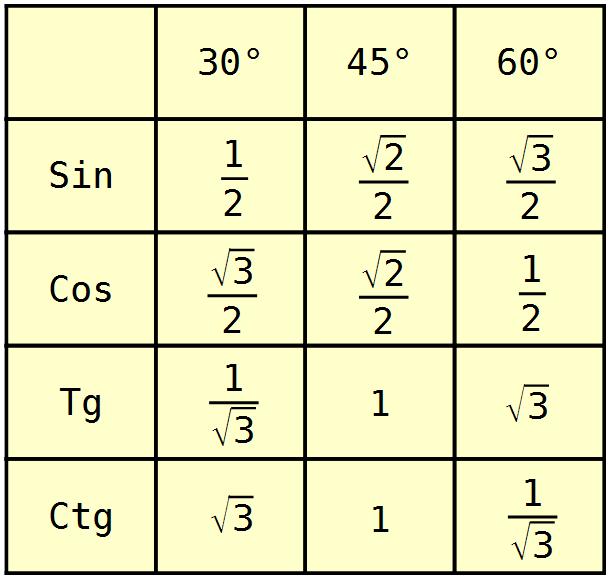
Зная, что два острых угла дополняют друг друга, то есть они складываются в 90 °, вы можете решить любой прямоугольный треугольник:
- Если вы знаете две из трех сторон, вы можете найти третью сторону и оба острых угла.
- Если вы знаете один острый угол и одну из трех сторон, вы можете найти другой острый угол и две другие стороны.
Формулы наклонных треугольников
Эти формулы работают для любого треугольника, будь то острый, тупой или прямой.Мы будем использовать стандартные обозначения, в которых три вершины треугольника обозначаются прописными буквами A , B и C , а три противоположные им стороны соответственно обозначаются строчными буквами a , . b и c .
Есть две важные формулы для наклонных треугольников. Их называют законом косинусов и законом синусов.
Закон косинусов обобщает формулу Пифагора на все треугольники.В нем говорится, что c 2 , квадрат одной стороны треугольника, равен a 2 + b 2 , сумме квадратов двух других сторон минус 2.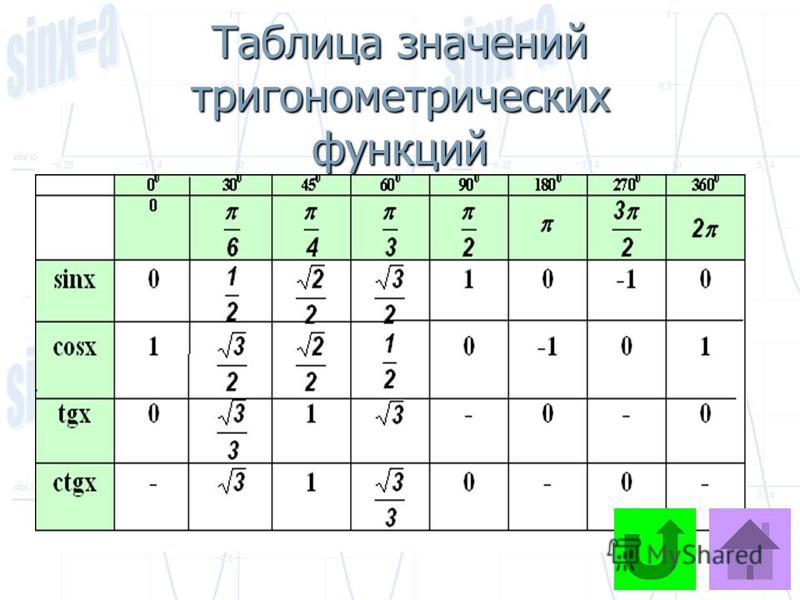 ab cos & nbsp C , удвоить их произведение, умноженное на косинус противоположного угла. Когда угол C правильный, он становится формулой Пифагора.
ab cos & nbsp C , удвоить их произведение, умноженное на косинус противоположного угла. Когда угол C правильный, он становится формулой Пифагора.
Закон синусов гласит, что отношение синуса одного угла к противоположной стороне является одинаковым отношением для всех трех углов.
С помощью этих двух формул вы можете решить любой треугольник:
- Если вы знаете два угла и сторону, вы можете найти третий угол и две другие стороны.
- Если вы знаете две стороны и включенный угол, вы можете найти третью сторону и оба других угла.
- Если вы знаете две стороны и угол, противоположный одной из них, есть две возможности для угла, противоположного другой (острый и тупой), и для обеих возможностей вы можете определить оставшийся угол и оставшуюся сторону.
Формулы площади для треугольников
Есть три разные полезные формулы для вычисления площади треугольника, и какая из них вы используете, зависит от того, какая информация у вас есть.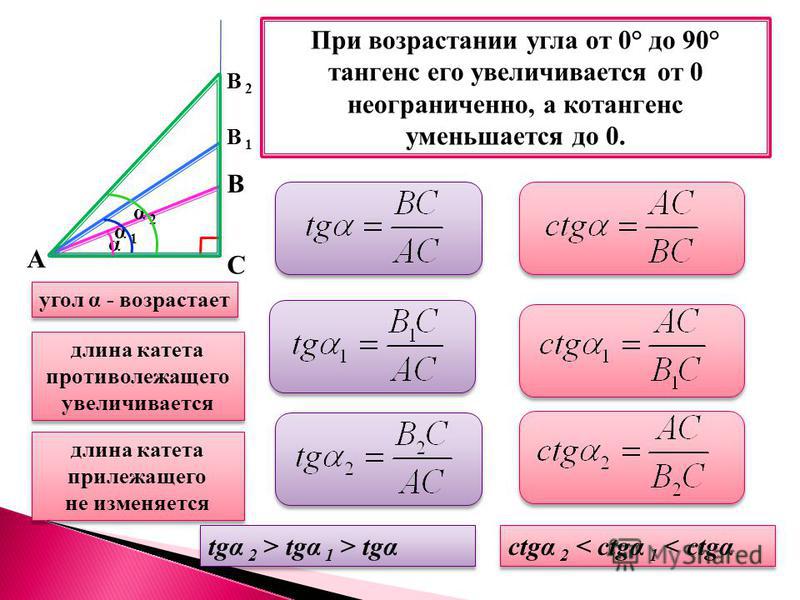
| Умножить половину основания на высоту. Это обычный вариант, поскольку он самый простой и обычно у вас есть такая информация. Выбирайте любую сторону, чтобы позвонить по базе b . Тогда, если h — это расстояние от противоположной вершины до b , то площадь равна половине bh . | |
| Формула Герона. Это полезно, когда вы знаете три стороны треугольника: a , b и c , и все, что вам нужно знать, это площадь. Пусть с будет половиной их суммы, называемой полупериметром . Тогда площадь является квадратным корнем из произведения s , s — a , s — b и s — c . | |
Формула стороны-угла-стороны. Используйте это, если вам известны две стороны, a и b , и включенный угол C . Площадь равна половине произведения двух сторон, умноженного на синус включенного угла. |
Углы поиска — тригонометрия
Если вы считаете, что контент, доступный через Веб-сайт (как определено в наших Условиях обслуживания), нарушает или несколько ваших авторских прав, сообщите нам об этом, отправив письменное уведомление («Уведомление о нарушении»), содержащее в информацию, описанную ниже, назначенному ниже агенту.Если репетиторы университета предпримут действия в ответ на ан Уведомление о нарушении, он предпримет добросовестную попытку связаться со стороной, которая предоставила такой контент средствами самого последнего адреса электронной почты, если таковой имеется, предоставленного такой стороной Varsity Tutors.
Ваше Уведомление о нарушении прав может быть отправлено стороне, предоставившей доступ к контенту, или третьим лицам, таким как в виде ChillingEffects.org.
Обратите внимание, что вы будете нести ответственность за ущерб (включая расходы и гонорары адвокатам), если вы существенно
искажать информацию о том, что продукт или действие нарушает ваши авторские права. Таким образом, если вы не уверены, что контент находится
на Веб-сайте или по ссылке с него нарушает ваши авторские права, вам следует сначала обратиться к юристу.
Таким образом, если вы не уверены, что контент находится
на Веб-сайте или по ссылке с него нарушает ваши авторские права, вам следует сначала обратиться к юристу.
Чтобы отправить уведомление, выполните следующие действия:
Вы должны включить следующее:
Физическая или электронная подпись правообладателя или лица, уполномоченного действовать от их имени;
Идентификация авторских прав, которые, как утверждается, были нарушены;
Описание характера и точного местонахождения контента, который, по вашему мнению, нарушает ваши авторские права, в \
достаточно подробностей, чтобы позволить репетиторам университетских школ найти и точно идентифицировать этот контент; например, мы требуем
а
ссылка на конкретный вопрос (а не только на название вопроса), который содержит содержание и описание
к какой конкретной части вопроса — изображению, ссылке, тексту и т. д. — относится ваша жалоба;
Ваше имя, адрес, номер телефона и адрес электронной почты; а также
Ваше заявление: (а) вы добросовестно считаете, что использование контента, который, по вашему мнению, нарушает
ваши авторские права не разрешены законом, владельцем авторских прав или его агентом; (б) что все
информация, содержащаяся в вашем Уведомлении о нарушении, является точной, и (c) под страхом наказания за лжесвидетельство, что вы
либо владелец авторских прав, либо лицо, уполномоченное действовать от их имени.
д. — относится ваша жалоба;
Ваше имя, адрес, номер телефона и адрес электронной почты; а также
Ваше заявление: (а) вы добросовестно считаете, что использование контента, который, по вашему мнению, нарушает
ваши авторские права не разрешены законом, владельцем авторских прав или его агентом; (б) что все
информация, содержащаяся в вашем Уведомлении о нарушении, является точной, и (c) под страхом наказания за лжесвидетельство, что вы
либо владелец авторских прав, либо лицо, уполномоченное действовать от их имени.
Отправьте жалобу нашему уполномоченному агенту по адресу:
Чарльз Кон
Varsity Tutors LLC
101 S. Hanley Rd, Suite 300
St. Louis, MO 63105
Или заполните форму ниже:
2. Sin, Cos и Tan суммы и разности двух углов
М. Борна
Синус суммы и разности двух углов имеет следующий вид:
sin ( α + β ) = sin α cos β + cos α sin β
sin ( α — β ) = sin α cos β — cos α sin β
Косинус суммы и разности двух углов имеет следующий вид:
cos ( α + β ) = cos α cos β — sin α sin β
cos ( α — β ) = cos α cos β + sin α sin β
Доказательства синуса и косинуса сумм и разностей двух углов
Мы можем доказать эти тождества разными способами.
Вот относительно простое доказательство с использованием единичной окружности:
Доказательство 1
Доказательство 1 — Использование единичной окружности
Начнем с единичного круга (что означает, что он имеет радиус 1) с центром в О.
Мы строим углы BOA = alpha и AOP = beta, как показано.
Затем мы опускаем перпендикуляр из P на ось x в T. Точка C — это пересечение OA и PT.
Затем строим линию PR перпендикулярно OA.
Наконец, мы опускаем перпендикуляр от R к оси x в точке S, а другой перпендикуляр от R к PT в точке Q, как показано.
Отметим следующее:
(1) `/ _TPR = alpha`, поскольку треугольники OTC и PRC подобны. (`/ _OTC = / _PRC = 90 °` и `/ _OCT = / _PCR = 90 ° — alpha`.)
(2) Длина | QT | = | RS |
(3) sin (α + β) = | PT | = | PQ | + | QT | = | PQ | + | RS |
(4) | PR | = грех (β)
(5) В треугольнике PQR, | PQ | = | PR | cos (α)
(6) Таким образом, из (4) и (5) | PQ | = sin (β) cos (α).
(7) | ИЛИ | = cos (β)
(8) В треугольнике OSR, | RS | = | ИЛИ | грех (α)
(9) Таким образом, из (7) и (8), | RS | = cos (β) sin (α)
(10) Таким образом, из (3), (6) и (9) мы доказали:
sin (α + β) = sin (β) cos (α) + cos (β) sin (α)
Перестановка дает:
sin (α + β) = sin (α) cos (β) + cos (α) sin (β)
(11) Из четных и нечетных функций имеем: cos (- β ) = cos (β) и sin (- β ) = −sin (β)
(12) Таким образом, заменяя β на (- β ), тождество в (10) становится
sin ( α — β ) = sin α cos β — cos α sin β
[Спасибо Дэвиду Макинтошу за набросок приведенного выше доказательства.]
Доказательства косинуса
Теперь нам нужно доказать
cos ( α + β ) = cos α cos β — sin α sin β
(13) | ОТ | = cos ( α + β )
(14) В треугольнике ORS имеем: `cos alpha = | OS | / | OR |`.
(15) cos (β) = | OR | из (7) выше.
(16) Из (14) и (15) получаем `cos alpha cos beta = | OS | / | OR | xx | OR | = | ОС | `.
(17) В треугольнике QPR имеем `sin alpha = | QR | / | PR |`.
(18) sin (β) = | PR | из (4) выше.
(19) Из (17) и (18) получаем `sin alpha sin beta = | QR | / | PR | xx | PR | = | QR | `.
(20) Сейчас | ОС | — | QR | = | ОТ |.
(21) Итак, `cos alpha cos beta — sin alpha sin beta« = cos (alpha + beta) `.
(22) Переставляя, получаем:
cos ( α + β ) = cos α cos β — sin α sin β
(23) Еще раз заменим β на (- β ), и тождество в (22) станет:
cos ( α — β ) = cos α cos β + sin α sin β
Следующее доказательство — стандартное, которое вы видите в большинстве учебников.Здесь также используется единичный круг, но это не так просто, как первое доказательство. Однако мы все еще можем многому научиться из этого следующего доказательства, особенно о том, как работают тригонометрические тождества.
Однако мы все еще можем многому научиться из этого следующего доказательства, особенно о том, как работают тригонометрические тождества.
Проба 2
Доказательство 2 — Использование единичной окружности
Сначала мы докажем тождество косинуса суммы двух углов, а затем покажем, что этот результат можно распространить на все другие данные тождества.
cos (α + β) = cos α cos β — sin α sin β
Нарисуем круг радиусом 1 единицу с точкой P на окружности в точке (1, 0).
Нарисуем угол α от центра с конечной точкой Q в точке (cos α, sin α), как показано. [ Q равно (cos α, sin α), потому что гипотенуза равна 1 единице.]
Мы расширяем эту идею, нарисовав:
а. Угол β с концевыми точками в Q (cos α, sin α) и R (cos (α + β), sin (α + β))
г. Угол −β с конечной точкой S (cos (−β), sin (−β))
г. Строки PR и QS эквивалентны по длине.
Теперь, используя формулу расстояния из Аналитической геометрии, мы имеем:
PR 2 = (cos (α + β) — 1) 2 + sin 2 (α + β)
= cos 2 (α + β) — 2 cos (α + β) + 1 + sin 2 (α + β)
= 2 — 2cos (α + β)
[поскольку sin 2 (α + β) + cos 2 (α + β) = 1]
Теперь используем формулу расстояния для расстояния QS :
QS 2 = (cos α — cos (−β)) 2 + (sin α — sin (−β)) 2
= cos 2 α — 2 cos α cos (−β) + cos 2 (−β) + sin 2 α — 2sin α sin (−β) + sin 2 (−β)
= 2 — 2cos α cos (−β) — 2sin α sin (−β)
[с
sin 2 α + cos 2 α = 1 и
sin 2 (−β) + cos 2 (−β) = 1]
= 2 — 2cos α cos β + 2sin α sin β
[с
cos (−β) = cos β (косинус — четная функция) и
sin (−β) = −sinβ (синус — нечетная функция — см. Четные и нечетные функции)]
Четные и нечетные функции)]
Поскольку PR = QS , мы можем приравнять 2 только что найденных расстояния:
2 — 2cos (α + β) = 2 — 2cos α cos β + 2sin α sin β
Вычитая 2 с обеих сторон и деля на −2, получаем:
cos (α + β) = cos α cos β — sin α sin β
Если мы заменим β на (−β), это тождество станет:
cos (α — β) = cos α cos β + sin α sin β
[поскольку cos (−β) = cos β и sin (−β) = −sinβ]
Синус суммы двух углов
Мы стремимся доказать, что
sin (α + β) = sin α cos β + cos α sin β
Напомним, что (см. Фазовый сдвиг)
sin ( θ ) = cos (π / 2− θ )
Если θ = α + β, то имеем:
грех (α + β)
= соз [π / 2 — (α + β)]
= cos [π / 2 — α — β)]
Затем мы перегруппируем углы внутри косинусного члена, так как он нам понадобится для остальной части доказательства:
cos [π / 2 — α — β)] = cos [(π / 2 — α) — β]
Используя косинус разности двух углов, тождество, которое мы только что нашли выше [где сказано
cos (α — β) = cos α cos β + sin α sin β],
имеем:
cos [(π / 2 — α) — β]
= cos (π / 2 — α) cos (β) + sin (π / 2 — α) sin (β)
= sin α cos β + cos α sin β
[Поскольку cos (π / 2 — α) = sin α; и sin (π / 2 — α) = cos α]
Следовательно:
sin (α + β) = sin α cos β + cos α sin β
Заменяя β на (−β), это тождество становится (из-за четных и нечетных функций):
sin (α — β) = sin α cos β — cos α sin β
Мы доказали 4 тождества, включающих синус и косинус суммы и разности двух углов.
Резюме:
sin (α + β) = sin α cos β + cos α sin β
sin (α — β) = sin α cos β — cos α sin β
cos (α + β) = cos α cos β — sin α sin β
cos (α — β) = cos α cos β + sin α sin β
Наконец, вот более простое доказательство личности с использованием комплексных чисел :
Доказательство 3
Доказательство 3 — Использование комплексных чисел
Экспоненциальная и полярная формы комплексного числа обеспечивают простой способ доказательства основных тригонометрических тождеств.
Предположим, у нас есть 2 комплексных числа, которые мы записываем как:
r 1 e jα = r 1 (cos α + j sin α)
и
r 2 e jβ = r 2 (cos β + j sin β)
Умножаем эти комплексные числа вместе.
Умножение левой части:
r 1 e jα × r 2 e jβ = r 1 r 2 e (α 900)
Мы можем записать этот ответ как:
r 1 r 2 e j (α + β) = r 1 r 2 (cos (α + β) + j sin ( α + β))… (1)
Умножение правых частей:
r 1 (cos α + j sin α) × r 2 (cos β + j sin β)
= r 1 r 2 (cos α cos β + j cos α sin β + j sin α cos β — sin α sin β)
= r 1 r 2 (cos α cos β — sin α sin β + j (cos α sin β + sin α cos β)). … (2)
… (2)
[начиная с j 2 = −1]
Теперь, приравняв (1) и (2) и разделив обе части на r 1 r 2 :
cos (α + β) + j sin (α + β) = cos α cos β — sin α sin β + j (cos α sin β + sin α cos β)
Приравнивание реальных частей дает:
cos (α + β) = cos α cos β — sin α sin β
Приравнивание мнимых частей дает:
sin (α + β) = sin α cos β + cos α sin β
Затем мы, как и раньше, заменим β на (−β), чтобы получить тождества для sin (α — β) и cos (α — β).
Касательная к сумме и разности двух углов
У нас есть следующие тождества для тангенса суммы и разности двух углов:
`загар (альфа + бета) = (загар альфа + загар бета) / (1-загар альфа \ загар бета)`
и
`загар (альфа-бета) = (загар альфа-загар бета) / (1 + загар альфа \ загар бета)`
Доказательство касательной суммы и разности двух углов
Наше доказательство для них использует тригонометрическое тождество для tan, которое мы встречали ранее.
Проба
Регистр: `tan (alpha + beta)`
Напомним, что
`tan theta = (sin theta) / (cos theta)`
Итак, положив θ = α + β и расширив с использованием наших новых тождеств синуса и косинуса, мы имеем:
`tan (alpha + beta)` = (sin (alpha + beta)) / (cos (alpha + beta)) « = (sin alpha cos beta + cos alpha sin beta) / (cos alpha cos beta-sin альфа грех бета) `
Деление числителя и знаменателя на cos α cos β:
`= (sin alpha cos beta + cos alpha sin beta) / (cos alpha cos beta-sin alpha sin beta)` — 🙁 cos alpha cos beta) / (cos alpha cos beta`
Упрощение дает нам:
`загар (альфа + бета) =` `(загар альфа + загар бета) / (1-загар альфа \ загар бета)`
Футляр: `tan (alpha-beta)`
Замена β на (−β) дает
`загар (альфа-бета) =` `(загар альфа-загар бета) / (1 + загар альфа \ загар бета)`
[касательная функция нечетная, поэтому tan (−β) = — tan β]
Мы доказали два тангенса тождества суммы и разности двух углов:
`загар (альфа + бета) =` `(загар альфа + загар бета) / (1-загар альфа \ загар бета)`
`загар (альфа-бета) =` `(загар альфа-загар бета) / (1 + загар альфа \ загар бета)`
Пример 1
Найдите точное значение для cos 75 o , используя 75 o = 30 o + 45 o . («o») `
(«o») `
`= sqrt3 / 2 (1) / sqrt2-1 / 2 (1) / sqrt2`
`= (sqrt3-1) / (2sqrt2)`
Это точное значение для cos 75 o .
Пример 2
Если sin α = 4/5 (в квадранте I) и cos β = -12 / 13 (в квадранте II), вычислите sin (α — β).
Ответ
Мы используем
sin ( α — β ) = sin α cos β — cos α sin β
Сначала нужно найти cos α и sin β.
Если sin α = 4/5, то мы можем нарисовать треугольник и найти значение неизвестной стороны, используя теорему Пифагора (в данном случае 3):
Проделаем то же самое для cos β = 12/13 и получим следующий треугольник.
Примечание 1: Мы используем положительное значение «12/13» для расчета необходимого опорного угла относительно «бета».
Примечание 2: Коэффициент синусоиды положительный как в квадранте I, так и в квадранте II.
Примечание 3: Мы использовали теорему Пифагора, чтобы найти неизвестную сторону, 5.
Теперь о неизвестных соотношениях в вопросе:
`cos α = 3/5`
(положительный, потому что в квадранте I)
`грех β = 5 / 13`(положительный, потому что в квадранте II)
Теперь мы готовы найти искомое значение sin ( α — β ):
`sin (alpha-beta) =` sin alpha \ cos beta-cos alpha \ sin beta`
`= 4/5 (-12/13) -3/5 (5/13)`
`= (- 48-15) / 65`
`= (- 63) / 65`
Это точное значение для sin ( α — β ).(«o») `
`= 1/2 (1) / sqrt2 + sqrt3 / 2 (1) / sqrt2`
`= (1 + sqrt3) / (2sqrt2)`
2. Если sin α = 4/5 (в квадранте I) и cos β = -12 / 13 (в квадранте II), оцените cos (β — α).
[Это не то же самое, что и в Примере 2 выше. На этот раз нам нужно найти косинус разности.]
Ответ
В этом случае для косинуса разности двух углов имеем:
`cos (beta-alpha) =` `cos beta cos alpha + sin beta sin alpha`
`= ((- 12) / 13) 3/5 + (5/13) 4/5`
`= (- 36 + 20) / 65`
`= (- 16) / 65`
3. Сократите следующее до одного члена. Не расширяться.
Сократите следующее до одного члена. Не расширяться.
cos ( x + y ) cos y + sin ( x + y ) sin y
Ответ
Мы узнаем это выражение как правую часть от:
cos ( α — β ) = cos α cos β + cos α cos β ,
с α = x + y и β = y.»o» \ sin x`
`= sqrt3 / 2 cos x-1 / 2sin x`
`= (sqrt3 \ cos x-sin x) / 2`
`=» RHS «`
Поскольку LHS = RHS, мы доказали тождество.
1.2: Тригонометрические функции острого угла
Рассмотрим прямоугольный треугольник \ (\ треугольник \, ABC \) с прямым углом в \ (C \) и длиной \ (a \), \ (b \), и \ (c \), как на рисунке справа. Для острого угла \ (A \) назовите ножку \ (\ overline {BC} \) его противоположной стороной и назовите ножку \ (\ overline {AC} \) его соседней стороной .Напомним, что гипотенуза треугольника — это сторона \ (\ overline {AB} \). Соотношения сторон прямоугольного треугольника встречаются в практических приложениях достаточно часто, чтобы оправдать их собственные названия, поэтому мы определяем шесть тригонометрических функций из \ (A \) следующим образом:
Таблица 1.2 Шесть тригонометрических функций \ (A \)
Обычно мы будем использовать сокращенные названия функций. Обратите внимание на таблицу 1.2, что пары \ (\ sin A \) и \ (\ csc A \), \ (\ cos A \) и \ (\ sec A \), а также \ (\ tan A \) и \ ( \ cot A \) являются обратными величинами:
Пример 1.5
Для прямоугольного треугольника \ (\ треугольник \, ABC \), показанного справа, найдите значения всех шести тригонометрических функций острых углов \ (A \) и \ (B \).
Раствор:
Гипотенуза треугольника \ (\ треугольник \, ABC \) имеет длину \ (5 \). Для угла \ (A \) противоположная сторона \ (\ overline {BC} \) имеет длину \ (3 \), а соседняя сторона \ (\ overline {AC} \) имеет длину \ (4 \). Таким образом:
\ [\ nonumber \ sin A ~ = ~ \ dfrac {\ text {напротив}} {\ text {hypotenuse}} ~ = ~ \ dfrac {3} {5} \ qquad \ qquad
\ cos A ~ = ~ \ dfrac {\ text {смежный}} {\ text {hypotenuse}} ~ = ~ \ dfrac {4} {5} \ qquad \ qquad
\ tan A ~ = ~ \ dfrac {\ text {напротив}} {\ text { смежный}} ~ = ~ \ dfrac {3} {4} \]
\ [\ nonumber \ csc A ~ = ~ \ dfrac {\ text {hypotenuse}} {\ text {напротив}} ~ = ~ \ dfrac {5} {3} \ qquad \ qquad
\ sec A ~ = ~ \ dfrac {\ text {hypotenuse}} {\ text {смежный}} ~ = ~ \ dfrac {5} {4} \ qquad \ qquad
\ cot A ~ = ~ \ dfrac {\ text {смежный}} {\ text { напротив}} ~ = ~ \ dfrac {4} {3} \]
Для угла \ (B \) противоположная сторона \ (\ overline {AC} \) имеет длину \ (4 \), а соседняя сторона \ (\ overline {BC} \) имеет длину \ (3 \).Таким образом:
\ [\ sin B ~ = ~ \ dfrac {\ text {напротив}} {\ text {hypotenuse}} ~ = ~ \ dfrac {4} {5} \ qquad \ qquad
\ cos B ~ = ~ \ dfrac { \ text {смежный}} {\ text {hypotenuse}} ~ = ~ \ dfrac {3} {5} \ qquad \ qquad
\ tan B ~ = ~ \ dfrac {\ text {противоположный}} {\ text {смежный} } ~ = ~ \ dfrac {4} {3} \]
\ [\ csc B ~ = ~ \ dfrac {\ text {hypotenuse}} {\ text {напротив}} ~ = ~ \ dfrac {5} {4} \ qquad \ qquad
\ sec B ~ = ~ \ dfrac { \ text {hypotenuse}} {\ text {смежный}} ~ = ~ \ dfrac {5} {3} \ qquad \ qquad
\ cot B ~ = ~ \ dfrac {\ text {смежный}} {\ text {напротив} } ~ = ~ \ dfrac {3} {4} \]
Уведомление в примере 1.5, что мы не указали единицы измерения длины. Это повышает вероятность того, что наши ответы зависели от треугольника определенного физического размера.
Например, предположим, что этот учебник читают два разных студента: один в США, а другой — в Германии. Американский студент думает, что длины \ (3 \), \ (4 \) и \ (5 \) в примере 1.5 измеряются в дюймах, тогда как немецкий студент думает, что они измеряются в сантиметрах. Поскольку \ (1 \) в \ (\ приблизительно \) \ (2.54 \) см, учащиеся используют треугольники разных физических размеров (см. Рис. 1.2.1 ниже, не в масштабе).
Рисунок 1.2.1: \ (△ ABC ∼ △ A ′ B ′ C ′ \)
Если американский треугольник \ (\ треугольник \, ABC \), а немецкий треугольник — \ (\ треугольник \, A’B’C ‘\), то из рисунка 1.2.1 мы видим, что \ (\ треугольник \, ABC \) подобен \ (\ треугольник \, A’B’C ‘\), и, следовательно, соответствующие углы равны и отношения соответствующих сторон равны.Фактически, мы знаем это общее отношение: стороны \ (\ треугольник \, ABC \) примерно в \ (2.54 \) раз длиннее, чем соответствующие стороны \ (\ треугольник \, A’B’C ‘\). Итак, когда американский студент вычисляет \ (\ sin A \), а немецкий студент вычисляет \ (\ sin A ‘\), они получают тот же ответ:
\ [\ треугольник \, ABC ~ \ sim ~ \ треугольник \, A’B’C ‘\ quad \ Rightarrow \ quad
\ dfrac {BC} {B’C’} ~ = ~ \ dfrac {AB} {A ‘B’} \ quad \ Rightarrow \ quad
\ dfrac {BC} {AB} ~ = ~ \ dfrac {B’C ‘} {A’B’} \ quad \ Rightarrow \ quad \ sin A ~ = ~ \ sin А ‘\]
Аналогично, другие значения тригонометрических функций \ (A \) и \ (A ‘\) одинаковы.Фактически, наш аргумент был достаточно общим, чтобы работать с любыми подобными прямоугольными треугольниками. Это приводит нас к следующему выводу:
При вычислении тригонометрических функций острого угла \ (A \) вы можете использовать любой прямоугольный треугольник , который имеет \ (A \) в качестве одного из углов.
Поскольку мы определили тригонометрические функции в терминах отношений сторон, вы можете думать об единицах измерения для этих сторон как о сокращении этих отношений. Это означает, что значения тригонометрических функций являются безразмерными числами .\ circ \; = \; \ dfrac {\ text {смежный}} {\ text {противоположный}} \; = \;
\ dfrac {\ sqrt {3}} {1} \; = \; \ sqrt {3} \]
Пример 1.8
\ (A \) — острый угол такой, что \ (\ sin A = \ frac {2} {3} \). Найдите значения других тригонометрических функций \ (A \).
Раствор:
В общем, рисование прямоугольного треугольника помогает решать задачи этого типа. Причина в том, что тригонометрические функции были определены в терминах отношения сторон прямоугольного треугольника, и вам дана одна такая функция (в данном случае синус) уже в терминах отношения: \ (\ sin \; A = \ frac {2} {3} \).2 ~ = ~ 9 ~ — ~ 4 ~ = ~ 5 \ quad \ Rightarrow \ quad
b ~ = ~ \ sqrt {5} \]
Теперь мы знаем длины всех сторон треугольника \ (\ треугольник \, ABC \), поэтому имеем:
\ [\ cos \; A \; = \; \ dfrac {\ text {смежный}} {\ text {hypotenuse}} \; = \; \ dfrac {\ sqrt {5}} {3} \ qquad
\ tan \; A \; = \; \ dfrac {\ text {напротив}} {\ text {смежный}} \; = \;
\ dfrac {2} {\ sqrt {5}} \ quad \ quad \]
\ [\ csc \; A \; = \; \ dfrac {\ text {hypotenuse}} {\ text {напротив}} \; = \; \ dfrac {3} {2} \ qquad
\ sec \; A \; = \; \ dfrac {\ text {hypotenuse}} {\ text {смежный}} \; = \; \ dfrac {3} {\ sqrt {5}} \ qquad
\ cot \; A \; = \; \ dfrac {\ text {смежный}} {\ text {противоположный}} \; = \; \ dfrac {\ sqrt {5}} {2} \]
Возможно, вы заметили связь между синусом и косинусом, секансом и косекансом, а также тангенсом и котангенсом дополнительных углов в примерах 1.5 и 1.7. Обобщение этих примеров дает нам следующую теорему:
Теорема 1.2 Теорема о функциях
Если \ (A \) и \ (B \) — дополнительные острые углы в прямоугольном треугольнике \ (\ треугольник \, ABC \), то выполняются следующие соотношения:
\ [\ sin \; A ~ = ~ \ cos \; B \ qquad \ qquad \ sec \; A ~ = ~ \ csc \; B \ qquad \ qquad \ tan \; A ~ = ~ \ cot \; B \]
\ [\ sin \; B ~ = ~ \ cos \; A \ qquad \ qquad \ sec \; B ~ = ~ \ csc \; A \ qquad \ qquad \ tan \; B ~ = ~ \ cot \; A \]
Мы говорим, что пары функций \ (\ lbrace \; \ sin, \ cos \; \ rbrace \), \ (\ lbrace \; \ sec, \ csc \; \ rbrace \) и \ (\ lbrace \ ; \ tan, \ cot \; \ rbrace \) являются \ (\ textbf {cofunctions} \).\ circ \), поместите \ (30-60-90 \) прямоугольный треугольник \ (\ треугольник \, ADB \) с катетами длиной \ (\ sqrt {3} \) и \ (1 \) поверх гипотенуза прямоугольного треугольника \ (45-45-90 \) \ (\ треугольник \, ABC \), длина гипотенузы которого равна \ (\ sqrt {3} \), как на рисунке справа. Из рисунка 1.2.2 (а) мы знаем, что длина каждого катета \ (\ треугольника \, ABC \) равна длине гипотенузы, деленной на \ (\ sqrt {2} \). Итак, \ (AC = BC = \ frac {\ sqrt {3}} {\ sqrt {2}} = \ sqrt {\ frac {3} {2}} \). Нарисуйте \ (\ overline {DE} \) перпендикулярно \ (\ overline {AC} \) так, чтобы \ (\ треугольник \, ADE \) был прямоугольным треугольником.\ circ \), поскольку это дополнение к \ (\ angle \, BDF \). Гипотенуза \ (\ overline {BD} \) треугольника \ (\ треугольник \, DFB \) имеет длину \ (1 \), а \ (\ треугольник \, DFB \) является \ (45-45-90 \) правой треугольник, поэтому мы знаем, что \ (DF = FB = \ frac {1} {\ sqrt {2}} \).
Теперь мы знаем, что \ (\ overline {DE} \ perp \ overline {AC} \) и \ (\ overline {BC} \ perp \ overline {AC} \), поэтому \ (\ overline {FE} \) и \ (\ overline {BC} \) параллельны. Аналогично, \ (\ overline {FB} \) и \ (\ overline {EC} \) оба перпендикулярны \ (\ overline {DE} \) и, следовательно, \ (\ overline {FB} \) параллельны \ ( \ overline {EC} \).\ circ` = `1 / (\ sqrt (3))`
Тригонометрических функций и единичная окружность
Радианы
Радианы — это еще один способ измерения углов, и величина угла может быть преобразована между градусами и радианами.
Цели обучения
Объясните определение радиан с точки зрения длины дуги единичного круга и используйте его для преобразования между градусами и радианами.
Основные выводы
Ключевые моменты
- Один радиан — это мера центрального угла окружности, при которой длина дуги равна радиусу
окружности.\ circ} {\ pi}} [/ латекс]. - Радианная мера угла — это отношение длины дуги к радиусу круга [латекс] \ displaystyle {\ left (\ theta = \ frac {s} {r} \ right)} [/ latex] . Другими словами, если [latex] s [/ latex] — это длина дуги круга, а [latex] r [/ latex] — это радиус круга, то центральный угол, содержащий эту дугу, измеряется в радианах.
Ключевые термины
- arc : Непрерывная часть окружности круга.
- окружность : длина линии, ограничивающей круг.
- радиан : Стандартная единица измерения углов в математике. Мера центрального угла круга, который пересекает дугу, равную по длине радиусу этого круга.
Введение в радианы
Напомним, что деление круга на 360 частей дает измерение в градусах. Это произвольное измерение, и мы можем выбрать другие способы разделить круг.Чтобы найти другую единицу, представьте себе процесс рисования круга. Представьте, что вы останавливаетесь до того, как круг замкнется. Нарисованная вами часть называется дугой. Дуга может быть частью полного круга, полного круга или более чем полного круга, представленного более чем одним полным оборотом. Длина дуги вокруг всего круга называется окружностью этого круга.
Окружность круга
[латекс] C = 2 \ pi r [/ латекс]
Если мы разделим обе части этого уравнения на [латекс] r [/ латекс], мы получим отношение окружности, которое всегда равно [латексу] 2 \ pi [/ латексу] к радиусу, независимо от длины радиус.Таким образом, длина окружности любого круга равна [латексу] 2 \ пи \ приблизительно в 6,28 [/ латексу] раз больше длины радиуса. Это означает, что если мы возьмем струну такой же длины, как радиус, и будем использовать ее для измерения последовательных длин по окружности, то будет место для шести полных длин струны и чуть больше четверти седьмой, как показано на диаграмме. ниже.
Длина окружности по сравнению с радиусом : Длина окружности чуть более чем в 6 раз превышает длину радиуса.
Это подводит нас к нашей новой угловой мере. Радиан — это стандартная единица измерения углов в математике. Один радиан — это мера центрального угла круга, который пересекает дугу, равную по длине радиусу этого круга.
Один радиан: Угол [латекс] t [/ латекс] выметает величину в один радиан. Обратите внимание, что длина перехваченной дуги равна длине радиуса круга.
Поскольку общая длина окружности равна [латексу] 2 \ pi [/ latex], умноженному на радиус, полный круговой поворот составляет [латекс] 2 \ pi [/ latex] радиан. {\ circ}} [/ latex].
Измерение угла в радианах
Длина дуги [латекс] s [/ латекс] — это длина кривой вдоль дуги. Так же, как полная длина окружности всегда имеет постоянное отношение к радиусу, длина дуги, образованная любым заданным углом, также имеет постоянную связь с радиусом, независимо от длины радиуса.
Это отношение, называемое радианной мерой, одинаково независимо от радиуса круга — оно зависит только от угла. Это свойство позволяет нам определять меру любого угла как отношение длины дуги [latex] s [/ latex] к радиусу [latex] r [/ latex].
[латекс] \ displaystyle {\ begin {align} s & = r \ theta \\ \ theta & = \ frac {s} {r} \ end {align}} [/ latex]
Измерительные радианы: (a) под углом 1 радиан; длина дуги равна радиусу [латекс] r [/ латекс]. (b) Угол в 2 радиана имеет длину дуги [латекс] s = 2r [/ латекс]. (c) Полный оборот составляет [латекс] 2 \ pi [/ латекс], или около 6,28 радиана.
Пример
Какова мера данного угла в радианах, если длина его дуги равна [латекс] 4 \ pi [/ latex], а радиус — [латекс] [/ латекс] 12?
Подставьте значения [latex] s = 4 \ pi [/ latex] и [latex] r = 12 [/ latex] в формулу угла:
[латекс] \ displaystyle {\ begin {align} \ theta & = \ frac {s} {r} \\ & = \ frac {4 \ pi} {12} \\ & = \ frac {\ pi} {3 } \\ & = \ frac {1} {3} \ pi \ end {align}} [/ latex]
Угол измеряется в [latex] \ displaystyle {\ frac {1} {3} \ pi} [/ latex] радианах.
Определение тригонометрических функций на единичной окружности
Определение точек на единичной окружности позволяет применять тригонометрические функции к любому углу.
Цели обучения
Используйте прямоугольные треугольники, нарисованные в единичной окружности, чтобы определить тригонометрические функции для любого угла
Основные выводы
Ключевые моменты
- Координаты [latex] x [/ latex] — и [latex] y [/ latex] в точке на единичной окружности, заданной углом [latex] t [/ latex], определяются функциями [latex] x = \ cos t [/ latex] и [latex] y = \ sin t [/ latex].{\ circ} [/ латекс].
- Единичный круг демонстрирует периодичность тригонометрических функций, показывая, что они приводят к повторяющемуся набору значений через равные промежутки времени.
Ключевые термины
- периодичность : качество функции с повторяющимся набором значений через равные промежутки времени.
- единичная окружность : окружность с центром в начале координат и радиусом 1.
- квадранты : Четыре четверти координатной плоскости, образованные осями [latex] x [/ latex] — и [latex] y [/ latex].
Тригонометрические функции и единичная окружность
Мы уже определили тригонометрические функции в терминах прямоугольных треугольников. В этом разделе мы переопределим их в терминах единичной окружности. Напомним, что единичный круг — это круг с центром в начале координат и радиусом 1. Угол [латекс] t [/ латекс] (в радианах) образует дугу длиной [латекс] s [/ латекс].
Оси x- и y- делят координатную плоскость (и единичную окружность, поскольку она центрирована в начале координат) на четыре четверти, называемых квадрантами.Мы помечаем эти квадранты, чтобы имитировать направление, в котором будет разворачиваться положительный угол. Четыре квадранта обозначены I, II, III и IV.
Для любого угла [latex] t [/ latex] мы можем обозначить пересечение его стороны и единичного круга его координатами, [latex] (x, y) [/ latex]. Координаты [latex] x [/ latex] и [latex] y [/ latex] будут выходными данными тригонометрических функций [latex] f (t) = \ cos t [/ latex] и [latex] f (t). = \ sin t [/ latex] соответственно. Это означает:
[латекс] \ displaystyle {\ begin {align} x & = \ cos t \\ y & = \ sin t \ end {align}} [/ latex]
Эти координаты показаны на диаграмме единичного круга.
Единичный круг: координаты точки на единичной окружности, центральный угол которой составляет [латекс] t [/ латекс] радиан.
Обратите внимание, что значения [latex] x [/ latex] и [latex] y [/ latex] задаются длинами двух сторон треугольника, окрашенных в красный цвет. Это прямоугольный треугольник, и вы можете видеть, как длины этих двух сторон (и значения [latex] x [/ latex] и [latex] y [/ latex]) задаются тригонометрическими функциями [latex] t [/латекс].
В качестве примера того, как это применимо, рассмотрим диаграмму, показывающую точку с координатами [latex] \ displaystyle {\ left (- \ frac {\ sqrt2} {2}, \ frac {\ sqrt2} {2} \ right)} [/ latex] по единичной окружности.
Точка на единичном круге: точка [латекс] \ displaystyle {\ left (- \ frac {\ sqrt2} {2}, \ frac {\ sqrt2} {2} \ right)} [/ latex] на единичном круге .
Мы знаем, что для любой точки единичного круга координата [latex] x [/ latex] равна [latex] \ cos t [/ latex], а координата [latex] y [/ latex] — [latex] ] \ sin t [/ латекс]. Применяя это, мы можем определить, что [latex] \ displaystyle {\ cos t = — \ frac {\ sqrt2} {2}} [/ latex] и [latex] \ displaystyle {\ sin t = — \ frac {\ sqrt2} {2}} [/ латекс] для угла [латекс] t [/ латекс] на схеме.
Напомним, что [латекс] \ displaystyle {\ tan t = \ frac {\ sin t} {\ cos t}} [/ latex]. Применяя эту формулу, мы можем найти тангенс любого угла, обозначенного единичной окружностью. Для угла [латекс] t [/ латекс], указанного на диаграмме единичного круга, показывающего точку [латекс] \ displaystyle {\ left (- \ frac {\ sqrt2} {2}, \ frac {\ sqrt2} {2 } \ right)} [/ latex], касательная:
[латекс] \ displaystyle {\ begin {align} \ tan t & = \ frac {\ sin t} {\ cos t} \\ & = \ frac {- \ frac {\ sqrt2} {2}} {- \ гидроразрыв {\ sqrt2} {2}} \\ & = 1 \ end {align}} [/ latex]
Ранее мы обсуждали тригонометрические функции применительно к прямоугольным треугольникам.{\ circ} [/ латекс].
Дальнейшее рассмотрение единичного круга
Координаты определенных точек на единичной окружности и мера каждого угла в радианах и градусах показаны на диаграмме координат единичной окружности. Эта диаграмма позволяет наблюдать за каждым из этих углов, используя тригонометрические функции.
Координаты единичной окружности : Единичная окружность, показывающая координаты и угловые размеры определенных точек.
Мы можем найти координаты любой точки единичной окружности.Учитывая любой угол [латекс] t [/ латекс], мы можем найти координату [latex] x [/ latex] или [latex] y [/ latex] в этой точке, используя [latex] x = \ text {cos} t [/ latex] и [latex] y = \ text {sin} t [/ latex].
Единичный круг демонстрирует периодичность тригонометрических функций. Периодичность относится к способу, которым тригонометрические функции приводят к повторяющемуся набору значений через равные промежутки времени. Взгляните на [latex] x [/ latex] -значения координат в единичном круге выше для значений [latex] t [/ latex] от [latex] 0 [/ latex] до [latex] 2 {\ pi} [/ latex]:
[латекс] {1, \ frac {\ sqrt {3}} {2}, \ frac {\ sqrt {2}} {2}, \ frac {1} {2}, 0, — \ frac {1} {2}, — \ frac {\ sqrt {2}} {2}, — \ frac {\ sqrt {3}} {2}, -1, — \ frac {\ sqrt {3}} {2}, — \ frac {\ sqrt {2}} {2}, — \ frac {1} {2}, 0, \ frac {1} {2}, \ frac {\ sqrt {2}} {2}, \ frac { \ sqrt {3}} {2}, 1} [/ латекс]
Мы можем определить закономерность в этих числах, которые колеблются между [латекс] -1 [/ латекс] и [латекс] 1 [/ латекс].Обратите внимание, что этот шаблон будет повторяться для более высоких значений [latex] t [/ latex]. Напомним, что эти значения [latex] x [/ latex] соответствуют [latex] \ cos t [/ latex]. Это показатель периодичности функции косинуса.
Пример
Решите [латекс] \ displaystyle {\ sin {\ left (\ frac {7 \ pi} {6} \ right)}} [/ latex].
Похоже, это будет сложно решить. Однако обратите внимание, что диаграмма единичного круга показывает координаты в [latex] \ displaystyle {t = \ frac {7 \ pi} {6}} [/ latex].Поскольку координата [latex] y [/ latex] соответствует [latex] \ sin t [/ latex], мы можем идентифицировать, что
[латекс] \ displaystyle {\ sin {\ left (\ frac {7 \ pi} {6} \ right)} = — \ frac {1} {2}} [/ latex]
Специальные уголки
Единичный круг и набор правил можно использовать для вызова значений тригонометрических функций специальных углов.
Цели обучения
Объясните, как свойства синуса, косинуса и тангенса и их знаки в каждом квадранте дают свои значения для каждого из специальных углов.
Основные выводы
Ключевые моменты
- Тригонометрические функции для углов в единичной окружности можно запомнить и вызвать с помощью набора правил.
- Знак тригонометрической функции зависит от квадранта, в который попадает угол, и мнемоническая фраза «Умный класс триггера» используется для определения того, какие функции в каком квадранте положительны.
- Опорные углы в квадранте I используются для определения значения любого угла в квадрантах II, III или IV. Базовый угол образует тот же угол с осью [latex] x [/ latex], что и рассматриваемый угол.
- В единичную окружность включаются только функции синуса и косинуса для особых углов.Однако, поскольку тангенс получается из синуса и косинуса, его можно вычислить для любого из специальных углов.
Ключевые термины
- специальный угол : угол, кратный 30 или 45 градусам; тригонометрические функции легко записываются под этими углами.
Тригонометрические функции специальных углов
Напомним, что определенные углы и их координаты, которые соответствуют [latex] x = \ cos t [/ latex] и [latex] y = \ sin t [/ latex] для данного угла [latex] t [/ latex], можно определить по единичному кругу.{\ circ} \ right)} & = 1 \\ \ end {align}} [/ latex]
Выражения для косинусных функций этих специальных углов также просты.
Обратите внимание, что, хотя только синус и косинус определяются непосредственно единичной окружностью, касательную можно определить как частное, включающее эти два:
[латекс] \ displaystyle {\ tan t = \ frac {\ sin t} {\ cos t}} [/ латекс]
Функции касания также имеют простые выражения для каждого из специальных углов.
Мы можем наблюдать эту тенденцию на примере.{\ circ} \ right)}} \\ & = \ frac {\ frac {\ sqrt {3}} {2}} {\ frac {1} {2}} \\ & = \ frac {\ sqrt {3 }} {2} \ cdot \ frac {2} {1} \\ & = \ sqrt {3} \ end {align}} [/ latex]
Запоминание тригонометрических функций
Понимание единичной окружности и способность быстро решать тригонометрические функции для определенных углов очень полезно в области математики. Применение правил и ярлыков, связанных с единичным кругом, позволяет быстро решать тригонометрические функции. Ниже приведены некоторые правила, которые помогут вам быстро решить такие проблемы.
Признаки тригонометрических функций
Знак тригонометрической функции зависит от квадранта, в который попадает угол. Чтобы помочь запомнить, какие из тригонометрических функций положительны в каждом квадранте, мы можем использовать мнемоническую фразу «Умный класс триггера». Каждое из четырех слов во фразе соответствует одному из четырех квадрантов, начиная с квадранта I и вращаясь против часовой стрелки. В квадранте I, который является «A», все тригонометрических функций положительны.В квадранте II «Умный» только синус положительный. В квадранте III «Триггер» только , касательная положительна. Наконец, в квадранте IV «Класс» только , косинус является положительным.
Знаковые правила для тригонометрических функций: Каждая тригонометрическая функция перечислена в тех квадрантах, в которых она положительна. {\ circ} [/ латекс].
Для любого заданного угла в первом квадранте существует угол во втором квадранте с тем же значением синуса. Поскольку значение синуса является координатой [latex] y [/ latex] на единичной окружности, другой угол с таким же синусом будет иметь такое же значение [latex] y [/ latex], но будет иметь противоположное значение [latex] x [/ latex] -значение. Следовательно, его значение косинуса будет противоположным значению косинуса первого угла.
Аналогично, в четвертом квадранте будет угол с таким же косинусом, что и исходный угол.Угол с таким же косинусом будет иметь одно и то же значение [latex] x [/ latex], но будет иметь противоположное значение [latex] y [/ latex]. Следовательно, его значение синуса будет противоположным значению синуса исходного угла.
Как показано на диаграммах ниже, угол [латекс] \ альфа [/ латекс] имеет то же значение синуса, что и угол [латекс] t [/ латекс]; значения косинуса противоположны. Угол [латекс] \ бета [/ латекс] имеет то же значение косинуса, что и угол [латекс] t [/ латекс]; значения синуса противоположны.
[латекс] \ displaystyle {\ begin {align} \ sin t = \ sin \ alpha \ quad & \ text {and} \ quad \ cos t = — \ cos \ alpha \\ \ sin t = — \ sin \ beta \ quad & \ text {and} \ quad \ cos t = \ cos \ beta \ end {align}} [/ latex]
Контрольные углы: На левом рисунке [латекс] t [/ latex] является контрольным углом для [латекс] \ альфа [/ латекс].{\ circ} [/ latex] или [latex] 0 [/ latex] и [latex] \ displaystyle {\ frac {\ pi} {2}} [/ latex] радиан. Для любого угла в квадранте II, III или IV существует опорный угол в квадранте I.
Базовые углы в каждом квадранте: Для любого угла в квадрантах II, III или IV существует опорный угол в квадранте I.
Таким образом, чтобы вызвать любой синус или косинус особого угла, вы должны иметь возможность идентифицировать его угол с осью [latex] x [/ latex], чтобы сравнить его с опорным углом.{\ circ})} \\ & = \ frac {- \ frac {\ sqrt {2}} {2}} {- \ frac {\ sqrt {2}} {2}} \\ & = — \ frac { \ sqrt {2}} {2} \ cdot — \ frac {2} {\ sqrt {2}} \\ & = 1 \ end {align}} [/ latex]
Синус и косинус как функции
Функции синуса и косинуса можно изобразить, используя значения из единичной окружности, и на обоих графиках можно наблюдать определенные характеристики.
Цели обучения
Опишите характеристики графиков синуса и косинуса
Основные выводы
Ключевые моменты
- И синусоидальная функция [latex] (y = \ sin x) [/ latex], и косинусная функция [latex] (y = \ cos x) [/ latex] могут быть построены на графике путем нанесения точек, полученных из единичной окружности, с каждая координата [latex] x [/ latex] представляет собой угол в радианах, а координата [latex] y [/ latex] представляет собой соответствующее значение функции под этим углом.
- Синус и косинус — периодические функции с периодом [латекс] 2 \ пи [/ латекс].
- И синус, и косинус имеют домен [latex] (- \ infty, \ infty) [/ latex] и диапазон [latex] [- 1, 1] [/ latex].
- График [latex] y = \ sin x [/ latex] симметричен относительно начала координат, потому что это нечетная функция, в то время как график [latex] y = \ cos x [/ latex] симметричен относительно [latex ] y [/ latex] -axis, потому что это четная функция.
Ключевые термины
- период : интервал, содержащий значения, повторяющиеся в функции.
- четная функция : непрерывный набор точек [latex] \ left (x, f (x) \ right) [/ latex], в которых [latex] f (-x) = f (x) [/ latex], с симметрией относительно оси [латекс] y [/ латекс].
- нечетная функция : Непрерывный набор точек [latex] \ left (x, f (x) \ right) [/ latex], в которых [latex] f (-x) = -f (x) [/ latex] , с симметрией относительно начала координат.
- периодическая функция : непрерывный набор точек [latex] \ left (x, f (x) \ right) [/ latex], который повторяется через равные промежутки времени.
Графические функции синуса и косинуса
Напомним, что функции синуса и косинуса связывают значения действительных чисел с координатами [latex] x [/ latex] и [latex] y [/ latex] точки на единичной окружности. Так как же они выглядят на графике на координатной плоскости? Начнем с синусоидальной функции [latex] y = \ sin x [/ latex]. Мы можем создать таблицу значений и использовать их для построения графика. Ниже приведены некоторые значения для функции синуса на единичном круге, где координата [latex] x [/ latex] представляет собой угол в радианах, а координата [latex] y [/ latex] — [latex] \ sin х [/ латекс]:
[латекс] \ displaystyle {(0, 0) \ quad (\ frac {\ pi} {6}, \ frac {1} {2}) \ quad (\ frac {\ pi} {4}, \ frac { \ sqrt {2}} {2}) \ quad (\ frac {\ pi} {3}, \ frac {\ sqrt {3}} {2}) \ quad (\ frac {\ pi} {2}, 1 ) \\ (\ frac {2 \ pi} {3}, \ frac {\ sqrt {3}} {2}) \ quad (\ frac {3 \ pi} {4}, \ frac {\ sqrt {2} } {2}) \ quad (\ frac {5 \ pi} {6}, \ frac {1} {2}) \ quad (\ pi, 0)} [/ latex]
Построение точек из таблицы и продолжение по оси [latex] x [/ latex] дает форму синусоидальной функции.
График синусоидальной функции: График точек с координатами [latex] x [/ latex], являющимися углами в радианах, и координатами [latex] y [/ latex], являющимися функцией [latex] \ sin x [/ latex] .
Обратите внимание на положительные значения синуса между [latex] 0 [/ latex] и [latex] \ pi [/ latex], которые соответствуют значениям синусоидальной функции в квадрантах I и II на единичной окружности, и синусоидальной значения отрицательны между [латекс] \ пи [/ латекс] и [латекс] 2 \ пи [/ латекс], что соответствует значениям синусоидальной функции в квадрантах III и IV на единичной окружности.
Построение значений синусоидальной функции: Точки на кривой [латекс] y = \ sin x [/ latex] соответствуют значениям синусоидальной функции на единичной окружности.
Теперь давайте посмотрим на функцию косинуса, [latex] f (x) = \ sin x [/ latex]. Опять же, мы можем создать таблицу значений и использовать их для построения графика. Ниже приведены некоторые значения синусоидальной функции на единичном круге, где координата [latex] x [/ latex] представляет собой угол в радианах, а координата [latex] y [/ latex] — [latex] \ cos х [/ латекс]:
[латекс] \ displaystyle {(0, 1) \ quad (\ frac {\ pi} {6}, \ frac {\ sqrt {3}} {2}) \ quad (\ frac {\ pi} {4} , \ frac {\ sqrt {2}} {2}) \ quad (\ frac {\ pi} {3}, \ frac {1} {2}) \ quad (\ frac {\ pi} {2}, 0 ) \\ (\ frac {2 \ pi} {3}, — \ frac {1} {2}) \ quad (\ frac {3 \ pi} {4}, — \ frac {\ sqrt {2}} { 2}) \ quad (\ frac {5 \ pi} {6}, — \ frac {\ sqrt {3}} {2}) \ quad (\ pi, -1)} [/ latex]
Как и в случае с функцией синуса, мы можем построить точки для построения графика функции косинуса.
График функции косинуса: Точки на кривой [latex] y = \ cos x [/ latex] соответствуют значениям функции косинуса на единичной окружности.
Поскольку мы можем вычислять синус и косинус любого действительного числа, обе эти функции определены для всех действительных чисел. Если рассматривать значения синуса и косинуса как координаты точек на единичной окружности, становится ясно, что диапазон обеих функций должен быть интервалом [latex] \ left [-1, 1 \ right] [/ latex].
Определение периодических функций
На графиках для функций синуса и косинуса форма графика повторяется после [latex] 2 \ pi [/ latex], что означает, что функции являются периодическими с периодом [latex] 2 \ pi [/ latex].Периодическая функция — это функция с повторяющимся набором значений через равные промежутки времени. В частности, это функция, для которой определенный горизонтальный сдвиг, [латекс] P [/ латекс], приводит к функции, равной исходной функции:
[латекс] f (x + P) = f (x) [/ латекс]
для всех значений [latex] x [/ latex] в домене [latex] f [/ latex]. Когда это происходит, мы называем наименьший такой сдвиг по горизонтали с [latex] P> 0 [/ latex] периодом функции. На приведенной ниже диаграмме показаны несколько периодов функций синуса и косинуса.
Периоды функций синуса и косинуса: Функции синуса и косинуса являются периодическими, что означает, что определенный горизонтальный сдвиг, [latex] P [/ latex], приводит к функции, равной исходной функции: [latex] f (x + P) = f (x) [/ латекс].
Четные и нечетные функции
Еще раз взглянув на функции синуса и косинуса в домене с центром на оси [latex] y [/ latex], можно выявить симметрии. Как мы можем видеть на графике синусоидальной функции, она симметрична относительно начала координат, что указывает на то, что это нечетная функция.На всем протяжении графика любые две точки с противоположными значениями [latex] x [/ latex] также имеют противоположные значения [latex] y [/ latex]. Это характерно для нечетной функции: два входа, которые являются противоположными, имеют выходы, которые также являются противоположными. Другими словами, если [латекс] \ sin (-x) = — \ sin x [/ latex].
Нечетная симметрия синусоидальной функции: Синусоидальная функция нечетная, что означает, что она симметрична относительно начала координат.
График функции косинуса показывает, что он симметричен относительно оси y .Это указывает на то, что это четная функция. Для четных функций любые две точки с противоположными значениями [latex] x [/ latex] имеют одинаковое значение функции. Другими словами, [латекс] \ cos (-x) = \ cos x [/ latex]. Мы можем видеть из графика, что это правда, сравнивая значения [latex] y [/ latex] графика с любыми противоположными значениями [latex] x [/ latex].
Четная симметрия функции косинуса: Функция косинуса четная, что означает, что она симметрична относительно оси [latex] y [/ latex].
Касательная как функция
Характеристики касательной функции можно увидеть на ее графике.
Цели обучения
Опишите характеристики графика касательной функции
Основные выводы
Ключевые моменты
- Функция касательной не определена при любом значении [latex] x [/ latex], где [latex] \ cos x = 0 [/ latex], и ее график имеет вертикальные асимптоты при этих значениях [latex] x [/ latex] .
- Касательная — периодическая функция с периодом [латекс] \ пи [/ латекс].
- График функции касательной симметричен относительно начала координат и, следовательно, является нечетной функцией.
Ключевые термины
- периодическая функция : непрерывный набор точек [latex] \ left (x, f (x) \ right) [/ latex] с набором значений, которые повторяются через равные промежутки времени.
- период : интервал, содержащий минимальный набор значений, которые повторяются в периодической функции.
- нечетная функция : Непрерывный набор точек [latex] \ left (x, f (x) \ right) [/ latex], в которых [latex] f (-x) = -f (x) [/ latex] , и есть симметрия относительно начала координат.
- вертикальная асимптота : прямая линия, параллельная оси [латекс] y [/ латекс], к которой кривая приближается произвольно близко, когда кривая уходит в бесконечность.
Построение касательной функции
Касательную функцию можно изобразить, нанеся точки [latex] \ left (x, f (x) \ right) [/ latex]. Форму функции можно создать, найдя значения тангенса под определенными углами. Однако невозможно найти касательные функции для этих особых углов с единичной окружностью.Мы применяем формулу [latex] \ displaystyle {\ tan x = \ frac {\ sin x} {\ cos x}} [/ latex], чтобы определить касательную для каждого значения.
Мы можем проанализировать графическое поведение касательной функции, посмотрев на значения некоторых специальных углов. Рассмотрим точки ниже, для которых координаты [latex] x [/ latex] представляют собой углы в радианах, а координаты [latex] y [/ latex] — [latex] \ tan x [/ latex]:
[латекс] \ displaystyle {(- \ frac {\ pi} {2}, \ text {undefined}) \ quad (- \ frac {\ pi} {3}, — \ sqrt {3}) \ quad (- \ frac {\ pi} {4}, -1) \ quad (- \ frac {\ pi} {6}, — \ frac {\ sqrt {3}} {3}) \ quad (0, 0) \\ (\ frac {\ pi} {6}, \ frac {\ sqrt {3}} {3}) \ quad (\ frac {\ pi} {4}, 1) \ quad (\ frac {\ pi} {3 }, \ sqrt {3}) \ quad (\ frac {\ pi} {2}, \ text {undefined})} [/ latex]
Обратите внимание, что [latex] \ tan x [/ latex] не определено в [latex] \ displaystyle {x = — \ frac {\ pi} {2}} [/ latex] и [latex] \ displaystyle {x = \ frac {\ pi} {2}} [/ латекс].Вышеупомянутые пункты помогут нам нарисовать наш график, но нам нужно определить, как граф ведет себя там, где он не определен. Давайте рассмотрим последние четыре пункта. Мы можем определить, что значения [latex] y [/ latex] увеличиваются по мере того, как [latex] x [/ latex] увеличивается и приближается к [latex] \ displaystyle {\ frac {\ pi} {2}} [/ latex]. Мы могли бы рассмотреть дополнительные точки между [latex] \ displaystyle {x = 0} [/ latex] и [latex] \ displaystyle {x = \ frac {\ pi} {2}} [/ latex], и мы увидим, что это держит. Точно так же мы видим, что [latex] y [/ latex] уменьшается по мере приближения [latex] x [/ latex] к [latex] \ displaystyle {- \ frac {\ pi} {2}} [/ latex], потому что выходные становиться все меньше и меньше.
Напомним, что существует несколько значений [latex] x [/ latex], которые могут дать [latex] \ cos x = 0 [/ latex]. В любой такой точке [latex] \ tan x [/ latex] не определено, потому что [latex] \ displaystyle {\ tan x = \ frac {\ sin x} {\ cos x}} [/ latex]. При значениях, при которых функция касания не определена, на ее графике наблюдаются разрывы. При этих значениях график касательной имеет вертикальные асимптоты.
График функции касательной: функция касательной имеет вертикальные асимптоты в [latex] \ displaystyle {x = \ frac {\ pi} {2}} [/ latex] и [latex] \ displaystyle {x = — \ frac {\ пи} {2}} [/ латекс].
Характеристики графика касательной функции
Как и функции синуса и косинуса, тангенс является периодической функцией. Это означает, что его значения повторяются через равные промежутки времени. Период касательной функции равен [latex] \ pi [/ latex], потому что график повторяется на [latex] x [/ latex] -осных интервалах [latex] k \ pi [/ latex], где [latex] k [/ latex] — это константа. На графике функции касательной на интервале [latex] \ displaystyle {- \ frac {\ pi} {2}} [/ latex] к [latex] \ displaystyle {\ frac {\ pi} {2}} [/ latex], мы можем увидеть поведение графика за один полный цикл функции.Если мы посмотрим на
любой больший интервал, мы увидим, что характеристики графика повторяются.
График функции касательной симметричен относительно начала координат и, следовательно, является нечетной функцией. Другими словами, [latex] \ text {tan} (- x) = — \ text {tan} x [/ latex] для любого значения [latex] x [/ latex]. Любые две точки с противоположными значениями [latex] x [/ latex] производят противоположные значения [latex] y [/ latex]. Мы можем видеть, что это правда, рассматривая значения [latex] y [/ latex] графика при любых противоположных значениях [latex] x [/ latex].Рассмотрим [latex] \ displaystyle {x = \ frac {\ pi} {3}} [/ latex] и [latex] \ displaystyle {x = — \ frac {\ pi} {3}} [/ latex]. Выше мы уже определили, что [латекс] \ displaystyle {\ tan (\ frac {\ pi} {3}) = \ sqrt {3}} [/ latex] и [latex] \ displaystyle {\ tan (- \ frac { \ pi} {3}) = — \ sqrt {3}} [/ latex].
Секанс и тригонометрические функции
Тригонометрические функции имеют обратные величины, которые можно вычислить с помощью единичной окружности.
Цели обучения
Расчет значений тригонометрических функций, являющихся обратными синусу, косинусу и тангенсу
Основные выводы
Ключевые моменты
- Секущая функция обратна функции косинуса [latex] \ displaystyle {\ left (\ sec x = \ frac {1} {\ cos x} \ right)} [/ latex].Его можно найти для угла [латекс] t [/ latex], используя координату [latex] x [/ latex] связанной точки на единичной окружности: [latex] \ displaystyle {\ sec t = \ frac { 1} {x}} [/ латекс].
- Функция косеканса является обратной функцией синусоидальной функции [latex] \ displaystyle {\ left (\ csc x = \ frac {1} {\ sin x} \ right)} [/ latex]. Его можно найти для угла [латекс] t [/ latex], используя координату [latex] y [/ latex] соответствующей точки на единичной окружности: [latex] \ displaystyle {\ csc t = \ frac { 1} {y}} [/ латекс].
- Функция котангенса является обратной функцией касательной [латекс] \ displaystyle {\ left (\ cot x = \ frac {1} {\ tan x} = \ frac {\ cos t} {\ sin t} \ right) }[/латекс]. Его можно найти для угла, используя координаты [latex] x [/ latex] и [latex] y [/ latex] соответствующей точки на единичной окружности: [latex] \ displaystyle {\ cot t = \ frac {\ cos t} {\ sin t} = \ frac {x} {y}} [/ latex].
Ключевые термины
- секанс : обратная функция косинуса
- косеканс : функция, обратная синусоиде
- котангенс : величина, обратная касательной функции
Введение в взаимные функции
Мы обсудили три тригонометрические функции: синус, косинус и тангенс.Каждая из этих функций имеет обратную функцию, которая определяется обратной величиной отношения исходной тригонометрической функции. Обратите внимание, что обратные функции отличаются от обратных функций. Обратные функции — это способ работы в обратном направлении или определения угла с учетом тригонометрического отношения; они предполагают работу с теми же соотношениями, что и исходная функция.
Три взаимные функции описаны ниже.
Секант
Секущая функция обратна функции косинуса и обозначается сокращенно как [латекс] \ сек [/ латекс].
Его можно описать как отношение длины гипотенузы к длине соседней стороны в треугольнике.
[латекс] \ displaystyle {\ begin {align} \ sec x & = \ frac {1} {\ cos x} \\ \ sec x & = \ frac {\ text {hypotenuse}} {\ text {смежный}} \ end {align}} [/ latex]
Секанс легко вычислить со значениями в единичной окружности. Напомним, что для любой точки круга значение [latex] x [/ latex] дает [latex] \ cos t [/ latex] для соответствующего угла [latex] t [/ latex].Следовательно, секущая функция для этого угла равна
.[латекс] \ displaystyle {\ sec t = \ frac {1} {x}} [/ латекс]
Косеканс
Функция косеканса является обратной функцией синусоиды и обозначается сокращенно как [latex] \ csc [/ latex]. Его можно описать как отношение длины гипотенузы к длине противоположной стороны треугольника.
[латекс] \ displaystyle {\ begin {align} \ csc x & = \ frac {1} {\ sin x} \\ \ csc x & = \ frac {\ text {hypotenuse}} {\ text {напротив}} \ end {align}} [/ latex]
Как и секанс, косеканс может быть вычислен со значениями в единичной окружности.Напомним, что для любой точки круга значение [latex] y [/ latex] дает [latex] \ sin t [/ latex]. Следовательно, функция косеканса для того же угла равна
.[латекс] \ Displaystyle {\ csc t = \ frac {1} {y}} [/ латекс]
Котангенс
Функция котангенса обратна функции тангенса и обозначается сокращенно как [latex] \ cot [/ latex]. Его можно описать как отношение длины соседней стороны к длине гипотенузы в треугольнике.
[латекс] \ displaystyle {\ begin {align} \ cot x & = \ frac {1} {\ tan x} \\ \ cot x & = \ frac {\ text {смежный}} {\ text {противоположный}} \ end {align}} [/ latex]
Также обратите внимание, что поскольку [latex] \ displaystyle {\ tan x = \ frac {\ sin x} {\ cos x}} [/ latex], его обратное значение равно
[латекс] \ displaystyle {\ cot x = \ frac {\ cos x} {\ sin x}} [/ латекс]
Котангенс также можно вычислить со значениями в единичной окружности.Применяя координаты [latex] x [/ latex] и [latex] y [/ latex], связанные с углом [latex] t [/ latex], получаем
[латекс] \ displaystyle {\ begin {align} \ cot t & = \ frac {\ cos t} {\ sin t} \\ \ cot t & = \ frac {x} {y} \ end {align}} [/ латекс]
Вычисление взаимных функций
Теперь мы распознаем шесть тригонометрических функций, которые можно вычислить, используя значения в единичном круге. Напомним, что мы использовали значения функций синуса и косинуса для вычисления функции тангенса.Мы будем следовать аналогичному процессу для обратных функций, ссылаясь на значения в единичном круге для наших расчетов.
Например, давайте найдем значение [latex] \ sec {\ left (\ frac {\ pi} {3} \ right)} [/ latex].
Применяя [латекс] \ displaystyle {\ sec x = \ frac {1} {\ cos x}} [/ latex], мы можем переписать это как:
[латекс] \ displaystyle {\ sec {\ left (\ frac {\ pi} {3} \ right)} = \ frac {1} {\ cos {\ left ({\ frac {\ pi} {3}} \ right)}}} [/ латекс]
Из единичного круга мы знаем, что [латекс] \ displaystyle {\ cos {\ left ({\ frac {\ pi} {3}} \ right)} = \ frac {1} {2}} [/ latex] .Используя это, можно найти значение [latex] \ displaystyle {\ sec {\ left (\ frac {\ pi} {3} \ right)}} [/ latex]:
[латекс] \ displaystyle {\ begin {align} \ sec {\ left (\ frac {\ pi} {3} \ right)} & = \ frac {1} {\ frac {1} {2}} \\ & = 2 \ end {align}} [/ латекс]
Остальные взаимные функции могут быть решены аналогичным образом.
Пример
Используйте единичный круг для вычисления [латекс] \ sec t [/ latex], [latex] \ cot t [/ latex] и [latex] \ csc t [/ latex] в точке [latex] \ displaystyle {\ left (- \ frac {\ sqrt {3}} {2}, \ frac {1} {2} \ right)} [/ latex].
Точка на единичном круге: Точка [латекс] \ displaystyle {\ left (- \ frac {\ sqrt {3}} {2}, \ frac {1} {2} \ right)} [/ latex] , показанный в единичном круге.
Поскольку нам известны координаты [latex] (x, y) [/ latex] точки на единичной окружности, обозначенной углом [latex] t [/ latex], мы можем использовать эти координаты для нахождения трех функций.
Напомним, что координата [latex] x [/ latex] дает значение для функции косинуса, а координата [latex] y [/ latex] дает значение для функции синуса.Другими словами:
[латекс] \ displaystyle {\ begin {align} x & = \ cos t \\ & = — \ frac {\ sqrt {3}} {2} \ end {align}} [/ latex]
и
[латекс] \ displaystyle {\ begin {align} y & = \ sin t \\ & = \ frac {1} {2} \ end {align}} [/ latex]
Используя эту информацию, можно вычислить значения обратных функций под углом [латекс] t [/ латекс]:
[латекс] \ displaystyle {\ begin {align} \ sec t & = \ frac {1} {\ cos t} \\ & = \ frac {1} {x} \\ & = \ left (\ frac {1 } {- \ frac {\ sqrt {3}} {2}} \ right) \\ & = — \ frac {2} {\ sqrt {3}} \\ & = \ left (- \ frac {2} { \ sqrt {3}} \ cdot \ frac {\ sqrt {3}} {\ sqrt {3}} \ right) \\ & = — \ frac {2 \ sqrt {3}} {3} \ end {align} } [/ латекс]
[латекс] \ displaystyle {\ begin {align} \ cot t & = \ frac {\ cos t} {\ sin t} \\ & = \ frac {x} {y} \\ & = \ left (\ frac {- \ frac {\ sqrt {3}} {2}} {\ frac {1} {2}} \ right) \\ & = \ left (- \ frac {\ sqrt {3}} {2} \ cdot \ frac {2} {1} \ right) \\ & = — \ sqrt {3} \ end {align}} [/ latex]
[латекс] \ displaystyle {\ begin {align} \ csc t & = \ frac {1} {\ sin t} \\ & = \ frac {1} {y} \\ & = \ left (\ frac {1 } {\ frac {1} {2}} \ right) \\ & = 2 \ end {align}} [/ latex]
Обратные тригонометрические функции
Каждая тригонометрическая функция имеет обратную функцию, которую можно изобразить. {- 1} x = y [/ latex].{-1} [/ латекс]
Введение в обратные тригонометрические функции
Обратные тригонометрические функции используются для нахождения углов треугольника, если нам заданы длины сторон. Обратные тригонометрические функции могут использоваться, чтобы определить, какой угол даст определенное значение синуса, косинуса или тангенса.
Чтобы использовать обратные тригонометрические функции, мы должны понимать, что обратная тригонометрическая функция «отменяет» то, что «делает» исходная тригонометрическая функция, как и в случае с любой другой функцией и ее обратной.{-1} (б) = а [/ латекс]. Однако функции синуса, косинуса и тангенса — это , а не взаимно однозначные функции. График каждой функции не прошел бы тест горизонтальной линии. Фактически, никакая периодическая функция не может быть взаимно однозначной, потому что каждый выход в ее диапазоне соответствует по крайней мере одному входу в каждом периоде, а количество периодов бесконечно. Как и в случае с другими функциями, которые не являются взаимно однозначными, нам нужно будет ограничить область определения каждой функции, чтобы получить новую функцию, которая является взаимно однозначной. Мы выбираем домен для каждой функции, который включает число [latex] 0 [/ latex].
Функции синуса и косинуса в ограниченных областях: (a) Функция синуса, показанная в ограниченной области [latex] \ left [- \ frac {\ pi} {2}, \ frac {\ pi} {2} \ справа] [/ латекс]; (b) Функция косинуса, показанная в ограниченной области [latex] \ left [0, \ pi \ right] [/ latex].
График функции синуса ограничен областью [latex] [- \ frac {\ pi} {2}, \ frac {\ pi} {2}] [/ latex] и графиком функции косинуса ограничено [латексом] [0, \ pi] [/ латексом]. График касательной функции ограничен [latex] \ left (- \ frac {\ pi} {2}, \ frac {\ pi} {2} \ right) [/ latex].
Касательная функция в ограниченной области
Функция касательной, показанная в ограниченной области [latex] \ left (- \ frac {\ pi} {2}, \ frac {\ pi} {2} \ right) [/ latex].
Эти варианты выбора ограниченных доменов в некоторой степени произвольны, но они имеют важные полезные характеристики. Каждый домен включает начало координат и некоторые положительные значения, и, что наиболее важно, каждый результат дает взаимно однозначную функцию, которая является обратимой. Обычный выбор для ограниченной области касательной функции также имеет то полезное свойство, что он распространяется от одной вертикальной асимптоты к другой, вместо того, чтобы разбиваться на части асимптотой.{-1} x \ quad \ text {имеет домен} \ quad \ left (- \ infty, \ infty \ right) \ quad \ text {и диапазон} \ quad \ left (- \ frac {\ pi} {2} , \ frac {\ pi} {2} \ right)} [/ latex]
Графики обратных тригонометрических функций
Функция синуса и функция обратного синуса (или арксинуса): функция арксинуса является отражением функции синуса относительно линии [latex] y = x [/ latex].
Чтобы найти область определения и диапазон обратных тригонометрических функций, мы меняем область определения и диапазон исходных функций.
Функция косинуса и функция обратного косинуса (или арккосинуса): Функция арккосинуса является отражением функции косинуса относительно линии [латекс] y = x [/ latex].
Каждый график обратной тригонометрической функции является отражением графика исходной функции относительно линии [латекс] y = x [/ latex].
Функция касательной и функция арктангенса (или арктангенса): Функция арктангенса является отражением функции касательной относительно линии [latex] y = x [/ latex].{-1} х = у [/ латекс].
Углы
Угол — это мера поворота. Углы измеряются в градусах . Один полный оборот измеряется как 360 °. Угол может быть положительным или отрицательным, в зависимости от направления вращения. Угловая мера — это величина поворота между двумя лучами, образующими угол. Вращение измеряется от начальной стороны до конечной стороны угла . Положительные углы (рисунок a) возникают в результате поворота на против часовой стрелки на , а отрицательные углы (рисунок b) возникают в результате поворота на по часовой стрелке на .Угол с его начальной стороной на оси x считается стандартным положением .
Рисунок 1
(a) Положительный угол и (b) отрицательный угол.
Углы, которые находятся в стандартном положении, называются квадрантными , если их конечная сторона совпадает с координатной осью. Углы в стандартном положении, которые не являются квадрантами, попадают в один из четырех квадрантов, как показано на рисунке 2.
Пример 1: Следующие углы (стандартное положение) заканчиваются в указанном квадранте.
94 ° | 2-й квадрант |
500 ° | 2-й квадрант |
−100 ° | 3-й квадрант |
180 ° | квадрант |
−300 ° | 1-й квадрант |
Два угла в стандартном положении, которые имеют общую клеммную сторону, называются на конце. Все углы на Рисунке 3 совпадают с углом 30 °.
Все углы, которые совпадают с d °, можно записать как
, где n — целое число (положительное, отрицательное или ноль).
Пример 2: Является ли угол 200 ° совпадающим с углом 940 °?
Если угол 940 ° и угол 200 ° совпадают, то
Поскольку 740 не кратно 360, эти углы не совпадают.
Пример 3: Назовите 5 углов, совпадающих с -70 °.
Угловые измерения не всегда являются целыми числами. Дробный градус может быть выражен либо в виде десятичной части градуса, например 34,25 °, либо с помощью стандартных делений градуса, называемых минутами и секундами. Между градусами, минутами и секундами существуют следующие отношения:
Пример 4: Запишите 34 ° 15 ′ в десятичных градусах
Пример 5: Запишите 12 ° 18′44 ″, используя десятичные градусы.

 Положение OA этого вектора, которое совпадает с положительным направлением оси Ox, назовем начальным положением радиус-вектора OM, а сам радиус-вектор
Положение OA этого вектора, которое совпадает с положительным направлением оси Ox, назовем начальным положением радиус-вектора OM, а сам радиус-вектор

 Синусы, косинусы, тангенсы и котангенсы. Значения тригонометрических функций нестандартных углов.
Синусы, косинусы, тангенсы и котангенсы. Значения тригонометрических функций нестандартных углов.
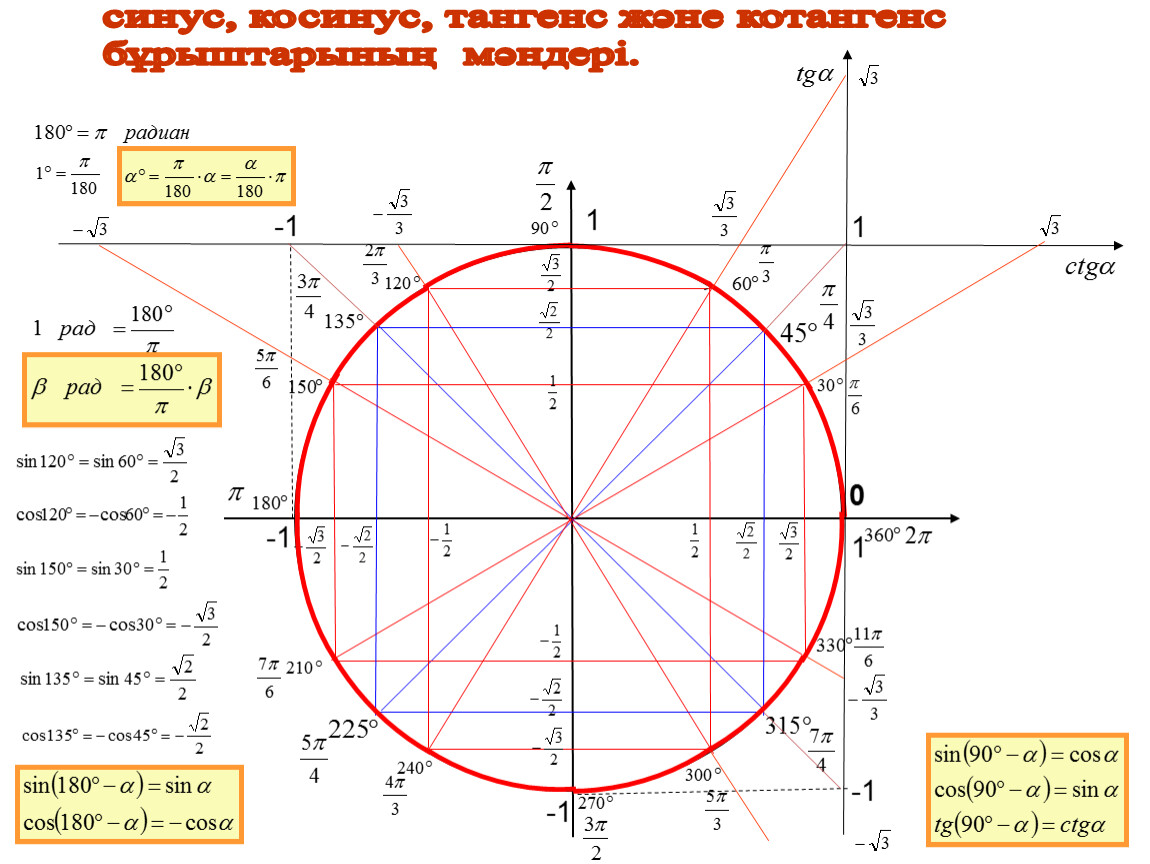 74)
74)