Угол между двумя векторами: Угол между векторами

Угол между двумя векторами

Пусть в n-мерном пространстве задан ортонормированный базис

Как известно скалярное произведение ненулевых векторов x и y называется произведение

(1)

где |·|-модуль вектора, φ -угол между векторами.

Если x=0 или y=0, то скалярное произведение равно нулю.

Вариант 1. Начальные точки всех векторов совпадают с началом координат.

Так как рассматривается пространство с ортонормированным базисом, то скалярное произведение можно вычислить также из выражения

(2)

где

координаты векторов x и y соответственно.

Из выражений (1) и (2) следует, что косинус угла между двумя векторами равен

И, следовательно, угол между двумя векторами будет равен

Вариант 2. Начальные точки векторов произвольные.

Пусть заданы векторы x=AB и y=CD, где ,,,.

Переместим параллельно векторы x и y так, чтобы начальные точки векторов совпали с началом координат. Получим векторы x’ и y’ с координатами (т.е. с конечными точками):

где

При таком перемещении угол между векторами x и y равен углу между векторами x’ и y’. Следовательно косинус угла между двумя векторами равен:

(3)

Угол между двумя векторами будет равен:

(4)

Вариант 1. Начальные точки всех векторов совпадают с началом координат.

Пример . Найти угол между векторами x=(7,2) и y=(4,5).

 

Рис. 1

На рисунке Рис. 1 в двухмерном пространстве представлены векторы x=(7,2) и y=(4,5).

Для вычисления угла между векторами x и y, вычислим нормы векторов x и y:

Косинус угла между векторами x и y, будет равен:

(5)

Из выражения (5) вычисляем угол φ:

Вариант 2. Начальные точки векторов произвольные.

Пример . Найти угол между векторами x=AB и y=CD, где A(-1,1), B(3, 7), C(3,2), D(12,5).

На рисунке Рис. 2 в двухмерном пространстве представлены векторы

x=AB и y=CD.

 

Рис. 2

Переместим параллельно векторы x и y так, чтобы начальные точки векторов совпали с началом координат. Получим векторы x’ и y’ с координатами (т.е. с конечными точками): x’=(3-(-1),7-1)=(4,6), y’=(12-3,5-2)=(9,3).

Угол φ между векторами x и y равен углу φ’ между векторами x’ и y’. Поэтому вычисляя угол φ’ , получим угол между векторами x и y.

Вычислим норму векторов x’ и y’:

Косинус угла между векторами x’ и y’:

Угол между двумя векторами будет равен:

Как найти косинус угла между двумя векторами: формула, пример задачи

Sign in

Password recovery

Восстановите свой пароль

Ваш адрес электронной почты

MicroExcel.ru Математика Геометрия Нахождение угла между векторами

В данной публикации мы рассмотрим, что такое угол меду двумя векторами, и приведем формулу, с помощью которой можно найти его косинус. Также разберем пример решения задачи по этой теме.

• Нахождение угла между векторами
• Пример задачи

Нахождение угла между векторами

Угол между двумя векторами, берущими начало в одной и той же точке – это наименьший угол, на который можно повернуть один из данных векторов вокруг своей начальной точки до положения, при котором он будет сонаправлен со вторым вектором.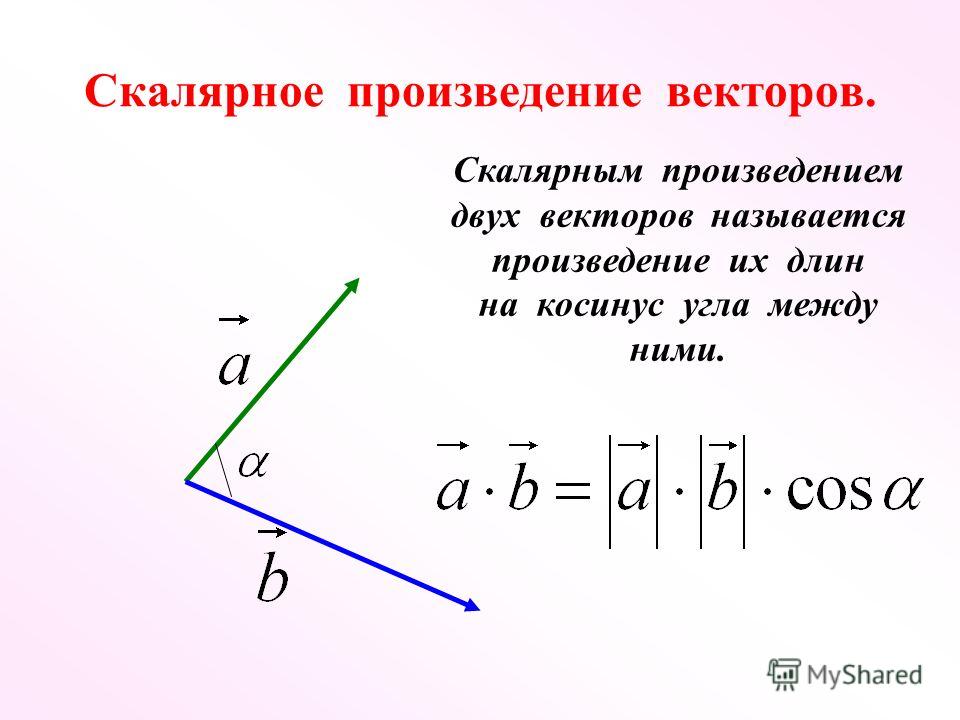

Косинус угла между двумя векторами равняется скалярному произведению векторов, разделенному на произведение длин (модулей) этих векторов.

Для расчета косинуса угла используется формула ниже:

Пример задачи

Найдем угол между векторами a = {4; 3} и b = {12; 5}.

Решение

1. Для начала рассчитаем их скалярное произведение:
a · b = 4 · 12 + 3 · 5 = 48 + 15 = 63.

2. Теперь найдем длины (модули) заданных векторов:

3. Применим формулу для нахождения косинуса угла:

4. Следовательно, угол приблизительно равняется 14,26° (arccos 0,9692).

ЧАЩЕ ВСЕГО ЗАПРАШИВАЮТ

Таблица знаков зодиака

Нахождение площади трапеции: формула и примеры

Нахождение длины окружности: формула и задачи

Римские цифры: таблицы

Таблица синусов

Тригонометрическая функция: Тангенс угла (tg)

Нахождение площади ромба: формула и примеры

Нахождение объема цилиндра: формула и задачи

Тригонометрическая функция: Синус угла (sin)

Геометрическая фигура: треугольник

Нахождение объема шара: формула и задачи

Тригонометрическая функция: Косинус угла (cos)

Нахождение объема конуса: формула и задачи

Таблица сложения чисел

Нахождение площади квадрата: формула и примеры

Что такое тетраэдр: определение, виды, формулы площади и объема

Нахождение объема пирамиды: формула и задачи

Признаки подобия треугольников

Нахождение периметра прямоугольника: формула и задачи

Формула Герона для треугольника

Что такое средняя линия треугольника

Нахождение площади треугольника: формула и примеры

Нахождение площади поверхности конуса: формула и задачи

Что такое прямоугольник: определение, свойства, признаки, формулы

Разность кубов: формула и примеры

Степени натуральных чисел

Нахождение площади правильного шестиугольника: формула и примеры

Тригонометрические значения углов: sin, cos, tg, ctg

Нахождение периметра квадрата: формула и задачи

Теорема Фалеса: формулировка и пример решения задачи

Сумма кубов: формула и примеры

Нахождение объема куба: формула и задачи

Куб разности: формула и примеры

Нахождение площади шарового сегмента

Что такое окружность: определение, свойства, формулы

Объяснение урока: Угол между двумя векторами в пространстве

В этом объяснении мы узнаем, как найти угол между двумя векторами в пространстве, используя их скалярное произведение.

Для начала вспомним, как вычислить скалярное произведение (или скалярное произведение) двух векторов в пространстве. Если мы рассмотрим два вектора одинаковой размерности, ⃑𝑢=(𝑢,𝑢,𝑢,…,𝑢) и ⃑𝑣=(𝑣,𝑣,𝑣,…,𝑣), тогда скалярное произведение двух векторов равно ⃑𝑢⋅⃑𝑣=𝑢𝑣+𝑢𝑣+𝑢𝑣+⋯+𝑢𝑣, что является скалярной величиной. Также напомним следующие свойства скалярного произведения.

Теорема: свойства скалярного произведения

Для любого скаляра 𝑐 и векторов ⃑𝑢, ⃑𝑣, и ⃑𝑤 той же размерности выполняются следующие свойства: ⃑𝑢om⃑𝑣 = ⃑𝑣om⃑𝑢 (), 𝑐⃑𝑢> ⃑𝑣 = 𝑐⃑𝑢om⃑𝑣 (), ⃑𝑢⋅⃑𝑣+⃑𝑤 = ⃑𝑢> ⃑𝑣+⃑𝑢om⃑𝑤 (), ⃑𝑢⋅⃑𝑢 = ‖⃑𝑢⃑𝑢 ‖‖.коммутативное свойство скалярное свойство умножения дистрибутивное свойство

Давайте рассмотрим геометрический смысл скалярного произведения, используя рисунок ниже.

Используя обозначения на рисунке, закон косинусов гласит, что ‖‖⃑𝑢‖‖+‖‖⃑𝑣‖‖−2‖‖⃑𝑢‖‖‖‖⃑𝑣‖‖𝜃=‖‖⃑𝑢−⃑𝑣‖‖.cos

Используя последнее свойство из списка, мы можем переписать правую часть уравнения как ⃑𝑢−⃑𝑣⋅⃑𝑢−⃑𝑣. Используя распределительное свойство скалярного произведения, получаем ⃑𝑢 — ⃑𝑣d⃑𝑢 — ⃑𝑣 = ⃑𝑢om⃑𝑢 -⃑𝑣 — ⃑𝑣 ⃑𝑣 -⃑𝑣 = ⃑𝑢om⃑𝑢 -⃑𝑢 ⃑𝑢 -⃑𝑣 ⃑𝑣 -⃑𝑣 -⃑𝑣 -⃑𝑣- = ⃑𝑢 ⃑𝑢 порядка

Мы знаем, что ⃑𝑢⋅⃑𝑢=‖‖⃑𝑢‖‖ и ⃑𝑣⋅⃑𝑣=‖‖⃑𝑣‖‖. По свойству коммутативности имеем ⃑𝑢⋅⃑𝑣=⃑𝑣⋅⃑𝑢. Применение этих тождеств к правой части приведенного выше уравнения сводит его к ‖‖⃑𝑢‖‖+‖‖⃑𝑣‖‖−2⃑𝑢⋅⃑𝑣.

Это приводит к уравнению ‖⃑𝑢⃑𝑢⃑𝑢‖+‖⃑𝑣⃑𝑣⃑𝑣‖ — 2‖⃑𝑢⃑𝑢⃑𝑢⃑𝑢‖⃑𝑣0003

Упрощая это уравнение, получаем −2‖⃑𝑢⃑𝑢⃑𝑢⃑𝑢‖‖⃑𝑣⃑𝑣⃑𝑣⃑𝑣 = −2⃑𝑢⋅⃑𝑣, ‖⃑𝑢⃑𝑢⃑𝑢‖‖‖⃑𝑣⃑𝑣⃑𝑣⃑𝑣𝜃 = ⃑𝑢⋅⃑𝑣.coscos

Следовательно, точечный продукт двух векторов, геометрически произведение величин двух векторов, умноженное на косинус угла между ними.

Теорема: геометрическая формула скалярного произведения

Пусть ⃑𝑢 и ⃑𝑣 ненулевые векторы, и пусть 𝜃 быть углом между двумя векторами. Затем, ⃑𝑢⋅⃑𝑣=‖‖⃑𝑢‖‖‖‖⃑𝑣‖‖𝜃.cos

Рассмотрим пример, в котором мы применяем эту геометрическую формулу для вычисления скалярного произведения.

Пример 1. Нахождение скалярного произведения между векторами

Угол между ⃑𝐴 и ⃑𝐵 равен 22∘. Если ‖‖⃑𝐴‖‖=3‖‖⃑𝐵‖‖=25,2, найти ⃑𝐴⋅⃑𝐵 с точностью до сотой.

Ответ

Вспомним, что скалярное произведение двух векторов есть произведение модулей двух векторов на косинус угла между ними. Другими словами, ⃑𝐴⋅⃑𝐵=‖‖⃑𝐴‖‖‖‖⃑𝐵‖‖𝜃, потому что где 𝜃 — угол между двумя векторами. Нам дано, что 𝜃=22∘ и ‖‖⃑𝐴‖‖=25,2. Мы можем вычислить ‖‖⃑𝐵‖‖=25,23=8,4.

Тогда, ⃑𝐴⋅⃑𝐵=25,2×8,4×22≈196,266.cos∘

Округляя до сотых, получаем ⃑𝐴⋅⃑𝐵=196,27.

В следующем примере мы используем свойства векторных операций вместе с геометрической интерпретацией скалярного произведения.

Пример 2. Нахождение скалярного произведения векторов с использованием свойств скалярного произведения

Если ⃑𝐴 и ⃑𝐵 — два перпендикулярных единичных вектора, найти 3⃑𝐴−⃑𝐵⋅−2⃑𝐴+⃑𝐵.

Ответ

Вспомним дистрибутивное свойство скалярного произведения; для любых векторов равной размерности, ⃑𝑢, ⃑𝑣 и ⃑𝑤: ⃑𝑢⋅⃑𝑣+⃑𝑤=⃑𝑢⋅⃑𝑣+⃑𝑢⋅⃑𝑤.

Заметим, что свойство дистрибутивности работает так же, когда знаки плюс с обеих сторон заменены знаками минус. Используя это свойство, мы вычисляем

3⃑𝐴 — ⃑𝐵 ⃑𝐵 -2⃑𝐴+⃑𝐵 = 3⃑𝐴 — ⃑𝐵 порядка  — 2⃑𝐴+3⃑𝐴 — ⃑𝐵 порядка.

(1)

Напомним также, что свойство перестановочности скалярного произведения; для любых векторов одинаковой размерности ⃑𝑢 и ⃑𝑣: ⃑𝑢⋅⃑𝑣=⃑𝑣⋅⃑𝑢.

Тогда правая часть уравнения (1) может быть записана как −2⃑𝐴⋅3⃑𝐴−⃑𝐵+⃑𝐵⋅3⃑𝐴−⃑𝐵.

Снова используя распределительное свойство, это равно

(2)

Далее мы вспоминаем свойство скалярного умножения скалярного произведения; для любого скаляра 𝑐 и векторов одинаковой размерности, ⃑𝑢 и ⃑𝑣: 𝑐⃑𝑢⋅⃑𝑣=⃑𝑢⋅𝑐⃑𝑣=𝑐⃑𝑢⋅⃑𝑣.

Тогда выражение (2) равно

−6⃑𝐴⋅⃑𝐴+2⃑𝐴⋅⃑𝐵+3⃑𝐵⋅⃑𝐴−⃑𝐵⋅⃑𝐵.

(3)

Наконец, напомним, что для любого вектора ⃑𝑢 ⃑𝑢⋅⃑𝑢=‖‖⃑𝑢‖‖.

Используя это свойство и свойство коммутативности скалярного произведения, выражение (3) можно записать в виде −6‖⃑𝐴⃑𝐴⃑𝐴⃑𝐴++2⃑𝐴⋅⃑𝐵+3⃑𝐴= ⃑𝐵-‖⃑𝐵⃑𝐵⃑𝐵⃑𝐵, −6‖⃑𝐴⃑𝐴⃑𝐴‖+5⃑𝐴⋅⃑𝐵-‖‖⃑𝐵⃑𝐵 ‖⃑𝐵⃑𝐵‖, −6‖⃑𝐴⃑𝐴⃑𝐴+5⃑𝐴⃑𝐴 ⃑𝐵⃑𝐵‖⃑𝐵 ‖⃑𝐵⃑𝐵‖, −6‖⃑𝐴⃑𝐴⃑𝐴+5 ⃑𝐴 ⃑𝐵⃑𝐵⃑𝐵‖. , который мыпль

Мы знаем, что величины ‖‖⃑𝐴‖‖ и ‖‖⃑𝐵‖‖ оба равны 1, так как они заданы как единичные векторы. Итак, осталось вычислить скалярное произведение ⃑𝐴⋅⃑𝐵. Мы помним, что ⃑𝐴⋅⃑𝐵=‖‖⃑𝐴‖‖‖‖⃑𝐵‖‖𝜃, потому что где 𝜃 — угол между двумя векторами. Поскольку нам известно, что два вектора перпендикулярны, мы имеем 𝜃=90∘. Затем, ⃑𝐴⋅⃑𝐵=1×1×90=0.cos∘

Затем мы можем подставить эти значения в наше выражение: −6‖‖⃑𝐴‖‖+5⃑𝐴⋅⃑𝐵−‖‖⃑𝐵‖‖=−6×1+5×0−1=−7. 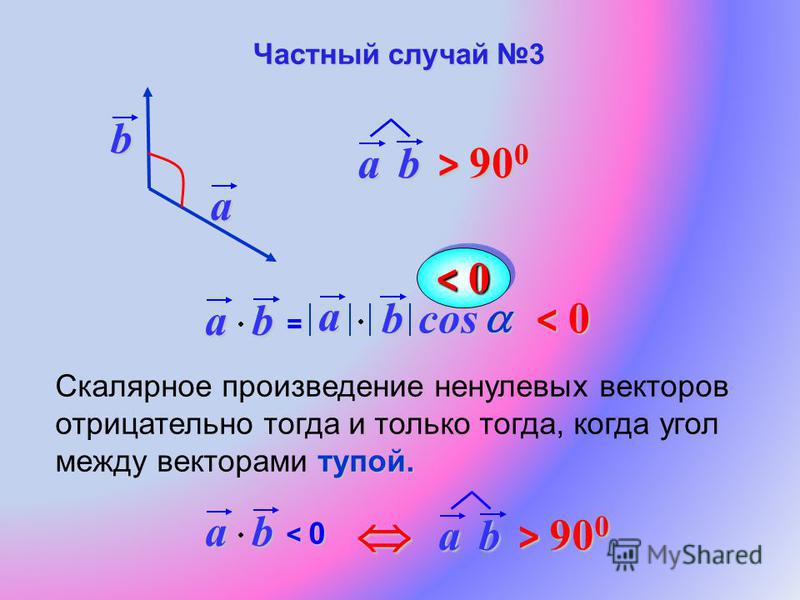

Следовательно, =-7.

Отметим, что существует два разных способа измерения угла 𝜃 между любыми двумя векторами: ⃑𝑢 и ⃑𝑣, как показано на рисунке ниже. Помните, что вектор — это величина, у которой есть величина и направление. которые мы можем рисовать, начиная с любого места в пространстве. Это означает, что мы можем рисовать как ⃑𝑢, так и ⃑𝑣. имеющих одну и ту же начальную точку.

Два угла 𝜃 и 𝜃 удовлетворяют уравнению 𝜃+𝜃=360∘, что означает 𝜃=360−𝜃∘. Геометрическая формула в теореме верна как для 𝜃, так и для 𝜃, потому что косинус четный и периодический с периодом 360∘. Точнее, у нас есть coscoscoscos𝜃=(−𝜃)=(−𝜃+360)=𝜃.∘

Заметим, что один из углов (𝜃 на рисунке выше) лежит между 0∘ и 180∘, а другой угол (𝜃 на картинке) лежит между 180∘ и 360∘. По соглашению, когда мы говорим угол между двумя векторами, мы имеем в виду наименьший неотрицательный угол между этими двумя векторами, то есть угол между 0∘ и 180∘.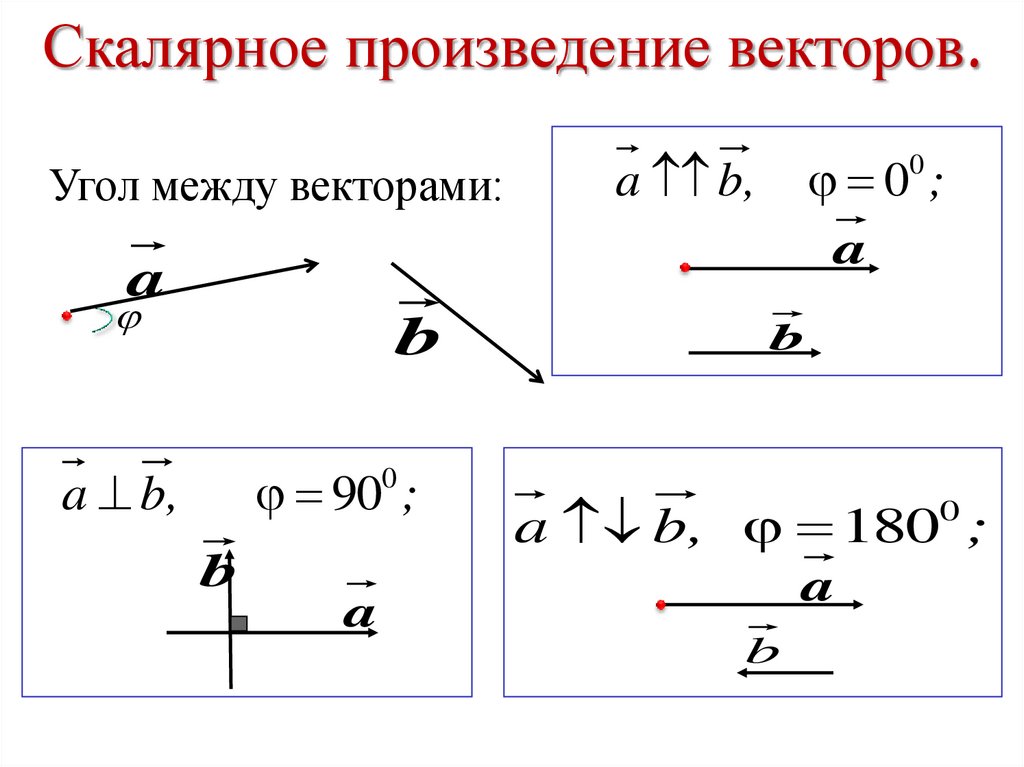

Мы обсудили геометрическую формулу скалярного произведения: ⃑𝑢⋅⃑𝑣=‖‖⃑𝑢‖‖‖‖⃑𝑣‖‖𝜃.cos

Чтобы вычислить угол между двумя векторами, мы можем изменить это уравнение так, чтобы 𝜃 было предметом уравнения. Если ⃑𝑢 и ⃑𝑣 ненулевые векторы, то ‖‖⃑𝑢‖‖≠0 и ‖‖⃑𝑣‖‖≠0 поэтому мы можем разделить обе части уравнения на ‖‖⃑𝑢‖‖‖‖⃑𝑣‖‖. Затем, Coscos𝜃 = ⃑𝑢⋅⃑𝑣⃑𝑣⃑𝑣⃑𝑢⃑𝑢⃑𝑢⃑𝑢‖⃑𝑣⃑𝑣⃑𝑣⃑𝑣𝜃 = ⃑𝑢⋅⃑𝑣⃑𝑣⃑𝑣⃑𝑣⃑𝑢⃑𝑢⃑𝑢‖‖⃑𝑣. .

Мы помним, что обратная косинусная функция имеет диапазон между 0∘ и 180∘, где также определяется угол между двумя векторами.

Теорема: угол между двумя векторами

Пусть ⃑𝑢 и ⃑𝑣 ненулевые векторы. Тогда угол 𝜃 между двумя векторами, который лежит между 0∘ и 180∘, определяется выражением 𝜃=⃑𝑢⋅⃑𝑣‖‖⃑𝑢‖‖‖‖⃑𝑣‖‖.cos

В следующем примере мы вычисляем угол между двумя векторами, зная их величины и скалярное произведение.

Пример 3. Нахождение меры меньшего угла между двумя векторами по их величинам и скалярному произведению

Учитывая, что ‖‖⃑𝐴‖‖=35, ‖‖⃑𝐵‖‖=23, и ⃑𝐴⋅⃑𝐵=−805√22, определить меру меньшего угол между двумя векторами.

Ответ

Напомним, что угол 𝜃 между любыми двумя ненулевыми векторами ⃑𝐴 и ⃑𝐵 задается 𝜃=⃑𝐴⋅⃑𝐵‖‖⃑𝐴‖‖‖‖⃑𝐵‖‖.cos

Нам дано, что ‖‖⃑𝐴‖‖=35, ‖‖⃑𝐵‖‖=23, и ⃑𝐴⋅⃑𝐵=−805√22, поэтому имеем 𝜃=⎛⎜⎜⎝35×23⎞⎟⎟⎠=−805√21610=−√22=135.coscoscos√9

0002 Следовательно, угол между 𝐴 и 𝐵 равен 135∘. Заметим, что ответ находится между 0∘ и 180∘, что является правильным диапазоном.

В следующем примере мы вычислим угол между двумя векторами, заданными в терминах единичных векторов направления.

Пример 4. Нахождение угла между векторами, заданными в терминах фундаментальных единичных векторов

Если ⃑𝐴=2⃑𝑖+5⃑𝑘 и ⃑𝐵=4⃑𝑖+3⃑𝑗+⃑𝑘, найдите меру угла между двумя векторами, округленную до сотых.

Ответ

Напомним, что угол между любыми двумя ненулевыми векторами ⃑𝐴 и ⃑𝐵 — угол 𝜃 между 0∘ и 180∘ удовлетворительно cos𝜃=⃑𝐴⋅⃑𝐵‖‖⃑𝐴‖‖‖‖⃑𝐵‖‖.

Дан вектор ⃑𝑣=𝑣⃑𝑖+𝑣⃑𝑗+𝑣⃑𝑘, мы знаем это ‖‖⃑𝑣‖‖=𝑣+𝑣+𝑣.

Так как ⃑𝐴=2⃑𝑖+5⃑𝑘 и ⃑𝐵=4⃑𝑖+3⃑𝑗+⃑𝑘, мы можем вычислить ‖‖⃑𝐴‖‖=√2+0+5=√29,‖‖⃑𝐵‖‖=√4+3+1=√26.

Кроме того, для любых двух векторов ⃑𝑢=𝑢⃑ 𝑢⃑𝑗+𝑢⃑𝑘 и ⃑𝑣=𝑣⃑𝑖+𝑣⃑𝑗+𝑣⃑𝑘, скалярное произведение двух векторов равно ⃑𝑢⋅⃑𝑣=𝑢𝑣+𝑢𝑣+𝑢𝑣.

Итак, ⃑𝐴⋅⃑𝐵=2×4+0×3+5×1=13.

Как уже отмечалось, угол 𝜃 должен удовлетворять cos𝜃=13√29×√26=0,4734….

Это приводит к 𝜃=(0,4734…)=61,742….cos∘

Следовательно, мера угла между двумя заданными векторами, округленная до сотых, равна 61,74∘. Мы обратите внимание, что ответ находится между 0∘ и 180∘, что является правильным диапазоном.

В следующем примере мы вычисляем угол между двумя параллельными векторами.

Пример 5. Нахождение угла между двумя заданными векторами в трехмерной плоскости

Найти угол 𝜃 между векторами ⃑𝑉=−⃑𝑖+2⃑𝑗+⃑𝑘 и 𝑊=−3⃑𝑖+6⃑𝑗+3⃑𝑘.

Ответ

В этом примере мы можем использовать два разных метода, чтобы найти угол между ⃑𝑉 и 𝑊. Первый метод заключается в использовании скалярного произведения для нахождения угла между двумя векторами. и второй способ заключается в использовании свойства параллельных векторов.

Метод 1

Напомним, что угол между любыми двумя ненулевыми векторами ⃑𝑉 и 𝑊 дается 𝜃=⃑𝑉⋅𝑊‖‖⃑𝑉‖‖‖‖𝑊‖‖.cos

Поскольку ⃑𝑉=−⃑𝑖+2⃑𝑗+⃑𝑘 и 𝑊=−3⃑𝑖+6⃑𝑗+3⃑𝑘, мы можем рассчитать ‖‖⃑𝑉‖‖=(−1)+2+1=√6,‖‖𝑊‖‖=(−3)+6+3=√54.

Их скалярный продукт дан кем-то ⃑𝑉⋅𝑊=(−1)×(−3)+2×6+1×3=18.

Тогда угол 𝜃 определяется выражением 𝜃=⃑𝑉⋅𝑊‖‖⃑𝑉‖‖‖‖𝑊‖‖=18√6√54=(1)=0.coscoscos∘

3, так что угол между ∘

3, и 𝑊 0∘.

Метод 2

Напомним, что два ненулевых вектора ⃑𝑉 и 𝑊 параллельны, если существует скаляр 𝑐≠0, удовлетворяющий ⃑𝑉=𝑐𝑊.

Кроме того, если 𝑐>0, то два вектора имеют одинаковое направление. В этом случае угол между два вектора равны 0∘. С другой стороны, если 𝑐0, то два вектора направлены в противоположные стороны, это означает, что угол между ними равен 180∘.

Нам дано, что ⃑𝑉=−⃑𝑖+2⃑𝑗+⃑𝑘 и 𝑊=−3⃑𝑖+6⃑𝑗+3⃑𝑘. Заметим, что каждая координата 𝑊 точно в 3 раза больше соответствующей координаты ⃑𝑉. Другими словами, 𝑊=−3⃑𝑖+6⃑𝑗+3⃑𝑘=3−⃑𝑖+2⃑𝑗+⃑𝑘=3⃑𝑉.

Итак, 𝑊=3⃑𝑉, что означает, что векторы ⃑𝑉 и 𝑊 параллельны. Поскольку скаляр 3 положителен, это означает что они имеют одинаковое направление.

Следовательно, угол между двумя векторами равен 0∘.

В нашем следующем примере мы идентифицируем угол между двумя векторами, заданными графически.

Пример 6. Нахождение угла между двумя заданными векторами из графика

Найдите меру угла между двумя векторами, показанными на рисунке. Округлите ответ до ближайшего степень.

Ответ

Напомним, что угол между любыми двумя ненулевыми векторами ⃑𝑣 и ⃑𝑤 это угол 𝜃=⃑𝑣⋅⃑𝑤‖‖⃑𝑣‖‖‖‖⃑𝑤‖‖.cos

На приведенном рисунке графически представлены два вектора. Начнем с поиска компонентов векторы из диаграмм.

Заметим, что оба вектора начинаются в точке (1,0,3). Фиолетовый вектор имеет конечную точку в (1,2,0), а красный вектор имеет конечную точку (0,2,0). Затем, фиолетовый вектор задается (1,2,0)−(1,0,3)=(0,2,−3).

Красный вектор задается (0,2,0)−(1,0,3)=(−1,2,−3).

Вычислим их величины и скалярное произведение по формуле угла между двумя векторами: ‖(0,2,−3)‖=0+2+(−3)=√13,‖(−1,2,−3)‖=(−1)+2+(−3)=√ 14,(0,2,−3)⋅(−1,2,−3)=0×(−1)+2×2+(−3)×(−3)=13.

Следовательно, угол между двумя векторами равен 𝜃=13√13×√14=(0,9636…)=15,51….coscos∘

Итак, угол между двумя заданными векторами, округленный до ближайшего градуса, равен 16∘. Заметим, что оба значения лежат между 0∘ и 180∘, что является правильным диапазоном.

В нашем последнем примере мы вычислим угол между двумя векторами, учитывая их конечные точки.

Пример 7. Определение угла между векторами

Дано 𝐴(−3,−5,6), 𝐵(0,3,−7), 𝐶(−8,10,−2) и 𝐷(−3,9,−6), определить меру угла между векторы 𝐴𝐵 и 𝐶𝐷 округлены до сотых.

Ответ

Напомним, что угол между любыми двумя ненулевыми векторами ⃑𝑣 и ⃑𝑤 это угол 𝜃=⃑𝑣⋅⃑𝑤‖‖⃑𝑣‖‖‖‖⃑𝑤‖‖.cos

Нам нужно идентифицировать векторы 𝐴𝐵 и 𝐶𝐷 перед вычислением их величин и скалярного произведения. У нас есть 𝐴𝐵=(0−(−3),3−(−5),−7−6)=(3,8,−13),𝐶𝐷=(−3−(−8),9−10,− 6−(−2))=(5,−1,−4).

Затем вычисляем ‖‖𝐴𝐵‖‖=3+8+(−13)=√242,‖‖𝐶𝐷‖‖=5+(−1)+(−4)=√42,𝐴𝐵⋅𝐶𝐷=3 ×5+8×(−1)+(−13)×(−4)=59.

Отсюда получаем 𝜃=59√242×√42=54,181….cos∘ что с точностью до сотых равно 54,18∘.

Мера угла между векторами 𝐴𝐵 и 𝐶𝐷 округленное до сотых равно 54,18∘. Мы наблюдаем что ответ находится между 0∘ и 180∘, что является правильным диапазоном.

Давайте резюмируем несколько важных понятий из этого объяснения.

Ключевые точки

• Скалярное произведение двух ненулевых векторов ⃑𝑢 и ⃑𝑣 определяется выражением ⃑𝑢⋅⃑𝑣=‖‖⃑𝑢‖‖‖‖⃑𝑣‖‖𝜃, потому что где 𝜃 — угол между двумя векторами.
• Угол 𝜃 между двумя ненулевыми векторами ⃑𝑢 и ⃑𝑣 дается 𝜃=⃑𝑢⋅⃑𝑣‖‖⃑𝑢‖‖‖‖⃑𝑣‖‖.cos
• По соглашению угол между двумя векторами относится к наименьшему неотрицательному углу между этими два вектора, который находится между 0∘ и 180∘. 9\circ???, вот так:

  Привет! Я Криста.

  Я создаю онлайн-курсы, чтобы помочь вам в учебе по математике. Читать далее.

  Если мы хотим найти острый угол между двумя линиями, мы можем преобразовать линии в стандартную векторную форму, а затем использовать формулу

  ???\cos{\theta}=\frac{a\cdot b}{|a ||б|}???

  где ???а??? и ???б??? данные векторы, ???a\cdot{b}??? скалярное произведение векторов, ???|a|??? величина вектора ???a??? (его длина) и ???|b|??? величина вектора ???b??? (его длина). Мы можем найти величину обоих векторов, используя формулу расстояния 9\circ???, и мы получим острый угол.

  Как найти острый угол между двумя прямыми, если прямые заданы векторами?

  Пройти курс

  Хотите узнать больше об исчислении 3? У меня есть пошаговый курс для этого. 🙂

  Учить больше

  Преобразование линий в векторы с последующим определением угла между этими двумя векторами

  Пример

  Найдите острый угол между прямыми.

  ???x+3y=2???

  ???3x-6y=5???

  Сначала мы преобразуем линии в стандартную векторную форму.

  ???x+3y=2???

  ???a=\langle1,3\rangle???

  и

  ???3x-6y=5???

  ???b=\langle3,-6\rangle???

  Прежде чем мы сможем использовать нашу формулу, нам нужно найти скалярное произведение ???a??? и ???б???.

  ???a\cdot{b}=(1)(3)+(3)(-6)??? 92}???

  ???|b|=\sqrt{9+36}???

  ???|b|=\sqrt{45}???

  Если мы хотим найти острый угол между двумя линиями, мы можем преобразовать линии в стандартную векторную форму.

  No related posts.