Планка угла наружного: характеристики, виды, монтаж
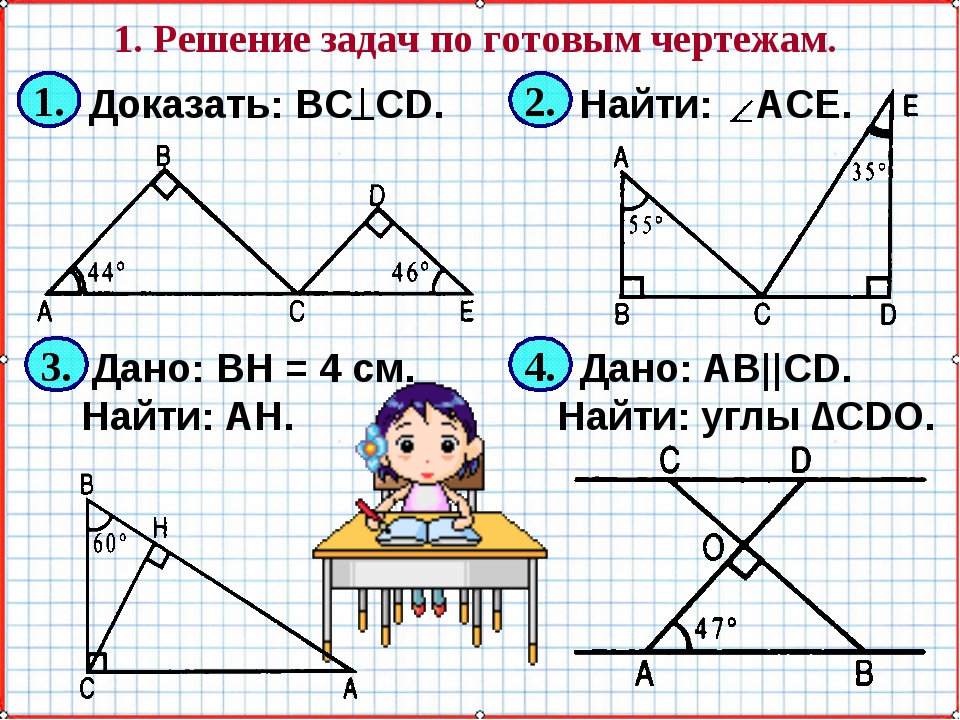
Обширный ассортимент доборных металлических элементов, выпускаемый компанией «СЭНДВИЧ ПАНЕЛИ», включает планки угла внутренние и наружные. Основное назначение этой детали состоит в установке в местах стыка наружных и внутренних углов металлочерепицы, профнастила и других облицовочных или кровельных материалов. Грамотная установка угловой планки обеспечивает защиту внутреннего пространства от ветра, дождя или снега.
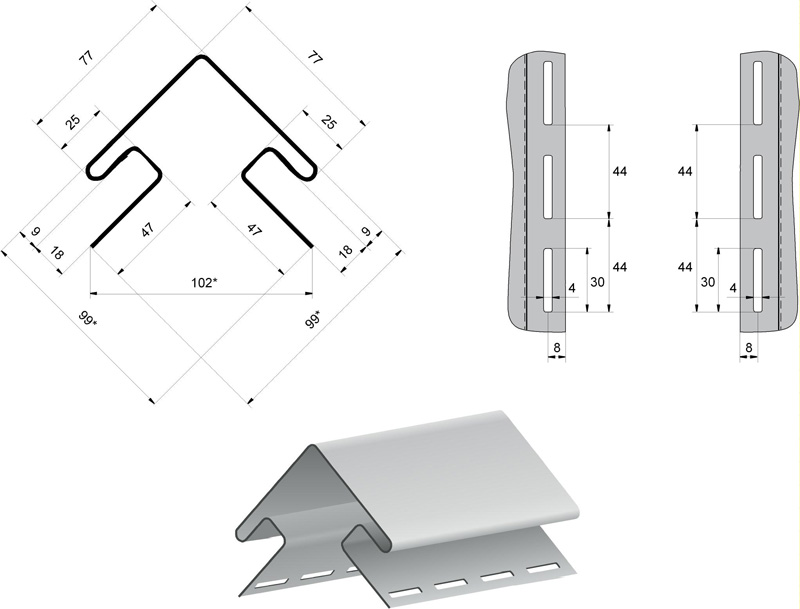
Планка угла наружного
Незаметный, но тем не менее очень важный элемент фасада — угол внешний. Все чаще и чаще мы можем наблюдать в процессе строительства или изучая уже готовые дома, красивое и правильное применение этого отделочного материала. Со стороны смотрится это очень эффектно, но просто эстетика не является самой главной и важной функцией отделки.
Это очень значимая и полезная вещь, которая скроет конструкцию и защитит ее от погодных явлений.
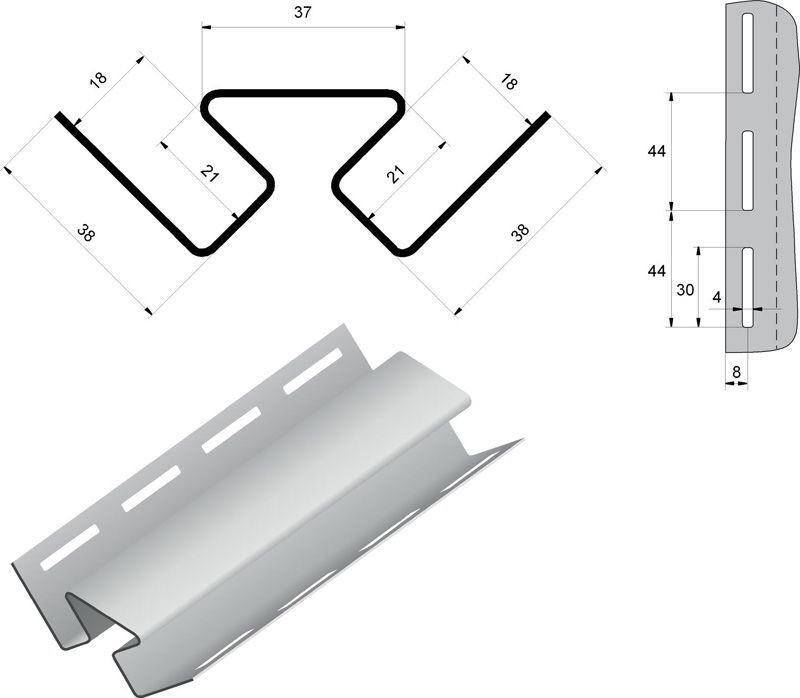
Планки углов делятся на простые с двумя гранями и сложные. Последние имеют не только внешние грани, но и внутренний паз для установки сайдинга, софита, металлических листов, сэндвич панелей и т. д.
Последние имеют не только внешние грани, но и внутренний паз для установки сайдинга, софита, металлических листов, сэндвич панелей и т. д.
Угол внешний простой
Угол оцинкованный или с полимерным покрытием (простой, наружный) – это доборная часть, представляющая собой прямой уголок. Чаще всего, он предназначен специально для того, чтобы закрыть стыкующиеся планки на всех внешних углах. Монтаж проводится на сам металлосайдинг, шапочки крепежей остаются открытыми.
Уголок монтируется на уже готовый материал из металла, при этом крепежные шапочки не закрываются. Если пренебрегать такими доборными элементами и оставлять конструкцию незащищенной, материал для кровли или фасада покроется ржавчиной и выйдет из строя.
Человеческий мозг устроен таким образом, что первое мнение, которое складывается о чем-либо, практически всегда зависит от вида того, на что мы посмотрели. Это относится и к домам. Хорошие, симпатичные домики воспринимаются нами как качественные, дорогие и уютные.
Далеко не последнюю роль в этом играет облицовка, способствующая красивому виду кровли и фасада.
Планка угла наружного сложного
Планка угла наружного сложного предназначена для облицовки и кровли внешних углов стен. За счет пазов панель сайдинга фиксируется без применения дополнительного видимого крепежа, что создает более цельный вид всего фасада. Стандартная длина элемента 2 м.
Использование угловых элементов для сайдингов и сэндвич панелей
Уголовая планка – это особое изделие, используемое для соединения панелей на наружных и внутренних углах фасада здания. Данный вид уголка для металлического сайдинга обрамляет внешние угловые выступы. Прежде всего, он используется для того, чтобы предотвратить попадание природных осадков в виде снега и дождя внутрь конструкции. Этот внешний сложный угол для панелей не требует особого ухода. Он устанавливается до основного прокладывания панелей на специальную подсистему. Сайдинг или сэндвич панели же потом вставляется в паз у данного углового элемента.
Изготовление планок угла
Для производства уголков применяется два способа – горячекатаный и холодногнутый. При первом варианте температура прокатки имеет выше показатель, чем во время рекристаллизации. Процедура изготовления предусматривает два этапа: для начала слиток проходит через валы и происходит формирование первоначальной заготовки. После чего заготовка направляется на прокатный стан с образованием окончательной формы. Для производства гнутого угла нужной формы используется профилегибочное оборудование, происходит изготовление изделия при помощи изгиба полосы из стали. Процесс изготовления четко определен государственными стандартами и нормами.
Четкий контроль на всех этапах производства позволяет получить высококачественные изделия, которые обладают высокими эксплуатационными параметрами. Планки угла стальной оцинкованный с покрытием полиэстер обладает высокой прочностью в поперечном направлении, при этом вес изделия небольшой. Такие характеристики сделали продукцию востребованной практически во всех сферах строительства.
При установке навесных фасадов, обустройстве софитов и фронтонов необходимо использовать доборные элементы. В нашем каталоге вы сможете выбрать и купить планки углов фасада, которые выполняют не только защитную, но и декоративную функцию.
Технические характеристики
- материал изделия – оцинкованная сталь;
- толщина листа – от 0,35 до 0,71 мм;
- стандартная длина планки – 2-3 метра;
- покрытие – одностороннее, толщиной 0,25 мкм: Drap, GreenCoat, Print Twincolor, PVDF, Safari, Полиэстер-double и ещё 14;
- цвета – имитация массива, камня и более 42 оттенков (палитры RR и RAL).
Преимущества продукции
- надёжная защита угловых стыков от пыли и осадков;
- безграничные возможности для персонализации экстерьера;
В нашем интернет-магазине мы предлагаем продукцию собственного производства и устанавливаем конкурентные цены, гарантируя качество.
Наша компания занимается производством кровельных и стеновых сэндвич-панелей, профилированных листов, металлочерепиц и доборных элементов для обустройства крыш и стен различных типов. Полностью готовый к монтажу материал предлагается нами на выгодных условиях.
Мы готовы предложить вам большой выбор цветовых решений палитры RAL, так же и порезку металлов под индивидуальный заказ. На сайте можно сразу заказать крепеж, аксессуары и элементы, необходимые для работы. Мы обеспечим вам наличие сертификатов, соответствие ГОСТам , бесплатную консультацию 8 (812) 603-49-30, качество и оригинальность продукции, оперативность поставок. Мы располагаем собственным автопарком грузового транспорта. Наша компания осуществляет доставку по Москве, Санкт Петербургу и по другим городам России. Стоимость доставки определяется в зависимости от географии и объема продаж.
Палитра RAL:
Параллелограмм – свойства, признаки, определение
Научим решать сложные задачи о параллелограммах
Начать учиться
Геометрические фигуры изучают не только восьмиклассники и технари, но и представители творческих специальностей. Нестандартные четырехугольные формы можно встретить как в дизайне обуви, так и в современных зданиях. В этой статье расскажем о параллелограмме и его отличительных особенностях.
Нестандартные четырехугольные формы можно встретить как в дизайне обуви, так и в современных зданиях. В этой статье расскажем о параллелограмме и его отличительных особенностях.
Определение параллелограмма
Параллелограмм — это четырехугольник, у которого противоположные стороны попарно параллельны и равны. Как выглядит параллелограмм:
Частные случаи параллелограмма: ромб, прямоугольник, квадрат.
Диагонали — отрезки, которые соединяют противоположные вершины.
Свойства диагоналей параллелограмма:
- В параллелограмме точка пересечения диагоналей делит их пополам.
- Любая диагональ параллелограмма делит его на два равных треугольника.
- Сумма квадратов диагоналей параллелограмма равна удвоенной сумме квадратов его двух смежных сторон.

Биссектриса угла параллелограмма
Свойства биссектрисы параллелограмма:
- Биссектриса параллелограмма отсекает от него равнобедренный треугольник.
- Биссектрисы углов, прилежащих к одной стороне параллелограмма пересекаются под прямым углом.
- Отрезки биссектрис противоположных углов равны и параллельны.
Как найти площадь параллелограмма:
- S = a × h, где a — сторона, h — высота.
- S = a × b × sinα, где a и b — две стороны, sinα — синус угла между ними. Для ромба формула примет вид S = a2 × sinα.

- Для ромба: S = 0,5 × (d1 × d2), где d1 и d2 — две диагонали.
Для параллелограмма: S = 0,5 × (d1 × d2) × sinβ, где β — угол между диагоналями.
Периметр параллелограмма — сумма длины и ширины, умноженная на два.
P = 2 × (a + b), где a — ширина, b — высота.
У нас есть отличные дополнительные курсы по математике для учеников с 1 по 11 классы!
Реши домашку по математике на 5.
Подробные решения помогут разобраться в самой сложной теме.
Свойства параллелограмма
Геометрическая фигура — это любое множество точек. У каждой фигуры есть свои свойства, которые отличают их между собой и помогают решать задачи по геометрии в 8 классе.
Рассмотрим основные свойства диагоналей и углов параллелограмма, узнаем чему равна сумма углов параллелограмма и другие особенности этой фигуры. Вот они:
- Противоположные стороны параллелограмма равны.

ABCD — параллелограмм, значит, AB = DC, BC = AD. - Противоположные углы параллелограмма равны.
ABCD — параллелограмм, значит, ∠A = ∠C, ∠B = ∠D. - Диагонали параллелограмма точкой пересечения делятся пополам.
ABCD — параллелограмм, AC и BD — диагонали, AC∩BD=O, значит, BO = OD, AO = OC. - Диагональ делит параллелограмм на два равных треугольника.
ABCD — параллелограмм, AC — диагональ, значит, △ABC = △CDA. - Сумма углов в параллелограмме, прилежащих к одной стороне, равна 180 градусам.
ABCD — параллелограмм, значит, ∠A + ∠D = 180°. - В параллелограмме диагонали d1, d2 и стороны a, b связаны следующим соотношением: d1 2 + d22 = 2 × (a2 + b2 ).
А сейчас докажем теорему, которая основана на первых двух свойствах.
Теорема 1. В параллелограмме противоположные стороны и противоположные углы равны.
В параллелограмме противоположные стороны и противоположные углы равны.
В любом выпуклом четырехугольнике диагонали пересекаются. Все, что мы знаем о точке их пересечения — это то, что она лежит внутри четырехугольника.
Если мы проведем обе диагонали в параллелограмме, точка пересечения разделит их пополам. Убедимся, так ли это:
- AB = CD как противоположные стороны параллелограмма.
- ∠1 = ∠2 как накрест лежащие углы при пересечении секущей AC параллельных прямых AB и CD; ∠3 = ∠4 как накрест лежащие углы при пересечении секущей BD параллельных прямых AB и CD.
- Следовательно, треугольник AOB равен треугольнику COD по второму признаку равенства треугольников, то есть по стороне и прилежащим к ней углам, из чего следует:
- CO = AO
- BO = DO
Теорема доказана. Наше предположение верно.
Наше предположение верно.
Признаки параллелограмма
Признаки параллелограмма помогают распознать эту фигуру среди других четырехугольников. Сформулируем три основных признака.
Первый признак параллелограмма. Если в четырехугольнике две противолежащие стороны равны и параллельны, то этот четырехугольник — параллелограмм.
Докажем 1 признак параллелограмма:
Шаг 1. Пусть в четырехугольнике ABCD:
- AB || CD
- AB = CD
Чтобы назвать этот четырехугольник параллелограммом, нужно внимательно рассмотреть его стороны.
Сейчас мы видим одну пару параллельных сторон. Нужно доказать, что вторая пара сторон тоже параллельна.
Шаг 2. Проведем диагональ. Получились два треугольника ABC и CDA, которые равны по первому признаку равенства, то есть по по двум сторонам и углу между ними:
- AC — общая сторона;
- По условию AB = CD;
- ∠1 = ∠2 как внутренние накрест лежащие углы при пересечении параллельных прямых AB и CD секущей АС.

Шаг 3. Из равенства треугольников также следует:
- ∠3 = ∠4
Эти углы тоже являются внутренними накрест лежащими для прямых CB и AD. А это как раз и есть признак параллельности прямых. Значит, CB || AD и ABCD — параллелограмм.
Вот так быстро мы доказали первый признак.
Второй признак параллелограмма. Если в четырехугольнике противоположные стороны попарно равны, то этот четырехугольник — параллелограмм.
Докажем 2 признак параллелограмма:
Шаг 1. Пусть в четырехугольнике ABCD:
- AB = CD
- BC = AD
Шаг 2. Проведем диагональ AC и рассмотрим треугольники ABC и CDA:
- AC — общая сторона;
- AB = CD по условию;
- BC = AD по условию.

Из этого следует, что треугольники ABC и CDA равны по третьему признаку, а именно по трем сторонам.
Шаг 3. Из равенства треугольников следует:
- ∠ DCA = ∠BAC
А так как эти углы — накрест лежащие при сторонах BC и AD и диагонали AC, значит, стороны BC и AD параллельны.
- ∠DAC = ∠BCA
Эти углы — накрест лежащие при сторонах AB и CD и секущей AC. Поэтому стороны AB и CD тоже параллельны. Значит, четырехугольник ABCD — параллелограмм, ЧТД.
Доказали второй признак.
Докажем 3 признак параллелограмма:
Шаг 1. Если диагонали четырехугольника ABCD делятся пополам точкой O, то треугольник AOB равен треугольнику COD по двум сторонам и углу между ними:
- CO = OA;
- DO = BO;
- углы между ними равны, как вертикальные, то есть угол AOB равен углу COD.

Шаг 2. Из равенства треугольников следует, что CD = AB.
Эти стороны параллельны CD || AB, по равенству накрест лежащих углов: ∠1 = ∠2 (следует из равенства треугольников AOB и COD).Значит, ABCD является параллелограммом по первому признаку, который мы доказали ранее. Что и требовалось доказать.
Теперь мы знаем свойства параллелограмма и то, что выделяет его среди других четырехугольников — признаки. Так как они совпадают, эти формулировки можно использовать для определения параллелограмма. Но самое распространенное определение все-таки связано с параллельностью противоположных сторон.
Шпаргалки для родителей по математике
Все формулы по математике под рукой
Лидия Казанцева
Автор Skysmart
К предыдущей статье
410.4K
Натуральные числа
К следующей статье
297.
Обыкновенные дроби
Получите план обучения, который поможет понять и полюбить геометрию
ПремиумНа вводном уроке с методистом
Проверим знание геометрии и других разделов математики, выявим пробелы
Подберём курс
Познакомим с интерактивной платформой
Самая сложная в мире задача «Простая геометрия»
Самая сложная в мире задача «Простая геометрия»
|
Комплексные числа: углы и полярные координаты
Комплексные числа: углы и полярные координаты Этот раздел предполагает знание тригонометрии. Для получения информации о тригонометрии см. Краткий курс Дейва по триггерам наhttp://www.clarku.edu/~djoyce/trig/
Полярные координаты помогут нам понять комплексные числа геометрически. С одной стороны, обычные прямоугольные координаты x и yi определяют комплексное число z = x + yi , задавая расстояние x вправо и расстояние y вверх.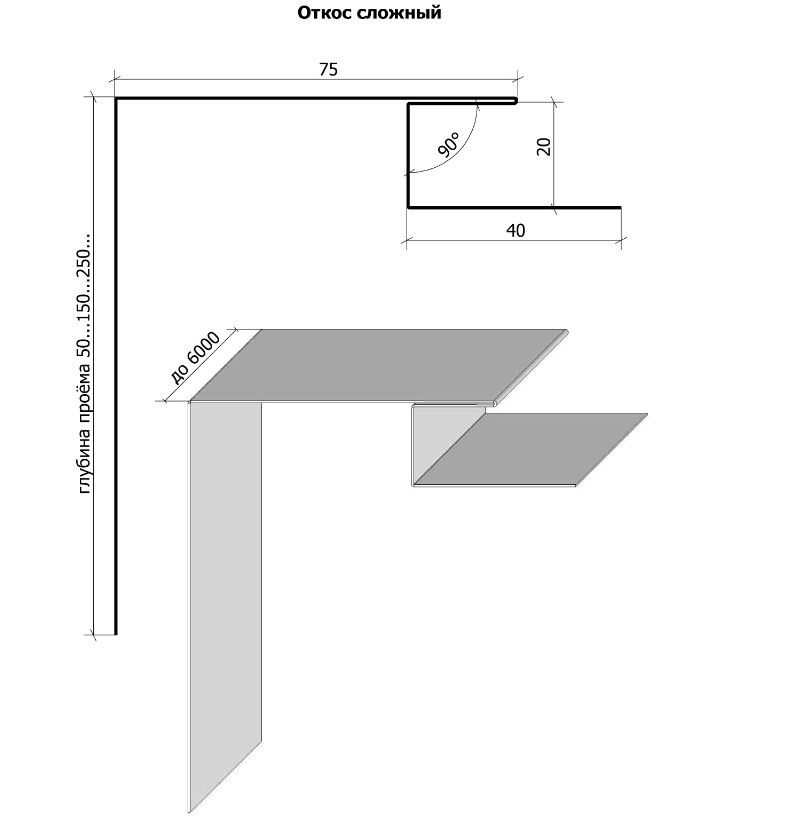 С другой стороны, полярные координаты определяют ту же самую точку z , говоря, как
far r от начала координат 0 и угол для линии от начала координат до точки.
Мы уже назвали расстояние r абсолютной величиной | из | z, , и мы увидели, как
Теорема Пифагора установила связь между ним и х и и :
С другой стороны, полярные координаты определяют ту же самую точку z , говоря, как
far r от начала координат 0 и угол для линии от начала координат до точки.
Мы уже назвали расстояние r абсолютной величиной | из | z, , и мы увидели, как
Теорема Пифагора установила связь между ним и х и и :
Далее нам нужно разобраться с углом . Мы будем следовать стандартному соглашению для указания угла
. Согласно этому соглашению положительная ось x (наша реальная ось) проходит под углом 0°, т.е.
положительная ось y (наша воображаемая ось) под углом 90°, отрицательная ось x под углом 180° и отрицательная y — ось под углом 270°. Кроме того, 360° можно добавить или вычесть из любого угла, и направление не изменится. Так,
0°, 360°, 720° и 360° относятся к положительному x — ось. Аналогично, 270° и 90°
оба относятся к отрицательной оси y . Угол 45° проходит вдоль линии y = x вверх вправо.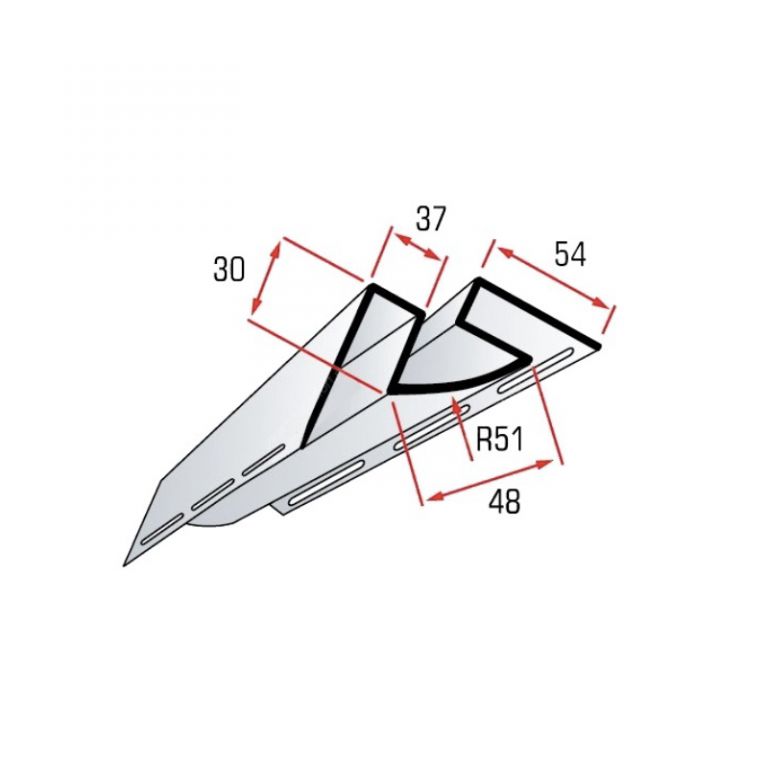 И так далее.
И так далее.
Точка z может быть задана любой парой, парой прямоугольных координат, x и y , или парой полярных координат. координаты, r, что | z | и , который является arg ( z ). Поскольку любая пара определяет точку, каждая пара должна определять другую пару. Должно быть четыре уравнения, связывающих их, и так есть. Пифагорейский тождество было упомянуто выше, но остальные требуют тригонометрии. Из того же треугольника мы используемые для теоремы Пифагора, мы находим следующие три соотношения:
Теперь, если мы применим эти отношения к нашему комплексному числу z = x + yi, , то мы получим альтернативное описание для z
| с | = | x + iy |
| = | r cos + i r sin | |
| = | r (cos + i sin ) | |
| = | | из | (cos + i sin ) |
Обратите внимание, что комплексное число cos + i sin имеет абсолютное значение 1, поскольку cos 2 + sin 2 равно 1 для любого угла . Таким образом, каждое комплексное число z является
произведение действительного числа | из | и комплексное число cos + i sin .
Таким образом, каждое комплексное число z является
произведение действительного числа | из | и комплексное число cos + i sin .
Мы почти подошли к тому моменту, когда можем доказать последнее недоказанное утверждение предыдущего раздела об умножении, а именно, что arg( zw ) = arg( z ) + arg( zw ). Как и выше, мы принимаем arg( z ) как , и теперь пусть arg( w ) будет . Затем,
Нам нужно показать, что arg( zw ) равно + . Другими словами
Если мы воспользуемся формулами сложения для косинуса и синуса в одном важном моменте, мы его получим. Напомним из тригонометрии эти сложения формулы:
sin ( + ) = cos sin + sin cos .






 При двух равных сторонах ДКЭ равнобедренный и заключаем:
При двух равных сторонах ДКЭ равнобедренный и заключаем: