Укажите прямую параллельную прямой x y 1: Укажите прямую, параллельную прямой x+y=1 варианты ответа: 1)y=−1/2 x+1 2)y=x−1 3)2x+2y+3=0 4)y=x+1 5)x−y=2 ———————————- Определите…

Уравнение параллельной прямой онлайн

Прямая, проходящая через точку K(x₀; y₀) и параллельная прямой y = kx + a находится по формуле:

y — y₀ = k(x — x₀) (1)

где k — угловой коэффициент прямой.

Альтернативная формула:
Прямая, проходящая через точку M₁(x₁; y₁) и параллельная прямой Ax+By+C=0, представляется уравнением

A(x-x₁)+B(y-y₁)=0. (2)

назначение сервиса. Онлайн-калькулятор предназначен для составления уравнения параллельной прямой (см. также как составить уравнение перпендикулярной прямой).

Составить уравнение прямой, проходящей через точку K(;) параллельно прямой y = ·x + .
Пример №1. Составить уравнение прямой, проходящей через точку M₀(-2,1) и при этом:
а) параллельно прямой 2x+3y -7 = 0;
б) перпендикулярно прямой 2x+3y -7 = 0.
Решение. Представим уравнение с угловым коэффициентом в виде y = kx + a. Для этого перенесем все значения кроме y в правую часть: 3y = -2x + 7. Затем разделим правую часть на коэффициент 3. Получим: y = -2/3x + 7/3
Найдем уравнение NK, проходящее через точку K(-2;1), параллельно прямой y = ^-2/₃x + ⁷/₃
Подставляя x₀ = -2, k = ^-2/₃, y₀ = 1 получим:
y-1 = ^-2/₃(x-(-2))
или
y = ^-2/₃x — ¹/₃ или 3y + 2x +1 = 0

Пример №2. Написать уравнение прямой, параллельной прямой 2x + 5y = 0 и образующей вместе с осями координат треугольник, площадь которого равна 5.
Решение. Так как прямые параллельны, то уравнение искомой прямой 2x + 5y + C = 0. Площадь прямоугольного треугольника , где a и b его катеты. Найдем точки пересечения искомой прямой с осями координат:

;
.
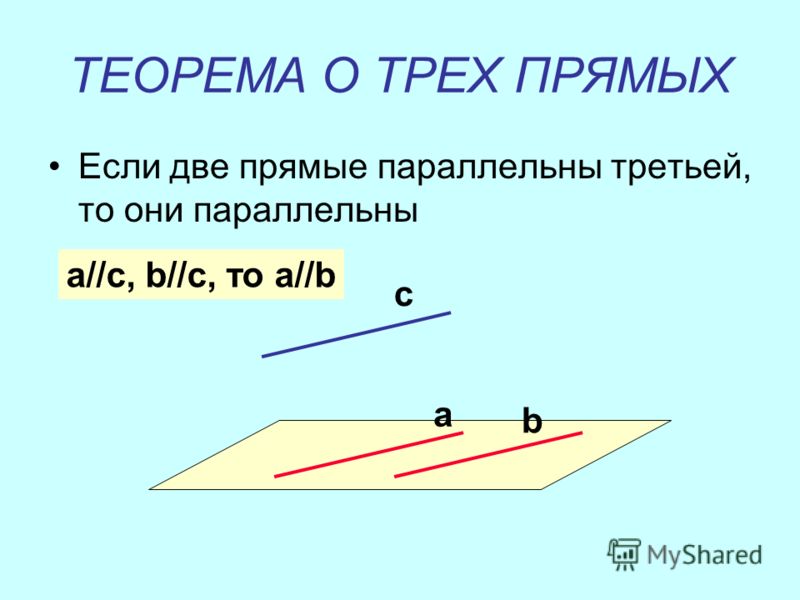
Итак, A(-C/2,0), B(0,-C/5). Подставим в формулу для площади: . Получаем два решения: 2x + 5y + 10 = 0 и 2x + 5y – 10 = 0.

Пример №3. Составить уравнение прямой, проходящей через точку (-2; 5) и параллельной прямой 5x-7y-4=0.
Решение. Данную прямую можно представить уравнением y = ⁵/₇x – ⁴/₇ (здесь a = ⁵/₇). Уравнение искомой прямой есть y – 5 = ⁵/^{7(x – (-2)), т.е. 7(y-5)=5(x+2) или 5x-7y+45=0.}

Пример №4. Решив пример 3 (A=5, B=-7) по формуле (2), найдем 5(x+2)-7(y-5)=0.

Пример №5. Составить уравнение прямой, проходящей через точку (-2;5) и параллельной прямой 7x+10=0.

Решение. Здесь A=7, B=0. Формула (2) дает 7(x+2)=0, т.е. x+2=0. Формула (1) неприменима, так как данное уравнение нельзя разрешить относительно y (данная прямая параллельна оси ординат).

Аналитическая геометрия в пространстве (Лекция №19)

УГОЛ МЕЖДУ ПЛОСКОСТЯМИ

Рассмотрим две плоскости α₁ и α₂, заданные соответственно уравнениями:

Под углом между двумя плоскостями будем понимать один из двугранных углов, образованных этими плоскостями. Очевидно, что угол между нормальными векторами и плоскостей α₁ и α₂ равен одному из указанных смежных двугранных углов или . Поэтому . Т.к. и , то

.

Пример. Определить угол между плоскостями x+2y-3z+4=0 и 2x+3y+z+8=0.

Условие параллельности двух плоскостей.

Две плоскости α₁ и α₂ параллельны тогда и только тогда, когда их нормальные векторы и параллельны, а значит .

Итак, две плоскости параллельны друг другу тогда и только тогда, когда коэффициенты при соответствующих координатах пропорциональны:

или

Условие перпендикулярности плоскостей.

Ясно, что две плоскости перпендикулярны тогда и только тогда, когда их нормальные векторы перпендикулярны, а следовательно, или .

Таким образом, .

Примеры.

1. Составить уравнение плоскости, проходящей через точку

   M(-2; 1; 4) параллельно плоскости 3x+2y-7z+8=0.

   Уравнение плоскости будем искать в виде Ax+By+Cz+D=0. Из условия параллельности плоскостей следует, что: . Поэтому можно положить A=3, B=2, C

   =-7. Поэтому уравнение плоскости принимает вид3x+2y-7z+D=0.

   Кроме того, так какMÎ α, то-6+2-28+D=0, D=32.

   Итак, искомое уравнение 3x+2y-7z+32=0.

2. Составить уравнение плоскости, проходящей через точки M₁(1; 1; 1), M₂(0; 1; –1) перпендикулярно плоскости x+y+z=0.

   Так как M₁Î α, то используя уравнение плоскости, проходящей через заданную точку, будем иметь A(x-1)+B(y-1)+C(z-1)=0.

   Далее, так как M₂Î α, то подставив координаты точки в выписанное уравнение, получим равенство -A-2C=0 или A+2C=0.

   Учтем, что заданная плоскость перпендикулярна искомой. Поэтому A+B+C=0.

   Выразим коэффициенты Aи Bчерез

   C: A=-2C, B=C и подставим их в исходное уравнение: -2C(x-1)+C(y-1)+C(z-1)=0.

   Окончательно получаем -2x+y+z=0.

3. Составить уравнение плоскости, проходящей через точку M(-2; 3; 6) перпендикулярно плоскостям 2x+3y-2z-4=0 и 3x+5y+z=0.

   Так как MÎ α, то A(x+2)+B(x-3)+C(z-6)=0.

   По условию задачи , поэтому

   Итак уравнение плоскости принимает вид 13(x+2)-8(y-3)+z-6=0 или 13x-8y+z+44=0.

ПРЯМАЯ В ПРОСТРАНСТВЕ.

ВЕКТОРНОЕ УРАВНЕНИЕ ПРЯМОЙ.

ПАРАМЕТРИЧЕСКИЕ УРАВНЕНИЯ ПРЯМОЙ

Положение прямой в пространстве вполне определяется заданием какой-либо её фиксированной точки М₁ и вектора , параллельного этой прямой.

Вектор , параллельный прямой, называется направляющим вектором этой прямой.

Итак, пусть прямая l проходит через точку М₁(x₁, y₁, z₁), лежащую на прямой параллельно вектору .

Рассмотрим произвольную точку М(x,y,z) на прямой. Из рисунка видно, что .

Векторы и коллинеарны, поэтому найдётся такое число t, что , где множитель t может принимать любое числовое значение в зависимости от положения точки M на прямой. Множитель t называется параметром. Обозначив радиус-векторы точек М₁ и М соответственно через и , получаем . Это уравнение называется векторным уравнением прямой. Оно показывает, что каждому значению параметра t соответствует радиус-вектор некоторой точки

М, лежащей на прямой.

Запишем это уравнение в координатной форме. Заметим, что , и отсюда

Полученные уравнения называются параметрическими уравнениями прямой.

При изменении параметра t изменяются координаты x, y и z и точка М перемещается по прямой.

КАНОНИЧЕСКИЕ УРАВНЕНИЯ ПРЯМОЙ

Пусть М₁(x₁, y₁, z₁) – точка, лежащая на прямой l, и – её направляющий вектор. Вновь возьмём на прямой произвольную точку М(x,y,z) и рассмотрим вектор .

Ясно, что векторы и коллинеарные, поэтому их соответствующие координаты должны быть пропорциональны, следовательно,

– канонические уравнения прямой.

Замечание 1. Заметим, что канонические уравнения прямой можно было получить из параметрических,исключив параметр

t. Действительно, из параметрических уравнений получаем или .

Пример. Записать уравнение прямой в параметрическом виде.

Обозначим , отсюда x = 2 + 3t, y = –1 + 2t, z = 1 –t.

Замечание 2. Пусть прямая перпендикулярна одной из координатных осей, например оси Ox. Тогда направляющий вектор прямой перпендикулярен Ox, следовательно, m=0. Следовательно, параметрические уравнения прямой примут вид

Исключая из уравнений параметр t, получим уравнения прямой в виде

Однако и в этом случае условимся формально записывать канонические уравнения прямой в виде. Таким образом, еслив знаменателе одной из дробей стоит нуль, то это означает, что прямая перпендикулярна соответствующей координатной оси.

Аналогично, каноническим уравнениям соответствует прямая перпендикулярная осям Ox и Oy или параллельная оси Oz.

Примеры.

1. Составить канонические и параметрические уравнения прямой, проходящей через точку М₁(1;0;-2) параллельно вектору .

   Канонические уравнения: .

   Параметрические уравнения:

2. Составить уравнения прямой, проходящей через две точки М₁(-2;1;3), М₂(-1;3;0).

   Составим канонические уравнения прямой. Для этого найдем направляющий вектор . Тогда l: .

ОБЩИЕ УРАВНЕНИЯ ПРЯМОЙ, КАК ЛИНИИ ПЕРЕСЕЧЕНИЯ ДВУХ ПЛОСКОСТЕЙ

Через каждую прямую в пространстве проходит бесчисленное множество плоскостей. Любые две из них, пересекаясь, определяют ее в пространстве. Следовательно, уравнения любых двух таких плоскостей, рассматриваемые совместно представляют собой уравнения этой прямой.

Вообще любые две не параллельные плоскости, заданные общими уравнениями

определяют прямую их пересечения. Эти уравнения называются общими уравнениями прямой.

Примеры.

Построить прямую, заданную уравнениями

Для построения прямой достаточно найти любые две ее точки. Проще всего выбрать точки пересечения прямой с координатными плоскостями. Например, точку пересечения с плоскостью xOy получим из уравнений прямой, полагая z= 0:

Решив эту систему, найдем точку M₁(1;2;0).

Аналогично, полагая y= 0, получим точку пересечения прямой с плоскостью xOz:

От общих уравнений прямой можно перейтик её каноническим или параметрическим уравнениям. Для этого нужно найти какую-либо точку М₁ на прямой и направляющий вектор прямой.

Координаты точки М₁ получим из данной системы уравнений, придав одной из координат произвольное значение. Для отыскания направляющего вектора, заметим, что этот вектор должен быть перпендикулярен к обоим нормальным векторам и . Поэтому за направляющий вектор прямой l можно взять векторное произведение нормальных векторов:

.

Пример. Привести общие уравнения прямой к каноническому виду.

Найдём точку, лежащую на прямой. Для этого выберем произвольно одну из координат, например, y= 0 и решим систему уравнений:

Нормальные векторы плоскостей, определяющих прямую имеют координаты Поэтому направляющий вектор прямой будет

. Следовательно, l: .

УГОЛ МЕЖДУ ПРЯМЫМИ

Углом между прямыми в пространстве будем называть любой из смежных углов, образованных двумя прямыми, проведёнными через произвольную точку параллельно данным.

Пусть в пространстве заданы две прямые:

Очевидно, что за угол φ между прямыми можно принять угол между их направляющими векторами и . Так как , то по формуле для косинуса угла между векторами получим

.

Условия параллельности и перпендикулярности двух прямых равносильны условиям параллельности и перпендикулярности их направляющих векторов и :

Две прямые параллельны тогда и только тогда, когда их соответствующие коэффициенты пропорциональны, т.е. l₁ параллельна l₂ тогда и только тогда, когда параллелен .

Две прямые перпендикулярны тогда и только тогда, когда сумма произведений соответствующих коэффициентов равна нулю: .

Примеры.

1. Найти угол между прямыми и .

2. Найти уравнения прямой проходящей через точку М₁(1;2;3) параллельно прямой l₁:

   Поскольку искомая прямая l параллельна l₁, то в качестве направляющего вектора искомой прямой l можно взять направляющий вектор прямой l₁.

3. Составить уравнения прямой, проходящей через точку М₁(-4;0;2) и перпендикулярной прямым: и .

   Направляющий вектор прямой l можно найти как векторное произведение векторов и :

УГОЛ МЕЖДУ ПРЯМОЙ И ПЛОСКОСТЬЮ

Углом между прямой и плоскостью будем называть угол, образованный прямой и её проекцией наплоскость. Пусть прямаяи плоскость заданы уравнениями

Рассмотрим векторы и . Если угол между ними острый, то он будет , где φ – угол между прямой и плоскостью. Тогда .

Если угол между векторами и тупой, то он равен . Следовательно . Поэтому в любом случае . Вспомнив формулу вычисления косинуса угла между векторами, получим .

Условие перпендикулярности прямой и плоскости. Прямая и плоскость перпендикулярны тогда и только тогда, когда направляющий вектор прямой и нормальный вектор плоскости коллинеарны, т.е. .

Условие параллельности прямой и плоскости. Прямая и плоскость параллельны тогда и только тогда, когда векторы и перпендикулярны.

Примеры.

1. Написать уравнение плоскости, проходящей через точку М₁(2;-3;4) параллельно прямым и .

   Так как M₁Î α, то уравнение плоскости будем искать в виде

   .

   Применяя условие параллельности прямой и плоскости, получим систему линейных уравнений

   Отсюда

   Итак, или .

2. Найти угол между прямой и плоскостью .

   Направляющий вектор прямой . Нормальный вектор плоскости . Следовательно,

3. Найдите точку, симметричную данной М(0;-3;-2) относительно прямой .

   Составим уравнение плоскости α перпендикулярной l. MÎ α, . Следовательно, или .

   Найдём точку пересечения прямой l и α:

   Итак, N(0.5;-0.5;0.5). Пусть искомая точка М₁ имеет координаты М₁(x,y,z). Тогда очевидно равенство векторов , т.е. (0,5;2,5;2,5)=(х-0.5;у+0.5;z-0.5). Откуда x=1, y=2, z=3 или М₁(1;2;3)..

3 6 Решить для ? cos(x)=1/2 7 Найти x sin(x)=-1/2 8 Преобразование градусов в радианы 225 9 Решить для ? cos(x)=(квадратный корень из 2)/2 10 Найти x cos(x)=(квадратный корень из 3)/2 11 Найти x sin(x)=(квадратный корень из 3)/2 92=9 14 Преобразование градусов в радианы 120 градусов 15 Преобразование градусов в радианы 180 16 Найти точное значение желтовато-коричневый(195) 92-4 38 Найти точное значение грех(255) 39 Оценить лог база 27 из 36 40 Преобразовать из радианов в градусы 2 шт. 92-3sin(x)+1=0 43 Найти x tan(x)+ квадратный корень из 3=0 44 Найти x sin(2x)+cos(x)=0 45 Упростить (1-cos(x))(1+cos(x)) 92=25 59 График f(x)=- натуральный логарифм x-1+3 60 Найдите значение с помощью единичного круга угловой синус(-1/2) 61 Найти домен квадратный корень из 36-4x^2 92=0 66 Найти x cos(2x)=(квадратный корень из 2)/2 67 График у=3 68 График f(x)=- логарифмическая база 3 x-1+3 92 71 Найти x квадратный корень из x+4+ квадратный корень из x-1=5 72 Решить для ? cos(2x)=-1/2 73 Найти x логарифмическая база x из 16=4 9х 75 Упростить (cos(x))/(1-sin(x))+(1-sin(x))/(cos(x)) 76 Упростить сек(х)sin(х) 77 Упростить кубический корень из 24 кубический корень из 18 92=0 96 Найти x 3x+2=(5x-11)/(8г) 97 Решить для ? sin(2x)=-1/2 98 Найти x (2x-1)/(x+2)=4/5 92+n-72)=1/(n+9)

Линии, параллельные осям — линии, параллельные осям x и y, уравнение, график линий, параллельных осям, решенные примеры

В двумерной геометрии есть две оси: ось x и ось Y. Линия, параллельная оси y, имеет вид «x=k», где «k» — любое действительное число, а «k» — расстояние линии от оси y. Например, уравнение прямой, имеющей форму x = 3, представляет собой прямую, параллельную оси y и отстоящую на 3 единицы от оси y. Точно так же линии можно рисовать параллельно оси X. Линия, параллельная оси x, имеет форму «y=k», где «k» — действительное число, а также расстояние линии от оси x. Например, уравнение прямой, имеющее форму y = 2, представляет собой прямую, параллельную оси x и отстоящую на 2 единицы от оси x.

1.	Линия, параллельная оси x
2.	Линия, параллельная оси Y
3.	Решенные примеры
4.	Практические вопросы
5.	Часто задаваемые вопросы о линиях, параллельных осям

Линия, параллельная оси x

Линия, параллельная оси x, имеет форму ‘y = k’, где ‘k’ — постоянное значение. В координатной плоскости прямую можно представить уравнением. Чтобы представить уравнение этой параллельной линии в более обобщенной форме, мы можем записать его как «y = k», где «k» — любое действительное число. Также говорят, что «k» — это расстояние от оси x до линии «y=k». Например, если уравнение линии y = 5, то мы можем сказать, что она находится на расстоянии 5 единиц выше линии оси x. Все точки прямой, параллельной оси x, находятся от нее на одинаковом расстоянии.

Рассмотрим уравнение y = 2 или y — 2 = 0. Это уравнение с одной переменной y . Однако мы можем думать об этом как о линейном уравнении с двумя переменными, в котором коэффициент x равен 0:

0(x) + 1(y) + (-2) = 0. 

Построим график график для уравнения и найдите, как будет выглядеть линия ‘y=2’.

х	-4	-3	-2	-1	0	1	2	3	4
у	2	2	2	2	2	2	2	2	2

Подставляя каждое значение ‘x’, данное в таблице, мы видим, что значение ‘y’ остается неизменным. Например, возьмем значение «x = -4» и подставим в уравнение 0(x) + 1(y) + (-2) = 0, 
0(-4) + 1(у) — 2 = 0
0 + у — 2 = 0
Следовательно, у = 2,
Возьмем положительное значение для «x = 3» и решим уравнение, чтобы найти значение «y».
0(3) + 1 (у) — 2 = 0
0 + у — 2 = 0
у = 2,
Таким образом, мы видим, что хотя значение «x» изменяется, значение «y» остается неизменным. Таким образом, все решения этого линейного уравнения имеют вид (k,2), где k — некоторое действительное число. График линии y=2 приведен ниже.

Это линия, параллельная оси x . Таким образом, уравнение формы y = a представляет прямую линию, параллельную оси x и пересекающую ось y в точке (0,a).

Линия, параллельная оси Y

Линия, параллельная оси Y, имеет вид x = k, где k — постоянное значение. Это означает, что для любого значения «y» значение «x» одинаково. Более обобщенный способ представить уравнение прямой линии, параллельной оси y, — это x = k, где k — действительное число. Здесь «k» представляет собой расстояние от оси y до линии «x = k». Например, если у нас есть уравнение линии как «x = 2», оно говорит, что линия находится на расстоянии 2 единиц от оси y. Все точки прямой, параллельной оси у, находятся от нее на одинаковом расстоянии.

Теперь рассмотрим уравнение x = 3. Его также можно записать в виде линейного уравнения с двумя переменными следующим образом:

1(x) + 0(y) + (-3) = 0. 

Давайте постройте график для уравнения и найдите, как будет выглядеть линия «x = 3».

х	3	3	3	3	3	3	3	3	3
у	-4	-3	-2	-1	0	1	2	3	4

При подстановке различных значений y в уравнение 1(x) + 0(y) + (-3) = 0 значение x остается неизменным. Например, если y = -3, то значение «x» равно
. 1(х) + 0(-3) +(-3) = 0,
х + 0 — 3 = 0
х-3 = 0
Следовательно, х = 3,
Возьмем положительное значение для ‘y’. Скажите «у=2». Подставив значение y=2, мы получим
1(х) + 0(2) + (-3) = 0
х + 0 -3 =0
Следовательно, х = 3, 
Мы можем заметить, что для любого значения y значение x = 3. Таким образом, все решения этого уравнения имеют форму (3,k), где k — некоторое действительное число. График этого уравнения будет состоять из всех точек, чья координата x равна 3, то есть линия, параллельная и -ось, проходящая через (3,0). График линии, уравнение которой x = 3, показан на рисунке ниже.

В общем случае уравнение вида x = a представляет собой прямую линию, параллельную оси  y  и пересекающую ось  x  в точке (a, 0).

Темы, относящиеся к линиям, параллельным осям

Ознакомьтесь с некоторыми интересными статьями, посвященными линиям, параллельным осям. Нажмите, чтобы узнать больше!

• Линии
• оси x и y
• Оси координат
• Декартовы координаты
• Уравнение прямой

Часто задаваемые вопросы о линиях, параллельных осям

Что означает параллельность осям?

Параллельно осям означает линии, которые параллельны либо оси x, либо оси y. Линия, параллельная оси x, – это горизонтальная линия, уравнение которой имеет форму y = k, где k   – расстояние от линии до оси x. Точно так же линия, параллельная оси y, является вертикальной линией, уравнение которой имеет вид x = k, где «k» — расстояние линии от оси y.

Что представляет собой уравнение прямой, параллельной оси X?

Уравнение оси x определяется как y = 0. Уравнение прямой, параллельной оси x, имеет вид y = k, где k – любое действительное число. Например, рассматривая уравнение линии y = 2, для любого значения «x» значение «y» всегда равно 2. Это можно понять, подставив различные значения «x» в уравнение линии, 0(x) + 1(y) — 2 = 0, что всегда приводит к y = 2. Эта линия параллельна оси x.

Что представляет собой уравнение прямой, параллельной оси Y?

Уравнение оси Y задается как x = 0. Уравнение прямой, параллельной оси Y, имеет вид x = k, где k – любое действительное число. Например, рассматривая уравнение линии, x = 3, для любого значения «y» значение «x» всегда равно 3. Это можно понять, подставив различные значения «y» в уравнение линии, 1(x) + 0(y) — 3 = 0, что всегда приводит к x = 3. Эта линия параллельна оси y.

Когда можно сказать, что две прямые параллельны осям?

Все вертикальные и горизонтальные линии на плоскости параллельны осям. Горизонтальные линии параллельны оси x, а вертикальные линии параллельны оси y. Линия параллельна осям, если либо координата x, либо координата y фиксированы или постоянны на протяжении всей линии, и она должна проходить либо из (0, a), либо из (a, 0). Например, линия с уравнением 3x — 6 = 0 параллельна оси y, поскольку для любого значения y значение x остается неизменным, то есть 2.