Укажите равные треугольники и признак равенства: ПОМОГИТЕ СРОЧНО ПОЖАЛУЙСТА!!!! Помогите с заданиями по геометрии Укажите равные треугольники изображенные на рисунке запишите признак равенства треугольников с помощью которого доказывается его равенство с указанием пар равных элементов

Равные треугольники – определение, свойства, признаки

4.5

Средняя оценка: 4.5

Всего получено оценок: 345.

Обновлено 11 Января, 2021

4.5

Средняя оценка: 4.5

Всего получено оценок: 345.

Обновлено 11 Января, 2021

Изучая тему треугольников, стоит обратить внимание на признаки равенства двух фигур. Их можно использовать во время решений различных заданий. О том, как определить признаки и свойства равенства треугольников – поговорим в этой статье.

Материал подготовлен совместно с учителем высшей категории Харитоненко Натальей Владимировной.

Опыт работы учителем математики — более 33 лет.

Определение

Треугольники ABC и $A_1B_1C_1$ считаются равными в том случае, если их можно совместить наложением. При этом, все стороны и вершины фигур полностью наложатся друг на друга, а все соответствующие углы совместятся.

Исходя из определения равных треугольников, в равных треугольниках все соотвествующие стороны равны и все соответствующие углы равны.

Используем это свойство для доказательства признаков равенства треугольников способом наложения.

Для обозначения равенства фигур используют знак “равно”, к примеру, $Δ ABC = Δ А_1В_1С_1$

Математик Фалес, чтобы вычесть расстояние от корабля до суши построил треугольник на суше равный треугольнику на «море». Он, таким образом, узнал точное расстояние.

Признаки равенства

Выделяют три признака равенства треугольников:

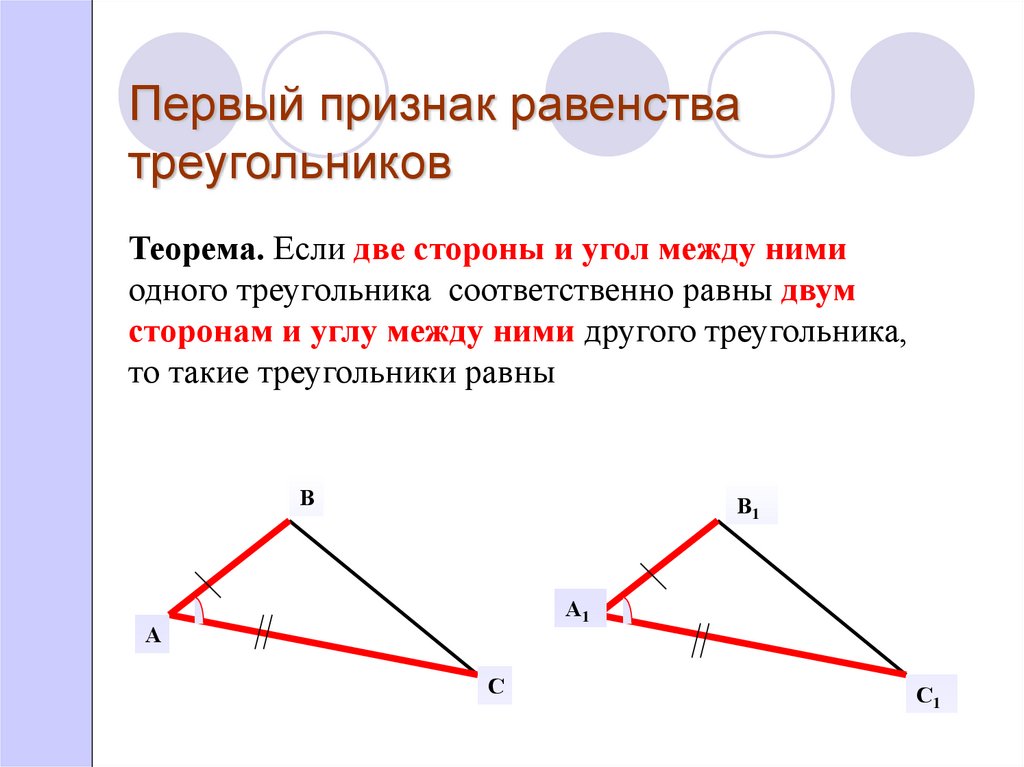
1. Если две стороны и угол между ними одного треугольника равны соответствующим двум сторонам и углу между ними другого треугольника, то такие фигуры равны.

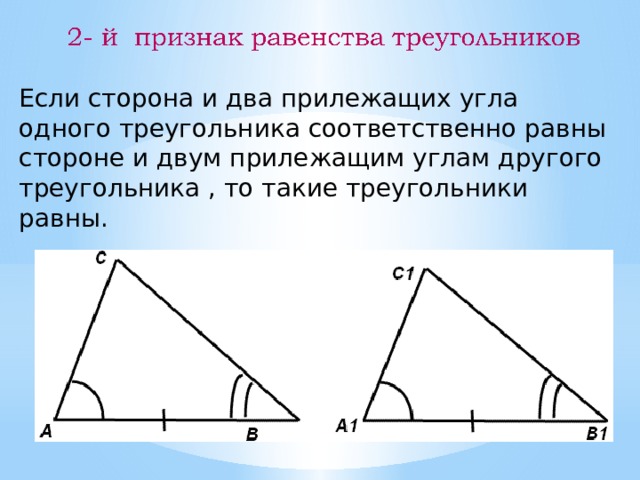
Рис. 1. Первый признак равенства

2. Если сторона и два прилегающих к ней угла одного треугольника равны соответствующей стороне и двум прилегающим к ней углам другого треугольника, то такие фигуры равны.

Рис. 2. Второй признак равенства

3. Если три стороны в одном треугольнике равны трем сторонам в другом треугольнике, то такие треугольники равны.

Кроме того, стоит выделить некоторые свойства:

• Сумма двух внутренних углов треугольника будет всегда меньше 180⁰.
• Внешний угол треугольника всегда больше внутреннего, при условии, если угол не смежный с ним.
• Внешний угол треугольника равен сумме двух внутренних углов, не смежных с ним.

Алгоритм доказательства равенства фигур

• Необходимо сориентироваться, для каких треугольников необходимо доказать равенство. Для удобства можно выделить их разными цветами.
• На рисунке отметить, все необходимые данные в условии задания.
• Проверить есть ли у двух треугольников общая сторона либо угол.
• Далее необходимо проанализировать, имеют ли треугольники по две пары равных сторон либо углов. А также необходимо поразмышлять, как можно доказать равенство третьей стороны, либо угла между ними.
• При недостатке данных необходимо выяснить: можно ли использовать равенство других треугольников, чтобы доказать равенство нужных по условию.
• При необходимости, можно сделать дополнительное построение.

Порядок названия вершин одного треугольника должен быть одинаковым с порядком названия вершин другого треугольника.

Стойки стремянки могут свободно раздвигаться, до того момента, когда их не зафиксировали перемычкой. Жесткость такой конструкции основывается на третьем признаке равенства фигур.

Пример

Задание:
Два отрезка пересекаются в точке О и делятся этой точкой пополам. Доказать, что $Δ ABO = Δ CDO$.

Решение:
Стоит обратить внимание на рисунок

Рис. 3. Два треугольника

В условии задания сказано, что $BO=OD$, $AO = OС$. А углы $AOB$ и $COD$ равны, так как они вертикальные. Поэтому $Δ ABO = Δ CDO$ по первому признаку равенства треугольников.

Что мы узнали?

Для того, чтобы доказать равенство фигур необходимо использовать один из трех признаков равенства треугольников. Треугольники могут быть равными по двум сторонами и углу между ними, по стороне и двум прилегающим к ней углам, а также по трем сторонам.

Тест по теме

Доска почёта

Чтобы попасть сюда — пройдите тест.

• Анна Ножеева

  5/5

• Ярик Яраслав

  5/5

• Данила Салин

  5/5

• Никита Ушаков

  5/5

Оценка статьи

4.5

Средняя оценка: 4.5

Всего получено оценок: 345.

---

А какая ваша оценка?

Признаки равенства прямоугольных треугольников 7 класс онлайн-подготовка на Ростелеком Лицей

Введение и доказательство первого признака равенства прямоугольных треугольников

 

Вспомним из материала предыдущего урока, прямоугольный треугольником называется треугольник, если у него хотя бы один из углов прямой (т. е. равен 90^о).

 

Рассмотрим первый признак равенства треугольников: если два катета одного прямоугольного треугольника соответственно равны двум катетам другого прямоугольного треугольника, то такие треугольники равны.

Проиллюстрируем данный случай:

Рис.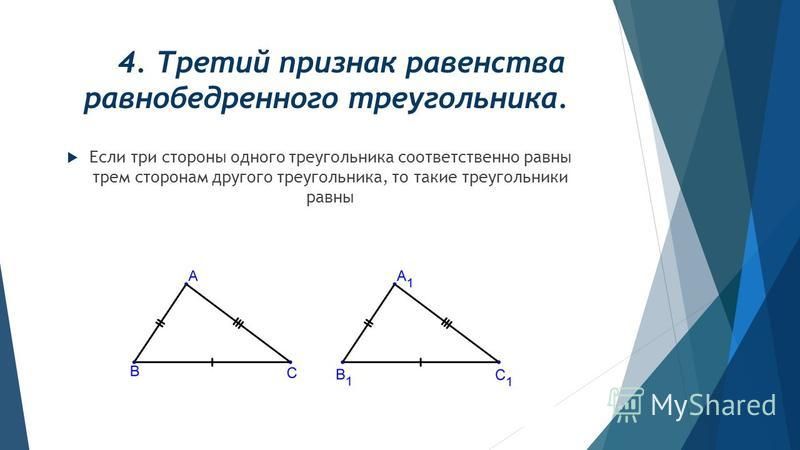 1. Равные прямоугольные треугольники

Доказательство:

Вспомним о первом равенстве произвольных треугольников.

 

 

 

 

 

 

 

Рис. 2

Если две стороны и угол между ними одного треугольника и соответствующие им две стороны и угол между ними второго треугольника равны, то данные треугольники равны. Об этом гласит первый признак равенства треугольников, то есть:

АВС = .

Аналогичное доказательство следует и для прямоугольных треугольников:

.

Треугольники равны по первому признаку.

 

Введение и доказательство второго признака равенства прямоугольных треугольников

 

 

Рассмотрим второй признак равенства прямоугольных треугольников. Если катет и прилежащий к нему острый угол одного прямоугольного треугольника соответственно равны катету и прилежащему острому углу другого прямоугольного треугольника, то такие треугольники равны.

 

Рис. 3

Доказательство:

Рис. 4

Воспользуемся вторым признаком равенства треугольников:

 

Аналогичное доказательство и для прямоугольных треугольников:

 

Треугольники равны по второму признаку.

 

Введение и доказательство третьего признака равенства прямоугольных треугольников

 

 

Рассмотрим третий признак равенства прямоугольных треугольников: если гипотенуза и прилежащий к ней угол одного прямоугольного треугольника соответственно равны гипотенузе и прилежащему углу другого треугольника, то такие треугольники равны.

 

Доказательство:

Рис. 5

Вспомним второй признак равенства треугольников:

 Рис. 6

Данные треугольники равны, если:

 

Поскольку известно, что одна пара острых углов у прямоугольных треугольников равна (∠А = ∠А₁), то равенство другой пары углов (∠B = ∠B₁) доказывается следующим образом:

.

Поскольку АВ = А₁В₁ ( по условию), ∠В = ∠В₁, ∠А = ∠А₁. Поэтому треугольники АВС и А₁В₁С₁ равны по второму признаку.

 

Введение и доказательство четвёртого признака равенства прямоугольных треугольников, введение понятия «внешний угол треугольника»

 

 

Рассмотрим следующий признак равенства треугольников:

 

Если катет и гипотенуза одного треугольника соответственно равны катету и гипотенузе другого треугольника, такие прямоугольные треугольники равны.

 

 

 

 

 

Рис. 7

Доказательство:

Совместим наложением треугольники АВС и А₁В₁С₁. Предположим, что вершины А и А₁, а также С и С₁ совместились наложением, а вершина В и точка В₁ не совпадают. Именно этот случай указан на следующем рисунке:

Рис. 8

В данном случае мы можем заметить равнобедренный треугольник АВВ₁ (по определению – по условию АВ = АВ₁). Поэтому по свойству, ∠АВ₁В = ∠АВВ₁. Рассмотрим определение внешнего угла. Внешним углом треугольника называется угол, смежный любому углу треугольника. Его градусная мера равна сумме двух углов треугольника, несмежных с ним. На рисунке указано данное соотношение:

Рис. 9

Угол 5 является внешним углом треугольника и равен ∠5 = ∠1 + ∠2. Отсюда следует, что внешний угол больше каждого из углов, несмежных с ним.

Таким образом, ∠АВВ₁ является внешним углом для треугольника АВС и равен сумме ∠АВВ₁  = ∠САВ + ∠АСВ = ∠АВС  = ∠САВ + 90^о. Таким образом, ∠АВ₁В (что является острым углом в прямоугольном треугольнике АВВ₁) не может быть равен углу ∠АВВ₁, ведь данный угол – тупой по доказанному.

Значит наше предположение касательно расположения точек В и В₁ оказалось неверным, следовательно данные точки совпадают. А значит треугольники АВС и А₁В₁С₁ совместились наложением. Поэтому они равны (по определению).

Таким образом, данные признаки вводятся не зря, ведь их можно использовать при решении некоторых задач.

 

Рекомендованные ссылки на ресурсы интернет

1. Омский государственный университет (Источник).
2. Справочный портал calc.ru (Источник).
3. Учительский портал (Источник).

 

Рекомендованное домашнее задание

1. № 38. Бутузов В.Ф., Кадомцев С.Б., Прасолов В.В., под редакцией Садовничего В. А. Геометрия 7. М.: Просвещение. 2010 г.

2. Исходя из данных, указанных на рисунке, укажите равные треугольники, если они есть.

3. Исходя из данных, указанных на рисунке, укажите равные треугольники, если они есть. Учитывайте, что АС = АF.

4. В прямоугольном треугольнике к гипотенузе проведены медиана и высота. Угол между ними равен 20^о. Определите величину каждого из острых углов данного прямоугольного треугольника.

 

Как определить конгруэнтность треугольников

Два треугольника равны, если они имеют: точно такие же с трех сторон и точно такие же три угла. Но нам не обязательно знать все три стороны и все три угла… обычно три из шести достаточно.

Существует пять способов определить конгруэнтность двух треугольников: SSS , SAS , ASA , AAS и HL .

1. SSS  

(сторона, сторона, сторона)

SSS означает «сторона, сторона, сторона» и означает, что у нас есть два треугольника со всеми тремя сторонами равными.

Например:

соответствует:

(дополнительную информацию см.

в разделе Решение треугольников SSS)

Если три стороны одного треугольника равны трем сторонам другого треугольника, треугольники конгруэнтны.

2. SAS  

(сторона, угол, сторона)

SAS означает «сторона, угол, сторона» и означает, что у нас есть два треугольника, две стороны и угол между которыми равны.

Например:

равно и соответствует:

(дополнительную информацию см. в разделе Решение треугольников SAS)

Если две стороны и угол между ними одного треугольника равны соответствующим сторонам и углу другого треугольника, треугольники конгруэнтны.

3. ASA  

(угол, сторона, угол)

ASA означает «угол, сторона, угол» и означает, что у нас есть два треугольника, в которых мы знаем, что два угла и прилежащая сторона равны.

Например:

равно и соответствует:

(дополнительную информацию см. в разделе Решение треугольников ASA)

Если два угла и прилежащая к ним сторона одного треугольника равны соответствующим углам и стороне другого треугольника, треугольники конгруэнтны.

4. ААС  

(угол, угол, сторона)

AAS означает «угол, угол, сторона» и означает, что у нас есть два треугольника, где мы знаем, что два угла и не включенная сторона равны.

Например:

равно и соответствует:

(дополнительную информацию см. в разделе Решение треугольников AAS)

Если два угла и не включенная в них сторона одного треугольника равны соответствующим углам и стороне другого треугольника, треугольники конгруэнтны.

5. HL  

(гипотенуза, катет)

Это относится только к прямоугольным треугольникам!

или

HL означает « H ypotenuse, L eg» (самая длинная сторона прямоугольного треугольника называется «гипотенуза», две другие стороны называются «каттерами»)

Это означает, что у нас есть два прямоугольных треугольника с

• одинаковой длиной гипотенузы и
• такой же длины для одной из двух других ножек .

Не имеет значения, какая сторона треугольника может вращаться.

Например:

равно и соответствует:

(Подробнее см.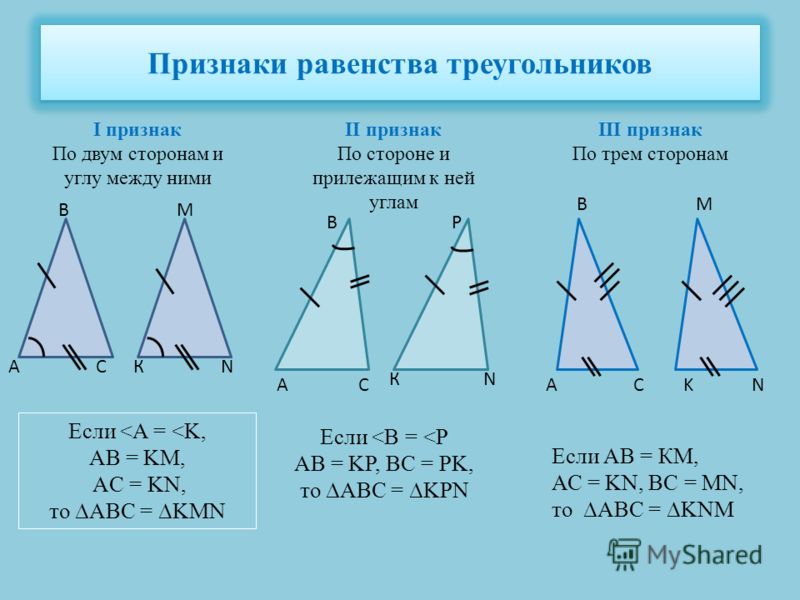 в Теореме Пифагора)

Если гипотенуза и катет одного прямоугольного треугольника равны соответствующим гипотенузе и катету другого прямоугольного треугольника, то эти два треугольника конгруэнтны.

Внимание! Не используйте «AAA»

AAA означает, что нам даны все три угла треугольника, но нет сторон.

Этой информации недостаточно, чтобы решить, конгруэнтны ли два треугольника!

Потому что треугольники могут иметь одинаковые углы, но быть разных размеров :

равно , а не соответствует:

Не зная хотя бы одной стороны, мы не можем быть уверены, что два треугольника конгруэнтны.

 

Конгруэнтные треугольники – объяснение и примеры

Вы должны хорошо знать фотокопировальную машину. Когда вы кладете A4 страницу внутри машины и активируйте ее, вы получите идентичную копию этой страницы.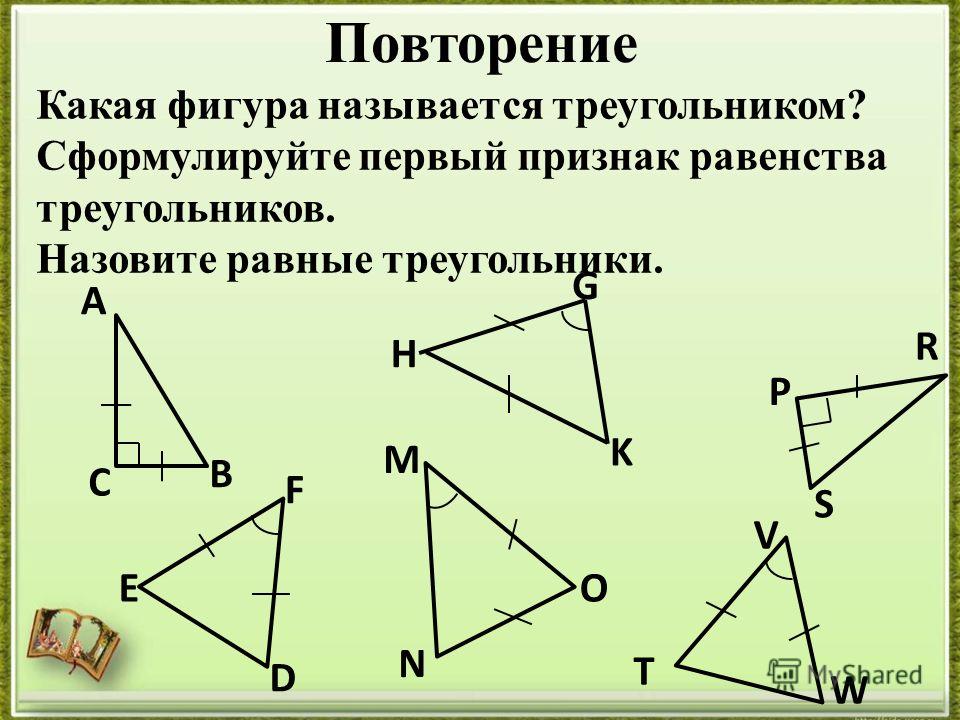 Если вы повернете или перевернете страницу, она останется такой же, как исходная страница. Даже если вы вырезаете их, вы можете легко выровнять их снова. Мы можем сказать, что страницы похожи или конгруэнтны.

Далее страница формата А4 имеет прямоугольную форму, поэтому при разрезании по диагонали получится треугольник. Если вы разрежете обе фотокопии одинаковым образом, вы увидите, что обе они образуют одинаковый треугольник с одинаковым набором углов и сторон.

Что такое конгруэнтный треугольник?

Вы, должно быть, уже хорошо знакомы с треугольником — это двумерная фигура с тремя сторонами, тремя углами и тремя вершинами. Два или более треугольника называются равными, если их соответствующие стороны или углы равны. Другими словами, конгруэнтных треугольников имеют одинаковую форму и размеры .

Конгруэнтность — это термин, используемый для описания двух объектов одинаковой формы и размера . Символ соответствия — ≅ .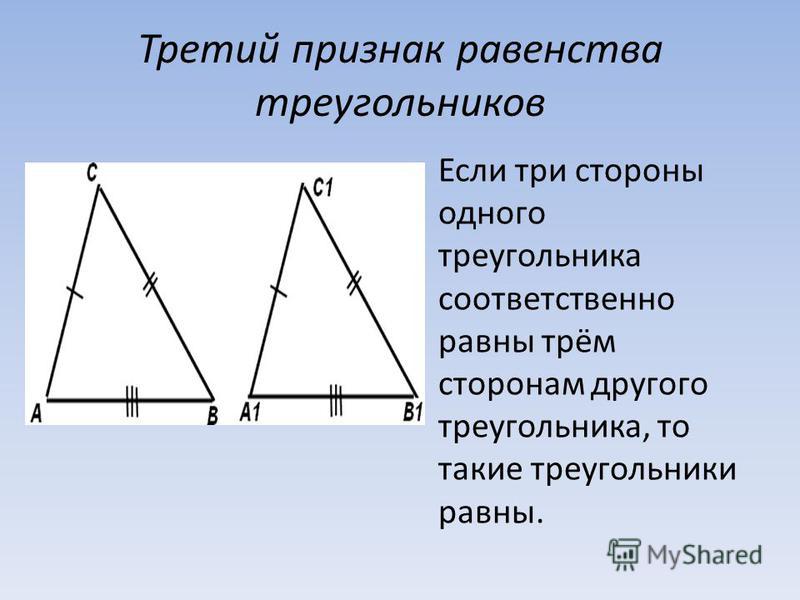 В треугольниках мы используем аббревиатуру CPCT , чтобы показать, что соответствующие части конгруэнтных треугольников одинаковы.

Конгруэнтность не рассчитывается и не измеряется, а определяется визуальным осмотром. Треугольники могут стать конгруэнтными в трех различных движениях, а именно: вращении, отражении и перемещении.

Что такое конгруэнтность треугольников?

Сравнения треугольников — это правила или методы, используемые для доказательства конгруэнтности двух треугольников. Два треугольника называются конгруэнтными тогда и только тогда, когда мы можем заставить один из них наложиться на другой так, чтобы он точно покрыл его.

Эти четыре критерия, используемые для проверки сходства треугольников, включают :

Сторона – Сторона – Сторона ( SSS ), Сторона – Угол – Сторона ( SAS ), Угол – Сторона – Угол ( ASA ) и Угол – Угол – Сторона ( AAS ).

Есть и другие способы доказать конгруэнтность треугольников, но в этом уроке мы ограничимся только этими постулатами.

Прежде чем перейти к подробностям этих постулатов конгруэнтности важно уметь обозначать разные стороны и углы определенным знаком, показывающим их соответствие. Вы часто будете видеть, что стороны и углы треугольника отмечены маленькими засечками, чтобы указать наборы конгруэнтных углов или конгруэнтных сторон.

На рисунках ниже видно, что стороны с одной засечкой имеют одинаковую длину, стороны с двумя засечками также имеют одинаковую длину, а стороны с засечками равны. То же самое касается углов.

Сторона – Угол – Сторона

Сторона Угол Сторона (SAS) – это правило, используемое для доказательства конгруэнтности данного набора треугольников . В этом случае два треугольника равны, если две стороны и один угол между ними в данном треугольнике равны соответствующим двум сторонам и одному углу между ними в другом треугольнике.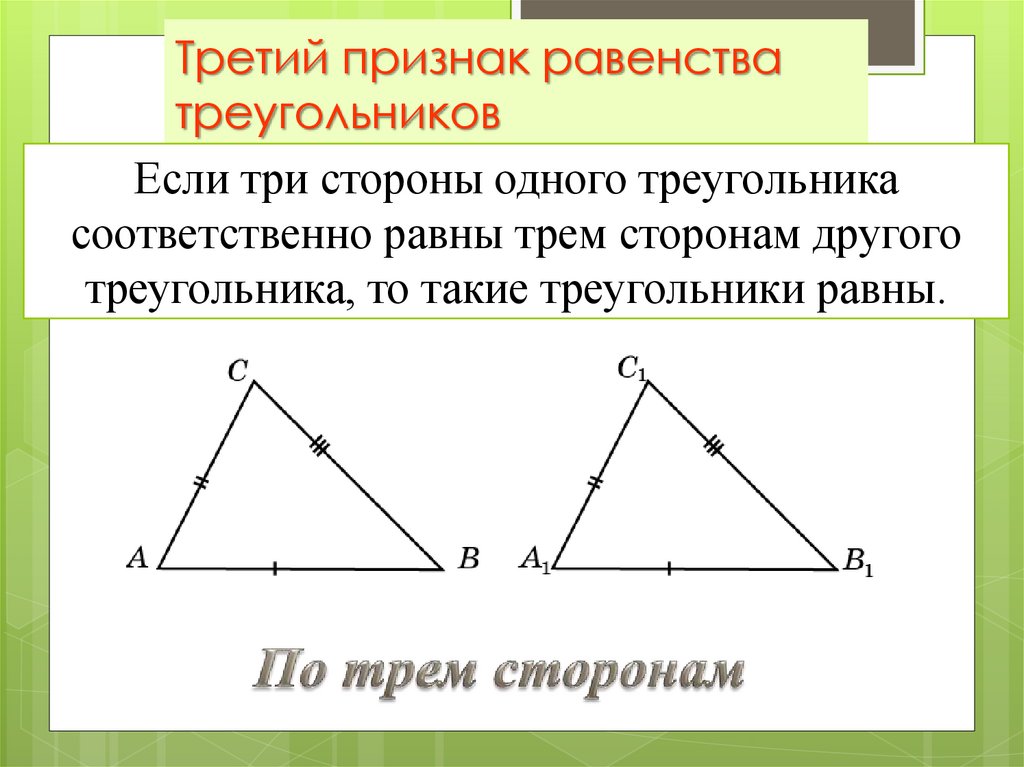

Помните, что угол должен быть образован двумя сторонами, чтобы треугольники были конгруэнтными.

Иллюстрация правила SAS:

Учитывая это; длина AB = PR, AC = PQ и ∠ QPR = ∠ BAC , затем; Треугольники ABC и PQR равны ( △ ABC ≅△ PQR).

Угол – Угол – Сторона

Правило «Угол – Угол – Сторона» (AAS) гласит, что два треугольника конгруэнтны, если два их соответствующих угла и одна не включенная сторона равны.

Иллюстрация:

Учитывая это;

∠ BAC = ∠ QPR, ∠ AC B = ∠ RQP and length AB = QR, then triangle ABC and PQR are congruent ( △ ABC ≅△ PQR).

Сторона – Сторона – Сторона

Правило стороны – стороны – стороны (SSS) утверждает, что: Два треугольника конгруэнтны, если их соответствующие длины трех сторон равны.

Illustration:

Triangle ABC and PQR are said to be congruent ( △ ABC ≅△ PQR)  if length AB = PR , AC = QP , и до н.э. = QR .

Угол – Сторона – Угол

Правило «Угол – Сторона – Угол» (ASA) гласит: Два треугольника конгруэнтны, если два соответствующих им угла и одна из сторон равны.

Illustration:

Triangle ABC and PQR are congruent ( △ ABC ≅△ PQR)  if length ∠ BAC = ∠ PRQ, ∠ ACB = ∠ PQR.

Примеры равенства треугольников:

Пример 1

Два треугольника ABC и PQR таковы, что AB = 3,5 см, BC = 7,1 см, AC = 5 см, PQ = 7,1 см, QR = 5 см и PR = 3,5 см. Проверьте, равны ли треугольники.

Решение

Дано: AB = PR = 3,5 см

BC = PQ = 7,1 см и

AC = QR = 5 см

Следовательно, ∆ABC ≅ ∆PQR (SSS).

Пример 2

Учитывая, что тий ABC = (2x + 30) °, ♂ PQR = 55 ° и PQR = 55 ° и PQR = 55 ° PQR = 55 ° PQR = 55 ° PQR = 55 ° . значение х.

Раствор

∆ABC ≅ ∆PQR

Следовательно,

55° + 65° + (2x + 30) ° = 180°

120° + 2x + 30° = 180°

150° + 2×9 08 = 080 30°

x = 15°

Пример 3

Опишите тип конгруэнтности двух треугольников, заданный формулой;

∆ ABC, AB = 7 см, BC = 5 см, ∠B = 50° и ∆ DEF, DE = 5 см, EF = 7 см, ∠E = 50° AB = EF = 7 см,

BC = DE = 5 см и

∠B =∠E = 50°

Следовательно, ∆ABC ≅ ∆FED (SAS)

Реальные примеры конгруэнтных объектов (h4)

Примеров бесконечное множество.