«Свойства степени с натуральным показателем»
Тема: «Свойства степени с натуральным показателем» 7 класс
Алгебра 7 кл.,Г.В. Дорофеев, С.Б. Суворова и др. «Просвещение», 2017г.
Учитель Кизилова В.А.
Цели урока: познакомить учащихся со свойствами степени с натуральным показателем; владеть правилами выполнения действий над степенями; обеспечить условия для развития умений работы с источниками учебной информации, выделять главное и второстепенное.
Задачи:
Образовательные (формирование познавательных УУД): изучить свойства степени (умножение, деление, возведение степени в степень) с натуральным показателем; научить выполнять действия на применение правил; совершенствование вычислительных навыков.
Развивающие (формирование регулятивных УУД): развивать умения наблюдать, сравнивать, анализировать, делать выводы, развивать устную математическую речь.
Воспитательные (формирование коммуникативных и личностных УУД): формировать трудолюбие, внимательность, активность, умение слушать мнения других, участвовать в коллективном обсуждении проблем, воспитывать самостоятельность.
Тип урока: Урок «открытия» нового знания.
Формы работы учащихся: фронтальная, индивидуальная, групповая.
Используемые технологии: проблемное обучение, обучение в сотрудничестве, личностно-ориентированное обучение, коммуникативные и здоровьесберегающие технологии.
Необходимое оборудование: компьютер, проектор, экран, учебники, карточки.
Ход урока.
1.Организационный момент.
Здравствуйте, ребята!
Начинаем наш урок, тему которого узнаем чуть позже.
-Запишем в тетрадях число, «Классная работа».
— Скажите, что нового вы узнали на предыдущих уроках? (ответы учеников)
Сегодня эпиграфом нашего урока станут слова М.В.Ломоносова:
«Пусть кто-нибудь попробует вычеркнуть из математики степени, и он увидит, что без них далеко не уедешь»
-Где особенно часто используют степени, в каких науках? (Проверка домашнего задания — найти дополнительный материал)
2.
Актуализация опорных знаний.
Устная работа. (Слайд)
-Что называют степенью числа? (Привести примеры).
-Назвать основание и показатель степени (Слайд)
-Любым ли числом может быть основание? (Привести примеры).
-Всегда ли степень с отрицательным основанием, есть число отрицательное? (Сформулируйте определение, приведите примеры).
— Что называют степенью числа с показателем 1?
Выполним вычисления и узнаем тему нашего урока (карточка 1 и 2)
ме | ой | ре | еп | св | к | да | ни | ва | нет | ра | ст | ро | см | сте | с | нь |
-36 | 25 | 12 | 81 | 16 | 8 | 4,5 | 7,9 | 10 | 7 | -6 | 9 | 6 | -9 | -8 | 36 | 1 |
|
|
|
| ||||||||||
сте | зате | нату | лем | пени | раль | ный | с | пока | ным | |||
-12 | 103 | 16 384 | 3026 | 10 609 | 59 049 | 177147 | 36 | 121 | 531 441 | |||
Запишем в тетради тему нашего урока: «Свойства степени».
Название целей и задач урока.
3. Освоение нового учебного материала.
Скажите, в чем возникла трудность при выполнении заданий второй части?
Работа в группах.
Карточка 3.
-Вам сейчас предстоит изучить карточки, проанализировать, обобщить материал, сделать выводы, и после этого вы сможете вычислить примеры в которых у вас возникли затруднения. (См Инструкцию к карточке)
Инструкция к карточке №3.
1.Повтори определение степени, вспомни, где записывается основание степени и показатель степени. (если забыл, можешь использовать карточки 1.1 и 1.2)
2. Внимательно прочитай определение 1. «Как умножать степени с одинаковым основанием», посмотри на схему- рисунок и запомни, что нужно сделать.
3. Посмотри на решение примеров. Выясни, как получается ответ.
4. Внимательно читай определение 2. Изучив схему-рисунок дополни определение необходимыми словами.
5.
Посмотри на решение примеров. Выясни, как получается ответ, и проверь все ли так ты сформулировал в определении. Повтори определение еще раз.
6. Внимательно читай начало определения 3, изучив схему-рисунок дополни определение необходимыми словами.
7. Посмотри на решение примеров. Выясни, как получается ответ, и проверь все ли так ты сформулировал в определении. Повтори определение еще раз.
8. Повтори все определения еще раз.
9.Обрати внимания на перечеркнутые свойства, сделай вывод, проверь на примерах. Возьми основание равное 2, а затем 3.
-Посмотрите на образец решения примеров.
-Сформулируйте свойства степеней.
Работа с учебником.
Что написано в учебнике про деление степеней (какая неточность написана в карточке), Что надо запомнить и как исправить? Обязательно ли чтобы основание ≠0? Как вы думаете, почему?
Докажите, на примере почему
Запишите формулы в тетрадь.
4. Закрепление учебного материала.
Устная работа на применение формул (фронтально). Работа по учебнику: № 524,530, 540. – Какие правилами применили при решении?
Физкультминутка.
Мы все вместе улыбнемся,
Подмигнем слегка друг другу,
Вправо-влево повернемся (поворот влево — вправо)
И кивнем затем по кругу (поклоны влево — вправо)
Все идеи победим,
Вверх взметнулись наши руки, (поднимают руки вверх- вниз)
Груз забот с себя стряхнули
И продолжим путь науки (встряхнули кистями рук)
Карточка 4.
Выполните задание 1 – 4.
Запишите ответы в тетрадь. (После того, как задание выполнено, ученики меняются тетрадями и проверяют тетради одноклассников, отмечая правильно решенные примеры знаком «+» ,проверяя решения по слайду)
Объяснение трудных моментов, повторение правил, работа в группах.
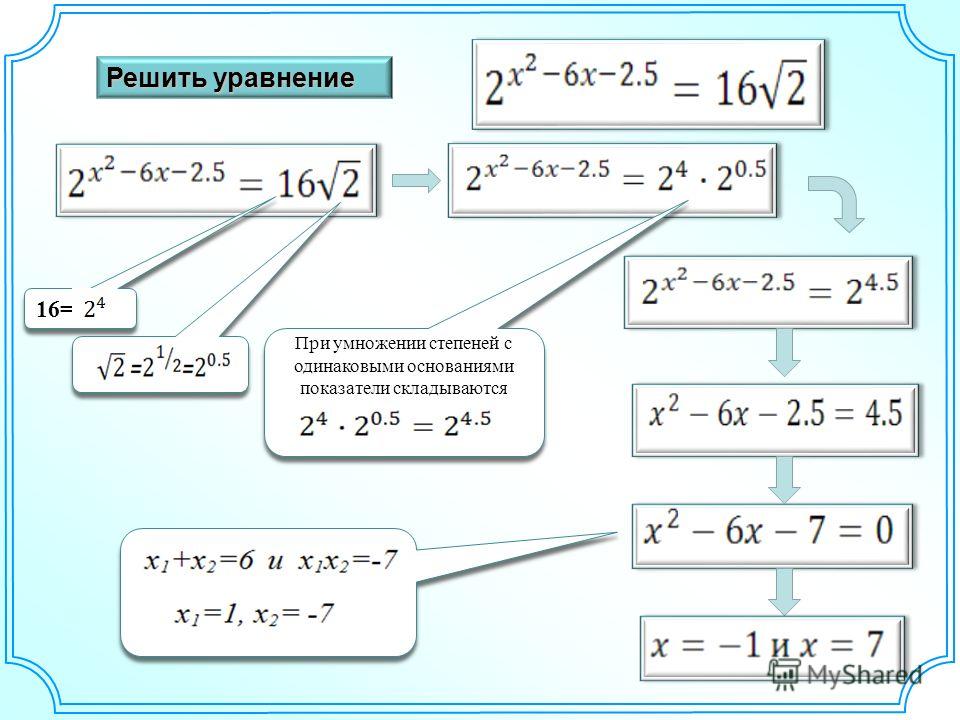
Обратимся к таблицам и попробуем решить задание, с которым мы не смогли справиться в начале урока.
; ; ; ; ; .
Степень числа «3» мы можем найти в учебнике — №549.
-Теперь кто готов полностью озвучить тему нашего урока?
-Как она будет звучать?
-Что значит натуральная степень?
-Натуральное число?
-Какие свойства мы выучили?
-Сформулируйте свойства степеней.
Можно ли умножать или делить степени с разными основаниями?
Какое обязательное условие?
Выполним устно: , , ? (Слайд)
Выполнить на доске и в тетрадях № 548, 549.
5.Задание на дом.
1.Сделать карточку – «помогайку» — записать формулы и свойства степеней (опорные сигналы), выписать степени чисел «2», «3» с показателями от 1 до 15. (П 6.1, 6.2 )
2.Зашифровать фразу или слово, используя выражения со степенями + №537
или выполнить №№ 525, 529, 537, 536.
6. Подведение итогов урока. Рефлексия.
-Что мы изучали сегодня на уроке?
-Какие свойства степени мы выучили?
— Сформулируйте свойства степеней.
— Можно ли умножать или делить степени с разными основаниями?
Рефлексия:
— Кто может сегодня о себе сказать:
— Я работал(а) отлично, в полную силу своих возможностей, чувствовал(а) себя уверенно.
— Я работал(а) хорошо, но не в полную силу, испытывал(а) чувство неуверенности, боязни, что отвечу неправильно.
— У меня сегодня не получилось. Сегодня не мой день.
Инструкция к карточке №3.
1.Повтори определение степени, вспомни, где записывается основание степени и показатель степени. (если забыл, можешь использовать карточки 1.1 и 1.2)
2. Внимательно прочитай определение 1. «Как умножать степени с одинаковым основанием», посмотри на схему- рисунок и запомни, что нужно сделать.
3. Посмотри на решение примеров. Выясни, как получается ответ.
4. Внимательно читай определение 2. Изучив схему-рисунок дополни определение необходимыми словами.
5. Посмотри на решение примеров.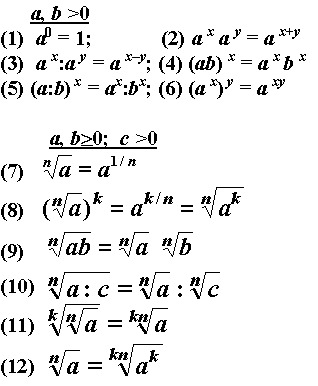
Выясни, как получается ответ, и проверь все ли так ты сформулировал в определении. Повтори определение еще раз.
6. Внимательно читай начало определения 3, изучив схему-рисунок дополни определение необходимыми словами.
7. Посмотри на решение примеров. Выясни, как получается ответ, и проверь все ли так ты сформулировал в определении. Повтори определение еще раз.
8. Повтори все определения еще раз.
9.Обрати внимания на перечеркнутые свойства, сделай вывод, проверь на примерах. Возьми основание равное 2, а затем 3.
Numbers in Different Bases
Numbers in Different Bases- About
- Statistics
- Number Theory
- Java
- Data Structures
- Cornerstones
- Calculus
Changing to base 10 from another база
Когда мы пишем обычное число (с основанием 10), например 5763, мы имеем в виду значение:
$5000 + 700 + 60 + 3$$или, выражаясь в более откровенной форме: 90$$
Обратите внимание, «цифры» нашего числа соответствуют коэффициентам при степенях десяти, которые складываются вместе, чтобы получить значение нашего числа.
Аналогичным образом мы можем указать числа в других «основаниях» (помимо 10), используя разные цифры, соответствующие коэффициентам при степенях (данного основания), которые нужно сложить, чтобы получить значение нашего числа.
Например, число «основание 8» (или « восьмеричное число «) (как указано в нижнем индексе) 90$$
Чтобы каждое число имело представление по основанию b, но ни одно число не имеет более одного такого представления, мы должны использовать только цифры от 0 до (b-1) в любом данном числе по основанию b.
Это согласуется с числами с основанием 10, где мы используем цифры 0-9.
Для меньших баз мы используем подмножество этих цифр. Например, в базе 5 мы используем только цифры 0-4; в базе 2 (которую также называют двоичной ) мы используем только цифры 0 и 1.
Для больших оснований нам нужно иметь однозначные числа для значений после 9.0 = 23288$$
( Примечание. Как показано выше, нижний индекс, указывающий на используемую базу, часто опускается в случае шестнадцатеричных и/или двоичных чисел.
В этих случаях контекст их использования обычно делает основу ясной. )
Переход с базы 10 на другую базу
Один (прямой, но неэффективный) способ преобразования базы 10 в другую:
- Определите наибольшую степень основания, которое входит в число ненулевое число раз.
- Определите, сколько раз эту степень можно вычесть из числа, чтобы результат не был отрицательным (т. е. разделить число на степень). Запишите эту цифру.
- Переопределите число, чтобы оно было наименьшим положительным остатком от деления на рассматриваемую степень
- Переопределите мощность как мощность, деленную на основание.
- Вернитесь к шагу 2, если сила теперь не меньше единицы — в этом случае все готово.
Например, чтобы преобразовать 1073 в основание 5, мы вспоминаем, что:
5 0 = 1 5 1 = 5 5 2 = 25 5 3 = 125 5 4 = 625 5 5 = 3125
Затем мы замечаем, что 5 4 = 625 — это наивысшая степень числа 5 меньше 1073.
1073 = 1 * 625 + 448 448 = 3 * 125 + 73 73 = 2 * 25 + 23 23 = 4* 5 + 3 3 = 3 * 1 + 0
Красные цифры 13243 показывают представление числа 1073 по основанию 5.
Этот процесс, однако, неэффективен, поскольку необходимо знать и использовать различные способности желаемого основания.
Есть более простой способ!
Рассмотрим остатки при делении следующих чисел на 5:
1073 = 214 * 5 + 3 214 = 42 * 5 + 4 42 = 8 * 5 + 2 8 = 1 * 5 + 3 1 = 0 * 5 + 1
Примечание: представление по основанию 5 происходит от считывания остатков (выделено красным) снизу вверх! На каждом шаге выше мы просто делим на 5 и смотрим как на частное, так и на остаток — никаких знаний о высших степенях числа 5 не требуется!
Удивительно, но эта техника работает на любой базе. ( Можете ли вы объяснить почему? )
Так, например, если мы хотим найти двоичное (с основанием 2) представление числа 1000, мы просто вычисляем следующее:
1000 = 500 * 2 + 0 500 = 250 * 2 + 0 250 = 125 * 2 + 0 125 = 62 * 2 + 1 62 = 31 * 2 + 0 31 = 15 * 2 + 1 15 = 7 * 2 + 1 7 = 3 * 2 + 1 3 = 1 * 2 + 1 1 = 0 * 2 + 1
Таким образом, 1000 в двоичном формате равно 1111101000 .
Подсчет в другой базе
Счет по другим основаниям не слишком отличается от счета по основанию 10. Чтобы увидеть сходство, давайте посчитаем до 41 по основанию 10 и 3 (как показано в таблице ниже).
Обратите особое внимание на то, что «2» в системе счисления 3 играет ту же роль, что и «9» в базе 10. Она представляет собой последнюю цифру, которую вы можете использовать перед увеличением цифры слева.
| База 10 | База 3 | База 3 | ||
|---|---|---|---|---|
| 0 | 0 | 21 | 210 | |
| 1 | 1 | 22 | 211 | |
| 2 | 2 | 23 | 212 | |
| 3 | 10 | 24 | 220 | |
| 4 | 11 | 25 | 221 | |
| 5 | 12 | 26 | 222 | |
| 6 | 20 | 27 | 1000 | |
| 7 | 21 | 28 | 1001 | |
| 8 | 22 | 29 | 1002 | |
| 9 | 100 | 30 | 1010 | |
| 10 | 101 | 31 | 1011 | |
| 11 | 102 | 32 | 1012 | |
| 12 | 110 | 33 | 1020 | |
| 13 | 111 | 34 | 1021 | |
| 14 | 112 | 35 | 1022 | |
| 15 | 120 | 36 | 1100 | |
| 16 | 121 | 37 | 1101 | |
| 17 | 122 | 38 | 1102 | |
| 18 | 200 | 39 | 1110 | |
| 19 | 201 | 40 | 1111 | |
| 20 | 202 | 41 | 1112 |
Добавление в другую базу
Вы можете добавить другое основание (без преобразования в основание 10), если вы помните, что вы «переносите», когда у вас есть сумма, которая больше или равна вашей базе (вместо больше или равна 10), и что то, что вы «несете», — это количество раз, которое вы можете вытащить из своей суммы.
Лучше всего это иллюстрируется примером. Предположим, вы хотите добавить шестнадцатеричные числа 4EF5A и 6ACF7:
1111 <---- Это "несущие" цифры 4EF5A +6ACF7 ------ B9C51
Давайте рассмотрим пример. Заметить, что
А + 7 = 11 (шестнадцатеричные вычисления) 10 + 7 = 17 = 1 * 16 + 1 (десятичные вычисления)
Итак, мы записываем 1 в столбце «единицы» и переносим 1. Затем
1 + 5 + F = 15 (шестнадцатеричные вычисления) 1 + 5 + 15 = 21 = 1 * 16 + 5 (десятичные вычисления)
Итак, мы записываем 5 в колонке «десятки/шестнадцать» и переносим 1. Затем
1 + F + C = 1C (шестнадцатеричные вычисления) 1 + 15 + 12 = 28 = 1 * 16 + 12 (десятичные вычисления)
Итак, мы записываем C в следующем столбце и переносим 1. Затем
1 + E + A = 19 (шестнадцатеричные вычисления) 1 + 14 + 10 = 25 = 1 * 16 + 9 (десятичные вычисления)
Итак, мы записываем 9 в следующем столбце и переносим 1.
Затем
1 + 4 + 6 = B (шестнадцатеричные вычисления) 1 + 4 + 6 = 11 (десятичные вычисления)
Итак, мы пишем букву B в следующем столбце, и все готово.
Ярлык для переключения между основанием 2 и основанием 16
Рассмотрим следующее преобразование из двоичного в шестнадцатеричное:
100100010101111 (двоичный) = 0100 1000 1010 1111
4 8 10 15
= 4 8 А F
Следовательно, 10010001010111 (двоичный) = 48AF (шестнадцатеричный)
Удивительно, но всегда можно разбить двоичное число на группы из 4 цифр (начиная справа и добавив начальные нули, если цифры заканчиваются), а затем интерпретировать эти группы из 4 цифр как шестнадцатеричные значения и получить шестнадцатеричное представление для исходное двоичное число. (
Обратный процесс так же прост.
Предположим, мы хотим преобразовать FC7 (hex) в двоичную форму.
Обратите внимание, что
F (шестнадцатеричный) = 15 = 1111 (двоичный) C (шестнадцатеричный) = 12 = 1100 (двоичный) 7 (шестнадцатеричный) = 7 = 0111 (двоичный) Следовательно, FC7 (шестнадцатеричный) = 111111000111 (двоичный)
Математический обзор умножения показателей
Математический обзор умножения показателей https://schooltutoring.com/help/wp-content/themes/movedo/images/empty/thumbnail.jpg 150 150 Дебора Дебора https://secure.gravatar.com/avatar/63fb4ad5c163b8f83de2f54371b9e040?s=96&d=mm&r=g
Обзор
Показатель степени используется как тип сокращения, определяющий, сколько раз базовое число умножается само на себя. Экспоненциальные выражения полезны при работе с очень большими или очень маленькими числами, как в экспоненциальном представлении.
Как и другие числа и переменные, экспоненциальные выражения можно умножать по определенным правилам.
Обзор упрощенных выражений
Если в выражении есть отрицательные показатели, оно не упрощается. Выражение x -3 можно определить как 1/x 3 . Точно так же, если одна и та же основа используется в выражении более одного раза, оно не упрощается. Предположим, что выражение равно x 2 x. На самом деле это означает x·x·x или x 3 . Кроме того, степени, возведенные в степени, не упрощаются, например [x 5 ] 2 . Если какие-либо коэффициенты имеют общие факторы, эти общие факторы должны быть упрощены. Например, (15а 2 )/ (10b 3 ) можно упростить до (3a 2 )/ (2b 3 ), поскольку 15 и 10 имеют общий делитель 5. показатель степени означает, сколько раз основание умножается само на себя, правило умножения показателей степени можно обнаружить, показывая каждую степень как повторное умножение.
Если выражение равно y 3 y 2 , его можно расширить как y·y·y·y·y или y 5 . Произведение степеней можно найти, сложив показатели степени, так как 3 + 2 = 5. Однако для сложения показателей степени основания должны быть одинаковыми. На языке алгебры для любого действительного числа a, не равного нулю, a m ·a n = a m+n .
Полномочия
Выражения, такие как [x 5 ] 2 фактически означает x 5 ·x 5 (x····x 5 , or x·x·x·x), используя значение показателей степени как многократное умножение. Произведение степеней степеней можно найти путем умножения показателей, так как 5 · 2 равно 10. На языке алгебры для любого действительного числа a, не равного нулю, (a m ) н = а мн . Способ узнать, следует ли складывать или умножать показатели степени, состоит в том, чтобы расширить выражение до многократного умножения.