Умножение и деление обыкновенных дробей – пример (5 класс, математика)
4.6
Средняя оценка: 4.6
Всего получено оценок: 66.
4.6
Средняя оценка: 4.6
Всего получено оценок: 66.
Умножение и деление обыкновенных дробей – это основа навыка умножения и деления любых дробей вообще. Ошибки при выполнении примеров на данную тему в математике 5 класса недопустимы, поскольку приводят к огромным ошибкам в более сложных вычислениях.
Виды дробей
Дробь это некоторое выражение, которое отражает, на сколько частей поделили целое и сколько получившихся частей взяли для расчета
Выделяют следующие виды дробей:
- Десятичные, у которых в знаменателе стоит число 10 и степени числа 10
- Обыкновенные, у которых числитель меньше знаменателя
- Неправильные, у которых числитель больше знаменателя
- Смешанные, то есть дроби, у которых выделили целую часть в отдельное число.
Кроме того, существует другое определение, согласно которому, дробь это незавершенная операция деления. В целях сокращения точности расчетов люди не производят операцию деления до конца. Вместо результата просто записывают дробь и считают дальше.
Умножение дробей
Умножение дробей осуществляется по принципу «каждый на каждый». Это значит, что числитель умножается на числитель, а знаменатель на знаменатель. Так можно умножить любое количество дробей, просто заменив пример одной дробью с произведениями в числителе и знаменателе.
Приведем пример:
$${3\over{4}}*{5\over{6}}*{7\over{12}}={{3*5*7}\over{4*6*12}}$$
В процессе умножения нужно обращать внимание на числа, которые можно сократить, чтобы уменьшить затраты времени на умножение.
Рассмотрим пример сокращения в процессе умножения на уже приведенном примере:
${3\over{4}}*{5\over{6}}*{7\over{12}}={{3*5*7}\over{4*6*12}}={{5*7}\over{4*6*4}}$ – мы сократили число 3 в числителе и число 12 в знаменателе на число 3, убрав один множитель из числителя и упростив выражение в знаменателе.
${{5*7}\over{4*6*4}}={35\over{64}}$ – помимо облегчения вычислений, сокращение избавляет нас от работы по упрощению конечной дроби. Можно сразу быть уверенным в том, что результат сократить невозможно.
Почему умножение производится именно так? Вспомним о том, что дробь это незавершенное деление. Тогда умножение дробей можно представить как умножение двух примеров на деление. Выглядеть это будет так:
(а:в)*(х:у) – правила деления при этом допускают перемножить делимые и делители, а потом выполнить деление с результатами. То есть:
(а:в)*(х:у)=(а*х):(в*у) – по этому принципу и выполняется умножение дробей.
Деление дробей
Деление дробей осуществляется с помощью приема переворота. Дробь-делитель переворачивается, то есть числитель становится знаменателем, а знаменатель числителем. После этого дробь-делимое умножается на перевернутое делимое согласно правилу «каждый на каждый».
Перечисленными способами делят только правильные дроби.
Неправильные, смешанные и десятичные дроби требуют некоторых преобразований для выполнения операций деления и умножения.
Что мы узнали?
Мы поговорили о видах дробей. Отдельно записали, как выполняется деление и умножение обыкновенных дробей. Привели небольшой пример умножения и деления обыкновенных дробей.
Тест по теме
Доска почёта
Чтобы попасть сюда — пройдите тест.
Пока никого нет. Будьте первым!
Оценка статьи
4.6
Средняя оценка: 4.6
Всего получено оценок: 66.
А какая ваша оценка?
Деление дробей с разными знаменателями 6. Умножение и деление дробей
Умножение десятичных дробей
Десятичная форма записи позволяет выполнять умножение дробей практически по тем же правилам, по которым умножают натуральные числа. Отличие заключается в том, что необходимо определять место запятой в полученном произведении.
Поясним сказанное на примере; вычислим произведение 2,5 1,02.
Перенесем запятую в первом множителе на одну цифру вправо, а во втором-на две цифры вправо. Тем самым первый множитель увеличится в 10 раз, второй-в 10 2 = 100 раз, а произведение-в 10 100 = 1000 раз.
Определим произведение натуральных чисел 25 и 102:
25 102 = 2550.
Это число в 1000 раз больше, чем требуемое произведение. Поэтому необходимо число 2550 уменьшить в 1000= 10 3 раз, т. е. перенести в этом числе запятую влево на 3 цифры. Таким образом,
2,5 1,02 = 2,550 = 2,55.
Можно рассуждать по-другому:
Таким образом, чтобы перемножить две десятичные дроби9 достаточно, не обращая внимания на запятые, перемножить их как натуральные числа9 а затем в полученном произведении справа отделить запятой столько цифр, сколько их было после запятых в обоих множителях вместе.
Например,
Деление десятичных дробей
Рассмотрим пример деления десятичной дроби на натуральное число.
Пример . Вычислить 46,8: 2.
Решение . 4 десятка делим на 2-получаем цифру частного 2 (2 десятка).
6 единиц делим на 2 — получаем цифру частного 3 (3 единицы).
Деление целой части закончено-отделяем в частном целую часть запятой.
8 десятых делим на 2 — получаем цифру частного 4 (4 десятых). Остаток равен 0-деление закончено.
Деление десятичной дроби на десятичную дробь сводится к делению на натуральное число переносом запятых в делимом и делителе на столько цифр вправо, чтобы делитель стал натуральным числом.
Пример . Вычислить 4,42:0,2.
Решение . Так как в делителе одна цифра после запятой, то достаточно перенести запятые в делимом и делителе на 1 цифру вправо. Тем самым делимое и делитель увеличиваются в 10 раз, поэтому частное не изменится. При этом делитель будет натуральным числом.
Можно рассуждать и таким образом:
Но не всегда получается точный результат при делении десятичных дробей. Чаще приходится довольствоваться приближенным частным.
Пример . Найти частное 1,723:0,03.
Решение . Освободимся от запятой в делителе: 1,723:0,03= 172,3:3. Выполним деление.
Начиная с разряда сотых, цифра 3 в частном повторяется без конца, потому что остаток, начиная с третьего этапа процесса деления, все время равен одному и тому же числу 1.
Если оставить у частного первые две цифры после запятой, то получится приближенное равенство: 172,3:3 ≈ 57,43.
§ 15. Умножение и деление обыкновенных дробей — Учебник по Математикe 6 класс (Зубарева, Мордкович)
Краткое описание:
В этом параграфе учебника вас ждет более сложные операции с умножением и делением, так как следует научится не только умножению и делению целых чисел, но также и дробей. Есть множество особенностей выполнения этих действий, но если понять принцип, вы сможете решать любые выражения!
Умножение дробей кажется очень сложным при первом взгляде на эти числа. Но для того, чтобы решать такие выражения, нужно просто по порядку проделать определенные действия.
Например, для умножения дробей на натуральное число, числитель умножается на множитель, а знаменатель остается таким же. После умножения эту дробь можно сократить, выявив в ней общее для числителя и знаменателя число и вынеся его как целое число. Так например, 2/3 4 = 2 4/3 = 8/3 = 2 2/3. При умножении смешанной дроби (с целым и дробью) на число, целое число и числитель умножаются между собой, а знаменатель по прежнему остается таким же. Если же нужно умножить между собой простые дроби, нужно перемножить между собой числители и записать значение в числитель и знаменатели перемножить между собой, записав значение в знаменатель. Если вам нужно умножить смешанные дроби между собой, в таком случае нужно перевести множители в неправильные дроби и определить значение выражение как в рассмотренном примере. Для деления дробей существуют другие правила, но они достаточно простые, если внимательно их изучить. При делении дроби на целое число, целое число записывают в знаменатель, но уже с действием умножения.
Технологическая карта урока.
ФИО учителя: Степанова Дарья Сергеевна
Место работы: МАОУ «СОШ №76»
Должность: учитель математики
Предмет: математика
Тема урока: «Деление обыкновенных дробей».
Тип урока : урок открытия нового знания .
ЦЕЛЬ УРОКА:
Образовательные: сформировать представление о делении обыкновенных дробей, выработать первичное умение выполнять деление чисел, записанных в виде дробей.
Развивающие: развитие математического мышления учащихся и вычислительных навыков.
Воспитательные: содействовать воспитанию интереса к математике, воспитывать культуру математических записей.
Оборудование : Учебник для 6 класса общеобразовательных учреждений/ Н. Я. Виленкин, В. И. Жохов, А. С. Чесноков, С. И. Шварцбурд.- издание.- М.: Мнемозина, 2007, мультимедийный проектор, презентация к уроку по данной теме., раздаточный материал.
План:
Организационный момент (1 мин.).
Целеполагание и мотивация (7 мин.).
Открытия нового знания (13 мин.).
Физкультминутка (1мин.).
Закрепление нового (15 мин.).
Подведение итогов. Рефлексия (3 мин.).
Домашнее задание (1 мин).
–Здравствуйте! Давайте проверим все ли у нас готово к уроку?
Проверяют. Достают тетради и ручки, если не достали.
–Вспомним, с каким новым понятием мы познакомились на предыдущих уроках?
–Какие числа называют взаимно обратными?
–Хорошо! Молодцы! А теперь давайте устно решим примеры на слайде.
–Из 1 вычесть мы получим?
– Что мы должны сделать, чтобы решить второй пример?
–Чему он равен?
– Тогда дополнительный множитель, для первой дроби равен?
–Молдец! Чему равен НОЗ в третьем примере?
– Как вычислим следующий пример? Как мы умножаем дробь на дробь?
–Что можно сделатьперед тем как перемножать?
–Верно, Молодец! Как умножить натуральное число на дробь?
– Что будем делать, перед тем как перемножать?
–Молодец! Как решить следующий пример?
–Верно, что получим?
Хорошо! Следующий пример.
–Молодец! Что нужно сделать, чтоб перемножить следющие два числа?
–Как будем решать следующий приер?
–С понятием взаимно обратных чисел
– Числа называют взаимно обратным, если в произведении они дают единицу.
(один ученик вслух разбирает один пример).
–Найти наименьший общий знаменатель.
–14, так как 14 делиться на 7 нацело.
–Двум. Домножим дробь на два, получим . Прибавим к дробь , получим ответ .
–Так как 7 и 5 взаимно простые числа, наименьший общий знаменатель равен 35.
Для первой дроби дополнительный множитель равен 5, для второй дроби 7. Домножим первую дробь на 5, получим , вторую дробь на 7, получим . Разность равна .
–Чтобы умножить дробь на дробь, нужно перемножить числители дробей и записать это произведение в числитель, перемножить знаменатели и записать произведение в знаменатель.
–Можно сократить 4 и 8 на 4, и 3 и 9 на 3, получим одну шестую
– Чтобы умножить натуральное число на обыкновенную дробь, нужно числитель умножить на это число, а знаменатель оставить без изменения.
–Сократим 23 и 23. Ответ 9.
– Сначала надо записать смешанное число в неправильную дробь, а потом перемножить.
–Получим дробь , перемножим ее с . Можем сократить 7 и 7. Ответ .
–Сократить ничего нельзя. Перемножаем 4 и 5,в числител запишем 20, в знаменателе 7 или .
– Нужно представить смешанные числа в виде неправильной дроби. Получим и .
Можем сократить 5 и 15 на 3 и 22 и 2 на 2. В числителе получим 11 взнаменателе 3 или .
– Мы не знаем как делить.
–Как вы думаете, какая тема нашего урока на сегодня?
–Врно! Откройте тетради запишите число и тему урока.
–Какую цель мы поставим на сегоднящний урок?
–А для того, чтобы научиться делить, что нам сначала надо узнать?
–Верно! Для этого, вначале, рассмотрим задачу. Площадь прямоугольника равна
. Длина одной стороны
. Найти длину другой стороны.
– Назовите формулу площади прямугольника.
– Ширина и площадь нам известны, а длина – нет. Как мы обозначаеим неизвестную величину?
– Можем мы с вами теперь составить уравнение?
–Мы с вами уже решали такие уравнения с помощью взаимно обратных чисел. Давайте решим его.
– Что получим в правой части уравнения?
–Что получим в левой части уравнения?
– Хорошо. Нашли чему равна длинна. Давайте вернемся к уравнению, и вспомним, как наити нейзвестный множитель?
–Верно! Примените это к нашему уравнению, что получим?
–Но мы уже знаем чему равен x .
– И как мы его нашли?
– А по отношению к какая дробь?
– То есть мы можем составить такое равенство:
.
– Исходя из этого равенства попробуйте сформулировать правило деления обыкновенных дробей.В этом вам поможет карточка №1, заполните пропуски в ней.
–Верно, молодцы! Запишите в тетрадь данное определение в буквенном виде, самостоятельно. Проверьте.
–Можем ли мы теперь решить тот пример, который в начале вызвал у нас затруднение(возрашаемся к примеру)?
– Деление обыкновенных дробей.
(Открывают тетради, записывают тему урока).
–Научиться выполнять деление дробей.
–Правило деления дробей.
– S = ab .
– x .
–Да.
.
– Нужно домножить обе части уравнение на обратное число, числу . То есть на .
–В правой части произведение двух взаимно обратных чисел дадут нам единицу.
–В левой части, произведение и . Сократить ничего нельзя, значит получим .
.
Чтобы найти неизвестный множитель, нужно произведение разделить на известный множитель.
–
.
–
. Мы умножили на .
–Обратная.
–Чтобы разделить одну дробь на другую, нужно делимое умножить на число обратную делителю.
– Да,
.
–А теперь разомнемся немного. Сожмите разожмите кулочки. Расправте плечики. Делайте движения головой, следуя за снежинкой.
–Верно! Учиться применять правило на практике.
(На слайде примеры. Вызываем учеников по одному к доске, остальные работают в тетрадях.)
–Молодцы! У вас на партах есть карточка №2. Выполните ее самостоятельно. Задание: Вставьте пропуски в примерах, чтобы получились верные равенства.
–Проверьте себя сами! Если все пропуски заполнены верно или одна ошибка – оценка «5», если 2-4 ошибки – оценка «4», если 5-7 ошибок –оценка «3».
–Решать примеры.
(выполняют карточки с заданиями №2)
(проверяют, оценивают себя)
–Давайте подведем итоги! Как вы считаете, добились ли мы поставленной в начале урока цели?
–Давайте повторим правило, которое мы сегодня узнали.
(спрашиваем нескольких учеников).
–Хорошо! Молодцы! У вас на столах лежат разного цвета карточки, оцените с помощью их результат вашей работы сегодня на уроке.
– Чтобы разделить одну дробь на другую, нужно делимое умножить на число обратную делителю.
(поднимают карточки).
–Откройте дневники и запишите домашнее задание.
–Спасибо за урок!
(Записывают домашнее задание в дневники).
Раздаточный материал.
Каточка №1
Правило деления обыкновенных дробей.
Чтобы разделить одну дробь на другую, надо делимое ___________ на число, ____________ делител ю.
Карточка №2
Fractions Обзор: Умножение и деление дробей
Сокращение дробейСмешанные и неправильные дробиСложение и вычитаниеполиномиальных дробей
Purplemath
Умножать дроби легко: вы умножаете верхние числа и умножаете нижние числа. Например:
Когда это возможно, вы уменьшаете дробь, сокращая общие множители; то есть вы вычеркиваете любые факторы с одной стороны линии дроби, которые дублируются с другой стороны линии.
Однако в приведенном выше примере ничего не уменьшается, потому что 8 и 45 не имеют общих множителей.
Содержание продолжается ниже
MathHelp.com
Умножение дробей
Если вы не уверены, можно ли что-либо сократить, вы всегда можете разложить числитель и знаменатель на множители и проверить наличие повторяющихся множителей:
3Ничто не дублируется между верхом и низом, поэтому ничто не отменяется.
Однако часто что-то отменяется:
Чтобы выполнить умножение, я умножаю все верхние числа (числители) друг на друга и умножаю все нижние числа (знаменатели) друг на друга. Однако, чтобы немного облегчить себе жизнь, я сначала отменю все множители, общие как для числителей, так и для знаменателей:
Тогда упрощенный продукт равен
7 / 2 .
Вы можете использовать виджет Mathway ниже, чтобы попрактиковаться в умножении дробей.
Попробуйте введенное упражнение, введите собственное упражнение. Затем нажмите кнопку, чтобы сравнить свой ответ с ответом Mathway. (Или пропустите виджет и продолжите урок).
(Нажав «Нажмите, чтобы просмотреть шаги» на экране ответов виджета, вы перейдете на сайт Mathway для платного обновления.)
Делить дроби так же просто, как и умножать их; есть только один дополнительный шаг. Когда вы делите на дробь, первое, что вы делаете, это «переворачиваете-умножаете». То есть вы берете вторую дробь, переворачиваете ее вверх ногами (то есть «находите обратную»), а затем умножаете первую дробь на эту перевернутую дробь.
Мой первый шаг будет заключаться в том, чтобы преобразовать это в умножение, перевернув 9 / 4 , чтобы получить 4 / 9 . Затем я могу приступить к простому умножению, отменив дублирующиеся множители:
Тогда мой упрощенный ответ будет
4 / 15 .
Это немного сложно, но я могу справиться с целым числом 5, преобразовав его в дробь. Помните, что любое целое число является дробью, если поставить его над «1». Итак, я конвертирую 5 в дробь 5 / 1 и переворачиваю-умножаю:
Тогда мой упрощенный ответ:
1 / 6 .
Упростить
Для этого упражнения мне сначала нужно преобразовать смешанные числа в (неправильную) дробную форму. (Умножение и деление дробей — это те места, где дроби оооочень намного приятнее, чем смешанные числа!) Когда у меня есть дроби, я могу их перевернуть и умножить.
Тогда мой смешанный ответ будет
1 37 / 68 .
Примечание. Если в качестве входных данных используются смешанные числа, как в последнем примере выше, книга (или преподаватель, или оценщик) обычно также ожидает в качестве выходных данных смешанные числа.
Итак, если ваш ответ представляет собой неправильную дробь, вам нужно будет преобразовать ее обратно в форму смешанного числа. Не забудьте этот шаг!
Вы можете использовать виджет Mathway ниже, чтобы попрактиковаться в делении дробей. Попробуйте введенное упражнение или введите свое собственное упражнение. Затем нажмите кнопку, чтобы сравнить свой ответ с ответом Mathway. (Или пропустите виджет и продолжите урок.)
Пожалуйста, примите куки-файлы настроек, чтобы включить этот виджет.
(Нажав «Нажмите, чтобы просмотреть шаги» на экране ответов виджета, вы перейдете на сайт Mathway для платного обновления.)
Далее мы переходим к гораздо более сложному сложению и вычитанию дроби…
URL: https://www.purplemath.com/modules/fraction3.htm
Страница 1 Страница 2 Страница 4 Страница 5
Как умножать и делить дроби (видео)
TranscriptFAQsPracticeWorksheets
Многие студенты по-настоящему боятся дробей.
Однако, если вы помните, что представляет собой дробь 90 139 90 140, и несколько математических правил алгебраической работы с ними, вы сможете уверенно сталкиваться с дробями. В этом видео мы рассмотрим как умножать и делить дроби. Давайте начнем.
Начнем с точного определения дроби. Дробь представляет отношение «части» к «целому» или части к целому. Значение выше линии деления называется числителем , а значение ниже линии деления называется знаменателем .
Умножение дробей
Чтобы умножить дроби, просто умножьте «прямо», что означает «числитель, умноженный на числитель», деленный на «знаменатель, умноженный на знаменатель». Давайте рассмотрим несколько простых примеров:
\(\frac{2}{3} \times \frac{2}{5}\)
Здесь мы хотим умножить \(\frac{2}{3}\) на \(\frac{2}{5}\). Как мы сказали ранее, мы собираемся умножать прямо. Итак, у нас будет 2 умножить на 2 на 3 на 5. Что равно четырем на пятнадцать.
Итак, наш ответ: \(\frac{4}{15}\).
\(\frac{2}{3} \times \frac{2}{5}= \frac{2 \times 2}{3 \times 5}= \frac{4}{15}\)
Теперь попробуем еще один. Мы попробуем \(\frac{4}{7}\) раз \(\frac{3}{11}\).
\(\frac{4}{7} \times \frac{3}{11}\)
Опять та же концепция. Мы собираемся умножить 4 на 3, разделить на 7 на 11. Что дает нам \(\frac{12}{77}\).
\(\frac{4}{7} \times \frac{3}{11}= \frac{4 \times 3}{7 \times 11}= \frac{12}{77}\)
Довольно просто, правда? Теперь займемся делением дробей.
Деление дробей
Деление дробей включает несколько иной процесс. Прежде чем мы перейдем к механике процесса, давайте начнем с интуитивного примера деления дроби на два. Эффект деления на 2 заключается в простом сокращении дроби пополам или простом умножении дроби на 1 на 2.
Итак, \(\frac{4}{5}\) разделить на 2 на самом деле то же самое, что и \(\frac{4}{5}\) умножить на \(\frac{1}{2}\) .
\(\frac{4}{5}\)\( \div \text{ } 2 \text{ }\)\( = \frac{4}{5} \times \frac{1}{2 }\)
Затем оно будет умножено, как мы делали это раньше. Итак, у нас 4 раза 1 равно четырем, более 5 раз 2 равно 10. Что затем упрощается до \(\frac{2}{5}\).
\(\frac{4}{5}\)\( \div \text{ } 2 \text{ }\)\( = \frac{4}{5} \times \frac{1}{2 }= \frac{4}{10}= \frac{2}{5}\)
Другими словами, \(\frac{2}{5}\) вдвое меньше \(\frac{4}{5}\).
Аналогично, деление дроби на 3 приведет к дроби, равной одной трети размера оригинала:
\(\frac{2}{5}\)\( \div \text{ } 3 \ text{ }\)\( = \frac{2}{5} \times \frac{1}{3}= \frac{2}{15}\)
\(\frac{2}{5 }\) разделить на 3 — это то же самое, что сказать \(\frac{2}{5}\) умножить на \(\frac{1}{3}\), что даст вам \(\frac{2}{15} \).
Таким образом, \(\frac{2}{15}\) составляет одну треть размера \(\frac{2}{5}\).
Прежде чем мы обобщим этот процесс, давайте рассмотрим некоторые важные термины.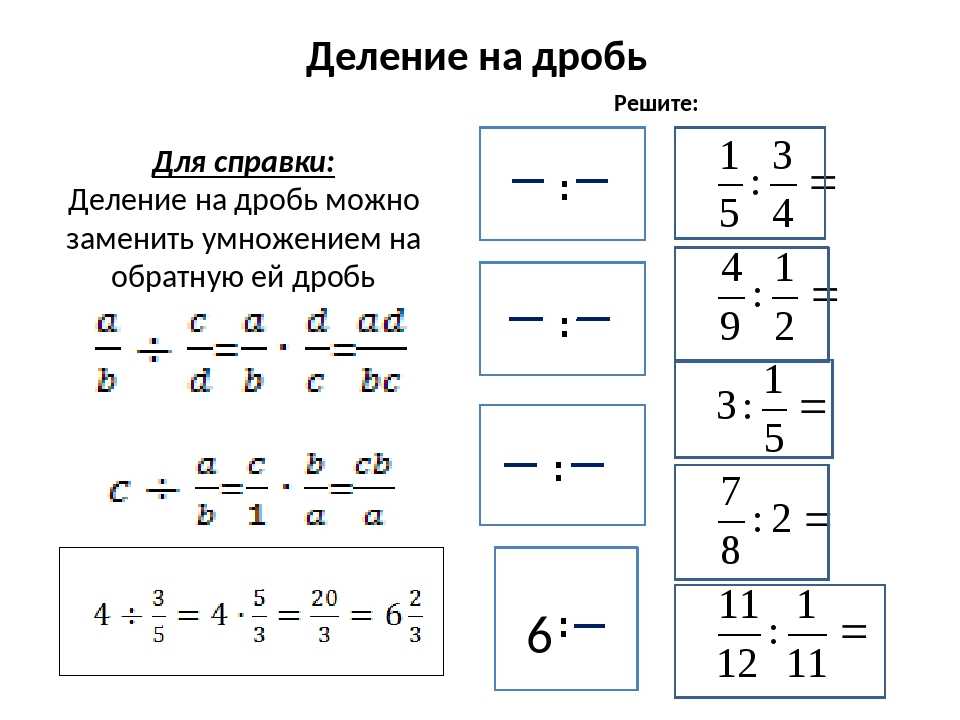
Рассмотрим связь между 2 и \(\frac{1}{2}\). Эти числа называются обратными друг другу, что означает, что числитель одного числа является знаменателем другого, и наоборот. Помните, что 2 можно записать в виде дроби, написав ее над 1, например: \(\frac{2}{1}\). Следовательно, \(\frac{2}{1}\) и \(\frac{1}{2}\) обратны. То же самое верно для 3 и \(\frac{1}{3}\), потому что 3 можно записать как \(\frac{3}{1}\). Следовательно, 3 и \(\frac{1}{3}\) обратны.
Имея это в виду, какую закономерность вы видите в процессе деления дробей?
Сохранить, изменить, перевернуть
Процесс деления дробей аналогичен умножению первой дроби на обратную вторую. Сокращенная версия этого многословного объяснения, которое может помочь вам запомнить процесс деления, звучит так: «Сохранить, изменить, перевернуть»:
Оставить первую дробь как есть
Изменить операцию деления на умножение;
Переверните (или возьмите обратное значение) вторую дробь.
После внесения этой корректировки просто следуйте правилам умножения дробей путем умножения числителей и деления на произведение знаменателей.
Вот пример использования процесса «Сохранить, изменить, перевернуть»:
Допустим, мы хотим разделить \(\frac{3}{5}\) на \(\frac{7}{5}\). Мы оставим первую дробь как есть, изменим операцию деления на умножение и перевернем второе число. Теперь мы просто умножаем наши числители, 3 умножить на 5 — это пятнадцать, более 5 умножить на 7 — это 35. А затем отсюда мы упрощаем до \(\frac{3}{7}\).
\(\frac{3}{5} \div \frac{7}{5}= \frac{3}{5} \times \frac{5}{7}= \frac{15}{35 }= \frac{3}{7}\)
Надеюсь, это видео было полезным! Спасибо за просмотр и удачной учебы!
Перемножение дробей | Неправильные дроби и смешанные числа
Часто задаваемые вопросы
Q
Как умножать дроби на целые числа?
A
Умножьте дроби на целые числа, превратив целое число в дробь, поместив ее над 1.
Любое число, разделенное само на себя, является самим собой, поэтому это не меняет значения целого числа. Затем умножьте как обычные дроби.
пр. \(\frac{2}{3}×4=\frac{2}{3}×\frac{4}{1}=\frac{8}{3}=2 \frac{2}{3}\ )
Q
Как умножать смешанные дроби?
A
Умножайте смешанные дроби, сначала превращая их в неправильные дроби, а затем умножая как обычно. Если в числителе и знаменателе есть общие множители, сначала сократите их, чтобы упростить умножение. Чтобы преобразовать дробь обратно в смешанное число, разделите числитель на знаменатель. Количество полных делений становится целым числом, а остаток становится числителем дробной части исходного знаменателя.
пр. \(3 \frac{1}{5}×2 \frac{7}{9}=\frac{16}{5}×\frac{25}{9}=\frac{16}{1}×\ frac{5}{9}=\frac{80}{9}=8 \frac{8}{9}\)
Пр. \(3 \frac{1}{5}×2 \frac{7}{9}=\frac{16}{5}×\frac{25}{9}=\frac{16}{5}×\ frac{5×5}{9}=\frac{16}{1}×\frac{5}{9}=\frac{80}{9}=8 \frac{8}{9}\)
Q
Как вы делите дроби?
A
Разделите дроби, используя фразу: «Сохранить, изменить, перевернуть».
Оставьте первую дробь такой же. Замените знак деления на знак умножения. Переверните вторую дробь. Затем умножьте и упростите, если необходимо.
пр. \(\frac{4}{7}÷\frac{8}{13}=\frac{4}{7}×\frac{13}{8}=\frac{52}{56}=\frac{ 13}{14}\)
Q
Как вы делите дроби с целыми числами?
A
Разделите дроби на целые числа, сначала превратив целое число в дробь, а затем разделив дроби как обычно, перевернув вторую дробь и умножив ее. Любое число можно превратить в дробь, поместив его над 1.
Упр. \(\frac{2}{3}÷4=\frac{2}{3}÷\frac{4}{1}=\frac{2}{3}×\frac{1}{4}=\ frac{2}{12}=\frac{1}{6}\)
Q
Как разделить смешанные дроби?
A
Разделите смешанные дроби, сначала преобразовав их в неправильные дроби, а затем разделив дроби как обычные.
пр. \(4 \frac{3}{5}÷2 \frac{1}{2}=\frac{23}{5}÷\frac{5}{2}=\frac{23}{5}×\ frac{2}{5}=\frac{46}{25}=1 \frac{21}{25}\)
Практические вопросы
Вопрос №1:
\(\frac{2} {3}\times\frac{7}{9}=\)
\(\frac{42}{9}\)
\(\frac{42}{47}\)
\(\frac{14}{27}\)
\(\frac{14}{9}\)
Показать ответ
Ответ:
Правильный ответ C: \(\frac{14}{27}\).
Чтобы умножить дроби, просто перемножьте числители, чтобы получить новый числитель, и перемножьте знаменатели, чтобы получить новый знаменатель.
\(\frac{2}{3}\times\frac{7}{9}=\frac{2\times7}{3\times9}=\frac{14}{27}\)
Скрыть ответ
Вопрос №2:
\(\frac{7}{6}\div\frac{2}{3}=\)
\(\frac{7}{4}\)
\(\frac{9}{) 9}\)
\(\frac{14}{18}\)
\(\frac{7}{2}\)
Показать ответ
Ответ:
Правильный ответ A: \(\ гидроразрыва{7}{4}\). Чтобы разделить дроби, используйте фразу: Keep, Change, Flip. Оставьте первую дробь такой же. Заменить знак деления на знак умножения. Переверните вторую дробь, чтобы она была обратной. Этот процесс выглядит так:
\(\frac{7}{6}\div\frac{2}{3}=\frac{7}{6}\times\frac{3}{2}\)
Затем умножьте и упростите дроби.
\(\frac{7}{6}\times\frac{3}{2}=\frac{7\times3}{6\times2}=\frac{21}{12}=\frac{7}{ 4}\)
Скрыть ответ
Вопрос №3:
\(\frac{1}{4}\times\frac{6}{7}\div\frac{2}{9}= \)
\(\frac{7}{108}\)
\(\frac{47}{52}\)
\(\frac{12}{252}\)
\(\frac {27}{28}\)
Показать ответ
Ответ:
Правильный ответ D: \(\frac{27}{28}\). Согласно Порядку операций (PEMDAS), умножение и деление могут происходить одновременно. Для этого примера давайте проработаем умножение и деление по порядку слева направо. Итак, мы начнем с умножения \(\frac{1}{4}\) и \(\frac{6}{7}\), при необходимости упрощая.
\(\frac{1}{4}\times\frac{6}{7}=\frac{1×6}{4×7}=\frac{6}{28}=\frac{3}{ 14}\)
Затем разделите \(\frac{3}{14}\) на \(\frac{2}{9}\).
\(\frac{3}{14}\div\frac{2}{9}=\frac{3}{14}\times\frac{9}{2}=\frac{27}{28}\ )
Следовательно, \(\frac{1}{4}\times\frac{6}{7}\div\frac{2}{9}=\frac{27}{28}\).
Скрыть ответ
Вопрос № 4:
Сара Энн печет печенье, и рецепт требует \(\frac{2}{3}\) чашек масла. Ей нужно много печенья, поэтому она решает увеличить рецепт в четыре раза. Быстро сообразив, что печенья много, она решает немного отступить и сделать рецепт только в \(3\frac{1}{2}\) раза больше оригинала. Для этого сколько чашек масла понадобится Саре-Энн?
\(2\frac{1}{3}\) чашки
\(\frac{4}{21}\) чашки
\(1\frac{2}{3}\) чашки
\ (\frac{1}{7}\) чашек
Показать ответ
Ответ:
Правильный ответ: A: \(2\frac{1}{3}\) чашек. Первое, что нужно сделать, чтобы решить эту проблему, это \(3\frac{1}{2}\) нужно преобразовать в неправильную дробь.
\(3\frac{1}{2}=\frac{3×2+1}{2}=\frac{7}{2}\)
Затем умножьте две дроби и упростите.
\(\frac{2}{3}\times\frac{7}{2}=\frac{14}{6}=\frac{7}{3}\)
Наконец, преобразуйте \(\frac {7}{3}\) в смешанное число.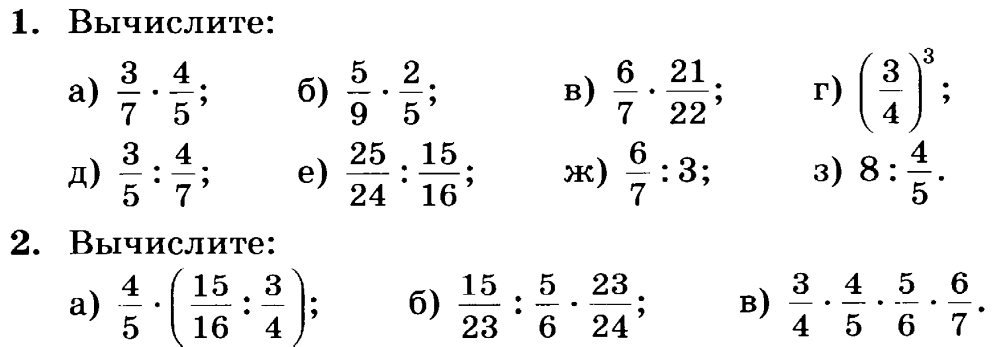
\(\frac{7}{3}=2\frac{1}{3}\)
Саре Энн нужно \(2\frac{1}{3}\) чашек масла.
Скрыть ответ
Вопрос №5:
У Антонио осталось \(\frac{6}{8}\) пиццы и два голодных друга. Если Антонио и его друзья поровну поделят пиццу, какая часть пиццы достанется каждому?
\(\frac{1}{3}\)
\(\frac{3}{4}\)
\(\frac{1}{4}\)
\(\frac{2}{3}\)
Показать ответ
Ответ :
Правильный ответ C: \(\frac{1}{4}\). Этот вопрос предлагает нам разделить \(\frac{6}{8}\) на 3. Помните, что любое целое число можно превратить в дробь, поместив его над 1. Вот как выглядит деление:
\(\ frac{6}{8}\div\frac{3}{1}=\frac{6}{8}\times\frac{1}{3}=\frac{6}{24}=\frac{1 }{4}\)
Каждый человек получает \(\frac{1}{4}\) пиццы.
Скрыть ответ
Рабочие листы
Используйте наши бесплатные печатные рабочие листы по умножению и делению дробей для дополнительной практики!
Умножение и разделение рабочих листов фракций
Умножение и разделение фракций (ключ ответа)
Умножение фракций
Фракции.