Свойства неопределенного интеграла
Вычислению интегралов от тех функций, которые не представлены в приведенной выше таблице интегралов, часто помогают приводимые ниже свойства интегралов.
1. Производная от интеграла равна подынтегральной функции:
.
2. Интеграл от производной равен самой функции (плюс, естественно, ) : .
3. Интеграл от суммы-разности равен сумме-разности интегралов:
4. Постоянный множитель можно выносить за знак интеграла:
Замечание 1.
Поскольку есть множество всех первообразных для
,
то в первом свойстве слева под знаком
производной стоит бесконечное множество
функций. Поэтому понимать это свойство
надо в том смысле, что производная от любой из указанных первообразных равна
.
Что сразу следует самого определения
первообразной. Остальные свойства легко
доказываются с помощью правила (*).
Докажем, например, по этому правилу
последнее свойство интегралов.
{постоянный множитель при вычислении производной можно выносить за знак производной}= {по первому свойству}= , что как раз является выражением под интегралом в левой части.
Замечание 2.
Сравним трудоемкость вычисления
интегралов и производных. Для вычисления
производных от различных функций тоже
(как и для интегралов) сначала была дана
таблица производных от основных
элементарных функций (степенных,
показательных, логарифмических,
тригонометрических и т.д.). Затем были
даны свойства производных, среди которых
присутствовало свойство вынесения
постоянного множителя за знак производной,
а также формулы для производных от
суммы-разности функций, произведения
и частного, производных от сложных
функций (т.е. функций от функций –
например, ).
Таким образом, пользуясь таблицей
производных и этими свойствами, можно
было вычислять производную от функций,
заданных сколь угодно сложными формулами,
в которых перечисленные элементарные
функции умножались бы на числа,
складывались, вычитались, умножались
и делились между собой, а также брались
бы функции от функций.
Есть
функции (даже достаточно простого вида),
интегралы от которых принципиально не могут быть выражены в виде «обычных»
формул (основных элементарных функций,
соединенных в формулу перечисленными
выше операциями ). Например, если выражается формулой просто (табличный
интеграл), то уже чуть усложненный «обычной» формулой не выражается (хотя 
Можно
считать, что для его выражения просто
не хватает запаса привычных формул и
их надо расширить, то есть выйти за рамки
множества функций, выражающихся через
основные элементарные функции с помощью
арифметических операций и функций от
функций. В науке и её приложениях в
технике, экономике и других дисциплинах
применяются такого типа функции, которые
называются специальными функциями.
К специальным функциям относятся и
многие «неберущиеся» интегралы от
элементарных функций. Вот некоторые
такие функции и их названия:а) − «почти» функция Лапласа б) − интегральный синус в) − интегральный косинус г) − интегральная экспонента д) − интегральный логарифм.
А теперь приведем примеры, в которых можно обойтись перечисленными свойствами интегралов и таблицей интегралов от основных элементарных функций.
Пример 1. Вычислить .
Решение.
= {свойство 3} = = = {свойство 4} = = {формулы 3, 2, 1 таблицы интегралов } = = .
Итак, = .
Пример 2. Вычислить .
Решение. = {свойство 3} = = {свойство 4} = = {формула 10 таблицы интегралов и формула 11 при } = . Итак, = .
Если при взятии интеграла использовались только приведенные выше свойства и приведенная выше простая таблица интегралов, то говорят, что интеграл вычислен методом непосредственного интегрирования.
Пример 3. Вычислить интеграл методом непосредственного интегрирования.
Решение. Сложность в том, что подынтегральная функция содержит операцию умножения, а формулы для интеграла от произведения функций нет! Но в этом случае легко избавиться от умножения, раскрыв скобки:
= {заменяем корни дробными степенями} = = {раскрываем скобки под знаком интеграла}= = {свойство 3 и 4 интегралов − интеграл от суммы равен сумме интегралов, а постоянные множители можно выносить за знак интеграла} = = = {формула 3 таблицы интегралов при и } = = .
Итак,
=
.
Пример 4. Вычислить .
Решение. Здесь под интегралом присутствует деление (на ), но формулы для интеграла от частного двух функций не существует. В этом примере тоже можно деление свести к сложению-вычитанию, деля каждое слагаемое в числителе на знаменатель:
={делим каждое слагаемое в числителе на знаменатель и заменяем корень дробной степенью}= = = = {интеграл от разности равен разности интегралов, числовые множители выносим за интегралы}= = {смотрим таблицу интегралов} = = .
Итак, = .
Интегрирование подстановкой (внесение под знак дифференциала). Первая часть.
Высшая математика » Неопределённые интегралы » Интегрирование подстановкой » Первая часть.
Первая часть
Вторая часть
Сначала немного поговорим о постановке задачи в общем виде, а затем перейдём к примерам интегрирования подстановкой. Допустим, в нас есть некий интеграл $\int g(x) \; dx$.
Однако в таблице интегралов нужной формулы нет, да и разбить заданный интеграл на несколько табличных не удаётся (т.е. непосредственное интегрирование отпадает). Однако задача будет решена, если нам удастся найти некую подстановку $u=\varphi(x)$, которая сведёт наш интеграл $\int g(x) \; dx$ к какому-либо табличному интегралу $\int f(u) \; du=F(u)+C$. После применения формулы $\int f(u) \; du=F(u)+C$ нам останется только вернуть обратно переменную $x$. Формально это можно записать так:
$$\int g(x) \; dx=|u=\varphi(x)|=\int f(u) \; du=F(u)+C=F(\varphi(x))+C.$$
Проблема в том, как выбрать такую подстановку $u$. Для этого понадобится знание, во-первых, таблицы производных и умение её применять для дифференцирования сложных функций, а во-вторых, таблицы неопределенных интегралов. Кроме того, нам будет крайне необходима формула, которую я запишу ниже. Если $y=f(x)$, то:$$ \begin{equation} dy=y’dx \end{equation} $$
Т.
е. дифференциал некоторой функции равен производной этой функции, умноженной на дифференциал независимой переменной. Это правило очень важно, и именно оно позволит применять метод подстановки. Здесь же укажем пару частных случаев, которые получаются из формулы (1). Пусть $y=x+C$, где $C$ – некая константа (число, попросту говоря). Тогда, подставляя в формулу (1) вместо $y$ выражение $x+C$, получим следующее:
Так как $(x+C)’=x’+C’=1+0=1$, то указанная выше формула станет такой:
$$ d(x+C)=(x+C)’ dx=1\cdot dx=dx.$$
Запишем полученный результат отдельно, т.е.
$$ \begin{equation} dx=d(x+C) \end{equation} $$
Полученная формула означает, что прибавление константы под дифференциалом не изменяет оный дифференциал, т.е. $dx=d(x+10)$, $dx=d(x-587)$ и так далее.
Рассмотрим еще один частный случай для формулы (1). Пусть $y=Cx$, где $C$, опять-таки, является некоторой константой. Найдем дифференциал этой функции, подставляя в формулу (1) выражение $Cx$ вместо $y$:
$$ d(Cx)=(Cx)’dx $$
Так как $(Cx)’=C\cdot (x)’=C\cdot 1=C$, то записанная выше формула $d(Cx)=(Cx)’dx$ станет такой: $d(Cx)=Cdx$. Если разделить обе части этой формулы на $C$ (при условии $C\neq 0$), то получим $\frac{d(Cx)}{C}=dx$. Этот результат можно переписать в несколько иной форме:
$$ \begin{equation} dx=\frac{1}{C}\cdot d(Cx)\;\;\;(C\neq 0) \end{equation} $$
Полученная формула говорит о том, что умножение выражения под дифференциалом на некую ненулевую константу требует введения соответствующего множителя, компенсирующего такое домножение. Например, $dx=\frac{1}{5} d(5x)$, $dx=-\frac{1}{19} d(-19x)$.
В примерах №1 и №2 формулы (2) и (3) будут рассмотрены подробно.
Замечание относительно формул
В данной теме будут использоваться как формулы 1-3, так и формулы из таблицы неопределённых интегралов, которые тоже имеют свои номера. Чтобы не было путаницы, условимся о следующем: если в теме встречается текст «используем формулу №1», то означает он буквально следующее «используем формулу №1, расположенную на этой странице«. Если нам понадобится формула из таблицы интегралов, то это будем оговаривать каждый раз отдельно. Например, так: «используем формулу №1 из таблицы интегралов».
И ещё одно небольшое примечание
Перед началом работы с примерами рекомендуется ознакомиться с материалом, изложенным в предыдущих темах, посвящённых понятию неопределённого интеграла и непосредственному интегрированию. Изложение материала в этой теме опирается на сведения, указанные в упомянутых темах.
Пример №1
Найти $\int \frac{dx}{x+4}$.
Решение
Если мы обратимся к таблице неопределённых интегралов, то не сможем найти формулу, которая точно соответствует интегралу $\int \frac{dx}{x+4}$.
Наиболее близка к этому интегралу формула №2 таблицы интегралов, т.е. $\int \frac{du}{u}=\ln|u|+C$. Проблема в следующем: формула $\int \frac{du}{u}=\ln|u|+C$ предполагает, что в интеграле $\int \frac{du}{u}$ выражения в знаменателе и под дифференциалом должны быть одинаковы (и там и там расположена одна буква $u$). В нашем случае в $\int \frac{dx}{x+4}$ под дифференциалом находится буква $x$, а в знаменателе – выражение $x+4$, т.е. налицо явное несоответствие табличной формуле. Попробуем «подогнать» наш интеграл под табличный. Что произойдёт, если под дифференциал вместо $x$ подставить $x+4$? Для ответа на этот вопрос применим формулу №1, подставив в неё выражение $x+4$ вместо $y$:
$$ d(x+4)=(x+4)’dx $$
Так как $(x+4)’=x’+(4)’=1+0=1$, то равенство $ d(x+4)=(x+4)’dx $ станет таким:
$$ d(x+4)=1\cdot dx=dx $$
Итак, $dx=d(x+4)$. Честно говоря, этот же результат можно было получить, просто подставив в формулу №2 вместо константы $C$ число $4$.
В дальнейшем мы так и будем делать, а на первый раз разобрали процедуру получения равенства $dx=d(x+4)$ подробно. Но что даёт нам равенство $dx=d(x+4)$?
А даёт оно нам следующий вывод: если $dx=d(x+4)$, то в интеграл $\int \frac{dx}{x+4}$ вместо $dx$ можно подставить $d(x+4)$, причём интеграл от этого не изменится:
$$ \int \frac{dx}{x+4}=\int \frac{d(x+4)}{x+4}$$
Сделали мы это преобразование лишь для того, чтобы полученный интеграл стал полностью соответствовать табличной формуле $\int \frac{du}{u}=\ln|u|+C$. Чтобы такое соответствие стало совсем явным, заменим выражение $x+4$ буквой $u$ (т.е. сделаем подстановку $u=x+4$):
$$ \int \frac{dx}{x+4}=\int \frac{d(x+4)}{x+4}=|u=x+4|=\int \frac{du}{u}=\ln|u|+C.$$
По сути, задача уже решена. Осталось лишь вернуть переменную $x$. Вспоминая, что $u=x+4$, получим: $\ln|u|+C=\ln|x+4|+C$. Полное решение без пояснений выглядит так:
$$ \int \frac{dx}{x+4}=\int \frac{d(x+4)}{x+4}=|u=x+4|=\int \frac{du}{u}=\ln|u|+C=\ln|x+4|+C.
{3x} dx$ под дифференциалом находится буква $x$, а в степени числа $e$ – выражение $3x$, т.е. налицо явное несоответствие табличной формуле. Попробуем «подогнать» наш интеграл под табличный. Что произойдёт, если под дифференциал вместо $x$ подставить $3x$? Для ответа на этот вопрос применим формулу №1, подставив в неё выражение $3x$ вместо $y$:
$$ d(3x)=(3x)’dx $$
Так как $(3x)’=3\cdot (x)’=3\cdot 1=3$, то равенство $d(3x)=(3x)’dx$ станет таким:
$$ d(3x)=3dx $$
Разделив обе части полученного равенства на $3$, будем иметь: $\frac{d(3x)}{3}=dx$, т.е. $dx=\frac{1}{3}\cdot d(3x)$. Вообще-то, равенство $dx=\frac{1}{3}\cdot d(3x)$ можно было получить, просто подставив в формулу №3 вместо константы $C$ число $3$. В дальнейшем мы так и будем делать, а на первый раз разобрали процедуру получения равенства $dx=\frac{1}{3}\cdot d(3x)$ подробно.
Что нам дало полученное равенство $dx=\frac{1}{3}\cdot d(3x)$? Оно означает, что в интеграл $\int e^{3x} dx$ вместо $dx$ можно подставить $\frac{1}{3}\cdot d(3x)$, причём интеграл от этого не изменится:
$$ \int e^{3x} dx= \int e^{3x} \cdot\frac{1}{3} d(3x) $$
Вынесем константу $\frac{1}{3}$ за знак интеграла и заменим выражение $3x$ буквой $u$ (т.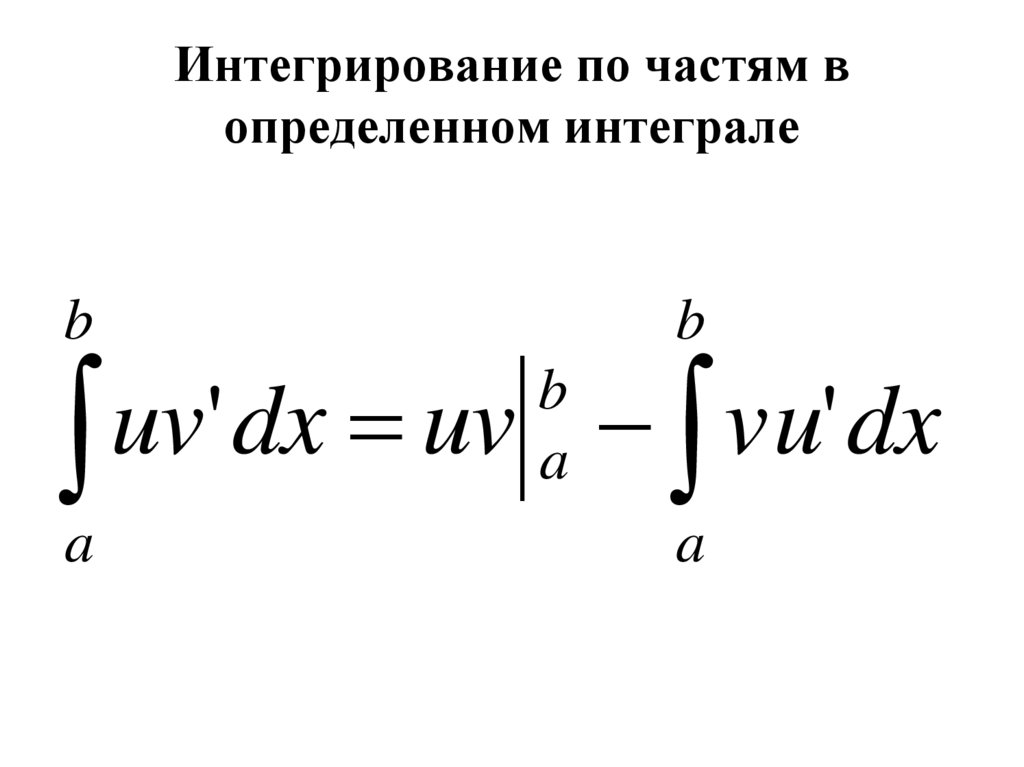
2+4x+C.
$$
Второй способ
Скобки раскрывать не будем. Попробуем сделать так, чтобы под дифференциалом вместо $x$ появилось выражение $3x+2$. Это позволит ввести новую переменную и применить табличную формулу. Нам нужно, чтобы под дифференциалом возник множитель $3$, посему подставляя в формулу №3 значение $C=3$, получим $d(x)=\frac{1}{3}d(3x)$. Кроме того, под дифференциалом не хватает слагаемого $2$. Согласно формуле №2 прибавление константы под знаком дифференциала не меняет оный дифференциал, т.е. $\frac{1}{3}d(3x)=\frac{1}{3}d(3x+2)$. Из условий $d(x)=\frac{1}{3}d(3x)$ и $\frac{1}{3}d(3x)=\frac{1}{3}d(3x+2)$ имеем: $dx=\frac{1}{3}d(3x+2)$.
Отмечу, что равенство $dx=\frac{1}{3}d(3x+2)$ можно получить и иным способом:
$$ d(3x+2)=(3x+2)’dx=((3x)’+(2)’)dx=(3\cdot x’+0)dx=3\cdot 1 dx=3dx;\\ dx=\frac{1}{3}d(3x+2). $$
Используем полученное равенство $dx=\frac{1}{3}d(3x+2)$, подставив в интеграл $\int (3x+2)^2 dx$ выражение $\frac{1}{3}d(3x+2)$ вместо $dx$.
{200}$, получив при этом сумму в двести одно слагаемое! А потом каждое слагаемое ещё и проинтегрировать придётся. Поэтому вывод тут такой: для больших степеней метод непосредственного интегрирования не годится. Второй способ, несмотря на кажущуюся сложность, более практичен.
Пример №4
Найти $\int \sin2x dx$.
Решение
Решение этого примера проведём тремя различными способами.
Первый способ
Заглянем в таблицу интегралов. Ниболее близка к нашему примеру формула №5 из этой таблицы, т.е. $\int \sin u du=-\cos u+C$. Чтобы подогнать интеграл $\int \sin2x dx$ под вид $\int \sin u du$, воспользуемся формулой №3, внеся множитель $2$ под знак дифференциала. Собственно, мы это делали уже в примере №2, так что обойдёмся без подробных комментариев:
$$
\int \sin 2x dx=\left|dx=\frac{1}{2}\cdot d(2x) \right|=\int \sin 2x \cdot\frac{1}{2}d(2x)=\\
=\frac{1}{2} \int \sin 2x d(2x)=|u=2x|=\frac{1}{2} \int \sin u du=-\frac{1}{2}\cos u+C=-\frac{1}{2}\cos 2x+C.
$$
Ответ: $\int \sin2x dx=-\frac{1}{2}\cos 2x+C$.
Второй способ
Для решения вторым способом применим простую тригонометрическую формулу: $\sin 2x=2\sin x\cos x$. Подставим вместо $\sin 2x$ выражение $2 \sin x \cos x$, при этом константу $2$ вынесем за знак интеграла:
$$ \int \sin 2x dx=\int 2 \sin x\cos x dx=2\cdot\int \sin x\cos x dx $$
Какова цель такого преобразования? В таблице интеграла $\int \sin x\cos x dx$ нет, но мы можем немного препобразовать $\int \sin x\cos x dx$, чтобы он стал больше походить на табличный. Для этого найдем $d(\cos x)$, используя формулу №1. Подставим в упомянутую формулу $\cos x$ вместо $y$:
$$ d(\cos x)=(\cos x)’dx=-\sin x dx. $$
Так как $d(\cos x)=-\sin x dx$, то $\sin x dx=-d(\cos x)$. Так как $\sin x dx=-d(\cos x)$, то мы можем в $\int \sin x\cos x dx$ вместо $\sin x dx$ подставить $-d(\cos x)$.
2x+C$.
Третий способ
Для решения третьим способом применим ту же тригонометрическую формулу: $\sin 2x=2\sin x\cos x$. Подставим вместо $\sin 2x$ выражение $2 \sin x \cos x$, при этом константу $2$ вынесем за знак интеграла:
$$ \int \sin 2x dx=\int 2 \sin x\cos x dx=2\cdot\int \sin x\cos x dx $$
Найдем $d(\sin x)$, используя формулу №1. Подставим в упомянутую формулу $\sin x$ вместо $y$:
$$ d(\sin x)=(\sin x)’dx=\cos x dx. $$
Итак, $d(\sin x)=\cos x dx$. Из полученного равенства следует, что мы можем в $\int \sin x\cos x dx$ вместо $\cos x dx$ подставить $d(\sin x)$. Значение интеграла при этом не изменится:
$$ 2\cdot\int \sin x\cos x dx=2\cdot\int \sin x \cdot d(\sin x) $$
Говоря иными словами, мы внесли под дифференциал $\sin x$.
2x+C$. Полагаю, теперь видно, что отличаются они друг от друга лишь некоторым числом. Т.е. дело опять оказалось в интегральной константе. Как видите, небольшое различие в интегральной константе способно, в принципе, сильно изменить внешний вид ответа, – но от этого ответ не перестанет быть правильным. К чему я веду: если в сборнике задач вы увидите ответ, не совпадающий с вашим, то это вовсе не означает, что ваш ответ неверен. Возможно, что вы просто пришли к ответу иным способом, чем предполагал автор задачи. А убедиться в правильности ответа поможет проверка, основанная на определении неопределённого интеграла. Например, если интеграл $\int \sin2x dx=-\frac{1}{2}\cos 2x+C$ найден верно, то должно выполняться равенство $\left( -\frac{1}{2}\cos 2x+C\right)’=\sin 2x$. Вот и проверим, правда ли, что производная от $\left( -\frac{1}{2}\cos 2x+C\right)$ равна подынтегральной функции $\sin 2x$:
$$
\left( -\frac{1}{2}\cos 2x+C\right)’=\left( -\frac{1}{2}\cos 2x\right)’+C’=-\frac{1}{2}\cdot(\cos 2x)’+0=\\
=-\frac{1}{2}\cdot (-\sin 2x)\cdot (2x)’=-\frac{1}{2}\cdot (-\sin 2x)\cdot 2=\sin 2x.
$$
Проверка пройдена успешно. Равенство $\left( -\frac{1}{2}\cos 2x+C\right)’=\sin 2x$ выполнено, поэтому формула $\int \sin2x dx=-\frac{1}{2}\cos 2x+C$ верна. В примере №5 также осуществим проверку результата, дабы убедиться в его правильности. Наличие проверки не является обязательным, хотя в некоторых типовых расчётах и контрольных работах требование проверять результат присутствует.
Первая часть
Вторая часть
Вернуться к списку тем
Задать вопрос на форуме
Записаться на занятия
Онлайн-занятия по высшей математике
Интегралы как умножение – BetterExplained
Интегралы часто описываются как нахождение площади под кривой. Это описание слишком узкое: это все равно, что сказать, что умножение существует для нахождения площади прямоугольников. Нахождение площади является полезным приложением , но не целью умножения.
Основная идея: интегралы помогают нам комбинировать числа, когда умножение не может.
Хотел бы я провести минутку с самим собой в школьном исчислении:
«Псс! Интегралы позволяют «перемножать» изменяющиеся числа. Мы привыкли к «3 x 4 = 12», но что, если одна величина меняется? Мы не можем умножать изменяющиеся числа, поэтому интегрируем.
Вы’ Я слышал много разговоров о площади — площадь — это просто один из способов визуализировать умножение. Ключ не в площади, а в идее объединения величин в новый результат. Конечно, мы можем интегрировать скорость и время, чтобы получить расстояние, или длину, ширину и высоту, чтобы получить объем.0005
Когда мы хотим использовать обычное умножение, но не можем, мы достаем большую пушку и интегрируем. Площадь — это всего лишь техника визуализации , не слишком зацикливайтесь на ней. Теперь иди, изучай исчисление!»
Это мой ага-момент: интегрирование — это «лучшее умножение», которое работает с вещами, которые изменяются. Давайте научимся видеть интегралы в этом свете. время:
- Для целых чисел (3 x 4) умножение равно повторному сложению
- С действительными числами (3,12 x $\sqrt{2}$) умножение равно масштабированию
- С отрицательными числами (-2,3 * 4,3) умножение равно с переворотом и масштабированием
- С комплексными числами (3 * 3i) умножение равно вращению и масштабированию
Мы движемся к общему понятию «применения» одного числа к другому, и свойства, которые мы применяем (повторяющийся счет, масштабирование, переворачивание или вращение), могут различаться.
Интеграция — еще один шаг на этом пути.
Понимание области
Область — это детальная тема. На сегодня давайте рассмотрим площадь как визуальное представление умножения :
С каждым счетом на другой оси мы можем «применить их» (3 применительно к 4) и получить результат (12 квадратных единиц). Свойства каждого входа (длина и длина) переносились в результат (квадратные единицы).
Просто, правда? Ну, становится сложно. Умножение может привести к «отрицательной области» (3 x (-4) = -12), которой не существует.
Мы понимаем, что граф представляет собой представление умножения, и используем аналогию так, как она нам служит. Если бы все были слепы и у нас не было диаграмм, мы все равно могли бы прекрасно умножать. Площадь — это просто интерпретация.
Умножение по частям
Теперь давайте умножим 3 x 4,5:
Что происходит? Ну, 4,5 не считается, но мы можем использовать операцию «по частям». Если 3×4 = 3 + 3 + 3 + 3, то
3 x 4,5 = 3 + 3 + 3 + 3 + 3×0,5 = 3 + 3 + 3 + 3 + 1,5 = 13,5
Берем 3 (значение) 4,5 раза.
То есть мы объединили 3 с 4 целыми отрезками (3 х 4 = 12) и одним неполным отрезком (3 х 0,5 = 1,5).
Мы так привыкли к умножению, что забыли, насколько хорошо оно работает. Мы можем разбить число на части (целые и частичные), умножить каждую часть и сложить результаты. Заметили, как мы поступили с дробной частью? Это начало интеграции.
Проблема с числами
Числа не всегда остаются на месте, чтобы мы могли их подсчитать. Сценарии типа «Вы едете со скоростью 30 миль в час в течение 3 часов» предназначены для удобства, а не для реализма.
Формулы типа «расстояние = скорость * время» только маскируют проблему; нам все еще нужно подключить статические числа и умножить. Так как же нам найти пройденное расстояние, если наша скорость меняется со временем?
Описание изменения
Наша первая задача — описать изменяющееся число. Мы не можем просто сказать: «Моя скорость изменилась с 0 до 30 миль в час». Это недостаточно конкретно: как быстро это меняется? Это гладко?
Теперь давайте конкретнее: каждую секунду я еду в два раза быстрее, чем в милях в час.
В 1 секунду я еду 2 мили в час. 2 секунды, 4 мили в час. 3 секунды это 6 миль в час, и так далее:
Вот это хорошее описание, достаточно подробное, чтобы знать мою скорость в любой момент. Формальное описание: «скорость есть функция времени», что означает, что мы можем подключить любое время (t) и найти нашу скорость в этот момент («2t» миль в час).
(Это не говорит , почему скорость и время связаны. Возможно, я ускоряюсь из-за гравитации или из-за того, что меня тянет лама. Мы просто говорим, что с изменением времени меняется и наша скорость.)
Итак, наше умножение «расстояние = скорость * время», пожалуй, лучше записать:
где скорость(t) это скорость в любой момент. В нашем случае скорость(t) = 2t, поэтому мы пишем:
Но это уравнение все равно выглядит странно! «t» по-прежнему выглядит как одно мгновение, которое нам нужно выбрать (например, t = 3 секунды), что означает, что скорость (t) примет одно значение (6 миль в час).
Это не хорошо.
При обычном умножении мы можем взять одну скорость и предположить, что она справедлива для всего прямоугольника. Но изменяющаяся скорость требует от нас объединения скорости и времени по частям (посекундно). Ведь каждое мгновение могло быть разным.
Это большой сдвиг перспективы:
- Обычное умножение (прямоугольное): возьмите расстояние, пройденное за одну секунду, предположим, что оно одинаково для всех секунд, и «увеличьте его».
- Интеграция (по частям): смотрите на время как на серию мгновений, каждое из которых имеет свою собственную скорость. Сложите расстояние, пройденное за секунду за секундой.
Мы видим, что регулярное умножение является частным случаем интегрирования, когда величины не меняются.
Насколько велик «кусок»?
Насколько велик «кусок» при сборке по частям? Второй? Миллисекунда? Наносекунда?
Быстрый ответ: Достаточно мало, чтобы значение выглядело одинаково на протяжении всего времени.
Нам не нужна идеальная точность.
Более длинный ответ: такие понятия, как пределы, были изобретены, чтобы помочь нам выполнять кусочное умножение. Хотя они и полезны, они представляют собой решение проблемы и могут отвлечь от понимания «объединения вещей». Меня беспокоит, что ограничения вводятся в самом начале исчисления, до того, как мы понимаем проблему, для решения которой они были созданы (например, показать кому-то ремень безопасности еще до того, как он увидит машину). Конечно, это полезная идея, но Ньютон, похоже, довольно хорошо разбирался в исчислении и без них.
Что насчет начала и конца?
Допустим, мы рассматриваем интервал от 3 до 4 секунд.
Скорость в начале (3×2 = 6 миль в час) отличается от скорости в конце (4×2 = 8 миль в час). Итак, какое значение мы используем, когда делаем «скорость * время»?
Ответ заключается в том, что мы разбиваем наши фрагменты на достаточно маленькие фрагменты (от 3,00000 до 3,00001 секунды) до тех пор, пока разница в скорости в начале и в конце интервала не будет иметь для нас значения.
Опять же, это более длинная дискуссия, но «поверьте мне», что есть период времени, который делает разницу бессмысленной.
На графике представьте каждый интервал как одну точку на линии. Вы можете нарисовать прямую линию для каждой скорости, и ваша «площадь» будет набором линий, которые измеряют умножение.
Где находится «кусок» и какова его стоимость?
Отделить часть от ее значения было для меня проблемой.
«Кусок» — это рассматриваемый нами интервал (1 секунда, 1 миллисекунда, 1 наносекунда). «Позиция» — это место, где начинается этот секундный, миллисекундный или наносекундный интервал. Значение — это наша скорость в этой позиции.
Например, рассмотрим интервал от 3,0 до 4,0 секунд:
- «Ширина» отрезка времени составляет 1,0 секунды
- Позиция (начальное время) 3.0
- Значение (скорость(t)) равно скорости(3,0) = 6,0 миль в час
Опять же, исчисление позволяет нам сжимать интервал до тех пор, пока мы не сможем определить разницу в скорости в начале и в конце интервала.
Следите за более широкой картиной: мы умножаем коллекцию кусочков.
Понимание целочисленного представления
У нас есть неплохое представление о «кусочном умножении», но мы не можем его выразить. «Расстояние = скорость (t) * t» по-прежнему выглядит как обычное уравнение, где t и скорость (t) принимают одно значение.
В исчислении мы записываем соотношение следующим образом:
Знак интеграла (кривая в форме буквы S) означает, что мы умножаем вещи по частям и складываем их вместе.
dt представляет конкретный «кусок» времени, который мы рассматриваем. Это называется «дельта t», а не «d умножить на t».
t представляет положение dt (если dt — это диапазон от 3,0 до 4,0, t равно 3,0).
скорость(t) представляет значение, на которое мы умножаем (скорость(3.0) = 6.0))
У меня есть несколько претензий к этому обозначению:
- То, как используются буквы, сбивает с толку.
«dt» выглядит как «d, умноженное на t», в отличие от всех уравнений, которые вы видели ранее. - Пишем скорость(t) * dt вместо скорости(t_dt) * dt. Последнее дает понять, что мы рассматриваем «t» в нашем конкретном фрагменте «dt», а не в какой-то глобальной «t» 9.0034
- Вы часто будете видеть $\int speed(t)$ с неявным dt. Это позволяет легко забыть, что мы выполняем пошаговое умножение на два элемента .
«dt» выглядит как «d, умноженное на t», в отличие от всех уравнений, которые вы видели ранее.Слишком поздно менять способ записи интегралов. Просто помните концепцию более высокого уровня «умножения» того, что изменяется.
Чтение в голове
Когда я вижу
, я думаю: «Расстояние равно скорости, умноженной на время» (читая сначала левую часть) или «объединить скорость и время, чтобы получить расстояние» (читая правую часть). первый).
Я мысленно перевожу «скорость(t)» в скорость и «dt» во время, и получается умножение, помня, что скорость может изменяться. Такое абстрагирование интеграции помогает мне сосредоточиться на том, что происходит («Мы комбинируем скорость и время, чтобы увеличить расстояние!»), а не на деталях операции.
Бонус: последующие идеи
Интегралы — это глубокая идея, как и умножение. У вас могут возникнуть дополнительные вопросы, основанные на этой аналогии:
- Если интегралы умножают изменяющиеся величины, есть ли что-то, что их делит? (Да — производные)
- А интегралы (умножение) и производные (деление) сокращаются? (Да, с некоторыми оговорками).
- Можем ли мы изменить уравнения с «расстояние = скорость * время» на «скорость = расстояние/время»? (Да.)
- Можем ли мы объединить несколько изменяющихся вещей? (Да — это называется множественной интеграцией)
- Имеет ли значение порядок, в котором мы объединяем несколько вещей? (обычно нет)
Когда вы начинаете рассматривать интегралы как «лучшее умножение», вы начинаете искать такие понятия, как «лучшее деление», «повторное интегрирование» и так далее. Придерживаясь «области под кривой», эти темы кажутся несвязанными. (Для ботаников-математиков, рассматривающих «площадь под кривой» и «наклон» как обратные величины, это многого требует от студента).
Чтение интегралов
Интегралы имеют множество применений. Один из них — объяснить, что две вещи «умножаются» вместе, чтобы получить результат.
Вот как можно выразить площадь круга:
Мы хотели бы получить площадь круга с помощью умножения. Но мы не можем — высота меняется по ходу движения. Если мы «развернём» круг, мы увидим, что площадь, вносимая каждой частью радиуса, равна «радиус * длина окружности». Мы можем записать это соотношение, используя приведенный выше интеграл. (Подробнее см. Введение в исчисление).
А вот и интеграл, выражающий идею «масса = плотность * объем»:
О чем это говорит? Rho: $\rho$ — это функция плотности, говорящая нам, насколько плотен материал в определенном положении, r. dv — это бит объема, на который мы смотрим. Итак, мы умножаем небольшую часть объема (dv) на плотность в этой позиции $\rho(r)$ и складываем их все, чтобы получить массу.
Мы хотели бы умножить плотность и объем, но если плотность меняется, нам нужно интегрировать.
Нижний индекс V означает сокращение от «интеграла объема», который на самом деле представляет собой тройной интеграл длины, ширины и высоты! Интеграл включает четыре «умножения»: 3 для нахождения объема и еще одно для умножения на плотность.
Возможно, мы не решим эти уравнения, но мы можем понять, что они выражают.
Вперед вверх
Сегодняшняя цель не в том, чтобы строго понять исчисление. Это чтобы расширить нашу ментальную модель и понять, что есть другой способ комбинировать вещи: мы можем складывать, вычитать, умножать, делить… и объединять.
Воспринимайте интегралы как лучший способ умножения: вычисления станут проще, и вы будете знать такие понятия, как множественные интегралы и производная. Счастливая математика.
(PS. Зак из SMBC поместил себя в… ммм… комикс об этой интуиции.)
.. = 1Видео-вопрос: нахождение интегрирования полинома, включающего умножение двух скобок и применение степенного правила 𝑥 в кубе плюс один относительно 𝑥.
В этом вопросе нас просят оценить неопределенный интеграл от произведения
два многочлена. И мы не знаем, как это сделать напрямую. Однако мы знаем, как умножить их вместе, используя FOIL.
метод. Это затем превратит наше подынтегральное выражение в многочлен, который мы знаем, как интегрировать.
почленно, используя степенное правило интегрирования. Итак, мы начнем с перемножения этих двух многочленов с помощью функции FOIL.
метод. Во-первых, нам нужно перемножить первые два члена вместе.
Таким образом, умножая первые два члена наших многочленов вместе, мы получаем отрицательное значение.
семь 𝑥 в квадрате умножить на минус 𝑥 в кубе.
И мы можем оценить это и упростить, используя наши законы показателей. Это равно семи 𝑥 в пятой степени. Мы продолжим расширять это, используя метод FOIL. Далее нам нужно перемножить два внешних члена вместе. Это означает, что нам нужно добавить к отрицательному члену семь 𝑥 в квадрате, умноженное на один. Конечно, умножение на единицу не меняет нашего значения, поэтому мы просто получаем минус семь. 𝑥 в квадрате. Затем метод FOIL говорит нам перемножить два внутренних члена вместе. Это дает нам отрицательные пять, умноженные на отрицательные 𝑥 в кубе, которые мы можем оценить как равно пяти 𝑥 в кубе.
Наконец, метод FOIL говорит нам, что нам нужно умножить два последних члена нашего
биномы вместе. Таким образом, мы должны добавить к термину минус пять, умноженный на один, что, конечно же,
равно минус пяти.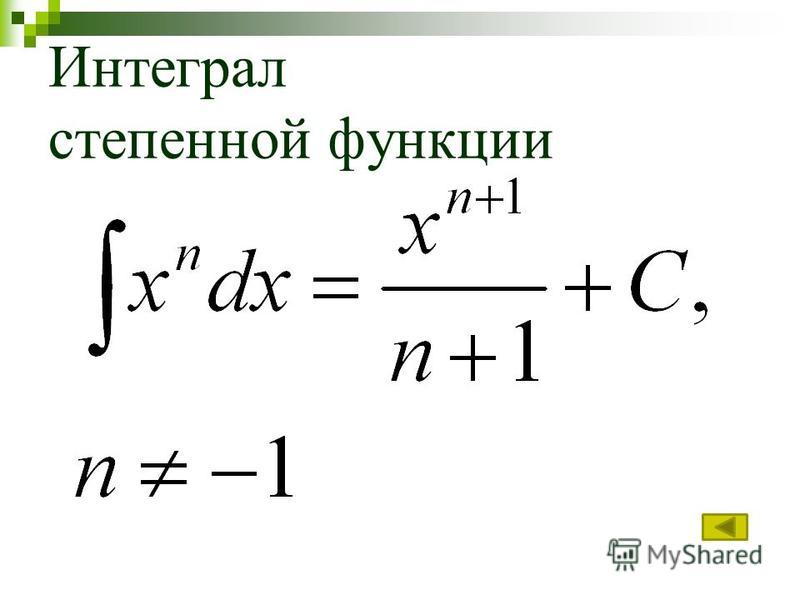
Итак, мы переписали наш интеграл как интеграл от семи 𝑥 в пятой степени минус
семь 𝑥 в квадрате плюс пять 𝑥 в кубе минус пять относительно 𝑥. Итак, теперь мы просто вычисляем интеграл многочлена.
И мы знаем, что можем делать это почленно, используя степенное правило для интегрирования, что говорит нам для любых реальных констант 𝑎 и 𝑛, где 𝑛 не равно отрицательному один, интеграл от 𝑎𝑥 в 𝑛-й степени по 𝑥 равен 𝑎 раз 𝑥 в степени 𝑛 плюс единица, деленная на 𝑛 плюс единица плюс наша постоянная интеграция 𝐶. Мы добавляем единицу к нашему показателю 𝑥, а затем делим на этот новый показатель. Мы хотим применять этот термин за термином.
Начнем с первого члена с семью 𝑥 в пятой степени. Мы видим, что наш показатель степени 𝑥 равен пяти. Мы хотим добавить единицу к этому показателю степени пяти, чтобы получить новый показатель степени шести, а затем
разделить на этот новый показатель степени.
Это дает нам семь 𝑥 в шестой степени, деленное на шесть. Мы хотим сделать то же самое со своим следующим сроком. Теперь мы можем видеть, что наш показатель степени 𝑥 равен двум. Мы добавляем единицу к нашему показателю степени двух, чтобы получить новый показатель степени трех, а затем делим
этим новым показателем. И помните, поскольку мы вычитали семь 𝑥 в квадрате, нам нужно вычесть это
стоимость. Это означает, что мы вычитаем семь 𝑥 в кубе из трех.
Мы можем сделать то же самое с нашим третьим членом; наш показатель 𝑥 равен трем. Итак, еще раз, мы добавляем единицу к этому показателю степени трех, чтобы получить новый показатель степени четырех.
а затем разделить на этот новый показатель степени. Это дает нам пять 𝑥 в четвертой степени над четырьмя. И есть несколько способов интегрировать наш последний термин. Например, мы могли бы переписать минус пять как минус пять раз 𝑥 с точностью до нуля.
мощность, потому что помните 𝑥 в нулевой степени равно единице.
Затем мы могли бы вычислить интеграл от этого члена, используя степенное правило для
интегрирование с нашим значением 𝑛, равным нулю.
Это дало бы минус пять 𝑥. Мы также можем помнить, что производная от минус пяти 𝑥 по отношению к 𝑥 равна минус пять. Итак, отрицательная пятерка 𝑥 является первообразной отрицательной пятерки. Наконец, помните, нам нужно добавить константу интегрирования. Мы назовем это 𝐶. Это дает нам семь 𝑥 в шестой степени больше шести минус семь 𝑥 в кубе над тремя. плюс пять 𝑥 в четвертой степени четыре минус пять 𝑥 плюс 𝐶.
И мы могли бы оставить наш ответ так. Однако, поскольку это многочлен, мы напишем так, чтобы наши показатели степени 𝑥 были
уменьшение. Итак, поменяв местами второй и третий члены, мы получим окончательный ответ. Таким образом, мы смогли показать интеграл минус семь 𝑥 в квадрате минус пять
умножить отрицательное 𝑥 в кубе плюс один по отношению к 𝑥 равно семи 𝑥 к
шестая степень больше шести плюс пять 𝑥 в четвертой степени больше четырех минус семь 𝑥 в кубе
больше трех минус пять 𝑥 плюс 𝐶.