Корень n-ой степени и свойства
ПРАКТИЧЕСКАЯ РАБОТА № 2
Тема: «Корень п-ой степени и свойства.
Цель занятия: Обобщить и систематизировать знания по теме «Корень п-ой степени и свойства»; закрепить умения использовать полученные знания для преобразования выражений.
Ход работы.
1. Записать теоретические сведения
Теоретические сведения
КОРНИ НАТУРАЛЬНОЙ СТЕПЕНИ ИЗ ЧИСЛА, ИХ СВОЙСТВА.
Корень n – степени: , n — показатель корня, а – подкоренное выражение
Если n – нечетное число, то выражение имеет смысл при а
Если n – четное число, то выражение имеет смысл при
Арифметический корень:
Корень нечетной степени из отрицательного числа:
ОСНОВНЫЕ СВОЙСТВА КОРНЕЙ
Правило извлечения корня из произведения:
Правило извлечения корня из дроби:
Правило извлечения корня из корня:
Правило вынесения множителя из под знака корня:
Внесение множителя под знак корня:
,
Показатель корня и показатель подкоренного выражения можно умножить на одно и тоже число.
Правило возведения корня в степень.
СТЕПЕНЬ С НАТУРАЛЬНЫМ ПОКАЗАТЕЛЕМ
=,a – основание степени, n – показатель степени
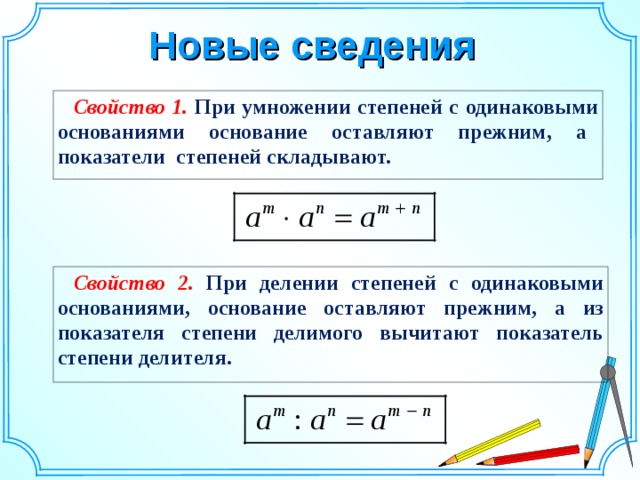
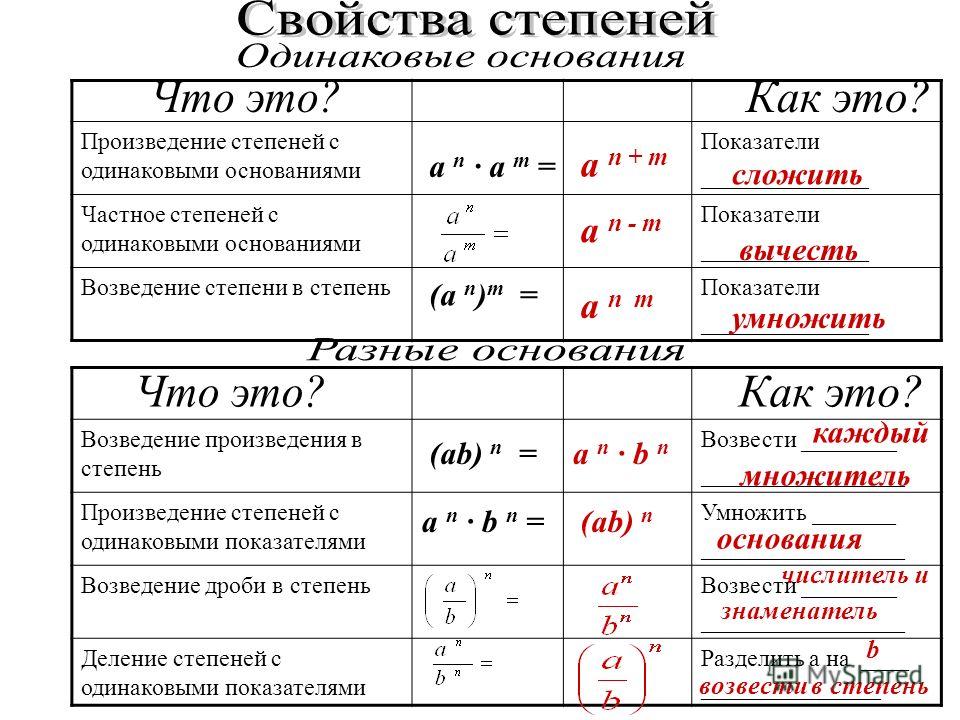
Свойства:
При умножении степеней с одинаковыми основаниями показатели складываются, а основание остается неизменным.
При делении степеней с одинаковыми основаниями показатели вычитаются, а основание остается неизменным.
При возведении степени в степень показатели перемножаются.
При возведении в степень произведения двух чисел, каждое число возводят в эту степень, а результаты перемножают.
Если в степень возводят частное двух чисел, то в эту степень возводят числитель и знаменатель, а результат делят друг на друга.
Если
СТЕПЕНЬ С ЦЕЛЫМ ПОКАЗАТЕЛЕМ
По определению:
Свойства:
Пусть r рациональное число , тогда
при r0 при r
7 .Для любого рациональных чисел r и s из неравенства следует
при a1 при
Формулы сокращённого умножения.
Пример 1. Упростите выражение .
Упростите выражение .
Решение
Применим свойства степеней (умножение степеней с одинаковым основанием и деление степеней с одинаковым основанием): .
Ответ: 9m7 .
Пример 2.Сократить дробь:
Решение. Так область определения дроби все числа, кроме х ≠ 1 и х ≠ -2.Вместе с тем .Сократив дробь, получим .Область определения полученной дроби: х ≠ -2, т.е. шире, чем область определения первоначальной дроби. Поэтому дроби и равны при х ≠ 1 и х ≠ -2.
Пример 3.Сократить дробь:
Пример 4.Упростить:
Пример 5.Упростить:
Пример 6. Упростить:
Пример 7. Упростить:
Пример 8.Упростить:
Пример 9. Вычислить: .
Решение.
Пример 10.Упростить выражение:
Решение.
Пример 11.Сократить дробь , если
Решение. .
2. Решить самостоятельно
1. Упростите выражение:
2. Найдите значение выражения:
Найдите значение выражения:
3. Представьте степень с дробным показателем в виде корня
4. Привести указанное выражение к виду , где а -рациональное число, b – натуральное число
,
5. Упростить:
;
6. Замените арифметические корни степенями с дробным показателем
, ,
7. Представьте выражение в виде дроби, знаменатель которой не содержит знака корня
8. Сократите дробь
9. Выполните действие
Логарифм произведения (сумма логарифмов с одинаковыми основаниями): формула, примеры
Sign in
Password recovery
Восстановите свой пароль
Ваш адрес электронной почты
MicroExcel.ru Математика Алгебра Логарифм произведения (сумма логарифмов)
Логарифм произведения – одно из основных логарифмических свойств; равняется сумме логарифмов множителя и множимого при неизменном основании.
logb (x ⋅ y) = logb x + logb y
При этом результат умножения x на y должен быть строго положительным, т.е. (x ⋅ y) > 0.
Данное свойство работает и в обратную сторону, т.е.:
Сумма логарифмов с одинаковыми основаниями равна логарифму произведения их подлогарифмических выражений по тому же основанию.
logb x + log
Примеры:
- log3 (5 ⋅ 6) = log3 5 + log3 6
- log9 (12 ⋅ 15) = log9 12 + log9 15
- log11 7 + log11 14 = log11 (7 ⋅ 14)
ЧАЩЕ ВСЕГО ЗАПРАШИВАЮТ
Таблица знаков зодиака
Нахождение площади трапеции: формула и примеры
Нахождение длины окружности: формула и задачи
Римские цифры: таблицы
Таблица синусов
Тригонометрическая функция: Тангенс угла (tg)
Нахождение площади ромба: формула и примеры
Нахождение объема цилиндра: формула и задачи
Тригонометрическая функция: Синус угла (sin)
Геометрическая фигура: треугольник
Нахождение объема шара: формула и задачи
Тригонометрическая функция: Косинус угла (cos)
Нахождение объема конуса: формула и задачи
Таблица сложения чисел
Нахождение площади квадрата: формула и примеры
Что такое тетраэдр: определение, виды, формулы площади и объема
Нахождение объема пирамиды: формула и задачи
Признаки подобия треугольников
Нахождение периметра прямоугольника: формула и задачи
Формула Герона для треугольника
Что такое средняя линия треугольника
Нахождение площади треугольника: формула и примеры
Нахождение площади поверхности конуса: формула и задачи
Что такое прямоугольник: определение, свойства, признаки, формулы
Разность кубов: формула и примеры
Степени натуральных чисел
Нахождение площади правильного шестиугольника: формула и примеры
Тригонометрические значения углов: sin, cos, tg, ctg
Нахождение периметра квадрата: формула и задачи
Теорема Фалеса: формулировка и пример решения задачи
Сумма кубов: формула и примеры
Нахождение объема куба: формула и задачи
Куб разности: формула и примеры
Нахождение площади шарового сегмента
Что такое окружность: определение, свойства, формулы
Умножение и деление подкоренных выражений
Умножение подкоренных выражений
При умножении подкоренных выражений с одинаковым индексом мы используем правило произведения для подкоренных. Если a и b представляют положительные действительные числа,
Если a и b представляют положительные действительные числа,
Пример 1: Умножьте: 2⋅6.
Решение: Эта задача представляет собой произведение двух квадратных корней. Примените правило произведения для радикалов, а затем упростите.
Ответ: 23
Пример 2: Умножьте: 93⋅63.
Решение: Эта задача является произведением кубических корней. Примените правило произведения для радикалов, а затем упростите.
Ответ: 3 23
Часто перед радикалами стоят коэффициенты.
Пример 3: Умножьте: 23⋅52.
Решение: Используя правило произведения радикалов и тот факт, что умножение коммутативно, мы можем перемножить коэффициенты и подкоренные числа следующим образом.
Обычно первый шаг, связанный с применением свойства коммутативности, не показан.
Ответ: 106
Пример 4: Умножьте: −2 5×3⋅3 25×23.
Решение:
Ответ: −30x
Используйте свойство дистрибутивности при умножении рациональных выражений, содержащих более одного члена.
Пример 5: Умножьте: 43(23−36).
Решение: Примените свойство распределения и умножьте каждое слагаемое на 43.
Ответ: 24-362
Пример 6: Умножьте: 4×23(2×3-5 4×23).
Решение: Примените свойство распределения, а затем упростите результат.
Ответ: 2x−10x⋅2×3
Процесс умножения радикальных выражений с несколькими членами аналогичен процессу умножения многочленов. Примените распределительное свойство, упростите каждый радикал, а затем объедините одинаковые члены.
Пример 7: Умножить: (5+2)(5−4).
Решение: Начните с применения свойства распределения.
Ответ: −3−25
Пример 8: Умножить: (3x−y)2.
Решение:
Ответ: 9x−6xy+y
Попробуйте! Умножить: (23+52)(3−26).
Ответ: 6−122+56−203
Решение для видео
(нажмите, чтобы посмотреть видео)Выражения (a+b) и (a−b) называются сопряженнымиМножители (a+b) и (a−b) являются сопряженными.. При умножении сопряженных чисел сумма произведений внутренний и внешний члены дают 0,
Пример 9: Умножьте: (2+5)(2−5).
Решение: Примените распределительное свойство, а затем объедините подобные условия.
Ответ: −3
Важно отметить, что при умножении сопряженных подкоренных выражений мы получаем рациональное выражение. Это верно в целом и часто используется в нашем изучении алгебры.
Следовательно, для неотрицательных действительных чисел a и b мы имеем следующее свойство:
Деление подкоренных выражений (рационализация знаменателя)
Чтобы разделить подкоренные выражения с одинаковым индексом, мы используем правило частного для подкоренных. Если a и b представляют собой неотрицательные числа, где b ≠ 0, то мы имеем
Если a и b представляют собой неотрицательные числа, где b ≠ 0, то мы имеем
Пример 10: Разделим: 8010.
Решение: 10,0014 В этом случае мы можем увидеть, что имеют общие факторы. Если мы применим правило отношения для радикалов и запишем его в виде одного квадратного корня, мы сможем уменьшить дробное подкоренное число.
Ответ: 22
Пример 11: Разделить: 16x5y42xy.
Решение:
Ответ: 2x2y2y
Пример 12: Разделить: 54a3b5316a2b23.
Решение:
Ответ: 3b⋅a32
Когда делитель подкоренного выражения содержит подкорень, общепринятой практикой является поиск эквивалентного выражения, в котором знаменатель является рациональным числом. Нахождение такого эквивалентного выражения называется рационализацией знаменателя. Процесс определения эквивалентного подкоренного выражения с рациональным знаменателем.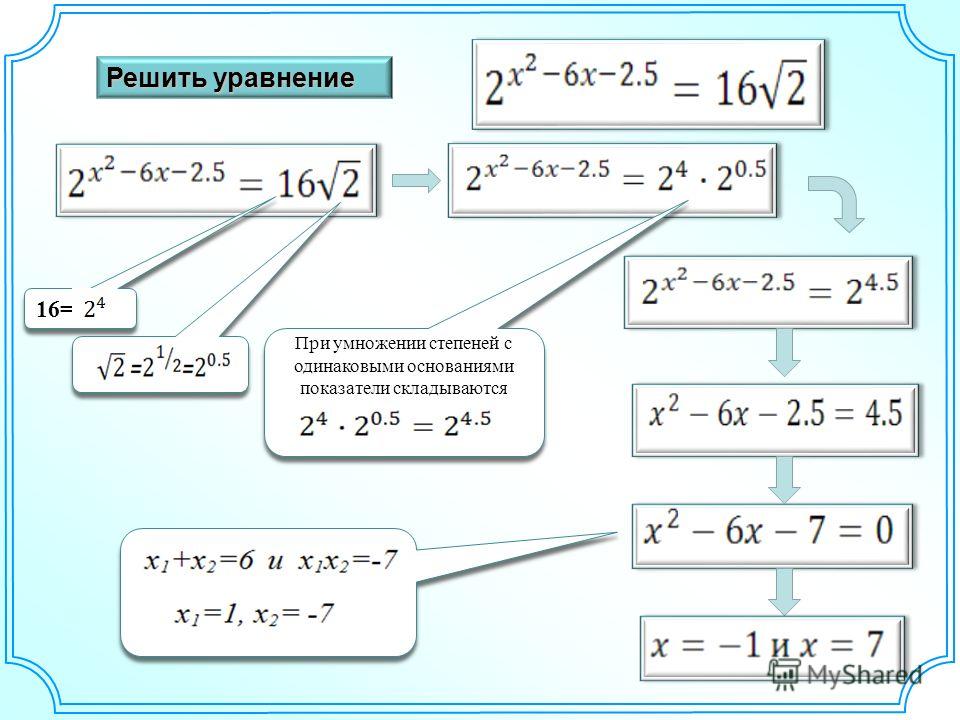 .
.
Для этого умножьте дробь на 1 особой формы, чтобы подкоренное число в знаменателе можно было записать со степенью, соответствующей индексу. После этого упростите и удалите радикал в знаменателе. Например,
Помните, чтобы получить эквивалентное выражение, вы должны умножить числитель и знаменатель на один и тот же ненулевой множитель.
Пример 13: Рационализируйте знаменатель: 32.
Решение: Цель состоит в том, чтобы найти эквивалентное выражение без корня в знаменателе. В этом примере умножьте на 1 в форме 22.
Ответ: 62
Пример 14: Объясните знаменатель: 123x.
Решение: Подкоренное число в знаменателе определяет факторы, которые необходимо использовать для его рационализации. В этом примере умножьте на 1 в виде 3x3x.
Ответ: 3x6x
Как правило, мы обнаружим необходимость уменьшить или отменить после рационализации знаменателя.
Пример 15: Рационализируем знаменатель: 525ab.
Решение: В этом примере мы умножим на 1 в форме 5ab5ab.
Обратите внимание, что a и b в этом примере не отменяются. Не отменяйте факторы внутри радикала с теми, что снаружи.
Ответ: 10abab
Попробуйте! Рационализируйте знаменатель: 4a3b.
Ответ: 23ab3b
Видеорешение
(нажмите, чтобы посмотреть видео)До этого момента мы видели, что умножение числителя и знаменателя на квадратный корень с одинаковыми подкоренными дает рациональный знаменатель. В общем случае это верно только тогда, когда знаменатель содержит квадратный корень. Однако это не относится к кубическому корню. Например,
Обратите внимание, что умножение на тот же коэффициент в знаменателе не оправдывает его. В этом случае, если мы умножаем на 1 в виде x23x23, то мы можем записать подкоренное число в знаменателе как степень числа 3. Упрощение результата дает рационализированный знаменатель. Например,
Упрощение результата дает рационализированный знаменатель. Например,
Поэтому, чтобы рационализировать знаменатель подкоренных выражений с одним подкоренным членом в знаменателе, начните с разложения подкоренной части знаменателя. Множители этого подкоренного числа и индекса определяют, на что мы должны умножать. Умножьте числитель и знаменатель на
Пример 16: Рационализируем знаменатель: 1253.
Решение: Радикал в знаменателе эквивалентен 523. Чтобы рационализировать знаменатель, он должен быть 533. Чтобы получить это, нам нужен еще один делитель 5. Поэтому умножьте на 1 в виде 5353.
Ответ: 535
Пример 17: Объясним знаменатель: 27a2b23.
Решение: В этом примере мы умножим на 1 в форме 22b322b3.
Ответ: 34ab32b
Пример 18: Объясните знаменатель: 1 4×35.
Решение: В этом примере мы умножим на 1 в виде 23x2523x25.
Ответ: 8x252x
Когда в знаменателе появляются два члена, содержащие квадратные корни, мы можем рационализировать это, используя очень специальную технику. Этот метод включает умножение числителя и знаменателя дроби на сопряженную часть знаменателя. Напомним, что умножение подкоренного выражения на его сопряженное дает рациональное число.
Пример 19: Рационализируйте знаменатель: 13−2.
Решение: В этом примере сопряжение знаменателя равно 3+2. Поэтому умножьте на 1 в виде (3+2)(3+2).
Ответ: 3+2
Обратите внимание, что члены, содержащие квадратный корень в знаменателе, исключаются путем умножения на сопряженное. Мы можем использовать свойство (a+b)(a−b)=a−b, чтобы ускорить процесс умножения выражений в знаменателе.
Пример 20: Рационализируйте знаменатель: 2−62+6.
Решение: Умножьте на 1 в виде 2−62−6.
Ответ: −2+3
Пример 21: Рационализируем знаменатель: x+yx−y.
Решение: В этом примере мы умножим на 1 в форме x−yx−y.
Ответ: x−2xy+yx−y
Попробуйте! Рационализируйте знаменатель: 35+525−3.
Ответ: 195+4511
Решение для видео
(нажмите, чтобы посмотреть видео)Ключевые выводы
- Чтобы умножить два одночленных подкоренных выражения, умножьте коэффициенты и умножьте подкоренные числа. Если возможно, упростите результат.
- Применять распределительное свойство при умножении подкоренных выражений с несколькими терминами. Затем упростите и объедините все как радикалы.
- Умножение двухчленного подкоренного выражения, содержащего квадратные корни, на его сопряженное дает рациональное выражение.
- Подкоренные выражения принято записывать без подкоренных в знаменателе.
 Процесс нахождения такого эквивалентного выражения называется рационализацией знаменателя.
Процесс нахождения такого эквивалентного выражения называется рационализацией знаменателя. - Если в выражении есть один член в знаменателе, содержащий радикал, то рационализируйте его, умножив числитель и знаменатель на n -й корень из множителей подкоренного и так, чтобы их степени были равны индексу.
- Если подкоренное выражение имеет в знаменателе два члена, содержащих квадратные корни, то рационализируйте его, умножив числитель и знаменатель на сопряженные с ними.
Тематические упражнения
Часть A: Умножение радикальных выражений
Умножение. ( Предположим, что все переменные неотрицательны. )
1. 3=5
2. 7 %
3. 2=6
4. 5om15
5. 7t7
6. 12 порядка12
7. 25 % 70009
8. 315 ОТДОЙ 26
9. (25) 2
10. (62) 2
11. 2xt2x
12. 5y порядка
13. 3а⋅12
14. 3а⋅2а
3а⋅2а
15. 42x> 36x
16. 510y порядка 22y
17. 53 порядка253
18. 43=23
19. 43z103
20. 183t63
21. (5 93). (2 63)
22. (2 43) (3 43)
23. (2 23) 3
24. (3 43) 3
25. 3a23t9a3
26. 7b3t49b23
27. 6x23t4x23
28. 12y3s9y23
29. 20x2y3t10x2y23
30. 63xy3⋅12x4y23
31. 5 (3-5)
32. 2 (3–2)
3333. 37(27−3)
34. 25(6−310)
35. 6(3−2)
36. 15(5+3)
37. х(х+ху)
38. у(ху+у)
39. 2ab(14a−210b)
40. 6ab(52a−3b)
41. (2−5)(3+7)
42. (3+2)(5−7)
43 , (23−4)(36+1)
44. (5−26)(7−23)
45. (5−3)2
46. (7−2)2
47. ( 23+2)(23−2)
48. (2+37)(2−37)
49. (a−2b)2
50. (ab+1)2
51. Какие периметр и площадь прямоугольника, длина которого 53 сантиметра, а ширина 32 сантиметра?
52. Каковы периметр и площадь прямоугольника, длина которого 26 сантиметров, а ширина 3 сантиметра?
53. Если основание треугольника 62 метра, а высота 32 метра, то какова его площадь?
Если основание треугольника 62 метра, а высота 32 метра, то какова его площадь?
54. Если основание треугольника 63 метра, а высота 36 метров, то какова его площадь?
Часть B: Деление подкоренных выражений
Разделить.
55. 753
56. 36010
57. 7275
58. 9098
59. 90x52x
60. 96y33y
61. 162x7y52xy
62. 363x4y93xy
63. 16a5b232a2b23
64. 192a2b732a2b23
Rationalize the denominator.
65. 15
66. 16
67. 23
68. 37
69. 5210
70. 356
71. 3–53
72. 6-22
73. 17x 17x.
74. 13 лет
75. a5ab
76. 3b223ab
77. 2363
78. 1473
79. 14×3
80. 13y23
81. 9x⋅239xy23
82. 5y2⋅x35x2y3
83. 3a2 3a2b23
84. 25n3 25m2n3
85. 327x2y5
86. 216xy25
87. ab9a3b5
88. abcab2c35
abcab2c35
89. 310−3
90. 26−2
91. 15+3
92. 17−2
93. 33+ 6
94. 55+15
95. 105−35
96. −224−32
97. 3+53−5
98. 10−210+2
99. 23−3243+2
100. 65+225−2
101. x+yx−y
902.004 1xy +y103. a-ba+b
104. ab+2ab-2
105. x5-2x
106. 1x-y
Часть C: Обсуждение
107. причины, по которым принято рационализировать знаменатель.
108. Объясните своими словами, как рационализировать знаменатель.
Ответы
1: 15
3: 23
5: 7
7: 702
9: 20
11: 2x
13: 6a
15: 24×3
17: 5
19: 2 53
21: 21: 30 23
23: 16
25: 3A
27: 2x порядка 3×3
29: 2xyцать 25×3
31: 35–5
33: 42–321
35: 32-23
37 37 : x+xy
39: 2a7b−4b5a
41: 6+14−15−35
43: 182+23−126−4
45: 8−215
97: 47: 182+23−126−4
0009
49: a−22ab+2b
51: Периметр: (103+62) сантиметров; area: 156 square centimeters
53: 18 square meters
55: 5
57: 265
59: 3×25
61: 9x3y2
63: 2a
65: 55
67: 63
69 : 104
71: 3–153
73: 7x7x
75: AB5B
77: 633
79: 2x232x
81: 3 6x2y3y
83: 9AB32B9999954 855. 8554 8554 8554 855. 855. 855. 8554545445.
8554 8554 8554 855. 855. 855. 8554545445.
5. 8554 8. 85545445.
5.
45.
5.
54 855.
45.
5.
5.
5.
454 85: 3 6x2y3y
83:
81: 3 6x2y3y
83:
81: 3.0004 87: 27A2B453
89: 310+
91: 5–32
93: −1+2
95: −5–352
97: −4-15
99: 15-7623
97: −4-1599: 15-7623
997: −4-1599: 15-7623
9101: x2+2xy+yx2−y
103: a−2ab+ba−b
105: 5x+2×25−4x
Радикалы | безграничная алгебра |
Знакомство с радикалами
Радикальные выражения дают корни и являются обратными экспоненциальным выражениям.
Цели обучения
Описать корень числа с точки зрения возведения в степень
Ключевые выводы
Ключевые моменты
Ключевые термины
- корень

- подкоренное выражение : математическое выражение, содержащее корень, записанное в виде
an\sqrt[n]{a}na
. - кубический корень : Корень степени 3, записанный в виде
a3\sqrt[3]{a}3a
. - квадратный корень : Корень второй степени, записанный в виде
a\sqrt{a}a
.
Корни — это обратная операция возведения в степень. Математические выражения с корнями называются подкоренными выражениями и их легко распознать, поскольку они содержат радикальный символ (
\sqrt{}
).
Вспомните, что показатели степени означают, что мы должны умножить данное целое число определенное количество раз. Например,
Например,
Поскольку корни являются обратной операцией возведения в степень, они позволяют нам работать в обратном направлении от решения экспоненциального выражения к числу в основании выражения.
Например, следующее радикальное выражение, которое переворачивает приведенное выше решение, работая в обратном порядке от 49 до его квадратного корня: символ известен как «радикал», а решение 7 называется «корень».
Найти значение конкретного корня может быть намного сложнее, чем решить экспоненциальное выражение. На данный момент важно упростить распознавание отношений между корнями и показателями: если корень
rrr
определен как
nthn \text{th}nth
корень из
xxx
, он представлен как
xn=r\sqrt [ n ]{ x } = rnx
=r
Поскольку корни обратны показателям степени, мы можем сократить корень в этом уравнении, возведя ответ в n-ю степень: 92 = 6 \cdot 6 = 3662=6⋅6=36
, и поэтому заключаем, что 6 является корнем
36\sqrt{36}36
. Таким образом, у нас есть ответ,
Таким образом, у нас есть ответ,
36=6\sqrt{36} = 636
=6
.
Кубические корни
Кубический корень числа (
x3\sqrt [ 3 ]{x}3x
) также можно вычислить. Кубический корень из значения
xxx
– это число, которое при возведении в куб (т. е. при возведении в степень 3) дает исходное число 9.3 = 2 \cdot 2\cdot 2=823=2⋅2⋅2=8
. Это также можно записать как
83=2\sqrt[3]{8}=238
=2
.
Другие корни
Существует бесконечное количество возможных корней, все они имеют форму
an\sqrt [n]{a}na
. Вместо
Вместо
nnn
можно заменить любое целое число, отличное от нуля. Например,
a4\sqrt[4]{a}4a
называется «корнем четвертой степени из
aaa 9».4 = 7\cdot 7\cdot 7\cdot 7 = 240174=7⋅7⋅7⋅7=2401
.
Сложение, вычитание и умножение радикальных выражений
Радикалы и экспоненты предъявляют особые требования к сложению и вычитанию, в то время как умножение выполняется более свободно.
Цели обучения
Различие между правильным и неправильным использованием операций над радикальными выражениями
Ключевые выводы
Ключевые моменты
- Чтобы добавить радикалы, подкоренное число (число под радикалом) должно быть одинаковым для каждого радикала.
- Вычитание выполняется по тем же правилам, что и сложение: подкоренное число должно быть одинаковым.

- Умножение радикалов просто требует, чтобы мы умножали термин под радикальными знаками.
Ключевые термины
- подкоренное число : Число или выражение, квадратный корень или другой корень которого рассматривается; например, 3 в
3n\sqrt[n]{3}n3
. Проще говоря, число под радикалом. - радикальное выражение : Выражение, представляющее корень числа или количества.
Корни — это обратная операция для показателей. Выражение с корнями называется радикальным выражением . Легко, хотя, возможно, и утомительно, вычислять показатели степени, зная корень. Например,
7⋅7⋅7⋅7=49⋅49=24017\cdot7\cdot7\cdot7 = 49\cdot49 = 24017⋅7⋅7⋅7=49⋅49=2401
. Итак, мы знаем, что корень в четвертой степени из 2401 равен 7, а квадратный корень из 2401 равен 49. Чему равен корень в третьей степени из 2401? Найти значение для конкретного корня сложно. Это связано с тем, что возведение в степень — это функция другого типа, чем сложение, вычитание, умножение и деление.
Чему равен корень в третьей степени из 2401? Найти значение для конкретного корня сложно. Это связано с тем, что возведение в степень — это функция другого типа, чем сложение, вычитание, умножение и деление.
Давайте рассмотрим некоторые основные математические операции с радикалами и показателями.
Сложение и вычитание подкоренных выражений
Чтобы сложить радикалы, подкоренное число и (число под радикалом) должны быть одинаковыми для каждого радикала, поэтому общее уравнение будет иметь вид:
ab+cb=(a+c)ba\sqrt{ b}+c\sqrt{b} = (a+c)\sqrt{b}ab
+cb
=(a+c)b
Вместо переменных подставим числа. :
3+23=33\sqrt 3 +2\sqrt 3 = 3\sqrt 33
+23
=33
a−c)ba\sqrt b — c\sqrt b = (a-c)\sqrt bab
−cb
=(a−c)b
Например:
33−23=33 \sqrt 3 -2\sqrt 3 = \sqrt 333
−23
=3
Умножение радикальных выражений
Умножение радикалов просто требует, чтобы мы умножали переменную под знаками радикалов.
a⋅b=a⋅b\sqrt a \cdot \sqrt b = \sqrt {a\cdot b}a
⋅b
=a⋅b
Некоторые примеры с вещественными числами:
3⋅6=18\sqrt 3 \cdot \sqrt 6 = \sqrt {18}3
⋅6
=18
Это уравнение можно еще упростить; мы рассмотрим упрощение в другом разделе.
Упрощение радикальных выражений
Подкоренное выражение можно упростить, если:
- значение под знаком корня можно записать в виде степени, 92}{3}} = 4\sqrt{\frac{1}{3}}316
=342
=431
Тогда можно обратиться к дроби под знаком корня. , а радикал в числителе снова можно упростить.

413 = 413 = 43 \ displaystyle 4 \ sqrt {\ frac {1} {3}} = \ frac {4 \ sqrt {1}} {\ sqrt {3}} = \ frac {4} {\ sqrt { 3}}431
=3
41
=3
4
Наконец, из знаменателя нужно удалить радикал.
43 = 43⋅33 = 433 = 433 \ displaystyle \ frac {4} {\ sqrt {3}} = \ frac {4} {\ sqrt {3}} \ cdot \ frac {\ sqrt {3}} { \sqrt{3}} = \frac{4\sqrt{3}}{3} = \frac{4}{3}\sqrt{3}3
4=3
4⋅3
3
=343
=343
Фракции, содержащие радикалы
8 Корневая рационализация — это процесс, посредством которого удаляются все корни в знаменателе иррациональной дроби.
Цели обучения
Преобразование между дробями с рационализированными знаменателями и без них
Ключевые выводы
Ключевые моменты
- Чтобы рационализировать знаменатель, умножьте и числитель, и знаменатель на радикал в знаменателе.
Ключевые термины
- рационализация : Процесс, посредством которого удаляются радикалы в знаменателе дроби.
В математике нам часто дают термины в виде дробей с радикалами в числителе и/или знаменателе. Когда нам даны выражения, в которых в знаменателе есть радикалы, проще вычислить выражение, если мы перепишем его таким образом, чтобы радикал больше не был в знаменателе. Этот процесс называется рационализация знаменателя .
Прежде чем мы начнем, помните, что все, что мы делаем с одной частью алгебраического уравнения, мы должны делать и с другой частью. Тот же принцип можно применить и к дробям: что бы мы ни делали с числителем, мы должны делать и со знаменателем, и наоборот.
 2}} = {\frac{10\sqrt{3}}{3}}3
2}} = {\frac{10\sqrt{3}}{3}}310⋅3
3
=3
210⋅3
=3103
Мнимые числа
3 9 07003 Не существует такого значения, которое при возведении в квадрат дает отрицательное значение; поэтому мы классифицируем корни отрицательных чисел как «мнимые».
Цели обучения
Объясните, что такое мнимые числа и зачем они нужны в математике
Ключевые выводы
Ключевые моменты
- 2=-1×2=-1 для
xxx
приводит к «числу», которое не является действительным числом, называемым мнимым числом. - Мнимое число
iii
определяется как квадратный корень из -1:i=−1i=\sqrt{-1}i=−1
.
Ключевые термины
- мнимое число : Квадратный корень из -1.

- radicand : Значение под знаком радикала.
Подкоренное выражение представляет собой корень данной величины. Что тогда означает, если значение под корнем отрицательное, например, в 92 =-1×2=-1
верное утверждение.
Здесь на помощь приходят мнимые числа. Когда подкоренное число (значение под знаком корня) отрицательное, говорят, что корень этого числа является мнимым числом. В частности, мнимое число ,
iii
определяется как квадратный корень из -1: таким образом,
i=-1i=\sqrt{-1}i=-1
.
Мы можем записать квадратный корень из любого отрицательного числа через
iii
. Вот несколько примеров:
Лицензии и атрибуции
Контент под лицензией CC, совместно используемый ранее
- Курирование и доработка.
 Автор : Boundless.com. Лицензия : Общественное достояние: Неизвестно Авторские права
Автор : Boundless.com. Лицензия : Общественное достояние: Неизвестно Авторские права
Лицензионный контент CC, конкретное указание авторства
- Радикальные функции. Предоставлено : Безгранично. Лицензия : CC BY-SA: Attribution-ShareAlike
- Корень. Предоставлено : Викисловарь . Расположен по адресу : https://en.wiktionary.org/wiki/root. Лицензия : CC BY-SA: Attribution-ShareAlike
- N-й корень. Предоставлено : Википедия. Лицензия : CC BY-SA: Attribution-ShareAlike
- подкорен. Предоставлено : Викисловарь. Лицензия : CC BY-SA: Attribution-ShareAlike
- N-й корень. Предоставлено : Википедия. Лицензия : CC BY-SA: Attribution-ShareAlike
- Алгебра/Корни и радикалы.


 Процесс нахождения такого эквивалентного выражения называется рационализацией знаменателя.
Процесс нахождения такого эквивалентного выражения называется рационализацией знаменателя.


 2}} = {\frac{10\sqrt{3}}{3}}3
2}} = {\frac{10\sqrt{3}}{3}}3
 Автор : Boundless.com. Лицензия : Общественное достояние: Неизвестно Авторские права
Автор : Boundless.com. Лицензия : Общественное достояние: Неизвестно Авторские права 