Умножение матрицы 2х2 на 2х2: Онлайн калькулятор. Умножение матриц

Компания DeepMind рассказала, как они используют глубокое обучение с подкреплением

Исследования в области машинного обучения развиваются все более быстрыми темпами. Вероятно, до достижения сингулярности еще несколько десятков лет, но ИИ уже стал модным словечком, которым пользуется каждая технологическая компания. Существует бесчисленное множество моделей ИИ, но многие из них полагаются на аналогичные методы обучения для развития и совершенствования своих возможностей. 

Обучение с подкреплением в широком смысле описывает методы, в которых используются вознаграждения и штрафы для управления моделью ИИ при выполнении сложной задачи. Человеческой аналогией может быть игра в любую игру с рейтинговой системой. Победа в играх вознаграждается продвижением вверх в таблице лидеров, а ошибки сопровождаются понижением рейтинга. В процессе обучения игроки будут пробовать разные тактики и стратегии, чтобы приспособиться к тому, что делают противники. Конечно, некоторые люди могут не заботиться о ранге в иерархии, но модели ИИ могут быть принуждены программным обеспечением.

AlphaTensor — это модель искусственного интеллекта, основанная на AlphaZero, перед которой стоит задача обнаружения алгоритмов для решения произвольных задач умножения матриц. Умножения матриц используются для описания преобразований в пространстве, а матрицы представляют математическую концепцию, называемую тензором, общим термином для скаляров и векторов. Тензорная математика лежит в основе линейной алгебры и имеет применение в различных областях, от материаловедения до самого машинного обучения.

Матричные умножения решаются в соответствии с определенными правилами и процессами. Как и в большей части математики, существуют оптимизации, позволяющие решать эти задачи за меньшее количество шагов. Усовершенствованные алгоритмы позволяют выполнять умножение больших матриц в допустимых временных масштабах.

Пример умножения двух матриц 2×2

AlphaTensor представлена игрой в виде одиночной головоломки. Доска состоит из сетки чисел, представляющих 3D-тензор, который AlphaTensor затем должен свести к нулю с помощью серии допустимых ходов, состоящих из матричных умножений.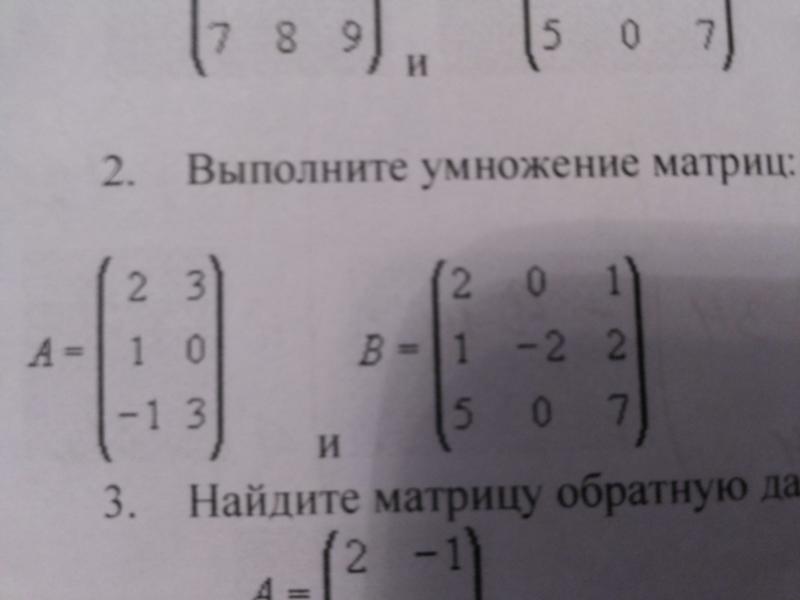 Возможный набор ходов ошеломляюще огромен, превосходя такие игры, как шахматы и го, по нескольким параметрам.

ИИ использует поиск по дереву Монте-Карло (MCTS) для планирования своих действий. По сути, это та же система, которую AlphaZero использует для освоения шахмат и го. В MCTS ИИ-игрок просматривает выборку потенциальных ходов, результаты которых отслеживаются как распределение потенциального успеха. Раунды игры ограничены определенным количеством запусков, чтобы избежать излишне длинных игр, но успешные матчи переигрываются для улучшения параметров принятия решений в сети.

Соавтор Хусейн Фавзи рассказал Nature: «AlphaTensor не встраивает человеческую интуицию в отношении матричного умножения», поэтому «ИИ в некотором смысле должен создавать свои собственные знания о проблеме с нуля». Благодаря этой обратной связи AlphaTensor узнает, какие шаги с большей вероятностью принесут успех. При размерах матриц до 5 x 5 пар AlphaTensor соответствует или превосходит эффективность известных алгоритмов с точки зрения количества шагов.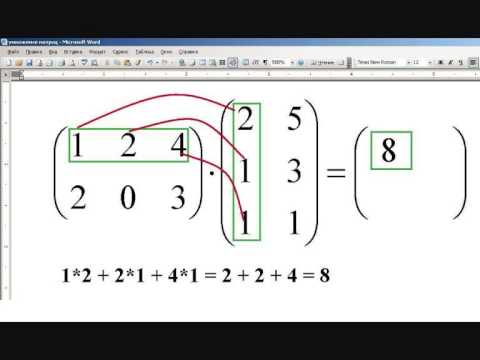

В частности, AlphaTensor обнаружил 47-шаговое решение парного матричного умножения 4 x 4, которое улучшает известное 49-шаговое решение, найденное в 1969 году. Он также сократил на пару шагов парное матричное умножение 5 x 5, сократив 98 шагов до 96.

Исследователи отмечают, что первоначальная предопределенная выборка наборов движений действительно имеет ограничения. Возможно, что более эффективные алгоритмы могли бы быть получены из исходных ходов, которые были исключены в начале. Помимо перебора всех возможных ходов, что требует значительных вычислительных ресурсов, исследователи считают, что они могут адаптировать AlphaTensor для поиска лучших стартовых наборов.

рекомендации

В действительности, однако, легко провести параллели между AlphaTensor, который учится решать эти огромные проблемы, и начинающим игроком в Starcraft, в котором ИИ DeepMind по совпадению также преуспел. Путем итерации он узнает, какие ходы максимизируют его шансы на успех, а какие с большей вероятностью закончатся неудачей — например, когда рой зерглингов поджаривается группой огнедышащих летучих мышей противника. В будущих матчах игрок за зерга может попытаться незаметно пробежать мимо, чтобы воспользоваться отсутствием мобильности адской летучей мыши, а не вступать в прямой бой. Умножение матриц может быть не таким захватывающим, но основной процесс, который ИИ использует для обучения, все тот же.

Этот материал написан посетителем сайта, и за него начислено вознаграждение.

Умножение матриц

1. Умножение матриц — это специфическая операция, со­ставляющая основу алгебры матриц. Строки и столбцы мат­риц можно рассматривать как векторы-строки и векторы-стол­бцы соответствующих размерностей: иными словами, любую матрицу можно интерпретировать как совокупность векторов-строк или векторов-столбцов.

Пусть даны матрица А размером т х п и матрица В разме­ром п х k. Будем рассматривать матрицу А как совокупность т векторов-строк _i размерности п каждый, а матрицу В — как совокупность k векторов-столбцов _j, каждый из которых содержит по п координат:

Векторы-строки матрицы А и векторы-столбцы матрицы В показаны в записи этих матриц (13. 3). Длина строки матри­цы А равна высоте столбца матрицы

В, и потому скалярное произведение этих векторов имеет смысл.

Определение 3. Произведением матриц А и В называется матрица С, элементы которой c_ij равны скалярным произве­дениям векторов-строк _i матрицы А на векторы-столбцы _j матрицы В:

Произведение матриц А и В — матрица С — имеет размер т х k, поскольку длина п векторов-строк и векторов-столбцов исчезает при суммировании произведений координат этих век­торов в их скалярных произведениях, как показано в формулах (13.4). Таким образом, для вычисления элементов первой строки матрицы С необходимо последовательно получить скаляр­ные произведения первой строки матрицы А на все столбцы матрицы В; вторая строка матрицы С получается как ска­лярные произведения второй вектор-строки матрицы

А на все векторы-столбцы матрицы В и так далее. Для удобства за­поминания размера произведения матриц нужно перемножить отношения размеров матриц-сомножителей:, т.е. размер матрицыС равен произведению оставшихся в отношении чисел: т х k.

В операции умножения матриц есть характерная особен­ность: произведение матриц А и В имеет смысл, если число столбцов в А равно числу строк в В. Тогда если А и В — прямоугольные матрицы, то произведение В и А уже не будет иметь смысла, так как в скалярных произведениях, формиру­ющих элементы соответствующей матрицы, должны участво­вать векторы с одинаковым числом координат.

Если матрицы А и В квадратные размером n х n, то име­ет смысл как произведение матриц

АВ, так и произведение матриц BA, причем размер этих матриц такой же, как и у ис­ходных сомножителей. При этом в общем случае перемноже­ния матриц правило перестановочности не соблюдается, т. е. АВ ≠ ВА.

Рассмотрим примеры на умножение матриц.

Решение. Поскольку число столбцов матрицы А равно числу строк матрицы В, то произведение матриц АВ имеет смысл. По формулам (13.4) получаем в произведении матрицу размером 3 х 2:

Произведение ВА не имеет смысла, так как число столбцов матрицы В не совпадает с числом строк матрицы А.

Решение. Здесь мы найдем произведения данных матриц АВ и ВА:

Как видно из результата, матрица произведения зависит от по­рядка расположения матриц в произведении. В обоих случаях произведения матриц имеют тот же размер, что и у исходных сомножителей: 2 х 2.

Решение. В данном случае матрица В представляет собой вектор-столбец, т. е. матрицу, у которой три строки и один столбец. Вообще, векторы — это частные случаи матриц: век­тор-строка длины п представляет собой матрицу с одной стро­кой и п столбцами, а вектор-столбец высоты n — матрицу с n строками и одним столбцом. Размеры данных матриц соот­ветственно 2 х 3 и 3 х 1, так что произведение этих матриц определено. Имеем

В произведении получена матрица размером 2 х 1 или вектор-столбец высоты 2.

Решение. Путем последовательного умножения матриц находим

2. Свойства произведения матриц. Пусть А, В и С — мат­рицы соответствующих размеров (чтобы произведения матриц были определены), а α — действительное число. Тогда следу­ющие свойства произведения матриц имеют место:

1) (АВ)С = А(ВС),

2) (А + В)С = AC + ВС,

3) А(В + С) = АВ + АС,

4) α(АВ) = (αА)В = А(αВ).

В п. 1 этого раздела введено понятие единичной матрицы Е. Нетрудно убедиться, что в алгебре матриц она играет роль единицы, т.е. можно отметить еще два свойства, связанные с умножением на эту матрицу слева и справа в случае квадрат­ных матриц:

5) АЕ = А,

6)

ЕА = А.

Иными словами, произведение любой матрицы на единич­ную матрицу, если оно имеет смысл, не меняет исходную мат­рицу.

алгоритмов. Как доказать, что матричное умножение двух матриц 2×2 не может быть выполнено менее чем за 7 умножений?

спросил 5 лет, 4 месяца назад

Изменено 5 лет, 4 месяца назад

Просмотрено 4к раз

$\begingroup$

В матричном умножении Штрассена мы констатируем один странный (по крайней мере для меня) факт, что матричное умножение двух 2 x 2 требует 7 умножения.

Вопрос : Как доказать невозможность умножения двух матриц 2 x 2 за 6 умножений?

Обратите внимание, что матрицы больше целых чисел.

• алгоритмы
• теория сложности
• нижние границы

$\endgroup$

5

$\begingroup$

Это классический результат Винограда: Об умножении матриц 2×2. 9{\log_27})$ из верхней границы $R(\langle 2,2,2 \rangle) \leq 7$.

Из результата Винограда следует, что $R(\langle 2,2,2 \rangle)=7$. Ландсберг показал, что граничный ранг $\langle 2,2,2 \rangle$ также равен 7, а Bläser et al. недавно расширил это, чтобы поддерживать ранг и ранг пограничной поддержки. Граничный ранг и опорный ранг являются более слабыми (= меньшими) понятиями ранга, которые использовались (в случае граничного ранга) или предлагались (в случае опорного ранга) в алгоритмах быстрого умножения матриц.

$\endgroup$

$\begingroup$

Узнать результат можно по адресу:

С.Виноград, Об умножении 2×2 матрицы , линейная алгебра и прил. 4 (1971), 381–388, MR0297115 (45:6173).

$\endgroup$

Зарегистрируйтесь или войдите в систему

Зарегистрируйтесь с помощью Google

Зарегистрироваться через Facebook

Зарегистрируйтесь, используя электронную почту и пароль

Опубликовать как гость

Электронная почта

Требуется, но никогда не отображается

Опубликовать как гость

Электронная почта

Требуется, но не отображается

Нажимая «Опубликовать свой ответ», вы соглашаетесь с нашими условиями обслуживания, политикой конфиденциальности и политикой использования файлов cookie

.

Калькулятор умножения матриц 2×2 | Калькулятор матриц

Меню

Популярные сегодня

• Преобразователь коэффициентов
• Калькулятор деления коэффициентов
• Калькулятор эквивалентного коэффициента
• Калькулятор коэффициента деления
• 3 Ratio Calculator
• Ratio Calculator
• Fraction Calculator
• Centroid of a Trapezoid Calculator
• Equivalent Ratios Calculator
• Annulus Calculator
• Equivalent Ratios of 3.5:17.5

2 x 2 matrix multiplication calculator is an online tool который запрограммирован таким образом, что может перемножить две матрицы порядка 2 x 2 в кратчайшие сроки. В отличие от обычного умножения, матричное умножение не так просто. Это требует много времени и усилий. Если вы думаете, что можете самостоятельно перемножить две матрицы, просто используя мозг и ручные вычисления, позвольте нам предупредить вас, поскольку это легче сказать, чем сделать. Это может стоить вам много времени, и процесс настолько длительный, что вам, вероятно, придется дважды проверять, чтобы подтвердить, являются ли результаты точными или нет.

2×2 Matrix Multiplication Calculator

Matrix A
Matrix B

2×2 Matrix Multiplication Calculator Results

2×2 Matrix Calculation
Результат умножения матриц 2×2

О калькуляторе умножения матриц 2 x 2

Итак, зачем мучиться и тратить время на вычисление умножения матриц 2×2 вручную, если вы можете использовать наш калькулятор умножения матриц 2 x 2, который может обеспечить наиболее точный результат без особых усилий. Умножение матриц порядка 2 x 2 может быть выполнено только тогда, когда количество столбцов в первой матрице равно количеству строк в другой матрице. Если вышеуказанное условие не выполняется, вы не можете перемножить две матрицы.

Полученная матрица будет иметь порядок в виде A x B, где A — количество строк первой матрицы, а B — количество столбцов второй матрицы.

При умножении двух матриц можно даже использовать мультипликативную идентичность матрицы. Мультипликативная идентичность матрицы — это такая матрица, которая при умножении на исходную матрицу (скажем, A) дает в результате ту же матрицу (A). Единичная матрица (мультипликативная единичная матрица) часто обозначается символом I. Вы также можете попытаться умножить матрицу на ее единичную матрицу с помощью приведенного выше калькулятора умножения матриц 2 x 2, чтобы доказать приведенное выше определение мультипликативной единичной матрицы. . Вам просто нужно ввести элементы двух матриц в необходимые поля, и вы получите результаты в мгновение ока, как только вы нажмете кнопку ввода.