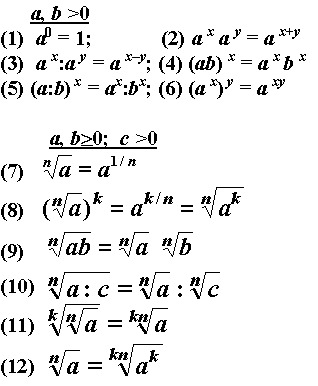Умножение сложение вычитание корней: Сложение корней урок. Умножение корней: основные правила

2 целых умножить на 3 10. Извлечение корня из числа

Математический-Калькулятор-Онлайн v.1.0

Калькулятор выполняет следующие операции: сложение, вычитание, умножение, деление, работа с десятичными, извлечение корня, возведение в степень, вычисление процентов и др. операции.

Решение:

Как работать с математическим калькулятором

Клавиша	Обозначение	Пояснение
5	цифры 0-9	Арабские цифры. Ввод натуральных целых чисел, нуля. Для получения отрицательного целого числа необходимо нажать клавишу +/-
.	точка (запятая)	Разделитель для обозначения десятичной дроби. При отсутствии цифры перед точкой (запятой) калькулятор автоматически подставит ноль перед точкой. Например: .5 — будет записано 0.5
+	знак плюс	Сложение чисел (целые, десятичные дроби)
—	знак минус	Вычитание чисел (целые, десятичные дроби)
÷	знак деления	Деление чисел (целые, десятичные дроби)
х	знак умножения	Умножение чисел (целые, десятичные дроби)
√	корень	Извлечение корня из числа. При повторном нажатие на кнопку «корня» производится вычисление корня из результата. Например: корень из 16 = 4; корень из 4 = 2
x 2	возведение в квадрат	Возведение числа в квадрат. При повторном нажатие на кнопку «возведение в квадрат» производится возведение в квадрат результата Например: квадрат 2 = 4; квадрат 4 = 16
1 / x	дробь	Вывод в десятичные дроби. В числителе 1, в знаменателе вводимое число
%	процент	Получение процента от числа. Для работы необходимо ввести: число из которого будет высчитываться процент, знак (плюс, минус, делить, умножить), сколько процентов в численном виде, кнопка «%»
(	открытая скобка	Открытая скобка для задания приоритета вычисления. Обязательно наличие закрытой скобки. Пример: (2+3)*2=10
)	закрытая скобка	Закрытая скобка для задания приоритета вычисления. Обязательно наличие открытой скобки
±	плюс минус	Меняет знак на противоположный
=	равно	Выводит результат решения. Также над калькулятором в поле «Решение» выводится промежуточные вычисления и результат.
←	удаление символа	Удаляет последний символ
С	сброс	Кнопка сброса. Полностью сбрасывает калькулятор в положение «0»

Алгоритм работы онлайн-калькулятора на примерах

Сложение.

Сложение целых натуральных чисел { 5 + 7 = 12 }

Сложение целых натуральных и отрицательных чисел { 5 + (-2) = 3 }

Сложение десятичных дробных чисел { 0,3 + 5,2 = 5,5 }

Вычитание.

Вычитание целых натуральных чисел { 7 — 5 = 2 }

Вычитание целых натуральных и отрицательных чисел { 5 — (-2) = 7 }

Вычитание десятичных дробных чисел { 6,5 — 1,2 = 4,3 }

Умножение.

Произведение целых натуральных чисел { 3 * 7 = 21 }

Произведение целых натуральных и отрицательных чисел { 5 * (-3) = -15 }

Произведение десятичных дробных чисел { 0,5 * 0,6 = 0,3 }

Деление.

Деление целых натуральных чисел { 27 / 3 = 9 }

Деление целых натуральных и отрицательных чисел { 15 / (-3) = -5 }

Деление десятичных дробных чисел { 6,2 / 2 = 3,1 }

Извлечение корня из числа.

Извлечение корня из целого числа { корень(9) = 3 }

Извлечение корня из десятичных дробей { корень(2,5) = 1,58 }

Извлечение корня из суммы чисел { корень(56 + 25) = 9 }

Извлечение корня из разницы чисел { корень (32 – 7) = 5 }

Возведение числа в квадрат.

Возведение в квадрат целого числа { (3) 2 = 9 }

Возведение в квадрат десятичных дробей { (2,2) 2 = 4,84 }

Перевод в десятичные дроби.

Вычисление процентов от числа

Увеличить на 15% число 230 { 230 + 230 * 0,15 = 264,5 }

Уменьшить на 35% число 510 { 510 – 510 * 0,35 =331,5 }

18% от числа 140 это { 140 * 0,18 = 25,2 }

Ребята, мы вкладываем душу в сайт. Cпасибо за то,
что открываете эту красоту. Спасибо за вдохновение и мурашки.
Присоединяйтесь к нам в Facebook и ВКонтакте

Таблица умножения — базовое понятие в математике, с которым мы знакомимся еще в начальной школе и которое потом используем всю жизнь вне зависимости от профессии. Вот только дети не спешат заучивать бесконечные столбики наизусть, особенно если задание пришлось на каникулы.

сайт даст советы, как легко выучить таблицу вместе с детьми и сделать этот процесс увлекательным.

Таблица Пифагора

Несмотря на то что задача — выучить, то есть заучить, таблицу наизусть, прежде всего важно понять суть самого действия. Для этого можно заменить умножение сложением: одинаковые числа складываются столько раз, на сколько мы умножаем. Например, 6×8 — это сложить 8 раз по 6.

Выделяем цветом одинаковые значения

Отличным помощником для изучения умножения станет таблица Пифагора, которая также демонстрирует некоторые закономерности. Например то, что от перемены мест множителей произведение не меняется: 4×6 = 6×4. Отметьте такие «зеркальные» ответы определенным цветом — это поможет запомнить и не запутаться при повторении.

Начинать изучение таблицы Пифагора лучше с самых простых и понятных частей: умножения на 1, 2, 5 и 10. При умножении на единицу число остается неизменным, а умножение на 2 дает нам удвоенное значение. Все ответы умножения на 5 оканчиваются либо на 0, либо на 5. А вот умножив на 10, в ответе мы получим двузначное число из цифры, которую умножали, и нуля.

Таблица для закрепления результата

Для закрепления результатов нарисуйте с ребенком пустую таблицу Пифагора и предложите ему заполнить клеточки правильными ответами. Для этого вам понадобится всего лишь листок бумаги, карандаш и линейка. Нужно нарисовать квадрат и поделить его на 10 частей по вертикали и горизонтали. А затем заполнить верхнюю строчку и крайний левый столбик числами от 1 до 9, пропустив первую клетку.

Конечно, все дети индивидуальны и универсального рецепта не существует. Главная задача родителя — найти подход и поддержать свое чадо, ведь все мы когда-то начинали с таких одновременно простых и сложных шагов.

С лучшей бесплатной игрой учится очень быстро. Проверьте это сами!

Учить таблицу умножения — игра

Попробуйте нашу обучающую электронную игру. Используя её, вы уже завтра сможете решать математические задачи в классе у доски без ответов, не прибегая к табличке, чтобы умножить числа. Стоит только начать играть, и уже минут через 40 будет отличный результат. А для закрепления результата тренируйтесь несколько раз, не забывая о перерывах. В идеале – каждый день (сохраните страницу, чтобы не потерять). Игровая форма тренажера подходит как для мальчиков, так и для девочек.

Смотрите ниже шпаргалки в полной форме.

Умножение прямо на сайте (онлайн)

*

Таблица умножения (числа от 1 до 20)

×	1	2	3	4	5	6	7	8	9	10	11	12	13	14	15	16	17	18	19	20
1	1	2	3	4	5	6	7	8	9	10	11	12	13	14	15	16	17	18	19	20
2	2	4	6	8	10	12	14	16	18	20	22	24	26	28	30	32	34	36	38	40
3	3	6	9	12	15	18	21	24	27	30	33	36	39	42	45	48	51	54	57	60
4	4	8	12	16	20	24	28	32	36	40	44	48	52	56	60	64	68	72	76	80
5	5	10	15	20	25	30	35	40	45	50	55	60	65	70	75	80	85	90	95	100
6	6	12	18	24	30	36	42	48	54	60	66	72	78	84	90	96	102	108	114	120
7	7	14	21	28	35	42	49	56	63	70	77	84	91	98	105	112	119	126	133	140
8	8	16	24	32	40	48	56	64	72	80	88	96	104	112	120	128	136	144	152	160
9	9	18	27	36	45	54	63	72	81	90	99	108	117	126	135	144	153	162	171	180
10	10	20	30	40	50	60	70	80	90	100	110	120	130	140	150	160	170	180	190	200
11	11	22	33	44	55	66	77	88	99	110	121	132	143	154	165	176	187	198	209	220
12	12	24	36	48	60	72	84	96	108	120	132	144	156	168	180	192	204	216	228	240
13	13	26	39	52	65	78	91	104	117	130	143	156	169	182	195	208	221	234	247	260
14	14	28	42	56	70	84	98	112	126	140	154	168	182	196	210	224	238	252	266	280
15	15	30	45	60	75	90	105	120	135	150	165	180	195	210	225	240	255	270	285	300
16	16	32	48	64	80	96	112	128	144	160	176	192	208	224	240	256	272	288	304	320
17	17	34	51	68	85	102	119	136	153	170	187	204	221	238	255	272	289	306	323	340
18	18	36	54	72	90	108	126	144	162	180	198	216	234	252	270	288	306	324	342	360
19	19	38	57	76	95	114	133	152	171	190	209	228	247	266	285	304	323	342	361	380
20	20	40	60	80	100	120	140	160	180	200	220	240	260	280	300	320	340	360	380	400

Как умножать числа столбиком (видео по математике)

Чтобы потренироваться и быстро выучить, можно также попробовать умножать числа столбиком.

Страница не найдена (ошибка 404)

• Родителям и ученикам
  • Полезная информация
    • Вакантные места для приема (перевода) обучающихся
    • Информационная безопасность
    • Помощь в трудной ситуации
    • Будущим первоклассникам
    • Правила приема, перевода, отчисления
    • Детям с ограниченными возможностями здоровья
    • Отдых и оздоровление учащихся
  • Мероприятия
  • Платные образовательные услуги
  • Новости
  • Каникулы
  • Секции и кружки
  • Олимпиады и конференции
  • Стипендии и меры поддержки обучающихся
  • Услуги и сервисы
• Наша школа
  • О школе
  • Администрация
  • Педагогический состав
  • Наши классы
  • Достижения и победы
    • Доска почета
• Педагогам и сотрудникам
  • Электронный журнал
  • Образовательные ресурсы
  • Профессиональные стандарты
  • Аттестация педагогических работников
  • Повышение квалификации
  • Профсоюзная организация
  • Вакансии
• Независимая оценка качества образования
  • Независимая оценка качества условий образовательной деятельности
  • Независимая оценка качества подготовки обучающихся
• Расписание
• Вопросы и ответы
• Контакты

Решение квадратных корней — упрощение, сложение, вычитание, умножение и деление

Содержание страницы

Упрощение квадратных корней

Грамматическое преобразование в английском языке: . .. of Speech

Первый шаг к извлечению квадратных корней — это умение их упростить. Например, если вам дан квадратный корень √4, вы можете думать о нем как о «числе, которое при возведении в квадрат (или умножении числа на само себя) равно четырем». Правильным ответом будет 2, потому что, когда 2 возводится в квадрат, получается 2 X 2 = 4. Узнайте, как выполнять основные операции с квадратным корнем. Но что, если число под знаком квадратного корня не является полным квадратом? В этом случае вам нужно будет учитывать это. Итак, если вам дали задачу √12, вы должны разложить ее на множители, чтобы получить √(2 X 2 X 3) или √(4 X 3). Затем просто уберите √4 и вместо этого напишите «2», оставив только «3» под знаком квадратного корня. Это оставило бы вас с 2√3.

Сложение и вычитание квадратных корней

Хотите верьте, хотите нет, но складывать и вычитать квадратные корни или другие иррациональные числа очень просто. Просто относитесь к квадратному корню как к переменной, такой как «x» или «y». Например, если вы складываете 2√2 и 3√2, представьте, что вы складываете 2x и 3x: 2√2 + 3√2 = 5√2. Сделайте то же самое для вычитания: 3√2 — 2√2. = 1√2 = √2

Умножение

Следующий шаг — научиться умножать квадратные корни. Чтобы умножить квадратные корни, обязательно отделите числа за пределами знака квадратного корня от тех, которые находятся внутри знака квадратного корня. Например, чтобы решить задачу 2 √ 2 X 3 √ 8, вы должны сначала перемножить 2 и 3, чтобы получить 6, а затем перемножить числа внутри квадратного корня и упростить свой ответ. Таким образом, задача будет выглядеть так: 2√2 X 3√8 = (2X3)√(2X8) = 6√16 = 6X4 = 24

Деление на квадратный корень

Деление на квадратный корень немного сложнее. Иногда вы можете просто сократить знаменатель или упростить его. Например, если вам дали задачу √8/√2, вы можете разделить числитель и знаменатель на √2, что даст вам √4/1 или 2. Таким образом, задача будет выглядеть так: √8 /√2 = √(8/2)/√(2/2) = √4/1 = √4 = 2 Вы также можете встретить более сложную разницу, такую ​​как √2/√3. Как вы можете упростить это? Помните одно простое правило: знаменатель никогда не может быть радикалом (квадратный корень). Чтобы получить квадратный корень из знаменателя, умножьте и числитель, и знаменатель на этот квадратный корень. Например, в задаче √2/√3 вы должны умножить и верх, и низ на √3. Результат будет выглядеть так: √2/√3 = √2/√3 X √3/√3 = √(2X3)/√(3X3) = (√6)/3 И это ваш окончательный ответ.

Примеры проблем

Не уверены, что поняли? Попробуйте некоторые из этих примеров задач на квадратный корень:

1. √16 = ?
2. √27 = ?
3. 2√24 = ?
4. 2√2 + 3√2 — 4√2 = ?
5. 4√2 Х √2 = ?
6. √2 х 3√15 х √3 = ?
7. √27/√3 = ?
8. 2√3/√2 = ?
9. 3√2/√3 = ?
10. (5√3)/(3√5) = ?

Ресурсы

Вот некоторые дополнительные ресурсы, которые вы можете использовать, чтобы узнать больше о решении квадратных корней — Purple Math. «Квадратные корни.» Спаркноты. «Экспоненты». Домашняя математика. «Как вычислить квадратный корень без калькулятора». Изображение предоставлено Clker-Free-Vector-Images с сайта Pixabay 9.0003

Этот пост является частью серии: Учебные пособия по математике

Запутались на уроке математики? Эти пособия по математике охватывают различные темы, от квадратных корней до неправильных дробей.

1. Сложение иррациональных чисел: пошаговое руководство
2. Два метода сложения смешанных дробей — с примерами
3. Шаги деления смешанных дробей с примерами и ресурсами
4. Узнайте, как решать математические задачи на квадратный корень: примеры и ресурсы

Как вычислять дроби и квадратные корни ｜ Hatsudy

Область, которую мы изучаем в математике, — это квадратный корень. Квадратный корень позволяет нам представлять числа до их возведения в квадрат.

Вычисления квадратного корня включают сложение и вычитание. Для умножения и деления мы можем просто умножить числа в корневом символе. С другой стороны, для сложения и вычитания правило состоит в том, что числа в корневом символе должны быть одинаковыми для вычисления.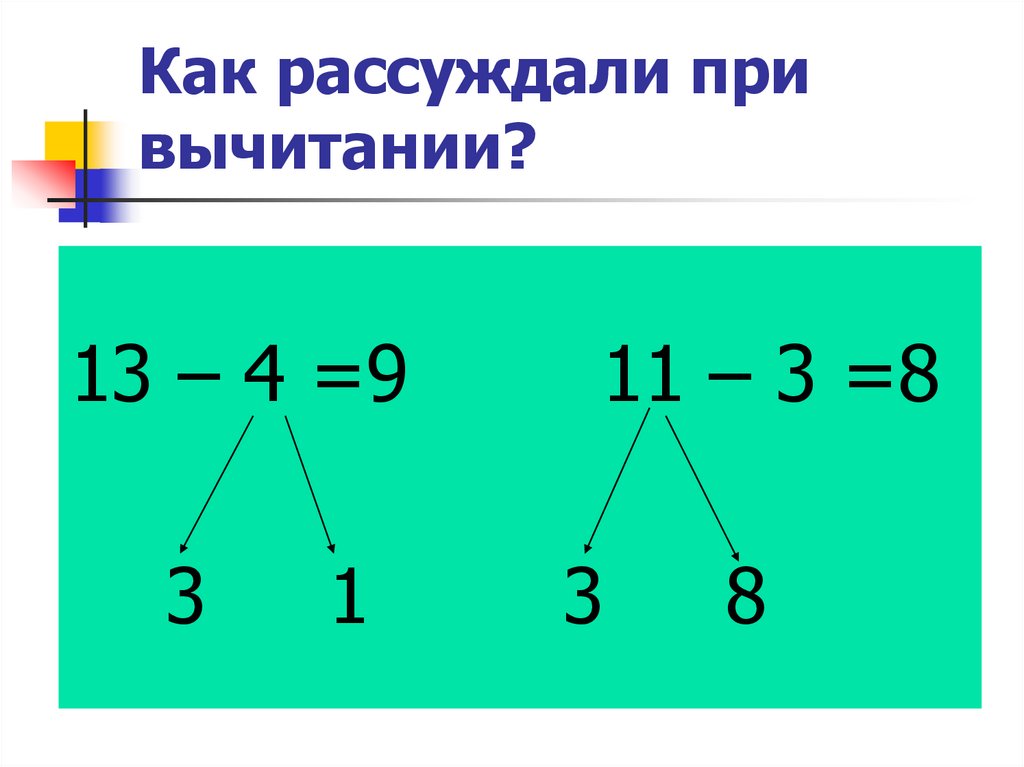

Кроме того, помимо сложения и вычитания, вам необходимо выполнить разложение на простые множители и рационализировать знаменатель. При вычислении квадратных корней сложение и вычитание сложнее, чем умножение.

Итак, мы объясним, как складывать и вычитать квадратные корни.

Содержание

• 1 Как складывать и вычитать квадратный корень
  • 1.1 Сложение и вычитание можно выполнять, если числа в радикальном символе одинаковы
  • 1.2 Сопоставление чисел в корневом символе с помощью простой факторизации
  • 1.3 Рационализируя знаменатель, приведите общий знаменатель и вычислите его
• 2 Умножение квадратного корня и деление с использованием распределительного свойства
  • 2.1 Расширение уравнения с помощью формул факторинга
• 3 Упражнения: сложение и вычитание квадратного корня
• 4 Сложение и вычитание квадратного корня в математике

Как складывать и вычитать квадратный корень

9002 Умножение квадратного корня 9002 и деление, мы можем умножать квадратные корни друг на друга. Хотя необходимо принять некоторые меры предосторожности, все, что вам нужно сделать, это умножить числа в корневом символе.

С другой стороны, что мы должны думать о сложении и вычитании? Для сложения и вычитания не следует складывать или вычитать квадратные корни, имеющие разные числа. Например, следующее неверно.

Метод вычисления отличается от умножения и деления. Почему мы не можем складывать квадратные корни из разных чисел друг в друга? Поскольку квадратный корень — это число до того, как оно возведено в квадрат, его свойства отличаются от целых чисел. 92}=5$. Однако на самом деле ответ должен быть 7. Итак, $\sqrt{9}+\sqrt{16}=\sqrt{25}=5$ неверно.

Поскольку квадрат числа — это квадратный корень, мы получаем следующее.

• $\sqrt{36}=6$
• $\sqrt{100}=10$
• $\sqrt{2500}=50$
• $\sqrt{10000}=100$

Как вы 90 Как видите, числа в корневом знаке намного больше, чем целые числа. Представьте, что целые числа (натуральные числа) и числа в подкоренном символе совершенно разные. Вот почему добавление или вычитание непосредственно к числам в корневом знаке является ошибкой.

Можно выполнять сложение и вычитание, если числа в радикальном символе одинаковы

Как мы можем складывать и вычитать квадратные корни? Складывать и вычитать можно только в том случае, если числа в корневом символе совпадают. Например, это следующее.

• $4\sqrt{2}-\sqrt{2}=3\sqrt{2}$

В этом случае число в корне совпадает с 2. Следовательно, можно складывать и вычитать целые числа перед знаком корня.

$4\sqrt{2}$ означает, что $\sqrt{2}$ четыре. Таким образом, если мы вычтем один $\sqrt{2}$, у нас останется три $\sqrt{2}$.

Вот почему, если числа в корневом знаке одинаковы, мы можем складывать и вычитать.

С другой стороны, что произойдет, если числа в корневом символе будут другими? Как мы уже объяснили, если числа в подкоренном символе одинаковы, мы можем складывать и вычитать. Однако, если числа в подкоренном символе разные, мы не можем ни складывать, ни вычитать их. Например, расчет выглядит следующим образом.

• $2\sqrt{\textcolor{red}{2}}-\sqrt{3}+3\sqrt{\textcolor{red}{2}}=5\sqrt{2}-\sqrt{3}$

Мы не можем складывать или вычитать числа с разными свойствами. Следовательно, ответ на этот расчет равен $5\sqrt{2}-\sqrt{3}$. Чтобы различить, возможно ли сложение и вычитание, посмотрите, совпадают ли числа в корневом символе или нет.

— Метод вычисления такой же, как и при вычислении алгебраических выражений.

Квадратные корни вычисляются так же, как и в алгебраических выражениях. В алгебраических выражениях можно умножать и делить даже разные алфавиты. Однако нельзя добавлять или вычитать разные буквы, как показано ниже.

• $2x+x-2y+4y=3x+2y$

Квадратные корни также можно умножать и делить, даже если числа в символе корня отличаются. Однако, если числа в подкоренном знаке разные, мы не можем складывать или вычитать, как показано ниже.

• $ 2 \ sqrt {\ textcolor {red} {2}} + \ sqrt {\ textcolor {red} {2}} — 2 \ sqrt {\ textcolor {синий} {3}} + 4 \ sqrt {\ textcolor {blue}{3}}=3\sqrt{2}+2\sqrt{3}$

Даже если свойства разные, мы все равно можем выполнять умножение и деление. Но если они различны по свойствам, мы не можем сложить или вычесть. В математике обязательно усвойте это правило.

Сопоставьте числа в корневом символе с помощью простой факторизации

Как только вы поймете правила, которые мы обсуждали, вы сможете складывать и вычитать квадратные корни. Однако во многих случаях перед сложением и вычитанием мы должны заранее провести разложение на простые множители. Выполняя простую факторизацию, числа в подкоренном знаке становятся более четкими.

При вычислении квадратного корня мы должны сделать простую факторизацию, чтобы получить $a\sqrt{b}$. Например, у нас есть следующее.

92×2}$

$=3\sqrt{2}+5\sqrt{2}-4\sqrt{2}$

$=4\sqrt{2}$

При вычислении важна простая факторизация квадратных корней, потому что это позволяет нам минимизировать число в знаке радикала. В результате доступны сложение и вычитание.

После рационализации знаменателя составьте общий знаменатель и вычислите его

Существует еще одна важная процедура при вычислении квадратного корня. Это рационализация знаменателя. Если знаменатель имеет квадратные корни (иррациональные числа), его нельзя вычислить. Итак, рационализируя знаменатель, если мы изменим число в знаменателе на целое число, мы сможем складывать и вычитать квадратные корни, создавая общий знаменатель.

Например, как мы можем сделать следующее вычисление?

• $\displaystyle\frac{1}{\sqrt{3}}+\sqrt{3}$

В математике ответ неверен, если знаменатель имеет знак корня. Причина этого в том, что рационализация знаменателя позволяет нам упростить числа.

В случае рационализации знаменателя можно вычислить следующее.

$\displaystyle\frac{1}{\sqrt{3}}+\sqrt{3}$

$=\displaystyle\frac{1\textcolor{red}{×\sqrt{3}}}{\ sqrt{3}\textcolor{red}{×\sqrt{3}}}+\sqrt{3}$

$=\displaystyle\frac{\sqrt{3}}{3}+\sqrt{3}$

$=\displaystyle\frac{\sqrt{3}}{3}+\textcolor{red}{ \displaystyle\frac{3\sqrt{3}}{3}}$ (Создайте общий знаменатель)

$=\displaystyle\frac{4\sqrt{3}}{3}$

Рационализация знаменателя в этом способ позволяет складывать или вычитать с общим знаменателем.

Умножение и деление квадратного корня с использованием распределительного свойства

Когда мы действительно вычисляем квадратный корень, мы не просто складываем и вычитаем. Во многих случаях уравнение включает умножение и деление. Следовательно, мы должны уметь вычислять выражения, включающие сочетание сложения, вычитания, умножения и деления.

Как упоминалось ранее, алгебраические выражения и квадратные корни вычисляются одинаково. Важным правилом алгебраических выражений является дистрибутивность. Следующее является распределительным свойством.

Распределительное свойство — это способ удаления скобок при умножении. Мы также должны использовать распределительное свойство для вычисления квадратного корня.

Например, как мы можем рассчитать следующее?

• $2(1+\sqrt{2})$

Чтобы решить эту проблему, воспользуемся свойством распределения. Это выглядит следующим образом.

После расширения уравнения приступайте к расчету путем сложения и вычитания.

Расширение уравнения с помощью формул факторинга

Однако при вычислении квадратных корней нам приходится вычислять более сложные выражения. Мы используем формулы факторинга, чтобы расширить выражение.

При расширении уравнения умножения с двумя скобками используется следующая формула. 92$

$=9+6\sqrt{5}+5$

$=14+6\sqrt{5}$

Целые числа и квадратные корни различны по свойствам. Следовательно, 14 и $6\sqrt{5}$ не могут быть вычислены дальше. Итак, расчет завершен. Давайте попробуем понять свойства квадратных корней, чтобы мы могли их вычислить.

Упражнения: сложение и вычитание квадратного корня

Q1: Выполните следующие вычисления.

1. $\sqrt{75}+\sqrt{98}-\sqrt{108}$
2. $\sqrt{8}-\displaystyle\frac{1}{\sqrt{2}}$
3. $\sqrt{6}(\sqrt{2}-\sqrt{3})+3\sqrt{ 3}$

A1: Ответы.

(a)

После факторизации простых чисел давайте выполним вычисление квадратного корня.

$\sqrt{75}+\sqrt{98}-\sqrt{108}$

$=5\sqrt{3}+7\sqrt{2}-6\sqrt{3}$

$= 7\sqrt{2}-\sqrt{3}$

(b)

После рационализации знаменателя давайте выполним вычисление квадратного корня.

$\sqrt{8}-\displaystyle\frac{1}{\sqrt{2}}$

$=2\sqrt{2}-\displaystyle\frac{1\textcolor{red}{×\sqrt {2}}}{\sqrt{2}\textcolor{red}{×\sqrt{2}}}$

$=2\sqrt{2}-\displaystyle\frac{\sqrt{2}}}{2 } $

$ = \ displaystyle \ frac {4 \ sqrt {2}} {2} — \ displaystyle \ frac {\ sqrt {2}} {2} $

$ = \ displaystyle \ frac {3 \ sqrt { 2}}{2}$

(c)

Вычислим, используя распределительное свойство.

$\sqrt{6}(\sqrt{2}-\sqrt{3})+3\sqrt{3}$

92=x(y-2x)$

Затем подставляем в это уравнение. Это происходит следующим образом.

$x(y-2x)$

$=(2+\sqrt{2})[4+2\sqrt{2}-2(2+\sqrt{2})]$

$=( 2+\sqrt{2})(4+2\sqrt{2}-4-2\sqrt{2})$

$=(2+\sqrt{2})×0$

$=0$

Сложение и вычитание квадратного корня в математике

Когда мы изучаем основы квадратных корней, после изучения умножения и деления мы изучаем сложение и вычитание.