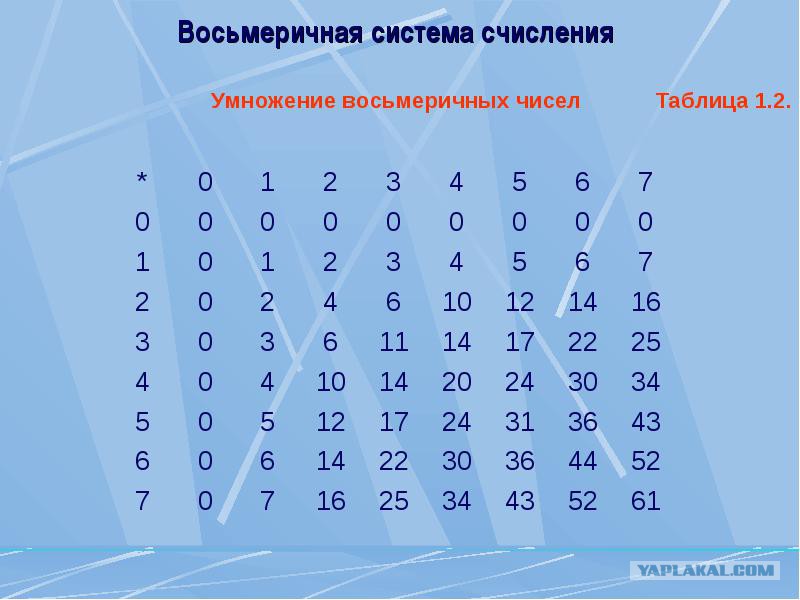
Сложение, вычитание, умножение и деление в системах счисления
Сложение в системах счисления
Как мы складываем в десятичной системе счисления?
Давайте вспомним о том, как мы складываем числа уже привычным нам способом, в десятичной системе счисления.
Самое главное стоит понять разряды. Вспомните алфавит каждой СС и тогда вам станет легче.
Сложение в двоичной системе счисления
Сложение в двоичной системе ничем не отличается от сложения в десятичной системе. Главное помнить, алфавит содержит всего две цифры: 0 и 1. Поэтому когда мы складываем 1 + 1, то получаем 0, и увеличиваем число еще на 1 разряд. Посмотрите на пример выше:
- Начинаем складывать как и привыкли справа налево. 0 + 0 = 0, значит записываем 0. Переходим к следующему разряду.
- Складываем 1 + 1 и получаем 2, но 2 нет в двоичной системе счисления, а значит мы записываем 0, а 1 добавляем к следующему разряду.
- У нас получается в этом разряде три единицы складываем 1 + 1 + 1 = 3, этой цифры также быть не может.
 Значит 3 – 2 = 1. И 1 добавляем к следующему разряду.
Значит 3 – 2 = 1. И 1 добавляем к следующему разряду. - У нас вновь получается 1 + 1 = 2. Мы уже знаем, что 2 быть не может, значит записываем 0, а 1 добавляем к следующему разряду.
- Складывать больше нечего, значит в ответе получаем: 10100.
Один пример мы разобрали, второй решите самостоятельно:
Сложение в восьмеричной системе счисления
Так же как и в любых других системах счисления необходимо помнить Алфавит. Давайте попробуем сложить выражение.
- Все как обычно, начинаем складывать справа налево. 4 + 3 = 7.
- 5 + 4 = 9. Девяти быть не может, значит из 9 вычитаем 8, получаем 1. И еще 1 добавляем к следующему разряду.
- 3 + 7 + 1 = 11. Из 11 вычитаем 8, получаем 3. И единицу добавляем к следующему разряду.
- 6 + 1 = 7.
- Складывать далее нечего. Ответ: 7317.
А теперь проделайте сложение самостоятельно:
Сложение в шестнадцатеричной системе счисления
- Выполняем уже знакомые нам действия и не забываем про алфавит.
 2 + 1 = 3.
2 + 1 = 3. - 5 + 9 = 14. Вспоминаем Алфавит: 14 = Е.
- С = 12. 12 + 8 = 20. Двадцати нет в шестнадцатеричной системе счисления. Значит из 20 вычитаем 16 и получаем 4. И единицу добавляем к следующему разряду.
- 1 + 1 = 2.
- Больше складывать нечего. Ответ: 24Е3.
Вычетание в системах счисления
Вычитание в десятичной системе счисления
Вспомним, как мы это делаем в десятичной системе счисления.
- Начинаем слева направо, от меньшего разряда к большему. 2 – 1 = 1.
- 1 – 0 = 1.
- 3 – 9 = ? Тройка меньше девяти, поэтому позаимствуем единицу из старшего разряда. 13 – 9 = 4.
- Из последнего разряда мы взяли единицу для предыдущего действия, поэтому 4 – 1 = 3.
- Ответ: 3411.
Вычитание в двоичной системе счисления
- Начинаем как обычно. 1 – 1 = 0.
- 1 – 0 = 1.
- От 0 отнять единицу нельзя. Поэтому заберем один разряд у старшего. 2 – 1 = 1.

- Ответ: 110.
А теперь решите самостоятельно:
Вычитание в восьмеричной системе счисления
- Ничего нового, главное помнить алфавит. 4 – 3 = 1.
- 5 – 0 = 5.
- От 3 отнять 7 мы сразу не можем, для этого нам необходимо заимствовать единицу у более старшего разряда. 11 – 7 = 4.
- Помним, что заимствовали единицу ранее, 6 – 1 = 5.
- Ответ: 5451.
Пример для самостоятельного решения:
Вычитание в шестнадцатеричной системе счисления
Возьмем предыдущий пример, и посмотрим каков будет результат в шестнадцатеричной системе. Такой же или другой?
- 4 – 3 = 1.
- 5 – 0 = 5.
- От 3 отнять 7 мы сразу не можем, для этого нам необходимо заимствовать единицу у более старшего разряда. 19 – 7 = 12. В шестнадцатеричной системе 12 = С.
- Помним, что заимствовали единицу ранее, 6 – 1 = 5
- Ответ: 5С51
Пример для самостоятельного решения:
Умножение в системах счисления
Умножение в десятичной системе счисления
Давайте запомним раз и навсегда, что умножение в любой системе счисления на единицу, всегда даст тоже самое число.
- Каждый разряд умножаем на единицу, как обычно справа налево, и получаем число 6748;
- 6748 умножаем на 8 и получаем число 53984;
- Проделываем операцию умножения 6748 на 3. Получаем число 20244;
- Складываем все 3 числа, по правилам. Получаем 2570988;
- Ответ: 2570988.
Умножение в двоичной системе счисления
В двоичной системе умножать очень легко. Мы всегда умножаем либо на 0, либо на единицу. Главное, это внимательно складывать. Давайте попробуем.
- 1101 умножаем на единицу, как обычно справа налево, и получаем число 1101;
- Проделываем эту операцию еще 2 раза;
- Складываем все 3 числа внимательно, помним про алфавит, не забывая про лесенку;
- Ответ: 1011011.
Пример для самостоятельного решения:
Умножение в восьмеричной системе счисления
Есть небольшой лайфхак, как считать в восьмеричной системе. Давайте рассмотрим на примере:
- 5 х 4 = 20.

- При умножении на 0, получаем четыре 0;
- При умножении на 7, у нас получается число 55164;
- Теперь складываем числа и получаем – 5556634;
- Ответ: 5556634.
Пример для самостоятельного решения:
Умножение в шестнадцатеричной системе счисления
Все как обычно, главное вспомните алфавит. Буквенные цифры, для удобства переводите в привычную для себя систему счисления, как умножите, переводите обратно в буквенное значение.
Давайте для наглядности разберем умножение на 5 числа 20А4.
- 5 х 4 = 20. А 20 = 16 + 4. Остаток от деления записываем в число – это будет 4, а 1 держим в уме.
- А х 5 + 1 = 10 х 5 + 1 = 51. 51 = 16 х 3 + 3. Остаток от деления записываем в число – это будет 3, а 3 держим в уме.
- При умножении на 0, получаем 0 + 3 = 3;
- 2 х 5 = 10 = А; В итоге у нас получается А334; Проделываем эту процедуру с двумя другими числами;
- Помним правило умножения на 1;
- При умножении на В, у нас получается число 1670С;
- Теперь складываем числа и получаем – 169В974;
- Ответ: 169В974.

Пример для самостоятельного решения:
Деление в системах счисления
С делением все так же, как и в привычной нам десятичной системе счисления.
Деление в двоичной системе счисления
В двоично системе счисления делить гораздо приятней, чем в десятичной системе. Потому что в десятичной надо угадывать числа и постоянно умножать, чтобы у нас получилось нужное значение. А в двоичной системе на какое еще число кроме единицы необходимо умножить, чтобы получить нужное значение? Правильно, ни на какое.
- Сколько в 101 получится 11? Правильно, 1. 101 – 11 = 10;
- 100 / 11? Так же 1 раз 11 поместится в 100. 100 – 11 = 1;
- 11 / 11 = 1, в остатке 0;
- Ответ: 111.
Деление в восьмеричной системе счисления
- 46 меньше 53, значит делить будем 462. Надо угадать сколько раз число 53 поместиться? Угадываем 7 и записываем;
- 53 / 53 = 1. Записываем к ответу, в остатке у нас 0;
- Последний 0 мы так же записываем к ответу, так как делить больше нечего;
- Ответ: 710.

Деление в шестнадцатеричной системе счисления
Осталось самое страшное – это научиться делить в шестнадцатеричной системе. Да прибудет с нами сила.
- 4С мы должны поделить на 2В. Методом подбора определяем что умножить можем только 1 раз. 4С – 2В = 21 и единицу записываем в ответ;
- Также методом подбора определяем, что 2В, мы можем умножить на С. 219 – 204 = 15;
- Опять, методом подбора определяем, что это 8. 158 – 158 = 0, решение закончено;
- Ответ: 1С8.
Related Articles
Шестнадцатиричная система счисления – умножение, вычитание в таблице
4.1
Средняя оценка: 4.1
Всего получено оценок: 191.
4.1
Средняя оценка: 4.1
Всего получено оценок: 191.
Для записи адресов и содержимого ячеек памяти компьютера используется шестнадцатеричная система счисления. Запись числовых значений в шестнадцатеричной системе счисления, а также выполнение арифметических операций над ними имеет ряд особенностей, о чем можно прочитать в данной статье. 0) = 256 + 240 + 4 = 500
0) = 256 + 240 + 4 = 500
Обратный перевод выполняется последовательным делением десятичного числа на 16 и взятия остатков от деления. Причем полученные остатки в диапазоне от 10 до 15 надо заменить соответствующей буквой.
Выполняя обратный перевод, следует помнить, что результирующее значение получают путем записи полученных от деления остатков в обратном порядке, начиная с последнего частного. Каждый остаток от деления должен получаться всегда меньше шестнадцати.
Например: 500 / 16 = 31 (остаток 4)
31 / 16 = 1 (остаток 15 заменяем на букву F)
Таким образом, получено шестнадцатеричное число 1F4.
Перевод 16 – 2
Для перевода шестнадцатеричного числа в десятичную систему каждую его цифру заменяют группой из четырех нулей и единиц, которую принято называть «тетрадой». Для перевода обычно пользуются таблицей соответствия шестнадцатеричных символов и двоичных тетрад.
Рис. 1. Таблица соответствия шестнадцатеричных чисел и их двоичных и десятичных эквивалентовНапример, 1F4 = (0001)(1111)(0100).
Арифметические действия в шестнадцатеричной системе счисления
Сложение и вычитание
Операции сложения и вычитания удобно выполнять с использованием таблицы сложения шестнадцатеричных чисел. И сложение или вычитание выполняются поразрядно, начиная с младшего разряда.
Рис. 2. Таблица сложения шестнадцатеричных чиселЕсли при сложении двух чисел одинакового разряда получается двузначное число, то значение его старшего разряда (единицу) добавляют в старший разряд.
Например, 1F + 2D = 4C.
Сначала складываются значения младших разрядов F + D. По таблице получается двузначное число1С, единицу старшего разряда которого переносим и добавляем к сумме следующих по величине разрядов суммируемых шестнадцатеричных чисел.
Сумма цифр старших разрядов 1 + 2 равна 3 и еще прибавляется переносимая единица, то есть получается в сумме 4.
Таким образом, получается число 4C.
При выполнении вычитания часто возникает ситуация, когда необходимо выполнять заем из старшего разряда, если уменьшаемое конкретного разряда меньше вычитаемого. Тогда занимается единица из старшего разряда. Значение разности смотрится по таблице.
Тогда занимается единица из старшего разряда. Значение разности смотрится по таблице.
Например, 2D – 1F = E.
Сначала находят разность цифр младших разрядов, то есть D – F (в десятичном представлении 13-15). Уменьшаемое меньше вычитаемого, поэтому происходит заем единицы из старшего разряда исходного числа. То есть вычисляют разность 1D – F = E.
После выполненных манипуляций с младшими разрядами переходят к следующим по величине. В текущем примере следует вычислить 2 – 1. Но ранее произошел заем единицы и в старшем разряде уменьшаемого остается не 2, а 1. Поэтому вычисляется разность 1 – 1 = 0.
Умножение и деление
Умножать и делить числа в шестнадцатеричной системе следует также поразрядно. При вычислениях удобно пользоваться таблицей умножения шестнадцатеричной системы счисления.
Рис. 3. Таблица умножения шестнадцатеричных чиселНапример, 1С * 2 = 38. Используя распределительный закон умножения: (10 + С) * 2 = 10 * 2 + С * 2 = 20 + 18 = 38
Операция деления также выполняется столбиком с использованием таблицы умножения: 1С / 2 = Е. В строке таблицы для числа 2, то есть делителя, находится значение 1С (делимое) и пересечение этой строки и столбца, где расположено 1С даст значение частного от деления числа, то есть Е.
В строке таблицы для числа 2, то есть делителя, находится значение 1С (делимое) и пересечение этой строки и столбца, где расположено 1С даст значение частного от деления числа, то есть Е.
Что мы узнали?
В шестнадцатеричной системе счисления для записи числовых значений используются цифры от 0 до 9 и латинские буквы от A до F. Прямой перевод шестнадцатеричного числа в десятичную систему выполняется с использованием развернутой формы записи числа. Обратный перевод выполняется путем деления и записи остатков. Каждую шестнадцатеричную цифру в числе можно заменить тетрадой двоичных чисел. Арифметические операции в шестнадцатеричной системе удобнее всего выполнять поразрядно с использованием таблиц сложения и умножения шестнадцатеричных чисел
Тест по теме
Доска почёта
Чтобы попасть сюда — пройдите тест.
Роман Журавлев
10/10
Татьяна Лазарева
10/10
Коля Приходько
8/10
Андрей Букин
10/10
Игорь Карабута
1/10
Александра Цалко
8/10
Оценка статьи
4. 1
1
Средняя оценка: 4.1
Всего получено оценок: 191.
А какая ваша оценка?
Умножение десятичных знаков — Примеры | Как умножать десятичные дроби?
Умножение десятичных знаков очень важно, когда мы говорим о группировке предметов. Предположим, вам нужно раздать по 0,25 части плитки шоколада каждому ребенку, а всего детей 12. Сколько плиток шоколада вам понадобится? Чтобы найти необходимое количество плиток шоколада, нужно умножить 12 на 0,25. Умножение десятичных знаков выполняется путем игнорирования десятичной точки и умножения чисел, и тогда количество знаков после запятой в произведении равно общему количеству знаков после запятой в обоих заданных числах.
| 1. | Как умножать десятичные дроби? |
| 2. | Умножение десятичных дробей на целые числа |
| 3. | Умножение двух десятичных чисел |
4. | Часто задаваемые вопросы об умножении десятичных дробей |
Как умножать десятичные дроби?
Умножение десятичных дробей имеет ту же процедуру, что и умножение целых чисел, за исключением размещения десятичной точки в произведении. В нашей повседневной жизни мы сталкивались с различными случаями, когда нам приходилось использовать операцию умножения на двух числах, из которых хотя бы одно или оба являются десятичными числами. Представьте, что вы идете с другом на обед. Вы оба заказываете блюдо стоимостью 6,75 долларов каждое. Общий счет составляет $ 15,75, включая налоги. Чтобы рассчитать общую стоимость тарелки в счете, вам нужно умножить 6,75 доллара на 2. Аналогичным образом предположим, что вы планируете подарить своей матери букет цветов на ее день рождения. Каждый цветок стоит 0,75 доллара, всего вы покупаете 6 цветов. Чтобы найти общую стоимость букета, вам нужно умножить 0,75 доллара на 6. В приведенных выше примерах используется умножение десятичных дробей.
Умножение десятичных дробей на целые числа
Умножение десятичных дробей на целые числа аналогично умножению целых чисел, единственное отличие заключается в расположении десятичной точки. Чтобы умножить десятичные дроби на целые числа, можно выполнить следующие шаги:
- Шаг 1: Сначала игнорируйте десятичную точку и умножайте два числа как обычно.
- Шаг 2: После умножения подсчитайте количество знаков после запятой в десятичном числе. Произведение, полученное после умножения, будет иметь такое же количество знаков после запятой.
- Шаг 3: Поставьте десятичную точку в полученном произведении после Шаг 2 .
Давайте разберемся в реальной ситуации умножения десятичных чисел на целые числа. Группа из 15 учеников решила внести свой вклад в благотворительный фонд. Каждый студент внес вклад в размере 6,5 долларов США. Какую сумму собрали со всего класса? Здесь вклад одного студента = $6,5. Общий вклад, сделанный 15 студентами = 6,5 × 15 = 9 долларов США.7.5.
Общий вклад, сделанный 15 студентами = 6,5 × 15 = 9 долларов США.7.5.
Умножение десятичных дробей на 10 100 и 1000
При умножении любой десятичной дроби на 10, 100, 1000 или любую другую степень 10 мы просто сдвигаем десятичную точку вправо на столько знаков, сколько нулей в степень числа 10.
- Если мы умножаем десятичную дробь на 10, мы сдвигаем десятичную точку на одну позицию вправо, так как в числе 10 1 ноль.
- Если мы умножим любое десятичное число на 100, мы сдвинем десятичную точку на два знака вправо.
- Точно так же, если мы умножаем десятичную дробь на 1000, мы сдвигаем десятичную точку на три знака вправо и так далее.
Например, 2,32 × 10 = 23,2, 2,32 × 100 = 232, 2,32 × 1000 = 2320.
Умножение двух десятичных чисел
Этот раздел поможет вам узнать об умножении двух десятичных чисел. Это то же самое, что и у целого числа, но с той лишь разницей, что в этом случае мы должны взять сумму общего количества знаков после запятой в обоих данных числах, и это должно быть равно количеству знаков после запятой в продукт. Чтобы умножить два десятичных знака, выполните шаги, перечисленные ниже:
Чтобы умножить два десятичных знака, выполните шаги, перечисленные ниже:
- Шаг 1: Сначала игнорируйте десятичную точку и умножайте два числа как обычно.
- Шаг 2: После умножения посчитайте общее количество знаков после запятой в обоих числах. Произведение, полученное после умножения, будет иметь это общее количество знаков после запятой.
- Шаг 3: Поставьте десятичную точку в полученном произведении после Шаг 2 .
Давайте посмотрим на умножение двух десятичных чисел на изображении ниже:
Примеры умножения десятичных дробей:
1. Умножьте 0,567 и 13,065
Следовательно, 7,567 × 17,040 = 8,567 × 13,040 После запятой 6 цифр.
2. Найдите произведение 16,45 и 8,5
Следовательно, 16,45 × 8,5 = 139,825. Произведение имеет 3 знака после запятой.
Важные примечания:
Это несколько важных примечаний, связанных с концепцией умножения десятичных дробей.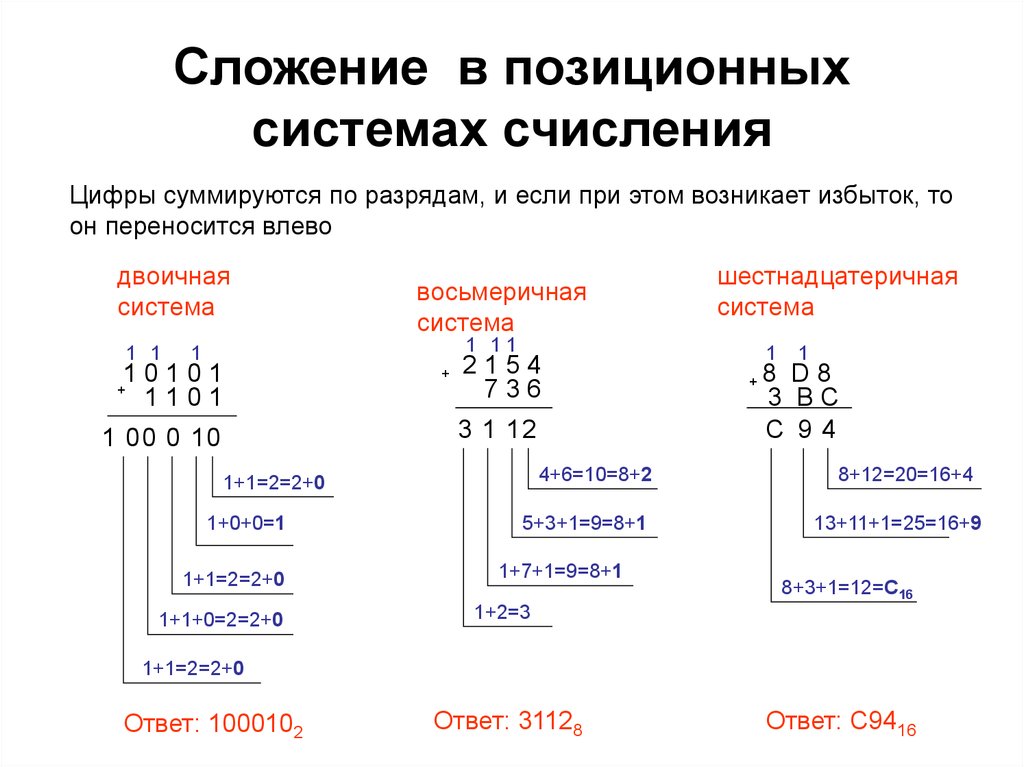 Взглянуть!
Взглянуть!
- Десятичное умножение следует той же процедуре, что и умножение целых чисел.
- Десятичная запятая должна быть поставлена в произведении таким образом, чтобы произведение имело количество знаков после запятой, равное сумме знаков после запятой всех множимых и множителей.
- Убедитесь, что в произведении сохранены все нули при размещении десятичной точки.
- Если в произведении больше знаков после запятой, чем количество цифр, слева перед запятой в произведении можно вставить нули.
- Конечные нули в результирующем произведении могут быть опущены.
Попробуйте решить эти сложные вопросы:
- Чарли платят 17,45 долларов в час, и на прошлой неделе он отработал 42,5 часа. Сколько денег он заработал на прошлой неделе (округлив до цента)?
- Какое общее расстояние проедет автомобиль, если он проехал со скоростью 31,5 км/час за 7 часов 15 минут?
Умножение десятичных знаков Связанные темы
Ознакомьтесь с этими статьями, посвященными умножению десятичных дробей.
- Калькулятор деления десятичных дробей
- Калькулятор добавления десятичных знаков
- Десятичные числа и дроби
- Как добавить десятичные дроби?
- Деление десятичных дробей
- Сложение и вычитание десятичных дробей
- Десятичные числа
Умножение десятичных дробей Примеры
Пример 1: Роуз изучает десятичное умножение. Поможешь ей умножить 0,6748 на 14,9?45?
Решение:
Посмотрим, как умножить 0,6748 на 14,945.
Примечание. Нули в конце можно опустить. Следовательно, 0,6748 × 14,945 = 10,084886.
Пример 2: Грейси пошла в продуктовый магазин со своей матерью. Ее мать купила 15 яблок по 1,25 доллара каждое. Помогите Грейси рассчитать сумму, которую должна заплатить ее мать, используя принцип умножения десятичных знаков.
Решение:
Стоимость одного яблока = 1,25 доллара.
 Таким образом, стоимость 15 яблок = 1,25 × 15 долларов. Следовательно, стоимость 15 яблок составляет 18,75 долларов.
Таким образом, стоимость 15 яблок = 1,25 × 15 долларов. Следовательно, стоимость 15 яблок составляет 18,75 долларов.
перейти к слайдуперейти к слайду
Разбивайте сложные концепции с помощью простых визуальных средств.
Математика больше не будет сложным предметом, особенно когда вы понимаете концепции с помощью визуализаций.
Запись на бесплатный пробный урок
Практические вопросы по умножению десятичных дробей
перейти к слайдуперейти к слайду
Часто задаваемые вопросы об умножении десятичных дробей
Как умножить десятичное число на целое?
Чтобы умножить десятичное число на целое, выполните следующие действия:
- Шаг 1: Не обращайте внимания на десятичную точку и умножайте оба числа.
- Шаг 2: Подсчитайте количество знаков после запятой в десятичном числе.
- Шаг 3: Затем поставьте запятую в произведении так, чтобы количество знаков после запятой в произведении и исходное десятичное число совпадали.

Как умножить десятичные дроби на 1000?
Чтобы умножить десятичные дроби на 1000, сдвиньте запятую на три знака вправо, так как в числе 1000 три нуля.
Как научить умножать десятичные дроби?
Давайте посмотрим, как научить учащихся десятичному умножению следующими способами:
- Сначала дайте учащимся понять значение десятичного умножения с помощью демонстрации и визуализации.
- Во-вторых, познакомьте учащихся с этапами умножения двух десятичных чисел.
- Дайте практические вопросы.
Что такое правило умножения десятичных дробей?
Правила умножения десятичных дробей приведены ниже:
Правила умножения десятичных дробей:
- Выполняйте умножение так же, как и с целыми числами.
- Если в произведении больше знаков после запятой, чем число цифр, перед размещением десятичной точки в произведении можно вставить нули, чтобы слева от десятичной точки был только один ноль, а десятичные знаки в произведении будут равно общему количеству знаков после запятой в обоих числах.

- Десятичная запятая должна быть поставлена в произведении таким образом, чтобы произведение имело количество знаков после запятой, равное сумме знаков после запятой всех множимых и множителей.
- Конечные нули в дробной части результирующего произведения могут быть опущены.
Как умножать десятичные дроби меньше 1?
Чтобы умножить два десятичных знака меньше 1, выполните следующие действия:
- Шаг 1: Сначала игнорируйте десятичную точку и умножайте два числа как обычно.
- Шаг 2: После умножения подсчитайте общее количество знаков после запятой в множимом и множитель. Произведение, полученное после умножения, будет иметь это общее количество знаков после запятой.
- Шаг 3: Поставьте десятичную точку в полученном произведении после Шаг 2 .
Например: 0,2 × 0,4 = 0,08.
Как умножать положительные и отрицательные десятичные дроби?
Положительные и отрицательные десятичные дроби умножаются так же, как два десятичных дроби.
- Умножьте обе числовые части, как при обычном десятичном умножении.
- Так как произведение одного отрицательного числа на одно положительное число отрицательно, поэтому сохраните отрицательный знак перед числовой частью полученного произведения.
Например, -0,5 × 0,3 = -0,15.
Скачать БЕСПЛАТНЫЕ учебные материалы
Рабочие листы по умножению десятичных дробей
Умножение десятичных дробей
Умножение десятичных дробейПоказать рекламу
Скрыть рекламу
О рекламе
Умножьте без десятичной точки, затем снова вставьте ее в нужное место!
Как умножать десятичные числа
Просто выполните следующие действия:
- Умножайте как обычно, игнорируя десятичные точки.
- Затем поставьте в ответе запятую — в нем будет столько знаков после запятой, сколько двух исходных чисел вместе взятых.
Другими словами, просто подсчитайте, сколько чисел после запятой в обоих чисел, которые вы умножаете, тогда ответ должен содержать столько же чисел после и десятичной запятой.
Пример: умножить 0,03 на 1,1
начать с: | 0,03 × 1,1 | |
умножить без десятичной точки: | 3 × 11 = 33 | |
0.03 имеет 2 десятичных знака , | 0,033 |
| См. анимацию умножения десятичных знаков |
Как это работает?
Потому что, когда вы умножаете без десятичной точки, вы действительно сдвигаете десятичную точку вправо до , уберите ее с пути :
| Оригинал: | 1 Перемещение: | 2 хода: | 3 хода: | |||
| 0,03 × 1,1 | 0,3 × 1,1 | 3. × 1,1 × 1,1 | 3. × 11. |
Затем мы выполняем (теперь простое) умножение:
3. × 11. = 33.
Но помните, мы сделали 3 перемещения десятичной точки, поэтому нам нужно отменить это:
| 3 хода: | 2 хода: | 1 Перемещение: | Правильно | |||
| 33. | 3,3 | 0,33 | 0,033 |
Вот еще несколько примеров:
Пример: умножьте 0,25 на 0,2
начните с: | 0,25 × 0,2 | |
умножить без десятичной точки: | 25 × 2 = 50 | |
0,25 имеет 2 знаков после запятой, | 0,050 |
Пример: умножьте 102 на 0,22
начните с: | 102 × 0,22 | |
умножить без десятичной точки: | 102 × 22 = 2244 | |
102 имеет 0 знаков после запятой, | 22,44 |
Здравый смысл
В качестве последней проверки вы можете надеть шляпу «здравого смысла» и подумать «это правильный размер?» , потому что вы не хотите ни за что платить в десять раз больше, ни получать только одну десятую того, что вам нужно!
И все.

 Значит 3 – 2 = 1. И 1 добавляем к следующему разряду.
Значит 3 – 2 = 1. И 1 добавляем к следующему разряду.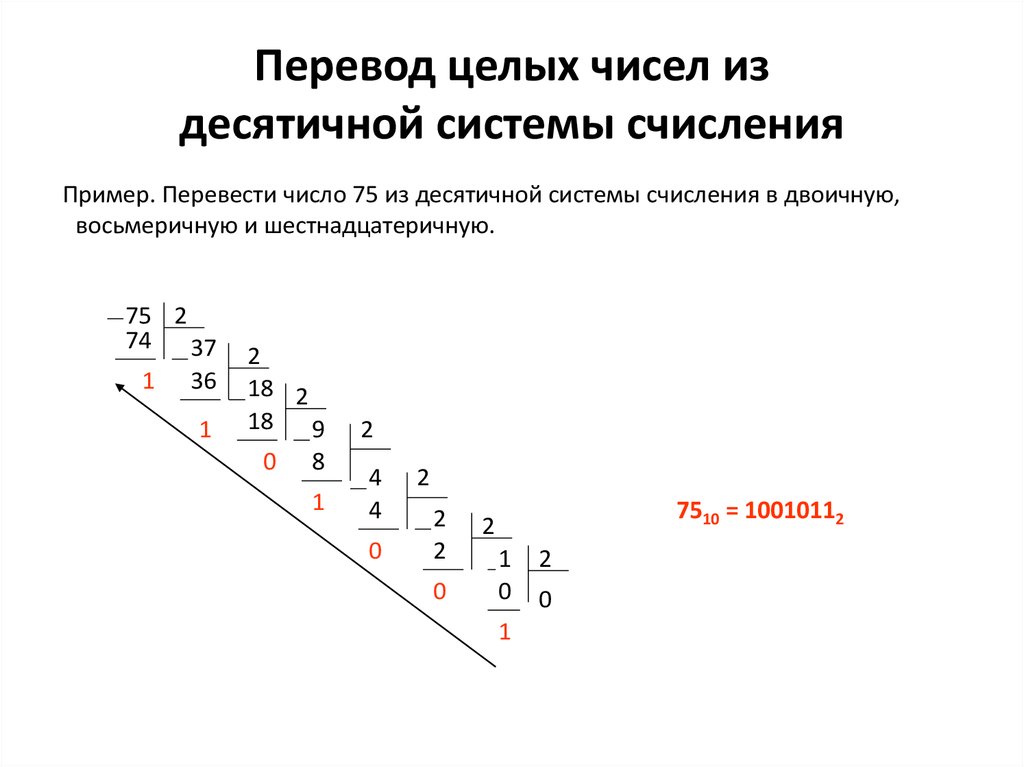 2 + 1 = 3.
2 + 1 = 3.



 Таким образом, стоимость 15 яблок = 1,25 × 15 долларов. Следовательно, стоимость 15 яблок составляет 18,75 долларов.
Таким образом, стоимость 15 яблок = 1,25 × 15 долларов. Следовательно, стоимость 15 яблок составляет 18,75 долларов.