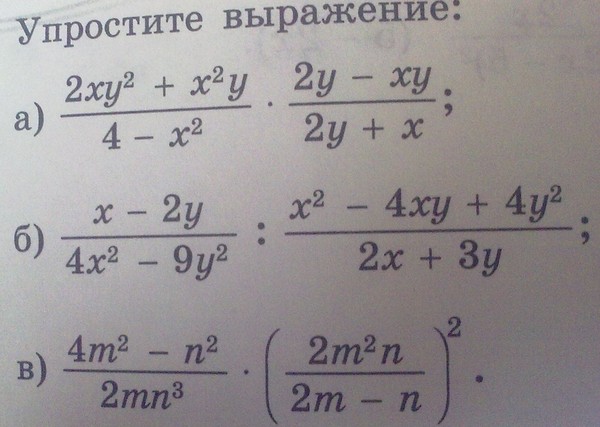Упростите выражение 9 класс: Упростите выражение:

2}$$

алгебра

задан 28 Мар ’13 15:10

Никита Sky
7●1●1●2

изменен 28 Мар ’13 17:05

Anatoliy
12.9k●8●46

старыеновыеценные

Все-таки второй уровень ДПА за 9 класс нужно решать. Там ведь есть еще третий и четвертый уровни. Успехов. $$\Big(\frac{x-2y}{x^2+2xy}-\frac{x+2y}{x^2-2xy}\Big):\frac{4y^2}{4y^2-x^2}=\Big(\frac{x-2y}{x(x+2y)}-\frac{x+2y)}{x(x-2y)}\Big):\frac{4y^2}{4y^2-x^2}=$$ $$=\frac{(x-2y)^2-(x+2y)^2}{x(x^2-4y^2)}:\frac{4y^2}{4y^2-x^2}=. ..$$ ссылка отвечен 28 Мар ’13 17:00 Anatoliy 12.9k●8●46

Ничего трудного дальше нет, вынести минус, перемножить, раскрыть скобки и всё сократится. ответ 1/y ссылка отвечен 11 Окт ’14 15:35 E1em -1

(y+1дробьy-1-yдробьy+1)/3y+1дробьy^2+y ссылка отвечен 28 Апр ’17 20:43 org/Person»>Серёжа -1

у меня получилось 2/у ссылка отвечен 14 Сен ’17 13:42 БАнгелина -1●1

(8 63 + 3 28-5 112):2 7 ссылка отвечен 21 Сен ’20 11:45 org/Person»>tohirbek -1

Ваш ответ

Если вы не нашли ответ, задайте вопрос.

Повторение: алгебраические выражения. 9 класс

Похожие презентации:

Элементы комбинаторики ( 9-11 классы)

Применение производной в науке и в жизни

Проект по математике «Математика вокруг нас. Узоры и орнаменты на посуде»

Знакомство детей с математическими знаками и монетами

Тренажёр по математике «Собираем урожай». Счет в пределах 10

Методы обработки экспериментальных данных

Лекция 6. Корреляционный и регрессионный анализ

Решение задач обязательной части ОГЭ по геометрии

Дифференциальные уравнения

Подготовка к ЕГЭ по математике. Базовый уровень Сложные задачи

1. Тема: «Повторение: алгебраические выражения»

9 класс. Алгебра
Учитель: Бекшаева М. Н.

2. Упростите выражение:

xy3 x 4 x y x 2 xy y 2
2
Упростите выражение: 5
4
2
y 4 x y x y x xy y
Решите уравнение:
y 5
4
24
2
y 3 y 3
y 9
2
2
x
5
y
x
2
20
Решите систему уравнений:
4 x y 8
2
2
3
x
1
1
3
x
1
3
x
2
1
x
Решите неравенство:
Решите систему неравенств:
Задача: одна из сторон треугольника на
20 см больше другой. Если меньшую
сторону увеличить вдвое, а большую
втрое, то периметр нового
прямоугольника станет равным 240 см.
Найдите стороны треугольника.
x 1
1 2 x 4
x 3 1 x 2
2
3

3. Цели:

вспомнить и закрепить методы работы с
алгебраическими выражениями:
правила раскрытия скобок
правила умножения одночлена на
многочлен и многочлена на многочлен
формулы сокращенного умножения
разложение многочлена на множители
действия над рациональными дробями;

4. Задачи урока:

• вспомнить и применить при решении
тренировочных упражнений
вышеперечисленные правила работы с
алгебраическими выражениями.

5. 1) Правила раскрытия скобок

Пример 1 5а (4с 3b) 5a 4c 3b
5а 1 (4с 3b) 5a 4c 3b
Пример 2 5а (4с 3b) 5a 4c 3b
5а 1 (4с 3b) 5a 4c 3b
Общее правило раскрытия в скобках
(a b) c ac bc

6. Устные примеры:

2a 3b 5c 4 8a 12b 20c
1
(8 x 3) 4 x 1,5
2
7 x 3(2 x 1,5) 4( x 3) 3x 7,5

7. 2) Правило умножения одночлена на многочлен

2) Правило умножения
2
2
2
a
b
a
2
ab
b
одночлена на
2
2
2
a
b
a
2
ab
b
многочлен
Пример 3
x (x 1)
x x
2
а 2 b 2 (a b)( a b)
a 3 b3 a b a 2 ab b 2
a 3 b3
a b a
2
ab b 2
2a (3 4a ) 6a 8a
Правило умножения многочлена на
многочлен
Пример 4 x 1 x 2 x 2 x 2 x 2 x 2 x 2
2
2x
2
2
3
5
y x y 2 x3 yx 2 2 x 2 y y 2 2 x3 x 2 y y 2
2

8.

3) Формулы сокращенного умноженияКарточка №1
(3a 1) 9a 6a 1
2
2
x 64 ( x 4)( x 4 x 16)
3
2
a b 2 a 2 2ab b 2
a b 2 a 2 2ab b 2
a 3 b3 a b a 2 ab b 2
а 2 b 2 (a b)( a b) a 3 b3 a b a 2 ab b 2

9. 3) Формулы сокращенного умножения

Карточка №2
(5 y 4 x) 25 y 40 yx 16 x
2
169a с
2
2
2
2
(13a с)(13a с)
a b 2 a 2 2ab b 2
a b 2 a 2 2ab b 2
a 3 b3 a b a 2 ab b 2
а 2 b 2 (a b)( a b) a 3 b3 a b a 2 ab b 2

10. 3) Формулы сокращенного умножения

Карточка №3
25a 64b (5a 8b)(5a 8b)
2
2
x 8 ( x 2)( x 2 x 4)
3
2
a b 2 a 2 2ab b 2
a b 2 a 2 2ab b 2
a 3 b3 a b a 2 ab b 2
а 2 b 2 (a b)( a b) a 3 b3 a b a 2 ab b 2

11. Соедините линиями задания и ответы:

2
4
2
1)( n 2 mn m 2 )( m n)
3
9
3
2) x 6 6 x 3 y 4 9 y 8
1) x 2 64
2)( a 2 2b) 2
3)( x 3 3 y 4 ) 2
4) 4 a 4 a b b
6
3 2
3)(8 x)( x 8)
4
5)(0,3c 0,2d )(0,3c 0,2d )
6)100 x y 20 xy
2
2
7)( a 10b) 2
8)(3 a )(9 6a a )
2
8 3
m n3
27
10)(10m 2 4n 3 )(10m 2 4n 3 )
9)
4)100m 4 80n 3 m 2 16n 6
5)9 a 3
6)0,09c 2 0,04d 2
7)a 4 4a 2b 4b
8)( 2a 3 b 2 ) 2
9)100а 2 20ab b 2
10)(10 x y ) 2

12.

4) Разложение на множители• Ответить на вопрос: что общего в
приведенных ниже примерах?
2
2
2
2
2
8
x
y
16
x
8
x
y
8
x
2
8
x
( y 2)
Пример 5
Пример 6
Пример 7
4a 2b 2 1 (2ab 1)( 2ab 1)
mx my 6 x 6 y m( x y ) 6( x y ) ( x y )( m 6)
Пример 8
2
9 x 2 25 x 6 9( x 3)( x ) ( x 3)(9 x 2)
9
2
D 841, x1 3, x2
9
Ответ: в ответах получаются произведения.

13. Определение.

• Представление многочлена в виде произведения двух
или нескольких многочленов называют разложением
на множители.
• Назвать, исходя из данных примеров, методы
разложения многочлена на множители.
• А) вынесение общего множителя за скобки
• Б) способ группировки
• В) с помощью формул сокращенного умножения
• Г) формула разложения на множители квадратного
трехчлена.
ax 2 bx c a( x x1 )( x x2 )

14. 5) Действия над рациональными дробями

• Сокращение дроби
( x 3) x x 3
( x 5) x x 5
• Сумма и разность дробей
5a
6
5a 6
a 8
a 8 a 8
5a
6
5a 6
a 8 a 8
a 8

15.

Сумма и разность дробей с разными знаменателямиb 8
a 8
b 8
a 8
5a(b 8) 6(a 8)
5a
6
(a 8)(b 8)
a 8 b 8
5a(b 8) 6(a 8)
5a
6
(a 8)(b 8)
a 8 b 8
• Произведение и частное дробей
a (6 a )
a (6 a )
3b
b
3
a (6 a )
3a
:
b
3
b (6 a )
3
a
a
2
b
2
(b 2)
2
6

17. Задание. Рассмотреть решение примера и найти ошибки

x
xx 33 x x 3 3 x
3 3 x x 3 3 x x3 (3x 3) x x3 3
( x 3)
2
x 3 x 3 2x 2 9
22 9
2
x
x
9
x 9 x 3 x 3 x 9
( x 3)
2
2
2
2
2
(
x
3
)(
x
6
x
9
x
6
x
9
)
2
x
18
2( x 3)( x 3)
2( x 3)
2
2
2
2
( xx 39))( x ( x3
)( 3x)( x3 ) 3)( x 3)( x 9)( x 3)
( x 9)(
22
2
xx 93

18. 4. Тренировочные упражнения № 1000(а, в, д, ж), 1004(а, в, д)

• 1 вариант — №1000(а, ж)
а)( x 2 y)( x 2 y) 4 y 2 x 2 4 y 2 4 y 2 x 2
ж)(3x 4 y) 2 (2 x 7 y)(4 x 2 y) x 2 30 y 2
• 2 вариант — №1000(в, д)
в)(5 x 1) 2 10 x 25 x 2 1
д)(m 2n)(m2 2mn 4n 2 ) 6n3 m3 2n 2

19.

№1004 учащиеся решают по рядам: 1 ряд – а), 2 ряд – в), 3 ряд – д).• Ответы выбрать из предложенных
выражений на слайде:
( x 5 y)
2
(2a c)(4a 2ac c )
2
2
( x 5 y)( x 5 y)
2
2
(2a c)(4a 2ac c )
(3b 4c)(3b 4c) ( x 5 y )( x 5 y )
2
2
(2a c)(4a 2ac c )
2
a(3b 4c)(3b 4c)
a(3b 4c)
2
2

20. №2 Упростите выражение:

x( x 6) 2( x 8)
2
( x 8) 16
x 2 6 x 2 x 16
x 2 8 x 16
( x 4)( x 4)
x 4
2
2
x 16 x 64 16 x 16 x 48 ( x 12)( x 4) x 12
x 2 8 x 16 0
D 0, x 4
x 2 16 x 48 0
D 64, x1 12, x2 4

21. №3 Упростите выражение:

2
2
xy x
x y x xy y
2
5
4
2
y 4 x y x y x xy y
3
4
x( y 3 x 3 ) ( x y )( x 2 xy y 2 ) ( x y )( x 2 xy y 2 )
4
4
2
2
y( y 4 x )
( x y )( x xy y )
x( y 3 x 3 )( x 3 yx 2 x 2 y xy2 xy2 y 3 x 3 x 2 y x 2 y xy2 y 2 x y 3 )
4
4
3
3
y ( y 4 x )( x y )
x(4 x 2 y 2 y 3 )
2 xy(2 x 2 y 2 )
2x
y( y 4 4 x 4 )
y ( y 2 2 x 2 )( y 2 2 x 2 ) y 2 2 x 2

22.

5. Итог урока1)(15a …) 2 …… 144 x 2
2)(… 3 xy) 2 … 24 xy …
3)(… b 2 )(b 2 …) 25 b 4
4)(17 …)(17 …) 289 9a 2
5) x 3 …0,125 ( x…0,5)( x 2 0,5 x 0,25)
18a 3b 4
6)
…
2
12ab
a 2 …
a 2
7)
3a …
3
4…
2
4
8)… x y :
3x 3
x

23. Проверяем!

1)(15a 12 x) 2 225a 360ax 144 x 2
2)( 4 3 xy) 2 16 24 xy 9 x 2 y 2
3)(5 b 2 )(b 2 5) 25 b 4
4)(17 3a)(17 3a) 289 9a 2
5) x 3 0,125 ( x 0,5)( x 2 0,5 x 0,25)
3a 2b 2
2
3 4
6)
7)
18a b
12ab 2
a2 4
3a 6
a 2
3
4 y3
8)12 x y :
3x 3
x
2
4
нет ошибок – оценка «5»,
2 ошибки – «4»,
3-4 ошибки – оценка «3»,
5 и более ошибок – оценка «2»

24. Домашнее задание п. 1-9, №1000(б, г, е, з), 1004(б, г, е).

English     Русский Правила

Bestmaths

Навигация

• Home
• • Год 9 (10 NZ, KS 3/4)
    • Год 9 Темы
      • Упрощающие выражения

2222222 в Algebra. стоять за числа.

Буквы часто называют переменными или прочислительными .

Необходимо уметь складывать, вычитать, умножать и делить алгебраические термины.

Определения

Алгебраический  член  может состоять из коэффициентов, переменных и показателей степени.
Подобные термины  имеют одинаковые переменные и показатели степени.	напр. { 2a, 4a, -6a } являются похожими на терминами. и  общий для всех.   { x, 3a 2 , 6 } являются в отличие от  терминов. Общепринятого термина нет.
Алгебраическое выражение  является группой терминов.	напр. 4x + 3y — это выражение .

 

 

Сложение и вычитание

Выражение, включающее сложение и вычитание, можно упростить, только если оно содержит аналогично терминам.

Термины и собираются вместе, а затем добавляются или вычитаются.

 

Примеры	Ответы
Упрощение:
(а) 5а + 6а − 2а	(а) 5а + 6а — 2а = 9а
(б) 18 шт. − 10 шт. + 4 шт.	(b) 18pq − 10pq + 4pq = 12pq
(в) 3c + 4d 2  + 5c − d 2	(в) 3c + 4d 2  + 5c − d 2 = 8с + 3d 2
(г) 4x 2  + 10x 2  − 3x 2	4x 2  + 10x 2  − 3x 2  = 11x 2

 

 

Умножение

3xy означает «3, умноженное на x, умноженное на y».

В терминах этого типа число идет первым, а переменные обычно располагаются в алфавитном порядке.

напр. 3q × 4p = 12pq

5c × 3e × 2d = 30cde

Обратите внимание, что сначала умножаются числа, а буквы (переменные) располагаются в алфавитном порядке.

Деление

^8xy ⁄ _4x означает «8xy разделить на 4x».

Этот тип выражения упрощается путем  отмены .

напр. 2 года

Примечание  Отменить можно только между цифрами или буквами в верхней строке и цифрами или буквами в нижней строке.

Слова в символы

Многие математические задачи записываются словами, и эти слова часто приходится преобразовывать в алгебраические выражения.

 

Слова	Алгебра
3 добавляется к х	х + 3
5 вычитается из у	г − 5
z умножается на 4	4з
w делится на 10	ш ⁄ 10
Произведение х и у	ху
Разница между а и 5	а − 5
Сумма 7 и w	7 + ш
p умножается на q и прибавляется 5	шт + 5
6 умножить на c равно 30	6с = 30

Открытые учебники | Siyavula

Загрузите наши открытые учебники в различных форматах, чтобы использовать их так, как вам удобно. Нажмите на обложку каждой книги, чтобы увидеть доступные для загрузки файлы на английском и африкаанс. Лучше, чем просто бесплатные, эти книги также имеют открытую лицензию! См. различные открытые лицензии для каждой загрузки и пояснения к лицензиям в нижней части страницы.

Математика

• • Читать онлайн

  • Учебники

    • Английский

      • • 7A PDF (CC-BY-ND)
        • 7B PDF (CC-BY-ND)

    • Африкаанс

      • • 7A PDF (CC-BY-ND)
        • 7B PDF (CC-BY-ND)
• • Читать онлайн

  • Учебники

    • Английский

      • • 8A PDF (CC-BY-ND)
        • 8B PDF (CC-BY-ND)

    • Африкаанс

      • • 8A PDF (CC-BY-ND)
        • 8B PDF (CC-BY-ND)
• • Читать онлайн

  • Учебники

    • Английский

      • • 9A PDF (CC-BY-ND)
        • 9B PDF (CC-BY-ND)

    • Африкаанс

      • • 9A PDF (CC-BY-ND)
        • 9B PDF (CC-BY-ND)
• • Читать онлайн

  • Учебники

    • Английский

      • • PDF (CC-BY-ND)
        • ePUB (CC-BY-ND)
        • ePUB (CC-BY)

    • Африкаанс

      • • PDF (CC-BY-ND)
        • ePUB (CC-BY-ND)
        • ePUB (CC-BY)

  • Пособия для учителя

    • Английский

      • • PDF (CC-BY-ND)

    • Африкаанс

      • • PDF (CC-BY-ND)
• • Читать онлайн

  • Учебники

    • Английский

      • • PDF (CC-BY-ND)
        • ePUB (CC-BY-ND)
        • ePUB (CC-BY)

    • Африкаанс

      • • PDF (CC-BY-ND)
        • ePUB (CC-BY-ND)
        • ePUB (CC-BY)

  • Пособия для учителя

    • Английский

      • • PDF (CC-BY-ND)

    • Африкаанс

      • • PDF (CC-BY-ND)
• • Читать онлайн

  • Учебники

    • Английский

      • • PDF (CC-BY-ND)
        • ePUB (CC-BY-ND)
        • ePUB (CC-BY)

    • Африкаанс

      • • PDF (CC-BY-ND)
        • ePUB (CC-BY-ND)
        • ePUB (CC-BY)

  • Пособия для учителя

    • Английский

      • • PDF (CC-BY-ND)

    • Африкаанс

      • • PDF (CC-BY-ND)
• • Читать онлайн

  • Учебники

    • Английский

      • • PDF (CC-BY-ND)
        • ePUB (CC-BY-ND)
        • ePUB (CC-BY)

    • Африкаанс

      • • PDF (CC-BY-ND)
        • ePUB (CC-BY-ND)
        • ePUB (CC-BY)

  • Пособия для учителя

    • Английский

      • • PDF (CC-BY-ND)

    • Африкаанс

      • • PDF (CC-BY-ND)

Наука

• • Читать онлайн

  • Учебники

    • Английский

      • • PDF (CC-BY-ND)
        • ePUB (CC-BY-ND)
        • ePUB (CC-BY)

    • Африкаанс

      • • PDF (CC-BY-ND)

  • Пособия для учителя

    • Английский

      • • PDF (CC-BY-ND)

    • Африкаанс

      • • PDF (CC-BY-ND)
• • Читать онлайн

  • Учебники

    • Английский

      • • PDF (CC-BY-ND)
        • ePUB (CC-BY-ND)
        • ePUB (CC-BY)

    • Африкаанс

      • • PDF (CC-BY-ND)
        • ePUB (CC-BY-ND)
        • ePUB (CC-BY)

  • Пособия для учителя

    • Английский

      • • PDF (CC-BY-ND)

    • Африкаанс

      • • PDF (CC-BY-ND)
• • Читать онлайн

  • Учебники

    • Английский

      • • PDF (CC-BY-ND)
        • ePUB (CC-BY-ND)
        • ePUB (CC-BY)

    • Африкаанс

      • • PDF (CC-BY-ND)
        • ePUB (CC-BY-ND)
        • ePUB (CC-BY)

  • Пособия для учителя

    • Английский

      • • PDF (CC-BY-ND)

    • Африкаанс

      • • PDF (CC-BY-ND)
• • Читать онлайн

  • Учебники

    • Английский

      • • PDF (CC-BY-ND)
        • ePUB (CC-BY-ND)
        • ePUB (CC-BY)

    • Африкаанс

      • • PDF (CC-BY-ND)
        • ePUB (CC-BY-ND)
        • ePUB (CC-BY)

  • Пособия для учителя

    • Английский

      • • PDF (CC-BY-ND)

    • Африкаанс

      • • PDF (CC-BY-ND)
• • Читать онлайн

  • Учебники

  • Пособия для учителя

    • Английский

      • Класс 7А

        • PDF (CC-BY-ND)

      • Класс 7Б

        • PDF (CC-BY-ND)

    • Африкаанс

      • Граад 7А

        • PDF (CC-BY-ND)

      • Граад 7Б

        • PDF (CC-BY-ND)
• • Читать онлайн

  • Учебники

  • Пособия для учителя

    • Английский

      • Класс 8А

        • PDF (CC-BY-ND)

      • Класс 8Б

        • PDF (CC-BY-ND)

    • Африкаанс

      • Граад 8А

        • PDF (CC-BY-ND)

      • Граад 8Б

        • PDF (CC-BY-ND)
• • Читать онлайн

  • Учебники

  • Пособия для учителя

    • Английский

      • Класс 9А

        • PDF (CC-BY-ND)

      • Класс 9Б

        • PDF (CC-BY-ND)

    • Африкаанс

      • Граад 9А

        • PDF (CC-BY-ND)

      • Граад 9Б

        • PDF (CC-BY-ND)
• • Читать онлайн

  • Учебники

  • Пособия для учителя

    • Английский

      • Класс 4А

        • PDF (CC-BY-ND)

      • Класс 4Б

        • PDF (CC-BY-ND)

    • Африкаанс

      • Граад 4А

        • PDF (CC-BY-ND)

      • Граад 4Б

        • PDF (CC-BY-ND)
• • Читать онлайн

  • Учебники

  • Пособия для учителя

    • Английский

      • Класс 5А

        • PDF (CC-BY-ND)

      • Класс 5Б

        • PDF (CC-BY-ND)

    • Африкаанс

      • Граад 5А

        • PDF (CC-BY-ND)

      • Граад 5Б

        • PDF (CC-BY-ND)
• • Читать онлайн

  • Учебники

  • Пособия для учителя

    • Английский

      • Класс 6А

        • PDF (CC-BY-ND)

      • Класс 6Б

        • PDF (CC-BY-ND)

    • Африкаанс

      • Граад 6А

        • PDF (CC-BY-ND)

      • Граад 6Б

        • PDF (CC-BY-ND)

Лицензирование наших книг

Лучше, чем просто бесплатные, эти книги также распространяются по открытой лицензии! Один и тот же контент, но разные версии (фирменные или нет) имеют разные лицензии, как объяснено:

CC-BY-ND (фирменные версии)

Вам разрешается и поощряется свободное копирование этих версий.

No related posts.