Уравнение асимптот: Как найти асимптоты графика функции, примеры решений

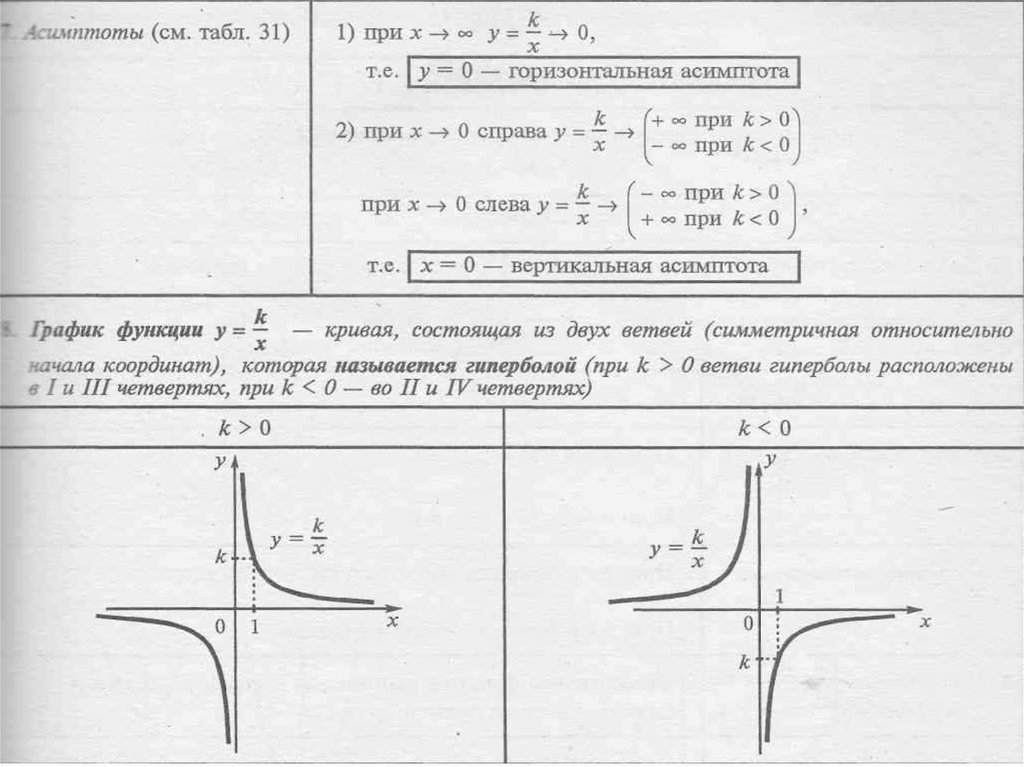
Асимптоты гиперболы

 

Пусть Г — какая-нибудь линия, М — переменная точка на ней, а — некоторая прямая. Если возможно такое движение точки М по линии Г, что:

1. точка М уходит в бесконечность;

2. при этом расстояние от точки М до прямой а стремится к нулю, —

то говорят, что линия Г ассимптотически приближается к прямой а. Прямая а в таком случае называется асимптотой линии Г.

Асимптотами гиперболы называются прямые, имеющие уравнения:

 

и . (3)

 

Эти прямые являются диагоналями основного прямоугольника. Построим гиперболу и рассмотрим какую-нибудь точку М(х;у), лежащую на гиперболе в первом квадранте.

 

Выясним, как в первом квадранте по мере возрастания х будет изменяться расстояние от точки М гиперболы до асимптоты .

Обозначим через N точку асимптоты с абсциссой х: N(x;Y), где Y=. Тогда

 

(4)

 

Так как а  х, то в скобках первое слагаемое всегда больше второго, следовательно, Y-y>0, а это означает, что при одной и той же абсциссе точка гиперболы лежит под соответствующей точкой асимптоты.

 

Преобразовав неравенство (4):

 

, (5)

 

убеждаемся, что длина отрезка MN по мере возрастания х уменьшается, и когда х неограниченно растет, MN стремится к нулю. Так как MN больше расстояния МК от точки M до асимптоты, то при этом МК и подавно стремится к нулю.

Аналогичное рассуждение можно провести в любом квадранте.

Итак, прямые в смысле определения асимптот к графику функции являются асимптотами гиперболы

 

.

При построении гиперболы обычно строят основной прямоугольник и проводят асимптоты, так как они позволяют точнее вычерчивать гиперболу.

 

Равнобочная гипербола

Возьмем каноническое уравнение гиперболы

 

.

 

В случае, когда а=b, уравнение гиперболы имеет вид

или

 

х² — у² = а². (6)

 

Гипербола, у которой полуоси а и b равны, называется равнобочной гиперболой. Уравнение (6) называется уравнением равнобочной гиперболы. Так как основной прямоугольник этой гиперболы является квадратом, то асимптоты равнобочной гиперболы будут перпендикулярны друг другу. (Рис. 5)

 

Рис. 5

 

 

Сопряженная гипербола

Рассмотрим уравнение

. (7)

Представим уравнение (7) в следующем виде:

. (8)

Очевидно, что уравнение (8) представляет собой уравнение гиперболы, у которой действительной осью является ось ординат, а мнимой — ось абсцисс.

 

Построим основной прямоугольник, проведем асимптоты и построим гиперболу (7). Далее в той же системе координат построим (пунктиром) (Рис. 6) гиперболу

 

 

Рис. 6

Очевидно, что гиперболы и имеют общие асимптоты. Такие гиперболы называются сопряженными.

Выведем теперь уравнение гиперболы, асимптотами которой служат оси координат. Возьмем уравнение равнобочной гиперболы х² — у² = а² и рассмотрим уравнение этой гиперболы в новой системе координат Х`OY`, полученной из старой поворотом осей координат на угол =(Рис. 2).

 

Используя для этого формулы поворота осей координат:

 

х = х`cos — y`sin;

y = x`sin + y`cos,

 

подставим значения х, у в уравнение гиперболы:

 

х² — у² = а².

 

Получим:

 

. (9)

 

Обозначая , получим х`y`=c.

Уравнение равнобочной гиперболы, для которой координатные оси ОХ и OY являются асимптотами, будет иметь вид:

ху = с

или

.

 

 

Отыскание асимптот в проективной плоскости

Данная работа посвящена исследованию методов отыскания асимптот плоских алгебраических кривых. Если кривая задана явным уравнением , то асимптоты кривой совпадают с асимптотами графика функции, определяющей эту кривую. В этом случае всем известно, как найти эти асимптоты. Если кривая определена уравнением , где  – многочлен степени n c действительными коэффициентами, то уравнения асимптот можно найти, получив параметрическое задание кривой [1, с.35]:

    (1)

В этом случае прямая y=kx+b будет асимптотой кривой при t→t₀, если существуют и конечны пределы Также прямая x=a является вертикальной асимптотой кривой при t→t₀, если  и  

Используя этот метод, найдены асимптоты кривых (в скобках указаны уравнения асимптот):

1. , ;
2. , ;
3. , .

Следует, однако, заметить, что переход к параметрическому заданию кривой является часто непростой задачей. В связи с этим в учебнике [2, с.69-71] предлагается метод отыскания асимптот кривой

,    (2)

заданной многочленом степени n c действительными коэффициентами вида

,    (3)

где – однородные многочлены степени i, но лишь при условии, что уравнение имеет действительные корни кратности 1. Также в этом учебнике доказывается следующая теорема (см. [2, с.67-68]):

Если касательная к кривой (1) стремится к предельному положению, когда точка касания стремится по кривой в бесконечность, то это предельное положение есть асимптота.

Эта теорема привела к мысли пополнить евклидову плоскость R², на которой рассматриваются кривые, бесконечно удаленной прямой. Каждая точка этой прямой будет общей точкой всех параллельных прямых заданного направления, то есть центром некоторого пучка параллельных прямых. Как известно, евклидова плоскость, пополненная бесконечно удаленной прямой, называется проективной.

Переход к проективной плоскости и теорема, сформулированная выше, позволяют определить асимптоту кривой как касательную в ее бесконечно удаленной точке.

Поскольку нам придется писать уравнения прямых не только на евклидовой плоскости, но и на проективной, то напомним, как связаны евклидовы координаты точки с проективными координатами этой же точки.

Если – евклидовы координаты точки M, а  – проективные или однородные координаты этой же точки, то , , где . Заметим, что проективные координаты точки не могут быть равны одновременно нулю и определяются с точностью до пропорциональности, то есть, если  – координаты некоторой точки, то при любом α≠0 набор чисел является координатами той же точки. Уравнение x₃=0 является уравнением бесконечно удаленной прямой на расширенной (проективной) плоскости.

Далее, если ax+by+c=0 – уравнение прямой на евклидовой плоскости, то уравнение этой прямой на расширенной плоскости будет иметь вид .

Уравнение кривой, заданной многочленом

 

которое в проектированных координатах  будет иметь вид:

  + ) +…     (4)

Уравнение касательной в точке , принадлежащей кривой, заданной на евклидовой плоскости уравнением (2) , имеет вид

    (5)

Уравнение касательной к кривой (4) в точке этой кривой записывается следующим образом

 .     (6)

Формулы (5) и (6) теряют смысл, если все частные производные равны нулю.

Точка M (x,y) на кривой (2) называется особой точкой кратности k, если все частные производные до порядка k-1 от многочлена  обращаются в этой точке в 0, но существует хотя бы одна производная k-ого порядка не равная 0 в ней.

В особой точке касательной к кривой в том смысле, в котором она определена выше формулами (5) и (6), не существует.

Чтобы понять, как получить уравнение касательной к кривой в ее особой точке  , предположим, что  и разложим многочлен  степени n в ряд Тейлора в окрестности точки этой точки:

Так как лежит на кривой , то Так как  – особая точка, то , , и всякая прямая y=kx, проходящая через M₀, пересекает кривую в этой точке по крайней мере 2 раза. Это следует из того, что система

которая равносильна системе

имеет по крайней мере двукратный корень x²=0 (при ∀k). Если кратность особой точки равна двум, то найдутся прямые, которые пересекаются с кривой в начале координат не два, а 3 раза. Угловые коэффициенты k этих прямых определяются из уравнения:

Относительно k это уравнение имеет 2 корня: различных или совпавших, а может быть и комплексных. Поэтому будем иметь 2 прямые, имеющие с кривой в точке  трехкратное пересечение. Эти прямые называют касательными к кривой в особой точке кратности 2. Если кривая имеет особую точку кратности 3, то в ней существуют 3 касательные, среди которых могут быть и совпавшие.

Перейдем теперь непосредственно к отысканию асимптот плоских алгебраических кривых. Остановимся лишь на методе, основанном на переходе к проективной плоскости и, соответственно, проективному замыканию кривой .

Асимптота плоской алгебраической кривой как предельное положение касательной

В данной части работы используется понятие асимптоты кривой, которое использует расширение евклидовой плоскости до проективной.

Определение. Касательная к кривой в её несобственной точке называется асимптотой этой кривой.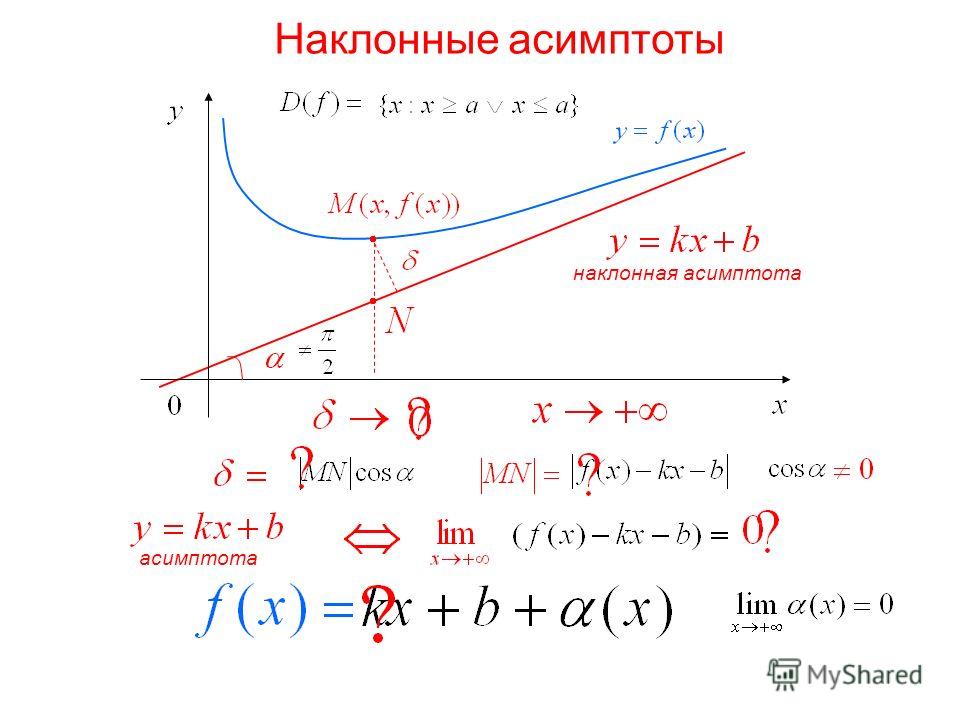

Задача 1. Найти асимптоты кривой, используя определение:

.

Решение. Запишем уравнение в однородных координатах. Так как , , то заданное уравнение перепишется в виде

Несобственная (бесконечно удалённая прямая) x₃=0 пересекает эту кривую в трех точках

Напишем уравнение касательной в каждой из этих точек. Уравнение касательной к кривой   в точке  M₁ этой кривой имеет вид

.

Для заданной кривой ,

1) =

Поэтому уравнение касательной к расширенной кривой в ее точке имеет вид  Переход к евклидовым координатам дает уравнение асимптоты к данной кривой: x+1=0.

2) =

Уравнение касательной к расширенной кривой в ее точке M₂=1,0,0 имеет вид x₂=0. Переход к евклидовым координатам дает уравнение асимптоты к данной кривой: y=0.

3)

Уравнение касательной к расширенной кривой в ее точке имеет вид x₁+x₂=0. Переход к евклидовым координата дает уравнение асимптоты к данной кривой: x+y=0.

Ответ. Асимптоты: x+1=0, y=0, x+y=0.

Применение рассуждений, которые использовались при решении задачи, в общем случае, то есть для уравнения кривой

приводит к доказательству следующей теоремы.

Теорема. Пусть γ – кривая, заданная уравнением

.

Тогда:

1. Если   приводим и содержит сомножитель (ax+by), то есть , то γ имеет асимптоту с уравнением:

     (7)

2) Если  приводим и (ax+by)  является для  множителем кратности 2, то есть

,

и  тоже имеет множитель (ax+by), но однократный, то есть

,

то γ имеет 2 параллельные асимптоты, уравнения которых определяются из равенства

    (8)

3) Если приводим и (ax+by) является для  множителем кратности 2, a  не содержит (ax+by) в качестве простого множителя, то асимптот в направлении прямой ax+by=0 нет.

Доказательство. Запишем уравнение кривой в однородных координатах:

.

Так как во всех трех случаях , то в однородных координатах

.

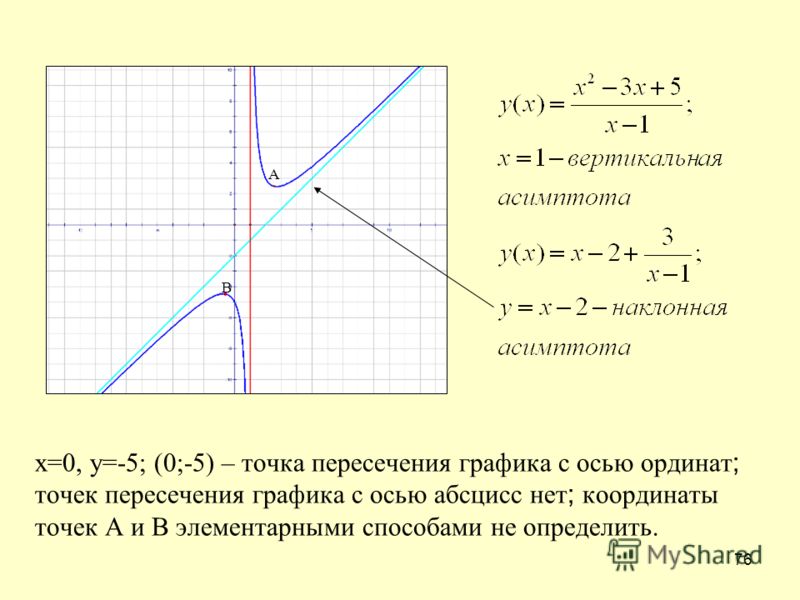
Среди точек пересечения кривой с бесконечно удаленной прямой x3=0 имеется точка  Итак,  является несобственной точкой кривой. Напишем уравнение касательной к γ в точке .

Рассмотрим случай 1. В этом случае

 

Поэтому уравнение касательной к γ в точке M(b,-a,0)  запишется следующим образом

Переход к евклидовым координатам: дает уравнение асимптоты кривой γ.

Случай 2. В этом случае     , а в разложении  на множители множителя нет.

Тогда значения частных производных в точке  соответственно равны

Это значит, что в этом случае  особой точкой не является, и уравнение касательной в ней к кривой на расширенной плоскости имеет вид x₃=0 . То есть касательная – это несобственная прямая. Поэтому кривая в евклидовой плоскости асимптот не имеет.

Таким образом доказана теорема, позволяющая не только определять наличие асимптот у плоской алгебраической кривой, расположенной в евклидовой плоскости, но и дающая алгоритм написания уравнения асимптот, если они существуют. 2

Асимптоты

Асимптотой кривой y = f ( x ), имеющей бесконечную ветвь, называется линия такая, что расстояние между точками ( x , f ( x )) кривая и прямая приближаются к нулю по мере того, как точка движется по ветви на бесконечность.

Асимптоты могут быть вертикальными, косыми (наклонными) и горизонтальными. Горизонтальную асимптоту часто рассматривают как частный случай наклонной асимптоты.

Вертикальная асимптота

Прямая x = a является вертикальной асимптотой графика функции y = f ( x ), если выполняется хотя бы одно из следующих условий:

\[\lim\limits_{x \to a — 0} f\left( x \right) = \pm \infty ,\;\;\lim\limits_{x \to a + 0} f\left( x \справа) = \pm \infty .\]

Другими словами, хотя бы один из односторонних пределов в точке x = должно быть равно бесконечности.

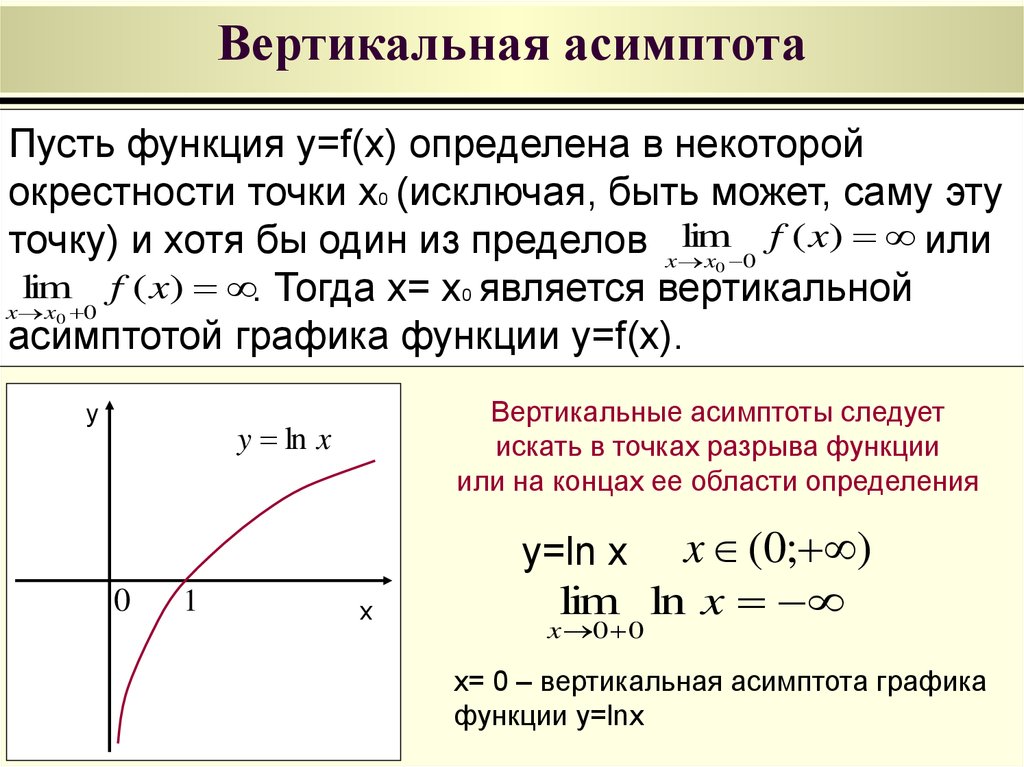
Вертикальная асимптота возникает у рациональных функций в точках, когда знаменатель равен нулю, а числитель не равен нулю (т.е. в точках разрыва второго рода). Например, график функции \(y = {\frac{1}{x}}\) имеет вертикальную асимптоту \(x = 0\) (рис. \(1\text{).}\). случае оба односторонних предела (слева и справа) стремятся к бесконечности:

\[\lim\limits_{x \to 0 — 0} \frac{1}{x} = — \infty ,\;\;\lim\limits_{x \to 0 + 0} \frac{1}{ х} = + \infty .\]

Рис. 1.

Функция, непрерывная на всем множестве действительных чисел, не имеет вертикальных асимптот.

Наклонная асимптота

Прямая \(y = kx + b\) называется наклонной (наклонной) асимптотой графика функции \(y = f\left( x \right)\) при \(x \to +\infty \) (Рисунок \(2\)) если

\[\lim\limits_{x \to + \infty } \left[ {f\left( x \right) — \left( {kx + b} \right)} \right]= 0.\]

Рис. 2.

Аналогично введем наклонные асимптоты как \(x \to -\infty.\)

Наклонные асимптоты графика функции \(y = f\left( x \right)\) могут быть различными как \(x \to +\infty\) и \(x \to -\infty. \)

Поэтому при нахождении наклонных (или горизонтальных) асимптот рекомендуется вычислять их отдельно.

Коэффициенты \(k\) и \(b\) наклонной асимптоты \(y = kx + b\) определяются следующей теоремой:

Прямая линия \(y = kx + b\) является асимптотой функции \(y = f\left( x \right)\) при \(x \to +\infty\) тогда и только тогда, когда выполняется следующее два предела конечны:

\[\lim\limits_{x \to + \infty} \frac{{f\left( x \right)}}{x} = k\;\;\text{and}\;\;\lim\ limit_{x \to + \infty} \left[ {f\left( x \right) — kx} \right] = b.\]

Доказательство.

Необходимость

Пусть прямая \(y = kx + b\) является асимптотой графика \(y = f\left( x \right)\) при \(x \to +\infty.\). Тогда условие верно:

\[\lim\limits_{x \to + \infty } \left[ {f\left( x \right) — \left( {kx + b} \right)} \right] = 0\]

или эквивалентно

\[f\left( x \right) = kx + b + \alpha \left( x \right),\;\;\text{где}\;\;\lim\limits_{x \to + \infty } \alpha \left( x \right) = 0. \]

Разделив обе части уравнения на \(x,\), получим:

\[\frac{{f\left( x \right)}}{x} = \frac{{kx + b + \alpha \left( x \right)}}{x},\;\; \Rightarrow \frac{{f\left( x \right)}}{x} = k + \frac{b}{x} + \frac{{\alpha \left( x \right)}}{x}. \]

Следовательно, в пределе при \(x \to +\infty,\) имеем

\[\lim\limits_{x \to + \infty } \frac{{f\left( x \right)}}{x} = \lim\limits_{x \to + \infty } \left[ {k + \frac{b}{x} + \frac{{\alpha \left( x \right)}}{x}} \right]= k,\]

\[\lim\limits_{x \to + \infty } \left[ {f\left( x \right) — kx} \right] = \lim\limits_{x \to + \infty } \left[ { b + \alpha \left( x \right)} \right]= b.\]

Достаточность

Предположим, что существуют конечные пределы

\[\lim\limits_{x \to + \infty} \frac{{f\left( x \right)}}{x} = k\;\;\text{and}\;\;\lim\ limit_{x \to + \infty} \left[ {f\left( x \right) — kx} \right] = b.\]

Второй предел может быть записан как

\[\lim\limits_{x \to + \infty } \left[ {f\left( x \right) — \left( {kx + b} \right)} \right] = 0,\]

, что соответствует определению наклонной асимптоты. Таким образом, прямая \(y = kx + b\) является асимптотой функции \(y = f\left( x \right).\)

Примечание:

Аналогично можно доказать теорему для случая \(x \to \infty.\)

Горизонтальная асимптота

В частности, если \(k = 0,\) мы получим горизонтальную асимптоту, которая описывается уравнением \(y = b.\) Теорема о необходимых и достаточных условиях существования горизонтальной асимптоты формулируется как следует:

Прямая линия \(y = b\) является асимптотой функции \(y = f\left( x \right)\) при \(x \to +\infty,\) тогда и только тогда, когда выполняется следующий предел конечно:

\[\lim\limits_{x \to + \infty} f\left( x \right) = b.\]

Аналогично рассматривается случай \(x \to -\infty\).

Асимптоты параметрически заданной кривой

Пусть плоская кривая задана параметрическими уравнениями

\[x = \varphi\left( t \right),\;\;y = \psi \left( t \right).\]

Эта кривая имеет вертикальную асимптоту \(x = a\) как \(t \to {t_1}\), если выполняются следующие условия:

\[\lim\limits_{t \to {t_1}} \varphi \left( t \right) = a\;\;\text{and}\;\;\lim\limits_{t \to {t_1} } \psi \left( t \right) = \pm \infty . \]

Аналогично, параметрически определенная кривая имеет горизонтальную асимптоту \(y = b\) как \(t \to {t_2}\), если

\[\lim\limits_{t \to {t_2}} \varphi \left( t \right) = \pm \infty\;\;\text{and}\;\;\lim\limits_{t \to {t_2}} \psi \left( t \right) = b.\]

Здесь \(а\) и \(Ь\) — конечные величины.

Параметрически заданная кривая имеет наклонную (наклонную) асимптоту \(y = kx + b\) при \(t \to {t_3}\), если при этом значении \(t,\) оба предела бесконечны:

\[\lim\limits_{t \to {t_3}} \varphi \left( t \right) = \pm \infty ,\;\;\lim\limits_{t \to {t_3}} \psi \left ( т \справа) = \pm \infty ,\]

, а коэффициенты \(k\) и \(b\) имеют конечные значения:

\[k = \lim\limits_{t \to {t_3}} \frac{{\psi \left( t \right)}}{{\varphi \left( t \right)}},\;\; b = \lim\limits_{t \to {t_3}} \left[ {\psi \left( t \right) — k\varphi \left( t \right)} \right].\]

Асимптота полярной кривой

Рассмотрим кривую, заданную в полярных координатах уравнением

\[\rho = \rho \left(\varphi\right)\;\;\text{or}\;\;F\left({\rho,\varphi} \right) = 0. \]

Его асимптота (если она существует) может быть описана двумя параметрами: расстоянием \(p\) от центра до асимптоты (отрезок \(OA\) на рис. \(3\text{)}\) и угол \(\alpha\) наклона асимптоты к полярной оси.

Рис. 3.

Эти параметры \(\alpha\) и \(p\) определяются формулами

\[\alpha = \lim\limits_{\rho \to \infty} \varphi,\;\;p = \lim\limits_{\rho \to \infty} \left[ {\rho \sin\left( {\alpha — \varphi} \right)} \right].\]

Примечания:

1. В последней формуле предельный переход \(\rho \to \infty\) можно заменить эквивалентным условием \(\varphi \to \alpha;\)
2. Параметр \(p\) может быть как положительным, так и отрицательным.

Асимптоты неявной кривой

Неявно определенная алгебраическая кривая описывается уравнением

\[F\влево({х,у}\вправо) = 0,\]

где левая часть представляет собой многочлен от переменных \(x\) и \(y.\)

В дифференциальной геометрии используется следующий метод нахождения наклонной асимптоты алгебраической кривой. Предположим, что асимптота описывается уравнением \(y = kx + b.\). Подставив это выражение вместо \(y\) в уравнение кривой, получим алгебраическое уравнение с одной переменной \(x:\) 9{n — 1}} + \ldots + {A_{n — 1}}x + {A_n} = 0,\]

, где коэффициенты \({A_i}\) зависят от параметров асимптоты \(k\) и \(b\) (коэффициент \({A_0}\) зависит только от \(k\)). Значения \(k\) и \(b\) можно определить из условия:

\[\left\{ \begin{массив}{l} {A_0}\влево(к\вправо) = 0\\ {A_1}\влево({k,b}\вправо) = 0 \конец{массив} \право..\]

Чтобы найти вертикальную асимптоту, надо подставить ее уравнение \(х = а\) в уравнение кривой и преобразовать последнее к виду: 9n}\) в последнем уравнении.

Значение параметра \(a\) определяется из условия

\[{B_1}\влево( а \вправо) = 0.\]

Приведенные выше формулы для асимптот неявной кривой справедливы, если кривая не имеет особых точек на бесконечности.

Решенные проблемы

Щелкните или коснитесь проблемы, чтобы увидеть решение.

Пример 1

Найдите асимптоты функции \[f\left( x \right) = \frac{x}{{x + 1}}.\] 92} — 2x — 3}}{x}}.\]

Пример 1.

Найдите асимптоты функции \[f\left( x \right) = \frac{x}{{x + 1}}.\]

Раствор.

При \(x = -1,\) функция имеет разрыв второго рода. Действительно:

\[\lim\limits_{x \to — 1 — 0} f\left( x \right) = \lim\limits_{x \to — 1 — 0} \frac{x}{{x + 1}} = \frac{{ — 1}}{{\left( { — 1 — 0} \right) + 1}} = \ frac{{ — 1}}{{ — 0}} = + \infty ,\]

\[\lim\limits_{x \to — 1 + 0} f\left( x \right) = \lim\limits_{x \to — 1 + 0} \frac{x}{{x + 1}} = \frac{{ — 1}}{{\left( { — 1 + 0} \right) + 1}} = \frac{{ — 1}}{{ + 0}} = — \infty .\]

Следовательно, \(x = -1\) есть уравнение вертикальной асимптоты.

Найдите горизонтальную асимптоту. Вычислить предел:

\[\lim\limits_{x \to \pm \infty } \frac{x}{{x + 1}} = \lim\limits_{x \to \pm \infty } \frac{1}{{1 + \frac{1}{x}}} = 1.\]

Таким образом, для кривой существует горизонтальная асимптота, и ее уравнение имеет вид \(y = 1. \)

Функция не имеет наклонных асимптот. В этом можно убедиться, вычислив коэффициенты \(k\) и \(b:\) 92} + x}} = \lim\limits_{x \to \pm \infty } \frac{{\frac{1}{x}}}{{1 + \frac{1}{x}}} = 0 ,\]

\[b = \lim\limits_{x \to \pm \infty } \left[ {y\left( x \right) — kx} \right] = \lim\limits_{x \to \pm \infty } \left( {\frac{x}{{x + 1}} — 0} \right) = \lim\limits_{x \to \pm \infty} \frac{1}{{1 + \frac{1} {х}}} = 1.\]

Видно, что фактически мы получили горизонтальную асимптоту, которая уже определена выше.

Итак, график функции имеет вертикальную асимптоту \(x = -1\) и горизонтальную асимптоту \(y = 1\) (рис. \(4\)).

Рис. 4.

Пример 2.

Найдите асимптоты функции \[f\left( x \right) = {\frac{{2x — 3}}{{x + 1}}}.\]

Раствор.

Функция определена для всех \(x \ne -1.\) Вычислить односторонние пределы при \(x = -1:\)

\[\lim\limits_{x \to — 1 — 0} f\left( x \right) = \lim\limits_{x \to — 1 — 0} \frac{{2x — 3}}{{x + 1}} = \frac{{ — 5}}{{ — 0}} = + \infty ;\]

\[\lim\limits_{x \to — 1 + 0} f\left( x \right) = \lim\limits_{x \to — 1 + 0} \frac{{2x — 3}}{{x + 1}} = \frac{{ — 5}}{{ + 0}} = — \infty . \]

Следовательно, \(x = -1\) является вертикальной асимптотой функции.

Найдите возможные горизонтальные асимптоты в точке \(x \to \pm\infty:\)

\[\lim\limits_{x \to \pm \infty } f\left( x \right) = \lim\limits_{x \to \pm \infty } \frac{{2x — 3}}{{x + 1}} = \lim \limits_{x \to \pm \infty } \frac{{2 — \frac{3}{x}}}{{1 + \frac{1}{x}}} = 2 .\]

Мы получили горизонтальную асимптоту при \(y = 2.\)

Проверка косых (наклонных) асимптот путем вычисления наклона \(k:\) 92} — 2x — 3}}{x} = x — 2 — \frac{3}{x}.\]

Член \(\frac{3}{x}\) стремится к нулю, когда \(x \to \pm \infty.\) Следовательно, функция имеет наклонную асимптоту \(y = x — 2.\)

Рисунок 7.

Дополнительные проблемы см. на стр. 2,3.

Наклонные асимптоты – свойства, графики и примеры

Графики и функции также могут иметь наклонные или наклонные асимптоты. Что происходит, когда асимптота функции сама является (линейной) функцией? В этой статье будет представлен уникальный элемент рациональных функций – наклонные асимптоты.

Наклонные асимптоты представляют собой линейные функции, определяющие конечное поведение рациональной функции с обоих концов.

Изучение наклонных асимптот может помочь нам предсказать поведение графиков при экстремальных значениях $x$. Поскольку в этой статье основное внимание будет уделено наклонным асимптотам рациональных функций, мы рекомендуем ознакомиться с некоторыми важными свойствами рациональных функций:

• Узнайте о рациональных функциях и их графиках здесь.
• Обязательно проверьте свои знания по горизонтали и вертикали.

Когда мы также узнаем о построении графиков наклонных асимптот, нам также нужно будет повторить наши знания о построении графиков линейных уравнений. Готовы ли вы расширить свои знания о наклонных асимптотах? Начнем с его определения.

Что такое наклонная асимптота?

Наклонные асимптоты также известны как наклонные асимптоты . Это из-за его наклонной формы, представляющей график линейной функции, $y = mx + b$. Рациональная функция может иметь наклонную асимптоту только тогда, когда степень ее числителя равна 9.0319 ровно на одну степень выше, чем степень его знаменателя.

Наклонные асимптоты — это линейные функции, которые мы можем использовать для предсказания конечного поведения рациональных функций, как показано в нашем примере ниже.

Как видно из графика, наклонная асимптота $f(x)$ представлена ​​пунктирной линией, определяющей поведение графика. Мы также видим, что $y= \dfrac{1}{2}x     +1$ является линейной функцией вида $y = mx + b$.

Наклонная асимптота дает нам представление о том, как ведет себя кривая $f(x)$ при приближении к $-\infty$ и $\infty$. График $f(x)$ также подтверждает то, что мы уже знаем: наклонные асимптоты будут линейными (и наклонными).

Заметили, что $f(x)$ не имеет горизонтальных асимптот? Это потому, что рациональная функция может иметь либо горизонтальную асимптоту, либо наклонную асимптоту, но никогда обе.

Как найти наклонную асимптоту?

При нахождении наклонной асимптоты рациональной функции нам может понадобиться освежить в памяти следующие темы:

• Повторить, как мы можем выполнять деление многочленов в длину.
• Нам также нужно будет использовать синтетическое деление, так что лучше освежить свои знания.

Обратите внимание, что оба метода должны возвращать один и тот же результат — мы будем зависеть только от форм числителя и знаменателя, чтобы решить, какой из двух методов лучше.

 Поскольку $f(x) = \dfrac{p(x)}{q(x)}$, является рациональной функцией, где $p(x)$ имеет одну степень выше, чем $q(x)$, мы можем найдите частное $\dfrac{p(x)}{q(x)}$, чтобы найти наклонную асимптоту.

$f(x) = \text{Частное} + \dfrac{\text{Остаток}}{q(x)}$

При нахождении наклонной асимптоты мы получаем только сосредоточиться на частном и игнорировать остаток .

Правила наклонной асимптоты для рациональных функций

При нахождении наклонной асимптоты рациональной функции мы всегда проверяем степени числителя и знаменателя, чтобы убедиться, что функция имеет наклонную асимптоту. Следите за тем, чтобы степень числителя была ровно на одну ступень выше.

Правило 1: Если числитель кратен знаменателю, наклонная асимптота будет упрощенной формой функции. 92 – 9$ эквивалентно $(x -3)(x +3)$ в факторизованной форме, поэтому знаменатель является множителем числителя.

Упрощенная форма $f(x)$: $ \dfrac{\cancel{(x-3)}(x+3)}{\cancel{x-3}} = x+3$. Это означает, что функция имеет наклонную асимптоту при $y = x + 3$.

Полезно помнить об этом, так как отмена факторов будет гораздо более быстрым подходом.

Правило 2: Если числитель не кратен знаменателю, используйте деление в длинное или синтетическое деление, чтобы найти частное функции. 92 – 6x + 9$ и $x – 1$. (Обязательно проверьте свои знания о делении многочленов.)

$\frac{\begin{array}{r|}1\end{array}}{\phantom{2}}\underline{\begin{array}{ rrr}1&-6&9 \\&1&-5\end{array}}$

$\begin{array}{rrrr}~~&1&-5\phantom{2}&4 \end{array}$

Это показывает, что частное равно $x – 5$. Мы также можем подтвердить это с помощью деления в длину, как показано ниже. 2-6x+92 – x ~~~~~\downarrow}\\0-5x+9 \\ \underline{-~\phantom{(}(-5x+5)}\\ \color{red}4\phantom{x} \end{array}$

Из этих двух методов мы видим, что $f(x) = x – 5 + \dfrac{4}{x + 1}$, поэтому, сосредоточив внимание на частном, наклонная асимптота $ f(x)$ находится при $y = x – 5$.

Как построить график наклонной асимптоты?

Получив уравнение, представляющее наклонную асимптоту, нарисуйте линейную функцию в виде наклонной пунктирной линии.

 Убедитесь, чтобы проверить свои знания о построении графиков линейных функций. Но не волнуйтесь, вот важные напоминания о построении графиков линейных функций: 92 – 6x + 9}{x – 1}$, мы используем отрезки его частного, $x – 5$.

$\boldsymbol{x}$ -intercept	$\begin{aligned}0 &= x-5\\x&= 5\\x_{\text{int}}&= (5, 0)\end{align}$
$\boldsymbol{y}$ -intercept	$\begin{align}0 -5 &=-5\\y_{\ text{int }}&=(0, -5)\end{aligned}$

Проверив знаменатель, мы видим, что $f(x)$ имеет вертикальную асимптоту при $x = 1$. Давайте также включим это в график $f(x)$, чтобы увидеть, как ведет себя кривая.

Как видно из графика, асимптоты также могут помочь нам узнать, как далеко покрываются кривые.

Изучив график наклонных асимптот, можно сразу заключить, что числитель функции на одну степень выше ее знаменателя.

Краткое изложение определения и свойств наклонных асимптот

Мы уже многое узнали о наклонных асимптотах, поэтому нам следует обобщить важные свойства наклонных асимптот, прежде чем мы попробуем другие примеры.

• Если числитель функции ровно на одну степень выше знаменателя, функция имеет наклонную асимптоту.
• Наклонная асимптота имеет общий вид $y = mx +b$, поэтому мы ожидаем, что она вернет линейную функцию.
• Постройте график линейной функции, используя точки пересечения наклонной асимптоты в качестве руководства.

Не забудьте также освежить свои знания по прошлым темам, которые мы упоминали в этой статье. Когда будете готовы, попробуйте эти примеры задач, которые мы подготовили! 94 -2}&=0\\ -x-1&=0\\ x&=-1\end{aligned}$

Мы видим, что $x$-координата пересечения равна $-1$. Чтобы найти координату $y$, подставьте $x=-1$ в уравнение наклонной асимптоты: $y = -1$.

Это означает, что $f(x)$ и ее наклонная асимптота пересекаются в точке $\boldsymbol{(-1,-1)}$.

Покажем, как будет выглядеть график и его асимптоты.

Пример 2

Найдите наклонные асимптоты следующих функций. 92-25$ можно разложить как $(x – 5)(x+5)$. Это означает, что $f(x)$ можно упростить как $\dfrac{\cancel{(x-5)}(x+5)}{\cancel{x – 5}} = x+5$.

а. Это означает, что $f(x)$ имеет наклонную асимптоту в точке $y = x+5$.

 Для второго выражения, поскольку делитель является биномом, лучше использовать синтетическое деление.

$\frac{\begin{array}{r|}-5\end{array}}{\phantom{2}}\underline{\begin{array}{rrr}1&-2&1 \\&-5&35\ конец{массив}}$

$\begin{массив}{рррр}~~&1&-7\фантом{х}&36 \конец{массив}$ 92 +2$ является квадратичным, поэтому он не будет образовывать линию (требование для наклонных или наклонных асимптот).

в. Это означает, что $h(x)$ не имеет наклонной асимптоты .

Пример 3

Функция $f(x) = \dfrac{p(x)}{q(x)}$ имеет наклонную асимптоту, проходящую через точки $(0, 10) $ и $(5, 0)$.

    а. Каково уравнение наклонной асимптоты $f(x)$?

    б. Чему равно частное $p(x)$ и $q(x)$?

Решение

Общий вид наклонных асимптот: $y=mx + b$, где $b$ — точка пересечения $y$. Поскольку $f(x)$ проходит через $(0, 10)$, уравнение для нашей наклонной асимптоты имеет вид $y = mx + 10$.

Найдите $m$ или наклон линии по формуле $m = \dfrac{y_2- y_1}{x_2 – x_1}$.

$\begin{align}m &= \dfrac{0-10}{5 – 0}\\&=\dfrac{-10}{5}\\&=-2\end{align}$

Следовательно, уравнение наклонной асимптоты равно $\boldsymbol{y = -2x + 10}$.

Напомним, что частное $\dfrac{p(x)}{q(x)}$ возвращает уравнение для наклонной асимптоты функции.

Это означает, что частное $\boldsymbol{p(x)}$ и $\boldsymbol{q(x)}$ равно $\boldsymbol{-2x + 10}$.

Документ без названия

Документ без названия

Рациональные уравнения

Лейтон Макинтайр

Цель: показать эффект изменения параметров a,b,c и d в рациональных уравнениях и распространить обсуждение на различные примеры

 

Рациональные уравнения — это уравнения вида , где f(x) и g(x) — многочлены, а g(x) не равно нулю.

Одной из форм рациональных функций, рассматриваемых в этом обсуждении, является

.

Типичный график уравнения этого типа выглядит следующим образом:

Горизонтальная асимптота этого графика равна y = 2, потому что график уравнения все ближе и ближе приближается к линии y = 2, но никогда не касается линии y = 2.

Вертикальная асимптота этого графика равна x=1, потому что график все ближе и ближе приближается к линии x = 1, но никогда не касается линии x = 1.

Значения констант и коэффициентов этого графика равны a = 2, b = 1, с = 1 и d = -1.

В задании 1 мы показали, что в общем случае для рациональной функции, где f(x) = ax + b и g(x) = cx + d, горизонтальные асимптоты возникают там, где разрывается область определения функции, то есть там, где знаменатель g(x) равен нулю. В этом случае cx + d = 0, поэтому вертикальная асимптота равна x = -d/c. Горизонтальные асимптоты возникают там, где y = a/c, потому что по мере того, как x становится бесконечно большим или маленьким, числитель стремится к чему-то чрезвычайно большому, умноженному на 9.0319 на или что-то очень малое умножить на на , а знаменатель стремится к чему-то очень большому на на или на что-то очень маленькое на на .

В случае гиперболы, приведенной в примере, мы видим, что асимптотами являются y = 2, горизонтальная линия, и x = 1, вертикальная линия. Поскольку асимптоты состоят из горизонтальной линии и вертикальной линии, то линии перпендикулярны. Гипербола, асимптоты которой пересекаются под прямым углом, называется прямоугольная гипербола . В приведенном выше примере центр гиперболы находится в точке (1,2). В общем случае центр прямоугольной гиперболы находится в точке (-d/c, a/c).

Изменение параметра a

Давайте посмотрим, что произойдет, если мы изменим параметр a

Давайте снова представим, что происходит при изменении параметра a.

пусть b = 1, c = 1, d = -1, а a изменяется в единицах от a = -2, — 1, 0, 1, 2

На этой диаграмме мы заметили несколько вещей:

1) Все графики проходят через точку y = -1. Эта точка является точкой пересечения по оси Y всего рационального уравнения. Точка пересечения с осью y — это точка, где значение x = 0. Таким образом, в общем случае точка пересечения с осью y — это точка (0, b/d)

2) Когда a = -2, график пересекает ось x на уровне 1/2, а когда a = 3, точка пересечения с x равна -1/3. Х-пересечение функций происходит в точке, где у = 0.

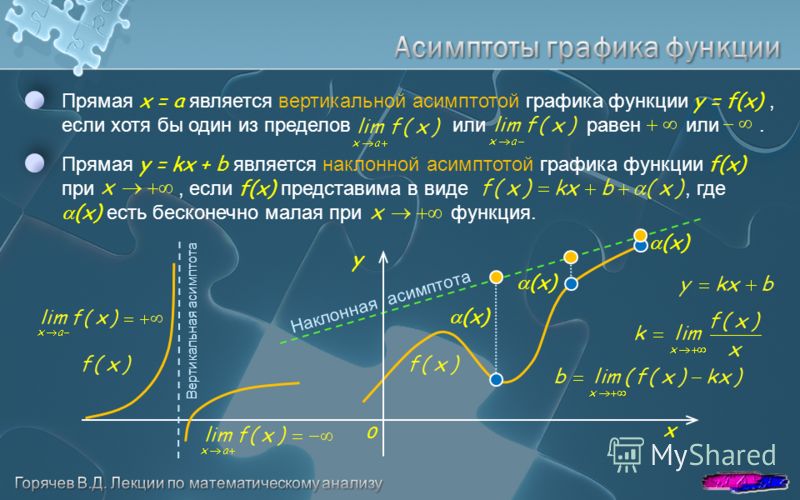Это то же самое, что приравнять числитель к нулю. Таким образом, точка пересечения по оси x рационального уравнения является точкой пересечения по оси x числителя. В общем случае точка пересечения с х — это точка (-b/a, 0). Изменения a вызывают изменения x-перехвата

3) Все графики, кроме того, в котором а = 0, являются гиперболами, поэтому при а = 0 имеет место частный случай рационального уравнения.

4) Все графики гипербол имеют вертикальную асимптоту в точке x=1. Вертикальная асимптота имеет место, когда значение знаменателя равно нулю. Так как в этом случае номинал сх + d равен х — 1; установка x — 1 = 0 дает вертикальную асимптоту как x = 1.

5) Графики гипербол имеют разные горизонтальные асимптоты, которые, по-видимому, прямо меняются при изменении а. Горизонтальная асимптота, где a = -2, лежит при y = -2, и эта идея видна при каждом значении a. Поскольку из предыдущего знания рациональной функции асимптота y возникает при y = a/c, мы можем сказать, что асимптота y здесь встречается при значении if a, потому что значение c равно 1, и, следовательно, значение a/c=a /1 = а.

Однако в целом асимптота y возникает при y = a/c.

6) Двигаясь слева направо по графику, мы замечаем, что графики переворачиваются, когда вы проходите вертикальную асимптоту. Фиолетовый график всегда является возрастающей функцией, а зеленый и голубой — всегда убывающей. Для этого есть причина, которая будет изучена по мере нашего продвижения в этом исследовании. Это связано с разницей между ad и bc. Обратите внимание, что для фиолетовой линии ad — bc > 0, а для зеленой и синей кривых ad и bc

< 0,9.0019

При использовании программного обеспечения Graphing Calculator для просмотра динамических изменений параметра a мы заменяем параметр a в уравнении параметром n (поскольку это параметр, который графический калькулятор распознает как параметр, который может легко изменять значения, и пусть параметр n принимает ряд значений, скажем, от -10 до 10, и наблюдайте, что происходит на графике График этого уравнения выглядит следующим образом в форме движения:

mov»>

Изменение параметра b

Посмотрим, что произойдет, если мы изменим параметр b

Обратите внимание, что происходит при изменении параметра b.

1) Пересечение по оси y изменяется при изменении параметра b. Когда b = 10, точка пересечения y равна -10, а когда b равна -5, точка пересечения y равна 5. Глядя на эту закономерность, можно сделать вывод, что точка пересечения y противоположна значению b в рациональном уравнении. Однако нужно быть осторожным, потому что в уравнении есть единичные значения. Поскольку значение d в уравнении равно -1, мы можем видеть, что если мы разделим значение b на значение d в каждом уравнении, это даст точное значение точки пересечения y, и, таким образом, мы можем утверждать, что y -перехват точка (0, b/d)

2) Когда b = 10, график пересекает ось x в точке -5, а когда b = -5, точка пересечения с x равна 2,5. Опять же, точка пересечения по оси x — это точка (-b/a, 0). Изменения в b вызывают изменения в x-перехвате.

3) Все графики, кроме того, в котором b = -2, являются гиперболами, поэтому при b = -2 имеет место частный случай рационального уравнения.

4) Все графики гипербол имеют вертикальную асимптоту в точке x = 1.

5) Графики гипербол имеют одинаковую горизонтальную асимптоту при y = 2. Горизонтальная асимптота как при a/c = 2/1 = 2. Поскольку a/c является одной и той же константой для всех уравнений, то горизонтальная асимптота для всех гипербол будет одинаковым.

6) Двигаясь слева направо по графику, мы замечаем, что графики переворачиваются, когда вы проходите вертикальную асимптоту. Светло-голубой график всегда является возрастающей функцией, а фиолетовый, красный и темно-синий — всегда убывающей функцией. Есть причина . Обратите внимание, что для светло-голубой гиперболы ad — bc > 0, а для фиолетовой, красной и синей кривых ad и bc

< 0,

График изменения b в движении выглядит следующим образом:

mov»>

Обратите внимание, что происходит, когда значение b изменяется от -10 до 10: точка, в которой график пересекает ось Y, перемещается от y = -10 до y = 10. График меняет направление при y = -2. Таким образом, между b = -10 и b = -2 график лежит во втором и четвертом квадрантах пересечения асимптот. Между b = -2 и b = 10 график лежит в первом и третьем квадрантах пересечения асимптот. Таким образом, мы можем видеть, что параметр b изменяет точку, в которой график пересекает ось y, на величину, равную букве b, и график становится все уже и уже по мере приближения к точке y=-2, и шире и шире по мере удаления от точки y = -2.

Изменение параметра c

Результаты наблюдения после изменения c следующие:

1) Точка пересечения с осью y для всех графиков находится в точке y = -1. Напомним, что точка пересечения с осью y представляет собой значение y при x = 0. поскольку при x=0 значение cx = 0, таким образом, меняется в c это не повлияет на y-перехват.

Точка пересечения y — это точка (0, b/d).

2) Точка пересечения по оси x для всех графиков находится в точке x = -1/2. Напомним, что точка пересечения с x — это значение x при y = 0. Точка пересечения с x — это точка (-b/a, 0 ). Изменения в c не вызывают изменений в x-отрезке.

3) Все графики, кроме тех, в которых с = 0 и с = -2, являются гиперболами, поэтому при с = 0 и с = -2 имеет место частный случай рационального уравнения.

4) Все графики гипербол имеют разные вертикальные асимптоты, которые изменяются в зависимости от значения c. Когда c = 10, вертикальная асимптота находится в точке x = 0,1, а когда c = -5, вертикальная асимптота находится в точке x = 0,4. Таким образом, можно сделать вывод, что значение вертикали является обратным значением c. Но вспомните, что вертикальная асимптота возникает там, где знаменатель равен нулю, поэтому, поскольку значение d равно -1, установка cx + d = 0 приведет к тому, что вертикальная асимптота будет иметь обратное значение, если значение c.

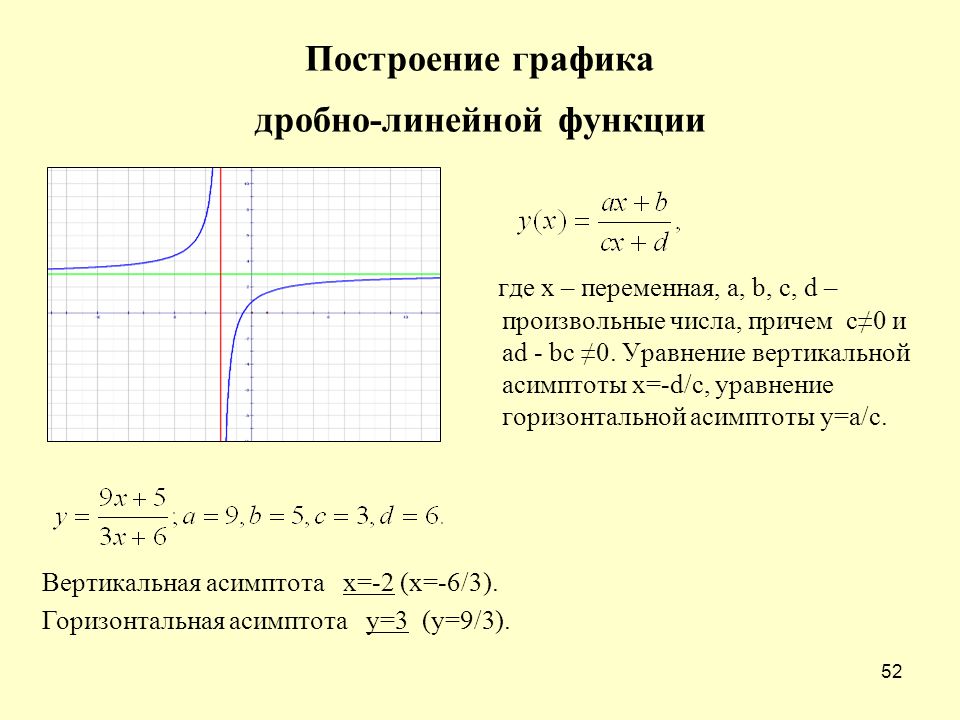
5) Графики гипербол имеют разные горизонтальные асимптоты для изменяющихся значений с, эквивалентных значению а/с в каждой точке.

6) Двигаясь слева направо по графику, мы замечаем, что графики переворачиваются, когда вы проходите вертикальную асимптоту. Светло-голубой график всегда является возрастающей функцией, а фиолетовый и красный — всегда убывающей функцией. Заметим, что для светло-голубой гиперболы ad — bc > 0, а для фиолетовой и красной кривых ad и bc

< 0,9.0019

Чтобы наблюдать, что происходит, когда график изменяется в динамической форме, мы затем позволяем c принимать значения от 10 до -10. Наблюдайте за изменениями графика и записывайте, что происходит.

Обратите внимание, как изменение значения c меняет график. При значении c = 1 вертикальная асимптота равна 1, при c = 2 вертикальная асимптота равна 0,5, при c = 4 вертикальная асимптота равна 0,25. Обратите внимание, что вертикальная асимптота является обратной величиной c.

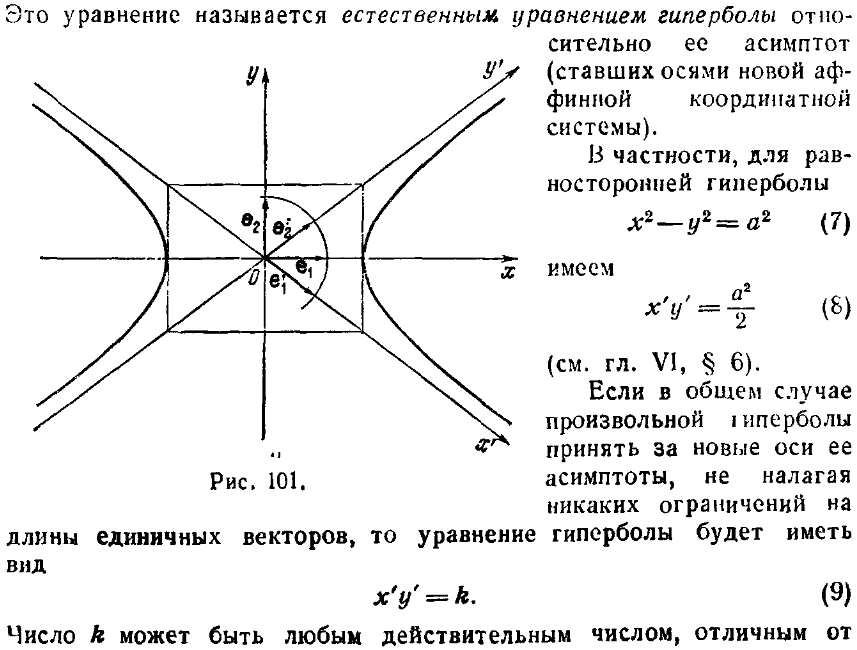Обратите внимание, что по мере того, как c становится все больше и больше, вертикальная асимптота все ближе и ближе к x = 0, но никогда не касается 0,9.0019

Изменение параметра d.

При сохранении параметров a, b и c постоянными параметр d теперь изменяется в соответствии со значениями d = 5, 2, 0, -2 и -5. На приведенной ниже диаграмме показано, что происходит, когда d принимает показанные значения.

Результаты наблюдения после изменения d следующие:

1) Y-пересечение для графиков изменяется при изменении d. Когда d = 5, точка пересечения с осью y составляет 1/5, а когда d = -2, точка пересечения с осью y составляет -1/2. Изменения d влияют на точку пересечения с осью y, поскольку точка пересечения с осью y происходит в точке (0, b/d).

2) Пересечение по оси x для всех графиков находится в точке x = -1/2. Х-пересечение — это точка (-b/a, 0). Изменения в d не вызывают изменений в x-отрезке.

3) Все графики для выбранных значений d являются гиперболами.

4) Все графики гипербол имеют разные вертикальные асимптоты, которые изменяются в зависимости от значения d. Когда d = 5, вертикальная асимптота находится в точке x = -5, а когда d = -2, вертикальная асимптота находится в точке x = 2. Таким образом, можно сделать вывод, что значение вертикали является отрицательным значением д. Но вспомните, что вертикальная асимптота возникает там, где знаменатель равен нулю, поэтому, поскольку значение d равно -2, установка cx + d = 0 приведет к тому, что вертикальная асимптота будет иметь отрицательное значение, если значение d.

5) Графики гипербол имеют одинаковую горизонтальную асимптоту при y = 2.

6) Двигаясь слева направо по графику, мы замечаем, что графики переворачиваются, когда вы проходите вертикальную асимптоту. В этом случае фиолетовый и красный графики всегда являются возрастающими функциями, а светло-голубой, зеленый и темно-синий — всегда убывающими. Обратите внимание, что для пурпурной и красной гипербол ad — bc > 0, а для голубой, зеленой и темно-синей кривых ad и bc

< 0,9. 0019

Чтобы наблюдать, что происходит, когда график изменяется в динамической форме, мы затем позволяем d принимать значения от 10 до -10. Посмотрите фильм ниже, чтобы увидеть изменения, которые происходят на графиках при изменении значения d.

Некоторые общие замечания о расследовании

1) Рациональные функции всегда имеют тенденцию переворачиваться при пересечении вертикальных асимптот, но функции либо всегда возрастают, либо всегда убывают в зависимости от разницы между ad и bc, если ad — dc > 0, то функция всегда возрастает, если ad — bc

< 0, то функция всегда убывает.

2) Горизонтальные асимптоты графиков встречаются при значении a/c.

3) Вертикальные асимптоты графиков приходятся на значение знаменателя cx + d = 0,

4) могут быть некоторые особые или вырожденные случаи, когда рациональные функции не являются гиперболами, а становятся прямыми линиями.

5) Х-пересечения происходят в точке (-b/a, 0)

6) Пересечение y происходит в точке (0, b/d)

До сих пор мы исследовали, как график меняется в зависимости от коэффициентов и констант рационального числа; изменения уравнения.

Рассмотрим еще несколько случаев изменения степени числителя и знаменателя.

Другие рациональные функции.

— это форма рациональной функции.

Во всех наших исследованиях до сих пор степень числителя f(x) и степень знаменателя g(x) были одинаковыми. И числитель, и знаменатель рационального уравнения были степени 1. Когда числитель и знаменатель оба имеют степень один, обратите внимание, что вертикальные асимптоты существуют, а вертикальные асимптоты встречаются в точке a/c.

Числитель меньше знаменателя.

Если в уравнении f(x)

< g(x), то в горизонтальной асимптоте возникает очень интересный результат, как показано на следующих диаграммах:

Обратите внимание, что на всех этих диаграммах кривые все ближе и ближе подходят к линии y = 0, но никогда не касаются линии y = 0. Следовательно, в случае, когда степень числителя меньше степени знаменателя, горизонтальная асимптота — это ось x.

Таким образом, можно дополнительно проиллюстрировать, нажав на ссылку фильма.

Числитель больше знаменателя

Если в уравнении f(x) > g(x), то результат будет выглядеть так, как показано на следующих диаграммах:

Обратите внимание, что происходит, когда значения становятся все больше (в абсолютном выражении). По мере того, как значения x становятся все больше (в абсолютном выражении), значения y также становятся все больше (в абсолютном выражении), поэтому горизонтальной асимптоты нет.

 

Резюме:

Учитывая рациональную функцию:

1) Горизонтальные асимптоты графиков встречаются при y = a/c, если степень f(x) совпадает со степенью g(x).

Горизонтальная асимптота равна y = 0, когда степень f(x)

< степени g(x).

Горизонтальная асимптота не существует, когда степень f(x) > степени g(x).

Для рациональной функции формы:

2) Рациональные функции либо возрастают, либо убывают в зависимости от разности между ad и bc, если ad — dc > 0, то функция возрастает; если ad — bc

< 0, то функция убывающая.

No related posts.