Уравнение касательной к графику функции параллельной прямой: Уравнение параллельной касательной — задание. Алгебра, 11 класс.

Решим это уравнение.

Сократим числитель и знаменатель дроби на 2:

Приведем правую часть уравнения к общему знаменателю. Получим:

Упростим числитель дроби и умножим обе части на — это выражение строго больше нуля. 2} {8-3x_0>=0} }}{ }»>

Решим первое уравнение.

Решим квадратное уравнение, получим

Второй корень не удовлетворяет условию title=»8-3x_0>=0″>, следовательно, у нас только одна точка касания и её абсцисса равна .

Напишем уравнение касательной к кривой в точке . Для этого подставим значение в уравнение — мы его уже записывали.

Ответ:
.

Пусть дана функция f , которая в некоторой точке x 0 имеет конечную производную f (x 0). Тогда прямая, проходящая через точку (x 0 ; f (x 0)), имеющая угловой коэффициент f ’(x 0), называется касательной.

А что будет, если производная в точке x 0 не существует? Возможны два варианта:

1. Касательная к графику тоже не существует. Классический пример — функция y = |x | в точке (0; 0).
2. Касательная становится вертикальной. Это верно, к примеру, для функции y = arcsin x в точке (1; π /2).

Уравнение касательной

Всякая невертикальная прямая задается уравнением вида y = kx + b , где k — угловой коэффициент. Касательная — не исключение, и чтобы составить ее уравнение в некоторой точке x 0 , достаточно знать значение функции и производной в этой точке.

Итак, пусть дана функция y = f (x ), которая имеет производную y = f ’(x ) на отрезке . Тогда в любой точке x 0 ∈ (a ; b ) к графику этой функции можно провести касательную, которая задается уравнением:

y = f ’(x 0) · (x − x 0) + f (x 0)

Здесь f ’(x 0) — значение производной в точке x 0 , а f (x 0) — значение самой функции.

Задача. Дана функция y = x 3 . Составить уравнение касательной к графику этой функции в точке x 0 = 2.

Уравнение касательной: y = f ’(x 0) · (x − x 0) + f (x 0). Точка x 0 = 2 нам дана, а вот значения f (x 0) и f ’(x 0) придется вычислять.

Для начала найдем значение функции. Тут все легко: f (x 0) = f (2) = 2 3 = 8;
Теперь найдем производную: f ’(x ) = (x 3)’ = 3x 2 ;
Подставляем в производную x 0 = 2: f ’(x 0) = f ’(2) = 3 · 2 2 = 12;
Итого получаем: y = 12 · (x − 2) + 8 = 12x − 24 + 8 = 12x − 16.
Это и есть уравнение касательной.

Задача. Составить уравнение касательной к графику функции f (x ) = 2sin x + 5 в точке x 0 = π /2.

В этот раз не будем подробно расписывать каждое действие — укажем лишь ключевые шаги. Имеем:

f (x 0) = f (π /2) = 2sin (π /2) + 5 = 2 + 5 = 7;
f ’(x ) = (2sin x + 5)’ = 2cos x ;
f ’(x 0) = f ’(π /2) = 2cos (π /2) = 0;

Уравнение касательной:

y = 0 · (x − π /2) + 7 ⇒ y = 7

В последнем случае прямая оказалась горизонтальной, т.к. ее угловой коэффициент k = 0. Ничего страшного в этом нет — просто мы наткнулись на точку экстремума.

В математике одним из параметров, описывающих положение прямой на декартовой плоскости координат, является угловой коэффициент этой прямой. Этот параметр характеризует наклон прямой к оси абцисс. Чтобы понять, как найти угловой коэффициент, сначала вспомним общий вид уравнения прямой в системе координат XY.

В общем виде любую прямую можно представить выражением ax+by=c, где a, b и c — произвольные действительные числа, но обязательно a 2 + b 2 ≠ 0.

Подобное уравнение с помощью несложных преобразований можно довести до вида y=kx+d, в котором k и d — действительные числа. Число k является угловым коэффициентом, а само уравнение прямой подобного вида называется уравнением с угловым коэффициентом. Получается, что для нахождения углового коэффициента, необходимо просто привести исходное уравнение к указанному выше виду. Для более полного понимания рассмотрим конкретный пример:

Задача: Найти угловой коэффициент линии, заданной уравнением 36x — 18y = 108

Решение: Преобразуем исходное уравнение.

Ответ: Искомый угловой коэффициент данной прямой равен 2.

В случае, если в ходе преобразований уравнения мы получили выражение типа x = const и не можем в результате представить y в виде функции x, то мы имеем дело с прямой, параллельной оси Х. Угловой коэффициент подобной прямой равен бесконечности.

Для прямых, которых выражены уравнением типа y = const, угловой коэффициент равняется нулю. Это характерно для прямых, параллельных оси абцисс.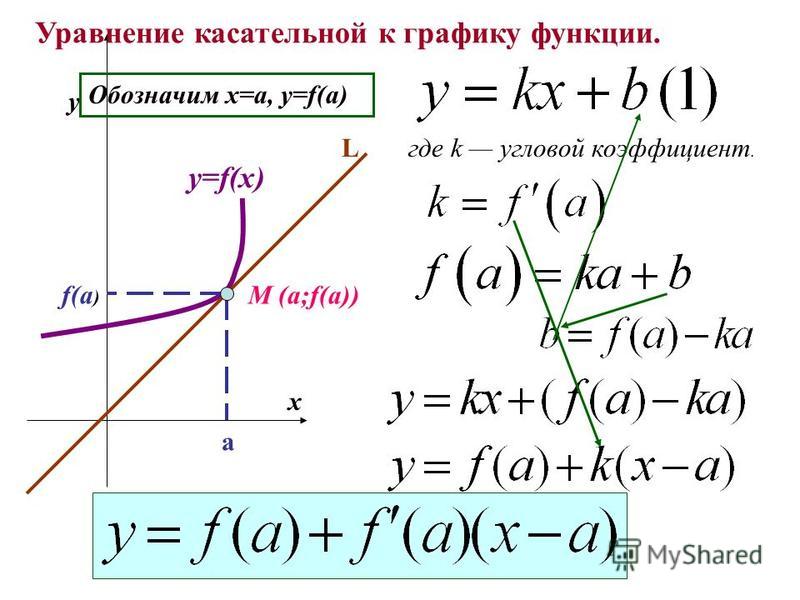 Например:

Задача: Найти угловой коэффициент линии, заданной уравнением 24x + 12y — 4(3y + 7) = 4

Решение: Приведем исходное уравнение к общему виду

24x + 12y — 12y + 28 = 4

Из полученного выражения выразить y невозможно, следовательно угловой коэффициент данной прямой равен бесконечности, а сама прямая будет параллельна оси Y.

Геометрический смысл

Для лучшего понимания обратимся к картинке:

На рисунке мы видим график функции типа y = kx. Для упрощения примем коэффициент с = 0. В треугольнике ОАВ отношение стороны ВА к АО будет равно угловому коэффициенту k. Вместе с тем отношение ВА/АО — это тангенс острого угла α в прямоугольном треугольнике ОАВ. Получается, что угловой коэффициент прямой равняется тангенсу угла, который составляет эта прямая с осью абцисс координатной сетки.

Решая задачу, как найти угловой коэффициент прямой, мы находим тангенс угла между ней и осью Х сетки координат. Граничные случаи, когда рассматриваемая прямая параллельна осям координат, подтверждают вышенаписанное. Действительно для прямой, описанной уравнением y=const, угол между ней и осью абцисс равен нулю. Тангенс нулевого угла также равен нулю и угловой коэффициент тоже равен нулю.

Для прямых, перпендикулярных оси абцисс и описываемых уравнением х=const, угол между ними и осью Х равен 90 градусов. Тангенс прямого угла равен бесконечности, так же и угловой коэффициент подобных прямых равен бесконечности, что подтверждает написанное выше.

Угловой коэффициент касательной

Распространенной, часто встречающейся на практике, задачей является также нахождение углового коэффициента касательной к графику функции в некоторой точке. Касательная — это прямая, следовательно к ней также применимо понятие углового коэффициента.

Чтобы разобраться, как найти угловой коэффициент касательной, нам будет необходимо вспомнить понятие производной. Производная от любой функции в некоторой точке — это константа, численно равная тангенсу угла, который образуется между касательной в указанной точке к графику этой функции и осью абцисс. Получается, что для определения углового коэффициента касательной в точке x 0 , нам необходимо рассчитать значение производной исходной функции в этой точке k = f»(x 0). Рассмотрим на примере:

Задача: Найти угловой коэффициент линии, касательной к функции y = 12x 2 + 2xe x при х = 0,1.

Решение: Найдем производную от исходной функции в общем виде

y»(0,1) = 24 . 0,1 + 2 . 0,1 . e 0,1 + 2 . e 0,1

Ответ: Искомый угловой коэффициент в точке х = 0,1 равен 4,831

С понятием касательной к графику функции вы уже знакомы. График дифференцируемой в точке х 0 функции f вблизи х 0 практически не отличается от отрезка касательной, а значит, он близок к отрезку секущей l, проходящей через точки (х 0 ; f (х 0)) и (х 0 +Δx; f (x 0 + Δx)). Любая из таких секущих проходит через точку А (х 0 ; f (х 0)) графика (рис. 1). Для того чтобы однозначно задать прямую, проходящую через данную точку A, достаточно указать ее угловой коэффициент. Угловой коэффициент Δy/Δx секущей при Δх→0 стремится к числу f ‘(x 0) (его мы примем за угловой коэффициент касательной) Говорят, что

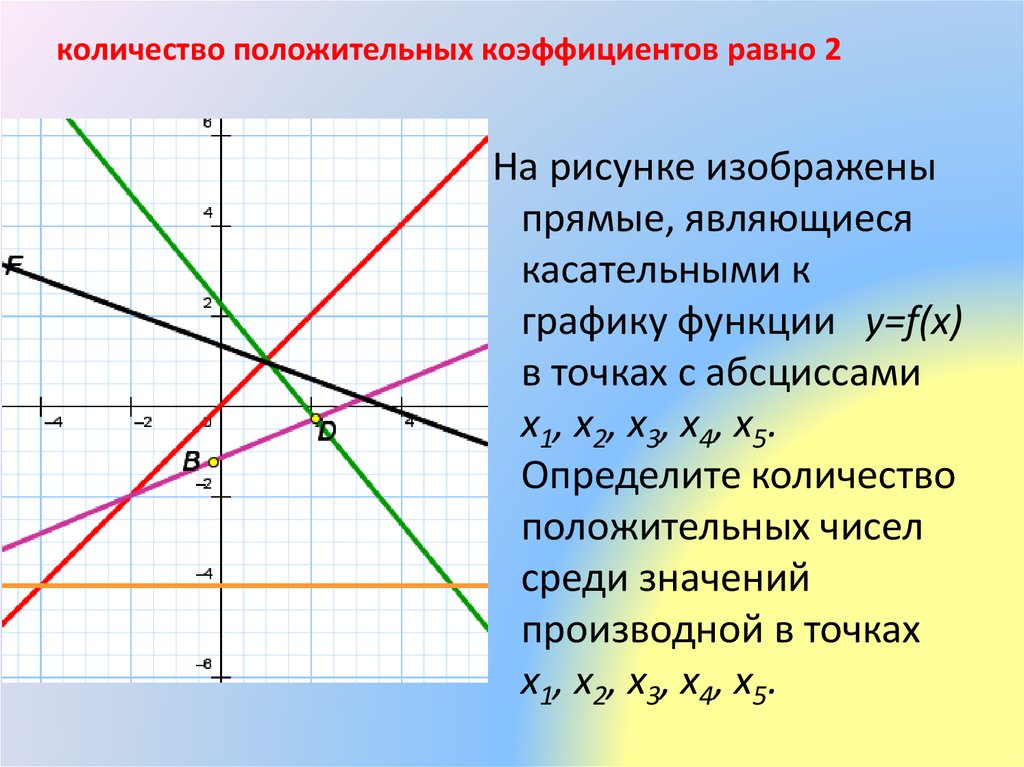
Если же f’(х 0) не существует, то касательная либо не существует (как у функции у = |x| в точке (0; 0), см. рис.), либо вертикальна (как у графика функции в точке (0; 0), рис.2).

Итак, существование производной функции f в точке хо эквивалентно существованию (невертикальной) касательной в точке (х 0 , f (х 0)) графика, при этом угловой коэффициент касательной равен f» (х 0). В этом состоитгеометрический смысл производной

Касательная к графику дифференцируемой в точке xо функции f — это прямая, проходящая через точку (x 0 ; f (x 0)) и имеющая угловой коэффициент f ‘(х 0).

Проведем касательные к графику функции f в точках x 1 , х 2 , х 3 (рис. 3) и отметим углы, которые они образуют с осью абсцисс. (Это угол, отсчитываемый в положительном направлении от положительного направления оси до прямой.) Мы видим, что угол α 1 острый, угол α 3 тупой, а угол α 2 равен нулю, так как прямая l параллельна оси Ох. Тангенс острого угла положителен, тупого — отрицателен, tg 0 = 0. Поэтому

F»(x 1)>0, f’(x 2)=0, f’(x 3)
Построение касательных в отдельных точках позволяет более точно строить эскизы графиков. Так, например, для построения эскиза графика функции синус предварительно находим, что в точках 0; π/2 и π производная синуса равна 1; 0 и -1 соответственно. Построим прямые, проходящие через точки (0; 0), (π/2,1) и (π, 0) с угловыми коэффициентами 1, 0 и -1 соответственно (рис. 4) Остается вписать в полученную трапецию, образованную этими прямыми и прямой Ох, график синуса так, чтобы при х, равном 0, π/2 и π, он касался соответствующих прямых.

Отметим, что график синуса в окрестности нуля практически не отличим от прямой у = х. Пусть, например, масштабы по осям выбраны так, что единице соответствует отрезок в 1см. Имеем sin 0,5 ≈ 0,479425, т. е. |sin 0,5 — 0,5| ≈ 0,02, и в выбранном масштабе это соответствует отрезку длиной 0,2 мм. Поэтому график функции y = sin x в интервале (-0,5; 0,5) будет отклоняться (в вертикальном направлении) от прямой у = х не более чем на 0,2 мм, что примерно соответствует толщине проводимой линии.

Инструкция

Определяем угловой коэффициент касательной к кривой в точке М.
Кривая, представляющая собой график функции y = f(x), непрерывна в некоторой окрестности точки М (включая саму точку М).

Если значения f‘(x0) не существует, то либо касательной нет, либо она проходит вертикально. Ввиду этого, наличие производной функции в точке х0 обусловлено существованием невертикальной касательной, соприкасающейся с графиком функции в точке (х0, f(х0)). В этом случае угловой коэффициент касательной равен будет f»(х0). Таким образом, становится ясен геометрический смысл производной – расчет углового коэффициента касательной.

Найдите значение абсциссы точки касания, которую обозначаются буквой «а». Если она совпадает с заданной точкой касательной, то «а» будет ее х-координате. Определите значение функции f(a), подставив в уравнение функции величину абсциссы.

Определите первую производную уравнения функции f’(x) и подставьте в него значение точки «а».

Возьмите общее уравнение касательной, которое определяется как y = f(a) = f (a)(x – a), и подставьте в него найденные значения a, f(a), f «(a). В результате будет найдено решение графика и касательной.

Решите задачу иным способом, если заданная точка касательной не совпала с точкой касания. В этом случае необходимо в уравнение касательной вместо цифр подставить «а». После этого вместо букв «х» и «у» подставьте значение координат заданной точки. Решите получившееся уравнение, в котором «а» является неизвестной. Поставьте полученное значение в уравнение касательной.

Составьте уравнение касательной с буквой «а», если в условии задачи задано уравнение функции и уравнение параллельной линии относительно искомой касательной. После этого необходимо производную функции , чтобы координату у точки «а». Подставьте соответствующее значение в уравнение касательной и решите функцию.

Уравнение касательной к графику функции

Тема: Уравнение касательной к графику функции.

Цель: Вывести уравнение касательной, начать формировать умение писать уравнение касательной к графику функции в точке.

План проведения урока:

1. Организационный момент (1 минута).

2. Проверочная работа (5 минут)

3. Введение нового материала (10 минут).

4. Решение упражнений (25 минут).

5. Подведение итогов урока (3 минуты).

6. Домашнее задание (1 минута).

Ход урока:

1. Организационный момент.

Добиться дисциплины в классе. Проверить готовность учеников к уроку, мобилизовать внимание. Собрать цикл задач ФИЗИЧЕСКИЙ СМЫСЛ ПРОИЗВОДНОЙ.

Проверочная работа (в двух вариантах)

Вариант 1

В чём заключается геометрический смысл производной?

Вариант 2

В чём заключается физический смысл производной?

3. Введение нового материала

Как найти уравнение касательной?

Касательная — это прямая линия. Уравнение прямой . Чтобы написать уравнение касательной, нужно знать числа k и b.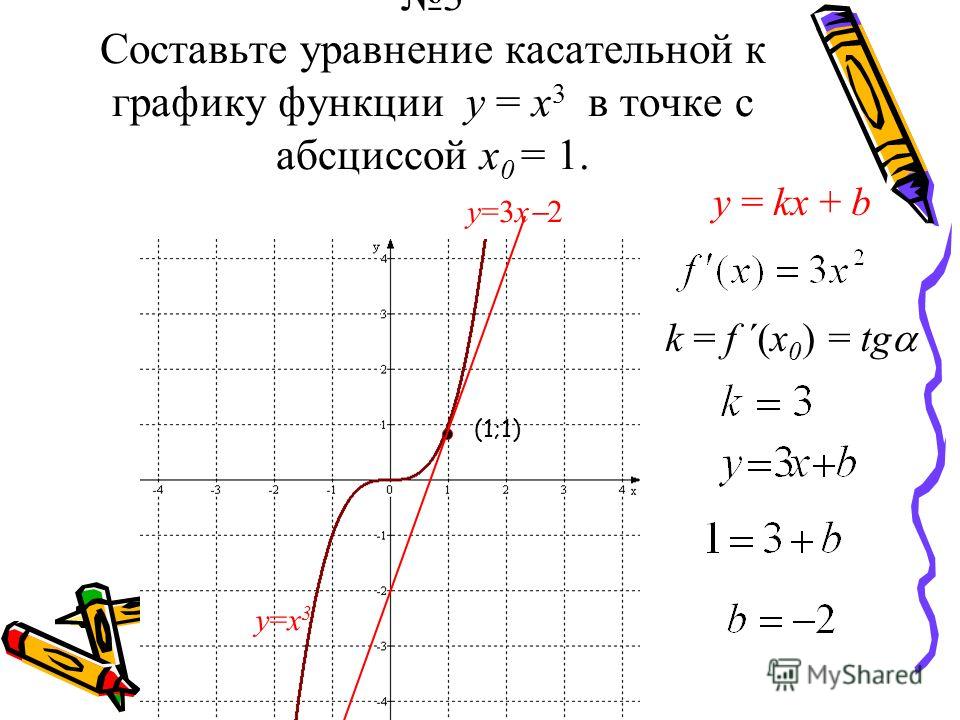 k — это угловой коэффициент касательной, который равен производной функции y = f(x) в точке.

(1)

Точка M принадлежит касательной AB, поэтому координаты удовлетворяют уравнению касательной:

(2)

Тогда уравнение касательной (1):

Уравнение касательной к кривой y = f(x) в точкеможно найти по плану:

1. Написать уравнение касательной в общем виде

2. Найти

3. Найти производную функции

4. Найти значение производной в точке

5. Подставить значение ив уравнение касательной.

Задача 1. Написать уравнение касательной к графику функции в точке с абсциссой .

Решение

1.

2.

3.

4.

5.

4. Решение упражнений

1.Написать уравнения касательной к графику функции в точке с абсциссой .

2.Написать уравнение касательной к графику функции в точке с абсциссой:

а) ; б) ; в)

3.Найти координаты точки, принадлежащей параболе, если известно, что касательная, проведенная к параболе в этой точке, образует с положительным направлением оси абсцисс угол .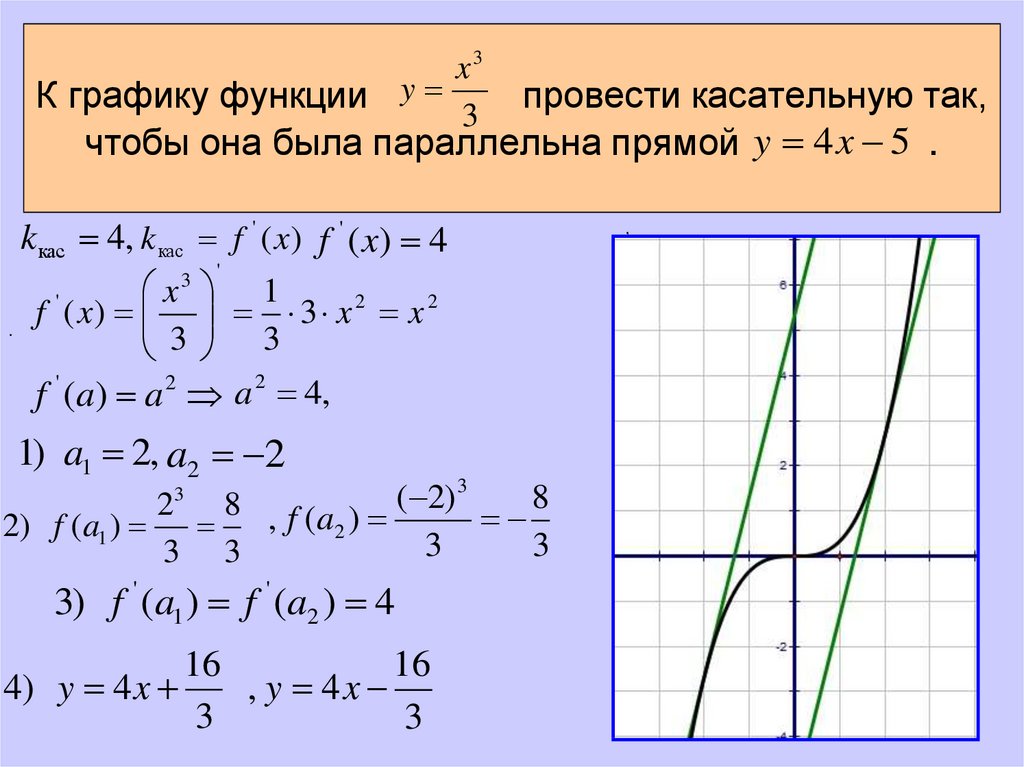

4.В каких точках кривой касательная параллельно оси?

5.Написать уравнение касательной, проведенной к графику функции ,параллельно прямой .

6.Докажите, что на графике функции нет точек, касательная в которых параллельно оси абсцисс.

 5. Подведение итогов урока.

Что такое производная?

В чем заключается физический смысл производной?

В чем заключается геометрический смысл производной?

Почему такое большое значение придают касательной в математике?

Какое отношение производная имеет к касательной?

6. Домашнее задание.

Тренажёр № 4 (задание 3 для всех функций)

Адрес публикации: https://www.prodlenka.org/metodicheskie-razrabotki/88622-uravnenie-kasatelnoj-k-grafiku-funkcii

исчисление — Касательная линия параллельна другой линии

Задавать вопрос

спросил 7 лет, 8 месяцев назад

Изменено 7 лет, 8 месяцев назад

Просмотрено 35 тысяч раз

$\begingroup$ 92-3x-5$ касательная параллельна $3x-y=2$? Найдите его уравнение. 2-3x-5$.

Это означает, что вопрос состоит в том, в какой точке производная параболы будет равна наклону $3x-y=2$.

Итак, чтобы решить задачу, определите наклон линии и приравняйте его к производной уравнения параболы, чтобы найти значение $x$ нужной точки. Затем используйте уравнение параболы, чтобы найти значение $y$, и все готово.

$\endgroup$

1

$\endgroup$

$\begingroup$

Изменить: поскольку касательная параллельна данной прямой: $3x-y=2$, следовательно, наклон касательной к параболе равен $\frac{-3}{-1}=3$

Пусть уравнение касательная будет $y=3x+c$

Теперь решим уравнение касательной: $y=3x+c$ и параболы: $y=x^2-3x-5$, подставив $y=3x+ c$ следующим образом $$3x+c=x^2-3x-5$$ $$\имеет x^2-6x-(c+5)=0\tag 1$$ Для касания выполняется следующее условие $$ \text{определитель},\ B^2-4AC=0$$ $$\подразумевает (-6)^2-4(1)(-(c+5))$$ $$\подразумевает c=\frac{ -56}{4}=-14$$ Следовательно, установив значение $c=-14$, получим $$x^2-6x-(-14+5)=0$$ $$\имеет x^2 -6х+92-3(3)-5=-5$$ Следовательно, точка касания $\color{blue}{(3, -5)}$

$\endgroup$

2

$\begingroup$

Если вы одновременно решаете кривую и прямую $y=3x+c$, чтобы получить квадратное уравнение относительно $x$, то это квадратное уравнение должно иметь двойные корни в точке касания.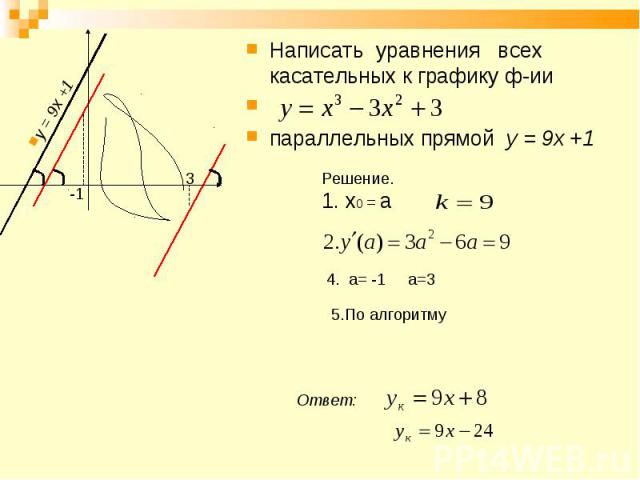 Это даст значение $c$, а требуемое значение $x$ определяется выражением $x=-\frac{b}{2a}$

$\endgroup$

Найдите уравнение прямой, касательной к графику F и параллельной данной прямой. 93 + 2, 3x — y — 4 = 0` Найдите уравнение прямой, касательной к графику функции f и параллельной данной прямой.

Ссылайтесь на эту страницу следующим образом:

«Найдите уравнение прямой, касательной к графику F и параллельной заданной прямой». Редакционная статья eNotes , 22 сентября 2015 г., https://www.enotes.com/homework-help/f-x-x-3-2-3x-y-4-0-find-an-equation-line-that-505614. По состоянию на 2 апреля 2023 г. 93 + 2 = 3
Наклон искомой линии равен 3, и теперь у нас есть точка на искомой прямой (1, 3), а также точка касания

Используя точку-наклон, уравнение для желаемого линию можно получить следующим образом. При заданном наклоне m = 3 и точке на искомой линии (x0, y0) уравнение линии задается как
(y — y0) = m (x — x0)
y — 3 = 3 (x — 1 )
г = 3x

Утверждено редакцией eNotes 93+2=1

Уравнение касательной можно записать, используя форму уравнения с точечным наклоном.

y-y_1=m(x-x_1)

y-3=3(x-1)

y-3=3x-3

y=3x

y-1=3(x- (-1)

y-1=3x+3

y=3x+4

См.

Начните 48-часовую бесплатную пробную версию , чтобы получить доступ к более чем 30 000 дополнительных руководств и более чем 350 000 вопросов помощи при выполнении домашних заданий, на которые наши эксперты ответили.

Уже зарегистрирован? Войдите здесь.

Утверждено редакцией eNotes

Задайте вопрос

Похожие вопросы

Математика

Последний ответ опубликован 07 сентября 2010 г. в 12:47:25.

Что означают буквы R, Q, N и Z в математике?

14 ответов воспитателя

математика

Последний ответ опубликован 07 октября 2013 г.