Лекции по математической физике
Лекции по математической физике
ОглавлениеПРЕДИСЛОВИЕГлава I.  ОСНОВНЫЕ УРАВНЕНИЯ МАТЕМАТИЧЕСКОЙ ФИЗИКИ И ПОСТАНОВКА НАЧАЛЬНО-КРАЕВЫХ ЗАДАЧ ОСНОВНЫЕ УРАВНЕНИЯ МАТЕМАТИЧЕСКОЙ ФИЗИКИ И ПОСТАНОВКА НАЧАЛЬНО-КРАЕВЫХ ЗАДАЧ§ 1. ФИЗИЧЕСКИЕ ЗАДАЧИ, СВЯЗАННЫЕ С ВОЛНОВЫМИ ПРОЦЕССАМИ 2. Малые поперечные колебания упругой струны 3. Случай многих пространственных переменных § 2. ПРОЦЕССЫ ТЕПЛОМАССОПЕРЕНОСА § 3. СТАЦИОНАРНЫЕ ПРОЦЕССЫ 1. Стационарное распределение тепла 2. Задачи электростатики 3. Установившиеся колебания 4. Установившиеся электромагнитные колебания 5. Постановка краевых задач § 4. ОБЩИЕ ЗАМЕЧАНИЯ Глава II. КЛАССИФИКАЦИЯ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ В ЧАСТНЫХ ПРОИЗВОДНЫХ ВТОРОГО ПОРЯДКА § 1. КЛАССИФИКАЦИЯ УРАВНЕНИЙ С ДВУМЯ НЕЗАВИСИМЫМИ ПЕРЕМЕННЫМИ § 2. ПРИВЕДЕНИЕ УРАВНЕНИЯ С ДВУМЯ НЕЗАВИСИМЫМИ ПЕРЕМЕННЫМИ К КАНОНИЧЕСКОМУ ВИДУ § 3. КЛАССИФИКАЦИЯ УРАВНЕНИЙ В СЛУЧАЕ МНОГИХ НЕЗАВИСИМЫХ ПЕРЕМЕННЫХ Глава III. МЕТОД РАЗДЕЛЕНИЯ ПЕРЕМЕННЫХ. РАЗЛОЖЕНИЕ ПО СОБСТВЕННЫМ ФУНКЦИЯМ ЗАДАЧИ ШТУРМА-ЛИУВИЛЛЯ § 2. ПЕРВАЯ И ВТОРАЯ ФОРМУЛЫ ГРИНА § 3. ПОЛНЫЕ И ЗАМКНУТЫЕ СИСТЕМЫ ФУНКЦИЙ § 4.  ОБЩАЯ СХЕМА МЕТОДА РАЗДЕЛЕНИЯ ПЕРЕМЕННЫХ ДЛЯ ОДНОРОДНОГО УРАВНЕНИЯ ОБЩАЯ СХЕМА МЕТОДА РАЗДЕЛЕНИЯ ПЕРЕМЕННЫХ ДЛЯ ОДНОРОДНОГО УРАВНЕНИЯ§ 5. МЕТОД РАЗДЕЛЕНИЯ ПЕРЕМЕННЫХ ДЛЯ НЕОДНОРОДНОГО УРАВНЕНИЯ § 6. НЕОДНОРОДНЫЕ ГРАНИЧНЫЕ УСЛОВИЯ § 7. РАЗЛОЖЕНИЕ ПО СОБСТВЕННЫМ ФУНКЦИЯМ ДЛЯ ЭЛЛИПТИЧЕСКОГО УРАВНЕНИЯ § 8. ПРОСТЕЙШИЕ ЗАДАЧИ ШТУРМА-ЛИУВИЛЛЯ Глава IV. СПЕЦИАЛЬНЫЕ ФУНКЦИИ § 1. УРАВНЕНИЕ СПЕЦИАЛЬНЫХ ФУНКЦИЙ И СВОЙСТВА ЕГО РЕШЕНИЙ § 2. ЦИЛИНДРИЧЕСКИЕ ФУНКЦИИ 2. Свойства гамма-функции 3. Степенной ряд для функций Бесселя 4. Рекуррентные формулы 5. Функции Бесселя полуцелого порядка 6. Интегральное представление функций Бесселя 7. Функции Ханкеля. Интегральное представление 8. Связь функций Ханкеля и Бесселя. Функция Неймана 10. Асимптотика цилиндрических функций 11. Цилиндрические функции чисто мнимого аргумента. Функции Инфельда и Макдональда § 3. КЛАССИЧЕСКИЕ ОРТОГОНАЛЬНЫЕ ПОЛИНОМЫ 2. Основные свойства классических ортогональных полиномов 3.  Производящая функция классических ортогональных полиномов Производящая функция классических ортогональных полиномов4. Полиномы Якоби 5. Полиномы Лежандра 6. Полиномы Лагерра 7. Полиномы Эрмита § 4. ПРИСОЕДИНЕННЫЕ ФУНКЦИИ ЛЕЖАНДРА 2. Краевая задача для присоединенных функций Лежандра 3. Полнота и замкнутость системы присоединенных функций Лежандра § 5. СФЕРИЧЕСКИЕ ФУНКЦИИ § 6. ШАРОВЫЕ ФУНКЦИИ § 7. СОБСТВЕННЫЕ ФУНКЦИИ ОПЕРАТОРА ЛАПЛАСА ДЛЯ КАНОНИЧЕСКИХ ОБЛАСТЕЙ 2. Собственные функции цилиндра 3. Собственные функции шара Глава V. УРАВНЕНИЯ ЭЛЛИПТИЧЕСКОГО ТИПА. КРАЕВЫЕ ЗАДАЧИ ДЛЯ УРАВНЕНИЯ ЛАПЛАСА 2. Основные свойства гармонических функций § 2. ВНУТРЕННИЕ КРАЕВЫЕ ЗАДАЧИ ДЛЯ УРАВНЕНИЯ ЛАПЛАСА 2. Внутренние вторая и третья краевые задачи § 3. ВНЕШНИЕ КРАЕВЫЕ ЗАДАЧИ 2. Единственность решения внешних задач в трехмерном случае 3. Единственность решения внешних задач для уравнения Лапласа на плоскости § 4. ФУНКЦИЯ ГРИНА ОПЕРАТОРА ЛАПЛАСА 2. Свойства функции Грина задачи Дирихле 3.  Функция Грина внутренней третьей краевой задачи Функция Грина внутренней третьей краевой задачи4. Функция Грина внутренней задачи Неймана 5. Функции Грина внешних краевых задач 6. Примеры построения функций Грина 7. Функция Грина задачи Дирихле на плоскости § 5. РЕШЕНИЕ КРАЕВЫХ ЗАДАЧ ДЛЯ УРАВНЕНИЯ ЛАПЛАСА В КРУГЕ И ПРЯМОУГОЛЬНИКЕ 2. Краевая задача для уравнения Лапласа в прямоугольнике § 6. ОСНОВЫ ТЕОРИИ ПОТЕНЦИАЛА 2. Несобственные интегралы, зависящие от параметра 4. Непрерывность потенциала простого слоя 5. Поверхности Ляпунова 6. Существование и непрерывность прямых значений потенциала двойного слоя на поверхности 7. Разрыв потенциала двойного слоя 8. Разрыв нормальной производной потенциала простого слоя § 7. МЕТОД ИНТЕГРАЛЬНЫХ УРАВНЕНИЙ РЕШЕНИЯ КРАЕВЫХ ЗАДАЧ 2. Интегральное уравнение для внутренней задачи Дирихле 3. Интегральное уравнение для внешней задачи Неймана 4. Интегральное уравнение для внутренней задачи Неймана и внешней задачи Дирихле Глава VI.  УРАВНЕНИЯ ПАРАБОЛИЧЕСКОГО ТИПА УРАВНЕНИЯ ПАРАБОЛИЧЕСКОГО ТИПА§ 1. ПОСТАНОВКА НАЧАЛЬНО-КРАЕВОЙ ЗАДАЧИ § 2. ПРИНЦИП МАКСИМУМА § 3. ТЕОРЕМЫ ЕДИНСТВЕННОСТИ И УСТОЙЧИВОСТИ § 4. СУЩЕСТВОВАНИЕ РЕШЕНИЯ УРАВНЕНИЯ ТЕПЛОПРОВОДНОСТИ В СЛУЧАЕ ОГРАНИЧЕННОЙ ОБЛАСТИ 2. Существование классического решения уравнения теплопроводности на отрезке § 5. ФУНКЦИЯ ГРИНА § 6. НЕОДНОРОДНОЕ УРАВНЕНИЕ ТЕПЛОПРОВОДНОСТИ И НЕОДНОРОДНЫЕ ГРАНИЧНЫЕ УСЛОВИЯ 2. Неоднородное граничное условие § 7. ЗАДАЧА КОШИ ДЛЯ УРАВНЕНИЯ ТЕПЛОПРОВОДНОСТИ 2. Теорема единственности 3. Фундаментальное решение. Интеграл Пуассона 4. Свойства фундаментального решения § 8. СУЩЕСТВОВАНИЕ РЕШЕНИЯ ЗАДАЧИ КОШИ ДЛЯ ОДНОРОДНОГО УРАВНЕНИЯ ТЕПЛОПРОВОДНОСТИ 2. Пример § 9. НЕОДНОРОДНОЕ УРАВНЕНИЕ ТЕПЛОПРОВОДНОСТИ НА БЕСКОНЕЧНОЙ ПРЯМОЙ § 10. НАЧАЛЬНАЯ ЗАДАЧА ДЛЯ УРАВНЕНИЯ ТЕПЛОПРОВОДНОСТИ В ПРОСТРАНСТВЕ § 11. РЕШЕНИЕ УРАВНЕНИЯ ТЕПЛОПРОВОДНОСТИ НА ПОЛУПРЯМОЙ 2. Однородные граничные условия 3. Краевой режим 4.  Неоднородное граничное условие второго рода Неоднородное граничное условие второго рода§ 12. ФОРМУЛА ГРИНА ДЛЯ УРАВНЕНИЯ ТЕПЛОПРОВОДНОСТИ § 13. УРАВНЕНИЕ НЕЛИНЕЙНОЙ ТЕПЛОПРОВОДНОСТИ И ГОРЕНИЯ Глава VII. УРАВНЕНИЯ ГИПЕРБОЛИЧЕСКОГО ТИПА § 5. ВЫНУЖДЕННЫЕ КОЛЕБАНИЯ ОГРАНИЧЕННОЙ СТРУНЫ § 6. ФОРМУЛА ГРИНА ДЛЯ УРАВНЕНИЯ КОЛЕБАНИЙ § 7. УРАВНЕНИЕ КОЛЕБАНИЙ НА НЕОГРАНИЧЕННОЙ ПРЯМОЙ 2. Формула Даламбера 3. Существование, единственность и устойчивость решения задачи Коши 4. Физическая интерпретация решения 5. Колебания струны под действием мгновенного сосредоточенного импульса 6. Существование и единственность решения § 8. ЗАДАЧИ ДЛЯ ПОЛУОГРАНИЧЕННОЙ ПРЯМОЙ § 9. КОЛЕБАНИЯ В НЕОГРАНИЧЕННОМ ПРОСТРАНСТВЕ 2. Формула Кирхгофа 3. Формула Пуассона 4. Метод спуска 5. Локальные начальные условия 6. Установившиеся колебания § 10. ЗАДАЧА С ДАННЫМИ НА ХАРАКТЕРИСТИКАХ (ЗАДАЧА ГУРСА) § 11. ОБЩАЯ ЗАДАЧА КОШИ.  ФУНКЦИЯ РИМАНА ФУНКЦИЯ РИМАНА§ 12. НЕЛИНЕЙНЫЕ УРАВНЕНИЯ 2. Обобщенное решение. Условия на разрыве 3. Уравнение Кортевега — де Фриза и законы сохранения 4. Схема метода обратной задачи 5. Солитонные решения Глава VIII. УРАВНЕНИЯ ЭЛЛИПТИЧЕСКОГО ТИПА. КРАЕВЫЕ ЗАДАЧИ ДЛЯ УРАВНЕНИЯ ГЕЛЬМГОЛЬЦА § 1. ЗАДАЧА ШТУРМА—ЛИУВИЛЛЯ ДЛЯ ОПЕРАТОРА ЛАПЛАСА 2. Свойства собственных значений и собственных функций § 2. СВОЙСТВА РЕШЕНИЙ УРАВНЕНИЯ ГЕЛЬМГОЛЬЦА 3. Потенциалы уравнения Гельмгольца 4. Принцип максимума для уравнения … § 3. ВНУТРЕННИЕ ЗАДАЧИ ДЛЯ УРАВНЕНИЯ ГЕЛЬМГОЛЬЦА § 4. ФУНКЦИЯ ГРИНА КРАЕВЫХ ЗАДАЧ ДЛЯ УРАВНЕНИЯ ГЕЛЬМГОЛЬЦА § 5. ЗАДАЧА ДЛЯ УРАВНЕНИЯ … В НЕОГРАНИЧЕННОЙ ОБЛАСТИ § 6. ЗАДАЧА ДЛЯ УРАВНЕНИЯ … В НЕОГРАНИЧЕННОЙ ОБЛАСТИ 2. Принцип предельного поглощения ЛИТЕРАТУРА ДОПОЛНЕНИЕ |
Методы математической физики. Семинары | Открытые видеолекции учебных курсов МГУ
В курсе «Методы математической физики» рассматриваются основные методы исследования краевых и начально-краевых задач для дифференциальных уравнений математической физики.
Список всех тем лекций
Семинар 1. Малые поперечные колебания струны.
Вступительное слово
Примеры уравнений, рассматриваемых в курсе
Уравнение малых поперечных колебаний струны
Начально краевая задача
Семинар 2. Задача Штурма-Лиувилля для оператора Лапласа в прямоугольных областях.
Вступление
Одномерное уравнение колебаний струны
Задача Штурма-Лиувилля
Общие свойства задач Штурма-Лиувилля
Теорема Стеклова
Двумерная задача Штурма-Лиувилля в прямоугольнике
Семинар 3. Уравнение Лапласа в прямоугольных координатах. Часть 1.
Вступление
Задача Штурма-Лиувилля
Задача Штурма-Лиувилля на отрезке с периодическими граничными условиями
Уравнение Лапласа в прямоугольных координатах
Теорема о существовании и единственности решения внутренней краевой задачи для уравнения Лапласа
Задача в прямоугольнике
Семинар 4. Уравнение Лапласа в прямоугольных координатах. Часть 2.
Задача в прямоугольнике (продолжение)
Краевая задача для уравнения Лапласа в прямоугольном параллелепипеде
Краевая задача для уравнения Пуассона
Семинар 5. Уравнение Лапласа в полярных координатах.
Вступление
Частные решения уравнения Лапласа в полярных координатах
Краевая задача для уравнения Лапласа в круге
Семинар 6. Внешняя краевая задача для уравнения Лапласа на плоскости. Часть 1.
Внешняя краевая задача для уравнения Лапласа на плоскости. Часть 1.
Вступление
Решение краевой задачи для уравнения Лапласа вне ограниченной области
Решение краевой задачи для уравнения Лапласа вне круга
Краевая задача для уравнения Лапласа в кольце
Семинар 7. Внешняя краевая задача для уравнения Лапласа на плоскости. Часть 2.
Вступление
Внутренняя краевая задача для уравнения Лапласа в круговом секторе
Внутренняя краевая задача для уравнения Лапласа в кольцевом секторе
Семинар 8. Задача Штурма-Лиувилля в полярных координатах. Часть 1.
Вступление
Задача Штурма-Лиувилля в круге
Общее решение уравнения Бесселя n-ного порядка
Граничное условие Дирихле (первого рода)
Граничное условие Неймана (второго рода)
Граничное условие третьего рода
Семинар 9. Задача Штурма-Лиувилля в полярных координатах. Часть 2.
Задача Штурма-Лиувилля в полярных координатах. Часть 2.
Задача Штурма-Лиувилля в круге
Задача Штурма-Лиувилля в круговом секторе
Задача Штурма-Лиувилля в кольце
Семинар 10. Уравнение Лапласа в сферических и цилиндрических координатах.
Вступление
Уравнение Лапласа в сферических координатах
Основные свойства присоединенных функций Лежандра
Основные свойства сферических функций
Семинар 11. Задача Штурма-Лиувилля и уравнение Лапласа в сферических и цилиндрических координатах.
Вступление
Задача Штурма-Лиувилля на единичной сфере
Уравнение Лапласа в шаре
Внешняя краевая задача для уравнения Лапласа в пространстве
Краевая задача для уравнения Лапласа вне шара
Краевая задача для уравнения Лапласа в шаровом слое
Семинар 12. Задача Штурма-Лиувилля для оператора Лапласа в цилиндрических координатах.
Задача Штурма-Лиувилля для оператора Лапласа в цилиндрических координатах.
Вступление
Задача Штурма-Лиувилля в цилиндре
Задача Штурма-Лиувилля в сферических координатах
Задача Штурма-Лиувилля в шаре
Семинар 13. Задача Штурма-Лиувилля в шаровом слое и уравнение Лапласа в цилиндре.
Вступление
Задача Штурма-Лиувилля в шаровом слое
Уравнение Лапласа в цилиндре
Семинар 14. Уравнение Лапласа в цилиндре (продолжение).
Вступление
Решение задачи 2
Пример с конкретными граничными условиями
Семинар 15. Решение краевых задач при помощи построения функции Грина.
Вступление
Фундаментальное решение уравнения Лапласа
Функция Грина внутренней задачи Дирихле для уравнения Лапласа
Внутренняя краевая задача для уравнения Пуассона
Способы нахождения функции Грина внутренней задачи Дирихле для уравнения Лапласа
Семинар 16. Нахождение функции Грина с помощью решения краевой задачи.
Вступление
Нахождение функции Грина с помощью решения краевой задачи
Функция Грина для других граничных условий
Семинар 17. Функция Грина для внешних краевых задач.
Вступление
Функция Грина для внешних краевых задач
Построение функции Грина методом зеркальных отображений
Задача Неймана в полупространстве
Задача Дирихле в круге
Построение функции Грина в плоской области методом конформных отображений
Семинар 18. Построение функции Грина.
Построение функции Грина.
Функция Грина для внешних краевых задач
Построение функции с помощью конформного отображения
Пример: построение функции Грина задачи Дирихле в полосе
Задача Дирихле в круге
Семинар 19. Решение начальной краевой задачи для уравнения колебаний.
Вступление
Начально-краевая задача для уравнения колебаний в ограниченной области с однородными граничными условиями
Пример: решение начальной краевой задачи для уравнения колебаний
Семинар 20. Решение начально-краевых задач с однородными и неоднородными условиями в ограниченной области.
Вступление
Начально-краевая задача для уравнения теплопроводности в ограниченной области с неоднородными граничными условиями
Начально-краевая задача для уравнения колебаний в ограниченной области с неоднородными граничными условиями
Пример: задача в единичном круге для уравнения теплопроводности
Пример: задача с неоднородными граничными условиями
Пример: уравнение колебаний в круге
Семинар 21. Решение начально-краевых задач с однородными и неоднородными условиями в неограниченной области.
Решение начально-краевых задач с однородными и неоднородными условиями в неограниченной области.
Вступление
Начально-краевая задача для уравнения теплопроводности в ограниченной области с неоднородными граничными условиями
Семинар 22. Уравнение теплопроводности на полупрямой.
Вступление
Уравнение теплопроводности на полупрямой
Пример задачи на полупрямой
Задача с неоднородными граничными условиями
Семинар 23. Уравнение колебаний в неограниченной области.
Уравнение колебаний на прямой
Метод распространяющихся волн
Неоднородное уравнение колебаний на прямой
Метод интегрирования по фазовой плоскости
Семинар 24. Начальная краевая задача для уравнения колебаний на полупрямой.
Начальная краевая задача для уравнения колебаний на полупрямой.
Вступление
Начальная краевая задача для уравнения колебаний на полупрямой
Начальная краевая задача с условиями Неймана
Семинар 25. Уравнение Гельмгольца.
Вступление
Уравнение Гельмгольца
Вывод волнового уравнения Гельмгольца
Краевые задачи для уравнения Гельмгольца в ограниченной области
Частные решения однородного уравнения Гельмгольца в полярных координатах
Волновое уравнение Гельмгольца
Неволновое уравнение Гельмгольца
Пример: задача Дирихле в круге для неволнового уравнения Гельмгольца
Пример: задача Дирихле в круге для волнового уравнения Гельмгольца
Семинар 26. Уравнение Гельмгольца в недекартовых координатах.
Уравнение Гельмгольца в недекартовых координатах.
Семинар 27. Дельта-функция.
18.2 Стандартные примеры
18.2 Стандартные примеры
|
| Далее: 18.3 Правильная поза |
Подразделы
18.
 2 Стандартные примеры
2 Стандартные примерыЕсть несколько стандартных примеров дифференциальных уравнений в частных производных. Вы должны знать их наизусть.
18.2.1 Уравнение Лапласа
Уравнение Лапласа определяет основную устойчивую теплопроводность, среди многих еще.
Пример проблемы показан на рисунке 18.1. Физически это устойчивая теплопроводность в прямоугольной пластине размерами . Неизвестным в этом примере является температура. Независимыми переменными являются декартовы координаты и . Домен представляет собой двумерную внутреннюю часть пластины. Граница – это одномерный периметр тарелка. (Граница может по-прежнему обозначаться вместо хотя здесь это не поверхность.)
Уравнение Лапласа также описывает идеальные течения, однонаправленные течения,
мембраны, электростатика и магнитостатика, сложные функции и
бесчисленное множество других проблем.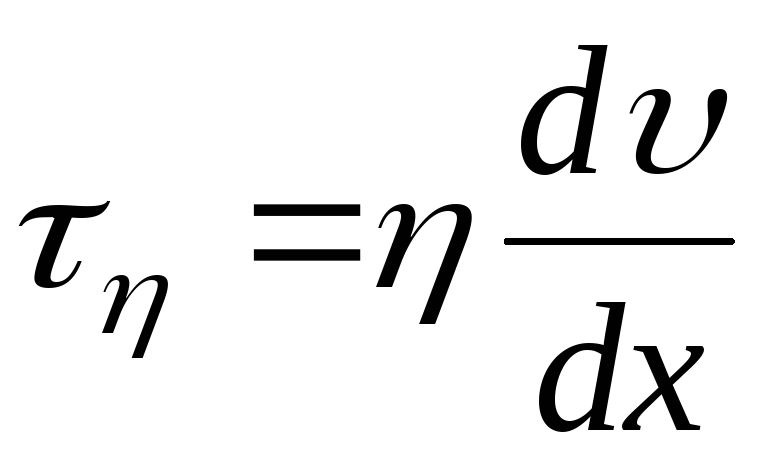
В любом количестве измерений уравнение Лапласа читается
| (18.1) |
В частности, в трех измерениях и декартовых координатах
Для координат, которые не являются декартовыми, лапласиан может можно найти в настольных книгах.
Некоторые важные свойства уравнения Лапласа:
- Установившиеся задачи: Уравнение Лапласа обычно описывает процессы, находящиеся в стационарном состоянии.
- Краевые задачи: Уравнение Лапласа требует
краевых задач.
В каждой точке на граница, следует задать одно граничное условие. Например, рассмотрим пример задачи на рисунке 18.1. На вертикальные границы, дана температура. Это Дирихле граничное условие. На горизонтальных границах тепловой поток выходит границы дается. Теперь поток тепла пропорционален градиент температуры. В частности, тепловой поток в
вертикальное направление пропорционально . Итак, горизонталь
границы имеют краевые условия Неймана; производная в
задано направление нормали к этим границам.
В частности, тепловой поток в
вертикальное направление пропорционально . Итак, горизонталь
границы имеют краевые условия Неймана; производная в
задано направление нормали к этим границам. - Бесконечная скорость распространения: Иногда решение Уравнение Лапласа может по-прежнему параметрически зависеть от времени. Для Например, уравнение Лапласа применимо к нестационарным идеальным потокам несжимаемые жидкости. Причина того, что уравнение Лапласа может применимы к таким потокам, заключается в том, что предположение о несжимаемости подразумевает бесконечная скорость звука. Если граничные условия где-то изменилось, поле течения моментально адаптируется к новому условия везде.
- Неограниченная область влияния: Уравнение Лапласа имеет
неограниченная область влияния. С точки зрения примера это означает
что если немного изменить температуру где-то на границе,
это повлияет на температуру в некоторой степени везде внутри
тарелка.

- Гладкость: Решения уравнения Лапласа гладкий. Даже если вы зададите сингулярные значения для решения на граница, раствор остается идеально гладким внутри домена. В частности, любая точка внутри имеет бесконечно много непрерывных производных, а также ряд Тейлора с конечным радиусом сходимости. {Г.2}
- Принцип максимума-минимума: Уравнение Лапласа имеет свойство, что максимум и минимум всегда встречаются на граница. Например, на рис. 18.1 задачи температура внутри пластины нигде не может быть выше Самая высокая температура на границе. {Г.3}
- Теорема о среднем значении: Предположим, определяется на и внутри некоторой сферической поверхности и удовлетворяет уравнению Лапласа. Затем среднее значение на сферической поверхности совпадает со значением в центре сферы. {Г.3}
(Для доменов, простирающихся до бесконечности, различные приведенные выше правила предполагают, что
вы считаете бесконечную область пределом конечной. )
)
Уравнение Лапласа является основным примером того, что называется эллиптическое
дифференциальное уравнение в частных производных. Решения
уравнение Лапласа называют гармоническими функциями.
18.2.1 Контрольные вопросы
- 1.
Выведите уравнение Лапласа для стационарной теплопроводности в двумерной пластине постоянной толщины. Сделайте это, рассмотрев небольшой прямоугольный декартов размер. Эскиз показан ниже:
Предположим, что закон Фурье:
Здесь – температура, предполагаемая независимой от . Кроме того, это коэффициент теплопроводности материала. Вектор – это плотность теплового потока. Вектор направлен в сторону теплового потока. Его величина равна теплу, проходящему через единицу площади по нормали к направлению потока.Если вам нужен поток тепла через элемент площади, который не перпендикулярен направлению потока тепла, выражение имеет вид
Вот единичный вектор нормали к элементу поверхности. Положительный означает тепловой поток через элемент поверхности в том же направлении, что и .
Положительный означает тепловой поток через элемент поверхности в том же направлении, что и .Предположим, что к маленькому прямоугольнику не поступает тепло от внешних источников.
Раствор станексл-а
- 2.
Выведите уравнение Лапласа для стационарной теплопроводности, используя векторный анализ. Предположим, что закон Фурье указан в предыдущем вопросе. В векторной форме
Предположим, что к телу не поступает тепла от внешних источников.
Раствор stanexl-b
- 3.
Рассмотрим уравнение Лапласа в пределах единичного круга:
Граничное условие на периметре круга
Чтобы найти значение в точке (0.1,0.2), могу ли я просто подставить координаты этой точки в граничное условие? Если нет, то каково правильное значение u в этой точке и что я получу из граничного условия?
Также ответьте на приведенные выше вопросы для следующей задачи:
Граничное условие на периметре круга
Найдите значение в точке (0. 1,0.2). Полностью защищайте свое решение.
1,0.2). Полностью защищайте свое решение.Раствор stanexl-b1
- 4.
Предположим, у вас есть задача с уравнением Лапласа, в которой граница симметрична относительно оси, как, скажем, в двух предыдущих задачах. В общем случае такая симметричная граница означает, что если — граничная точка, то и . Также предположим, что задано как антисимметричная функция x на этой границе; для любой граничной точки. Покажите, что в этом случае является антисимметричной функцией везде, т. е. везде.
Затем покажите, что это означает, что решение будет равно нулю на оси.
Также объясните, почему вышеизложенное больше не было бы верным, если бы у вас была производная первого порядка в УЧП, например, 0.
Раствор stanexl-b2
- 5.
Рассмотрим уравнение Лапласа внутри единичного круга, но теперь в полярных координатах:
Граничное условие на периметре круга
где заданная функция.
Решением является интегральная формула Пуассона
Теперь предположим, что функция немного увеличилась, на величину , и только в очень маленьком интервале .
Изменяется ли решение везде в окружности или только в непосредственной близости от интервала на границе, на котором было изменено. Каков знак изменения в положительном?
Раствор stanexl-b3
- 6.
- Покажите, что если функция является гармонической в конечной области и положительна на границе, то она положительна везде в области.
- Покажите на примере, что это не обязательно должно быть верно для бесконечной области.
- Позвольте , и быть гармоническими функциями. Показать, что если на границе конечной области, то и везде внутри области.
Раствор stanexl-b5
- 7.
Рассмотрим следующую задачу уравнения Лапласа в единичном квадрате:
Как показано, проблема имеет единственное решение.
 Это относится к случаю теплопроводности в квадратной пластине с температурой. Кто-то предложил, чтобы решение было простым: в верхнем треугольнике решение равно 0, а в нижнем — 1.
Это относится к случаю теплопроводности в квадратной пластине с температурой. Кто-то предложил, чтобы решение было простым: в верхнем треугольнике решение равно 0, а в нижнем — 1.Тщательно обсудите предлагаемое решение. Определить, удовлетворяются ли граничные условия и начальные условия. Выполняется ли уравнение в частных производных в обоих треугольниках?
Объясните, почему все изотермы, кроме 0 и 1, совпадают с линией 45. И почему изотермы ноль и 1 неопределимы.
Наконец обсудите, верно ли решение.
Раствор stanexl-c
- 8.
Если для задачи предыдущего вопроса предложенное решение неверно, то и описанные изотермы неверны.
Чтобы получить представление о правильном решении и изотермах, рассмотрим следующую более простую задачу. В этой задаче верхняя и правая границы искажены в четверть круга:
Решите эту проблему. Затем аккуратно нарисуйте изотермы 0, 0,25, 0,5, 0,75 и 1 для этой задачи.
Также аккуратно нарисуйте полярный угол в 0,5. На отдельном графике изобразите решение, предложенное в предыдущем разделе, 1 для и 0 для , снова против 0,5.
Теперь вернитесь к задаче из предыдущего вопроса и очень аккуратно нарисуйте правильные изотермы 0, 0,25, 0,5, 0,75 и 1 для этой задачи. Обратите особое внимание на то, где изотермы 0,25, 0,5 и 0,75 встречаются с границами и под каким углом.
Раствор станексл-д
- 9.
Вернемся еще раз к проблеме предпоследнего вопроса.
Правильное решение этой проблемы, которое вы найдете, используя так называемый метод разделения переменных:
Убедитесь, что это решение удовлетворяет как уравнению в частных производных, так и всем граничным условиям.Теперь прольем свет на вопрос, почему это решение является гладким для любого произвольного 0. Для этого сначала объясним, почему любая сумма синусов вида
является гладким, пока сумма конечна. Конечная сумма означает, что коэффициенты равны нулю после некоторого максимального значения .
Конечная сумма означает, что коэффициенты равны нулю после некоторого максимального значения .Далее вы можете использовать тот факт, что функция остается гладкой, если коэффициенты достаточно быстро стремятся к нулю. В частности, , если можно показать, что
для любого, сколь угодно большого, функция бесконечно гладкая.Используйте это, чтобы показать, что приведенное выше действительно бесконечно гладкое для любого 0. И покажите, что это неверно для 0, где решение скачком в начале координат.
Раствор станексл-е
18.2.2 Уравнение теплопроводности
Уравнение теплопроводности регулирует основную нестационарную теплопроводность, среди многих еще.
Пример проблемы показан на рисунке 18.2. Физически это
нестационарная теплопроводность в стержне длиной . Неизвестный
это температура. Независимыми переменными в этом случае являются
координата вдоль полосы и время. Домен
в этом примере это бар. Математически это линия
сегмент 0 с длиной бара.
граница состоит в этом случае всего из двух точек:
0 и .
Неизвестный
это температура. Независимыми переменными в этом случае являются
координата вдоль полосы и время. Домен
в этом примере это бар. Математически это линия
сегмент 0 с длиной бара.
граница состоит в этом случае всего из двух точек:
0 и .
Уравнение теплопроводности также описывает нестационарные вязкие однонаправленные течения. и многие другие диффузионные явления.
В любом количестве измерений уравнение теплопроводности читается
| (18.2) |
Здесь есть время и постоянная теплопроводности. В в частности, в трех измерениях и декартовых координатах
Некоторые важные свойства уравнения теплопроводности:
- Переходные проблемы: Уравнение теплопроводности обычно описывает процессы, которые развиваются во времени.
- Начальные или начально-краевые задачи: Тепловая
уравнению нужны задачи с начальным значением или начальное/граничное значение
проблемы.
 Пример рисунка 18.2 представляет собой
начально-краевая задача. Дана начальная температура.
Кроме того, существует граничное условие Дирихле (данное
температура ), при 0. Существует также граница Неймана
условие (нулевой тепловой поток за границу, поэтому 0), при
. Если вы позволите концам полосы уйти в бесконечность, вы получите
чистая начальная задача. (Однако на самом деле есть еще
некоторые ограничения на бесконечности. В частности, температура должна
не становиться слишком сингулярным на бесконечности.)
Пример рисунка 18.2 представляет собой
начально-краевая задача. Дана начальная температура.
Кроме того, существует граничное условие Дирихле (данное
температура ), при 0. Существует также граница Неймана
условие (нулевой тепловой поток за границу, поэтому 0), при
. Если вы позволите концам полосы уйти в бесконечность, вы получите
чистая начальная задача. (Однако на самом деле есть еще
некоторые ограничения на бесконечности. В частности, температура должна
не становиться слишком сингулярным на бесконечности.) - Бесконечная скорость распространения: Если изменить начальную температура или граничная температура немного, это сразу меняет решение везде. Точнее, в любое время после изменение, температура будет разной везде . Может быть, очень мало отличается, но отличается.
- Область влияния ограничена по времени: Если
граничные условия меняются, это меняет решение только при
более поздние времена.

- Гладкость: Решения гладкие. Даже если ты задают сингулярное начальное распределение температуры, решение будет гладким для всех последующих времен. В частности, для более поздних времен распределение температуры будет иметь бесконечно много непрерывных производные. Аналогичное наблюдение справедливо и для граничных условий.
- Принцип максимума-минимума: Максимум и минимум решение должно происходить изначально и/или на границах.
- Диссипативный: Предполагая, что граничные условия устойчиво, решение в конечном итоге будет приближаться к устойчивому состоянию.
Уравнение теплопроводности является основным примером того, что называется параболическое
дифференциальное уравнение в частных производных.
18.2.2 Контрольные вопросы
- 1.
Это продолжение соответствующего вопроса в подразделе об уравнении Лапласа.
 См. там определение терминов.
См. там определение терминов.Выведите уравнение теплопроводности для нестационарной теплопроводности в двумерной пластине толщиной , Сделайте это, рассмотрев небольшой декартов прямоугольник с размерами .
В частности, выведите коэффициент теплопроводности через коэффициент теплопроводности материала , толщину пластины и удельную теплоемкость твердого тела .
Раствор станекса-а
- 2.
Это продолжение соответствующего вопроса в подразделе об уравнении Лапласа. См. там определение терминов.
Выведите уравнение теплопроводности для нестационарной теплопроводности, используя векторный анализ.
Раствор stanexh-b
18.2.3 Волновое уравнение
Это уравнение, помимо всего прочего, управляет базовыми вибрациями.
Пример задачи о колебаниях струны показан на рис. 18.3. Неизвестным является поперечное отклонение
нить. Независимые переменные снова и как для
Пример уравнения теплопроводности. Домен снова -интервал
вдоль строки, а граница — это два конца
точки.
18.3. Неизвестным является поперечное отклонение
нить. Независимые переменные снова и как для
Пример уравнения теплопроводности. Домен снова -интервал
вдоль строки, а граница — это два конца
точки.
Уравнение теплопроводности также описывает акустику, стационарное сверхзвуковое течение, волны на воде, оптика, электромагнитные волны и многие другие основные явления, характеризующиеся распространением волн.
В любом количестве измерений волновое уравнение читается
| (18.3) |
Здесь есть время и постоянная скорость распространения волны. В в частности, в трех измерениях и декартовых координатах
Вот некоторые важные свойства волнового уравнения:
- Переходные задачи: Волновое уравнение обычно описывает процессы, которые развиваются во времени.
- Начальные или начальные/краевые задачи: Аналогично
уравнение теплопроводности, волновое уравнение нуждается в начальных задачах или
начально-краевые задачи.
 Однако для этого требуется два начальных
условия вместо одного, так как уравнение второго порядка по
время. Для примера на рисунке 18.2 это означает, что оба
начальный поперечный прогиб и начальный поперечный
должна быть задана скорость каждой точки струны. Строка
обычно фиксируется в своих конечных точках, производя Дирихле
граничные условия. Однако то же уравнение, что и в примере
также управляет акустикой в трубе, и либо Дирихле, либо Неймана
граничные условия могут относиться к концам трубы.
Однако для этого требуется два начальных
условия вместо одного, так как уравнение второго порядка по
время. Для примера на рисунке 18.2 это означает, что оба
начальный поперечный прогиб и начальный поперечный
должна быть задана скорость каждой точки струны. Строка
обычно фиксируется в своих конечных точках, производя Дирихле
граничные условия. Однако то же уравнение, что и в примере
также управляет акустикой в трубе, и либо Дирихле, либо Неймана
граничные условия могут относиться к концам трубы. - Конечная скорость распространения: Эффекты распространяются вместе с волной скорость .
- Область влияния ограничена скоростью волны: Предположим, что граничное или начальное условие где-то изменилось кусочек. Изменение не повлияет на решение в других местах. до тех пор, пока волна, бегущая из точки изменения скорости, не успел до них добраться.
- Распространение особенностей: Если сингулярный начальный или
заданы граничные условия, волновое уравнение не будет
сгладить их.
 Вместо этого сингулярности обычно будут распространяться
в одном или нескольких направлениях со скоростью распространения волны .
Вместо этого сингулярности обычно будут распространяться
в одном или нескольких направлениях со скоростью распространения волны . - Принципы отсутствия максимума или минимума: Например, если струна имеет нулевое начальное отклонение, но ненулевую начальную скорость, прогиб со временем будет расти.
- Сохранение энергии: Волновое уравнение сохраняет сумму потенциальной и кинетической энергии движения струны. Итак, если волновое уравнение было точным, струна будет колебаться вечно.
Волновое уравнение является основным примером того, что называется гиперболическое
дифференциальное уравнение в частных производных.
18.2.3 Контрольные вопросы
- 1.
Выведите волновое уравнение для малых поперечных колебаний струны, рассмотрев небольшой отрезок струны длиной .
Раствор stanexw-a
- 2.

Уравнения Максвелла для электромагнитного поля в вакууме имеют вид
Вот электрическое поле, магнитное поле, плотность заряда, плотность тока, постоянная скорость света и есть постоянная, называемая диэлектрической проницаемостью пространства. Плотности заряда и тока связаны уравнением неразрывности
Покажите, что если вы знаете, как решать стандартное волновое уравнение, вы знаете, как решать уравнения Максвелла. По крайней мере, если известны плотность заряда и тока.
Определите скорость волны.
Раствор stanexw-b
- 3.
Рассмотрим следующую задачу волнового уравнения в единичном квадрате:
Это в основном идентично задаче уравнения Лапласа в первом подразделе. Как и эта проблема, вышеприведенная задача волнового уравнения имеет единственное решение. Это относится к случаю акустики в трубе, с давлением. Кто-то предложил, чтобы решение было простым: в верхнем треугольнике решение равно 0, а в нижнем — 1.

Тщательно обсудите предлагаемое решение. Определить, удовлетворяются ли граничные условия и начальные условия. Выполняется ли уравнение в частных производных в обоих треугольниках? Наконец обсудите, верно ли решение. Учитывайте значение скорости волны в своем ответе.
Нарисуйте изобары правильного решения. В частности, зарисуйте изобары 0 0,25, 0,5, 0,75 и 1, если это возможно. Нарисуйте оба случая, что 1 и что .
Раствор stanexw-c
- 4.
Вернемся снова к проблеме последнего вопроса. Предположим 1.
Правильное решение этой проблемы, которое вы найдете, используя так называемый метод разделения переменных:
Убедитесь, что это решение удовлетворяет как уравнению в частных производных, так и всем граничным и начальным условиям.Объясните, что он производит движущийся скачок в решении, как указано в предыдущем вопросе.
Разрывное решение, данное в предыдущем вопросе, верно в этом случае.
 Это правильно, потому что это правильный предельный случай гладкого решения, которое всюду удовлетворяет уравнению в частных производных. В частности, если вы просуммируете приведенную выше сумму до очень высокого, но не бесконечного значения , вы получите гладкое решение уравнения в частных производных, которое удовлетворяет всем начальным и граничным условиям, за исключением того, что значение в 0 все еще показывает малое отклонения от 1. Чем больше членов вы суммируете, тем меньше становятся эти отклонения. (Всегда будут некоторые различия прямо в сингулярности, но они будут ограничены пренебрежимо малой окрестностью 0.)
Это правильно, потому что это правильный предельный случай гладкого решения, которое всюду удовлетворяет уравнению в частных производных. В частности, если вы просуммируете приведенную выше сумму до очень высокого, но не бесконечного значения , вы получите гладкое решение уравнения в частных производных, которое удовлетворяет всем начальным и граничным условиям, за исключением того, что значение в 0 все еще показывает малое отклонения от 1. Чем больше членов вы суммируете, тем меньше становятся эти отклонения. (Всегда будут некоторые различия прямо в сингулярности, но они будут ограничены пренебрежимо малой окрестностью 0.)Раствор stanexw-e
- 5.
Найдите возможные решения плоской волны для двумерного волнового уравнения
Какова скорость волны?Также найдите возможные решения стоячей волны. Предположим, что однородные граничные условия Дирихле или Неймана на некотором прямоугольнике 0 , 0 .
 Какова частота?
Какова частота?Повторите для обобщенного уравнения
где , , и – положительные постоянные.Раствор stanexw-f
| Далее: 18.3 Правильная поза |
ЭЦП и комплексный анализ
EDP и комплексный анализ 5. 00 кредитов
00 кредитов
30.0 ч + 30.0 ч
Q1
> Расписание
Язык
Французский
Предварительные требования
Основные методы дифференциального анализа решение ОДУ 1-го и 2-го порядка, функций нескольких переменных и частных производных), а также градиента, дивергенции и лапласиана, как преподается в курсах LEPL1102 и LEPL1105.
Наконец, предполагается следовать параллельно курсу Физики LEPL1203 для понятия волнового уравнения, к которому там приближаются.
Основные темы
Уравнения в частных производных (УЧП): классификация (гиперболические, параболические, эллиптические), связи с физическими явлениями, метод характеристик для гиперболических УЧП, решения в бесконечной области (по функциям Грина), решения в конечной области ( разделением переменных) с самосопряженными операторами, собственными значениями и собственными функциями, ортогональностью и разверткой решения собственных функций в ряд, решений в полубесконечной одномерной области (по переменной подобия).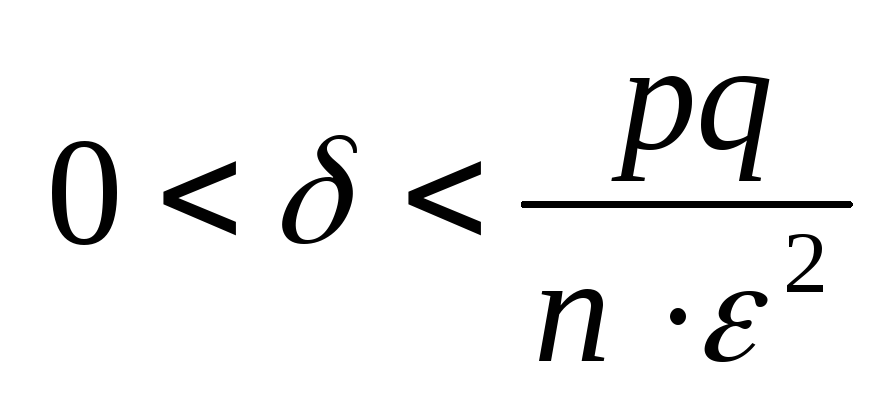 Функции комплексного переменного: элементарные функции, точка (точки) ветвления и разрез (ы), предел и непрерывность, дифференцируемость и уравнения Коши-Римана, интегрирование, теорема Коши и интегральные формулы Коши, ряды, теорема о вычетах и отображения (определенные интегралы) , конформные преобразования.
Функции комплексного переменного: элементарные функции, точка (точки) ветвления и разрез (ы), предел и непрерывность, дифференцируемость и уравнения Коши-Римана, интегрирование, теорема Коши и интегральные формулы Коши, ряды, теорема о вычетах и отображения (определенные интегралы) , конформные преобразования.
Результаты обучения
По окончании этого раздела обучения учащийся способен: | |
| 1 | Вклад курса в структуру программы AA1.1, AA1.2 AA6.1 Конкретные результаты обучения по курсу По окончании этого курса учащийся сможет: Определять и объяснять фундаментальные свойства различных типов первого и второго порядка, линейных и квазилинейных УЧП. Понимать и различать фундаментальные физические явления, описываемые УЧП: гиперболический случай (также уравнение переноса и волновое уравнение), параболический случай (уравнение диффузии), эллиптический случай (уравнения Лапласа и Пуассона). 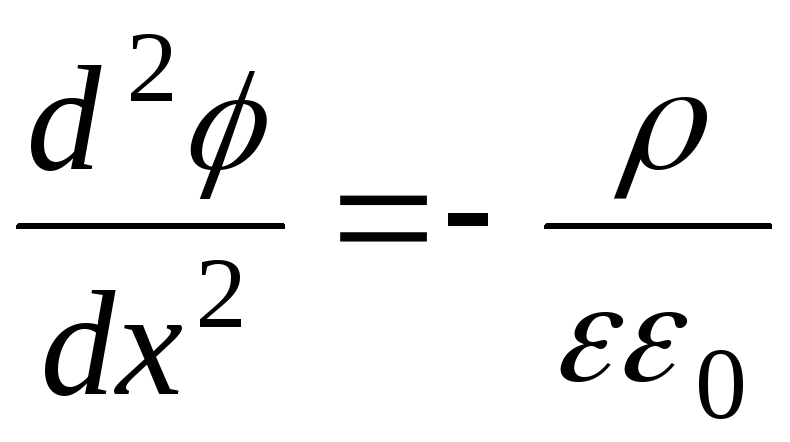 Для каждого типа определите и примените соответствующие начальные и/или граничные условия (Дирихле, Неймана, Робина). Примените метод характеристик для решения дифференциальных уравнений в частных производных порядка 1 и для решения одномерного волнового уравнения. Понимать общую теорию самосопряженных операторов: собственные значения и собственные функции, ортогональность собственных функций, разложение функции как ряда собственных функций. Применить метод разделения переменных для решения уравнения Лапласа в прямоугольнике, (секторе) окружности, (секторе) кольца. Применить метод разделения переменных для решения волнового уравнения на отрезке, прямоугольнике, окружности (уравнение Бесселя). Применить метод разделения переменных для решения уравнения диффузии в отрезке, прямоугольнике, окружности. Получить решение подобия уравнения диффузии на полубесконечном отрезке: случай с фиксированным скачком в начале координат, случай с временными колебаниями в начале координат. 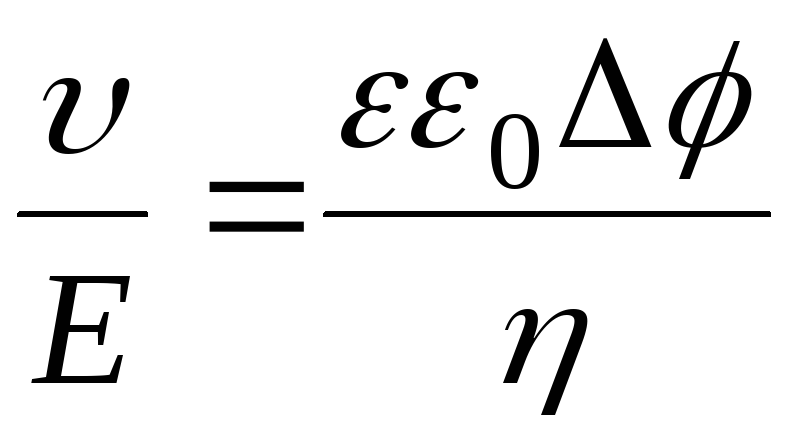 Понять определение элементарных функций сложной переменной, получить возможную точку (точки) ветвления функции и выбрать соответствующий разрез (отрезки), оценить функцию в одной или нескольких ветвях. Понимать понятия предела, непрерывности и дифференцируемости функции и устанавливать связи с уравнением Лапласа. Получить последовательное расширение функции. Вычислить полюс(ы) функции и использовать теорему о вычетах для вычисления определенных интегралов. Понимать концепцию конформного преобразования и уметь применять ее в простых случаях. Вклад этой учебной единицы в развитие и овладение навыками и достижениями программы (программ) можно найти в конце этого листа в разделе «Программы/обучение, предлагающие эту учебную единицу (ТУ)». |
Содержание
Уравнения в частных производных (УЧП) :
1-й и 2-й -й порядок УЧП: представление, классификация (гиперболическая, параболическая, эллиптическая) и связи с физическими явлениями (уравнение переноса, волновое уравнение, уравнение диффузии, уравнение Лапласа, уравнение Пуассона), задача Коши и метод характеристик для гиперболическое УЧП, начальные и/или граничные условия (Дирихле, Неймана, Робина), решения в бесконечной области (по функциям Грина) для уравнения диффузии и уравнения Пуассона.
самосопряженных операторов, собственные значения и собственные функции, ортогональность собственных функций. Развитие функций в ряды собственных функций. Проблема Гельмгольца. Функции Бесселя 1-й и 2-й и вид.
Метод разделения переменных для задач в бесконечной области: уравнение Лапласа в 2D (прямоугольник, окружность, кольцо, сектор окружности или кольцо) ; волновое уравнение в 1D и 2D, уравнение Диффисона в 1D и 2D.
Решения подобия для уравнения диффузии в одномерной полубесконечной области.
Функции комплексной переменной, f(z) :
Вспомните комплексную плоскость и комплексные числа.
Определение элементарных функций: z a , exp(z), log(z), a z , sin(z), sh(z), arcsin(z) и т. д.
Точка(ы) ветвления и разрез(ы) ветвления, риманова поверхность( с).
Пределы и непрерывность, выводимость, голоморфные (аналитические) функции, целые функции, уравнения Коши-Римана и связи с уравнением Лапласа.
Интегрирование, теорема Коши и следствия: интегральная формула Коши, ряды Тейлора и Лорана, полюсы, теорема о вычетах.
Вычисление определенных интегралов (также с использованием леммы Жордана).
Введение в конформные преобразования и примеры приложений.
Методы обучения
Курс состоит из 12 курсов (от CM1 до CM12), проводимых в большой аудитории, и 12 сессий «обучения через упражнения» (от APE1 до APE12), которые частично реализуются в группы (с одним ассистентом-тьютором на группу), а для остальных — вне тьюторских групп.
Методы оценивания
Учащиеся оцениваются индивидуально с письменным экзаменом.
APE (от APE1 до APE12) не оцениваются, но решения размещаются на сайте Moodle. Это также позволяет учащимся постоянно оценивать свой уровень понимания и приобретения компетенций
Интернет-ресурсы
Библиография
Вечеринка EDP :
Ж.-Ф. Remacle et G. Winckelmans, учебный план «LEPL1103: Support partiel pour la partie ésuations aux dérivées partielles (EDP)», дополнительные примечания: «Modèle LWR du traffic routier», «Fonctions de Bessel de 1ère et de 2ème espèces», «Méthodes de резолюция о диффузии».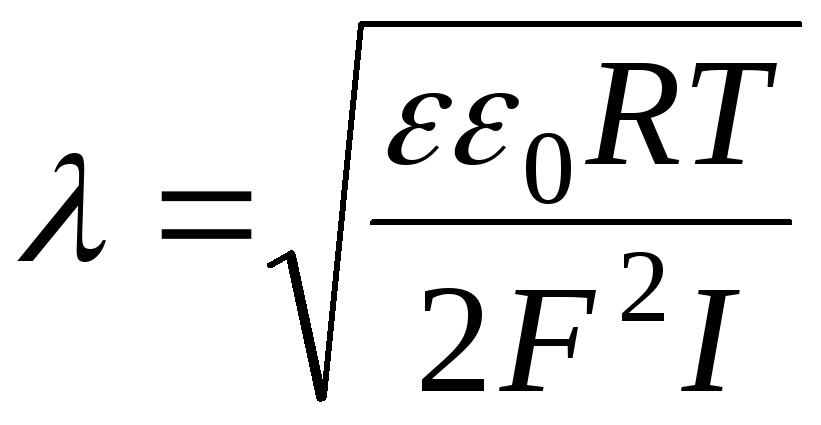

 В частности, тепловой поток в
вертикальное направление пропорционально . Итак, горизонталь
границы имеют краевые условия Неймана; производная в
задано направление нормали к этим границам.
В частности, тепловой поток в
вертикальное направление пропорционально . Итак, горизонталь
границы имеют краевые условия Неймана; производная в
задано направление нормали к этим границам.
 Положительный означает тепловой поток через элемент поверхности в том же направлении, что и .
Положительный означает тепловой поток через элемент поверхности в том же направлении, что и .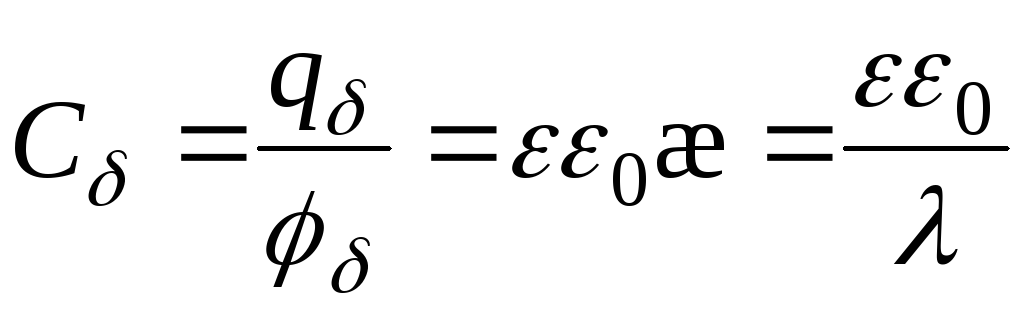 1,0.2). Полностью защищайте свое решение.
1,0.2). Полностью защищайте свое решение.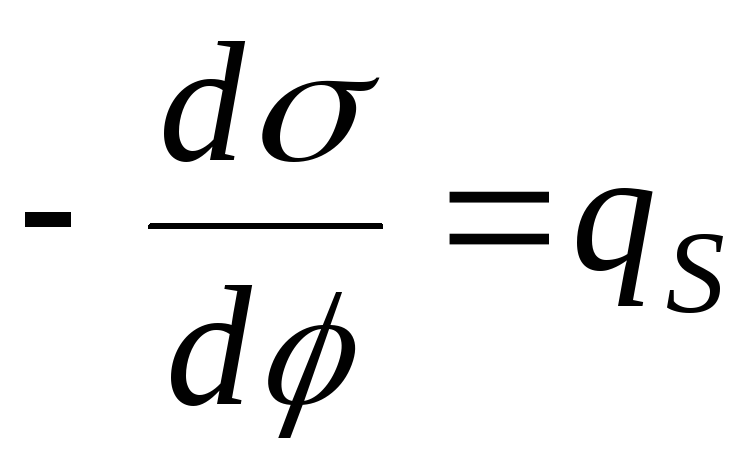
 Это относится к случаю теплопроводности в квадратной пластине с температурой. Кто-то предложил, чтобы решение было простым: в верхнем треугольнике решение равно 0, а в нижнем — 1.
Это относится к случаю теплопроводности в квадратной пластине с температурой. Кто-то предложил, чтобы решение было простым: в верхнем треугольнике решение равно 0, а в нижнем — 1.
 Конечная сумма означает, что коэффициенты равны нулю после некоторого максимального значения .
Конечная сумма означает, что коэффициенты равны нулю после некоторого максимального значения . Пример рисунка 18.2 представляет собой
начально-краевая задача. Дана начальная температура.
Кроме того, существует граничное условие Дирихле (данное
температура ), при 0. Существует также граница Неймана
условие (нулевой тепловой поток за границу, поэтому 0), при
. Если вы позволите концам полосы уйти в бесконечность, вы получите
чистая начальная задача. (Однако на самом деле есть еще
некоторые ограничения на бесконечности. В частности, температура должна
не становиться слишком сингулярным на бесконечности.)
Пример рисунка 18.2 представляет собой
начально-краевая задача. Дана начальная температура.
Кроме того, существует граничное условие Дирихле (данное
температура ), при 0. Существует также граница Неймана
условие (нулевой тепловой поток за границу, поэтому 0), при
. Если вы позволите концам полосы уйти в бесконечность, вы получите
чистая начальная задача. (Однако на самом деле есть еще
некоторые ограничения на бесконечности. В частности, температура должна
не становиться слишком сингулярным на бесконечности.)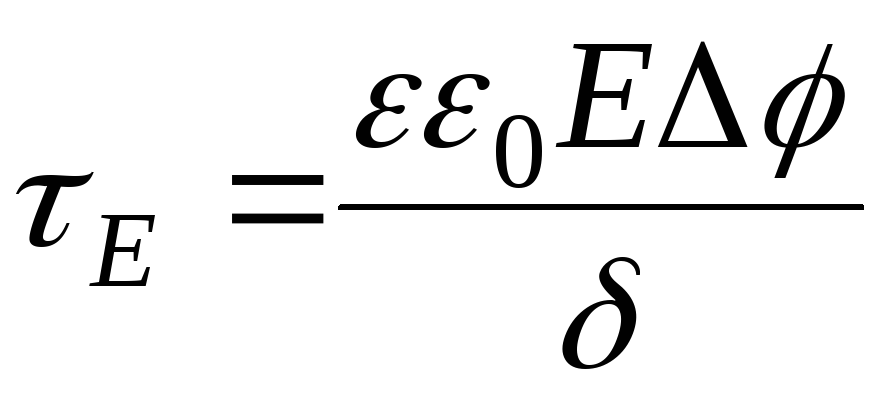
 См. там определение терминов.
См. там определение терминов. Однако для этого требуется два начальных
условия вместо одного, так как уравнение второго порядка по
время. Для примера на рисунке 18.2 это означает, что оба
начальный поперечный прогиб и начальный поперечный
должна быть задана скорость каждой точки струны. Строка
обычно фиксируется в своих конечных точках, производя Дирихле
граничные условия. Однако то же уравнение, что и в примере
также управляет акустикой в трубе, и либо Дирихле, либо Неймана
граничные условия могут относиться к концам трубы.
Однако для этого требуется два начальных
условия вместо одного, так как уравнение второго порядка по
время. Для примера на рисунке 18.2 это означает, что оба
начальный поперечный прогиб и начальный поперечный
должна быть задана скорость каждой точки струны. Строка
обычно фиксируется в своих конечных точках, производя Дирихле
граничные условия. Однако то же уравнение, что и в примере
также управляет акустикой в трубе, и либо Дирихле, либо Неймана
граничные условия могут относиться к концам трубы. Вместо этого сингулярности обычно будут распространяться
в одном или нескольких направлениях со скоростью распространения волны .
Вместо этого сингулярности обычно будут распространяться
в одном или нескольких направлениях со скоростью распространения волны .

 Это правильно, потому что это правильный предельный случай гладкого решения, которое всюду удовлетворяет уравнению в частных производных. В частности, если вы просуммируете приведенную выше сумму до очень высокого, но не бесконечного значения , вы получите гладкое решение уравнения в частных производных, которое удовлетворяет всем начальным и граничным условиям, за исключением того, что значение в 0 все еще показывает малое отклонения от 1. Чем больше членов вы суммируете, тем меньше становятся эти отклонения. (Всегда будут некоторые различия прямо в сингулярности, но они будут ограничены пренебрежимо малой окрестностью 0.)
Это правильно, потому что это правильный предельный случай гладкого решения, которое всюду удовлетворяет уравнению в частных производных. В частности, если вы просуммируете приведенную выше сумму до очень высокого, но не бесконечного значения , вы получите гладкое решение уравнения в частных производных, которое удовлетворяет всем начальным и граничным условиям, за исключением того, что значение в 0 все еще показывает малое отклонения от 1. Чем больше членов вы суммируете, тем меньше становятся эти отклонения. (Всегда будут некоторые различия прямо в сингулярности, но они будут ограничены пренебрежимо малой окрестностью 0.) Какова частота?
Какова частота?