Уравнение с дискриминантом решить: Дискриминант онлайн

2

Решение квадратных уравнений с помощью дискриминанта.

Репетиторы ❯ Математика ❯ Решение квадратных уравнений с помощью дискриминанта.

Автор: Валентина Галиневская

●

01.07.2015

●

Раздел: Математика

Надеюсь, изучив данную статью, вы научитесь находить корни полного квадратного уравнения.

С помощью дискриминанта решаются только полные квадратные уравнения, для решения неполных квадратных уравнений используют другие методы, которые вы найдете в статье «Решение неполных квадратных уравнений».

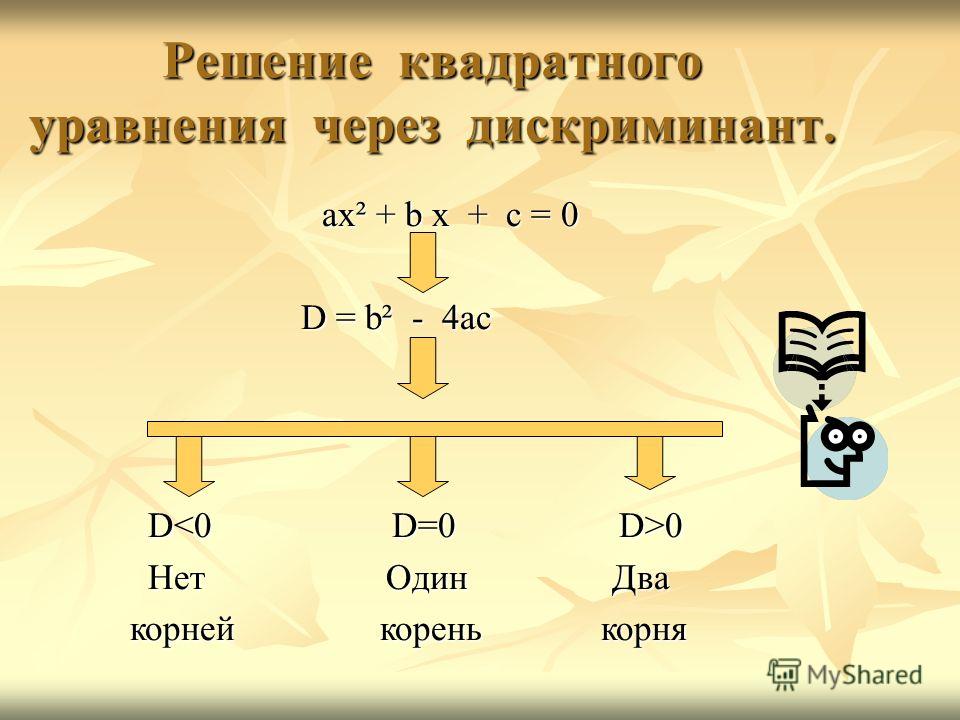
Какие же квадратные уравнения называются полными? Это уравнения вида ах² + b x + c = 0, где коэффициенты a, b и с не равны нулю. Итак, чтобы решить полное квадратное уравнение, надо вычислить дискриминант D.

D = b² – 4ас .

В зависимости от того какое значение имеет дискриминант, мы и запишем ответ.

Если дискриминант отрицательное число (D < 0),то корней нет.

Если же дискриминант равен нулю, то х = (-b)/2a. Когда дискриминант положительное число (D > 0),

тогда х₁ = (-b — √D)/2a ,  и  х₂ = (-b + √D)/2a .

Например. Решить уравнение х² – 4х + 4= 0.

D = 4² – 4 · 4 = 0

x = (- (-4))/2 = 2

Ответ: 2.

Решить уравнение 2х² + х + 3 = 0.

D = 1² – 4 · 2 · 3 = – 23

Ответ: корней нет.

Решить уравнение 2х² + 5х – 7 = 0.

D = 5² – 4 · 2 · (–7) = 81

х₁ = (-5 — √81)/(2·2)= (-5 — 9)/4= – 3,5

х₂ = (-5 + √81)/(2·2) = (-5 + 9)/4=1

Ответ: – 3,5 ; 1.

Итак представим решение полных квадратных уравнений схемой на рисунке1. 

По этим формулам можно решать любое полное квадратное уравнение. Нужно только внимательно следить за тем, чтобы уравнение было записано многочленом стандартного вида

ах² + bx + c, иначе можно допустить ошибку. Например, в записи уравнения х + 3 + 2х² = 0, ошибочно можно решить, что

а = 1, b = 3 и с = 2. Тогда

D = 3² – 4 · 1 · 2 = 1 и тогда уравнение имеет два корня. А это неверно. (Смотри решение примера 2 выше).

Поэтому, если уравнение записано не многочленом стандартного вида, вначале полное квадратное уравнение надо записать многочленом стандартного вида (на первом месте должен стоять одночлен с наибольшим показателем степени, то есть ах², затем с меньшим  – bx, а затем свободный член с.

При решении приведенного квадратного уравнения и квадратного уравнения с четным коэффициентом при втором слагаемом можно использовать и другие формулы. Давайте познакомимся и с этими формулами. Если в полном квадратном уравнении при втором слагаемом коэффициент будет четным (b = 2k), то можно решать уравнение по формулам приведенным на схеме рисунка 2. 

Полное квадратное уравнение называется приведенным, если коэффициент при х² равен единице и уравнение примет вид х² + px + q = 0. Такое уравнение может быть дано для решения, либо получается делением всех коэффициентов уравнение на коэффициент а, стоящий при х².

На рисунке 3 приведена схема решения приведенных квадратных уравнений. Рассмотрим на примере применение рассмотренных в данной статье формул.

Пример. Решить уравнение

3х² + 6х – 6 = 0.

Давайте решим это уравнение применяя формулы приведенные на схеме рисунка 1.

D = 6² – 4 · 3 · (– 6) = 36 + 72 = 108

√D = √108 = √(36 · 3) = 6√3

х₁ = (-6 — 6√3 )/(2 · 3) = (6 ( -1- √(3)))/6 = –1 – √3

х₂ = (-6 + 6√3 )/(2 · 3) = (6 ( -1+ √(3)))/6 = –1 + √3

Ответ: –1 – √3; –1 + √3

Можно заметить, что коэффициент при х в этом уравнении четное число, то есть b = 6 или b = 2k , откуда k = 3. Тогда попробуем решить уравнение по формулам , приведенным на схеме рисунка D₁ = 3² – 3 · (– 6) = 9 + 18 = 27

√(D₁) = √27 = √(9 · 3) = 3√3

х₁ = (-3 — 3√3)/3 = (3 (-1 — √(3)))/3 = – 1 – √3

х₂ = (-3 + 3√3)/3 = (3 (-1 + √(3)))/3 = – 1 + √3

Ответ: –1 – √3; –1 + √3. Заметив, что все коэффициенты в этом квадратном уравнении делятся на 3 и выполнив деление, получим приведенное квадратное уравнение x² + 2х – 2 = 0 Решим это уравнение, используя формулы для приведенного квадратного уравнения рисунок 3.

D₂ = 2² – 4 · (– 2) = 4 + 8 = 12

√(D₂) = √12 = √(4 · 3) = 2√3

х₁= (-2 — 2√3)/2 = (2 (-1 — √(3)))/2 = – 1 – √3

х₂= (-2 + 2√3)/2 = (2 (-1+ √(3)))/2 = – 1 + √3

Ответ: –1 – √3; –1 + √3.

Как видим, при решении этого уравнения по различным формулам мы получили один и тот же ответ. Поэтому хорошо усвоив формулы приведенные на схеме рисунка 1 , вы всегда сможете решить любое полное квадратное уравнение.

© blog.tutoronline.ru, при полном или частичном копировании материала ссылка на первоисточник обязательна.

Остались вопросы?

Задайте свой вопрос и получите ответ от профессионального преподавателя.

Задать вопрос

Математика

Курсы по математике 10 класс

Математика

Курсы по математике 9 класс

Математика

Математика 11 класс

Математика

Курсы по геометрии 7 класс

Математика

Курсы по алгебре 7 класс

Математика

Алгебра 8 класс

Математика

Курсы по геометрии 8 класс

Французский язык

Курсы французского языка для начинающих

Квадратные уравнения и его корни привести примеры.

Уравнение дискриминанта по математике

Более простым способом. Для этого вынесите z за скобки. Вы получите : z(аz + b) = 0. Множители можно расписать: z=0 и аz + b = 0, так как оба могут давать в результате ноль. В записи аz + b = 0 перенесем второй вправо с другим знаком. Отсюда получаем z1 = 0 и z2 = -b/а. Это и есть корни исходного .

Если же имеется неполное уравнение вида аz² + с = 0, в данном случае находятся простым переносом свободного члена в правую часть уравнения. Также поменяйте при этом его знак. Получится запись аz² = -с. Выразите z² = -с/а. Возьмите корень и запишите два решения — положительное и отрицательное значение корня квадратного.

Обратите внимание

При наличии в уравнении дробных коэффициентов помножьте все уравнение на соответствующий множитель так, чтобы избавиться от дробей.

Знание о том, как решать квадратные уравнения, необходимо и школьникам, и студентам, иногда это может помочь и взрослому человеку в обычной жизни. Существует несколько определенных методов решений. 2 — 4*a*c. Значение D может быть больше, меньше или равно нулю. Если D больше или меньше нуля, то корня будет два, если D=0, то остается всего один корень, более точно можно сказать, что D в этом случае имеет два равнозначных корня. Подставьте известные коэффициенты a, b, c в формулу и вычислите значение.

После того как вы нашли дискриминант, для нахождения х воспользуйтесь формулами: x(1) = (- b+sqrt{D})/2*a; x(2) = (- b-sqrt{D})/2*a, где sqrt — это функция, означающая извлечение квадратного корня из данного числа. Посчитав эти выражения, вы найдете два корня вашего уравнения, после чего уравнение считается решенным.

Если D меньше нуля, то он все равно имеет корни. В школе данный раздел практически не изучается. Студенты вузов должны знать о том, что появляется отрицательное число под корнем. От него избавляются выделяя мнимую часть, то есть -1 под корнем всегда равно мнимому элементу «i», который умножается на корень с таким же положительным числом. К примеру, если D=sqrt{-20}, после преобразования получается D=sqrt{20}*i. После этого преобразования, решение уравнения сводится к такому же нахождению корней, как было описано выше.

Теорема Виета заключается в подборе значений x(1) и x(2). Используется два тождественных уравнения: x(1) + x(2)= -b; x(1)*x(2)=с. Причем очень важным моментом является знак перед коэффициентом b, помните, что этот знак противоположен тому, который стоит в уравнении. С первого взгляда кажется, что посчитать x(1) и x(2) очень просто, но при решении вы столкнетесь с тем, что числа придется именно подбирать.

Элементы решения квадратных уравнений

По правилам математики некоторые можно разложить на множители: (a+x(1))*(b-x(2))=0, если вам посредством формул математики удалось преобразовать подобным образом данное квадратное уравнение, то смело записывайте ответ. x(1) и x(2) будут равны рядом стоящим коэффициентам в скобках, но с противоположным знаком.

Также не стоит забывать про неполные квадратные уравнения. У вас может отсутствовать какое-то из слагаемых, если это так, то все его коэффициенты просто равны нулю. 2 или x ничего не стоит, то коэффициенты а и b равны 1.

В современном обществе умение производить действия с уравнениями, содержащими переменную, возведённую в квадрат, может пригодиться во многих областях деятельности и широко применяется на практике в научных и технических разработках. Свидетельством тому может служить конструирование морских и речных судов, самолётов и ракет. При помощи подобных расчётов определяют траектории перемещения самых разных тел, в том числе и космических объектов. Примеры с решением квадратных уравнений находят применение не только в экономическом прогнозировании, при проектировании и строительстве зданий, но и в самых обычных житейских обстоятельствах. Они могут понадобиться в туристических походах, на спортивных состязаниях, в магазинах при совершении покупок и в других весьма распространённых ситуациях.

Разобьём выражение на составляющие множители

Степень уравнения определяется максимальным значением степени у переменной, которую содержит данное выражение. В случае, если она равна 2, то подобное уравнение как раз и называется квадратным.

Если изъясняться языком формул, то указанные выражения, как бы они ни выглядели, всегда можно привести к виду, когда левая часть выражения состоит из трёх слагаемых. Среди них: ax 2 (то есть переменная, возведённая в квадрат со своим коэффициентом), bx (неизвестное без квадрата со своим коэффициентом) и c (свободная составляющая, то есть обычное число). Всё это в правой части приравнивается 0. В случае, когда у подобного многочлена отсутствует одно из его составляющих слагаемых, за исключением ax 2 , оно называется неполным квадратным уравнением. Примеры с решением таких задач, значение переменных в которых найти несложно, следует рассмотреть в первую очередь.

Если выражение на вид выглядит таким образом, что слагаемых у выражения в правой части два, точнее ax 2 и bx, легче всего отыскать х вынесением переменной за скобки. Теперь наше уравнение будет выглядеть так: x(ax+b). Далее становится очевидно, что или х=0, или задача сводится к нахождению переменной из следующего выражения: ax+b=0. Указанное продиктовано одним из свойств умножения. Правило гласит, что произведение двух множителей даёт в результате 0, только если один из них равен нулю.

Пример

x=0 или 8х — 3 = 0

В результате получаем два корня уравнения: 0 и 0,375.

Уравнения такого рода могут описывать перемещение тел под действием силы тяжести, начавших движение из определённой точки, принятой за начало координат. Здесь математическая запись принимает следующую форму: y = v 0 t + gt 2 /2. Подставив необходимые значения, приравняв правую часть 0 и найдя возможные неизвестные, можно узнать время, проходящее с момента подъёма тела до момента его падения, а также многие другие величины. Но об этом мы поговорим позднее.

Разложение выражения на множители

Описанное выше правило даёт возможность решать указанные задачи и в более сложных случаях. Рассмотрим примеры с решением квадратных уравнений такого типа.

X 2 — 33x + 200 = 0

Этот квадратный трёхчлен является полным. Для начала преобразуем выражение и разложим его на множители. Их получается два: (x-8) и (x-25) = 0. В результате имеем два корня 8 и 25.

Примеры с решением квадратных уравнений в 9 классе позволяют данным методом находить переменную в выражениях не только второго, но даже третьего и четвёртого порядков.

Например: 2x 3 + 2x 2 — 18x — 18 = 0. При разложении правой части на множители с переменной, их получается три, то есть (x+1),(x-3) и (x+3).

В результате становится очевидно, что данное уравнение имеет три корня: -3; -1; 3.

Извлечение квадратного корня

Другим случаем неполного уравнения второго порядка является выражение, на языке букв представленное таким образом, что правая часть строится из составляющих ax 2 и c. Здесь для получения значения переменной свободный член переносится в правую сторону, а после этого из обеих частей равенства извлекается квадратный корень. Следует обратить внимание, что и в данном случае корней уравнения обычно бывает два. Исключением могут служить лишь только равенства, вообще не содержащие слагаемое с, где переменная равна нулю, а также варианты выражений, когда правая часть оказывается отрицательной. В последнем случае решений вообще не существует, так как указанные выше действия невозможно производить с корнями. Примеры решений квадратных уравнений такого типа необходимо рассмотреть.

В данном случае корнями уравнения окажутся числа -4 и 4.

Вычисление пощади земельного участка

Потребность в подобного рода вычислениях появилась в глубокой древности, ведь развитие математики во многом в те далёкие времена было обусловлено необходимостью определять с наибольшей точностью площади и периметры земельных участков.

Примеры с решением квадратных уравнений, составленных на основе задач такого рода, следует рассмотреть и нам.

Итак, допустим имеется прямоугольный участок земли, длина которого на 16 метров больше, чем ширина. Следует найти длину, ширину и периметр участка, если известно, что его площадь равна 612 м 2 .

Приступая к делу, сначала составим необходимое уравнение. Обозначим за х ширину участка, тогда его длина окажется (х+16). Из написанного следует, что площадь определяется выражением х(х+16), что, согласно условию нашей задачи, составляет 612. Это значит, что х(х+16) = 612.

Решение полных квадратных уравнений, а данное выражение является именно таковым, не может производиться прежним способом. Почему? Хотя левая часть его по-прежнему содержит два множителя, произведение их совсем не равно 0, поэтому здесь применяются другие методы.

Дискриминант

Прежде всего произведём необходимые преобразования, тогда внешний вид данного выражения будет выглядеть таким образом: x 2 + 16x — 612 = 0. Это значит, мы получили выражение в форме, соответствующей указанному ранее стандарту, где a=1, b=16, c=-612.

Это может стать примером решения квадратных уравнений через дискриминант. Здесь необходимые расчёты производятся по схеме: D = b 2 — 4ac. Данная вспомогательная величина не просто даёт возможность найти искомые величины в уравнении второго порядка, она определяет количество возможных вариантов. В случае, если D>0, их два; при D=0 существует один корень. В случае, если D

О корнях и их формуле

В нашем случае дискриминант равен: 256 — 4(-612) = 2704. Это говорит о том, что ответ у нашей задачи существует. Если знать, к , решение квадратных уравнений нужно продолжать с применением ниже приведённой формулы. Она позволяет вычислить корни.

Это значит, что в представленном случае: x 1 =18, x 2 =-34. Второй вариант в данной дилемме не может являться решением, потому что размеры земельного участка не могут измеряться в отрицательных величинах, значит х (то есть ширина участка) равна 18 м. Отсюда вычисляем длину: 18+16=34, и периметр 2(34+18)=104(м 2).

Примеры и задачи

Продолжаем изучение квадратных уравнений. Примеры и подробное решение нескольких из них будут приведены далее.

1) 15x 2 + 20x + 5 = 12x 2 + 27x + 1

Перенесём всё в левую часть равенства, сделаем преобразование, то есть получим вид уравнения, который принято именовать стандартным, и приравняем его нулю.

15x 2 + 20x + 5 — 12x 2 — 27x — 1 = 0

Сложив подобные, определим дискриминант: D = 49 — 48 = 1. Значит у нашего уравнения будет два корня. Вычислим их согласно приведённой выше формуле, а это значит, что первый из них буде равен 4/3, а второй 1.

2) Теперь раскроем загадки другого рода.

Выясним, есть ли вообще здесь корни x 2 — 4x + 5 = 1? Для получения исчерпывающего ответа приведём многочлен к соответствующему привычному виду и вычислим дискриминант. В указанном примере решение квадратного уравнения производить не обязательно, ведь суть задачи заключается совсем не в этом. В данном случае D = 16 — 20 = -4, а значит, корней действительно нет.

Теорема Виета

Квадратные уравнения удобно решать через указанные выше формулы и дискриминант, когда из значения последнего извлекается квадратный корень. Но это бывает не всегда. Однако способов для получения значений переменных в данном случае существует множество. Пример: решения квадратных уравнений по теореме Виета. Она названа в честь который жил в XVI веке во Франции и сделал блестящую карьеру благодаря своему математическому таланту и связям при дворе. Портрет его можно увидеть в статье.

Закономерность, которую заметил прославленный француз, заключалась в следующем. Он доказал, что корни уравнения в сумме численно равны -p=b/a, а их произведение соответствует q=c/a.

Теперь рассмотрим конкретные задачи.

3x 2 + 21x — 54 = 0

Для простоты преобразуем выражение:

x 2 + 7x — 18 = 0

Воспользуемся теоремой Виета, это даст нам следующее: сумма корней равна -7, а их произведение -18. Отсюда получим, что корнями уравнения являются числа -9 и 2. Сделав проверку, убедимся, что эти значения переменных действительно подходят в выражение.

График и уравнение параболы

Понятия квадратичная функция и квадратные уравнения тесно связаны. Примеры подобного уже были приведены ранее. Теперь рассмотрим некоторые математические загадки немного подробнее. Любое уравнение описываемого типа можно представить наглядно. Подобная зависимость, нарисованная в виде графика, называется параболой. Различные её виды представлены на рисунке ниже.

Любая парабола имеет вершину, то есть точку, из которой выходят её ветви. В случае если a>0, они уходят высоко в бесконечность, а когда a

Наглядные изображения функций помогают решать любые уравнения, в том числе и квадратные. Этот метод называется графическим. А значением переменной х является координата абсцисс в точках, где происходит пересечение линии графика с 0x. Координаты вершины можно узнать по только что приведённой формуле x 0 = -b/2a. И, подставив полученное значение в изначальное уравнение функции, можно узнать y 0 , то есть вторую координату вершины параболы, принадлежащую оси ординат.

Пересечение ветвей параболы с осью абсцисс

Примеров с решением квадратных уравнений очень много, но существуют и общие закономерности. Рассмотрим их. Понятно, что пересечение графика с осью 0x при a>0 возможно только если у 0 принимает отрицательные значения. А для a0. В противном случае D

По графику параболы можно определить и корни. Верно также обратное. То есть если получить наглядное изображение квадратичной функции нелегко, можно приравнять правую часть выражения к 0 и решить полученное уравнение. А зная точки пересечения с осью 0x, легче построить график.

Из истории

С помощью уравнений, содержащих переменную, возведённую в квадрат, в старину не только делали математические расчёты и определяли площади геометрических фигур. Подобные вычисления древним были нужны для грандиозных открытий в области физики и астрономии, а также для составления астрологических прогнозов.

Как предполагают современные деятели науки, одними из первых решением квадратных уравнений занялись жители Вавилона. Произошло это за четыре столетия до наступления нашей эры. Разумеется, их вычисления в корне отличались от ныне принятых и оказывались гораздо примитивней. К примеру, месопотамские математики понятия не имели о существовании отрицательных чисел. Незнакомы им были также другие тонкости из тех, которые знает любой школьник современности.

Возможно, ещё раньше учёных Вавилона решением квадратных уравнений занялся мудрец из Индии Баудхаяма. Произошло это примерно за восемь столетий до наступления эры Христа. Правда, уравнения второго порядка, способы решения которых он привёл, были самыми наипростейшими. Кроме него, подобными вопросами интересовались в старину и китайские математики. В Европе квадратные уравнения начали решать лишь в начале XIII столетия, но зато позднее их использовали в своих работах такие великие учёные, как Ньютон, Декарт и многие другие.

», то есть уравнения первой степени. В этом уроке мы разберем, что называют квадратным уравнением и как его решать.

Что называют квадратным уравнением

Важно!

Степень уравнения определяют по наибольшей степени, в которой стоит неизвестное.

Если максимальная степень, в которой стоит неизвестное — «2 », значит, перед вами квадратное уравнение.

Примеры квадратных уравнений

• 5x 2 − 14x + 17 = 0
• −x 2 + x + = 0
• x 2 + 0,25x = 0
• x 2 − 8 = 0

Важно! Общий вид квадратного уравнения выглядит так:

A x 2 + b x + c = 0

«a », «b » и «c » — заданные числа.

• «a » — первый или старший коэффициент;
• «b » — второй коэффициент;
• «c » — свободный член.

Чтобы найти «a », «b » и «c » нужно сравнить свое уравнение с общим видом квадратного уравнения «ax 2 + bx + c = 0 ».

Давайте потренируемся определять коэффициенты «a », «b » и «c » в квадратных уравнениях.

5x 2 − 14x + 17 = 0 −7x 2 − 13x + 8 = 0 −x 2 + x + = 0 x 2 + 0,25x = 0

Уравнение	Коэффициенты
a = 5 b = −14 с = 17
a = −7 b = −13 с = 8
a = −1 b = 1 с =
a = 1 b = 0,25 с = 0
x 2 − 8 = 0	a = 1 b = 0 с = −8

Как решать квадратные уравнения

В отличии от линейных уравнений для решения квадратных уравнений используется специальная формула для нахождения корней .

Запомните!

Чтобы решить квадратное уравнение нужно:

• привести квадратное уравнение к общему виду «ax 2 + bx + c = 0 ». То есть в правой части должен остаться только «0 »;
• использовать формулу для корней:

Давайте на примере разберем, как применять формулу для нахождения корней квадратного уравнения. Решим квадратное уравнение.

X 2 − 3x − 4 = 0

Уравнение « x 2 − 3x − 4 = 0 » уже приведено к общему виду «ax 2 + bx + c = 0 » и не требует дополнительных упрощений. Для его решения нам достаточно применить формулу нахождения корней квадратного уравнения .

Определим коэффициенты «a », «b » и «c » для этого уравнения.

x 1;2 =
x 1;2 =
x 1;2 =
x 1;2 =

С её помощью решается любое квадратное уравнение.

В формуле «x 1;2 = » часто заменяют подкоренное выражение
«b 2 − 4ac » на букву «D » и называют дискриминантом . Более подробно понятие дискриминанта рассматривается в уроке «Что такое дискриминант ».

Рассмотрим другой пример квадратного уравнения.

x 2 + 9 + x = 7x

В данном виде определить коэффициенты «a », «b » и «c » довольно сложно. Давайте вначале приведем уравнение к общему виду «ax 2 + bx + c = 0 ».

X 2 + 9 + x = 7x
x 2 + 9 + x − 7x = 0
x 2 + 9 − 6x = 0
x 2 − 6x + 9 = 0

Теперь можно использовать формулу для корней.

X 1;2 =
x 1;2 =
x 1;2 =
x 1;2 =
x =

x = 3
Ответ: x = 3

Бывают случаи, когда в квадратных уравнениях нет корней. Такая ситуация возникает, когда в формуле под корнем оказывается отрицательное число.

Библиографическое описание: Гасанов А. Р., Курамшин А. А., Ельков А. А., Шильненков Н. В., Уланов Д. Д., Шмелева О. В. Способы решения квадратных уравнений // Юный ученый. — 2016. — №6.1. — С. 17-20..02.2019).



Наш проект посвящен способам решения квадратных уравнений. Цель проекта: научиться решать квадратные уравнения способами, не входящими в школьную программу. Задача: найти все возможные способы решения квадратных уравнений и научиться их использовать самим и познакомить одноклассников с этими способами.

Что же такое «квадратные уравнения»?

Квадратное уравнение — уравнение вида ax 2 + bx + c = 0 , где a , b , c — некоторые числа (a ≠ 0 ), x — неизвестное.

Числа a, b,c называются коэффициентами квадратного уравнения.

• a называется первым коэффициентом;
• b называется вторым коэффициентом;
• c — свободным членом.

А кто же первый «изобрёл» квадратные уравнения?

Некоторые алгебраические приемы решения линейных и квадратных уравнений были известны еще 4000 лет назад в Древнем Вавилоне. Найденные древние вавилонские глиняные таблички, датированные где-то между 1800 и 1600 годами до н.э., являются самыми ранними свидетельствами об изучении квадратных уравнений. На этих же табличках изложены методы решения некоторых типов квадратных уравнений.

Необходимость решать уравнения не только первой, но и второй степени еще в древности была вызвана потребностью решать задачи, связанные с нахождением площадей земельных участков и с земляными работами военного характера, а также с развитием астрономии и самой математики.

Правило решения этих уравнений, изложенное в вавилонских текстах, совпадает по существу с современным, однако неизвестно, каким образом дошли вавилоняне до этого правила. Почти все найденные до сих пор клинописные тексты приводят только задачи с решениями, изложенными в виде рецептов, без указаний относительно того, каким образом они были найдены. Несмотря на высокий уровень развития алгебры в Вавилоне, в клинописных текстах отсутствуют понятие отрицательного числа и общие методы решения квадратных уравнений.

Вавилонские математики примерно с IV века до н.э. использовали метод дополнения квадрата для решения уравнений с положительными корнями. Около 300 года до н.э. Эвклид придумал более общий геометрический метод решения. Первым математиком, который нашел решения уравнения с отрицательными корнями в виде алгебраической формулы, был индийский ученый Брахмагупта (Индия, VII столетие нашей эры).

Брахмагупта изложил общее правило решения квадратных уравнений, приведенных к единой канонической форме:

ax2 + bх = с, а>0

В этом уравнении коэффициенты, могут быть и отрицательными. Правило Брахмагупты по существу совпадает с нашим.

В Индии были распространены публичные соревнования в решении трудных задач. В одной из старинных индийских книг говорится по поводу таких соревнований следующее: «Как солнце блеском своим затмевает звезды, так ученый человек затмит славу в народных собраниях, предлагая и решая алгебраические задачи». Задачи часто облекались в стихотворную форму.

В алгебраическом трактате Аль-Хорезми дается классификация линейных и квадратных уравнений. Автор насчитывает 6 видов уравнений, выражая их следующим образом:

1) «Квадраты равны корням», т. е. ах2 = bх.

2) «Квадраты равны числу», т. е. ах2 = с.

3) «Корни равны числу», т. е. ах2 = с.

4) «Квадраты и числа равны корням», т. е. ах2 + с = bх.

5) «Квадраты и корни равны числу», т. е. ах2 + bх =с.

6) «Корни и числа равны квадратам», т. е. bх + с == ах2.

Для Аль-Хорезми, избегавшего употребления отрицательных чисел, члены каждого из этих уравнений слагаемые, а не вычитаемые. При этом заведомо не берутся во внимание уравнения, у которых нет положительных решений. Автор излагает способы решения указанных уравнений, пользуясь приемами ал-джабр и ал-мукабала. Его решение, конечно, не совпадает полностью с нашим. Уже не говоря о том, что оно чисто риторическое, следует отметить, например, что при решении неполного квадратного уравнения первого вида Аль-Хорезми, как и все математики до XVII в., не учитывает нулевого решения, вероятно, потому, что в конкретных практических задачах оно не имеет значения. При решении полных квадратных уравнений Аль-Хорезми на частных числовых примерах излагает правила решения, а затем их геометрические доказательства.

Формы решения квадратных уравнений по образцу Аль-Хорезми в Европе были впервые изложены в «Книге абака», написанной в 1202г. итальянским математиком Леонардом Фибоначчи . Автор разработал самостоятельно некоторые новые алгебраические примеры решения задач и первый в Европе подошел к введению отрицательных чисел.

Эта книга способствовала распространению алгебраических знаний не только в Италии, но и в Германии, Франции и других странах Европы. Многие задачи из этой книги переходили почти во все европейские учебники XIV-XVII вв. Общее правило решения квадратных уравнений, приведенных к единому каноническому виду x2 + bх = с при всевозможных комбинациях знаков и коэффициентов b, c, было сформулировано в Европе в 1544 г. М. Штифелем.

Вывод формулы решения квадратного уравнения в общем виде имеется у Виета, однако Виет признавал только положительные корни. Итальянские математики Тарталья,Кардано, Бомбелли среди первых в XVI в. учитывают, помимо положительных, и отрицательные корни. Лишь в XVII в. благодаря трудам Жирара, Декарта, Ньютона и других ученых способ решения квадратных уравнений принимает современный вид.

Рассмотрим несколько способов решения квадратных уравнений.

Стандартные способы решения квадратных уравнений из школьной программы:

1. Разложение левой части уравнения на множители.
2. Метод выделения полного квадрата.
3. Решение квадратных уравнений по формуле.
4. Графическое решение квадратного уравнения.
5. Решение уравнений с использованием теоремы Виета.

Остановимся подробнее на решение приведенных и не приведенных квадратных уравнений по теореме Виета.

Напомним, что для решения приведенных квадратных уравнений достаточно найти два числа такие, произведение которых равно свободному члену, а сумма — второму коэффициенту с противоположным знаком.

Пример. x 2 -5x+6=0

Нужно найти числа, произведение которых равно 6, а сумма 5. Такими числами будут 3 и 2.

Ответ: x 1 =2, x 2 =3.

Но можно использовать этот способ и для уравнений с первым коэффициентом не равным единице.

Пример. 3x 2 +2x-5=0

Берём первый коэффициент и умножаем его на свободный член: x 2 +2x-15=0

Корнями этого уравнения будут числа, произведение которых равно — 15, а сумма равна — 2. Эти числа — 5 и 3. Чтобы найти корни исходного уравнения, полученные корни делим на первый коэффициент.

Ответ: x 1 =-5/3, x 2 =1

6. Решение уравнений способом «переброски».

Рассмотрим квадратное уравнение ах 2 + bх + с = 0, где а≠0.

Умножая обе его части на а, получаем уравнение а 2 х 2 + аbх + ас = 0.

Пусть ах = у, откуда х = у/а; тогда приходим к уравнению у 2 + by + ас = 0, равносильному данному. Его корни у 1 и у 2 найдем с помощью теоремы Виета.

Окончательно получаем х 1 = у 1 /а и х 2 = у 2 /а.

При этом способе коэффициент a умножается на свободный член, как бы «перебрасывается» к нему, поэтому его называют способом «переброски». Этот способ применяют, когда можно легко найти корни уравнения, используя теорему Виета и, что самое важное, когда дискриминант есть точный квадрат.

Пример. 2х 2 — 11х + 15 = 0.

«Перебросим» коэффициент 2 к свободному члену и сделав замену получим уравнение у 2 — 11у + 30 = 0.

Согласно обратной теореме Виета

у 1 = 5, х 1 = 5/2, х 1 =2,5 ;у 2 = 6, x 2 = 6/2, x 2 = 3.

Ответ: х 1 =2,5; х 2 = 3.

7. Свойства коэффициентов квадратного уравнения.

Пусть дано квадратное уравнение ах 2 + bх + с = 0, а ≠ 0.

1. Если a+ b + с = 0 (т.е. сумма коэффициентов уравнения равна нулю), то х 1 = 1.

2. Если а — b + с = 0, или b = а + с, то х 1 = — 1.

Пример. 345х 2 — 137х — 208 = 0.

Так как а + b + с = 0 (345 — 137 — 208 = 0), то х 1 = 1, х 2 = -208/345.

Ответ: х 1 =1; х 2 = -208/345 .

Пример. 132х 2 + 247х + 115 = 0

Т.к. a-b+с = 0 (132 — 247 +115=0), то х 1 = — 1, х 2 = — 115/132

Ответ: х 1 = — 1; х 2 =- 115/132

Существуют и другие свойства коэффициентов квадратного уравнения. но ихиспользование более сложное.

8. Решение квадратных уравнений с помощью номограммы.

Рис 1. Номограмма

Это старый и в настоящее время забытый способ решения квадратных уравнений, помещенный на с.83 сборника: Брадис В.М. Четырехзначные математические таблицы. — М., Просвещение, 1990.

Таблица XXII. Номограмма для решения уравнения z 2 + pz + q = 0 . Эта номограмма позволяет, не решая квадратного уравнения, по его коэффициентам определить корни уравнения.

Криволинейная шкала номограммы построена по формулам (рис. 1):

Полагая ОС = р, ED = q, ОЕ = а (все в см), из рис. 1 подобия треугольников САН и CDF получим пропорцию

откуда после подстановок и упрощений вытекает уравнение z 2 + pz + q = 0, причем буква z означает метку любой точки криволинейной шкалы.

Рис. 2 Решение квадратных уравнения с помощью номограммы

Примеры.

1) Для уравнения z 2 — 9z + 8 = 0 номограмма дает корни z 1 = 8,0 и z 2 = 1,0

Ответ:8,0; 1,0.

2) Решим с помощью номограммы уравнение

2z 2 — 9z + 2 = 0.

Разделим коэффициенты этого уравнения на 2, получим уравнение z 2 — 4,5z + 1 = 0.

Номограмма дает корни z 1 = 4 и z 2 = 0,5.

Ответ: 4; 0,5.

9. Геометрический способ решения квадратных уравнений.

Пример. х 2 + 10х = 39.

В оригинале эта задача формулируется следующим образом: «Квадрат и десять корней равны 39».

Рассмотрим квадрат со стороной х, на его сторонах строятся прямоугольники так, что другая сторона каждого из них равна 2,5, следовательно, площадь каждого равна 2,5x. Полученную фигуру дополняют затем до нового квадрата АВСD, достраивая в углах четыре равных квадрата, сторона каждого из них 2,5, а площадь 6,25

Рис. 3 Графический способ решения уравнения х 2 + 10х = 39

Площадь S квадрата ABCD можно представить как сумму площадей: первоначального квадрата х 2 , четырех прямоугольников (4∙2,5x = 10х) и четырех пристроенных квадратов (6,25∙ 4 = 25) , т.е. S = х 2 + 10х = 25. Заменяя х 2 + 10х числом 39, получим что S = 39+ 25 = 64, откуда следует, что сторона квадрата АВСD, т.е. отрезок АВ = 8. Для искомой стороны х первоначального квадрата получим

10. Решение уравнений с использованием теоремы Безу.

Теорема Безу. Остаток от деления многочлена P(x) на двучлен x — α равен P(α) (т.е. значению P(x) при x = α).

Если число α является корнем многочлена P(x), то этот многочлен делится на x -α без остатка.

Пример. х²-4х+3=0

Р(x)= х²-4х+3, α: ±1,±3, α =1, 1-4+3=0. Разделим Р(x) на (х-1):(х²-4х+3)/(х-1)=х-3

х²-4х+3=(х-1)(х-3), (х-1)(х-3)=0

х-1=0; х=1, или х-3=0, х=3; Ответ: х 1 =2, х 2 =3.

Вывод: Умение быстро и рационально решать квадратные уравнения просто необходимо для решения более сложных уравнений, например, дробно-рациональных уравнений, уравнений высших степеней, биквадратных уравнений, а в старшей школе тригонометрических, показательных и логарифмических уравнений. Изучив все найденные способы решения квадратных уравнений, мы можем посоветовать одноклассникам, кроме стандартных способов, решение способом переброски (6) и решение уравнений по свойству коэффициентов (7), так как они являются более доступными для понимания.

Литература:

1. Брадис В.М. Четырехзначные математические таблицы. — М., Просвещение, 1990.
2. Алгебра 8 класс: учебник для 8 кл. общеобразоват. учреждений Макарычев Ю. Н., Миндюк Н. Г., Нешков К. И., Суворова С. Б. под ред. С. А. Теляковского 15-е изд., дораб. — М.: Просвещение, 2015
3. https://ru.wikipedia.org/wiki/%D0%9A%D0%B2%D0%B0%D0%B4%D1%80%D0%B0%D1%82%D0%BD%D0%BE%D0%B5_%D1%83%D1%80%D0%B0%D0%B2%D0%BD%D0%B5%D0%BD%D0%B8%D0%B5
4. Глейзер Г. 2 + b*x + c = 0 ,где x — переменная, a,b,c – константы; a0 . Задача состоит в отыскании корней уравнения.

   Геометрический смысл квадратного уравнения

   Графиком функции, которая представлена квадратным уравнением является парабола. Решения (корни) квадратного уравнения — это точки пересечения параболы с осью абсцисс (х) . Из этого следует, что есть три возможных случая:
   1) парабола не имеет точек пересечения с осью абсцисс. Это означает, что она находится в верхней плоскости с ветками вверх или нижней с ветками вниз. В таких случаях квадратное уравнение не имеет действительных корней (имеет два комплексных корня).

   2) парабола имеет одну точку пересечения с осью Ох . Такую точку называют вершиной параболы, а квадратное уравнение в ней приобретает свое минимальное или максимальное значение. В этом случае квадратное уравнение имеет один действительный корень (или два одинаковых корня).

   3) Последний случай на практике интересный больше — существует две точки пересечения параболы с осью абсцисс. 2 и осуществим преобразование

   Отсюда находим

   Формула дискриминанта и корней квадратного уравнения

   Дискриминантом называют значение подкоренного выраженияЕсли он положительный то уравнение имеет два действительных корня, вычисляемые по формулеПри нулевом дискриминант квадратное уравнение имеет одно решение (два совпадающих корня), которые легко получить из приведенной выше формулы при D=0 При отрицательном дискриминант уравнения действительных корней нет. Однако исують решения квадратного уравнения в комплексной плоскости, и их значение вычисляют по формуле

   Теорема Виета

   Рассмотрим два корня квадратного уравнения и построим на их основе квадратное уравнение.С записи легко следует сама теорема Виета: если имеем квадратное уравнение видато сумма его корней равна коэффициенту p , взятому с противоположным знаком, а произведение корней уравнения равен свободному слагаемому q . Формульная запись вышесказанного будет иметь видЕсли в классическом уравнении константа а отлична от нуля, то нужно разделить на нее все уравнение, а затем применять теорему Виета. 2+x-6=0 .

   Решение: В случаях когда есть малые коэффициенты при х целесообразно применять теорему Виета. По ее условию получаем два уравнения

   С второго условия получаем, что произведение должно быть равно -6 . Это означает, что один из корней отрицателен. Имеем следующую возможную пару решений{-3;2}, {3;-2} . С учетом первого условия вторую пару решений отвергаем.
   Корни уравнения равны

   Задача 5. Найти длины сторон прямоугольника, если его периметр 18 см, а площадь 77 см 2 .

   Решение: Половина периметра прямоугольника равна сумме соседних сторон. Обозначим х – большую сторону, тогда 18-x меньшая его сторона. Площадь прямоугольника равна произведению этих длин:
   х(18-х)=77;
   или
   х 2 -18х+77=0.
   Найдем дискриминант уравнения

   Вычисляем корни уравнения
   
   Если х=11 , то 18-х=7 , наоборот тоже справедливо (если х=7 , то 21-х=9 ).

   Задача 6. Разложить квадратное 10x 2 -11x+3=0 уравнения на множители.

   Решение: Вычислим корни уравнения, для этого находим дискриминант
   
   Подставляем найденное значение в формулу корней и вычисляем
   
   Применяем формулу разложения квадратного уравнения по корнями
   
   Раскрыв скобки получим тождество. 2+(2а+6)х-3а-9=0 имеет более одного корня?

   Решение: Рассмотрим сначала особые точки, ими будут значения а=0 и а=-3 . При а=0 уравнение упростится до вида 6х-9=0; х=3/2 и будет один корень. При а= -3 получим тождество 0=0 .
   Вычислим дискриминант
   
   и найдем значения а при котором оно положительно
   
   С первого условия получим а>3 . Для второго находим дискриминант и корни уравнения

   
   Определим промежутки где функция принимает положительные значения. Подстановкой точки а=0 получим 3>0 . Итак, за пределами промежутка (-3;1/3) функция отрицательная. Не стоит забывать о точке а=0 , которую следует исключить, поскольку в ней исходное уравнение имеет один корень.
   В результате получим два интервала, которые удовлетворяют условию задачи
   
   Подобных задач на практике будет много, постарайтесь разобраться с заданиями самостоятельно и не забывайте учитывать условия, которые взаимоисключают друг друга. Хорошо изучите формулы для решения квадратных уравнений, они довольна часто нужны при вычислениях в разных задачах и науках.

   Квадратичная формула: решения и дискриминант

   Квадратичная формулаДиск. & Графики

   Purplemath

   Давайте сделаем еще несколько примеров.

   В данный момент я не только не могу применить квадратичную формулу, но и не могу факторизовать. Почему? Потому что это уравнение еще в правильной форме.

   И я , конечно, не могу утверждать с серьезным видом, что « х = 4, х — 2 = 4», потому что это , а не , как работает «разложение на множители».

   Независимо от того, какой метод решения я намереваюсь использовать — раскладываю ли я на множители или использую квадратную формулу, чтобы найти свои ответы — я должен сначала преобразовать уравнение в форму «(квадратичное) = 0».

   Содержание продолжается ниже

   MathHelp.com

   Квадратичная формула

   Первое, что я сделаю здесь, это умножу слева, а затем перенесу 4 справа влево:

   x ( x — 2) = 4

   x ² — 2 x = 4

   x ² — 2 x — 4 = 0

   С. (1)(−4) = −4, которые в сумме дают −2, то этот квадрат не учитывается. (Другими словами, нет никакой возможности, чтобы решение ложного факторинга « x = 4, x − 2 = 4» могло быть хотя бы немного правильным.)

   Таким образом, факторинг не сработает, но я может использовать квадратную формулу; в этом случае я подставлю значения a = 1, b = -2 и c = -4:

   Тогда ответ:

   x = -1,24, x = 3,24, округленное до двух знаков после запятой.

   ---

   Для справки, вот как выглядит график связанного квадратичного уравнения y = x ² − 2 x − 4:

   Формула совпадает с точками пересечения x . Места, где график пересекает 9Ось 0011 x дает значения, которые решают исходное уравнение.

   Существует еще одна связь между решениями квадратичной формулы и графиком параболы: вы можете сказать, сколько x -пересечений у вас будет, исходя из значения внутри квадратного корня. Аргумент (т. то есть уметь различать) различные типы решений.

   В этом случае значение дискриминанта b ² − 4 ac равно 20; в частности, значение было , а не нуля, и было , а не отрицательным. Поскольку значение не было отрицательным, уравнение должно было иметь по крайней мере одно (действительное) решение; поскольку значение не равно нулю, два решения будут разными (то есть, они будут отличаться друг от друга).

   ---

   Использование a = 9, b = 12 и c = 4, квадратичная формула дает мне:

   Тогда ответ:

   x = ⁻² / ₃

   ---

   В первом примере на этой странице я получил два решения, потому что значение дискриминанта (то есть значение внутри квадратного корня) было ненулевым и положительным. В результате часть формулы «плюс-минус» дала мне два разных значения; один для «плюсовой» части числителя, а другой для «минусовой» части. Однако в данном случае квадратный корень уменьшился до нуля, так что плюс-минус ничего не значил.

   Такое решение, в котором вы получаете только одно значение, потому что «плюс-минус ноль» ничего не меняет, называется «повторным» корнем, потому что x равно

   ⁻² / ₃ , но равно этому значению как бы дважды: ⁻² / ₃ + 0 и ⁻² / ₃ − 0.

   Вы можете увидеть это повторение лучше, если разложите на множители квадратное число (и, поскольку решения представляли собой аккуратные дроби, квадратное число должен иметь множитель ): 9 x ² + 12 x + 4 = (3 x + 2)(3 x + 2) = 0, поэтому первый множитель дает нам 3 x + 2 = 0, поэтому

   x = ^-2 / ₃ , и (из второго, тождественного множителя) 3 x + 2 = 0, поэтому x = ^{-2 903}

   / 39043 опять таки.

   Каждый раз, когда вы получаете ноль внутри квадратного корня квадратной формулы, вы получаете только одно решение уравнения, в том смысле, что получаете одно число, которое решает уравнение. Но вы получите два решения, в том смысле, что одно значение считается дважды. Другими словами, дискриминант (то есть выражение b ² − 4 ac ) со значением, равным нулю, означает, что вы получите одно «повторяющееся» значение решения.

   ---

   Ниже приведен график ассоциированной функции y = 9 x ² + 12 x + 4:

   2 -01 только парабола в

   x = ⁻² / ₃ ; на самом деле не пересекается. Это соотношение всегда верно: если у вас есть корень, который встречается ровно дважды (или, что то же самое, если вы получаете нуль внутри квадратного корня), то график будет «целовать» ось в значении решения, но это не так. не пройдет через ось.

   ---

   Поскольку в (3)(2) = 6 нет множителей, которые в сумме дают 4, этот квадрат не дает множителей. Но квадратичная формула работает всегда; в этом случае я подставлю значения a = 3, b = 4 и c = 2:

   На данный момент у меня есть отрицательное число внутри квадратного корня. Если вы еще не узнали о комплексных числах, то вам придется остановиться здесь, и ответом будет «нет решения»; если вы знаете о комплексных числах, то можете продолжить вычисления:

   Таким образом, в зависимости от вашего уровня знаний, ваш ответ будет одним из следующих:

   решения с вещественными числами: нет решения

   решения с комплексными числами:

   ---

   ---

   знайте, что вы не можете построить свой ответ, потому что вы не можете изобразить квадратный корень из отрицательного числа в обычном декартовом разряде. На оси x таких значений нет. Поскольку вы не можете найти графическое решение квадратного уравнения, разумно не должно быть никаких x — перехваты (потому что вы можете отобразить x -перехват).

   ---

   Вот график ассоциированной функции, y = 3 x ² + 4 x + 2:

   Как видите, на графике нет ни крестика, ни даже касания. x — ось. Это соотношение всегда верно: если вы получите отрицательное значение внутри квадратного корня, то не будет решения действительного числа , и, следовательно, не будет x — перехваты. Другими словами, если дискриминант (являющийся выражением b ² − 4 ac ) имеет отрицательное значение, то у вас не будет графически отображаемых нулей.

   (Отношение между дискриминантом (являющимся значением внутри квадратного корня), типом решений (два различных решения, одно повторяющееся решение или отсутствие графически отображаемых решений) и количеством x -отрезков на графике ( два, один или ни одного) представлены в таблице на следующей странице.)

   ---

   URL: https://www.purplemath.com/modules/quadform2. htm

   Page 1Page 3

   Заполнение квадрата и квадратной формулы

   Результаты обучения

   • Заполните квадрат, чтобы решить квадратное уравнение.
   • Используйте квадратную формулу для решения квадратного уравнения.
   • Используйте дискриминант, чтобы определить количество и тип решений квадратного уравнения.

   Не все квадратные уравнения можно разложить на множители или решить в исходной форме с использованием свойства квадратного корня. В этих случаях мы можем использовать другие методы для решения квадратное уравнение.

   Завершение квадрата

   Один метод известен как завершение квадрата . Используя этот процесс, мы добавляем или вычитаем члены с обеих сторон уравнения, пока у нас не получится идеальный квадратный трехчлен с одной стороны от знака равенства. Затем мы применяем свойство квадратного корня. Для завершения квадрата старший коэффициент [latex]a[/latex] должен быть равен 1. Если это не так, то разделите все уравнение на [latex]a[/latex]. Затем мы можем использовать следующие процедуры для решения квадратного уравнения путем завершения квадрата. 9{2}-6x=13[/латекс].

   Показать решение

   Использование квадратной формулы

   Четвертый метод решения квадратного уравнения заключается в использовании квадратной формулы , которая решает все квадратные уравнения. Хотя квадратная формула работает с любым квадратным уравнением в стандартной форме, легко сделать ошибку при подстановке значений в формулу. Будьте внимательны при подстановке и используйте круглые скобки при вставке отрицательного числа. 9{2}-10x+15=0[/латекс]

Показать решение

Попробуйте

Внесите свой вклад!

У вас есть идеи по улучшению этого контента? Мы будем признательны за ваш вклад.

Улучшить эту страницуПодробнее

Решение квадратных уравнений с помощью квадратичной формулы — промежуточная алгебра

Квадратные уравнения и функции

Цели обучения

К концу этого раздела вы сможете:

• Решать квадратные уравнения с помощью квадратичной формулы
• Использование дискриминанта для предсказания количества и типа решений квадратного уравнения
• Определите наиболее подходящий метод решения квадратного уравнения

Прежде чем начать, пройдите этот тест на готовность.

1. Оценить, когда и

   Если вы пропустили эту проблему, просмотрите (рисунок).

2. Упростить:

   Если вы пропустили эту проблему, просмотрите (рисунок).

3. Упростить:

   Если вы пропустили эту проблему, просмотрите (рисунок).

Решение квадратных уравнений с помощью квадратной формулы

Когда мы решали квадратные уравнения в последнем разделе, завершая квадрат, мы каждый раз выполняли одни и те же действия. К концу набора упражнений вы, возможно, задавались вопросом: «А нет ли более простого способа сделать это?» Ответ «да». Математики ищут закономерности, когда делают что-то снова и снова, чтобы облегчить себе работу. В этом разделе мы выведем и используем формулу для нахождения решения квадратного уравнения.

Мы уже видели, как решить формулу для конкретной переменной «в общем», так что мы проделаем алгебраические шаги только один раз, а затем используем новую формулу, чтобы найти значение конкретной переменной. Теперь мы пройдем этапы заполнения квадрата, используя общую форму квадратного уравнения, чтобы решить квадратное уравнение для x.

Начнем со стандартной формы квадратного уравнения и решим его для x , заполнив квадрат.

Add this value to both sides of the equation. X squared plus b divided by a times x plus b squared divided by the product 4 a squared equals negative c divided by a plus the quotient b squared divided by the product 4 times a squared. Factor the perfect square trinomial on the left side of the equation. The square of x plus the quotient b divided by 2 a equals the quotient negative c divided by a plus the quotient b squared divided by the product 4 times a squared. Find the common denominator of the right side of the equation and write equivalent fractions using the common denominator. Multiply the term negative c divided by a on the right side of the equation by the fraction 4 a divided by 4 a. Rearrange terms on the right side of the equation, and it becomes the square of the sum x plus the quotient b divided by 2 a equals the quotient b squared divided by the product 4 times a squared plus the quotient negative c times 4 a divided by a times 4 a. Combining to one fraction, the square of the sum x plus the quotient b divided by 2 a equals the quotient of the difference b squared minus 4 a c divided by 4 a squared. Use the Square Root Property. X plus the quotient b divded by 2 a equals the positive or negative square root of the quotient of the difference b squared minus 4 a c divided by 4 a squared. Simplify the radical. X plus the quotient b divded by 2 a equals the positive or negative quotient of the square root of the difference b squared minus 4 a c divided by 2 a. Add negative b divided by 2 a to both sides of the equation. So x equals negative b divided by the product 2 a plus or minus the quotient of the square root of the difference b squared minus 4 a c divided by 2 a. Combine the terms on the right side of the equation to get the final form of the Quadratic Formula. X equals the quotient negative b plus or minus the square root of the difference b squared minus 4 a c divided by 2 a.» data-label=»»>

Изолируйте переменные термины с одной стороны.
Сделать коэффициент равным 1, путем разделить на .
Упрощение.
Чтобы завершить квадрат, найдите и добавьте его к обеим частям уравнения.
Левая сторона представляет собой идеальный квадрат, разложите его на множители.
Найдите общий знаменатель права и напишите эквивалентные дроби с общий знаменатель.
Упрощение.
Объединить в одну фракцию.
Используйте свойство квадратного корня.
Упростите радикальное.
Добавьте к обеим частям уравнения.
Объедините термины справа.
	Это уравнение является квадратичной формулой.

Квадратная формула

Решения квадратного уравнения вида ax ² + bx + c = 0, где даются по формуле: замените значения a , b и c из стандартной формы в выражение в правой части формулы. Тогда упростим выражение. Результатом является пара решений квадратного уравнения.

Обратите внимание, что формула представляет собой уравнение. Убедитесь, что вы используете обе части уравнения.

Как решить квадратное уравнение с помощью квадратичной формулы

Решить с помощью квадратичной формулы:

Решить с помощью квадратичной формулы: .

Решите с помощью квадратичной формулы: .

Решите квадратное уравнение, используя квадратную формулу.

1. Запишите квадратное уравнение в стандартной форме: x ² + bx + c = 0. Определите значения a , b 2 5 1 c и 905 .
2. Напишите квадратную формулу. Затем замените значения на , на b и на .
3. Упростить.
4. Проверьте решения.

Если вы произносите формулу, когда пишете ее в каждой задаче, вы быстро ее запомните! И помните, квадратичная формула — это УРАВНЕНИЕ. Убедитесь, что вы начали с « x =».

Решите с помощью квадратичной формулы:

Simplify. X equals the quotient of the expression 6 plus or minus the square root of the difference 36 minus 20 divided by 2. This further simplifies to the quotient of 6 plus or minus square root 16 and 2, so x equals the quotient of 6 plus or minus 4 and 2. Rewrite to show two solutions The first is x equals the quotient 6 plus 4 divided by 2, or 10 divided by 2 which equals 5. The second solution is the quotient 6 minus 4 divided by 2, or 2 divided by 2 which equals 1. Check the solutions in the original equation. Substitute x equals 5 into the original equation, x squared minus 6 x plus 5 equals zero to get 5 squared minus 6 times 5 plus 5 on the left side of the equation we must show that this equals 0. Simplifying the expression yields 25 minus 30 plus 5, or 0. So x equals 5 is a solution. Next check x equals 1 in the original equation. X squared minus 6 x plus 5 becomes 1 squared minus 6 times 1 plus 5. We must show this equals 0. 1 minus 6 plus 5 does equal 0, so x = 1 is a solution. » data-label=»»>

Запишите уравнение в стандартной форме, добавив 5 с каждой стороны.
Теперь это уравнение имеет стандартную форму.
Определите значения
Напишите квадратную формулу.
Затем подставьте значения
Упрощение.
Перепишите, чтобы показать два решения.
Упрощение.
Проверить:

Решите с помощью квадратичной формулы: .

Решите с помощью квадратичной формулы: .

Когда мы решали квадратные уравнения, используя свойство квадратного корня, мы иногда получали ответы, содержащие радикалы. Это может произойти и при использовании квадратичной формулы. Если мы получаем радикал в качестве решения, окончательный ответ должен иметь радикал в его упрощенной форме.

Решите с помощью квадратичной формулы:

The constant term is c equals 11. Write the quadratic formula, x equals the quotient negative b plus or minus the square root of the expression b squared minus 4 a c divided by 2 a. Then substitute the values for a, b, and c. x equals the quotient of the difference negative 10 plus or minus the square root of the difference 10 squared minus the product 4 times 2 times 11 divided by the product 2 times 2. Simplify. X equals the quotient of the expression negative 10 plus or minus the square root of the difference 100 minus 88 divided by 4. This further simplifies to the quotient negative 10 plus or minus square root 12 divided by 4. Simplify the radical. x equals the quotient negative 10 plus or minus 2 times the square root of 3 divided by 2. Factor out the common factor in the numerator. X equals the quotient of 2 times the expression negative 5 plus or minus 2 square root 3 and 4. Remove the common factor to yield x equals the quotient negative 5 plus or minus square root 3 divided by 2. Rewrite to show two solutions The first solution is x equals the quotient of negative 5 plus square root 3 and 2. The second is x equals the quotient of negative 5 minus square root 3 and 2. Remember to check the solutions in the original equation. We leave that to you!» data-label=»»>

Это уравнение имеет стандартную форму.
Определите значения a , b и c .
Напишите квадратную формулу.
Затем подставьте значения на , на b и на .
Упрощение.
Упростите радикальное.
Вынесите общий множитель из числителя.
Удалите общие множители.
Перепишите, чтобы показать два решения.
Проверить: Мы оставляем вам чек!

Решите с помощью квадратичной формулы: .

Решите с помощью квадратичной формулы: .

Когда мы подставляем a , b и c в квадратную формулу, а подкоренное число отрицательное, квадратное уравнение будет иметь мнимые или комплексные решения. Мы увидим это в следующем примере.

Решите с помощью квадратичной формулы:

This further simplifies to p equals the quotient negative 2 plus or minus the square root of negative 104 divided by 6. Simplify the radical using complex numbers. p equals the quotient negative 2 plus or minus square root 104 times I divided by 6. Simplify the radical. p equals the quotient negative 2 plus or minus 2 times square root 104 times I divided by 6. Factor the common factor in the numerator. P equals the quotient of 2 times the expression negative 1 plus or minus square root 26 times I divided by 6. Remove the common factor to yield p equals the quotient negative 1 plus or minus square root 26 times I divided by 3. Rewrite in standard a plus b I form. P equals negative one third plus or minus square root 26 divided by 3 times I. Write as show two solutions The first solution is p equals negative one third plus square root 26 thirds I. The second is p equals negative one third minus square root 26 thirds I.» data-label=»»>

Это уравнение в стандартной форме
Определите значения
Напишите квадратную формулу.
Затем подставьте значения .
Упрощение.
Упростите радикал, используя комплексные числа.
Упростите радикальное.
Умножьте общий множитель в числителе.
Удалите общие множители.
Переписать в стандартной форме.
Запишите двумя решениями.

Решите с помощью квадратичной формулы: .

Решите с помощью квадратичной формулы: .

Помните, что для использования квадратичной формулы уравнение должно быть записано в стандартной форме: ax ² + bx + c = 0. Иногда нам нужно будет выполнить некоторые алгебраические вычисления, чтобы получить уравнение в стандартную форму, прежде чем мы сможем использовать квадратную формулу.

Решите с помощью квадратичной формулы:

Наш первый шаг — привести уравнение к стандартной форме.

Identify the values of a, b, and c. The coefficient of x squared is a = 1. The coefficient of x is b equals 6. The constant term is c equals 4. Write the quadratic formula, x equals the quotient negative b plus or minus the square root of the difference b squared minus 4 a c divided by 2 a. Then substitute the values for a, b, and c. x equals the quotient of the expression negative 6 plus or minus the square root of the difference 6 squared minus the product 4 times 1 times 4 divided by the product 2 times 1. Simplify. X equals the quotient of the expression negative 6 plus or minus the square root of the difference 36 minus 16 divided by 2. This further simplifies to the quotient of negative 6 plus or minus square root 20 and 2. Simplify the radical. X equals the quotient negative 6 plus or minus 2 square root 5 divided by 2. Factor the common factor in the numerator. X equals the quotient 2 times the expression negative 3 plus or minus 2 square root 5 divided by 2. Remove the common factor, and x equals negative 3 plus or minus 2 square root 5. Rewrite to show two solutions, x equals negative 3 plus 2 square root 5 and x equals negative 3 minus 2 square root 5. Remember to check the solutions in the original equation. We leave that to you!» data-label=»»>

Распределите, чтобы получить уравнение в стандартной форме.
Это уравнение теперь имеет стандартную форму
Определите значения
Напишите квадратную формулу.
Затем подставьте значения .
Упрощение.
Упростите радикальное.
Умножьте общий множитель в числителе.
Удалите общие множители.
Запишите двумя решениями.
Проверить: Мы оставляем вам чек!

Решить с помощью квадратичной формулы:

Решить с помощью квадратичной формулы:

Когда мы решали линейные уравнения, если в уравнении было слишком много дробей, мы очищали дроби, умножая обе части уравнения на ЖК. Это дало нам эквивалентное уравнение — без дробей — для решения. Мы можем использовать ту же стратегию с квадратными уравнениями.

Решите с помощью квадратичной формулы:

Наш первый шаг — очистить дроби.

Simplify. u equals the quotient of the expression negative 4 plus or minus the square root of the sum 16 plus 24 divided by 6. This further simplifies to the quotient of negative 4 plus or minus square root 40 and 6. Simplify the radical. U equals the quotient of the expression negative 4 plus or minus 2 square root 10 and 6. Factor the common factor in the numerator. U equals the quotient of 2 times the expression negative 2 plus or minus square root 10 and 6. Remove the common factor yielding u equals the quotient of negative 2 plus or minus square root 10 and 3. Rewrite to show two solutions. u equals the quotient negative 2 plus square root 10 divided by 3 and u equals the quotient negative 2 minus square root 10 divided by 3 Check the solutions in the original equation. We leave that to you!» data-label=»»>

Умножьте обе части на ЖК-дисплей, 6, чтобы очистить дроби.
Умножить.
Вычтите 2, чтобы получить уравнение в стандартной форме.
Определите значения a , b и c .
Напишите квадратную формулу.
Затем замените значения на , на b и на .
Упрощение.
Упростите радикальное.
Умножьте общий множитель в числителе.
Удалите общие множители.
Перепишите, чтобы показать два решения.
Проверить: Мы оставляем вам чек!

Решите с помощью квадратичной формулы: .

Решите с помощью квадратичной формулы: .

Подумайте об уравнении ( x − 3) ² = 0. Из свойства нулевого произведения мы знаем, что это уравнение имеет только одно решение,

x = 3,

Мы увидим в следующий пример того, как использование квадратичной формулы для решения уравнения, стандартная форма которого представляет собой идеальный квадратный трехчлен, равный 0, дает только одно решение. Обратите внимание, что после упрощения подкоренной дроби оно становится равным 0, что приводит только к одному решению.

Решите с помощью квадратичной формулы:

Then substitute the values for a, b, and c. x equals the quotient of the expression the opposite of negative 20 plus or minus the square root of the difference negative 20 squared minus the product 4 times 4 times 25 divided by the product 2 times 4. Simplify. X equals the quotient of the expression 20 plus or minus the square root of the difference 400 minus 400 divided by 8. This further simplifies to the quotient of 20 plus or minus 0 and 2, so x equals 20 divided by 8 or 5 halves. We leave it to you to check the solution in the original equation.» data-label=»»>

Добавьте 25, чтобы получить уравнение в стандартной форме.
Определите значения a , b и c .
Напишите формулу квадрата.
Затем подставьте значения на , на b и на .
Упрощение.
Упростите радикальное.
Упростите дробь.
Проверить: Мы оставляем вам чек!

Знаете ли вы, что 4 x ² − 20 x + 25 — это трехчлен в виде квадрата. Это эквивалентно (2 x − 5) ² ? Если вы решите

4 x ² − 20 x + 25 = 0, разложив на множители, а затем используя свойство квадратного корня, вы получите тот же результат?

Решить с помощью квадратичной формулы:

Решить с помощью квадратичной формулы:

Использование дискриминанта для предсказания количества и типа решений квадратного уравнения

Когда мы решали квадратные уравнения в предыдущих примерах, иногда мы получали два действительных решения, одно действительное решение, а иногда два комплексных решения. Есть ли способ предсказать количество и тип решений квадратного уравнения без фактического решения уравнения?

Да, выражение под радикалом квадратной формулы позволяет нам легко определить количество и тип решений. Это выражение называется дискриминантом.

Дискриминант

Давайте посмотрим на дискриминант уравнений в некоторых примерах, а также на количество и тип решений этих квадратных уравнений.

Квадратное уравнение (в стандартной форме)	Дискриминант	Значение дискриминанта	Количество и тип растворов
		+	2 действительных
		0	1 реальный
		—	2 комплекс

Использование дискриминанта, b ² − 4 ac , для определения количества и типа решений квадратного уравнения

для квадратичного уравнения формы AX ² + BX + C = 0,

• IF B ² — 4 5555 B ² — 4 55555 B ² — 4 5555> 00012 ² — 4 5555. .
• , если b ² − 4 ac = 0, уравнение имеет 1 действительное решение.
• , если b ² − 4 ac < 0, уравнение имеет 2 комплексных решения.

Определите количество решений каждого квадратного уравнения.

ⓐⓑⓒ

Чтобы определить количество решений каждого квадратного уравнения, мы посмотрим на его дискриминант.

ⓐ

Поскольку дискриминант положительный, уравнение имеет два действительных решения.

ⓑ

Поскольку дискриминант отрицателен, уравнение имеет два комплексных решения.

ⓒ

Поскольку дискриминант равен 0, уравнение имеет 1 действительное решение.

Определите количество и тип решений каждого квадратного уравнения.

ⓐⓑⓒ

ⓐ 2 комплексных раствора; ⓑ 2 реальных решения; ⓒ 1 действительное решение

Определите количество и тип решений каждого квадратного уравнения.

ⓐⓑⓒ

ⓐ 2 действительных решения; ⓑ 2 комплексных решения; ⓒ 1 реальный раствор

Определите наиболее подходящий метод для решения квадратного уравнения

Ниже мы суммируем четыре метода, которые мы использовали для решения квадратных уравнений.

Методы решения квадратных уравнений

1. Факторинг
2. Свойство квадратного корня
3. Завершение квадрата
4. Квадратичная формула

Учитывая, что у нас есть четыре метода решения квадратного уравнения, как решить, какой из них использовать? Факторинг часто является самым быстрым методом, поэтому мы пробуем его в первую очередь. Если уравнение или мы используем свойство квадратного корня. Для любого другого уравнения, вероятно, лучше всего использовать квадратную формулу. Помните, что вы можете решить любое квадратное уравнение, используя квадратную формулу, но это не всегда самый простой метод.

Как насчет метода завершения квадрата? Большинство людей считают этот метод громоздким и предпочитают его не использовать. Нам нужно было включить его в список методов, потому что мы завершили квадрат в целом, чтобы вывести квадратную формулу. Вы также будете использовать процесс заполнения квадрата в других областях алгебры.

Определите наиболее подходящий метод решения квадратного уравнения.

1. Сначала попробуйте Факторинг . Если квадратичные факторы легко, этот метод очень быстро.
2. Далее попробуйте свойство квадратного корня . Если уравнение соответствует форме или его можно легко решить с помощью свойства Square Root.
3. Используйте квадратичную формулу . Любое другое квадратное уравнение лучше всего решать с помощью квадратной формулы.

В следующем примере эта стратегия используется, чтобы решить, как решать каждое квадратное уравнение.

Определите наиболее подходящий метод для решения каждого квадратного уравнения.

ⓐⓑⓒ

ⓐ

Поскольку уравнение находится в форме, наиболее подходящим методом является использование свойства квадратного корня.

ⓑ

Мы понимаем, что левая часть уравнения представляет собой совершенный квадратный трехчлен, поэтому наиболее подходящим методом будет факторизация.

ⓒ

Хотя нашей первой мыслью может быть попытка разложения на множители, размышления обо всех возможностях метода проб и ошибок приводят нас к выбору квадратичной формулы как наиболее подходящего метода.

Определите наиболее подходящий метод для решения каждого квадратного уравнения.

ⓐⓑⓒ

ⓐ факторинг; ⓑ Свойство квадратного корня; ⓒ Квадратная формула

Определите наиболее подходящий метод для решения каждого квадратного уравнения.

ⓐⓑⓒ

ⓐ Квадратичная формула;

ⓑ Факторинг или свойство квадратного корня ⓒ Свойство квадратного корня

Доступ к этим онлайн-ресурсам для получения дополнительных инструкций и практических занятий по использованию квадратичной формулы.

• Использование квадратичной формулы
• Решение квадратного уравнения с использованием формулы квадратного уравнения с комплексными решениями
• Дискриминант в квадратичной формуле

Ключевые понятия

• Квадратичная формула
  • Решения квадратного уравнения вида ах ² + bx + с = 0 находятся по формуле:
• Как решить квадратное уравнение с помощью квадратной формулы.
  1. Напишите квадратное уравнение в стандартной форме: x ² + bx + c = 0. Найдите значения a , b , c .
  2. Напишите квадратную формулу. Затем замените значения на , на b , на .
  3. Упростить.
  4. Проверьте решения.
• Использование дискриминанта, b ² − 4 ac , для определения количества и типа решений квадратного уравнения
  • для квадратного уравнения формы AX ² + BX + C = 0,
    • IF B ² — 4 5555.
    • , если b ² − 4 ac = 0, уравнение имеет 1 действительное решение.
    • , если b ² − 4 ac < 0, уравнение имеет 2 комплексных решения.
• Методы решения квадратных уравнений:
  • Факторинг
  • Свойство квадратного корня
  • Завершение квадрата
  • Квадратичная формула
• Как определить наиболее подходящий метод решения квадратного уравнения.
  1. Сначала попробуйте факторинг. Если квадратичные факторы легко, этот метод очень быстро.
  2. Далее попробуйте свойство квадратного корня . Если уравнение соответствует форме x ² = k или a ( x − h ) ² = k , его можно легко решить, используя свойство квадратного корня.
  3. Используйте квадратичную формулу . Любое другое квадратное уравнение лучше всего решать с помощью квадратной формулы.

Практика ведет к совершенству

Решение квадратных уравнений с помощью квадратичной формулы

В следующих упражнениях решите с помощью квадратичной формулы.

3

Используйте дискриминанту для прогнозирования числа реальных решений квадратичного уравнения

.