Асимптоты графика функции
Часто оказывается, что график функции неограниченно приближается к некоторой прямой. Такого рода прямые называются асимптотами. Неограниченность приближения графика функции к асимптоте означает, что расстояние от графика до этой прямой (перпендикуляр, опущенный из произвольной точки графика на прямую) стремится к нулю.
Различают три вида асимптот: вертикальные, горизонтальные и наклонные.
Определение 4. Прямая х = а называется вертикальной асимптотой графика функции у = f(x), если хотя бы одно из предельных значений f(x) или f(x) равно + или -.
Вертикальные асимптоты обычно сопутствуют точкам разрыва второго рода. Например, график функции у = е1/x имеет вертикальную асимптоту
Определение 5. Прямая у = kx + b называется наклонной асимптотой графика функции у = f(x) при х ±, если f(x) можно представить в виде
где α(х) 0 прих ±.
Это определение относится как к наклонной, так и к горизонтальной асимптотам: в случае горизонтальной асимптоты угловой коэффициент k в (5.9) равен нулю.
Укажем способ нахождения коэффициентов k и b в уравнении наклонной асимптоты. Разделив обе части равенства (5.9) на x и перейдя к пределу при х , получим
т.е. k = . Затем из равенства (5.9) находим:
Рассмотрим примеры: найти асимптоты графиков функций.
Пример 5. f(x)
=
.
Решение. Найдем вертикальную асимптоту. Точка x = -1 является точкой разрыва 2-го рода, причем
Затем находим наклонные асимптоты:
Таким образом, получаем уравнение наклонной асимптоты
Пример 6. f(x) = х + e-x.
Решение. Вертикальных асимптот здесь нет, поскольку точки разрыва 2-го рода отсутствуют. Отыщем наклонную асимптоту:
Таким образом, уравнение наклонной асимптоты имеет вид
Схема исследования графика функции
Приведем схему исследования поведения функции и построения ее графика.
1. Найти область определения функции.
2. Определить
возможный тип симметрии функции:
четность или нечетность функции.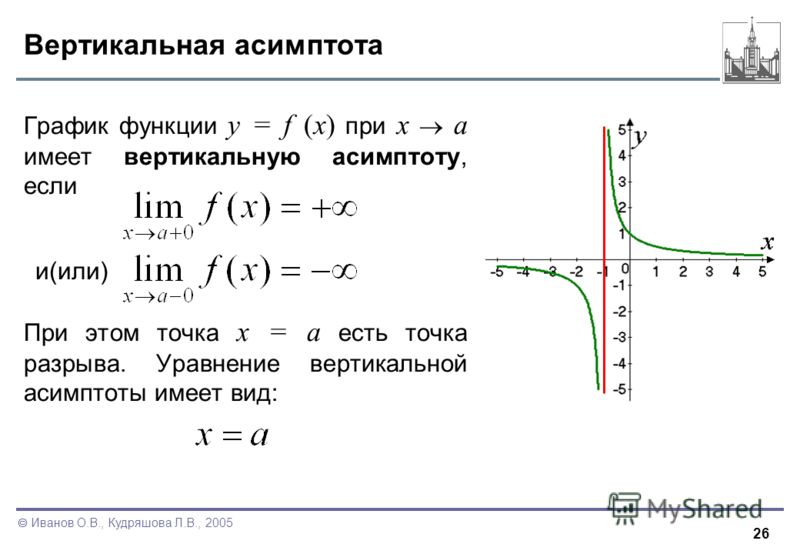
Функция f(x)
называется четной, если выполнено условие симметрии ее
графика относительно оси Оу:
Функция f(x) называется нечетной, если выполнено условие симметрии ее графика относительно начала координат O (0, 0):
При наличии симметрии достаточно построить график функции на правой координатной полуплоскости и затем отобразить его на левую половину: зеркально относительно оси Оу в случае (5.10) (рис. 5.8,а) или с центральной симметрией в случае (5.11) (рис. 5.8,6).
3. Найти точки пересечения графика функции с осями координат Ох и Оу, т.е. решить соответственно уравнения у = f(0) и f(x) = 0.
4. Найти асимптоты.
5. Найти точки возможного экстремума.
6. Найти критические
точки.
7. Исследовать знаки первой и второй производных, определить участки монотонности функции, направление выпуклости графика, точки экстремума и перегиба.
8. Определить максимум и минимум функции на области ее определения. Если областью определения функции является отрезок [а, b], необходимо вычислить значения функции в его концах и сопоставить их с локальными экстремумами.
Пример 7. Исследовать и построить график функции
Решение. Действуем по приведенной выше схеме.
1. Область определения функции: х ≠ 0 или х (-, 0) (0, ).
2. Функция (5.12) является нечетной, так как f(-x) = — f(x).
3. Уравнение f(x) = 0 дает корни х
= ±1 (точки
пересечения с осью Ох).
Пересечения с осью Оу нет в силу п.1.
4. Имеется вертикальная асимптота — ось Оу, так как предел f(x) при х 0 бесконечен:f(x) +прих 0-,f(x) -прих 0+.
Определяем наклонную асимптоту:Итак, уравнение наклонной асимптоты: у = х.
5. f'(x) = , т.е. производная нигде не равна нулю и точек возможного экстремума нет. В области определения везде f‘(x) положительна.
6. f»(x) = —2/х3 — критических точек нет.
7. Функция (5.12)
монотонно возрастает на всей области
своего определения, так как ее производная
всюду положительна. В левой координатной
полуплоскости выпуклость графика
функции направлена вниз (f«(x)
> 0), в правой полуплоскости выпуклость
направлена вверх (f»(x) < 0).
8. Наибольшего и наименьшего значений функции не существует, поскольку область ее значений неограничена.
9. График функции (5.12) приведен на рис. 5.9.
Объяснение урока: Горизонтальные и вертикальные асимптоты функции
В этом объяснении мы научимся находить горизонтальные и вертикальные асимптоты функции.
Прежде чем мы подробно рассмотрим, как найти асимптоту рациональной функции, давайте вспомним что такое асимптота.
Определение: Асимптота
Асимптота – это линия, которая сколь угодно близко подходит к заданной кривой. Это проиллюстрировано графиком 𝑦=1𝑥.
Здесь асимптотами являются линии 𝑥=0 и 𝑦=0.
Чтобы идентифицировать вертикальные асимптоты функции, нам нужно идентифицировать любой вход, который
не имеет определенного выхода, а также часто можно идентифицировать горизонтальные асимптоты
путем рассмотрения выходных данных, которые не могут быть получены ни на одном входе в области определения функции.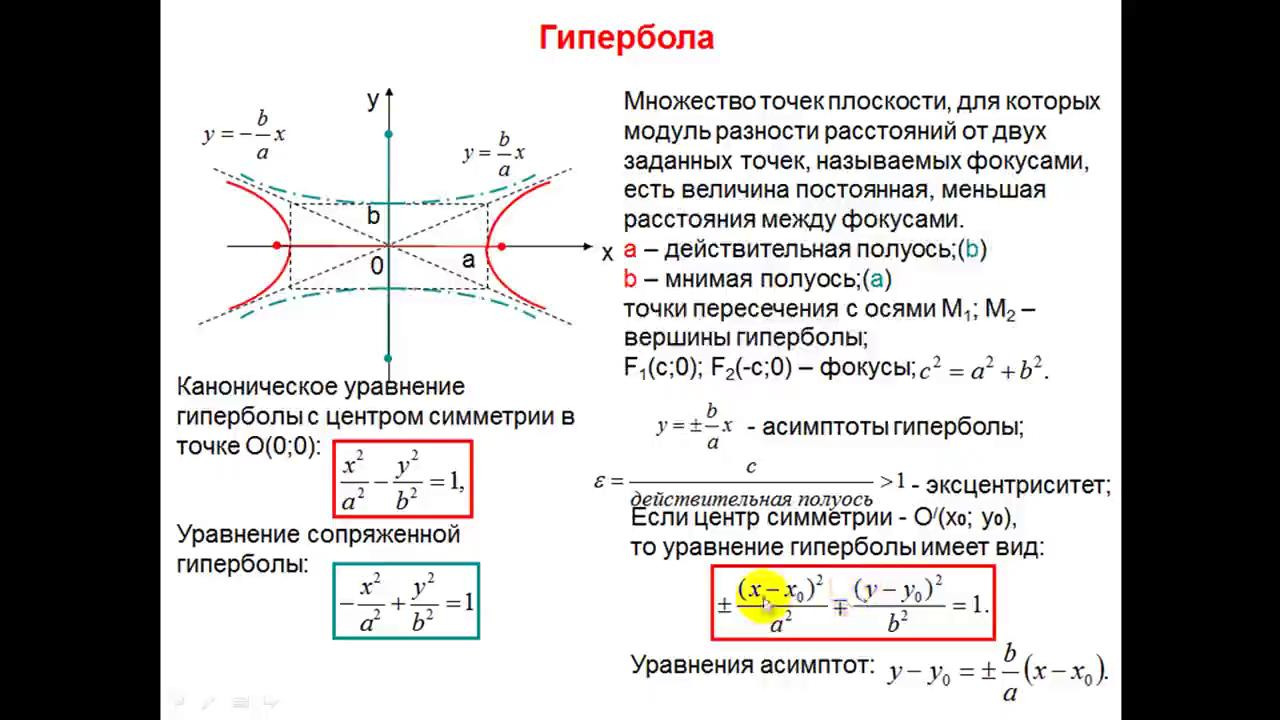
В
В частности, для рациональных функций знание области определения и диапазона поможет нам определить
асимптота и наоборот. Поэтому, если мы хотим найти асимптоты
рациональной функции, мы применяем очень похожий подход к тому, как мы определяем область и диапазон
рациональная функция.
Если мы рассмотрим функцию 𝑦=33−𝑥,
, нам нужно найти, есть ли у нее какие-либо неопределенные входные данные и, в равной степени, какие-либо значения, не существующие в его диапазон. Мы знаем, что рациональная функция не определена, если ее знаменатель равен нулю. Здесь, 3−𝑥 равно нулю, когда 𝑥=3.
Таким образом, это уравнение асимптоты. Есть ли другие? Ну а если рассматривать
все возможные выходы функции и рассмотрим, что происходит, когда входы получают
прогрессивно увеличиваясь, мы можем видеть, что выходы функции становятся все ближе и ближе к нулю
но никогда не может туда добраться. Следовательно, мы имеем другую асимптоту при
𝑦=0.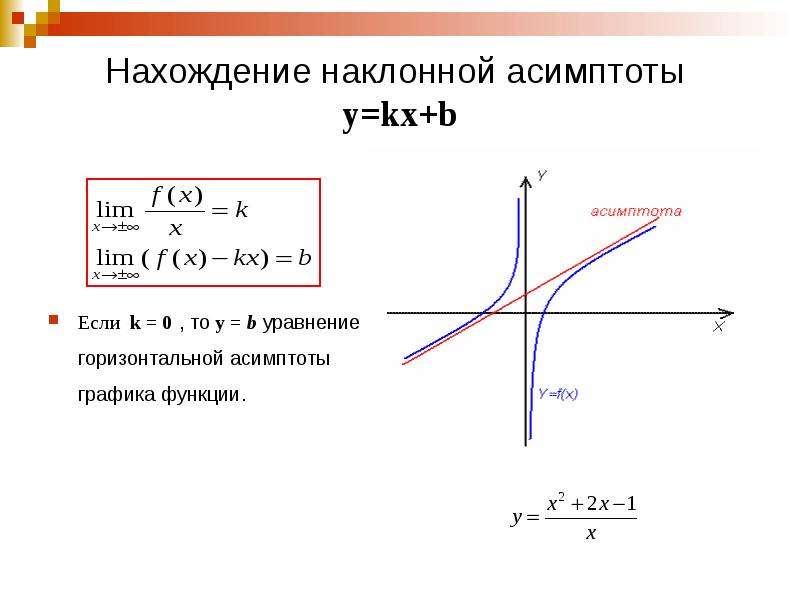
Идентифицируя асимптоты рациональной функции, мы можем легко определить область определения и диапазон. Функция имеет область определения, состоящую из всех действительных чисел, кроме 3, и диапазон, это все действительные числа, кроме 0.
Давайте теперь рассмотрим пару примеров.
Пример 1. Определение асимптот рациональных функций
Определение вертикальной и горизонтальной асимптот функции 𝑓(𝑥)=−1+3𝑥−4𝑥.
Ответ
Чтобы найти вертикальные асимптоты функции, нам нужно определить, существует ли ввод, который приводит к неопределенным результатам. Функция 𝑓(𝑥) содержит два рациональных выражения, которые не определены, когда их знаменатели равны нулю. выражение 3𝑥 не определено, когда 𝑥=0, а выражение −4𝑥, опять же, не определено, когда 𝑥=0. Следовательно, мы имеем вертикальную асимптоту с уравнением 𝑥=0.
Чтобы найти горизонтальные асимптоты, нам нужно найти, есть ли значения, которые не
существуют в диапазоне функции.
Если мы посмотрим на выходы функции как на
входные данные становятся все больше, мы можем видеть, что выражения
3𝑥 и −4𝑥 все ближе и ближе
к нулю, и функция становится все ближе и ближе к −1, но на самом деле никогда
достичь этого значения. Таким образом, мы имеем горизонтальную асимптоту с уравнением
𝑦=−1.
Прежде чем мы рассмотрим следующий пример, стоит отметить, что гипербола — это тип рационального функция с двумя асимптотами.
Пример 2. Определение асимптот рациональных функций
Каковы две асимптоты гиперболы 𝑦=84𝑥−3+53?
Ответ
Чтобы найти вертикальные асимптоты функции, нужно определить, существует ли
ввод, который приводит к неопределенным результатам. Функция содержит рациональное выражение
это не определено, когда его знаменатель равен нулю. Выражение не определено, когда
4𝑥−3=0 и, следовательно, имеет асимптоту с уравнением
𝑥=34.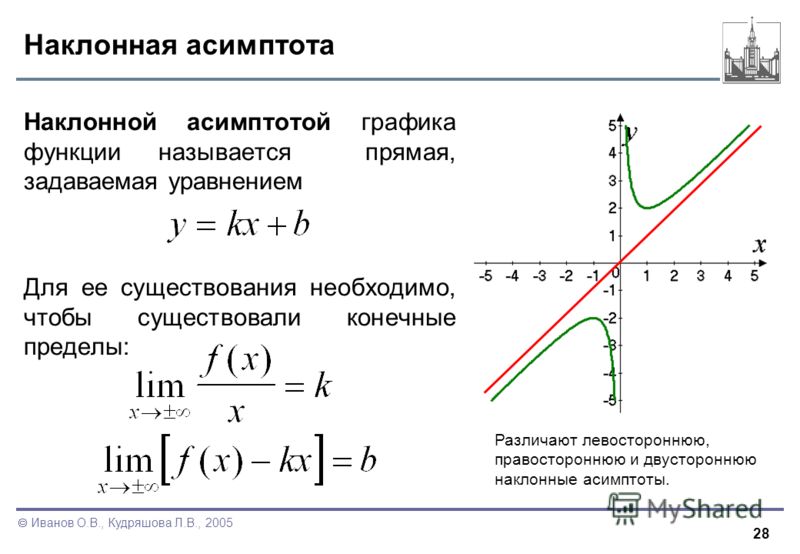
Чтобы найти горизонтальные асимптоты, нам нужно найти, есть ли значения, которые не существуют в диапазоне функции. Если мы посмотрим на выходы функции как на входные данные становятся все больше, мы можем видеть, что выражение 84𝑥−3 все ближе и ближе к нулю, а значение функция становится все ближе и ближе к 53, но на самом деле никогда не будет достичь этого значения. Таким образом, мы имеем горизонтальную асимптоту с уравнением 𝑦=53.
Как упоминалось ранее, если мы идентифицируем асимптоты рациональной функции, мы можем использовать эту информацию, чтобы легко найти домен и диапазон функции, и, в равной степени, мы можем использовать информация об асимптотах, чтобы помочь нам нарисовать или идентифицировать график функции. Давайте теперь посмотрим на примеры этого.
Пример 3. Использование асимптот рациональной функции для нахождения ее области определения и области значений
Определение области определения и области значений функции 𝑓(𝑥)=1𝑥−5
в ℝ.
Ответ
В этом вопросе нам повезло получить график рациональной функции. Это позволяет нам легко идентифицировать уравнения асимптот: мы можем видеть, что уравнение вертикальной асимптоты равно 𝑥=0, а уравнение горизонтальной асимптота равна 𝑦=−5. Используя эту информацию, мы можем констатировать, что домен функции ℝ−{0} и что диапазон функция ℝ−{−5}.
Предположим, нам не дан график функции. Мы могли бы определить асимптоты по
поиск любых входных данных, которые приводят к неопределенным выходным данным, и поиск любых выходных данных, которые
не может быть достигнуто независимо от ввода. Здесь мы видим, что у нас есть неопределенное
вывод для ввода нуля как 10 не определен. Следовательно, у нас есть
асимптота с уравнением 𝑥=0. Мы также можем видеть, что когда 𝑥 получает
прогрессивно большие выходы функции становятся все ближе и ближе к
−5, но никогда не может принимать это значение.
Следовательно, мы также имеем асимптоту
с уравнением 𝑦=−5.
Пример 4. Нахождение асимптот функции для определения ее графика
Какой из следующих графиков представляет 𝑓(𝑥)=1𝑥+1?
Ответ
В этом вопросе мы можем определить график рациональной функции, определив положение его асимптот. Если мы посмотрим на уравнение функции, мы можем определить любую вертикальную асимптоту, идентифицируя любые входные данные, которые приводят к неопределенным выходным данным. функция не определена, когда знаменатель равен нулю, т. е. когда 𝑥+1=0. Следовательно, мы имеем асимптоту с уравнением 𝑥=−1.
Чтобы найти горизонтальные асимптоты, нам нужно найти, есть ли значения, которые не
существуют в диапазоне функции. По мере того, как входные данные становятся все больше, мы можем видеть, что
функция 1𝑥+1 все ближе и ближе к нулю, но она будет
никогда на самом деле не достичь этого значения.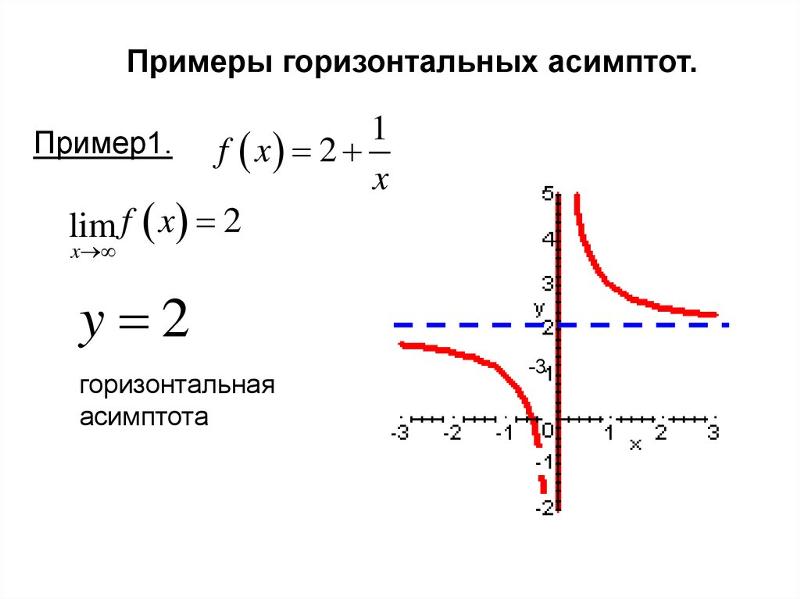
Таким образом, мы имеем горизонтальную асимптоту с уравнением
𝑦=0.
Используя эту информацию, мы видим, что правильный график (c).
Пример 5. Определение области определения рациональной функции
Найти домен функции 𝑓(𝑥)=𝑥−36𝑥𝑥+6𝑥.
Ответ
Это особенно интересный вопрос, так как не сразу понятно, как график совпадает с функцией. С таким вопросом очень легко ошибочно указывают домен и диапазон и в равной степени делают предположения о природе функции, включая наличие у нее асимптот.
Если мы разложим числитель и знаменатель функции, мы получим, что 𝑓(𝑥)=𝑥(𝑥+6)(𝑥−6)𝑥(𝑥+6).
На данный момент мы видим, что функция не определена в двух точках: 𝑥=0 и
𝑥=−6. Если вы введете любое из этих значений, вы получите 00, что не является
определенный. Используя то, что мы знаем о рациональных функциях, было бы справедливо предположить, что
поэтому функция имеет асимптоты в этих двух точках.
Однако это не так. При условии, что 𝑥 не равно 0 или −6, мы можем упростить нашу функцию следующим образом:
𝑓(𝑥)=𝑥(𝑥+6)(𝑥−6)𝑥(𝑥+6),
, что упрощается до 𝑓(𝑥)=𝑥−6.
Это показывает нам, что для всех значений 𝑥, кроме 0 и −6, функция упрощается. к линии. На этом этапе мы можем определить, что область определения функции равна ℝ−{−6,0}.
Распространенная ошибка здесь состоит в том, чтобы сначала упростить функцию, а затем указать, что домен это целые действительные числа, но это не так.
Обратите внимание, что в этом примере область определения функции не говорит нам об асимптотах функции. На самом деле функция не имеет ни вертикальных, ни горизонтальных асимптот. Это будет случай, когда у нас есть рациональные функции, определяемые выражением, которое можно упростить с помощью сокращая общие множители в числителе и знаменателе.
Ключевые точки
- Чтобы найти вертикальные асимптоты функции, нам нужно определить любую точку, которая приведет к знаменателю
нуля, но будьте осторожны, если функция упрощается — как в последнем примере.
- Чтобы найти горизонтальные асимптоты рациональной функции, нам нужно определить любое значение, которое функция не может брать. Часто бывает полезно взглянуть на пределы функции, чтобы помочь вам в этом процессе.
- Мы можем использовать асимптоты, чтобы определить диапазон и область определения функции.
- Мы можем использовать асимптоты, чтобы набросать или идентифицировать график функции.
Асимптоты — Алгебра II
Все ресурсы по Алгебре II
10 Диагностических тестов 630 практических тестов Вопрос дня Карточки Learn by Concept
Помощь по алгебре II » Математические отношения и основные графики » Экспоненты » Решение экспоненциальных уравнений и построение графиков » Асимптоты
Какова горизонтальная асимптота графика уравнения ?
Возможные ответы:
Правильный ответ:
Объяснение:
Асимптоту этого уравнения можно найти, заметив, что независимо от .
Таким образом, мы находим значение as, приближающееся к нулю.
Таким образом, значение, которое не может быть больше, равно , а линия – это асимптота.
Сообщить об ошибке
Что такое асимптота(ы) графика функции
?
Возможные ответы:
Правильный ответ:
Пояснение:
Показательное уравнение вида имеет только одну асимптоту — горизонтальную при . В заданной функции , значит, есть ее единственная асимптота.
Сообщить об ошибке
Найдите вертикальную асимптоту уравнения.
Вертикальные асимптоты отсутствуют.
Правильный ответ:
Пояснение:
Чтобы найти вертикальные асимптоты, приравняем знаменатель функции к нулю и решим.
Сообщить об ошибке
Определите асимптоты, если они есть:
Возможные ответы:
Правильный ответ:
Объяснение:
Разложить на множители числитель и знаменатель.
Обратите внимание, что один из биномов отменяется.
Область определения этого уравнения не может включать .
Упрощенное уравнение:
Поскольку член отменен, член будет иметь дыру вместо асимптоты.
Установить знаменатель равным нулю.
Вычесть единицу с обеих сторон.
Асимптота будет только:
Ответ:
Сообщить об ошибке
Какой из вариантов представляет асимптоту(ы), если они есть?
Возможные ответы:
Правильный ответ:
Пояснение:
Разложите числитель и знаменатель на множители.
Обратите внимание, что условия будут отменены. Отверстие будет расположено в потому что это устранимый разрыв.
Знаменатель не может быть равен нулю. Установите знаменатель, чтобы найти место, где переменная x не может существовать.
Асимптота находится в .
Сообщить об ошибке
Где находится асимптота, если она есть?
Возможные ответы:
Правильный ответ:
Пояснение:
Разложите числитель и знаменатель на множители.
Перепишите уравнение.
Обратите внимание, что отмена. Это означает, что корень будет дырой, а не асимптотой.
Приравняйте знаменатель к нулю и найдите x.
Асимптота находится по адресу:
Ответ:
Сообщить об ошибке
Рассмотрим экспоненциальную функцию .