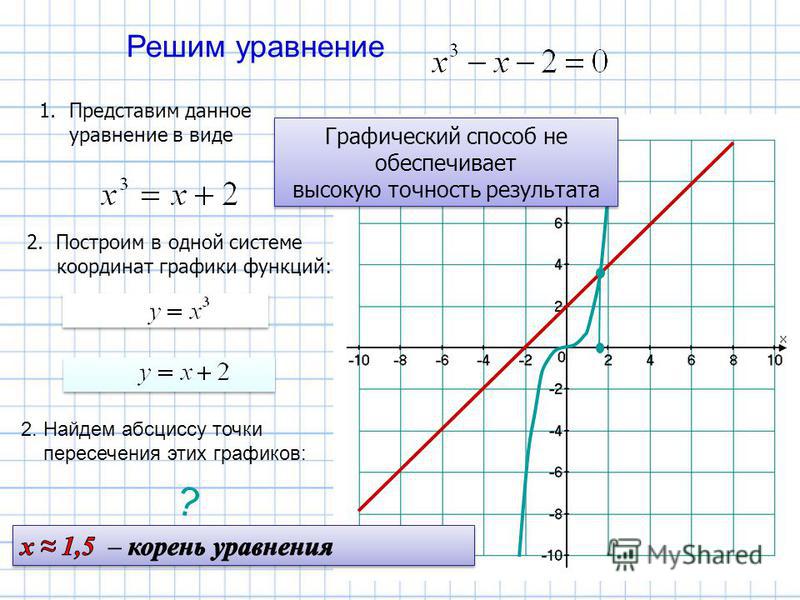
П.1.3. Функциональное уравнение логарифмической функции
Все непрерывные решения функционального уравнения
f (xy) = f(x) + f(y), (6)
справедливого для всех положительных значений x и y, имеют вид
f(x) = loga x (a > 0, a 1).
Докажем это. Для этого введём новую переменную ξ, изменяющуюся в промежутке (-; +), и положим
x = eξ (ведь x > 0), φ(ξ) = f(eξ),
откуда
ξ = lnx, f(x) = φ(lnx).
Тогда функция φ удовлетворяет функциональному уравнению (4):
а потому
и f(x)
= clnx.
Если исключить случай c = 0 (тогда f(x) 0), то полученный результат может быть написан в виде
f(x) = logax, a = e1/c.
П.1.4. Функциональное уравнение степенной функции
Функциональному уравнению
f(xy) = f(x)·f(y) (x > 0, y > 0) (7)
удовлетворяют в классе непрерывных функций только функции вида
f(x) = xa.
Прибегая к той же подстановке, что и в п. 1.3, мы приведём уравнение (7) к уравнению (4):
,
откуда
φ(ξ) = cξ (c >0), и, значит, f(x) =
clnx = xa (a = lnc).
Метод последовательного анализа можно применить к решению других уравнений.
Пример 1. Функция f определена и непрерывна на множестве R, f(1) = 1 и для любых действительных x и y
Чему равно f(x)?
Решение. Из данного равенства при x = y = 0 получаем, что f(0) = 0, а при y = 0 имеем f(x) = f(|x|), так что функция f чётная и достаточно рассматривать только положительные значения аргумента.
По индукции легко получить равенство
;
в самом деле, по предположению индукции
Положив в доказанном равенстве
,
будем иметь
,
т. е.
е.
.
Если теперь – положительное рациональное число, то
,
если же x — иррациональное число, то x является пределом последовательности рациональных чисел, , и в силу непрерывностиf будем иметь
П.1.5. Одно обобщение уравнения Коши.
Пусть n — фиксированное натуральное число. Рассмотрим функциональное уравнение
(1.11)
где D (f) = R. При n = 1 оно обращается в уравнение Коши. Как было показано, в классе непрерывных функций единственным решением уравнения Коши является линейная однородная функция. Из результатов Гамеля следует, что и разрывные функции могут удовлетворять уравнению Коши. Покажем, что решение уравнения (1.11) при n > 1 является непрерывной функцией.
Полагая х
= у = 0,
получим f (0) = 0.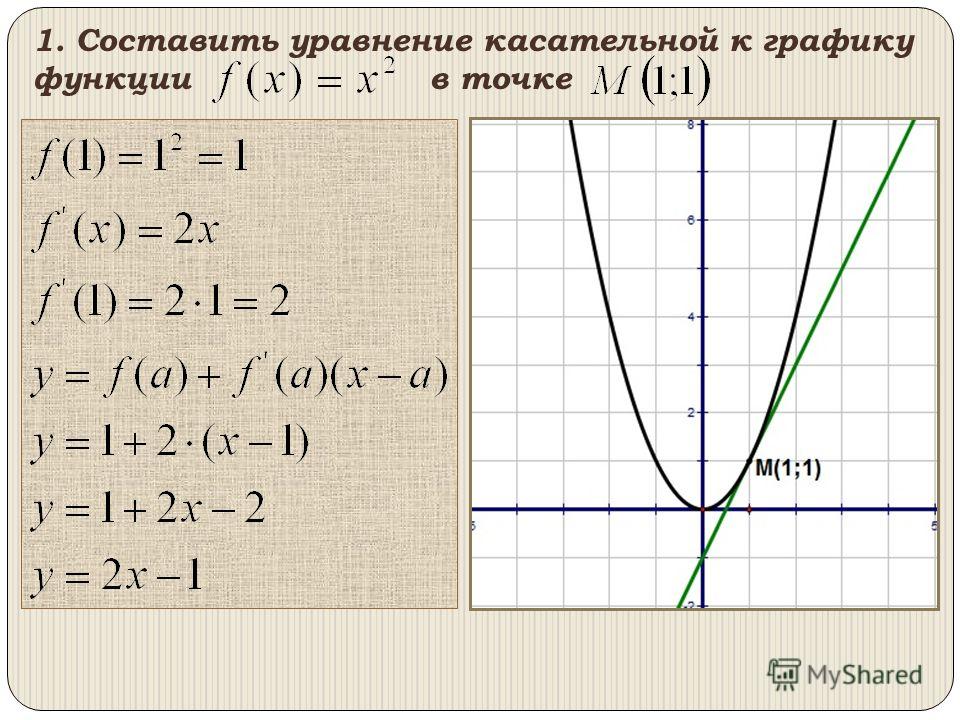 Поэтому
при х = 0 из (1.11) имеем f(уn)
= (f(y))n для всех у
R. Каждое неотрицательное число z может
быть записано в видеz
= уn.
Отсюда
Поэтому
при х = 0 из (1.11) имеем f(уn)
= (f(y))n для всех у
R. Каждое неотрицательное число z может
быть записано в видеz
= уn.
Отсюда
В частности, при х = -z
т. е. f(-z) = — f (z), z R. Если , то
Отсюда следует что f(х + w) = f(х) + f(w) для всех х R,w R, т. е.f(х) — аддитивная функция. Для аддитивной функции при рациональных
(1.12)
Воспользовавшись формулой Ньютона
,
и аддитивностью f(x), преобразуем отдельно левую и правую части (1.12) при рациональных t:
;
Правые части
последних двух равенств представляют
собой многочлены от t. Приравнивая коэффициенты при одинаковых
степенях t,
получим
Приравнивая коэффициенты при одинаковых
степенях t,
получим
, .
В частности, для k = 2 имеем
. (1.13)
Если (f(1))n-2 > 0, то f(x) — неубывающая функция. Действительно,
всякое у >
0 представимо
в виде у =
х2,
поэтому из (1.13) имеем f(у)
= f(x2)
≥ 0. При х1 > x2, х1 – x2>
0, f(x1 – x2)
≥ 0, или, в
силу аддитивности f(х), f (x1)
– f (х2) ≥ 0. Если
же (f(1))n -2 < 0,
аналогично доказывается, что функция f(х) — невозрастающая.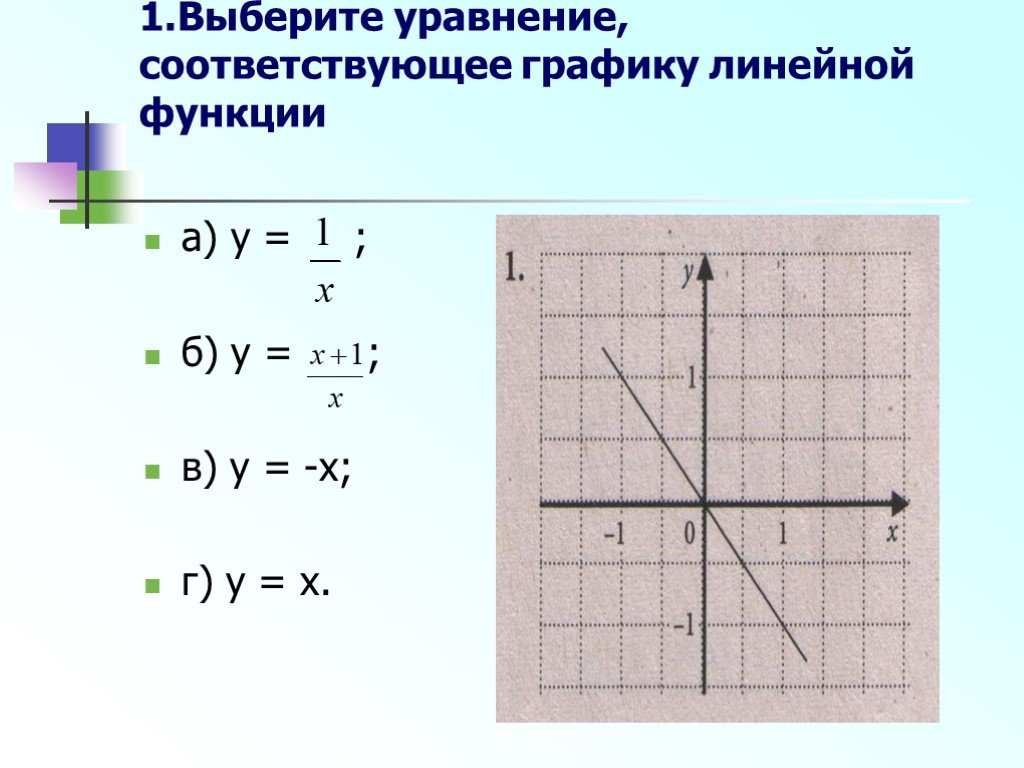
Ранее было доказано, что если аддитивная функция монотонна, то она имеет вид f(х) = ах.
Итак, f (х) = х либо f(х) = 0 при четных n; f (x) = х, либо f (х) = -х, либо f(х) = 0 при нечетных n > 1.
Тем самым доказана не только непрерывность решения уравнения (1.11) при n > 1, но и получен его вид.
«Необычные» функции/уравнения : Свободный полёт
Сообщения без ответов | Активные темы | Избранное
| LebedKun |
| ||
12/10/13 |
| ||
| |||
| Aritaborian |
| |
11/06/12 | ||
| ||
| Deggial |
| |||||||
20/11/12 |
| |||||||
| ||||||||
| Aritaborian |
| ||
11/06/12 |
| ||
| |||
| arseniiv |
| |||
27/04/09 |
| |||
| ||||
| Urnwestek |
| ||
03/10/13 |
| ||
| |||
| Aritaborian |
| ||
11/06/12 |
| ||
| |||
| arseniiv |
| |||
27/04/09 |
| |||
| ||||
| Aritaborian |
| ||
11/06/12 |
| ||
| |||
| arseniiv |
| |||
27/04/09 |
| |||
| ||||
| Cash |
| |||
12/09/10 |
| |||
| ||||
| Droog_Andrey |
| |||
09/02/09 |
| |||
| ||||
| Показать сообщения за: Все сообщения1 день7 дней2 недели1 месяц3 месяца6 месяцев1 год Поле сортировки АвторВремя размещенияЗаголовокпо возрастаниюпо убыванию |
| Страница 1 из 1 | [ Сообщений: 12 ] |
Модератор: Модераторы
Кто сейчас на конференции |
Сейчас этот форум просматривают: нет зарегистрированных пользователей |
| Вы не можете начинать темы Вы не можете отвечать на сообщения Вы не можете редактировать свои сообщения Вы не можете удалять свои сообщения Вы не можете добавлять вложения |
| Найти: |
Пересмотр полезности уравнений прогнозирования функции легких в зависимости от расы
. 2022 1 апреля; 205 (7): 819-829.
2022 1 апреля; 205 (7): 819-829.
doi: 10.1164/rccm.202105-1246OC.
Аарон Д. Боуг 1 , Стивен Шибоски 1 , Надя Н. Гензель 2 , Виктор Ортега 3 , Игорь Барьяктаревич 4 , Р. Грэм Барр 5 , Рассел Боулер 6 , Алехандро П. Комельяс 7 , Кристофер Б Купер 2 , Дэвид Купер 8 , Джерард Крайнер 9 , Джеффри Л. Кертис 10
11 , Марк Дрансфилд 12 , Чинеду Эджике 2 , МэйЛан К Хан 10 , Эрик Хоффман 7 , Джамуна Кришнан 13 , Джерри Кришнан 14 , Дэвид Маннино 15 , Роберт Пейн 3-й 16 , Триша Парех 12 , Стивен Питерс 3 , Нирупама Путча 2 , Стивен Реннард 17 , Нита Тхакур 1 , Прескотт Г. Вудрафф 1
Вудрафф 1
Принадлежности
- 1 Калифорнийский университет Сан-Франциско, Сан-Франциско, Калифорния.
- 2 Университет Джона Хопкинса, Балтимор, Мэриленд.
- 3 Медицинская школа Уэйк Форест, Уинстон-Сейлем, Северная Каролина.
- 4 Медицинская школа Дэвида Геффена Калифорнийского университета в Лос-Анджелесе, Лос-Анджелес, Калифорния.
- 5 Медицинский центр Колумбийского университета, Колумбийский университет, Нью-Йорк, Нью-Йорк.
- 6 Национальное еврейское здравоохранение, Денвер, Колорадо.

- 7 Медицинский колледж Карвера, Университет Айовы, Айова-Сити, Айова.
- 8 Департамент биостатистики, Университет Северной Каролины, Чапел-Хилл, Северная Каролина.
- 9 Медицинская школа Льюиса Каца, Университет Темпл, Филадельфия, Пенсильвания.
- 10 Мичиганский университет, Анн-Арбор, Мичиган.
- 11 Управление по делам ветеранов Система здравоохранения Анн-Арбор, Анн-Арбор, Мичиган.
- 12 Университет Алабамы, Бирмингем, Алабама.
- 13 Weill Cornell Medicine, Нью-Йорк, Нью-Йорк.

- 14 Университет Иллинойса в Чикаго, Чикаго, Иллинойс.
- 15 Университет Кентукки, Лексингтон, Кентукки.
- 16 Университет Юты, Солт-Лейк-Сити, Юта; и.
- 17 Университет Небраски, Омаха, Небраска.
- PMID: 34913855
- DOI: 10.1164/rccm.202105-1246OC
Аарон Д. Боуг и др.
Am J Respir Crit Care Med. .
. 2022 1 апреля; 205 (7): 819-829.
doi: 10.1164/rccm.202105-1246OC.
Авторы
Аарон Д. Боуг 1 , Стивен Шибоски 1 , Надя Н. Гензель 2 , Виктор Ортега 3 , Игорь Барьяктаревич 4 , Р. Грэм Барр 5 , Рассел Боулер 6 , Алехандро П. Комельяс 7 , Кристофер Б Купер 2 , Дэвид Купер 8 , Джерард Крайнер 9 , Джеффри Л. Кертис 10
11 , Марк Дрансфилд 12 , Чинеду Эджике 2 , МэйЛан К Хан 10 , Эрик Хоффман 7 , Джамуна Кришнан 13 , Джерри Кришнан 14 , Дэвид Маннино 15 , Роберт Пейн 3-й 16 , Триша Парех 12 , Стивен Питерс 3 , Нирупама Путча 2 , Стивен Реннард 17 , Нита Тхакур 1 , Прескотт Г. Вудрафф 1
Вудрафф 1
Принадлежности
- 1 Калифорнийский университет Сан-Франциско, Сан-Франциско, Калифорния.
- 2 Университет Джона Хопкинса, Балтимор, Мэриленд.
- 3 Медицинская школа Уэйк Форест, Уинстон-Сейлем, Северная Каролина.
- 4 Медицинская школа Дэвида Геффена Калифорнийского университета в Лос-Анджелесе, Лос-Анджелес, Калифорния.
- 5 Медицинский центр Колумбийского университета, Колумбийский университет, Нью-Йорк, Нью-Йорк.
- 6 Национальное еврейское здравоохранение, Денвер, Колорадо.

- 7 Медицинский колледж Карвера, Университет Айовы, Айова-Сити, Айова.
- 8 Департамент биостатистики, Университет Северной Каролины, Чапел-Хилл, Северная Каролина.
- 9 Медицинская школа Льюиса Каца, Университет Темпл, Филадельфия, Пенсильвания.
- 10 Мичиганский университет, Анн-Арбор, Мичиган.
- 11 Управление по делам ветеранов Система здравоохранения Анн-Арбор, Анн-Арбор, Мичиган.
- 12 Университет Алабамы, Бирмингем, Алабама.
- 13 Weill Cornell Medicine, Нью-Йорк, Нью-Йорк.

- 14 Университет Иллинойса в Чикаго, Чикаго, Иллинойс.
- 15 Университет Кентукки, Лексингтон, Кентукки.
- 16 Университет Юты, Солт-Лейк-Сити, Юта; и.
- 17 Университет Небраски, Омаха, Небраска.
- PMID: 34913855
- DOI: 10.1164/rccm.202105-1246OC
Абстрактный
Обоснование: афроамериканцев имеют худшие результаты при хронической обструктивной болезни легких (ХОБЛ). Цели: Оценить, способствуют ли расовые подходы к оценке функции легких расовому неравенству, поскольку они не могут распознать патологические декременты и считать их нормальными. Методы: В когорте с ХОБЛ и с риском развития ХОБЛ мы оценили, лучше ли моделируют взаимосвязь между ОФВ 9 уравнения прогнозирования функции легких, применяемые в расовой или универсальной манере.0295 1 , ФЖЕЛ и другие исходы ХОБЛ, включая оценочный тест ХОБЛ, респираторный опросник Святого Георгия, процент эмфиземы при компьютерной томографии, толщину стенки дыхательных путей и тест 6-минутной ходьбы. Мы связали эти результаты с различиями в ОФВ 1 , используя множественную линейную регрессию, и сравнили прогностическую эффективность между подобранными моделями, используя среднеквадратичную ошибку и парный тест Алпайдина F . Измерения и основные результаты: Используя расовые уравнения, было подсчитано, что у афроамериканцев функция легких лучше, чем у неиспаноязычных белых людей (ОФВ 1 , 76,8% против прогнозируемых 71,8%; P = 0,02).
Цели: Оценить, способствуют ли расовые подходы к оценке функции легких расовому неравенству, поскольку они не могут распознать патологические декременты и считать их нормальными. Методы: В когорте с ХОБЛ и с риском развития ХОБЛ мы оценили, лучше ли моделируют взаимосвязь между ОФВ 9 уравнения прогнозирования функции легких, применяемые в расовой или универсальной манере.0295 1 , ФЖЕЛ и другие исходы ХОБЛ, включая оценочный тест ХОБЛ, респираторный опросник Святого Георгия, процент эмфиземы при компьютерной томографии, толщину стенки дыхательных путей и тест 6-минутной ходьбы. Мы связали эти результаты с различиями в ОФВ 1 , используя множественную линейную регрессию, и сравнили прогностическую эффективность между подобранными моделями, используя среднеквадратичную ошибку и парный тест Алпайдина F . Измерения и основные результаты: Используя расовые уравнения, было подсчитано, что у афроамериканцев функция легких лучше, чем у неиспаноязычных белых людей (ОФВ 1 , 76,8% против прогнозируемых 71,8%; P = 0,02). Используя универсально применяемые уравнения, было подсчитано, что у афроамериканцев функция легких хуже. Используя уравнение Ханкинсона для неиспаноязычных белых, ОФВ 1 составил 64,7% по сравнению с 71,8% ( P <0,001). Используя уравнение другой расы Global Lung Initiative, FEV 1 составил 70,0% по сравнению с 77,9% ( P < 0,001). Ошибки прогнозирования линейной регрессии были меньше для универсальных уравнений по сравнению с уравнениями для конкретных рас при изучении ОФВ9.0295 1 % предсказано с помощью оценочного теста ХОБЛ ( P < 0,01), респираторного опросника Св. Георгия ( P < 0,01) и толщины стенки дыхательных путей ( P < 0,01). Хотя у афроамериканских участников были более тяжелые последствия ( P < 0,001), меньшие неблагоприятные условия были связаны только с лучшим ОФВ 1 у неиспаноязычных белых участников ( P для взаимодействия = 0,041). Выводы: Уравнения для конкретных рас могут недооценивать тяжесть ХОБЛ у афроамериканцев.
Используя универсально применяемые уравнения, было подсчитано, что у афроамериканцев функция легких хуже. Используя уравнение Ханкинсона для неиспаноязычных белых, ОФВ 1 составил 64,7% по сравнению с 71,8% ( P <0,001). Используя уравнение другой расы Global Lung Initiative, FEV 1 составил 70,0% по сравнению с 77,9% ( P < 0,001). Ошибки прогнозирования линейной регрессии были меньше для универсальных уравнений по сравнению с уравнениями для конкретных рас при изучении ОФВ9.0295 1 % предсказано с помощью оценочного теста ХОБЛ ( P < 0,01), респираторного опросника Св. Георгия ( P < 0,01) и толщины стенки дыхательных путей ( P < 0,01). Хотя у афроамериканских участников были более тяжелые последствия ( P < 0,001), меньшие неблагоприятные условия были связаны только с лучшим ОФВ 1 у неиспаноязычных белых участников ( P для взаимодействия = 0,041). Выводы: Уравнения для конкретных рас могут недооценивать тяжесть ХОБЛ у афроамериканцев. Клиническое исследование, зарегистрированное на сайте www.clinicaltrials.gov (NCT019).69344).
Клиническое исследование, зарегистрированное на сайте www.clinicaltrials.gov (NCT019).69344).
Ключевые слова: хроническая обструктивная болезнь легких; различия в состоянии здоровья; расизм; тесты функции дыхания.
Похожие статьи
Генотип альфа-1-антитрипсина PiMZ связан с хронической обструктивной болезнью легких в двух расовых группах.
Форман М.Г., Уилсон С., ДеМео Д.Л., Херш С.П., Бити Т.Х., Чо М.Х., Зинити Дж., Карран-Эверетт Д., Крайнер Г., Хокансон Д.Е., Брантли М., Рухани Ф.Н., Сандхаус Р.А., Крапо Д.Д., Сильверман Э.К.; Генетическая эпидемиология ХОБЛ (COPDGene) Исследователи *. Форман М.Г. и соавт. Энн Ам Торак Соц. 2017 авг;14(8):1280-1287. doi: 10.1513/AnnalsATS.201611-838OC. Энн Ам Торак Соц. 2017. PMID: 28380308 Бесплатная статья ЧВК.

Различия между абсолютными и прогнозируемыми значениями объемов форсированного выдоха для классификации вентиляционных нарушений при хронической обструктивной болезни легких.
Checkley W, Foreman MG, Bhatt SP, Dransfield MT, Han M, Hanania NA, Hansel NN, Regan EA, Wise RA; Исследователи исследования COPDGene. Чекли В. и др. Респир Мед. 2016 Февраль; 111:30-8. doi: 10.1016/j.rmed.2015.11.004. Epub 2015 11 ноября. Респир Мед. 2016. PMID: 26712569Бесплатная статья ЧВК.
Новая стратегия оценки ответа на бронхорасширяющие средства идентифицирует отдельные группы пациентов.
Хансен Дж. Э., Дилектасли А. Г., Поршас Дж., Стрингер В. В., Пак Ю., Росситер Х. Б., Касабури Р. Хансен Дж. Э. и соавт. Энн Ам Торак Соц.
 2019 декабря; 16 (12): 1504-1517. doi: 10.1513/AnnalsATS.201901-030OC.
Энн Ам Торак Соц. 2019.
PMID: 31404502
Бесплатная статья ЧВК.
2019 декабря; 16 (12): 1504-1517. doi: 10.1513/AnnalsATS.201901-030OC.
Энн Ам Торак Соц. 2019.
PMID: 31404502
Бесплатная статья ЧВК.Относительный вклад эмфиземы и ремоделирования дыхательных путей в ограничение воздушного потока при ХОБЛ: согласованные результаты двух когорт.
Тхо Н.В., Рюджин Ю., Огава Э., Транг ле Т.Х., Канда Р., Гото К., Ямагути М., Нагао Т., Лан ле Т.Т., Накано Ю. Тхо Н.В. и соавт. Респирология. 2015 май; 20(4):594-601. doi: 10.1111/соответственно 12505. Epub 2015 18 марта. Респирология. 2015. PMID: 25788016
Комбинированный объем форсированного выдоха за 1 секунду и форсированная жизненная емкость легких, ответ на бронхорасширяющее средство, обострения и смертность при хронической обструктивной болезни легких.

Fortis S, Comellas A, Make BJ, Hersh CP, Bodduluri S, Georgopoulos D, Kim V, Criner GJ, Dransfield MT, Bhatt SP; Исследователи COPDGene – основные подразделения:
Административный центр , Исследователи COPDGene – клинические центры:Анн-Арбор, Вирджиния . Фортис С. и др. Энн Ам Торак Соц. 2019Июль; 16 (7): 826-835. doi: 10.1513/AnnalsATS.201809-601OC. Энн Ам Торак Соц. 2019. PMID: 30908927 Бесплатная статья ЧВК.
Посмотреть все похожие статьи
Цитируется
Исследуйте референтные значения для расы и нарушения функции легких, одышку и прогноз: анализ NHANES 2007-2012.
Экстрем М., Маннино Д. Экстрем М. и соавт. Дыхание Рез. 2022 1 октября; 23 (1): 271. дои: 10.1186/с12931-022-02194-4. Дыхание Рез. 2022. PMID: 36182912 Бесплатная статья ЧВК.

Сравнение расовых различий в распространенности эмфиземы среди взрослых с нормальной спирометрией: анализ вторичных данных исследования легких CARDIA.
Лю Г.Ю., Хан С.С., Коланджело Л.А., Меза Д., Вашко Г.Р., Sporn PHS, Джейкобс Д.Р. младший, Дрансфилд М.Т., Карнетон М.Р., Калхан Р. Лю Г.Ю. и соавт. Энн Интерн Мед. 2022 авг;175(8):1118-1125. дои: 10.7326/M22-0205. Epub 2022 19 июля. Энн Интерн Мед. 2022. PMID: 35849828
Риск обострения ХОБЛ увеличивается при плохом качестве сна и модифицируется социальными невзгодами.
Боуг А., Бур Р.Г., Кибрера П., Барьяктаревич И., Барр Р.Г., Боулер Р., Хан М.К., Кауфман Д.Д., Кох А.Л., Кришнан Дж., Лабаки В., Мартинес Ф.Дж., Мкоромбиндо Т., Намен А., Ортега В., Пейн Р., Питерс С.
 П., Шотланд Х., Сундар К., Зейдлер М.Р., Хансель Н.Н., Вудрафф П.Г., Такур Н.
Боуг А и др.
Спать. 2022, 11 августа; 45(8):zsac107. дои: 10.1093/сон/zsac107.
Спать. 2022.
PMID: 35665826
П., Шотланд Х., Сундар К., Зейдлер М.Р., Хансель Н.Н., Вудрафф П.Г., Такур Н.
Боуг А и др.
Спать. 2022, 11 августа; 45(8):zsac107. дои: 10.1093/сон/zsac107.
Спать. 2022.
PMID: 35665826Достижение справедливости через науку и целостность: демонтаж медицины, основанной на расе.
Райт Д.Л., Фрид Г.Л., Хендрикс-Муньос К.Д., Джарвис Д.Н., Мальдонадо Я.А., Рафаэль Д.Л., Шнадауэр Д., Симс Б., Бог К.В., Леонард М.Б., Койн-Бизли Т.Д.; Комитет по разнообразию, интеграции и справедливости от имени Американского педиатрического общества. Райт Дж.Л. и соавт. Педиатр Рез. 2022 июн;91(7):1641-1644. doi: 10.1038/s41390-022-02041-8. Epub 2022 5 апр. Педиатр Рез. 2022. PMID: 35383261 Аннотация недоступна.
Контролируемое воздействие выхлопных газов дизельных двигателей на человека: результаты освещают последствия для здоровья загрязнения воздуха, связанного с дорожным движением, и дают информацию для будущих направлений.

Лонг Э., Карлстен К. Лонг Э. и др. Часть клетчатки Toxicol. 2022 9 февраля; 19 (1): 11. дои: 10.1186/с12989-022-00450-5. Часть клетчатки Toxicol. 2022. PMID: 35139881 Бесплатная статья ЧВК. Рассмотрение.
Типы публикаций
термины MeSH
Грантовая поддержка
- HHSN2682009C/HL/NHLBI NIH HHS/США
- U24 HL141762/HL/NHLBI NIH HHS/США
- HHSN2682006C/HL/NHLBI NIH HHS/США
- K24HL137013/HL/NHLBI NIH HHS/США
- HL137013/HL/NHLBI NIH HHS/США
- HHSN2682004C/HL/NHLBI NIH HHS/США
- F32HL158160/HL/NHLBI NIH HHS/США
- K23HL125551/HL/NHLBI NIH HHS/США
- HHSN2682008C/HL/NHLBI NIH HHS/США
- U01HL137880/HL/NHLBI NIH HHS/США
- P30 DK054759/DK/NIDDK NIH HHS/США
- HHSN2682003C/HL/NHLBI NIH HHS/США
- HHSN2682005C/HL/NHLBI NIH HHS/США
- F32 HL158160/HL/NHLBI NIH HHS/США
- HHSN268200
0C/HL/NHLBI NIH HHS/США
- HHSN2682007C/HL/NHLBI NIH HHS/США
Формула линейной функции — Изучите формулу линейной функции
Прежде чем приступить к изучению формул линейной функции, давайте вспомним, что такое линейное уравнение и что такое функция. Линейное уравнение — это уравнение, в котором каждый член является либо просто константой, либо произведением константы и переменной степени 1. Функция — это отношение, в котором каждый вход имеет ровно один выход. Каждое линейное уравнение представляет собой линию. Все линии, кроме вертикальных, являются функциями. Давайте изучим формулы линейной функции вместе с несколькими решенными примерами.
Линейное уравнение — это уравнение, в котором каждый член является либо просто константой, либо произведением константы и переменной степени 1. Функция — это отношение, в котором каждый вход имеет ровно один выход. Каждое линейное уравнение представляет собой линию. Все линии, кроме вертикальных, являются функциями. Давайте изучим формулы линейной функции вместе с несколькими решенными примерами.
Существует несколько формул линейной функции для нахождения уравнения линии в зависимости от доступной информации. Формулы линейной функции применимы для нахождения уравнения любой линии, кроме вертикальной, поскольку вертикальная линия НЕ является функцией. Формулы линейной функции:
Здесь
- (x, y) в каждом уравнении является общей точкой на прямой.
- \((x_1,y_1)\) — любая фиксированная точка на прямой.
- м – уклон линии. Его можно определить как \(\dfrac{\text{Rise}}{\text{Run}}\) (или) \(\dfrac{y_2-y_1}{x_2-x_1}\), где \((x_1 , y_1)\) и \((x_2,y_2)\) — любые две точки на прямой.
 90 135 (a, 0) и (0, b) – точки пересечения по оси x и y соответственно.
90 135 (a, 0) и (0, b) – точки пересечения по оси x и y соответственно. - A, B и C являются константами.
Давайте посмотрим, как использовать формулы линейной функции в следующем разделе примеров решения.
Разбивайте сложные концепции с помощью простых визуальных средств.
Математика больше не будет сложным предметом, особенно когда вы понимаете концепции с помощью визуализаций.
Записаться на бесплатный пробный урок
Пример 1. Найдите линейную функцию вида y = f(x), имеющую две точки (3, -1) и (2, 4), используя одну из формул линейной функции.
Решение:
Даны две точки:
\((x_1,y_1)\) = (3, -1)
\((x_2,y_2)\) = (2, 4)
Наклон равен \(m=\dfrac{y_2-y_1}{x_2-x_1}= \dfrac{4+1}{2-3}=-5\)
Линейная функция находится с помощью точки- наклонная форма.
\(y-y_1=m(x-x_1)\)
y + 1 = -5 (x — 3)
y + 1 = -5x + 15
y = -5x + 14
Ответ: Требуемая линейная функция y = -5x + 14.



 12.2013, 17:10
12.2013, 17:10 
 12.2013, 19:05
12.2013, 19:05  12.2013, 22:27
12.2013, 22:27  )
) Из неё сразу вытекает следствие , которое не имеет решений в вещественных. Пустое множество точек на плоскости выглядит, безусловно, очень мило, но это ли нам хотел донести LebedKun
Из неё сразу вытекает следствие , которое не имеет решений в вещественных. Пустое множество точек на плоскости выглядит, безусловно, очень мило, но это ли нам хотел донести LebedKun вздох.мюсли
вздох.мюсли Да, интересно, выглядит самоподобной.
Да, интересно, выглядит самоподобной. вздох.мюсли
вздох.мюсли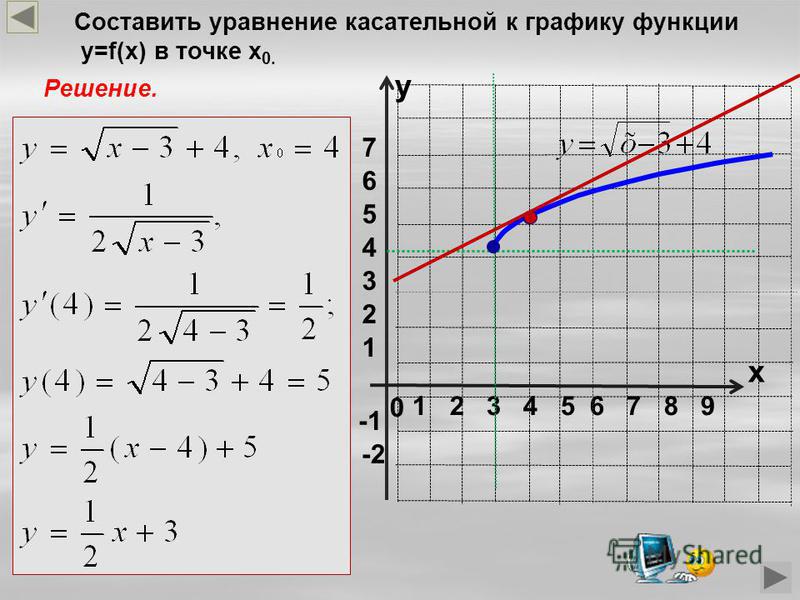 12.2013, 16:40
12.2013, 16:40  12.2013, 18:11
12.2013, 18:11  12.2013, 17:06
12.2013, 17:06 




 2019 декабря; 16 (12): 1504-1517. doi: 10.1513/AnnalsATS.201901-030OC.
Энн Ам Торак Соц. 2019.
PMID: 31404502
Бесплатная статья ЧВК.
2019 декабря; 16 (12): 1504-1517. doi: 10.1513/AnnalsATS.201901-030OC.
Энн Ам Торак Соц. 2019.
PMID: 31404502
Бесплатная статья ЧВК.
 П., Шотланд Х., Сундар К., Зейдлер М.Р., Хансель Н.Н., Вудрафф П.Г., Такур Н.
Боуг А и др.
Спать. 2022, 11 августа; 45(8):zsac107. дои: 10.1093/сон/zsac107.
Спать. 2022.
PMID: 35665826
П., Шотланд Х., Сундар К., Зейдлер М.Р., Хансель Н.Н., Вудрафф П.Г., Такур Н.
Боуг А и др.
Спать. 2022, 11 августа; 45(8):zsac107. дои: 10.1093/сон/zsac107.
Спать. 2022.
PMID: 35665826