|
Навигация: Главная Случайная страница Обратная связь ТОП Интересно знать Избранные Топ: Оснащения врачебно-сестринской бригады. Особенности труда и отдыха в условиях низких температур: К работам при низких температурах на открытом воздухе и в не отапливаемых помещениях допускаются лица не моложе 18 лет, прошедшие… Комплексной системы оценки состояния охраны труда на производственном объекте (КСОТ-П): Цели и задачи Комплексной системы оценки состояния охраны труда и определению факторов рисков по охране труда… Интересное: Наиболее распространенные виды рака: Раковая опухоль — это самостоятельное новообразование, которое может возникнуть и от повышенного давления… Инженерная защита территорий, зданий и сооружений от опасных геологических процессов: Изучение оползневых явлений, оценка устойчивости склонов и проектирование противооползневых сооружений — актуальнейшие задачи, стоящие перед отечественными. Лечение прогрессирующих форм рака: Одним из наиболее важных достижений экспериментальной химиотерапии опухолей, начатой в 60-х и реализованной в 70-х годах, является… Дисциплины: Автоматизация Антропология Археология Архитектура Аудит Биология Бухгалтерия Военная наука Генетика География Геология Демография Журналистика Зоология Иностранные языки Информатика Искусство История Кинематография Компьютеризация Кораблестроение Кулинария Культура Лексикология Лингвистика Литература Логика Маркетинг Математика Машиностроение Медицина Менеджмент Металлургия Метрология Механика Музыкология Науковедение Образование Охрана Труда Педагогика Политология Правоотношение Предпринимательство Приборостроение Программирование Производство Промышленность Психология Радиосвязь Религия Риторика Социология Спорт Стандартизация Статистика Строительство Теология Технологии Торговля Транспорт Фармакология Физика Физиология Философия Финансы Химия Хозяйство Черчение Экология Экономика Электроника Энергетика Юриспруденция |
⇐ ПредыдущаяСтр 5 из 5
Определение 1. Теорема 1.6.1. Определитель произведения матриц равен произведению определителей. Для двух матриц: . Следствие 1.6.1. Произведение любых невырожденных матриц само будет невырожденной матрицей. Определение 1.6.2. Обратной к квадратной матрице называется матрица , которая удовлетворяет условию .(1.6.1) Теорема 1.6.2. Матрица Доказательство. Необходимость.Пусть матрица A имеет обратную матрицу , тогда и .По теореме 1.6.1 .Так как , имеем . Значит и , т. е. матрицы A и невырожденные, а Достаточность.Для матрицы ; , составим матрицу из алгебраических дополнений и затем транспонируем ее. где –алгебраическое дополнениеэлемента . Вычисляя произведения и матриц, с учетом теоремы 1.3.1 получим . Разделив последнее соотношение на величину , имеем: откуда c учетом равенств (1.6.1), (1.2.4), найдем: . Мы получили формулу нахождения обратной матрицы и, следовательно, доказали ее существование. Таким образом, формула для вычисления обратной матрицы имеет вид:
(1.6.2)
Замечание 1.6.1. Для каждой невырожденной матрицы А существует единственная обратная матрица . Пример 1.6.1. Дано Найти . Решение. Следовательно, матрица А невырожденная и существует. Найдем алгебраические дополнения элементов данной матрицы: Подставляя полученное в формулу (1.
Проверка: . Замечание 1.6.1.Существует еще один способ нахождения обратной матрицы при помощи элементарных преобразований. Этот способ состоит в следующем: составляется матрица размера , при помощи приписывания к матрице Пример 1.6.2. Для матрицы из примера 1.6.1 найти обратную матрицу при помощи элементарных преобразований. Решение. Свойства обратных матриц: 1. . Непосредственно следует из равенства 1.6.1. 2. . Доказательство. . Следовательно, матрицы и обратные по отношению друг к другу, т. е. . 3. . Доказательство. Из соотношения 1.6.1: . По свойству 4 операции транспонирования (см. §2) .Следовательно, матрицы и взаимообратные, т. е. . Определение 1.6.2. Простейшими матричными уравнениями будем называть уравнения следующих трех типов: , , , (1.6.3) где , , – некоторые числовые матрицы, а – неизвестная матрица, которую нужно найти. Под решением матричного уравнения будем понимать матрицу X, которая обращает матричное уравнение в тождество. Искать решение матричных уравнений будем с помощью обратных матриц в зависимости от типа уравнения следующими тремя способами: 1) Если , то домножая обе части уравнения на слева, получим . 2) Если , то домножая обе части уравнения на справа, получим . 3) Если и , то домножая уравнение на .
Пример 1.6.3. Решить матричные уравнения: a) b) c) Решение: a)Матричное уравнение можно переписать в виде: , где Получили уравнение вида (1.6. ), решение которого – матрица . Найдем матрицу : существует; Таким образом, b) Матричное уравнение можно переписать в виде: , где Получили уравнение вида (1.6. ), решение которого ищется в виде: . Найдем матрицу : существует; c) Матричное уравнение можно переписать в виде (1.6. ): , где Решение данного уравнения ищется в виде: . Найдем матрицы и : существует; Окончательно, находим Замечание 1.6.2. В случае, когда и , приведенные способы решений применять нельзя. В этом случае неизвестную матрицу X находят, сводя матричное уравнение к системе линейных уравнений. Пример 1.6.4. Решить матричное уравнение: Решение: Так как , то решать матричное уравнение с помощью обратной матрицы нельзя. Пусть матрица X состоит из элементов , тогда по правилу умножения матриц (1.2.3) имеем: Используя определение 1.1.2 равенства матриц, составим систему: Таким образом, матрица X имеет вид: . Замечание 1.6.3. Более подробно решение систем линейных уравнений мы будем рассматривать в следующей главе. * Пьер Ф. Саррюс (1798–1858) – французский математик. В 1833 году сформулировал правило для вычисления определителя 3-го порядка, основанное на приписывании к матрице определителя строк или столбцов. ⇐ Предыдущая12345 Кормораздатчик мобильный электрифицированный: схема и процесс работы устройства… Организация стока поверхностных вод: Наибольшее количество влаги на земном шаре испаряется с поверхности морей и океанов (88‰). Индивидуальные и групповые автопоилки: для животных. Схемы и конструкции… Механическое удерживание земляных масс: Механическое удерживание земляных масс на склоне обеспечивают контрфорсными сооружениями различных конструкций… |
Как решить уравнение с помощью обратной матрицы. Линейные уравнения
Пусть дана система линейных уравнений снеизвестными:
Будем
предполагать, что основная матрица
невырожденная.
Тогда, по теореме 3.1,
существует обратная матрица
Помножив матричное уравнение
на матрицу
слева, воспользовавшись определением
3.2, а также утверждением 8) теоремы 1.1,
получим формулу, на которой основан
матричный метод решения систем линейных
уравнений:
Замечание.
Отметим, что матричный метод решения систем линейных уравнений в отличие от метода Гаусса имеет ограниченное применение: этим методом могут быть решены только такие системы линейных уравнений, у которых, во-первых, число неизвестных равно числу уравнений, а во-вторых, основная матрица невырожденная.
Пример. Решить систему линейных уравнений матричным методом.
Задана
система трёх линейных уравнений с тремя
неизвестными
где
Основная матрица системы уравнений невырожденная, поскольку её определитель отличен от нуля:
Обратную
матрицу
составим одним из методов, описанных в
пункте 3.
По формуле матричного метода решения систем линейных уравнений получим
5.3. Метод Крамера
Данный метод так же, как и матричный, применим только для систем линейных уравнений, у которых число неизвестных совпадает с числом уравнений. Метод Крамера основан на одноимённой теореме:
Теорема 5.2. Система линейных уравнений снеизвестными
основная матрица которой невырожденная, имеет единственное решение, которое может быть получено по формулам
где
определитель
матрицы, полученной из основной матрицысистемы уравнений заменой её
го
столбца столбцом свободных членов.
Пример. Найдём решение системы линейных
уравнений, рассмотренной в предыдущем
примере, методом Крамера. Основная
матрица системы уравнений невырожденная,
поскольку
Вычислим определители
По формулам, представленным в теореме 5.2, вычислим значения неизвестных:
6. Исследование систем линейных уравнений.
Базисное решение
Исследовать систему линейных уравнений – означает определить, какой является эта система – совместной или несовместной, и в случае её совместности выяснить, определённая эта система или неопределённая.
Условие совместности системы линейных уравнений даёт следующая теорема
Теорема 6.1 (Кронекера–Капелли).
Система линейных уравнений совместна тогда и только тогда, когда ранг основной матрицы системы равен рангу её расширенной матрицы:
Для
совместной системы линейных уравнений
вопрос о её определённости или
неопределённости решается с применением
следующих теорем.
Теорема 6.2. Если ранг основной матрицы совместной системы равен числу неизвестных, то система является определённой
Теорема 6.3. Если ранг основной матрицы совместной системы меньше числа неизвестных, то система является неопределённой.
Таким
образом, из сформулированных теорем
вытекает способ исследования систем
линейных алгебраических уравнений.
Пусть n – количество неизвестных,
Тогда:
Определение 6.1. Базисным решением неопределённой системы линейных уравнений называют такое её решение, в котором все свободные неизвестные равны нулю.
Пример. Исследовать систему линейных уравнений. В случае неопределённости системы найти её базисное решение.
Вычислим ранги основной и расширенной матрицданной системы уравнений, для чего приведём расширенную (а вместе с тем и основную) матрицу системы к ступенчатому виду:
Вторую
строку матрицы сложим с её первой
строкой, умноженной на
третью строку – с первой строкой,
умноженной на
а четвёртую строку – с первой, умноженной
наполучим матрицу
К
третьей строке этой матрицы прибавим
вторую строку, умноженную на
а к четвёртой строке – первую, умноженную
на
В результате получим матрицу
удаляя из которой третью и четвёртую строки получим ступенчатую матрицу
Таким
образом,
Следовательно, данная система линейных
уравнений совместна, а поскольку величина
ранга меньше числа неизвестных, система
является неопределённой. Полученной
в результате элементарных преобразований
ступенчатой матрице соответствует
система уравнений
Полученной
в результате элементарных преобразований
ступенчатой матрице соответствует
система уравнений
Неизвестные
иявляются главными, а неизвестныеи
свободными. Придавая свободным неизвестным
нулевые значения, получим базисное
решение данной системы линейных
уравнений.
Матричный метод решения СЛАУ применяют к решению систем уравнений, у которых количество уравнений соответствует количеству неизвестных. Метод лучше применять для решения систем низкого порядка. Матричный метод решения систем линейных уравнений основывается на применении свойств умножения матриц.
Этот способ, другими словами метод обратной матрицы, называют так, так как решение сводится к обычному матричному уравнению, для решения которого нужно найти обратную матрицу.
Матричный метод решения СЛАУ с определителем, который больше или меньше нуля состоит в следующем:
Предположим, есть СЛУ (система линейных уравнений) с n неизвестными (над произвольным полем):
Значит, её легко перевести в матричную форму:
AX=B , где A — основная матрица системы, B и X — столбцы свободных членов и решений системы соответственно:
Умножим это матричное уравнение слева на A −1 — обратную матрицу к матрице A: A −1 (AX)=A −1 B.
Т.к. A −1 A=E , значит, X=A −1 B . Правая часть уравнения дает столбец решений начальной системы. Условием применимости матричного метода есть невырожденность матрицы A . Необходимым и достаточным условием этого есть неравенство нулю определителя матрицы A :
detA≠0.
Для однородной системы линейных уравнений , т.е. если вектор B=0 , выполняется обратное правило: у системы AX=0 есть нетривиальное (т.е. не равное нулю) решение лишь когда detA=0 . Эта связь между решениями однородных и неоднородных систем линейных уравнений называется альтернатива Фредгольма.
Т.о., решение СЛАУ матричным методом производится по формуле . Либо, решение СЛАУ находят при помощи обратной матрицы A −1 .
Известно, что у квадратной матрицы А порядка n на n есть обратная матрица A −1 только в том случае, если ее определитель ненулевой. Таким образом, систему n линейных алгебраических уравнений с n неизвестными решаем матричным методом только в случае, если определитель основной матрицы системы не равен нулю.
Не взирая на то, что есть ограничения возможности применения такого метода и существуют сложности вычислений при больших значениях коэффициентов и систем высокого порядка, метод можно легко реализовать на ЭВМ.
Пример решения неоднородной СЛАУ.
Для начала проверим, не равен ли нулю определитель матрицы коэффициентов у неизвестных СЛАУ.
Теперь находим союзную матрицу , транспонируем её и подставляем в формулу для определения обратной матрицы.
Подставляем переменные в формулу:
Теперь находим неизвестные, перемножая обратную матрицу и столбик свободных членов.
Итак, x=2; y=1; z=4.
При переходе от обычного вида СЛАУ к матричной форме будьте внимательными с порядком неизвестных переменных в уравнениях системы. Например :
НЕЛЬЗЯ записать как:
Необходимо, для начала, упорядочить неизвестные переменные в кадом уравнении системы и только после этого переходить к матричной записи:
Кроме того, нужно быть внимательными с обозначением неизвестных переменных, вместо x 1 , x 2 , …, x n могут оказаться другие буквы. К примеру :
К примеру :
в матричной форме записываем так:
Матричным методом лучше решать системы линейных уравнений, в которых количество уравнений совпадает с числом неизвестных переменных и определитель основной матрицы системы не равен нулю. Когда в системе более 3-х уравнений, на нахождение обратной матрицы потребуется больше вычислительных усилий, поэтому, в этом случае целесообразно использовать для решения метод Гаусса.
Уравнения вообще, линейные алгебраические уравнения и их системы, а также методы их решения занимают в математике, как теоретической, так и прикладной, особое место.
Это связано с тем обстоятельством, что подавляющее большинство физических, экономических, технических и даже педагогических задач могут быть описаны и решены с помощью разнообразных уравнений и их систем. В последнее время особую популярность среди исследователей, ученых и практиков приобрело математическое моделирование практически во всех предметных областях, что объясняется очевидными его преимуществами перед другими известными и апробированными методами исследования объектов различной природы, в частности, так называемых, сложных систем. Существует великое многообразие различных определений математической модели, данных учеными в разные времена, но на наш взгляд, самое удачное, это следующее утверждение. Математическая модель – это идея, выраженная уравнением. Таким образом, умение составлять и решать уравнения и их системы – неотъемлемая характеристика современного специалиста.
Существует великое многообразие различных определений математической модели, данных учеными в разные времена, но на наш взгляд, самое удачное, это следующее утверждение. Математическая модель – это идея, выраженная уравнением. Таким образом, умение составлять и решать уравнения и их системы – неотъемлемая характеристика современного специалиста.
Для решения систем линейных алгебраических уравнений наиболее часто используются методы: Крамера, Жордана-Гаусса и матричный метод.
Матричный метод решения — метод решения с помощью обратной матрицы систем линейных алгебраических уравнений с ненулевым определителем.
Если выписать коэффициенты при неизвестных величинах xi в матрицу A, неизвестные величины собрать в вектор столбец X, а свободные члены в вектор столбец B, то систему линейных алгебраических уравнений можно записать в виде следующего матричного уравнения A · X = B, которое имеет единственное решение только тогда, когда определитель матрицы A не будет равен нулю. При этом решение системы уравнений можно найти следующим способом X = A -1 · B , где A -1 — обратная матрица.
Матричный метод решения состоит в следующем.
Пусть дана система линейных уравнений с n неизвестными:
Её можно переписать в матричной форме: AX = B , где A — основная матрица системы, B и X — столбцы свободных членов и решений системы соответственно:
Умножим это матричное уравнение слева на A -1 — матрицу, обратную к матрице A : A -1 (AX ) = A -1 B
Так как A -1 A = E , получаем X = A -1 B . Правая часть этого уравнения даст столбец решений исходной системы. Условием применимости данного метода (как и вообще существования решения неоднородной системы линейных уравнений с числом уравнений, равным числу неизвестных) является невырожденность матрицы A . Необходимым и достаточным условием этого является неравенство нулю определителя матрицы A : detA ≠ 0.
Для однородной системы линейных уравнений, то есть когда вектор B = 0 , действительно обратное правило: система AX = 0 имеет нетривиальное (то есть не нулевое) решение только если detA = 0. Такая связь между решениями однородных и неоднородных систем линейных уравнений носит название альтернативы Фредгольма.
Такая связь между решениями однородных и неоднородных систем линейных уравнений носит название альтернативы Фредгольма.
Пример решения неоднородной системы линейных алгебраических уравнений .
Убедимся в том, что определитель матрицы, составленный из коэффициентов при неизвестных системы линейных алгебраических уравнений не равен нулю.
Следующим шагом будет вычисление алгебраических дополнений для элементов матрицы, состоящей из коэффициентов при неизвестных. Они понадобятся для нахождения обратной матрицы.
Уравнения вообще, линейные алгебраические уравнения и их системы, а также методы их решения занимают в математике, как теоретической, так и прикладной, особое место.
Это связано с тем обстоятельством, что подавляющее большинство физических, экономических, технических и даже педагогических задач могут быть описаны и решены с помощью разнообразных уравнений и их систем. В последнее время особую популярность среди исследователей, ученых и практиков приобрело математическое моделирование практически во всех предметных областях, что объясняется очевидными его преимуществами перед другими известными и апробированными методами исследования объектов различной природы, в частности, так называемых, сложных систем. Существует великое многообразие различных определений математической модели, данных учеными в разные времена, но на наш взгляд, самое удачное, это следующее утверждение. Математическая модель – это идея, выраженная уравнением. Таким образом, умение составлять и решать уравнения и их системы – неотъемлемая характеристика современного специалиста.
Существует великое многообразие различных определений математической модели, данных учеными в разные времена, но на наш взгляд, самое удачное, это следующее утверждение. Математическая модель – это идея, выраженная уравнением. Таким образом, умение составлять и решать уравнения и их системы – неотъемлемая характеристика современного специалиста.
Для решения систем линейных алгебраических уравнений наиболее часто используются методы: Крамера, Жордана-Гаусса и матричный метод.
Матричный метод решения — метод решения с помощью обратной матрицы систем линейных алгебраических уравнений с ненулевым определителем.
Если выписать коэффициенты при неизвестных величинах xi в матрицу A, неизвестные величины собрать в вектор столбец X, а свободные члены в вектор столбец B, то систему линейных алгебраических уравнений можно записать в виде следующего матричного уравнения A · X = B, которое имеет единственное решение только тогда, когда определитель матрицы A не будет равен нулю. При этом решение системы уравнений можно найти следующим способом X = A -1 · B , где A -1 — обратная матрица.
Матричный метод решения состоит в следующем.
Пусть дана система линейных уравнений с n неизвестными:
Её можно переписать в матричной форме: AX = B , где A — основная матрица системы, B и X — столбцы свободных членов и решений системы соответственно:
Умножим это матричное уравнение слева на A -1 — матрицу, обратную к матрице A : A -1 (AX ) = A -1 B
Так как A -1 A = E , получаем X = A -1 B . Правая часть этого уравнения даст столбец решений исходной системы. Условием применимости данного метода (как и вообще существования решения неоднородной системы линейных уравнений с числом уравнений, равным числу неизвестных) является невырожденность матрицы A . Необходимым и достаточным условием этого является неравенство нулю определителя матрицы A : detA ≠ 0.
Для однородной системы линейных уравнений, то есть когда вектор B = 0 , действительно обратное правило: система AX = 0 имеет нетривиальное (то есть не нулевое) решение только если detA = 0. Такая связь между решениями однородных и неоднородных систем линейных уравнений носит название альтернативы Фредгольма.
Такая связь между решениями однородных и неоднородных систем линейных уравнений носит название альтернативы Фредгольма.
Пример решения неоднородной системы линейных алгебраических уравнений .
Убедимся в том, что определитель матрицы, составленный из коэффициентов при неизвестных системы линейных алгебраических уравнений не равен нулю.
Следующим шагом будет вычисление алгебраических дополнений для элементов матрицы, состоящей из коэффициентов при неизвестных. Они понадобятся для нахождения обратной матрицы.
Метод обратной матрицы не представляет ничего сложного, если знать общие принципы работы с матричными уравнениями и, конечно, уметь производить элементарные алгебраические действия.
Решение системы уравнений методом обратной матрицы. Пример.
Удобнее всего постигать метод обратной матрицы на наглядном примере. Возьмем систему уравнений:
Первый шаг, который необходимо сделать для решения этой системы уравнений — найти определитель. Поэтому преобразим нашу систему уравнений в следующую матрицу:
Поэтому преобразим нашу систему уравнений в следующую матрицу:
И найдем нужный определитель:
Формула, использующаяся для решения матричных уравнений, выглядит следующим образом:
Таким образом, для вычисления Х нам необходимо определить значение матрицы А-1 и умножить его на b. В этом нам поможет другая формула:
Ат в данном случае будет транспонированной матрицей — то есть, той же самой, исходной, но записанной не строками, а столбцами.
Не следует забывать о том, что метод обратной матрицы , как и метод Крамера, подходит только для систем, в которых определитель больше или меньше нуля. Если же определитель равен нулю, нужно использовать метод Гаусса.
Следующий шаг — составление матрицы миноров, представляющей собой такую схему:
В итоге мы получили три матрицы — миноров, алгебраических дополнений и транспонированную матрицу алгебраических дополнений. Теперь можно переходить к собственно составлению обратной матрицы. Формулу мы уже знаем. Для нашего примера это будет выглядеть так.
Формулу мы уже знаем. Для нашего примера это будет выглядеть так.
Многомерные линейные уравнения с постоянными коэффициентами
12.1Оператор монодромии
Рассмотрим линейное уравнение
˙z=Az,z(t)∈Rn(12.1)
Ранее мы разобрали случаи уравнений на плоскости (когда n=2). Сегодня мы рассмотрим общий случай.
Когда мы рассматривали линейные системы на плоскости, у нас получалось, что решение задается в виде
z(t)=M(t)z0,
где M(t) — некоторая матрица (зависящая от t), причём M(0)=E: см. уравнения (10.6) и (10.14)предыдущей главы. Это неспроста.
Пусть φ(t;z0) — решение уравнения (12.1) с начальным условием z(0)=z0. Зафиксируем некоторое t и рассмотрим отображение последования (оно также называется преобразованием фазового потока) за время t:
gt(z0)=φ(t;z0)
То есть для каждой точки фазового пространства z0 отобразим её туда, где она окажется через время t.
Пример 1. Рассмотрим систему
˙x=2x,˙y=3y
Для неё
g1(x0y0)=(e200e3)⋅(x0y0),
а в общем виде
gt(x0y0)=(e2t00e3t)(x0y0)
или просто
gt=(e2t00e3t)
Теорема 1. Для системы (12.1) и любого t отображение gt является линейным.
Доказательство. Пусть u и v — некоторые векторы из фазового пространства Rn. Тогда
gt(u+v)=φ(t;u+v)
Пусть ψ(t)=φ(t;u)+φ(t;v). Функция ψ является решением уравнения (12.1) (в силу линейности). При этом ψ(0)=φ(0;u)+φ(0;v)=u+v. Значит, это решение с начальным условием u+v. Но решение с начальным условием u+v задаётся функцией φ(t;u+v). Значит (по теореме о существовании и единственности), ψ(t)=φ(t;u+v). Таким образом,
gt(u+v)=φ(t;u)+φ(t;v)=gt(u)+gt(v)
Аналогично проверяется и вторая аксиома линейности для gt. (Упражнение:
завершить доказательство.)∎
(Упражнение:
завершить доказательство.)∎
Следствие 1. Пространство решений линейного дифференциального уравнения имеет такую же размерность, как фазовое пространство.
12.2Матричная экспонента
Таким образом, для решения уравнения (12.1) нам нужно будет найти матрицу M(t) (она иногда называется «матрицей монодромии»), которая задаёт решение. Как её найти? Если бы A была не матрицей, а числом (вещественным и комплексным), мы бы мгновенно записали решение в виде экспоненты. Нельзя ли с матрицей сделать то же самое, то есть записать решение уравнения (12.1) в виде экспоненты от матрицы?
z(t)=eAtz0(12.2)
На первый взгляд, это кажется безумием. (Хотя возможно вас с ним уже познакомили на курсе линейной алгебры.) Что значит «возвести число e в степень матрицы»? Ерунда какая-то. Впрочем, не большая ерунда, чем возведение числа e в степень π (вы ведь помните, что изначально возвести число в степень — это умножить его на себя сколько-то раз — как это можно сделать иррациональное число раз?). Так что может быть и с матрицей получится?
Так что может быть и с матрицей получится?
Напомним, что экспоненту от числа x можно определить как сумму ряда
ex=∞∑n=0xnn!
Оказывается, нет ничего невозможного в том, чтобы подставить в этот ряд матрицу A. Действительно, чтобы посчитать значение этого ряда, нам нужно только уметь складывать матрицы и возводить их в натуральные степени — а это мы делать умеем. Итак, по определению,
eA=∞∑n=0Ann!,A0=E(12.3)
Вы, безусловно, изучали анализ, и при взгляде на такую запись у вас неминуемо должен возникнуть вопрос: а почему этот ряд сходится? И всегда ли он сходится? Оказывается, да, сходится, причём всегда и, более того, абсолютно сходится. Мы не будем давать аккуратного доказательства, но наметим его основные шаги:
- Ввести норму на пространстве линейных операторов. Делается это так:
пусть ∥v∥ — норма вектора v (то есть на фазовом
пространстве какая-то норма введена). В этом случае определим норму
оператора A следующим образом:
∥A∥=supv:∥v∥=1∥Av∥
- Доказать, что эта норма обладает следующим свойством:
∥A⋅B∥≤∥A∥⋅∥B∥.

- Доказать, что каждое слагаемое ряда (12.3) ограничено сверху по норме соответствующим слагаемым для ряда e∥A∥.
- Ряд для e∥A∥ сходится абсолютно, а значит и ряд (12.3) тоже сходится абсолютно.
12.2.1Матричная экспонента даёт решение линейного уравнения
Покажем, функция, заданная формулой (12.2), является решением уравнения (12.1). Действительно,
ddteAtz0=ddt∞∑n=0tnAnz0n!=∞∑n=1ntn−1Anz0n!=A∞∑n=0tnAnn!=AeAtz0.
Дифференцирование ряда допустимо, поскольку он сходится абсолютно (чего мы правда не доказали).
Вопрос 1. Правда ли, что eA+B=eAeB?
Правда, потому что это верно для обычной экспоненты
Неверный ответ. Ну тогда попробуйте это доказать.
Неправда.
Верный ответ.
Действительно, в отличие от чисел, матрицы не обязаны
коммутировать по умножению. Поэтому ожидать выполнения этого
равенства кажется странно: его левая часть не меняется от того, что
мы поменяем A и B местами, а правая часть может и измениться.
Подобрать теперь конкретный контрпример не очень сложно: сделайте
это самостоятельно. На самом деле, именно отсутствие коммутирования
для матриц не даёт нам доказать это утверждение.
Поэтому ожидать выполнения этого
равенства кажется странно: его левая часть не меняется от того, что
мы поменяем A и B местами, а правая часть может и измениться.
Подобрать теперь конкретный контрпример не очень сложно: сделайте
это самостоятельно. На самом деле, именно отсутствие коммутирования
для матриц не даёт нам доказать это утверждение.
12.2.2Нахождение матричной экспоненты
Утверждение 1. Справедливо следующее соотношение
eCAC−1=CeAC−1
Оно означает, что вычисление экспоненты корректно определено на пространстве операторов: оно «дружит» с заменой базиса.
Доказательство. Имеем:
CeAC−1=C(∞∑n=0Ann!)C−1=∞∑n=0CAnC−1n!=eCAC−1
∎
Это означает, что для нахождения экспоненты можно перейти в «хороший» базис
(например, собственный или на худой конец жорданов), найти экспоненту там, а
затем перейти в исходный базис. Рассмотрим теперь два случая.
Рассмотрим теперь два случая.
12.2.3Экспонента диагонализируемой матрицы
Пусть A диагонализируема, то есть существует такая матрица C, что CAC−1 диагональная. Обозначим её за D. Тогда A=C−1DC. Заметим, что
exp⎛⎜ ⎜⎝λ1…0⋮⋱⋮0…λn⎞⎟ ⎟⎠=⎛⎜ ⎜ ⎜ ⎜ ⎜⎝∑∞k=0λk1k!…0⋮⋱⋮0…∑∞k=0λknk!⎞⎟ ⎟ ⎟ ⎟ ⎟⎠=⎛⎜ ⎜⎝eλ1…0⋮⋱⋮0…eλn⎞⎟ ⎟⎠
Решение уравнения (12.1) для диагонализируемой матрицы A теперь представляется в виде:
z(t)=exp(At)z0=C−1⋅exp(Dt)⋅C⋅z0,
где z0 — начальное условие.
12.2.4Экспонента жордановой клетки
Если матрица не диагонализируема, то она по крайней мере приводится к жордановой нормальной форме. Рассмотрим случай жордановой клетки.
Пусть
Jλ=⎛⎜ ⎜ ⎜ ⎜ ⎜ ⎜⎝λ1…0⋮⋱⋱⋮⋮…λ10…0λ⎞⎟ ⎟ ⎟ ⎟ ⎟ ⎟⎠
Чтобы найти eJλ, заметим для начала, что
Jλ=λE+N,
где N — это нильпотентный оператор, матрица которого состоит из единичек на
диагонали, сдвинутой на 1 вверх.
Заметим, что λE коммутирует с любой другой матрицей, в том числе и с матрицей N. Можно показать (мы этого не делали), что благодаря коммутированию
eλE+N=eλEeN=eλeN.
Однако матрица N нильпотентная, то есть существует такое k, что Nk=0. В этом случае ряд для экспоненты имеет лишь конечное число ненулевых слагаемых и становится полиномом:
∞∑i=0Nii!=k∑i=0Nii!
Его можно посчитать явно, а значит можно найти экспоненту от жордановой клетки.
Пример 2. Рассмотрим линейное уравнение на плоскости с оператором A, имеющим совпадающие собственные значения (равные λ), но не являющимся диагональным. Для нахождения решения по формуле (12.2) нам потребуется найти экспоненту от матрицы, пропорциональной жордановой клетке:
exp((λ10λ)t)=exp((λt00λt))⋅[(1001)+11!(0t00)]=eλt(1t01)=(eλtteλt0eλt)
Фазовый портрет этой системы см. на рис. 10.7.
10.7.
12.2.5Общий случай
Пусть ЖНФ матрицы имеет несколько клеток. Каждая из них соответствует некоторому инвариантному подпространству линейного оператора: оператор действует на различных инвариантных подпространствах независимо. Это означает, что мы можем вычислить экспоненту от каждой жордановой клетки и затем составить большую блочно-диагональную матрицу, состоящую из таких же блоков, как исходная (в ЖНФ).
Таким образом, мы можем вычислить экспоненту от любой матрицы — самым сложным этапом при этом является её приведение к ЖНФ и отыскание жорданова базиса.
Значит, мы умеем решать любые системы линейных уравнений!
← Предыдущая глава Следующая глава →
Карта механики — Матричные уравнения
Система уравнений — это любой набор уравнений, которые имеют общие переменные. Линейное уравнение — это уравнение, полностью состоящее из констант и простых переменных. Эти переменные можно умножать только на константу, их нельзя умножать вместе, возводить в степень, использовать с логарифмами или квадратными корнями или использовать другие более сложные математические функции. Ниже приведен пример системы линейных уравнений.
Эти переменные можно умножать только на константу, их нельзя умножать вместе, возводить в степень, использовать с логарифмами или квадратными корнями или использовать другие более сложные математические функции. Ниже приведен пример системы линейных уравнений.
| \[F_{AX}+F_{BX}=0\] |
| \[F_{AY}-8=0\] |
| \[-16+4F_{AY}+8F_{AX}=0\] |
В таких курсах, как статика и динамика, мы часто сталкиваемся с системой линейных уравнений и должны найти неизвестные в этих уравнениях. Когда в нашей системе всего несколько уравнений, мы обычно решаем уравнения вручную, используя алгебраические методы, такие как подстановка или исключение, сложение или вычитание. Для более крупных и сложных задач мы можем столкнуться с более крупными системами уравнений, и в какой-то момент математику может стать трудно обрабатывать вручную. Для этих больших систем линейных уравнений самый простой способ найти неизвестные — это преобразовать систему уравнений в одно матричное уравнение, а затем использовать компьютерные инструменты для решения матричного уравнения для неизвестных.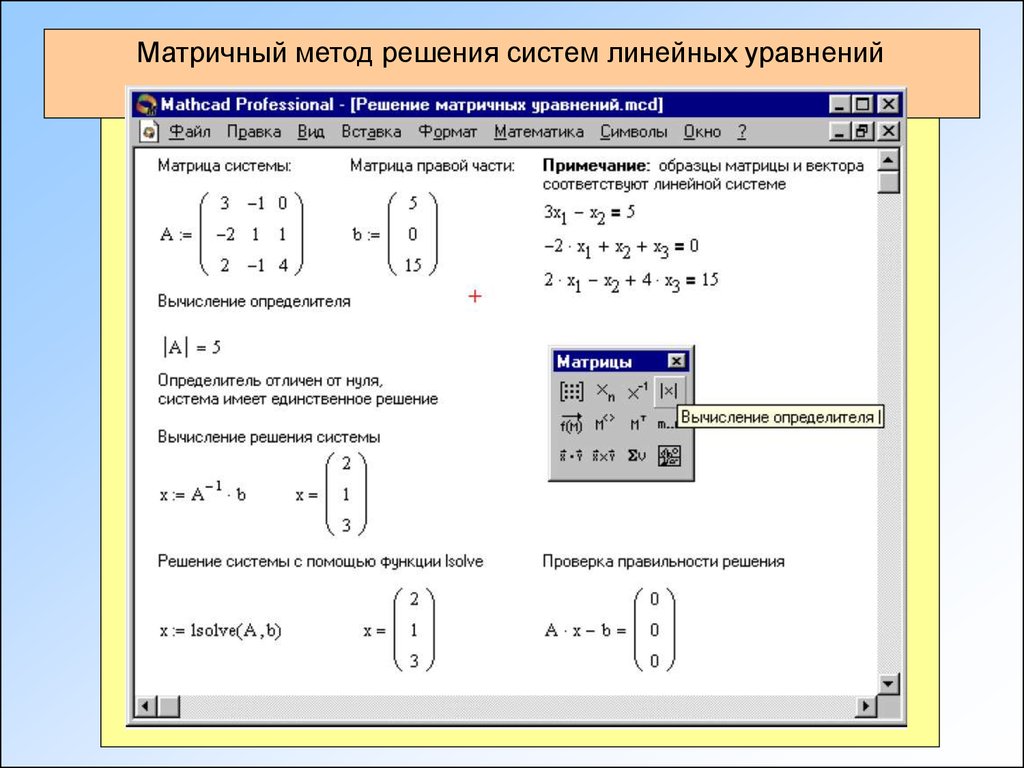 Некоторые компьютерные инструменты позволяют вам вводить систему уравнений вручную, но в фоновом режиме компьютер, вероятно, просто преобразует ее в матричное уравнение в фоновом режиме. По этой причине может быть полезно понять этот процесс.
Некоторые компьютерные инструменты позволяют вам вводить систему уравнений вручную, но в фоновом режиме компьютер, вероятно, просто преобразует ее в матричное уравнение в фоновом режиме. По этой причине может быть полезно понять этот процесс.
Что касается предположений, важно отметить, что этот метод будет работать только с системами из линейных уравнений , и чтобы получить разрешимое матричное уравнение, нам потребуется столько же уравнений, сколько и неизвестных переменных . Например, выше у нас есть система уравнений с тремя уравнениями и тремя неизвестными переменными. Если эти числа не совпадают, мы не сможем решить матричное уравнение описанным ниже методом.
Преобразование системы уравнений в матричное уравнение:
Первым шагом в преобразовании системы уравнений в матричное уравнение является преобразование уравнений в согласованный формат. Обычно мы помещаем все переменные с их коэффициентами на одну сторону уравнения, а константы — на другую сторону уравнения. Кроме того, лучше всего перечислять переменные в одном и том же порядке в каждом уравнении. Этот процесс перестановки уравнений в дальнейшем облегчит преобразование.
Кроме того, лучше всего перечислять переменные в одном и том же порядке в каждом уравнении. Этот процесс перестановки уравнений в дальнейшем облегчит преобразование.
Далее мы начнем процесс записи трех матриц, составляющих матричное уравнение. Этими тремя матрицами являются матрица коэффициентов (часто называемая матрицей A), матрица переменных (часто называемая матрицей X) и матрица констант (часто называемая матрицей B).
- Матрица коэффициентов (или матрица A) представляет собой матрицу N x N (где N — количество уравнений/количество неизвестных переменных), которая содержит все коэффициенты для переменных. Каждая строка матрицы представляет собой одно уравнение, а каждый столбец представляет одну переменную (иногда полезно записывать переменную вверху каждого столбца).
 Для случаев, когда переменная не фигурирует в уравнении, мы принимаем коэффициент равным 0,9.0042
Для случаев, когда переменная не фигурирует в уравнении, мы принимаем коэффициент равным 0,9.0042 - Матрица переменных (или матрица X) представляет собой матрицу размера 1 x N, содержащую все неизвестные переменные. Важно, чтобы порядок переменных в матрице коэффициентов соответствовал порядку переменных в матрице переменных.
- Наконец, с другой стороны знака равенства у нас есть константная матрица (или матрица B). Это матрица N x 1, содержащая все константы из правой части уравнений. Важно, чтобы порядок констант соответствовал порядку уравнений в матрице коэффициентов.
После настройки трех матриц мы готовы найти неизвестные в матрице переменных.
Решение матричного уравнения:
Начиная с наших матриц A, X и B в матричном уравнении ниже, мы пытаемся найти значения неизвестных переменных, содержащихся в нашей матрице X.
| \[[A][X]=[B]\] |
Для скалярного уравнения мы просто разделим обе его части на A, где значение X будет равно B/A. Вместо этого с матричным уравнением нам нужно будет умножить обе части уравнения на обратную матрицу A. Это отменит матрицу A с левой стороны, оставив только искомую матрицу X. Слева у нас будет обратная матрица A, умноженная на матрицу B. Результатом этой операции будет матрица 1 x N, содержащая решение для всех переменных. Значение в каждой строке решения будет соответствовать переменной, указанной в той же строке матрицы X. 9{-1}[Б]\]
Вместо этого с матричным уравнением нам нужно будет умножить обе части уравнения на обратную матрицу A. Это отменит матрицу A с левой стороны, оставив только искомую матрицу X. Слева у нас будет обратная матрица A, умноженная на матрицу B. Результатом этой операции будет матрица 1 x N, содержащая решение для всех переменных. Значение в каждой строке решения будет соответствовать переменной, указанной в той же строке матрицы X. 9{-1}[Б]\]
Можно найти обратную матрицу A вручную, а затем умножить ее на матрицу B, но этот процесс займет больше времени, чем простое решение уравнений с помощью алгебры. Истинная сила метода заключается в том, что компьютерные инструменты, такие как MATLAB или Wolfram Alpha, могут выполнять обращение и умножение матриц за вас.
Матричные линейные односторонние и двусторонние уравнения с двумя переменными над коммутативными кольцами
На этой странице
АннотацияПредварительные материалыСсылкиАвторские праваСтатьи по теме
Предлагается метод решения матричных линейных уравнений 𝐴𝑋+𝐵𝑌=𝐶 и 𝐴𝑋+𝑌𝐵=𝐶 над коммутативными областями Безу с помощью стандартной формы пары обобщенных эквивалентностей относительно пары обобщенных эквивалентностей. Выведены формулы общих решений таких уравнений. Установлены критерии единственности частных решений таких матричных уравнений.
Выведены формулы общих решений таких уравнений. Установлены критерии единственности частных решений таких матричных уравнений.
1. Предварительные
1.1. Введение
Матричные линейные уравнения играют фундаментальную роль во многих докладах по теории управления и теории динамических систем [1–4]. Такие уравнения представляют собой матричные линейные двусторонние уравнения с одной и двумя переменными𝐴𝑋+𝑋𝐵=𝐶,(1.1)𝐴𝑋+𝑌𝐵=𝐶,(1.2) и матричные линейные односторонние уравнения𝐴𝑋+𝐵𝑌=𝐶, (1.3) где 𝐴, 𝐵 и 𝐶 — матрицы соответствующего размера над некоторым полем ℱ или над кольцом ℛ, 𝑋, 𝑌 — неизвестные матрицы. Уравнения (1.1), (1.2) называются уравнениями Сильвестра. Уравнение 𝐴𝑋+𝑋𝐴𝑇=𝐶, где матрица 𝐴𝑇 транспонирована 𝐴, называется уравнением Ляпунова и является частным случаем уравнения Сильвестра. Уравнение (1.3) называют матричным линейным диофантовым уравнением [3, 4].
Рот [5] установил критерии разрешимости матричных уравнений (1.1), (1.2), коэффициенты которых 𝐴, 𝐵, 𝐶 являются матрицами над полем ℱ.
Теорема 1.1 ([5]). Матричное уравнение (1.1), где 𝐴, 𝐵 и 𝐶 — матрицы с элементами из поля ℱ, имеет решение 𝑋 с элементами из ℱ тогда и только тогда, когда матрицы ‖‖‖‖‖‖‖‖‖‖‖‖‖‖‖‖‖‖‖‖𝑀=𝐴𝐶0𝐵,𝑁=𝐴00𝐵(1.4) похожи.
Матричное уравнение (1.2), где 𝐴, 𝐵 и 𝐶 — матрицы с элементами из ℱ, имеет решение 𝑋, 𝑌 с элементами из ℱ тогда и только тогда, когда матрицы 𝑀 и 𝑁 эквивалентны.
Теорема Рота была распространена многими авторами на матричные уравнения (1.1), (1.2) в случаях, когда их коэффициенты являются матрицами над кольцами главных идеалов [6–8], над произвольными коммутативными кольцами [9] и над другие кольца [10–14].
Матричное линейное одностороннее уравнение (1.3) имеет решение тогда и только тогда, когда выполняется одно из следующих условий: (а) наибольший общий левый делитель матриц 𝐴 и B является левым делителем матрицы 𝐶; (б) матрицы ‖𝐴𝐵𝐶‖ и ‖𝐴𝐵0‖ эквивалентны справа.
В случае, когда 𝐴, 𝐵 и 𝐶 в (1.3) — матрицы над кольцом многочленов ℱ[𝜆], где ℱ — поле, эти условия были сформулированы в [1, 4]. Нетрудно показать, что эти условия разрешимости выполняются для матричного линейного одностороннего уравнения (1.3) над коммутативной областью Безу.
Нетрудно показать, что эти условия разрешимости выполняются для матричного линейного одностороннего уравнения (1.3) над коммутативной областью Безу.
Матричные уравнения (1.1), (1.2), (1.3), где коэффициенты 𝐴, 𝐵, 𝐶 — матрицы над полем ℱ, сводятся с помощью произведения Кронекера к эквивалентным системам линейных уравнений [15] . Следовательно, (1.1) над алгебраическим замкнутым полем имеет единственное решение тогда и только тогда, когда матрицы 𝐴 и −𝐵 не имеют общих характеристических корней.
Один из методов решения уравнения матричного полинома,𝐴(𝜆)𝑋(𝜆)+𝑌(𝜆)𝐵(𝜆)=𝐶(𝜆),(1.5) где 𝐴(𝜆), 𝐵(𝜆) и 𝐶(𝜆) — матрицы над кольцом полиномов ℱ[𝜆], основан на сводимости полиномиального уравнения к эквивалентному уравнению с матричными коэффициентами над полем ℱ, т. е. 𝐴𝑍+ 𝑍𝐵=𝐷, (1.6) где 𝐴 и 𝐵 — матрицы-компаньоны матричных полиномов ∑𝐴(𝜆)=𝑟𝑖=0𝐴𝑖𝜆𝑟−𝑖 и ∑𝐵(𝜆)=𝑠𝑗=0𝐵𝑗𝜆𝑠−𝑖 — соответственно матрица 𝐷, 𝐷 — матрица над 16, 17].
Уравнение (1.5) имеет единственное решение 𝑋0(𝜆), 𝑌0(𝜆) ограниченной степени deg𝑋0(𝜆)
Файнштейн и Бар-Несс [18] установили, что для уравнения (1.5), в котором хотя бы один из матричных коэффициентов 𝐴(𝜆) или 𝐵(𝜆) является регулярным, существует единственное минимальное решение 𝑋0(𝜆), 𝑌0( 𝜆), такой, что deg𝑋0(𝜆) В работе предлагается метод решения матричных линейных уравнений (1.2), (1.3) над коммутативной областью Безу. Этот метод основан на использовании стандартной формы пары матриц относительно обобщенной эквивалентности, введенной в [20, 21], и на сравнениях. Введем понятие частных решений таких матричных уравнений. Устанавливаются критерии единственности частных решений и выписываются формулы общих решений таких уравнений. Пусть ℛ — коммутативная область Безу. Далее, 𝑈(ℛ) обозначает группу единиц ℛ, ℛ𝑚 обозначает полный набор вычетов по модулю идеала (𝑚), порожденный элементом 𝑚∈ℛ, или полный набор вычетов по модулю 𝑚. Элемент 𝑎 из ℛ называется ассоциированным с элементом 𝑏 из ℛ, если 𝑎=𝑏𝑢, где 𝑢 принадлежит 𝑈(ℛ). Множество элементов ℛ, по одному из каждого ассоциированного класса, называется полным набором неассоциатов, которые мы обозначали через ℛ′ [24]. Например, если ℛ=ℤ — кольцо целых чисел, то ℤ′ можно выбрать как множество натуральных чисел с нулем, то есть ℤ′={0,1,2,…}, а ℤ𝑚 можно выбрать как множество наименьших неотрицательных остатков, то есть ℤ𝑚={0,1,2,…,𝑚−1}. Многие свойства делимости в кольцах главных идеалов [24–27] легко обобщаются на коммутативную область Безу. В дальнейшем ℛ всегда будет обозначать коммутативную область Безу. Лемма 1.2. Каждый класс вычетов 𝑎(mod𝑚) над ℛ может быть представлен как объединение 𝑎(mod𝑚)=𝑟∈𝑅𝑑𝑎+𝑚𝑟(mod𝑚𝑑),(1.7) где объединение берется по всем вычетам произвольного полного набора вычетов ℛ𝑑 по модулю 𝑑, где 𝑑≠0. В случае, когда ℛ — евклидово кольцо, эта лемма доказана в [27]. Точно так же эта лемма доказывается и в случае, когда ℛ — коммутативная область Безу. Класс элементов 𝑥≡𝑥0(mod𝑚), удовлетворяющих сравнению 𝑎𝑥≡𝑏(mod𝑚), называется решением этого сравнения. Лемма 1.3. Пусть 𝑎𝑥≡𝑏(mod𝑚)(1.8) и (𝑎,𝑚)=𝑑, где 𝑎,𝑏, 𝑚, 𝑑∈ℛ. Сравнение (1.8) имеет решение тогда и только тогда, когда 𝑑∣𝑏, то есть 𝑏=𝑏1𝑑. Доказательство. Необходимость. Это очевидно. Следствие 1.4. Сравнение (1.8) имеет единственное решение 𝑥≡𝑥0(mod𝑚), такое что 𝑥0∈ℛ𝑚 тогда и только тогда, когда (𝑎,𝑚)=1. Пусть𝑎𝑥+𝑏𝑦=𝑐(1.11)
— линейное диофантово уравнение над ℛ и (𝑎,𝑏)=𝑑. Уравнение (1.11) имеет решение тогда и только тогда, когда 𝑑∣𝑐. Предположим, что 𝑎=𝑎1𝑑, 𝑏=𝑏1𝑑 и 𝑐=𝑐1𝑑, где (𝑎1,𝑏1)=1. Тогда из (1.11) следует𝑎1𝑥+𝑏1𝑦=𝑐1. (1.12)
Пусть 𝑥0, 𝑦0 — решение уравнения (1. Решение 𝑥0, 𝑦0 уравнения (1.12), очевидно, является решением (1.11). Определение 1.5. Решение 𝑥0, 𝑦0 уравнения (1.11) такое, что 𝑥0∈ℛ𝑏, называется частным решением этого уравнения. Тогда по леммам 1.2 и 1.3 общее решение (1.11) имеет вид
где 𝑟 — произвольный элемент ℛ𝑑, а 𝑘 — любой элемент ℛ. Следствие 1.6. Частное решение 𝑥0, 𝑦0 уравнения (1.11) с 𝑥0∈ℛ𝑏 единственно тогда и только тогда, когда (𝑎,𝑏)=1. Пример 1.7. Пусть
9𝑥+6𝑦=6(1,14)
— линейное диофантово уравнение над кольцом ℤ. Тогда (9,6)=3=𝑑 и (1.14) разрешимо. Тогда частными решениями уравнения (1.14) являются
𝑥1(0)=0,𝑦1(0)𝑥=1,2(0)=2,𝑦2(0)𝑥=−2,3(0)=4,𝑦3(0)=−5,(1.15)
потому что 𝑥1(0), 𝑥2(0),𝑥3(0)∈ℤ6={0,1,2,3,4,5}. Пусть ℛ — коммутативная область Безу с диагональной редукцией матриц [28], т. е. для каждой матрицы 𝐴 кольца матриц 𝑀(𝑛,ℛ) существуют обратимые матрицы 𝑈, (1.18)
Если 𝜑𝑖∈ℛ′, 𝑖=1,…,𝑛, то матрица 𝐷𝐴 единственна и называется канонической диагональной формой (нормальной формой Смита) матрицы 𝐴. Такие кольца называются адекватными кольцами. Кольцо ℛ называется адекватным, если ℛ — коммутативная область, в которой каждый конечно порождённый идеал является главным и для любого 𝑎 𝑏∈ℛ с 𝑎≠0; 𝑎 можно представить как 𝑎=𝑐𝑑, где (𝑐,𝑏)=1 и (𝑑𝑖,𝑏)≠1 для каждого неединичного фактора 𝑑𝑖 из 𝑑 [29]. Определение 1.8. Пары (𝐴1,𝐴2) и (𝐵1,𝐵2) матриц 𝐴𝑖, 𝐵𝑖∈𝑀(𝑛,ℛ), 𝑖=1,2, называются обобщенно эквивалентными парами, если 𝐴𝑖=𝖈𝐵 , для некоторых обратимых матриц 𝑈 и 𝑉𝑖 над ℛ. В [20, 21] установлены формы пары матриц относительно обобщенной эквивалентности. Теорема 1. Пара (𝐷𝐴,𝑇𝐵), определенная в теореме 1.9, называется стандартной формой пары матриц (𝐴,𝐵) или стандартной парой матриц (𝐴,𝐵). Определение 1.10. Пара (𝐴,𝐵) называется диагонализируемой , если она в обобщенном виде эквивалентна паре диагональных матриц (𝐷𝐴,𝐷𝐵), то есть ее стандартная форма есть пара диагональных матриц (𝐷𝐴,𝐷𝐵). Следствие 1.11. Пусть 𝐴, 𝐵∈𝑀(𝑛,ℛ). Если (𝜑𝑛/𝜑1,𝜓𝑛/𝜓1)=1, то пара матриц (𝐴,𝐵) диагонализируема. С учетом следствия 1.11 ясно, что если (det𝐴,det𝐵)=1, то стандартной формой матриц (𝐴,𝐵) является пара диагональных матриц (𝐷𝐴,𝐷𝐵). Сформулируем критерий диагонализуемости пары матриц. Теорема 1.12. Пусть 𝐴, 𝐵∈𝑀(𝑛,ℛ) и 𝐴 — невырожденная матрица. Тогда пара матриц (𝐴,𝐵) обобщенно эквивалентна паре диагональных матриц (𝐷𝐴,𝐷𝐵) тогда и только тогда, когда эквивалентны матрицы (adj𝐴)𝐵 и (adj𝐷𝐴)𝐷𝐵, где adj𝐴 — присоединенная матрица. Предположим, что матричное линейное одностороннее уравнение (1.3) разрешимо, и пусть (𝐷𝐴,𝑇𝐵) — стандартная форма пары матриц (𝐴,𝐵) из (1.3) относительно обобщенной эквивалентности, т.е. = Φ = 𝑈𝐴𝑉𝐴𝜑 = diag1,…, 𝜑𝑛, 𝑇𝐵 = 𝑈𝐵𝑉𝐵 = ‖‖‖‖‖‖‖‖‖ 𝜓1𝑡0 ⋯ 021𝜓1𝜓2𝑡 ⋯ 0 ⋯⋯⋯⋯ 𝑛1𝜓1𝑡𝑛2𝜓2 ⋯ 𝜓𝑛𝜓𝑛‖‖‖‖‖‖‖ (2.1 )
— нижняя треугольная матрица вида (1.20) с главной диагональю𝐷𝐵𝜓=Ψ=diag1,…,𝜓𝑛, (2.2)
где 𝑈, 𝑉𝐴, 𝑉𝐵∈𝐺𝐿(𝑛,ℛ). Тогда (1.3) эквивалентно уравнению 𝐷𝐴𝑋+𝑇𝐵𝑌=𝐶, (2.3)
где 𝑋=𝑉𝐴−1𝑋, 𝑌=𝑉𝐵−1𝑌 и 𝐶=𝑈𝐶. Пара матриц 𝑋0, 𝑌0, удовлетворяющая (2. Уравнение матрицы (2,3) эквивалентно системе линейного уравнения: 𝜑1̃𝑥11+𝜓1̃𝑦11 = ̃𝑐11, 𝜑1̃𝑥12+𝜓1̃𝑦12 = ̃𝑐12, ⋮1̃𝑥1̃𝑥+𝜓1̃𝑦1𝑛 = ̃𝑐1𝑛, 𝜑21+𝜓1𝑡1̃𝑦11 +1̃𝑦1𝑛1𝑛1𝑛1𝑛1𝑛1𝑛1𝑛1𝑛1𝑛1𝑛1𝑛1𝑛1𝑛1𝑛1𝑛1𝑛1𝑛1𝑛1𝑛1𝑛1𝑛1𝑛1𝑛1𝑛1𝑛1𝑛1𝑛1𝑛1𝑛1𝑛1𝑛1𝑛1𝑛1𝑛1𝑛1𝑛1𝑛1𝑛1𝑛1𝑛1𝑛1𝑛1𝑛1𝑛1𝑛1𝑛1𝑛1𝑛1𝑛1𝑛1𝑛1𝑛1 * 𝜓12 = ̃𝑐12, ⋮1𝑡1𝑛1 +1𝑛1𝑛15. +𝜓𝑛−1𝑡𝑛,𝑛−1̃𝑦𝑛−1,𝑛+𝜓𝑛̃𝑦𝑛𝑛=̃𝑐𝑛𝑛, (2.5)
с переменными ̃𝑥𝑖𝑗, ̃𝑦𝑖𝑗, 𝑖, 𝑗 = 1,…, 𝑛, где 𝑡𝑖𝑗, 𝑖, 𝑗 = 1,…, 𝑛, из (2.3), или+𝑖 -1𝑙 = 1𝜓𝑙𝑡𝑖𝑙̃𝑦𝑙𝑗+𝜓𝑖̃𝑦𝑖𝑗 = ̃𝑐𝑖𝑗, 𝑖 𝑖 ,𝑗=1,…,𝑛, (2.6)
где 𝑋=‖̃𝑥𝑖𝑗‖𝑛1, 𝑌=‖̃𝑦𝑖𝑗‖𝑛1 и 𝐶=‖̃𝑐𝑖𝑗‖𝑛1. Решение этой системы сводится к последовательному решению линейных диофантовых уравнений вида 2.3). Тогда 𝑋=𝑉𝐴𝑋 и 𝑌=𝑉𝐵𝑌 являются решениями матричного уравнения (1.3). Предположим, что пара матриц (𝐴,𝐵) диагонализируема, т.е.
(2.8)
для некоторых матриц 𝑈, 𝑉𝐴, 𝑉𝐵∈𝐺𝐿(𝑛,ℛ). Тогда (1. Из уравнения матрицы (2.9) мы получаем систему линейного диофантинского уравнения: 𝜑𝑖̃𝑥𝑖𝑗+𝜓𝑖̃𝑦𝑖𝑗 = ̃𝑐𝑖𝑗, 𝑖, 𝑗 = 1,…, 𝑛. (2.10) Пусть ̃𝑥 (0) 𝑖𝑗, ̃𝑦 (0) 𝑖𝑗, 𝑖, 𝑗=1,…,𝑛, — частное решение соответствующего уравнения системы (2.10), т. е. ̃𝑥(0)𝑖𝑗 — решение сравнения 𝜑𝑖̃𝑥𝑖𝑗≡̃𝑐𝑖𝑗(mod𝥜𝑖), ∈𝑅𝜓𝑖 и ̃𝑦(0)𝑖𝑗=(̃𝑐𝑖𝑗−𝜑𝑖̃𝑥(0)𝑖𝑗)/𝜓𝑖. Общее решение соответствующего уравнения системы (2.10) по формуле (1.13) будет иметь следующую форму: ̃𝑥𝑖𝑗 = ̃𝑥 (0) 𝑖𝑗+𝜓𝑖𝑑𝑖𝑖𝑟𝑖+𝜓𝑖𝑘𝑖𝑗, ̃𝑦𝑖𝑗 = ̃𝑦 (0) 𝑖𝑗 — 𝜑𝑖𝑑𝑖𝑖𝑟𝑖 -𝜑𝑖𝑘𝑖𝑗, 𝑖 ,𝑗=1,…,𝑛, (2.11)
где 𝑑𝑖𝑖=(𝜑𝑖,𝜓𝑖), 𝑟𝑖 — произвольные элементы из ℛ𝑑𝑖𝑖, а 𝑘𝑖𝑗 — любые элементы из ℛ, 𝑖, 𝑗=1,…,𝑛. Частное решение матричного уравнения (2.9) is𝑋0=‖‖̃𝑥(0)𝑖𝑗‖‖𝑛1,𝑌0=‖‖̃𝑦(0)𝑖𝑗‖‖𝑛1, (2.12)
где ̃𝑥(0)𝑖𝑗, ̃𝑦(0)𝑖𝑗, 𝑖, 𝑗=1,…,𝑛, — частное решение соответствующего уравнения системы (2.10). Тогда𝑋0=𝑉𝐴𝑋0,𝑌0=𝑉𝐵𝑌0(2.13)
является частным решением матричного уравнения (1.3). Таким образом, мы получаем следующую теорему. Теорема 2.1. . Пусть пара матриц (𝐴,𝐵) из матричного уравнения (1.3) диагонализируема и ее стандартной парой является пара матриц (Φ,Ψ) в виде (2.8). Пусть 𝑋0, 𝑌0 — частное решение матричного уравнения (2.9). Тогда общее решение матричного уравнения (2.9) есть 𝑋𝑋 = 0𝜓+diag1𝑑11𝑟1𝜓,…, 𝑛𝑑𝑛𝑛𝑟𝑛𝑌𝐿+𝐾𝐾, 𝑌 = 0𝜑 -diag1𝑑11𝑟1𝜑,…, 𝑛𝑑𝑛𝑛𝑟𝑛𝐿 φ𝐾, (2.14) где 𝑑𝑖𝑖=(𝜑𝑖,𝜓𝑖), 𝑟𝑖 — произвольные элементы из ℛ𝑑𝑖𝑖, 𝑖=1,…,𝑛; 𝐿=‖𝑙𝑖𝑗‖𝑛1, 𝑙𝑖𝑗=1, 𝑖, 𝑗=1,…,𝑛; 𝐾=‖𝑘𝑖𝑗‖𝑛1, 𝑘𝑖𝑗 — произвольные элементы ℛ. Пример 2.2. Рассмотрим уравнение
𝐴𝑋+𝐵𝑌=𝐶, (2.16)
для матриц
‖‖‖‖‖‖‖‖‖‖‖‖‖‖‖‖‖‖‖‖‖‖‖‖‖‖‖‖‖‖𝐴=−1735−918,𝐵=26761236,𝐶=1534615(2,17)
матрицы над ℤ и
(2.18)
являются неизвестными матрицами. Условия единственности решений ограниченной степени (минимальных решений) матричных линейных полиномиальных уравнений (1.5) найдены в [16–19]. Приводятся условия единственности частных решений матричного линейного уравнения над коммутативной областью Безу ℛ. Теорема 2.3. Матричное уравнение (2.3) имеет единственное частное решение 𝑋0=‖‖̃𝑥(0)𝑖𝑗‖‖𝑛1,𝑌0=‖‖̃𝑦(0)𝑖𝑗‖‖𝑛1(2.30) такое, что ̃𝑥(0)𝑖𝑗∈ℛ𝜓𝑖, 𝑖, 𝑗=1,…,𝑛 тогда и только тогда, когда (det𝐷𝐴,det𝑇𝐵)=1. Доказательство. Из матричного уравнения (2.3) получаем систему линейных уравнений (2.6). Решение этой системы сводится к последовательному решению линейных диофантовых уравнений вида (2. Теорема 2.4. Пусть 𝑋0=‖̃𝑥(0)𝑖𝑗‖𝑛1, 𝑌0=‖̃𝑦(0)𝑖𝑗‖𝑛1, где ̃𝑥(0)𝑖𝑗∈ℛ𝜓𝑖,𝑖=1,…, — частное решение матрицы уравнение (2.3). Доказательство. Частное решение вида (2.30) уравнения (2. Рассмотрим линейное двустороннее уравнение матрицы (1.2), где 𝐴, 𝐵 и 𝐶 являются матрицами над коммутативным доменом bezout ℛ и 𝑈𝐴𝐴𝑉𝐴 = φ = diag1,…,𝜑𝑛,𝜑𝑖∣𝜑𝑖+1,𝑈𝐵𝐵𝑉𝐵=𝐷𝐵𝜓=Ψ=diag1,…,𝜓𝑛,𝜓𝑖∣𝜓𝑖+1,𝑑.3𝑖=1,𝑑.3𝑖=1,𝑑.
— канонические диагональные формы матриц 𝐴 и 𝐵 соответственно и 𝑈𝐴, 𝑉𝐴, 𝑈𝐵, 𝑉𝐵∈𝐺𝐿(𝑛,ℛ). Тогда (1.2) эквивалентно Φ𝑋+𝑌Ψ=𝐶, (3.2)
где 𝑋=𝑉𝐴−1𝑋𝑉𝐵, 𝑌=𝑈𝐴𝑌𝑈𝐵−1 и 𝐶=𝑈𝐴𝐶𝑉𝐵. Такой подход к решению (1.2), где 𝐴, 𝐵 и 𝐶 — матрицы над кольцом многочленов ℱ[𝜆], где ℱ — поле, применялся в [3]. Уравнение (3. Аналогично (2.3) докажем, что частное решение (3.2) единственно тогда и только тогда, когда (detΦ,detΝ) =1. Затем так же, как и для (1.3), запишем общее решение матричного уравнения (1.2). Теорема 3.2. Предположим, что 𝑋0=‖̃𝑥(0)𝑖𝑗‖𝑛1 и 𝑌0=‖̃𝑦(0)𝑖𝑗‖𝑛1, где ̃𝑥(0)𝑖𝑗∈ℛ𝜓𝑖 — единственное частное решение матрицы, 𝑖=1,… уравнение (3.2) и 𝐷𝐴𝜑=Φ=diag1,…,𝜑𝑛,𝐷𝐵𝜓=Ψ=diag1,…,𝜓𝑛(3. T. Kaczorek, Полиномиальные и рациональные матрицы , серия инженерии связи и управления, Springer, London, UK , 2007. Просмотр по адресу: Zentralblatt MATH В. Кучера, “Алгебраическая теория дискретного оптимального управления для систем с одной переменной. I. Предварительные», Кибернетика , том. 9, стр. 94–107, 1973. Посмотреть по адресу: Google Scholar | Zentralblatt MATH В. Посмотреть по адресу: Google Scholar В. А. Волович и П. Дж. Анцаклис, «Канонические диофантовы уравнения с приложениями», SIAM Journal on Control and Optimization , том. 22, нет. 5, стр. 777–787, 1984. Посмотреть по адресу: Сайт издателя | ученый Google | Zentralblatt MATH WE Roth, «Уравнения AX-YB=C и AX-XB=C в матрицах», Proceedings of the American Mathematical Society , vol. 3, стр. 392–396, 1952. Посмотреть по адресу: Google Scholar | Zentralblatt MATH M. Newman, «Нормальная форма Смита для разделенной матрицы», Journal of Research of the National Bureau of Standards , том. Посмотреть по адресу: Google Scholar | Zentralblatt MATH C. R. Johnson and M. Newman, «Условие диагонализируемости разделенной матрицы», Journal of Research of the National Bureau of Standards , vol. 79, нет. 1–2, стр. 45–48, 1975. Посмотреть по адресу: Google Scholar | Zentralblatt MATH Р. Б. Фейнберг, «Эквивалентность секционированных матриц», Журнал исследований Национального бюро стандартов , том. 80, нет. 1, стр. 89–97, 1976. Посмотреть по адресу: Google Scholar | Zentralblatt MATH WH Gustafson, «Теоремы Рота о коммутативных кольцах», Linear Algebra and its Applications , vol. 23, стр. 245–251, 1979. Посмотреть по адресу: Сайт издателя | ученый Google | Zentralblatt MATH RE Hartwig, «Проблема эквивалентности Рота в единичных правильных кольцах», Proceedings of the American Mathematical Society , том. Посмотреть по адресу: Google Scholar | Zentralblatt MATH WH Gustafson и JM Zelmanowitz, «О матричной эквивалентности и матричных уравнениях», Linear Algebra and its Applications , vol. 27, стр. 219–224, 1979. Посмотреть по адресу: Сайт издателя | ученый Google | Zentralblatt MATH Р. М. Гуральник, «Теоремы Рота и разложение модулей», Линейная алгебра и ее приложения , том. 39, стр. 155–165, 1981. Посмотреть по адресу: Сайт издателя | ученый Google | Zentralblatt MATH L. Huang и J. Liu, «Расширение теоремы Рота для матричных уравнений над кольцом», Linear Algebra and its Applications , vol. 259, стр. 229–235, 1997. Посмотреть по адресу: Сайт издателя | ученый Google | Zentralblatt MATH Р. Посмотреть по адресу: Google Scholar | Zentralblatt MATH П. Ланкастер и М. Тисменецкий, Теория матриц , Информатика и прикладная математика, Academic Press, Орландо, Флорида, США, 2-е издание, 1985. С. Барнетт, “ Правильные полиномиальные матрицы с относительно простыми определителями», Proceedings of the Cambridge Philosophical Society , том. 65, стр. 585–590, 1969. Посмотреть по адресу: Google Scholar | Zentralblatt MATH В. Петрычкович, «Клеточно-треугольная и клеточно-диагональная факторизация клеточно-треугольных и клеточно-диагональных полиномиальных матриц», Mathematical Notes , vol. 37, нет. Просмотр по адресу: Google Scholar Фейнштейн Дж., Бар-Несс Ю. О единственности минимального решения матричного полиномиального уравнения A(λ) X(λ)+Y(λ)B(λ)=C(λ)», Журнал Института Франклина , том. 310, нет. 2, стр. 131–134, 1980. Посмотреть по адресу: Сайт издателя | ученый Google | Zentralblatt MATH Прокип В. М., «О единственности решения матричного полиномиального уравнения A(λ)X(λ)−Y(λ)B(λ)=C(λ)», Лобачевский журнал математики , об. 29, нет. 3, стр. 186–191, 2008 г. Посмотреть по адресу: Сайт издателя | ученый Google | Zentralblatt MATH В. Петрычкович, «Обобщенная эквивалентность пар матриц», Линейная и полилинейная алгебра , том. 48, нет. 2, стр. Посмотреть по адресу: Сайт издателя | ученый Google | Zentralblatt MATH В. Петрычкович, «Стандартная форма пар матриц относительно обобщенной эквивалентности», Вестник Львовского университета , вып. 61, стр. 153–160, 2003. Посмотреть по адресу: Google Scholar П. М. Кон, Свободные кольца и их отношения , Academic Press, Лондон, Великобритания, 1971. С. Фридланд, «Матрицы над областями целочисленности», в CRC Handbook of Linear Algebra , стр. 23-1–23-11, Chapman & Hall, New York, NY, USA, 2007. Посмотреть по адресу: Google Scholar M. Newman, Integral Matrices , Academic Press, New York, NY, USA, 1972. B.L. , NY, USA, 1991. А. И. Боревич и И. Р. Шафаревич, Теория чисел , том. 20 из Перевод с русского Ньюкомб Гринлиф. Pure and Applied Mathematics , Academic Press, New York, NY, USA, 1966. Родосский К.А., Алгоритм Евклида , Наука, Москва, Россия, 1988. 1.2. Линейные сравнения и диофантовы уравнения
 Коммутативная область ℛ называется областью Безу, если любые два элемента 𝑎, 𝑏∈ℛ имеют наибольший общий делитель (𝑎,𝑏)=𝑑, 𝑑∈ℛ и 𝑑=𝑝𝑎+𝑞𝑏, для некоторых 𝑝, 𝑞∈ℛ [22]. , 23]. Обратите внимание, что коммутативная область ℛ является областью Безу тогда и только тогда, когда любой конечно порожденный идеал является главным.
Коммутативная область ℛ называется областью Безу, если любые два элемента 𝑎, 𝑏∈ℛ имеют наибольший общий делитель (𝑎,𝑏)=𝑑, 𝑑∈ℛ и 𝑑=𝑝𝑎+𝑞𝑏, для некоторых 𝑝, 𝑞∈ℛ [22]. , 23]. Обратите внимание, что коммутативная область ℛ является областью Безу тогда и только тогда, когда любой конечно порожденный идеал является главным. Напомним некоторые из них, которые будут использованы позже.
Напомним некоторые из них, которые будут использованы позже.
Пусть 𝑎=𝑎1𝑑, 𝑏=𝑏1𝑑,𝑚=𝑚1𝑑, где (𝑎1,𝑚1)=1, и 𝑥≡𝑥0(mod𝑚1) — решение сравнения 𝑎1𝑥≡𝑏1mod𝑚1.(1.9) Тогда общее решение сравнения (1.8) имеет вид: 𝑥≡𝑥0+𝑚1𝑟(mod𝑚),(1. 10) где 𝑟 — любой элемент из ℛ𝑑.
10) где 𝑟 — любой элемент из ℛ𝑑.
Достаточность. Пусть (𝑎,𝑚)=𝑑 и 𝑑∣𝑏. Тогда, разделив обе части сравнения (1.8) и 𝑚 на 𝑑, получим сравнение (1.9), где (𝑎1,𝑚1)=1. Существуют элементы 𝑢, 𝑣 из ℛ такие, что 𝑎1𝑢+𝑚1𝑣=1. Таким образом, мы имеем 𝑎1𝑢≡1(mod𝑚1). Умножьте две части этого сравнения на 𝑏1≠0, то есть 𝑎1𝑢𝑏1≡𝑏1(mod𝑚1). Следовательно, 𝑥≡𝑢𝑏1(mod𝑚1) является решением сравнения (1.9). Установите 𝑢𝑏1=𝑥0. Тогда по лемме 1.2 получаем общее решение сравнения (1.8): 𝑥≡𝑥0+𝑚1𝑟(mod𝑚), где 𝑟 — произвольный элемент из ℛ𝑑. Это доказывает лемму. 12), т. е. 𝑥0 — решение сравнения 𝑎1𝑥≡𝑐1(mod𝑏1), 𝑥0∈ℛ𝑏1 и 𝑦0=(𝑐1−𝑎1𝑥0)/𝑏1. Легко проверить, что если 𝑥0∈ℛ𝑏1, то 𝑥0∈ℛ𝑏.
12), т. е. 𝑥0 — решение сравнения 𝑎1𝑥≡𝑐1(mod𝑏1), 𝑥0∈ℛ𝑏1 и 𝑦0=(𝑐1−𝑎1𝑥0)/𝑏1. Легко проверить, что если 𝑥0∈ℛ𝑏1, то 𝑥0∈ℛ𝑏.
Тогда общее решение (1.14) можно записать, используя (1.13)
6𝑥=0+39𝑟+6𝑘,𝑦=1−3𝑟−9𝑘, (1.16)
то есть,
𝑥=2𝑟+6𝑘,𝑦=1−3𝑟−9𝑘, (1. 17)
где 𝑟 — произвольный элемент ℤ3={0,1,2}, а 𝑘 — любой элемент ℤ.
17)
где 𝑟 — произвольный элемент ℤ3={0,1,2}, а 𝑘 — любой элемент ℤ. 1.3. Стандартная форма пары матриц
 9. Пусть ℛ — адекватное кольцо, а 𝐴, 𝐵∈𝑀(𝑛,ℛ) — неособые матрицы и 𝐷𝐴𝜑=Φ=diag1,…,𝜑𝑛,𝐷𝐵𝜓=Ψ=diag1,…,𝜓𝑛(1,19) — их канонические диагональные формы.
9. Пусть ℛ — адекватное кольцо, а 𝐴, 𝐵∈𝑀(𝑛,ℛ) — неособые матрицы и 𝐷𝐴𝜑=Φ=diag1,…,𝜑𝑛,𝐷𝐵𝜓=Ψ=diag1,…,𝜓𝑛(1,19) — их канонические диагональные формы.
Тогда пара матриц (𝐴,𝐵) в обобщенном виде эквивалентна паре (𝐷𝐴,𝑇𝐵), где 𝑇𝐵 имеет следующий вид: 𝑇𝐵 = ‖‖‖‖‖‖‖‖ 𝜓1𝑡0 ⋯ 021𝜓1𝜓2𝑡 ⋯ 0 𝑛 𝑛1𝜓1𝑡𝑛2𝜓2 ⋯ 𝜓𝑛𝜓𝑛𝜓𝑛‖‖‖‖‖‖, (1.20) 𝑡𝑖𝑗∈ℛ𝛿𝑖𝑗, где 𝛿𝑖𝑗 = (𝜑𝑖/𝜑𝑗, (1.20) . 𝜓𝑖/𝜓𝑗), 𝑖, 𝑗=1,…,𝑛, 𝑖>𝑗. 
2. Матричные линейные односторонние уравнения 𝐴𝑋+𝐵𝑌=𝐶
2.1. Построение решений матричных линейных односторонних уравнений с двумя переменными
 3), называется решением этого уравнения. Тогда𝑋0=𝑉𝐴𝑋0,𝑌0=𝑉𝐵𝑌0(2.4)
является решением (1.3).
3), называется решением этого уравнения. Тогда𝑋0=𝑉𝐴𝑋0,𝑌0=𝑉𝐵𝑌0(2.4)
является решением (1.3). 2.2. Общее решение матричного уравнения 𝐴𝑋+𝐵𝑌=𝐶 с диагонализируемой парой матриц (𝐴,𝐵)
 3) эквивалентно уравнению Φ𝑋+Ψ𝑌=𝐶, (2.9)
где 𝑋=𝑉𝐴−1𝑋, 𝑌=𝑉𝐵−1𝑌 и 𝐶=𝑈𝐶.
3) эквивалентно уравнению Φ𝑋+Ψ𝑌=𝐶, (2.9)
где 𝑋=𝑉𝐴−1𝑋, 𝑌=𝑉𝐵−1𝑌 и 𝐶=𝑈𝐶.
Общее решение матричного уравнения (1.3) имеет вид 𝑋=𝑉𝐴𝑋,𝑌=𝑉𝐵𝑌.(2.15)
Матричное уравнение (2.16) разрешимо.
Пара матриц (𝐴,𝐵) из матричного уравнения (2.16) по теореме 1.12 диагонализируема, так как матрицы
‖‖‖‖‖‖‖‖‖‖‖‖‖‖‖‖‖‖‖‖‖ ‖ ‖‖‖‖‖‖ ‖‖‖‖‖‖‖‖‖‖‖‖‖‖‖‖=‖‖‖‖‖‖‖‖‖‖0012180012(2. 19)
эквивалентны. Следовательно,
𝑈𝐴𝑉𝐴=𝐷𝐴=Φ=diag(1,9),𝜑1=1,𝜑2=9,𝑈𝐵𝑉𝐵=𝐷𝐵=Ψ=diag(2,12),𝜓1=2,𝜓2=12,(2.20)
куда
‖‖‖‖‖‖‖‖‖‖𝑈=1−201,𝑉𝐴=‖‖‖‖‖‖‖‖‖‖2111,𝑉𝐵=‖‖‖‖‖‖‖‖‖‖‖‖−1,3.3.3 )
19)
эквивалентны. Следовательно,
𝑈𝐴𝑉𝐴=𝐷𝐴=Φ=diag(1,9),𝜑1=1,𝜑2=9,𝑈𝐵𝑉𝐵=𝐷𝐵=Ψ=diag(2,12),𝜓1=2,𝜓2=12,(2.20)
куда
‖‖‖‖‖‖‖‖‖‖𝑈=1−201,𝑉𝐴=‖‖‖‖‖‖‖‖‖‖2111,𝑉𝐵=‖‖‖‖‖‖‖‖‖‖‖‖−1,3.3.3 )
Тогда (2.16) эквивалентно уравнению
Φ𝑋+Ψ𝑌=𝐶, (2.22)
куда
𝑋 = 𝑉𝐴 -1‖‖‖‖‖𝑋 = ̃𝑥11̃𝑥12̃𝑥21̃𝑥22‖‖‖‖‖, 𝑌 = 𝑉𝐵 -1‖‖‖‖‖𝑌 = ̃𝑦11̃𝑦12̃𝑦21̃𝑦22‖‖‖, ‖‖‖‖‖‖ ‖𝐶=𝑈𝐶=34615.(2.23)
Из матричного уравнения (2.22) получаем систему линейных диофантовых уравнений:
̃𝑥11+2̃𝑦11=3,̃𝑥12+2̃𝑦12=4,9̃𝑥21+12̃𝑦21=6,9̃𝑥22+12̃𝑦22=15.(2.24)
Частное решение каждого линейного уравнения системы (2.24) имеет следующий вид:
̃𝑥(0)11=1,̃𝑦(0)11=1,̃𝑥(0)12=0,̃𝑦(0)12=2,̃𝑥(0)21=2,̃𝑦(0)21=−1,̃𝑥 (0)22=3,̃𝑦(0)22=−1.(2.25)
Частным решением матричного уравнения (2.22) является
𝑋0=‖‖‖‖‖‖‖‖‖‖,𝑌10230=‖‖‖‖‖‖‖‖‖‖12−1−1.(2.26)
Тогда в силу (2.14) общее решение матричного уравнения (2.22 ) является
‖‖‖‖‖‖‖‖++‖‖‖‖‖𝑋 = 10232𝑟12𝑟14𝑟24‖2‖‖‖‖+‖‖‖‖2𝑘112𝑘1212𝑘212‖‖‖++‖‖‖ ‖ ‖ ‖ ‖ ‖ ‖ ‖‖ ‖ ‖‖ ‖‖ ‖‖ ‖‖ ‖‖ ‖‖ ‖ ‖ ‖‖‖‖‖‖ ‖‖‖‖‖𝑟𝑌=12−1−11𝑟13𝑟23𝑟2‖‖‖‖‖−‖‖‖‖‖𝑘11𝑘129𝑘219𝑘22‖‖‖‖‖, (2,27)
или же
‖‖‖‖𝑋 = 1+2𝑘112𝑘122+4𝑟2+12𝑘213+4𝑟2+12𝑘22‖‖‖‖, ‖‖‖𝑌 = 1 — 𝑘112–12–1–2𝑟21-1–2𝑟2-9𝑘22 ‖‖‖‖‖, (2. 28)
где 𝑟1 — из ℤ1={0}, 𝑟2 — произвольный элемент из ℤ3={0,1,2}, а 𝑘𝑖𝑗, 𝑖, 𝑗=1,2 — произвольные элементы из ℤ.
28)
где 𝑟1 — из ℤ1={0}, 𝑟2 — произвольный элемент из ℤ3={0,1,2}, а 𝑘𝑖𝑗, 𝑖, 𝑗=1,2 — произвольные элементы из ℤ.
Наконец, общее решение матричного уравнения (2.16) имеет вид
𝑋 = 𝑉𝐴𝑉𝐴‖‖‖‖𝑋 = 4+4𝑟2+4𝑘11+12𝑘213+4𝑟2+4𝑘12+12𝑘223+4𝑟2+2𝑘11+12𝑘213+4𝑟2+2𝑘12+12𝑘22‖‖‖, 𝑌 = 𝑉𝐵𝑉𝐵‖‖ (9)0007 2.3. Единственность частных решений матричного линейного одностороннего уравнения
 7).
7).
Матричное уравнение (2.3) имеет единственное частное решение 𝑋0=‖̃𝑥(0)𝑖𝑗‖𝑛1, 𝑌0=‖̃𝑦(0)𝑖𝑗‖𝑛1 такое, что ,…,𝑛, тогда и только тогда, когда каждое линейное диофантово уравнение вида (2.7) имеет единственное частное решение ̃𝑥(0)𝑖𝑗, ̃𝑦(0)𝑖𝑗 такое, что ̃𝑥(0)𝑖𝑗∈ℛ𝜓𝑖, 𝑖, 𝑗=1 ,…,𝑛. По следствию 1.6 это верно тогда и только тогда, когда (𝜑𝑖,𝜓𝑖)=1 для всех 𝑖=1,…,𝑛. Отсюда следует, что (det𝐷𝐴,det𝑇𝐵)=1. Это завершает доказательство.
Тогда общее решение матричного уравнения (2.3) имеет вид 𝑋𝑋=0𝑌+Ψ𝐾,𝑌=0−Φ𝐾, (2.31) где Φ=𝐷𝐴 и Ψ=𝐷𝐵 — канонические диагональные формы 𝐴 и 𝐵 из матричного уравнения (1.3) соответственно, 𝐾=‖𝑘𝑖𝑗‖𝑛1, 𝑘𝑖𝑗 — произвольные элементы ℛ, 𝑖, 𝑗=1,…,𝑛.
Общее решение матричного уравнения (1.3) есть пара матриц 𝑋=𝑉𝐴𝑋,𝑌=𝑉𝐵𝑌. (2.32) 3) единственно тогда и только тогда, когда (det𝐷𝐴,det𝑇𝐵)=1, то есть (det𝐴,det𝐵)=1. Тогда по следствию 1.11 пара матриц (𝐴,𝐵) диагонализируема и (1.3) дает уравнение вида (2.9).
3) единственно тогда и только тогда, когда (det𝐷𝐴,det𝑇𝐵)=1, то есть (det𝐴,det𝐵)=1. Тогда по следствию 1.11 пара матриц (𝐴,𝐵) диагонализируема и (1.3) дает уравнение вида (2.9).
Таким образом, по теореме 2.1 получаем формулу (2.31) общего решения (2.3) и формулу (2.32) для вычисления общего решения (1.3) в случае, когда (2.3) имеет единственное частное решение вида (2.30). Теорема доказана. 3. Линейные двусторонние уравнения матрицы 𝐴𝑋+𝑌𝐵 = 𝐶
 2) эквивалентно системе линейных диофантовых уравнений Пусть 𝑋0=‖‖̃𝑥(0)𝑖𝑗‖‖𝑛1,𝑌0=‖‖̃𝑦(0)𝑖𝑗‖‖𝑛1(3.4) — частное решение матричного уравнения (3.2), т. е. ̃𝑥(0)𝑖𝑗, ̃𝑦(0)𝑖𝑗, 𝑖, 𝑗=1,…,𝑛 — частные решения линейных диофантовых уравнений системы (3.3).
2) эквивалентно системе линейных диофантовых уравнений Пусть 𝑋0=‖‖̃𝑥(0)𝑖𝑗‖‖𝑛1,𝑌0=‖‖̃𝑦(0)𝑖𝑗‖‖𝑛1(3.4) — частное решение матричного уравнения (3.2), т. е. ̃𝑥(0)𝑖𝑗, ̃𝑦(0)𝑖𝑗, 𝑖, 𝑗=1,…,𝑛 — частные решения линейных диофантовых уравнений системы (3.3).
Общее решение матричного уравнения (3.2) имеет вид 𝑋𝑋=0+𝑊Ψ𝑌+𝐾Ψ,𝑌=0−𝑊Φ−𝐾Φ, (3.5) где 𝑊𝑊 = ‖ (𝜓𝑗/𝑑𝑖𝑗) 𝑤𝑖𝑗𝑤𝑖𝑗1, 𝑊φ = ‖ (𝜑𝑗/𝑑𝑖𝑗) 𝑤𝑖𝑗𝑤𝑖𝑗1, где 𝑤𝑖𝑗 являются произвольными элементами ℛ𝑑𝑖𝑗, и 𝐾 = 𝑘𝑖𝑗𝑘𝑖𝑗1, где 𝑘𝑖𝑗 являются произвольными элементами ℛ, 𝑖 𝑖 , 𝑗=1,…,𝑛.
Общее решение матричного уравнения (1.2) имеет вид 𝑋=𝑉𝐴𝑋𝑉𝐵−1,𝑌=𝑈𝐴−1𝑌𝑈𝐵.(3.6) 7) являются каноническими диагональными формами матриц 𝐴, 𝐵 из матричного уравнения (1.2) соответственно.
7) являются каноническими диагональными формами матриц 𝐴, 𝐵 из матричного уравнения (1.2) соответственно.
Тогда общее решение матричного уравнения (3.2) имеет вид 𝑋𝑋=0𝑌+𝐾Ψ,𝑌=0−𝐾Φ, (3.8) где 𝐾=‖𝑘𝑖𝑗‖𝑛1; 𝑘𝑖𝑗 — произвольные элементы ℛ, 𝑖, 𝑗=1,…,𝑛.
Общее решение матричного уравнения (1.2) имеет вид 𝑋 = 𝑉𝐴𝑋𝑉𝐵 -1, 𝑌 = 𝑈𝐴 -1𝑌𝑈𝐵. (3.9) Ссылки
 Кучера, «Алгебраическая теория дискретного оптимального управления для систем с несколькими переменными», Кибернетика , том. 10/12, приложение, стр. 3–56, 1974.
Кучера, «Алгебраическая теория дискретного оптимального управления для систем с несколькими переменными», Кибернетика , том. 10/12, приложение, стр. 3–56, 1974. 78, стр. 3–6, 1974.
78, стр. 3–6, 1974. 59, нет. 1, стр. 39–44, 1976.
59, нет. 1, стр. 39–44, 1976. Э. Хартвиг и П. Патрисио, «О псевдоэквивалентности Рота над кольцами», Электронный журнал линейной алгебры , том. 16, стр. 111–124, 2007 г.
Э. Хартвиг и П. Патрисио, «О псевдоэквивалентности Рота над кольцами», Электронный журнал линейной алгебры , том. 16, стр. 111–124, 2007 г. 6, pp. 431–435, 1985.
6, pp. 431–435, 1985. 179–188, 2000.
179–188, 2000.
Посмотреть по адресу:
Сайт издателя | ученый Google | Zentralblatt МАТЕМАТИКА
О. Хелмер, «Теорема об элементарных делителях для некоторых колец без условия цепи», Бюллетень Американского математического общества , том. 49, стр. 225–236, 1943.
Посмотреть по адресу:
Сайт издателя | ученый Google | Zentralblatt MATH
Copyright
Copyright © 2012 Н. С. Джалюк и В. М. Петрычкович. Это статья с открытым доступом, распространяемая в соответствии с лицензией Creative Commons Attribution License, которая разрешает неограниченное использование, распространение и воспроизведение на любом носителе при условии надлежащего цитирования оригинальной работы.
Это статья с открытым доступом, распространяемая в соответствии с лицензией Creative Commons Attribution License, которая разрешает неограниченное использование, распространение и воспроизведение на любом носителе при условии надлежащего цитирования оригинальной работы.
Решение систем уравнений с использованием матриц — алгебра среднего уровня
Системы линейных уравнений
Цели обучения
К концу этого раздела вы сможете:
- Записывать расширенную матрицу для системы уравнений
- Использовать операции со строками на матрице
- Решение систем уравнений с использованием матриц
Прежде чем начать, пройдите этот тест на готовность.
- Решить:
Если вы пропустили эту проблему, просмотрите (рисунок).
- Решить:
Если вы пропустили эту проблему, просмотрите (рисунок).
- Оценить, когда и
Если вы пропустили эту проблему, просмотрите (рисунок).

Напишите расширенную матрицу для системы уравнений
Решение системы уравнений может быть утомительной операцией, где простая ошибка может испортить поиск решения. Доступен альтернативный метод, использующий основные процедуры исключения, но с более простыми обозначениями. Метод предполагает использование матрицы. Матрица представляет собой прямоугольный массив чисел, расположенных в строках и столбцах.
Матрица
Матрица представляет собой прямоугольный массив чисел, расположенных в строках и столбцах.
Матрица с m строк и n столбцов имеет порядок. Матрица слева внизу имеет 2 строки и 3 столбца, поэтому она имеет порядок Мы говорим, что это матрица 2 на 3.
Каждое число в матрице называется элементом или записью в матрице.
Мы будем использовать матрицу для представления системы линейных уравнений. Мы записываем каждое уравнение в стандартной форме, а коэффициенты переменных и константы каждого уравнения становятся строкой в матрице. Тогда каждый столбец будет коэффициентом одной из переменных в системе или констант. Вертикальная черта заменяет знаки равенства. Полученную матрицу назовем расширенной матрицей системы уравнений.
Мы записываем каждое уравнение в стандартной форме, а коэффициенты переменных и константы каждого уравнения становятся строкой в матрице. Тогда каждый столбец будет коэффициентом одной из переменных в системе или констант. Вертикальная черта заменяет знаки равенства. Полученную матрицу назовем расширенной матрицей системы уравнений.
Обратите внимание, что первый столбец состоит из всех коэффициентов x , второй столбец содержит все коэффициенты y , а третий столбец содержит все константы.
Запишите каждую систему линейных уравнений в виде расширенной матрицы:
ⓐⓑ
ⓐ Второе уравнение не в стандартной форме. Перепишем второе уравнение в стандартной форме.
Заменим второе уравнение его стандартной формой. В расширенной матрице первое уравнение дает нам первую строку, а второе уравнение дает нам вторую строку. Вертикальная черта заменяет знаки равенства.
ⓑ Все три уравнения имеют стандартную форму. В расширенной матрице первое уравнение дает нам первую строку, второе уравнение дает нам вторую строку, а третье уравнение дает нам третью строку. Вертикальная черта заменяет знаки равенства.
В расширенной матрице первое уравнение дает нам первую строку, второе уравнение дает нам вторую строку, а третье уравнение дает нам третью строку. Вертикальная черта заменяет знаки равенства.
Запишите каждую систему линейных уравнений в виде расширенной матрицы:
ⓐⓑ
ⓐ
ⓑ
Запишите каждую систему линейных уравнений в виде расширенной матрицы:
900ⓑ0002 ⓐ
ⓑ
Когда мы решаем системы уравнений с использованием матриц, важно иметь возможность переключаться между системой и матрицей. В следующем примере нас просят взять информацию из матрицы и написать систему уравнений.
Запишите систему уравнений, соответствующую расширенной матрице:
Мы помним, что каждая строка соответствует уравнению и что каждая запись является коэффициентом переменной или константой. Вертикальная черта заменяет знак равенства. Поскольку эта матрица представляет собой , мы знаем, что она преобразуется в систему трех уравнений с тремя переменными.
Напишите систему уравнений, соответствующую расширенной матрице:
Напишите систему уравнений, соответствующую расширенной матрице:
Использование операций со строками над матрицей
Как только система уравнений будет представлена в форме расширенной матрицы, мы будем выполнять операции над строками, которые приведут нас к решению.
Для решения методом исключения не имеет значения, в каком порядке мы располагаем уравнения в системе. Точно так же в матрице мы можем поменять местами строки.
При решении методом исключения мы часто умножаем одно из уравнений на константу. Поскольку каждая строка представляет собой уравнение, и мы можем умножить каждую часть уравнения на константу, аналогичным образом мы можем умножить каждую запись в строке на любое действительное число, кроме 0.
При исключении мы часто добавляем кратное одной строке к другой ряд. В матрице мы можем заменить строку на ее сумму, кратную другой строке.
Эти действия называются операциями со строками и помогут нам использовать матрицу для решения системы уравнений.
Операции со строками
В матрице следующие операции могут выполняться над любой строкой, и результирующая матрица будет эквивалентна исходной матрице.
- Поменяйте местами любые два ряда.
- Умножить строку на любое действительное число, кроме 0.
- Добавить ненулевое кратное одной строки к другой строке.
Выполнение этих операций несложно, но все арифметические действия могут привести к ошибке. Если мы используем систему для записи операций со строками на каждом этапе, гораздо проще вернуться и проверить нашу работу.
Мы используем заглавные буквы с нижними индексами для представления каждой строки. Затем мы показываем операцию слева от новой матрицы. Чтобы показать перестановку строки:
Чтобы умножить строку 2 на:
Чтобы умножить строку 2 на и добавить к строке 1:
Выполните указанные операции над расширенной матрицей:
␓ меняет местами строки 2 и 3.
ⓑ Умножить строку 2 на 5.
ⓒ Умножить строку 3 на и прибавить к строке 1.
ⓐ Поменяем местами 2 и 3 строки.
ⓑ 2 строку умножим на 5.
ⓒ 3 строку умножим на и прибавим к 1 строке.
ⓐ Поменять местами строки 1 и 3.
ⓑ Умножить строку 3 на 3.
ⓒ Умножить строку 3 на 2 и добавить ко второй строке. 1 и 2,
ⓑ Умножить 1-ю строку на 2,
ⓒ 2-ю строку умножить на 3 и прибавить к 1-й строке. использовать для достижения цели. Это именно то, что мы сделали, когда мы сделали исключение. Мы решили, на какое число умножить строку, чтобы при сложении строк исключалась переменная.
Учитывая эту систему, что бы вы сделали, чтобы устранить х ?
Следующий пример делает то же самое, но с матрицей.
Выполните необходимую операцию со строками, чтобы первая запись в строке 2 была равна нулю в расширенной матрице:
Чтобы сделать 4 равными 0, мы могли бы умножить строку 1 на и затем добавить ее к строке 2.
Выполнить необходимую операцию со строками, чтобы первая запись в строке 2 была равна нулю в расширенной матрице:
Выполнить необходимую операцию со строками, чтобы первая запись в строке 2 была равна нулю в расширенной матрице:
Решение систем уравнений с использованием матриц
Чтобы решить систему уравнений с использованием матриц, мы преобразуем расширенную матрицу в матрицу в виде строк-ступенчатых операций, используя операции со строками. Для непротиворечивой и независимой системы уравнений ее расширенная матрица имеет форму эшелона строк, когда слева от вертикальной линии каждая запись на диагонали равна 1, а все записи ниже диагонали — нули.
Форма Row-Echelon
Для непротиворечивой и независимой системы уравнений ее расширенная матрица находится в строка-эшелон формы , когда слева от вертикальной линии каждая запись на диагонали равна 1, а все записи ниже диагонали — нулями.
Как только мы приведем расширенную матрицу к ступенчатой форме, мы можем написать эквивалентную систему уравнений и прочитать значение по крайней мере одной переменной. Затем мы подставляем это значение в другое уравнение, чтобы продолжить решение для других переменных. Этот процесс проиллюстрирован в следующем примере.
Как решить систему уравнений с помощью матрицы
Решите систему уравнений, используя матрицу:
Решите систему уравнений, используя матрицу:
Решение:
Решите систему уравнений, используя матрицу:
Решение:
Шаги суммированы здесь .
Решить систему уравнений с помощью матриц.
- Напишите расширенную матрицу для системы уравнений.
- С помощью операций со строками значение записи в строке 1 столбца 1 равно 1.
- Используя операции со строками, получить нули в столбце 1 ниже 1.
- Используя операции со строками, сделайте запись в строке 2 столбца 2 равной 1.

- Продолжайте процесс до тех пор, пока матрица не будет иметь форму строки-эшелона.
- Напишите соответствующую систему уравнений.
- Используйте подстановку, чтобы найти оставшиеся переменные.
- Запишите решение в виде упорядоченной пары или тройки.
- Убедитесь, что решение соответствует исходным уравнениям.
Вот изображение, показывающее порядок расположения единиц и нулей в правильных позициях для эшелонированной формы.
Мы используем ту же процедуру, когда система уравнений состоит из трех уравнений.
Решить систему уравнений с помощью матрицы:
строка 1, столбец 1 будет 1.

имеет рядно-эшелонную форму.
Решить систему уравнений с помощью матрицы:
Решить систему уравнений с помощью матрицы:
имеют ровно одно решение. Давайте теперь посмотрим, что происходит, когда мы используем матрицу для зависимой или противоречивой системы.
Решить систему уравнений с помощью матрицы:

Решить систему уравнений с помощью матрицы:
нет решения
Решите систему уравнений, используя матрицу:
нет решения
Последняя система была противоречивой и поэтому не имела решений. Следующий пример является зависимым и имеет бесконечно много решений.
Следующий пример является зависимым и имеет бесконечно много решений.
Решить систему уравнений с помощью матрицы:


Решите систему уравнений с помощью матрицы:
бесконечно много решений где — любое действительное число.
Решите систему уравнений, используя матрицу:
бесконечно много решений где любое действительное число.
Получите доступ к этому онлайн-ресурсу для получения дополнительных инструкций и практики с методом исключения Гаусса.
- Исключение Гаусса
Ключевые понятия
Практика ведет к совершенству
Напишите расширенную матрицу для системы уравнений
В следующих упражнениях запишите каждую систему линейных уравнений в виде расширенной матрицы.
ⓐ
ⓑ
ⓐ
ⓑ
Запишите систему уравнений, соответствующую расширенной матрице.
Использование операций со строками над матрицей
В следующих упражнениях выполните указанные операции над матрицами.
ⓐ Поменять местами строки 1 и 2
ⓑ Умножить строку 2 на 3
ⓒ Умножить строку 2 на и добавить к ней строку 1.
ⓐ Поменять местами строки 1 и 2
ⓑ Умножить строку 1 на 4
ⓒ Умножить строку 2 на 3 и добавить к ней строку 1.
ⓐ Строки обмена 2 и 3
ⓑ Умножение строки 1 на 4
ⓒ Умножьте строку 2 на и добавьте в строку 3.
ⓐ Строки обмена 2 и 3
ⓑ Строка 2 на 5
ⓒ Умножьте строку 3 на и прибавьте к строке 1.
Выполните необходимую операцию над строками, которая сделает первый элемент в строке 2 равным нулю в расширенной матрице:
Выполните необходимые операции над строками, чтобы получить первый элемент в обе строки 2 и 3 равны нулю в расширенной матрице:
Решение систем уравнений с помощью матриц
В следующих упражнениях решите каждую систему уравнений с помощью матрицы.
В следующих упражнениях решите каждую систему уравнений, используя матрицу.
970002
Нет решения
Нет решения
Бесконечно многие растворы, где любое реальное число
БЕЗОПАСНОСТЬ МОЖЕСТВЕННЫ
Решите систему уравнений ⓐ с помощью графика и ⓑ с помощью замены.


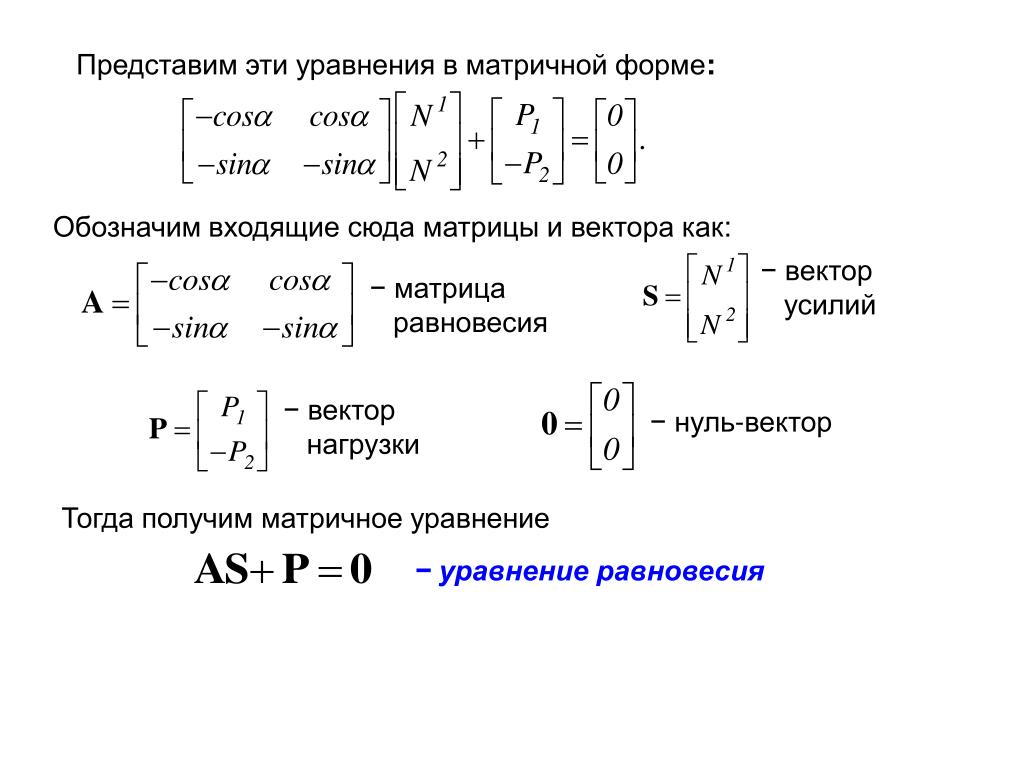
 6.1. Квадратная матрица называется невырожденной, если ее определитель отличен от нуля. В противном случае она называется вырожденной.
6.1. Квадратная матрица называется невырожденной, если ее определитель отличен от нуля. В противном случае она называется вырожденной. Получившуюся в результате матрицу обозначим и назовем присоединенной (или союзной) к A. Иными словами,
Получившуюся в результате матрицу обозначим и назовем присоединенной (или союзной) к A. Иными словами, 6.2), находим
6.2), находим




 Для случаев, когда переменная не фигурирует в уравнении, мы принимаем коэффициент равным 0,9.0042
Для случаев, когда переменная не фигурирует в уравнении, мы принимаем коэффициент равным 0,9.0042
