Уравнения «дробь равна нулю»: метод решения, примеры
Отдельного внимания заслуживают уравнения «дробь равна нулю», то есть, уравнения f(x)/g(x)=0, где f(x) и g(x) – произвольные выражения с переменной x. В этой статье мы, во-первых, разберем, в чем состоит метод решения таких уравнений, на чем он базируется и как обосновывается. А во-вторых, запишем алгоритм решения уравнений «дробь равна нулю» и решим несколько характерных примеров.
В чем состоит метод решения и на чем он базируется?
Метод решения уравнений «дробь равна нулю», то есть уравнений, имеющих вид f(x)/g(x)=0, состоит в нахождении решения через решение уравнения «числитель равен нулю», то есть, через решение уравнения f(x)=0. Пример для наглядности: решение уравнения можно найти через решения уравнения (x−1)·(x2−4)=0.
Базируется метод на следующем утверждении:
Утверждение
Множество решений уравнения f(x)/g(x)=0 совпадает с множеством решений уравнения f(x)=0 на ОДЗ для уравнения f(x)/g(x)=0.
Докажем это утверждение в следующем пункте.
К началу страницы
Обоснование метода
В основе доказательства утверждения из предыдущего пункта лежит хорошо известный факт: дробь a/b, b≠0 равна нулю тогда и только тогда, когда ее числитель есть нуль. Этот факт вытекает из определения дроби (дробь a/b, b≠0 есть такое число c, что b·c=a) и из того, что произведение двух чисел тогда и только тогда равно нулю, когда одно из чисел есть нуль.
Начнем с доказательства частных случаев.
Докажем, что решение уравнения 0/g(x)=0 есть ОДЗ для него. В силу того, что дробь равна нулю тогда и только тогда, когда ее числитель есть нуль, равенство 0/g(x 0)=0 является верным для любого числа x0, при котором оно имеет смысл. Очевидно, что равенство 0/g(x0)=0 имеет смысл тогда и только тогда, когда x0 принадлежит ОДЗ для уравнения 0/g(x)=0. Значит, решение уравнения 0/g(x)=0 есть ОДЗ для этого уравнения.
Очевидно, что равенство 0/g(x0)=0 имеет смысл тогда и только тогда, когда x0 принадлежит ОДЗ для уравнения 0/g(x)=0. Значит, решение уравнения 0/g(x)=0 есть ОДЗ для этого уравнения.
Докажем, что уравнение C/g(x)=0, где С – отличное от нуля число, не имеет решений. Так как дробь равна нулю тогда и только тогда, когда ее числитель есть нуль, то равенство C/g(x0)=0, C≠0 не может быть верным ни для какого числа x0. Следовательно, уравнение C/g(x)=0, C≠0 не имеет решений.
Теперь будем считать, что числитель дроби f(x)/g(x) есть выражение с переменной, а не число, и докажем, что множество решений уравнения f(x)/g(x)=0 совпадает с множеством решений уравнения f(x)=0 на ОДЗ для уравнения f(x)/g(x)=0. Для этого достаточно доказать два момента: первый — что любой корень уравнения f(x)/g(x)=0 является корнем уравнения f(x)=0, второй — что любой корень уравнения f(x)=0, принадлежащий ОДЗ для уравнения f(x)/g(x)=0, является корнем уравнения f(x)/g(x)=0.
Приступаем к доказательству первой части. Пусть x0 – корень уравнения f(x)/g(x)=0. Тогда f(x0)/g(x0)=0 – верное числовое равенство. Из этого неравенства и из того факта, что дробь равна нулю тогда и только тогда, когда ее числитель есть нуль, следует, что f(x0)=0. А это равенство означает, что x0 – корень уравнения f(x)=0.
Первая часть доказана. Приступаем к доказательству второй части.
Пусть x0 принадлежит ОДЗ для уравнения f(x)/g(x)=0 и при этом x0 — корень уравнения f(x)=0. Так как x 0 принадлежит ОДЗ для уравнения f(x)/g(x)=0, то дробь f(x0)/g(x0) имеет смысл. Так как x0 – корень уравнения f(x)=0, то f(x0)=0 – верное числовое равенство. Из этих результатов, а также из того факта, что дробь равна нулю тогда и только тогда, когда ее числитель есть нуль, следует, что дробь f(x0)/g(x0) равна нулю, то есть, f(x0)/g(x0)=0. А это равенство означает, что x0 – корень уравнения f(x)/g(x)=0.
А это равенство означает, что x0 – корень уравнения f(x)/g(x)=0.
Так доказана вторая часть и все утверждение в целом.
К началу страницы
Алгоритм решения уравнений «дробь равна нулю»
Доказанное утверждение позволяет записать алгоритм решения уравнений «дробь равна нулю»:
- Если уравнение имеет вид 0/g(x)=0, то надо найти область допустимых значений для этого уравнения – она и есть искомое решение уравнения.
- Если уравнение имеет вид C/g(x)=0, C – отличное от нуля число, то сразу записываем ответ – нет решений.
-
Если уравнение имеет вид f(x)/g(x)=0, где f(x) – выражение с переменной, а не число, то
- приравниваем числитель к нулю и решаем полученное уравнение f(x)=0,
-
отсеиваем посторонние корни (отбрасываем все корни, не принадлежащие ОДЗ для исходного уравнения, как посторонние).

Заметим, что записанный алгоритм находится в полном согласии с принципами решения дробно-рациональных уравнений, имеющих вид «дробь равна нулю». Принципы решения таких уравнений раскрываются на уроках алгебры в 8 классе. Оттуда нам известно, что для решения дробно-рационального уравнения, имеющего вид f(x)/g(x)=0 нужно приравнять к нулю числитель, решить полученное уравнение и отбросить те корни, при которых обращается в нуль знаменатель [1, с.26-30]. По сути, отбрасывание значений, при которых обращается в нуль знаменатель решаемого дробно-рационального уравнения f(x)/g(x)=0, есть отсеивание посторонних корней по ОДЗ, так как в этом случае ОДЗ определяется условием g(x)≠0.
К началу страницы
Решение примеров
Рассмотрим решения трех характерных уравнений «дробь равна нулю»: с нулем в числителе, с отличным от нуля числом в числителе, и с выражением с переменной в числителе. Ими мы закроем все три типичные ситуации.
Ими мы закроем все три типичные ситуации.
Сначала решим уравнение с нулем в числителе: .
Пример
Решите уравнение
Смотреть решение
Теперь решим уравнение , в числителе которого отличное от нуля число.
Пример
Решите уравнение
Смотреть решение
Осталось рассмотреть решение уравнения «дробь равна нулю» в случае, когда в числителе находится выражение с переменной, а не число. В этом случае, согласно алгоритму, нужно приравнять к нулю числитель, решить полученное уравнение и отсеять посторонние корни.
Пример
Решите уравнение
Смотреть решение
Литература
-
Мордкович А.
 2
2Практические уравнения FRACTIONS Материалы для занятий
Информация об освобождении от налогов
СИСТЕМА ОБУЧЕНИЯ ПРАКТИЧНЫМ УРАВНЕНИЯМ FRACTIONS [HF-1000]
Цена: $29,50
Полная программа для использования с одним учащимся. Включает руководства для Уровней I и II, рабочие листы, ключи к ответам и один комплект игровых фигур для учащихся, состоящий из плоских ламинированных весов, набора из 8 пронумерованных кубиков и набора из 33 блоков дробей.
Это программа, которая представляет собой конкретное введение в дробно-линейные уравнения.
РАБОЧАЯ ТЕТРАДЬ ДЛЯ ПРАКТИЧЕСКИХ ЗАДАЧ НА УЧАСТИЕ В УРОВНЯХ [HOEF-VP]
Цена: $20.00
Учебник для практических задач в области уравнений и дробей содержит более 60 вербальных задач, связанных с отношениями между дробями. Каждая из задач может быть решена с использованием стратегий, представленных в соответствующем уроке Системы обучения практическим уравнениям.
 Права на воспроизведение в классе включены.
Права на воспроизведение в классе включены.НАБОР ПРАКТИЧЕСКИХ УРАВНЕНИЙ ДРОБЕЙ ДЛЯ УЧИТЕЛЯ И ДЕСЯТИ (10) УЧАЩИХСЯ [HF-C1010]
Цена: 89,50 долларов США
Включает ОБУЧАЮЩУЮ СИСТЕМУ EQUATIONS® FRACTIONS®, десять (10) комплектов для учащихся, каждый из которых состоит из ламинированной шкалы, набора числовых кубиков и набора блоков дробей с пластиковой чашкой. Включены права на воспроизведение рабочих листов в классе.
НАБОР ДЛЯ ПРАКТИЧЕСКОГО ОБУЧЕНИЯ EQUATIONS® FRACTIONS ДЛЯ УЧИТЕЛЯ И ДВАДЦАТИ (20) СТУДЕНТОВ [HF-C1020]
Цена: $149,50
Включает СИСТЕМУ ОБУЧЕНИЯ ПРАКТИЧНЫМ УРАВНЕНИЯМ®, двадцать (20) комплектов для учащихся, каждый из которых состоит ламинированной шкалы, набора числовых кубиков и набора блоков дробей с пластиковой чашей. Включены права на воспроизведение рабочих листов в классе.
НАБОР ДЛЯ ПРАКТИЧЕСКИХ УРАВНЕНИЙ FRACTIONS ДЛЯ УЧИТЕЛЯ И ТРИДЦАТИ (30) СТУДЕНТОВ [HF-C1030]
Цена: 209,50 долл. состоит из ламинированной шкалы, набора числовых кубиков и набора блоков дробей с пластиковой чашей.
 Включены права на воспроизведение рабочих листов в классе.
Включены права на воспроизведение рабочих листов в классе. Учебный комплект для практических занятий по уравнениям дробей [HF-K1000]
Цена: $7,50
Учебный набор для практических уравнений: дроби: один набор.
Чтобы получить дополнительные наборы для учащихся, нажмите на ссылку выше Запасные материалы для практических уравнений.
Дроби HOE для SMART Board — для одного пользователя [HF-SB-01]
Цена: $25,00
Это приложение SMART Board позволяет учителю отображать решения двух учебных примеров для каждого из 12 уроков ручного труда. Система обучения дробям уравнений. Рабочая страница позволяет учителю составить любое уравнение из рабочих листов. ТРЕБУЕТСЯ ИСПОЛЬЗОВАНИЕ SMART BOARD® и ПРОГРАММНОГО ОБЕСПЕЧЕНИЯ SMART NOTEBOOK 15.0 ИЛИ ПОЗЖЕ. Один диск.
Дроби HOE для SMART Board — пять пользователей [HF-SB-05]
Цена: 100,00 долларов США
Это приложение SMART Board позволяет учителю отображать решения двух обучающих примеров для каждого из 12 уроков ручного труда.
 Система обучения дробям уравнений. Рабочая страница позволяет учителю составить любое уравнение из рабочих листов. ТРЕБУЕТСЯ ИСПОЛЬЗОВАНИЕ SMART BOARD® и ПРОГРАММНОГО ОБЕСПЕЧЕНИЯ SMART NOTEBOOK 15.0 ИЛИ ПОЗЖЕ. Пять дисков.
Система обучения дробям уравнений. Рабочая страница позволяет учителю составить любое уравнение из рабочих листов. ТРЕБУЕТСЯ ИСПОЛЬЗОВАНИЕ SMART BOARD® и ПРОГРАММНОГО ОБЕСПЕЧЕНИЯ SMART NOTEBOOK 15.0 ИЛИ ПОЗЖЕ. Пять дисков.Дроби HOE для интерактивной доски — для одного пользователя [HF-WB-01]
Цена: $25,00
Эта интерактивная доска позволяет учителю отображать решения двух учебных примеров для каждого из 12 уроков Системы обучения практическим уравнениям. Рабочая страница позволяет учителю составить любое уравнение из рабочих листов. Это приложение на базе WINDOWS. Свяжитесь с нашим офисом, если вы используете MAC. Один диск.
(может использоваться с Promethean Whiteboard, Mimio и т. д.)
Фракции HOE для интерактивной доски — пять пользователей [HF-WB-05]
Цена: $100,00
Это приложение для интерактивной доски позволяет учителю отображать решения к двум учебным примерам для каждого из 12 уроков Системы обучения практическим уравнениям с дробями.
 Рабочая страница позволяет учителю составить любое уравнение из рабочих листов. Это приложение на базе WINDOWS. Свяжитесь с нашим офисом, если вы используете MAC. Пять дисков.
Рабочая страница позволяет учителю составить любое уравнение из рабочих листов. Это приложение на базе WINDOWS. Свяжитесь с нашим офисом, если вы используете MAC. Пять дисков.(может использоваться с Promethean Whiteboard, Mimio и т. д.)
2.4 Дробные линейные уравнения — алгебра среднего уровня
Перейти к содержимомуГлава 2. Линейные уравнения
При работе с дробями, встроенными в линейные уравнения, зачастую проще всего удалить дробь на самом первом шаге. Обычно это означает нахождение LCD дроби, а затем умножение каждого члена во всем уравнении на LCD.
Найдите [латекс]x[/латекс] в уравнении [латекс]\dfrac{3}{4}x — \dfrac{7}{2} = \dfrac{5}{6}.[/latex]
Для этого уравнения LCD равно 12, поэтому каждый член этого уравнения будет умножен на 12.
[латекс]\dfrac{3}{4}x(12) — \dfrac{7}{2}(12) = \dfrac{5}{6}(12)[/latex]
Отмена знаменатель дает:
[латекс]3x(3) — 7(6) = 5(2)[/латекс]
Результат умножения:
[латекс]\begin{array}{rrrrr} 9x&-&42&=&10 \\ &+&42&&+42 \\ \hline &&\dfrac{9x}{9}&=&\dfrac{52}{9} \\ \\ &&x&=&\dfrac{52}{9} \end{array }[/латекс]
Найдите [латекс]x[/латекс] в уравнении [латекс]\dfrac{3\left(\dfrac{5}{9)}x+\dfrac{4}{27}\right)}{2}=3.

Сначала удалите внешний знаменатель 2, умножив обе части на 2:
[латекс]\left(2\ справа)\dfrac{3\left(\dfrac{5}{9}x+\dfrac{4}{27}\right)}{2}=3(2)[/latex]
[латекс]3\left (\dfrac{5}{9}x+\dfrac{4}{27}\right)=6[/latex]
Теперь разделите обе части на 3, что даст:
[латекс]\dfrac{5}{ 9}x + \dfrac{4}{27} = 2[/latex]
Чтобы удалить 9 и 27, умножьте обе стороны на LCD, 27:
[latex]\dfrac{5}{9}x\left(27\right) + \dfrac{4}{27}\left(27\right) = 2(27)[/latex]
Это оставляет:
[latex]\begin{array}{ rrrrl} 5x(3)&+&4&=&54 \\ &-&4&&-4 \\ \hline &&15x&=&50 \\ \\ &&x&=&\dfrac{50}{15}\text{ или }\dfrac{10} {3} \end{массив}[/latex]
В вопросах с 1 по 18 решите каждое линейное уравнение.
- [латекс]\dfrac{3}{5}\left(1 + p\right) = \dfrac{21}{20}[/latex]
- [латекс]-\dfrac{1}{2} = \dfrac{3k}{2} + \dfrac{3}{2}[/latex]
- [латекс]0 = -\dfrac{5}{4}\left(x-\dfrac{6}{5}\right)[/latex]
- [латекс]\dfrac{3}{2}n — 8 = -\dfrac{29}{12}[/latex]
- [латекс]\dfrac{3}{4} — \dfrac{5}{4}m = \dfrac{108}{24}[/latex]
- [латекс]\dfrac{11}{4} + \dfrac{3}{4}r = \dfrac{160}{32}[/latex]
- [латекс]2b + \dfrac{9}{5} = -\dfrac{11}{5}[/латекс]
- [латекс]\dfrac{3}{2} — \dfrac{7}{4}v = -\dfrac{9}{8}[/latex]
- [латекс]\dfrac{3}{2}\left(\dfrac{7}{3}n+1\right) = \dfrac{3}{2}[/latex]
- [латекс]\dfrac{41}{9} = \dfrac{5}{2}\left(x+\dfrac{2}{3}\right) — \dfrac{1}{3}x[/latex]
- [латекс]-a — \dfrac{5}{4}\left(-\dfrac{8}{3}a+ 1\right) = -\dfrac{19}{4}[/latex]
- [латекс]\dfrac{1}{3}\left(-\dfrac{7}{4}k + 1\right) — \dfrac{10}{3}k = -\dfrac{13}{8} [/латекс]
- [латекс]\dfrac{55}{6} = -\dfrac{5}{2}\left(\dfrac{3}{2}p-\dfrac{5}{3}\right)[/latex]
- [латекс]-\dfrac{1}{2}\left(\dfrac{2}{3}x-\dfrac{3}{4}\right)-\dfrac{7}{2}x=-\ dfrac{83}{24}[/latex]
- [латекс]-\dfrac{5}{8}=\dfrac{5}{4}\left(r-\dfrac{3}{2}\right)[/latex]
- [латекс]\dfrac{1}{12}=\dfrac{4}{3}x+\dfrac{5}{3}\left(x-\dfrac{7}{4}\right)[/latex]
- [латекс]-\dfrac{11}{3}+\dfrac{3}{2}b=\dfrac{5}{2}\left(b-\dfrac{5}{3}\right)[/ латекс]
- [латекс]\dfrac{7}{6}-\dfrac{4}{3}n=-\dfrac{3}{2}n+2\left(n+\dfrac{3}{2}\right) [/латекс]
Ключ ответа 2.



 2
2 Права на воспроизведение в классе включены.
Права на воспроизведение в классе включены.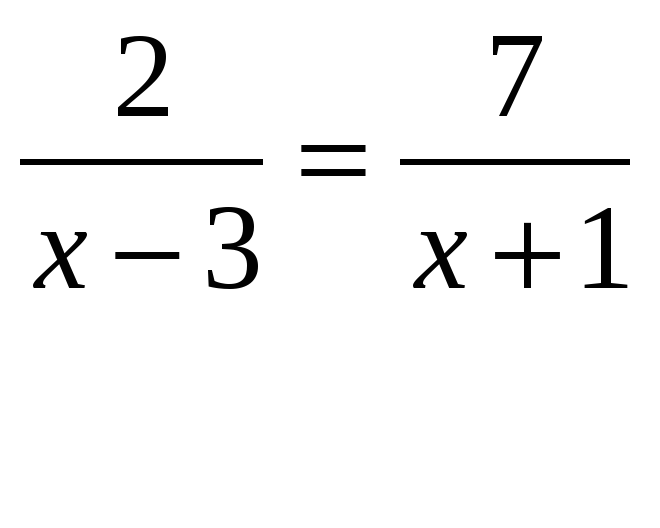 Включены права на воспроизведение рабочих листов в классе.
Включены права на воспроизведение рабочих листов в классе.  Система обучения дробям уравнений. Рабочая страница позволяет учителю составить любое уравнение из рабочих листов. ТРЕБУЕТСЯ ИСПОЛЬЗОВАНИЕ SMART BOARD® и ПРОГРАММНОГО ОБЕСПЕЧЕНИЯ SMART NOTEBOOK 15.0 ИЛИ ПОЗЖЕ. Пять дисков.
Система обучения дробям уравнений. Рабочая страница позволяет учителю составить любое уравнение из рабочих листов. ТРЕБУЕТСЯ ИСПОЛЬЗОВАНИЕ SMART BOARD® и ПРОГРАММНОГО ОБЕСПЕЧЕНИЯ SMART NOTEBOOK 15.0 ИЛИ ПОЗЖЕ. Пять дисков. Рабочая страница позволяет учителю составить любое уравнение из рабочих листов. Это приложение на базе WINDOWS. Свяжитесь с нашим офисом, если вы используете MAC. Пять дисков.
Рабочая страница позволяет учителю составить любое уравнение из рабочих листов. Это приложение на базе WINDOWS. Свяжитесь с нашим офисом, если вы используете MAC. Пять дисков.
