Занятие элективного курса «Методы решения уравнений. содержащих модуль»
Цели и задачи:
- познакомить с методами решения уравнений, содержащих под знаком модуля выражение с переменной;
- формирование умения решать данные уравнения, научить выбирать наиболее рациональный метод решения уравнений;
- развитие логического мышления, речи;
- создание условий, способствующих воспитанию у учащихся внимательности и аккуратности в решении уравнения.
Методы обучения: объяснение, выполнение тренировочных упражнений.
Формы контроля: самопроверка самостоятельно решенных задач.
Оборудование: компьютер, мультимедийный проектор, экран, папка с файлами (практикум), презентация урока (слайды).
Ход занятия
Фронтальный опрос.
Сформулируйте определение модуля числа.
Сформулируйте геометрическое истолкование модуля.
Может ли быть отрицательным значение суммы 2+?
Может ли равняться нулю значение разности 2-?
Как сравниваются два отрицательных числа?
Устная работа. Раскрыть модуль:
| 1. ; | 6. ; |
| 2. ; | 7. ; |
| 3. ; | 8. при ; |
| 4. ; | 9. при ; |
| 5. ; | 10. при . |
Проверка домашнего задания (класс разбит на 6
групп, каждая группа готовила презентацию по
заранее выбранному методу, которая и будет
представлять, и защищать ее).
Изучение нового материала.
1. Метод интервалов
Для того, чтобы решить уравнение, содержащее неизвестную под знаком модуля, необходимо освободиться от знака модуля, используя его определение. Для этого следует:
1) Найти критические точки, т.е. значение неизвестной, при которых выражение, стоящее под знаком модуля, обращается в нуль;
2) Разбить область допустимых значений уравнения на промежутки, на каждом из которых, выражения, стоящие под знаком модуля сохраняют знак;
3) На каждом из этих промежутков уравнение записать без знака модуля, а затем решить его.
Объединение решений, найденных на всех промежутках, и составляет решение исходного уравнения.
Пример 1. Решите уравнение: |x+4|=2x -10.
| [-4;+ ) | |
| — х — 4 = 2х -10 3х=6 х=2 (- ;-4) |
х+4=2х-10 х=14 [-4;+ ) |
Ответ: 14.
Пример 2. Решите уравнение: х 2-5|x|+6=0
| (- ;0) | [0;+ ) |
| х +5х+6=0 х1 =-2 (- ;0) х2 =-3 (- ;0) |
х -5х+6=0 х1 =2 [0;+ ) х2=3 [0;+ ) |
Ответ: 2; 3.
Пример 3. Решите уравнение: |5-2x|+|x+3|=2-3x
5-2x=0 x+3=0
х=2,5 х=-3
| (- ;-3) | [-3;+2,5) | [-2,5;+ ) | |
| 5-2х | + | + | — |
| х+3 | — | + | + |
| (- ;-3) | [-3;+2,5) | [-2,5;+ ) |
| 5-2х-х-3-2+3х=0 0х=0 х-любое число (- ;-3) |
5-2x+x+3-2+3x=0 2х=-6 х=-3 [-3;2,5) |
6х=4 x=2/3 [2,5;+ ) |
(- ;-3) {-3}=(- ;-3]
Ответ: (- ;-3].
2. Возведение обеих частей уравнения в квадрат.
Для того, чтобы решить уравнение содержащее модуль, необходимо освободиться от знака модуля. Для этого следует: возвести в квадрат обе части уравнения, решить его. Но не забывать, что при возведении в квадрат появляются лишние корни, поэтому, надо найти ОДЗ и выявить принадлежат ли корни данному условию.
Пример 4. Решите уравнение: |x+4|=2x-10.
Возведем в квадрат обе части уравнения
X2 +8x+16=4x2 -40x+100
3x2 -48x+84=0 /3
X2 -16x+28=0
X1=14, X2=2
Найдём ОДЗ:
2x-100;2×10 ;
x5.
x1=14 [5;+ ), х2=2 [5;+ )
Ответ:14
Пример 5. Решите уравнение: |x+3|=2x-3
Возведем в квадрат обе части уравнения
х2 +6x+9=4x2 -12x+9; 3x2 -18x=0 /:3
х2 -6x=0; x(x-6)=0
x=0, x=6.
Найдём ОДЗ: 2х-30, 2×3, x1,5
x=0 [1,5;+)
x=6 [1,5;+ )
Ответ: 6.
3. Метод введения новой переменной
Иногда уравнение, содержащее переменную под знаком модуля, можно решить довольно просто, используя метод введения новой переменной.
Продемонстрируем данный метод на конкретных примерах:
Пример 6. Решите уравнение: х2 -5|x|+6=0.
Пусть |x |=t,тогда
|x|2 =x2 =t2
t2 -5t+6=0
t1=2, |x |=2, x1,2= 2,
t2=3, |x |=3, x3,4= 3.
Ответ: 2, 3.
Пример 7. Решите уравнение: (x-2)2 — 8|x-2|+15=0.
Пусть |x-2|=t ,|x-2|2 =(x-2)2 =t2 ,
тогда уравнение примет вид: t2 -8t+15=0, D=16-15=1.
t1=3, t2=5.
t1=3, |x-2|=3, x1=5, x2=-1.
t2=5, |x-2|=5, x3=7, x4=3.
Ответ: -1; 3; 5; 7.
4. Метод замены уравнения совокупностью систем.
Рассмотрим ещё один метод решения подобных уравнений — метод замены уравнения совокупностью систем. Методом замены уравнения совокупностью систем можно решать уравнения вида
(2)
Причём данное уравнение можно заменять совокупностью систем двумя способами.
I способ:
II способ:
Если в уравнении функция имеет более простой вид, нежели функция , то имеет смысл исходное уравнение заменять первой совокупностью систем, а если более простой вид имеет функция , тогда исходное уравнение следует заменять второй совокупностью систем.
В частности, используя определение модуля, уравнение: ,
при С 0 равносильно совокупности уравнений и , т.е.
при С=0
при С0 уравнение решений не имеет.
Воспользуемся данным методом при решении
следующих уравнений.
Пример 8. Решите уравнение: 2|х2+2х-5|=х-1.
Данное уравнение равносильно совокупности систем:
| 2х2+4х-10-1+х=0 2х2+5х-11=0 Д=113 |
2х2+4х-10-х+1=0 2х2+3х-9=0 Д=81=92.
|
Ответ: .
Пример 9. Решите уравнение: |2|x-1|-3|=5.
Используя определение модуля уравнение <=> совокупности двух уравнений:
Первое уравнение совокупности равносильно совокупности двух уравнений:
Второе уравнение совокупности решений не имеет, т.к.
Ответ: -3; 5.
5. Графический метод
Существует ещё один метод решения уравнений с модулем. Он основан на геометрической интерпретации понятия абсолютной величины числа, а именно модуль х равен расстоянию от точки с координатой х до точки с координатой 0 на числовой прямой Ох. Используя геометрическую интерпретацию, легко решаются уравнения вида:
(4)
(5)
(6) где а,в,с — числа.
Решить уравнение (4) — это значит найти все точки на числовой оси Ох, которые отстоят от точки с координатой а на расстояние с.
При уравнение решений не имеет;
при уравнение имеет один корень;
при уравнение имеет два корня
Решить уравнение (5) — это значит найти все точки на числовой оси Ох, для каждой из которых сумма расстояний от неё до точки с координатами а и в равна с.
Аналогично интерпретируется решение уравнения
вида (6).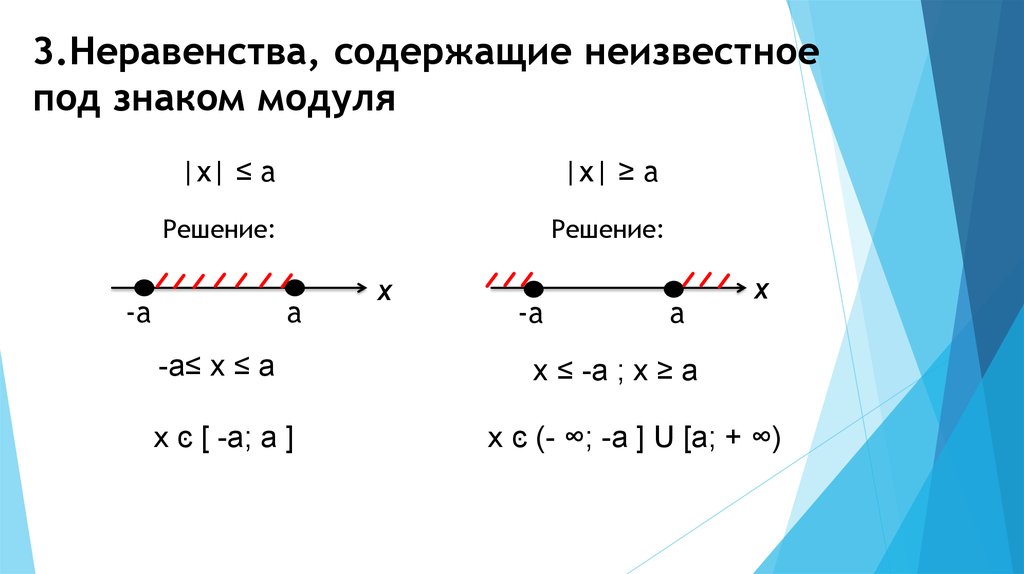
Пример 12. Решите уравнение: |x-1|-|x-3|=2
Для того, чтобы решить данное уравнение, нужно на числовой оси Ох найти все такие точки, для каждой из которых разность расстояния от нее до точки с координатой 1 и расстояния от неё до точки с координатой 3 равна 2. Так как длина отрезка [1;3] равна 2,то ясно, что любая точка с координатой х3 удовлетворяет данному уравнению, а любая точка с координатой х<3 не удовлетворяет ему. Таким образом, решением исходного уравнения является множество чисел промежутка [3;+ ).
Ответ: [3;+ ).
Рассмотренный метод можно отнести к
графическим методам решения уравнения. Все
необходимые построения здесь производились на
числовой оси. Рассмотрим теперь метод решения
уравнения, в котором будем использовать
построения на координатной плоскости. Этим
методом, теоретически, можно решать уравнения с
модулем любого вида, однако практическая
реализация метода иногда бывает довольно
сложной.
Суть метода состоит в следующем. Решить уравнение f(х)=q(x) это значит найти все значения х, для которых значение функций y=f(x) и y=q(x) равны, т.е. найти абсциссы всех точек пересечения графиков этих функций. Если же графики не имеют общих точек, то уравнение не имеет корней. Следует, однако, иметь в виду, что точное построение графиков функций практически невозможно, поэтому решение, найденное графическим способом требует проверки подстановкой.
Воспользуемся этим методом для решения уравнения вида (3).
Пример 13. Решите уравнение: |- 1| = 3.
Решение. Построим графики двух функций y=|-1| и y=3
Из чертежа видно, что графики имеют 2 общие точки. Координаты одной точки: (8; 3) , другой: (-4; 3).
Следовательно, исходное уравнение имеет два
решения: х1=8, x2= -4. Как уже говорилось,
при каждом методе значения корней уравнения
определяются приблизительно, и только проверка
позволит доказать, что найденные значения
действительно являются корнями исходного
уравнения. При подстановке х1=8, x2= -4 в
уравнение получаем, соответственно два верных
числовых равенства: |-3|=3 и |3|=3.
При подстановке х1=8, x2= -4 в
уравнение получаем, соответственно два верных
числовых равенства: |-3|=3 и |3|=3.
Ответ: -4; 8.
Так как при графическом методе решения зачастую не удается найти точное значение корня, но применение данного метода бывает обосновано, если требуется найти не сами корни, а всего лишь определить их количество.
6. Решение уравнений, содержащих модуль под знаком модуля.
При решении уравнения, в котором под знаком модуля находится выражение, также содержащее модуль, можно сначала освобождаться от внутренних модулей, а затем в полученных уравнениях раскрывать оставшиеся модули.
Пример 10. Решите уравнение: |x-|4-х||- 2x = 4
Уравнение |x-|4-х||-2x=4 совокупности двух систем:
|
совокупности двух следующих систем ЛОЖНО! (-; 2) |
(4; +), значит система решения не имеет. |
Ответ: .
Иногда внимательный взгляд на уравнение позволяет упростить процесс нахождения его корней.
Пример 11. Решите уравнение: |2|х|-6| =- 4-х.
Левая часть уравнения неотрицательна для всех х, следовательно правая часть его должна быть такой же: .
Значит . т.е. |-2 х — 6 | =- 4 — х, , значит
, -2 х — 6 =- 4 — х,
-х = 2 , х = — 2 .
Ответ: корней нет.
Закрепление. Решить самостоятельно (двумя способами):
Самопроверка (на слайде презентации):
1 способ: Решим методом интервалов:
1. Найдем значения переменной, при которых выражение, стоящее под знаком модуля, обращается в нуль:
, , .
2. Разобьем область допустимых значений уравнения на промежутки, на каждом из которых, выражения, стоящие под знаком модуля сохраняют знак:
| (- ;0) | [0;1) | [1;2) | [2;+ ) | |
| х2 — х | + | — | + | + |
| х — 2 | — | — | — | + |
3. На каждом из этих промежутков уравнение
записать без знака модуля, а затем решить его.
На каждом из этих промежутков уравнение
записать без знака модуля, а затем решить его.
| (- ;0), [1;2) | [0;1) | [2;+ ) |
| х2 — х — х + 2 = х2 -2 -2х = -4 х = 2 (- ;0), х = 2 [1;2). |
— х2 + х — х + 2 = х2 -2 — 2х2 = — 4 х = 2 [1;2). |
х2 — х + х — 2 = х2 -2 0х=0 х-любое число [2;+ ) |
Объединение решений, найденных на всех промежутках, и составляет решение исходного уравнения.
Ответ: [2;+ ).
2 способ: Решим методом замены уравнения совокупностью систем:
.
Сумма двух неотрицательных выражений
неотрицательна, значит левая часть уравнения
неотрицательна для всех х, следовательно и
правая часть его должна быть такой же, т. е. ; Данное уравнение
равносильно совокупности систем:
е. ; Данное уравнение
равносильно совокупности систем:
| совокупности
двух следующих систем: 1) 2) верно! |
) система решения не имеет. |
Домашнее задание.
1. Проработать теоретический материал.
2. Практикум «Уравнения с модулем». Решите уравнения с модулем рациональным способом:
Подведение итогов.
Список используемой литературы
- Сборник задач по алгебре. 8-9 класс. М.Л. Галицкий, А.М. Гольдман, Л.И. Звавич, М.: Просвещение, 1992 г.
- Алгебра для 8-9 класса: пособие для учащихся школ
и классов с углубленным изучением математики.
Н.Я. Виленкин, Г.
 С. Сурвилло, А.С. Симонов, А.И.
Кудрявцев, под редакцией Н.Я. Виленкина — М.:
Просвещение, 1998 г.
С. Сурвилло, А.С. Симонов, А.И.
Кудрявцев, под редакцией Н.Я. Виленкина — М.:
Просвещение, 1998 г. - Алгебраический тренажер: пособие для школьников и абитуриентов. А.Г. Мерзляк, В.Б. Полонский, М.С. Якир — М.: «Илексо» Харьков: «Гимназия» 1998 г.
- Задачи по математике. Алгебра. В.В. Вавилов, И.И. Мельников, С.Н. Олехин, П.И. Пасиченко — М.: Наука - главная редакция физико-математической литературы. 1987 г.
- Система тренировочных задач и упражнений по математике. А.Я. Симонов, Д.С. Бакаев, А.Г. Эпельман, А.А. Бесчинская, Р.М. Мостовой, А.Л. Абрамов — М.: Просвещение, 1991 г.
Приложение.
Уравнения и неравенства, содержащие знак модуля
Е.П. Нелин, В.А. Лазарев
АЛГЕБРА
и начала математического
анализа
10 класс
Учебник для
общеобразовательных
учреждений. Базовый и
Базовый и
профильный уровень
(Оформление и автор интерактивных технологий Морозова Е.)
Объяснение и обоснование
Решать любое уравнение или неравенство, содержащее знак модуля, можно одним из трех основных способов: по определению модуля, исходя из геометрического смысла модуля или по общей схеме. Некоторые уравнения или неравенства с модулем могут быть также решены с использованием специальных соотношений.
В зависимости от выбранного способа решения получаем разные записи решения.
Пример Решите уравнение | 2x – 4 | = 6.
I способ (по определению модуля)
II способ (использование геометрического смысла модуля)
Замечание. При решении уравнения с использованием геометрического смысла модуля знак модуля раскрывается неявно, то есть определение модуля в явном виде не применяется.
Общая схема решения уравнений и неравенств, содержащих знак модуля — это фактически немного измененный метод интервалов. Поясним содержание этой схемы на примере уравнения с двумя модулями вида
|f (x)| + |g (x)| = a (a > 0).
Чтобы решить это уравнение, необходимо раскрыть знаки модулей, а для этого необходимо знать, где функции f (x) и g (x) будут положительными, а где — отрицательными. То есть фактически мы должны решить неравенства
f (x) ≥ или ≤0, (1)
g (x) ≥ или ≤0. (2)
Каждое из этих неравенств мы умеем решать методом интервалов. Перестроим прием решения неравенств методом интервалов таким образом, чтобы он давал возможность одновременно решать каждое из последних неравенств. Как известно, решение неравенства (1) методом интервалов начинается с нахождения его ОДЗ (то есть области определения функции f (x)), а решение неравенства (2) — с нахождения его ОДЗ (то есть области определения функции g (x)). Чтобы начать одновременно решать оба неравенства, необходимо найти общую область определения для функций f (x) и g (x), то есть найти ОДЗ данного уравнения (это и есть первый из ориентиров необходимой схемы).
Чтобы начать одновременно решать оба неравенства, необходимо найти общую область определения для функций f (x) и g (x), то есть найти ОДЗ данного уравнения (это и есть первый из ориентиров необходимой схемы).
Чтобы продолжить решение неравенств f (x) ≥или≤0 и g (x) ≥или≤ 0 методом интервалов, необходимо найти нули функций f (x) и g (x), то есть найти нули всех подмодульных функций (это и есть второй ориентир).
Если далее применить схему метода интервалов одновременно для двух неравенств, необходимо на ОДЗ отметить нули подмодульных функций и разбить ОДЗ на промежутки (это третий ориентир).
В каждом из полученных промежутков знаки функций f (x) и g (x) не могут измениться. Тогда мы можем найти знаки подмодульных функций на каждом промежутке (в любой точке этого промежутка), раскрыть знаки модулей и найти решение данного уравнения в каждом из этих промежутков (это и есть четвертый ориентир общей схемы).
Обоснование возможности применения приведенной схемы к решению неравенств с модулями проводится аналогично.
ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ
Вопросы для контроля
- Объясните, какими способами можно решать уравнения и неравенства, содержащие знак модуля. Проиллюстрируйте эти способы на примерах.
- Обоснуйте специальные соотношения. Проиллюстрируйте их применение к решению уравнений и неравенств, содержащих знак модуля.
- Обоснуйте обобщения использования геометрического смысла модуля. Проиллюстрируйте их применение к решению уравнений и неравенств, содержащих знак модуля.
Упражнения
Решите уравнения и неравенства, содержащие знак модуля (1–15).
Постройте график функции
ТЕСТ
Уравнения и неравенства
Модульная арифметика — Решение систем модульных уравнений
Вопрос задан
Изменено 7 лет, 9 месяцев назад
Просмотрено 3к раз
$\begingroup$
Я готовлюсь к тесту по дискретной математике и создал свой вопрос, но не могу его решить.
Можно ли решить следующую систему уравнений (без безмозглых испытаний), и если да, то как?
$$x \экв 5 \pmod 3\\ x \equiv 2 \pmod 7$$
Моя попытка: $$x=3a + 5 $$
$$x=7b + 2$$
$$3\mid(x-5)$$ $$7\mid(x-2)$$
Я не могу продолжать дальше этой точки. Могу ли я решить это с наименьшим общим кратным или что-то в этом роде?
- модульная арифметика
- сравнения
- китайская теорема об остатках
$\endgroup$
1
$\begingroup$
В общем решение 9n a_iM_iM_i’ \text{ мод } \prod m_i$
$\endgroup$
1
$\begingroup$
На самом деле это довольно простая задача. $5\equiv2\pmod3$, так что $x$ на $2$ больше, чем кратно $3$, и на $2$ больше, чем кратно $7$. Объедините эти условия, и $x$ должно быть на $2$ больше, чем кратное $21$, или $x\equiv2\pmod{21}$.
Объедините эти условия, и $x$ должно быть на $2$ больше, чем кратное $21$, или $x\equiv2\pmod{21}$.
Мы можем усложнить задачу, изменив первое условие на $x\equiv3\pmod5$. В этом случае у вас есть
$$x=7b+2\equiv3\pmod5$$ $$2b\эквив1\эквив6\pmod5$$ $$b\equiv3\pmod5$$
В сочетании с $x=7b+2$ получается
$$x=7(5k+3)+2=35k+21+2=35k+23$$ $$x\equiv23\pmod{35}$$
$\endgroup$
4
$\begingroup$
можно написать $$x=5+3k_1$$ и $$x=2+7k_2$$, где $k_1,k_2$ — целые числа, поэтому нужно решить диофнтово уравнение $$3=-3k_1+7k_2$ $
$\endgroup$
$\begingroup$
Используя китайскую теорему об остатках, сначала заметим, что $\gcd (3,7) = 1$.
Мы можем разобраться с этим, просмотрев разделы, раздел $\mod 3$, раздел $\mod 7$. Теперь вы сначала выбираете раздел и ставите нулевой эквивалент на другие разделы, чтобы они исчезли, например, $3 \equiv 0\mod 3$, поэтому мы пишем
Теперь вы сначала выбираете раздел и ставите нулевой эквивалент на другие разделы, чтобы они исчезли, например, $3 \equiv 0\mod 3$, поэтому мы пишем
$$x = \underbrace{\ }_{\mod 3 } + \underbrace{3}_{\mod 7} $$
Далее у нас будет
$$x = \underbrace{7}_{\mod 3} + \underbrace{3}_{\mod 7} $$
Обратите внимание, что $7 \экв 1 \mod 3$, то если вы умножите на $5$, вы получите $35 \экв 5 \mod 3$. Если вы нажмете $x \mod 3$, мы получим
$$x = 5 \mod 3$$
Используя ту же идею, мы получим, что $3\dot \ 5 \equiv 1\mod 7$, затем $2 \dot\ 3 \dot \ 5 \equiv2 \mod 7$
а затем
$$x = 35 + 30 = 65$$
проще говоря, мы имеем это, применяя китайскую теорему об остатках
$$x \equiv 65 \equiv 2\mod 3\dot \ 7$$
что дает $$x \equiv 2 \mod 21$$
$\endgroup$
Зарегистрируйтесь или войдите в систему
Зарегистрируйтесь с помощью Google
Зарегистрироваться через Facebook
Зарегистрируйтесь, используя электронную почту и пароль
Опубликовать как гость
Электронная почта
Требуется, но никогда не отображается
Опубликовать как гость
Электронная почта
Требуется, но не отображается
Нажимая «Опубликовать свой ответ», вы соглашаетесь с нашими условиями обслуживания, политикой конфиденциальности и политикой использования файлов cookie
.
Уравнения модуля: Примеры — DoubleRoot.in
Еще раз привет.
В этом уроке мы обсудим несколько примеров уравнений, связанных с модулем. Этот урок является своего рода продолжением предыдущего, поэтому убедитесь, что вы сначала прошли его.
Начнем.
Пример 1 Найдите x: |x – 2| + |х + 4| = 8
Решение Как мы обсуждали в предыдущем уроке, для решения таких уравнений мы разделим числовую прямую на несколько областей. В каждой такой области выражения внутри «стенок» модуля сохраняют свой знак.
В результате мы сможем удалить модуль, освободив переменные и сделав уравнение легко решаемым.
Первое выражение |x – 2| можно решить, согласно определению, как
\( |x-2| = \begin{case}
x – 2& \text{ if } x\ge 2 \\
2 – x& \text{ if } x < 2
\end{cases} \)
Второе выражение может быть аналогично разрешено как
\( |x+4| = \begin{case}
x +4& \text{ if } x\ge -4 \\
– x – 4& \ text{ if } x < -4
\end{cases} \)
Перетащите ползунок в апплете ниже, чтобы посмотреть, как эти два выражения меняют свои знаки.
Подобно уравнению из предыдущего урока, это уравнение также постоянно меняет свою форму в зависимости от области, в которой находится x.
Итак, еще раз разделим числовую прямую на отдельные участки, в которых уравнение «сохраняет» свой вид, и попытаемся решить уравнение в каждом участке.
Случай 1 : x ≥ 2
Когда x ≥ 2, |x – 2| превращается в x – 2 и остается таким. Кроме того, x ≥ 2 означает x > –4, поэтому |x + 4| превращается в x + 4 (и остается таким).
Уравнение принимает вид
(x – 2) + (x + 4) = 8
, что дает x = 3.
Попробуйте подставить это значение в исходное уравнение для проверки. Мы закончили с областью x ≥ 2. Давайте перейдем к следующей.
Случай 2 : –4 ≤ x < 2
Сначала давайте подумаем, почему мы решили ограничить x этой областью.
Если x < 2, то |x – 2| становится 2 – x (и остается 2 – x), но |x + 4| может равняться x + 4 или – x – 4, в зависимости от того, x ≥ –4 или x < –4.
Итак, если мы ограничим x областью –4 ≤ x < 2, |x + 4| также сохранит свой вид, т. е. x + 4.
Исходное уравнение превратится в
(2 – x) + (x + 4) = 8
, что упрощается до 6 = 8,
Это означает, что когда x находится между –4 и 2, левая сторона всегда будет равна 6, что никогда не может равняться правой стороне. Попробуйте подставить некоторые значения x, чтобы убедиться в этом.
Это означает, что нет решения этого уравнения, когда –4 ≤ x < 2. Остался последний случай.
Случай 3 : x < –4
Здесь |x – 2| = 2 – x (поскольку x < –4 также подразумевает x < 2) и |x + 4| превратится в –x – 4 (и останется таким).
Наше уравнение теперь становится
2 – x – 4 – x = 8
Это дает x = –5 . Еще раз подставьте это в исходное уравнение, чтобы проверить. И, поскольку мы охватили всю числовую прямую, больше нечего искать.
В остальных примерах используется тот же метод.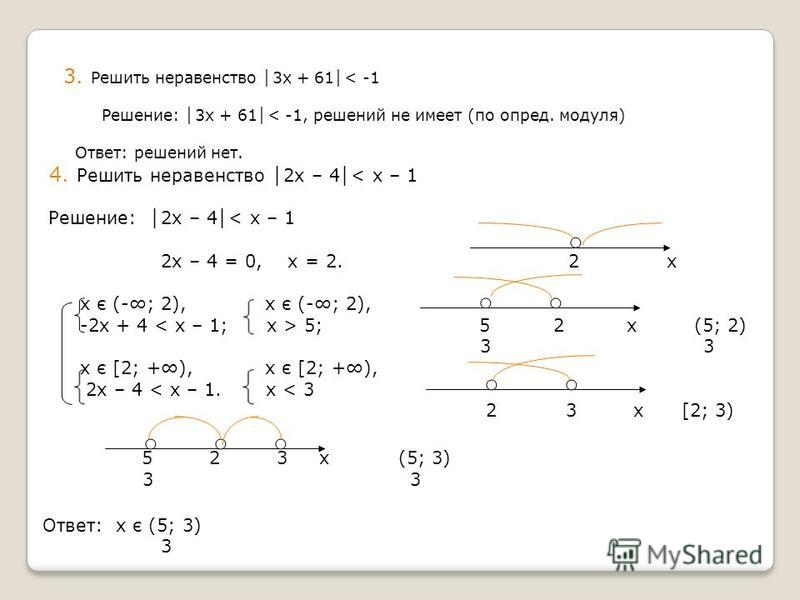 Но все равно пройдите их, так как в каждом из них вы столкнетесь с интересными ситуациями.
Но все равно пройдите их, так как в каждом из них вы столкнетесь с интересными ситуациями.
Пример 2 Найдите u: |u + 5| – |у + 1| = 2
Решение Начнем с разбора случаев. На этот раз мы будем двигаться немного быстрее.
Случай 1: u ≥ –1
В этом случае |u + 1| = u + 1 и |u + 5| = u + 5. Уравнение принимает вид
(u + 5) – (u + 1) = 2
, что дает 4 = 2.
Это означает, что в этой области не будет никакого решения, так как LHS всегда будет оставаться равным 4. Чтобы убедиться в этом, выберите любые случайные значения u ≥ –1.
Случай 2: –5 ≤ u < 1
В этом случае |u + 1| = – u – 1 и |u + 5| = u + 5. Уравнение принимает вид
(u + 5) – (– u – 1) = 2
, что дает u = –2.
Случай 3: u < –5
В этом случае |u + 1| = – u – 1 и |u + 5| = – u – 5. Уравнение принимает вид
(–u – 5) – (– u – 1) = 2
, что дает –4 = 2. Еще одна странная ситуация. Нет решения!
Еще одна странная ситуация. Нет решения!
В том, почему мы не получаем никакого решения в случаях 1 и 3, есть геометрический смысл. Напомним, что |u + 5| и |и + 1| соответственно расстояния между u и –5 и u и –1.
И, |у + 5| – |у + 1| есть разница этих двух расстояний. Если P представляет u на числовой прямой, а A и B соответственно представляют -5 и -1, то уравнение просто спрашивает нас
«Найдите точку P на числовой прямой так, что PA — PB = 2»
Итак , что происходит, когда P перемещается вправо от –1 или влево от –5? Посмотрите в апплете ниже. Вы можете перетащить точку P.
Когда P перемещается вправо от –1, тогда PA – PB равно , всегда равно AB (что равно 4). Вот почему мы получаем 4 на LHS в случае 1.
Аналогично, когда P лежит слева от –5, тогда PB – PA равно , всегда равно AB, или 4. Это означает, что PA – PB = –4. Проверьте LHS варианта 3, чтобы сопоставить.
В обоих этих случаях PA – PB не может равняться 2. Следовательно, нет решения.
Следовательно, нет решения.
Как насчет между А и Б?
Если P находится точно посередине между A и B, то PA – PB равно 0. И, если мы переместим P к B, значение PA – PB увеличится до 4. Где-то между 0 и 4, PA – PB будет также равно 2, правой части уравнения.
Следовательно, мы получим решение (т. е. между A и B). Давайте интересоваться не , что это за решение, а тем, что решение существует.
Позвольте всему этому впитаться. 😑
Пример 3 Решите для y: |y – 5| + |у – 1| = 4
Решение Давайте сразу приступим к рассмотрению трех случаев.
Случай 1: y ≥ 5
Уравнение принимает вид
(y – 5) + (y – 1) = 4
, что дает y = 5,
Случай 2: 1 ≤ y < 5
Уравнение принимает вид
(– y + 5) + (y – 1) = 4
, что дает 4 = 4.
Хмм. Что это может означать? Сделайте паузу и подумайте об этом, прежде чем продолжить.
4 = 4 означает, что при 1 ≤ y < 5 левая сторона всегда равна 4 и, следовательно, всегда равна правой. Другими словами, 90 276 каждых 90 277 значений y, таких что 1 ≤ y < 5, является решением исходного уравнения.
Давайте попробуем несколько.
Если y = 1,3, то LHS = |1,3 – 5| + |1,3 – 1| = |–3,7| + |–0,3| = 3,7 + 0,3 = 4 = RHS
y = 4,2, тогда LHS = |4,2 – 5| + |4.2 – 1| = |–0,8| + |3.2| = 0,8 + 3,2 = 4 = RHS
y = 2, тогда LHS = |2 – 5| + |2 – 1| = |–3| + |1| = 3 + 1 = 4 = RHS
Потрясающе!
Случай 3: y < 1
Уравнение принимает вид
(– y + 5) + (1 – y) = 4
, что дает y = 1. Внимательно посмотрите на это решение.
Все в порядке? Ну нет.
Уравнение (– y + 5) + (1 – y) = 4 было только верным, когда мы ограничили y в области y < 1. Но мы получили решение y = 1, которое не лежит в этой области.
Это означает, что это решение недействительно. И мы отвергнем это.
Но если вы подставите y = 1 в исходное уравнение, вы обнаружите, что LHS = RHS для этого значения y.
Что происходит?
Вернемся к случаю 2. Мы обнаружили, что любое значение y, такое что 1 ≤ y < 5, является решением исходного уравнения. Это решение включает y = 1. Так что не о чем беспокоиться.
Но помните – любое решение, лежащее вне области, которую мы выбираем, должно быть отвергнуто.
Давайте также посмотрим, что происходит геометрически в случае 2.
Как и в предыдущем примере, если P представляет y на числовой прямой, а A и B соответственно представляют 1 и 5, тогда уравнение задает нам
«Найдите точку P на числовой прямой, такую, что PA + PB = 4»
Итак, что происходит, когда P лежит между A и B? Посмотрите в апплете ниже. Вы можете перетащить точку P.
Когда P лежит между A и B, то PA + PB равно , всегда равно AB (что равно 4). Вот почему в Случае 2 мы получаем 4 на левой стороне.
А что, если P лежит справа от 5 (т. е. y > 5)?
PA + PB начинает увеличиваться с 4 и продолжает увеличиваться по мере продвижения вправо. Следовательно, PA + PB никогда больше не будет равно 4 в этом регионе. То же самое происходит, когда P лежит левее 1,
Следовательно, мы не получим никакого решения для y > 5 и y < 1,
Объединив решения Случая 1 и Случая 2, мы получим окончательное решение как 1 ≤ y ≤ 5 .
Позвольте и этому впитаться. 😑😑
Пример 4 Найдите z: |z – 3| + |г – 7| = 2
Решение Я знаю, вы думаете: «Но я все это знаю!», но в этом примере есть и кое-что новое.
Случай 1: z ≥ 7
Уравнение принимает вид
(z – 3) + (z – 7) = 2
, что дает z = 6. Отклонено!
Почему? Потому что мы ограничили z областью z ≥ 7, и действительными будут только те решения, которые лежат в этой области.
Давайте проверим это, подставив z = 6 в LHS. Получим
Получим
LHS = |6 – 3| + |6 – 7| = |3| + |–1| = 3 + 1 = 4 ≠ RHS
Я же говорил!
Случай 2: 3 ≤ z < 7
Уравнение принимает вид
(z – 3) + (7 – z) = 2
, что дает 4 = 2.
Ба! Мы уже видели этот абсурд. Давайте двигаться дальше.
Случай 3: z < 3
Уравнение принимает вид
(3 – z) + (7 – z) = 2
, что дает z = 4. Снова отклонено! Вы поймете, почему.
Если мы посмотрим на все случаи, то это уравнение вообще не имеет решения. 😥
Что происходит геометрически? Взгляните на аналогичный апплет. Вы можете перетащить точку P.
Когда P лежит между A и B, PA + PB равно AB или 4. Когда мы перемещаем P за пределы AB, PA + PB становится больше 4. И оно продолжает увеличиваться, если мы двигаемся дальше слева от A или справа от B.
В любом случае PA + PB или |z – 3| + |г – 7| никогда не будет равно 2 (правая сторона), и, следовательно, уравнение не будет иметь решения.


 С. Сурвилло, А.С. Симонов, А.И.
Кудрявцев, под редакцией Н.Я. Виленкина — М.:
Просвещение, 1998 г.
С. Сурвилло, А.С. Симонов, А.И.
Кудрявцев, под редакцией Н.Я. Виленкина — М.:
Просвещение, 1998 г.