Условная вероятность это вероятность: Электронная библиотека БГУ: Invalid Identifier

Условная вероятность – что это такое?



Случайное событие  является зависимым, если помимо случайных факторов его вероятность зависит от появления либо непоявления события . Вероятность события , вычисленная в предположении того, что событие  уже произошло, называется условной вероятностью наступления события  и обозначается через .
При этом события  и  называют зависимыми событиями (хотя, строго говоря, зависимо только одно из них).

Карты в руки:

Задача 47
Из колоды в 36 карт последовательно извлекаются 2 карты. Найти вероятность того, что вторая карта окажется червой, если до этого:
а) была извлечена черва, б) была извлечена карта другой масти.

Решение: рассмотрим событие:  – вторая карта будет червой. Совершенно понятно, что вероятность этого события зависит от того, черву вытянули ранее или нет.

а) Если сначала была извлечена черва (событие ), то в колоде осталось 35 карт, среди которых осталось 8 карт червовой масти. По классическому определению:
 – вероятность того, что вторая карта окажется червой при условии, что до этого была извлечена черва.

б) Если же сначала была извлечена карта другой масти (событие ), то все 9 черв остались в колоде. По классическому определению:
 – вероятность того, что вторая карта окажется червой при условии, что до этого была извлечена карта другой масти.

Ответ:

И здесь всё логично – если вероятность извлечения червы из полной колоды составляет , то при извлечении следующей карты аналогичная вероятность изменится: в первом случае – уменьшится:  (т.к. черв стало меньше), а во втором – возрастёт:  (т.к. все червы остались в колоде).

Зависимых событий, разумеется, может быть и больше. Пока задача не остыла, добавим ещё одно: – третьей картой будет извлечена черва. Предположим, что произошло событие , а затем событие ; тогда в колоде осталось 34 карты, среди которых 7 черв. По классическому определению:
 – вероятность наступления события  при условии, что до этого были извлечены две червы.
Для самостоятельной тренировки:

Задача 48
В конверте находится 10 лотерейных билетов, среди которых 3 выигрышных. Из конверта последовательно извлекаются билеты. Найти вероятности того, что:

а) 2-й извлечённый билет будет выигрышным, если 1-й был выигрышным;
б) 3-й будет выигрышным, если предыдущие два билета были выигрышными;

в) 4-й будет выигрышным, если предыдущие билеты были выигрышными.

Краткое решение с комментариями в конце книги.

А теперь обратим внимание на один принципиально важный момент: в рассмотренных примерах требовалось найти лишь условные вероятности, при этом предыдущие события считались достоверно состоявшимися. Но ведь в действительности и они являются случайными! Так, в демо-примере извлечение червы из полной колоды  – есть событие случайное, вероятность которого равна

Поэтому на практике гораздо чаще требуется отыскать вероятность совместного появления зависимых событий. Как, например, найти вероятность события , состоящего в том, что из полной колоды будет извлечена черва

и затем ещё одна черва? Ответ на этот вопрос даёт

1.6.6. Теорема умножения вероятностей зависимых событий

1.6.4. Задачи на теоремы сложения и умножения

| Оглавление |



Полную и свежую версию этой книги в pdf-формате,
а также курсы по другим темам можно найти здесь.

Также вы можете изучить эту тему подробнее – просто, доступно, весело и бесплатно!

С наилучшими пожеланиями, Александр Емелин

Условная вероятность.

Независимость событий

При решении вероятностных задач часто возникает необходимость определить вероятность события в ситуации, когда о нем имеются дополнительные сведения.

Постановка задачи: нужно определить вероятность события A после того, как стало известно, что некоторое событие B произошло, иными словами, имел место исход, благоприятствующий событию A.

ПРИМЕР 1 Бросается игральная кость. Пусть событие A состоит в выпадении четного числа очков. Стало известно, что произошло событие B, состоящее в выпадении числа очков меньше четырех. Определить вероятность события A при условии, что наступило событие B.

Решение. Пространство элементарных исходов при бросании игральной кости определяется шестью исходами U = {1, 2, 3, 4, 5, 6}. Известно, что произошло событие B, которому благоприятствуют три исхода = {1, 2, 3}. В этих условиях вероятность события А равна , так как событию А благоприятствует исход {2} из = {1, 2, 3}.

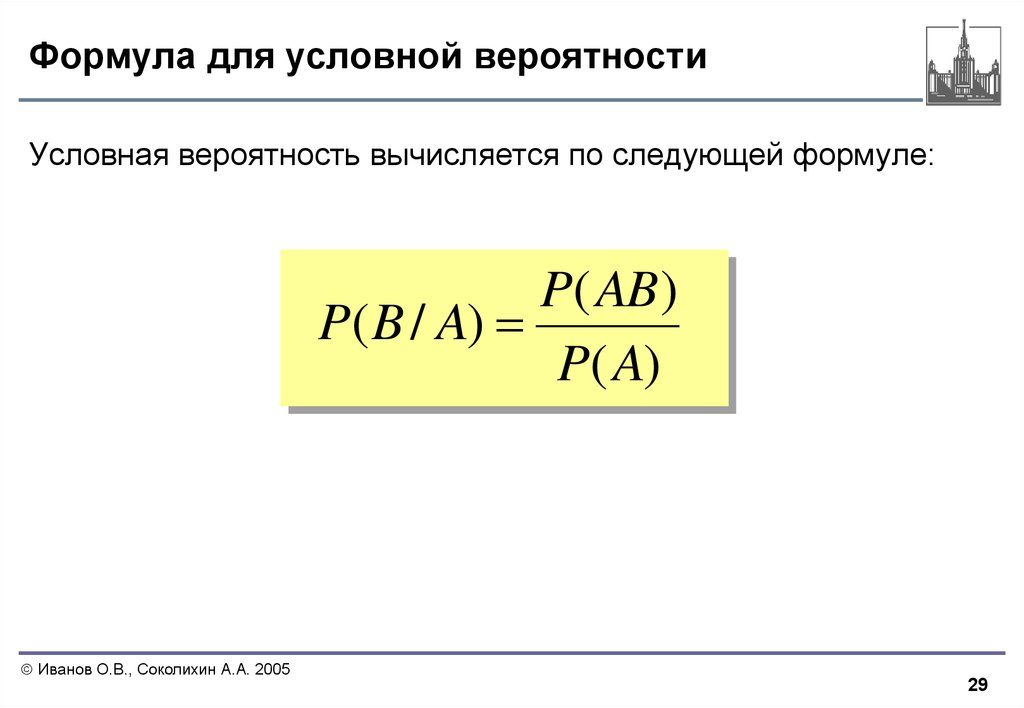
Условная вероятность

Определение. Условной вероятностью события A при условии, что наступило событие B, называется отношение числа k тех благоприятствующих A исходов, которые и благоприятствуют B, к числу m всех исходов, благоприятствующих B.

Условная вероятность обозначается P(A|B)

По определению ; если B — невозможное событие, то P(A|B) не определена.

Заметим, что , но , .

Поэтому

Эта формула служит для определения условий вероятности в общем случае. Вероятности и  , называются безусловными.

Свойства условных вероятностей 

1. Всегда 0 ≤ P(A|B) ≤ 1, причем P(A|B) = 0, если А — невозможное событие, и P(A|B) = 1, если А ⊂ B (A включено в B)
2. Если C = A∪B и A∩B = Ø, то для любого события D:
3. Если — событие противоположное , то

ПРИМЕР 2. Изучается качество техобслуживания, обеспечиваемое пятьюдесятью автомеханиками в определенном городе. Результаты изучения представлены в таблице.

	Хорошее обслуживание	Плохое обслуживание
Стаж работы более 10 лет	16	4
Стаж работы менее 10 лет	10	20

1. Какова вероятность, что случайно выбранный автомеханик хорошо обслуживает автомобили?

2. Если автомеханик случайно выбран и его стаж более 10 лет, то какова вероятность, что он хорошо обслуживает автомобили?

Решение 

1. В данном случае объем выборочного пространства . Пусть A – событие, состоящее в том, что выбранный автомеханик хорошо обслуживает автомашины. Используя данные из таблицы, имеем Тогда вероятность события A

2. Пусть событие B состоит в том, что выбранный механик имеет стаж более 10 лет. В данном случае объем выборочного пространства уменьшается, он равен сумме элементов первой строки: . Число благоприятных для события исходов , поэтому

Ответ: вероятность того, что случайно выбранный автомеханик хорошо обслуживает автомобили равна 0,52 или 52%

Вероятность того, что автомеханик со стажем более 10 лет хорошо обслуживает автомобили равна 0,8 или 80%.

ПРИМЕР 3. В условиях предыдущего примера определить вероятность того, что выбранный случайным образом механик проработал менее 10 лет и хорошо обслуживает автомобили.

Решение. Пусть D – событие, состоящее в том, что механик проработал меньше 10 лет. Событие C состоит в том, что механик хорошо обслуживает автомобили. Для определения условной вероятности  используем формулу

Отсюда

Ответ: вероятность равна примерно 0,3333… или 33,33%

Если обе стороны равенства, определяемого формулой , умножить на , то получим следующее правило умножения вероятностей в общем случае:

Правило умножения вероятностей в общем случае, если поменять местами и и использовать факт, что A∩B = B∩A, получаем следующее:

Независимость событий

Перед тем как изложить теорему умножения вероятностей, введем одно важное понятие: понятие о зависимых и независимых событиях.

Событие A называется независимым от события B, если вероятность события A не зависит от того, произошло событие B или нет.

Событие A называется зависимым от события B, если вероятность события A меняется в зависимости от того, произошло событие B или нет.

ПРИМЕР 4. Подбрасываются 2 монеты. Рассмотрим события: A – появления герба на первой монете; B – появление герба на второй монете.

Решение. Очевидно, событие A не зависит от того, произошло событие B или нет. Событие A независимо от события B.

ПРИМЕР 5. В урне два белых шара и один черный. Два человека последовательно вынимают по одному шару, не возвращая их в урну. Рассмотрим события: A – появление белого шара у первого человека, B – появление белого шара у второго человека.

Решение. Вероятность события A равна 2/3. Если стало известно, что событие A произошло, то в урне осталось два шара, из которых только один белый. Тогда вероятность события B становится равной 1/2. Из этого заключаем, что событие B зависит от события A.

Вероятность события B, вычисленная при условии, что имело место другое событие A, называется условной вероятностью события B и обозначается: .

Для ПРИМЕРА 5.

Теперь условие зависимости или независимости событий можно выразить математически. Если соотношение

верно, то события A и B называются независимыми.

Если верно выражение

≠ ,

то события A и B называются зависимыми.

Рассмотрим еще раз ПРИМЕР 5, это так называемая «урновая схема». В урне (закрытой емкости) находится a белых и b черных шаров. Два человека поочередно вынимают по одному шару из урны. Если реализуется схема без возвращения, то события – зависимые. Если реализуется схема с возвращением, после каждого опыта шар возвращается в урну, то события – независимые.

Условная вероятность: формула и примеры из жизни

Что такое условная вероятность?

Условная вероятность определяется как вероятность наступления события или исхода, основанная на наступлении предыдущего события или исхода. Условная вероятность рассчитывается путем умножения вероятности предыдущего события на обновленную вероятность последующего или условного события.

Условной вероятности можно противопоставить безусловную вероятность. Безусловная вероятность относится к вероятности того, что событие произойдет независимо от того, произошли ли какие-либо другие события или присутствуют какие-либо другие условия.

Основные выводы

• Условная вероятность относится к шансам того, что произойдет некоторый результат при условии, что произошло другое событие.
• Часто указывается как вероятность B при задании A и записывается как P(B|A), где вероятность B зависит от вероятности A.
• Условной вероятности можно противопоставить безусловную вероятность.
• Вероятности классифицируются как условные, предельные или совместные.
• Теорема Байеса — это математическая формула, используемая для вычисления условной вероятности.

Понимание условной вероятности

Условные вероятности зависят от предыдущего результата или события. Условная вероятность рассматривает такие события во взаимосвязи друг с другом. Условная вероятность, таким образом, представляет собой вероятность того, что событие или результат произойдет на основе возникновения некоторого другого события или предшествующего результата.

Два события называются независимыми, если появление одного из них не влияет на вероятность появления другого события. Однако, если одно событие происходит или не происходит, на самом деле влияет на вероятность того, что другое событие произойдет, то говорят, что эти два события являются зависимыми. Если события независимы, то вероятность некоторого события B не зависит от того, что происходит с событием A. Таким образом, условная вероятность относится к тем событиям, которые зависят друг от друга.

Условная вероятность часто изображается как «вероятность A при задании B», обозначаемая как P(A|B).

Условная вероятность используется в различных областях, таких как страхование, экономика, политика и многие другие области математики.

Формула условной вероятности

P(B|A) = P(A и B) / P(A)

Или:

P(B|A) = P(A∩B) / P(A)

Где

P = Вероятность

А = Событие А

Б = Событие Б

Безусловная вероятность также известна как предельная вероятность и измеряет вероятность события, игнорируя любые знания, полученные из предыдущих или внешних событий. Поскольку эта вероятность игнорирует новую информацию, она остается постоянной.

Примеры условной вероятности

В качестве примера предположим, что вы достаете из мешка три шарика — красный, синий и зеленый. Каждый шарик имеет равные шансы быть вытащенным. Какова условная вероятность вытащить красный шарик после того, как уже вытащен синий?

Во-первых, вероятность вытащить синий шарик составляет около 33%, потому что это один возможный результат из трех.

Предполагая, что это первое событие произойдет, останется два шарика, каждый из которых будет вытащен с вероятностью 50%. Таким образом, шанс вытащить синий шарик после того, как уже вытащен красный шарик, будет около 16,5% (33% х 50%).

В качестве еще одного примера, чтобы лучше понять эту концепцию, представьте, что был брошен правильный кубик, и вас попросили указать вероятность того, что выпала пятерка. Существует шесть равновероятных исходов, поэтому ваш ответ — 1/6.

Но представьте, что перед тем, как ответить, вы получите дополнительную информацию о том, что выпавшее число было нечетным. Поскольку возможны только три нечетных числа, одно из которых равно пяти, вы наверняка пересмотрите свою оценку вероятности того, что пятерка выпадет с 1/6 до 1/3.

Эта пересмотренная вероятность того, что событие A произошло, с учетом дополнительной информации о том, что другое событие B определенно произошло в этом испытании эксперимента, называется условная вероятность   A   при данном   B и обозначается P(A|B).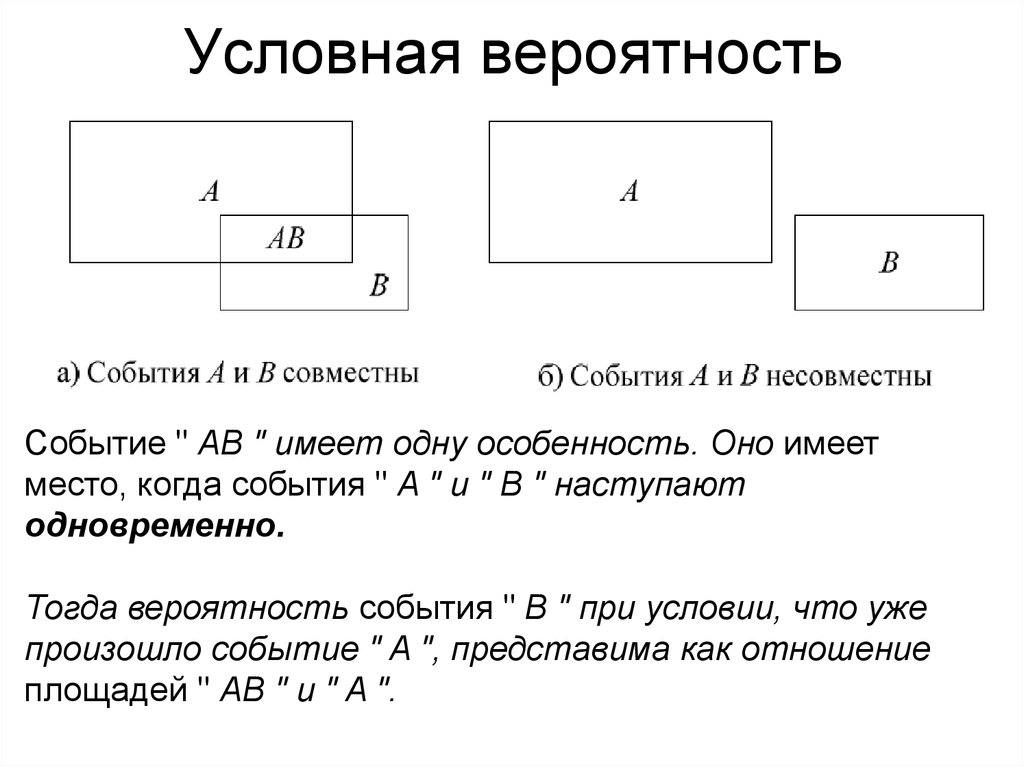

Другой пример условной вероятности

В качестве другого примера предположим, что студент подает заявку на поступление в университет и надеется получить академическую стипендию. Школа, в которую они подают заявление, принимает 100 из каждых 1000 абитуриентов (10%) и присуждает академические стипендии 10 из каждых 500 принятых студентов (2%).

Из получателей стипендий 50% также получают университетские стипендии на книги, питание и жилье. Для студентов вероятность того, что они будут приняты, а затем получат стипендию, составляет 0,2% (0,1 x 0,02). Вероятность их принятия, получения стипендии, а затем получения стипендии на книги и т. д. составляет 0,1% (0,1 х 0,02 х 0,5).

Условная вероятность в сравнении с совместной вероятностью и предельной вероятностью

• Условная вероятность : p(A|B) — вероятность наступления события A, при условии, что событие B произойдет. Например, учитывая, что вы вытащили красную карточку, какова вероятность того, что это четверка (p(четыре|красная))=2/26=1/13. Таким образом, из 26 красных карточек (учитывая красную карточку) есть две четверки, поэтому 2/26 = 1/13.
• Предельная вероятность : вероятность события (p(A)) в отдельности. Его можно рассматривать как безусловную вероятность. Это не обусловлено другим событием. Пример: вероятность того, что вытянутая карта будет красной (p(red) = 0,5). Другой пример: вероятность того, что вынутая карта равна 4 (p(four)=1/13).
• Совместная вероятность : p(A ∩B). Совместная вероятность — это вероятность события A и события B. Это вероятность пересечения двух или более событий. Вероятность пересечения A и B можно записать как p(A ∩ B). Пример: вероятность того, что на карте четыре и красное = p(четыре и красное) = 2/52=1/26. (В колоде из 52 карт две красные четверки: 4 черви и 4 бубны).

Теорема Байеса и условная вероятность

Теорема Байеса, названная в честь британского математика XVIII века Томаса Байеса, представляет собой математическую формулу для определения условной вероятности. Теорема предоставляет способ пересмотреть существующие предсказания или теории (обновить вероятности) с учетом новых или дополнительных доказательств. В финансах теорему Байеса можно использовать для оценки риска кредитования потенциальных заемщиков.

Теорема Байеса также называется правилом Байеса или законом Байеса и является основой области байесовской статистики. Этот набор правил вероятности позволяет обновлять свои прогнозы происходящих событий на основе новой полученной информации, обеспечивая более качественные и динамичные оценки.

Теорема Байеса хорошо подходит и широко используется в машинном обучении.

Как рассчитать условную вероятность?

Условная вероятность рассчитывается путем умножения вероятности предшествующего события на вероятность последующего или условного события. Условная вероятность рассматривает вероятность того, что произойдет одно событие, на основе вероятности того, что произойдет предыдущее событие.

Что такое калькулятор условной вероятности?

Калькулятор условной вероятности — это онлайн-инструмент для расчета условной вероятности. Это обеспечит вероятность появления первого события и второго события. Калькулятор условной вероятности избавляет пользователя от необходимости заниматься математикой вручную.

В чем разница между вероятностью и условной вероятностью?

Вероятность оценивает вероятность наступления одного события. Условная вероятность рассматривает два события, происходящие по отношению друг к другу. Он рассматривает вероятность возникновения второго события на основе вероятности возникновения первого события.

Что такое априорная вероятность?

Априорная вероятность — это вероятность того, что событие произойдет до того, как будут собраны какие-либо данные для определения вероятности. Это вероятность, определяемая предшествующим убеждением. Априорная вероятность является компонентом байесовского статистического вывода.

Что такое сложная вероятность?

Составная вероятность определяет вероятность возникновения двух независимых событий. Сложная вероятность умножает вероятность первого события на вероятность второго события. Наиболее распространенным примером является подбрасывание монеты дважды и определение того, будет ли второй результат таким же или отличным от первого.

Итог

Условная вероятность исследует вероятность возникновения события на основе вероятности возникновения предшествующего события. Второе событие зависит от первого события. Он рассчитывается путем умножения вероятности первого события на вероятность второго события.

Условная вероятность

Как обрабатывать Зависимые события

Жизнь полна случайных событий! Вам нужно «почувствовать» их, чтобы быть умным и успешным человеком.

Независимые события

События могут быть «независимыми», что означает, что каждое событие не зависит от других событий.

Пример: подбрасывание монеты.

Каждый бросок монеты — это совершенная изолированная вещь.

То, что он делал в прошлом, не повлияет на текущий бросок.

Шанс просто 1 к 2, или 50%, как при ЛЮБОМ подбрасывании монеты.

Таким образом, каждый бросок является независимым событием .

Зависимые события

Но события также могут быть «зависимыми»… это означает, что они могут быть затронуты предыдущими событиями …

Пример: Шарики в мешочке

2 синих и 3 красных шарика в мешке.

Каковы шансы получить синий шарик?

Шанс 2 из 5

Но после того, как вы вынули один из , шансы изменились!

Итак, в следующий раз:

если мы получили красный шарик раньше, то шанс выпадения синего шарика равен 2 из 4

если мы получили синий шарик до этого, то вероятность того, что следующий синий шарик будет 1 из 4

Это потому что мы удаляем шарика из мешка.

Итак, следующее событие зависит от того, что произошло в предыдущем событии, и называется зависимым .

Замена

Примечание: если мы заменяем шарики в мешочке каждый раз, то шансы не равны меняются и события независимы:

• С Замена: события Независимые (шансы не меняются)
• Без Замена: события Зависимые (шансы меняются)

Зависимые события — это то, что мы рассматриваем здесь.

Древовидная диаграмма

Древовидная диаграмма: прекрасный способ изобразить происходящее, поэтому давайте построим ее для нашего примера с шариками.

Вероятность вытащить синий шарик составляет 2/5, а красный — 3/5:

Мы можем сделать еще один шаг и посмотреть, что произойдет, когда мы вытащим второй шарик:

Если синий шарик был выбран первым, теперь есть 1/4 шанса получить синий шарик и 3/4 шанса получить красный шарик.

Если сначала был выбран красный шарик, теперь есть шанс 2/4 получить синий шарик и 2/4 шанс получить красный шарик.

Теперь мы можем ответить на такие вопросы, как «Каковы шансы вытащить 2 синих шарика?»

Ответ: это шанс 2/5 , за которым следует шанс 1/4 :

Вы видели, как мы умножили шансы? В результате получил 1/10.

Шанс вытащить 2 синих шарика равен 1/10

Обозначения

Мы любим обозначения в математике! Это означает, что мы можем использовать силу алгебры, чтобы поиграть с идеями. Итак, вот обозначение вероятности:

P(A) означает «вероятность события A»

В нашем примере с шариками событие A — это «получить синий шарик первым» с вероятностью 2/5:

P(A) = 2/5

И событие B «получить синий шарик вторым» … но для этого у нас есть 2 варианта:

• Если мы получили синий шарик первым , шанс теперь 1/4
• Если мы получили Красный мрамор первым , шанс теперь 2/4

Итак, мы должны сказать какой из них мы хотим , и используем символ «|» означает «дано»:

P(B|A) означает «Событие B дано Событие A»

Другими словами, событие A уже произошло, какова вероятность события B?

P(B|A) также называется «условной вероятностью» B при заданном A.

И в нашем случае:

P(B|A) = 1/4

Таким образом, вероятность получить 2 синих шарика это:

И мы пишем это как

«Вероятность события A и события B равна
вероятность события A умножить на вероятность события B при данном событии A »

6

Пример: Вытягивание 2 королей из колоды

Событие A сначала вытягивает короля, а Событие B вытягивает короля вторым.

Для первой карты шанс вытянуть короля 4 из 52 (в колоде из 52 карт 4 короля):

P(A) = 4/52

Но после удаления короля из колоды вероятность того, что вторая карта будет вытянута, составляет минус вероятность того, что это будет король (только 3 из 51 оставшейся карты являются королями):

P(B|A) = 3/51

Итак:

P(A и B) = P(A) x P(B|A) = (4/52) x (3/51) = 12/2652 = 1/221

Таким образом, шанс получить двух королей равен 1 из 221, или около 0,5% :

Начните с:		P(A и B) = P(A) x P(B|A)
Поменять стороны:		P(A) x P(B|A) = P(A и B)
Разделить на P(A):		P(B|A) = P(A и B) / P(A)

И у нас есть еще одна полезная формула:

«Вероятность события B при данном событии A равна
вероятности событие A и событие B разделить на вероятность события A

Пример: Мороженое

70% ваших друзей любят шоколад, а 35% любят шоколад И любят клубнику.

Какой процент тех, кто любит шоколад, также любит клубнику?

P(Клубника|Шоколад) = P(Шоколад и клубника) / P(Шоколад)

0,35 / 0,7 = 50%

50% ваших друзей, которые любят шоколад, также любят клубнику

 

Большой пример: футбольный матч

Вы собираетесь играть в футбол и хотите быть вратарем, но это зависит от того, кто сегодня является тренером:

• с тренером Сэмом вероятность быть вратарем равна 0,5
• с тренером Алексом вероятность быть вратарем равна 0,3

Сэм будет тренером чаще … примерно в 6 из каждых 10 игр (вероятность 0,6 ).

Итак, какова вероятность того, что вы сегодня будете вратарем?

 

Построим древовидную диаграмму. Сначала мы показываем двух возможных тренеров: Сэма или Алекса:

Вероятность получить Сэма равна 0,6, поэтому вероятность Алекса должна быть 0,4 (вместе вероятность равна 1)

Теперь, если вы получите Сэма, есть 0,5 вероятность быть вратарем (и 0,5 не быть вратарем):

Если вы получаете Алекса, существует 0,3 вероятность быть вратарем (и 0,7 нет):

Древовидная диаграмма завершена, теперь давайте посчитаем общие вероятности. Помните, что:

P(A и B) = P(A) x P(B|A)

Вот как это сделать для ветки «Сэм, да»: будучи тренером, умножив шанс 0,5 на то, что Сэм позволит тебе стать вратарем, мы получаем шанс 0,3.)

Но мы еще не закончили! Мы не включили Алекса в качестве тренера:

Шанс 0,4 для Алекса в качестве тренера, за которым следует шанс 0,3, дает 0,12

И две ветви дерева «Да» вместе составляют:

0,3 + 0,12 = 0,42 вероятность стать вратарем сегодня

(это вероятность 42 %)

Проверить

Последний шаг: выполнить расчеты и убедиться, что они складываются в 1:

6

4

4 0,3 + 0,3 + 0,12 + 0,28 = 1

Да, они добавляют к 1 , так что это выглядит правильно.

Друзья и случайные числа

Вот еще один совсем другой пример условной вероятности.

4 друга (Алекс, Блейк, Крис и Дасти) выбирают случайное число от 1 до 5. Какова вероятность того, что кто-то из них выбрал одно и то же число?

Давайте добавим наших друзей по одному. ..

 

Во-первых, какова вероятность того, что у Алекса и Блейка одинаковые номера?

Блейк сравнивает свой номер с номером Алекса. Вероятность совпадения 1 к 5.

В виде дерева:

Примечание: «Да» и «Нет» вместе составляют 1
(1/5 + 4/5 = 5/5 = 1)

 

Теперь давайте включим Криса…

Но теперь есть два случая для рассмотрения:

• Если Алекс и Блейк совпали , то у Криса есть только одно число для сравнения.
• Но если Алекс и Блейк не совпадают с , то у Криса есть два числа для сравнения.

И получаем это:

Для верхней строки (Алекс и Блейк сделали совпадение) у нас уже есть совпадение (шанс 1/5).

Но для «Алекс и Блейк не совпали с » теперь есть шанс 2/5 совпадения Криса (потому что Крис может сопоставить свое число с Алексом и Блейком).

И мы можем рассчитать общий шанс на , умножив шансы , которые потребовались, чтобы добраться туда:

Следуя по пути «Нет, Да» .

No related posts.