В модуле число: Модуль числа — урок. Математика, 6 класс.

Модуль числа | Фізика – легко!

Противоположные числа – это числа, которые отличаются друг от друга только знаком. Выражение –а обозначает, что это число противоположное числу а.

Например, 7  и – 7;
                       41  и – 41  и т.д.

Число 0 противоположно самому себе!

То есть, для того, чтобы показать противоположность чисел в математике используют знак « – ».

Приписав знак « – » перед положительным числом 5, мы получим отрицательное число – 5.

Приписав знак « – » перед отрицательным числом – 5, мы получим противоположное ему положительное число 5, то есть – (–5) = 5.

– (–а) = а

На координатной прямой точки, у которых противоположные координаты, расположены на одинаковом расстоянии от начала отсчёта.

AO = OC

BO = OD

Модуль числа

Модуль числа – это расстояние (в единичных отрезках) от начала отсчёта до точки, которая изображает это число на координатной прямой.

Точки А(– 4) и В (4) отдалены от начала отсчёта на 4 единичных отрезков, а числа – 4 и 4 имеют одинаковые модули, равные 4.

Модуль числа а обозначают | а |

Так как модуль – это расстояние, а расстояние не может быть отрицательным, то модуль числа не может быть отрицательным числом!!!

Модулем положительного числа и нуля является тоже самое число, а модулем отрицательного числа – противоположное ему число:

| а | = а, если а  ≥ 0  (если а – неотрицательное число)

| а | = – а, если а  <  0  (если а – отрицательное число)

Выводы

Свойства модуля числа:

1. Модуль числа не может быть отрицательным. Модуль числа всегда или положительное число или равен 0.

| 4| = 4

| 0 | = 0

|– 4| = 4

2. Противоположные числа имеют равные модули.

| – а | = | а | = а

Пример, | – 12 | = | 12 | = 12

Решение уравнений (примеры)

1.

  – x = 7
вместо – x   и   7  напишем противоположные им числа, используя знак «–»
–(– x) = – 7
воспользуемся правилом, что – (–а) = а получим
x = – 7

2. – x = – 10

–(– x) = –(– 10)
x = 10

3. x = –(– 32)

x = 32

4. | x | = 4

x = 4 или x = – 4
Ответ: 4; – 4

5. | x | = 0

x = 0
Ответ: 0

6. | y | = – 8

модуль не может быть отрицательным числом, а значит данное уравнение не имеет решения
Ответ: нет корней

7. | – x | = 12

вспомним второе свойство модуля, что | – а | = | а | = а, тогда
| x | = 12
x = 12 или x = – 12
Ответ: 12; – 12

8. | y | – 2 = 12

подобные уравнения решаются как простые уравнения, только с учётом модуля
| y | = 12 + 2
| y | = 14
y = 14 или y = – 14
Ответ: 14; – 14

9.  10 – 2| x | = 4

2| x | = 10 – 4
2| x | = 6
| x | = 6 : 2
| x | = 3
x = 3 или x = – 3
Ответ: 3; – 3

То есть при решении уравнений, содержащих модуль мы получим три вида ответа:

два корня (если под знаком модуля положительное число), один корень (если под знаком модуля 0)
нет корней (если под знаком модуля отрицательное число).

Решение простейших неравенств, содержащих модуль

В 5 классе мы решали примеры с простейшими неравенствами. Линейные неравенства бывают строгие и нестрогие.
Строгие неравенства – это неравенства со знаками больше (>) или меньше (<).
x > a; x < a;
Нестрогие неравенства – это неравенства со знаками больше либо равно (≥) или меньше либо равно (≤).
x ≥ a; x ≤ a.

Примеры

1. Найдите все натуральные значения x, при которых является правильным неравенство x < 9

Решение.
Данное неравенство будет правильным при таких значениях x: 1; 2; 3; 4; 5; 6; 7; 8.
Ответ: х = {1; 2; 3; 4; 5; 6; 7; 8} – натуральные решения данного неравенства.

Примечание:
Число 0 не является решением этого неравества, так как 0 не является натуральным числом;
Число 9 не является решением этого неравества, так как данное неравенство строгое, то есть х строго меньше 9 и не может быть равным 9.

2. Какое наименьшее натуральное значение а удовлетворяет неравенство а > 12?

Решение.
Поскольку неравенство строгое, то число 13 является наименьшим натуральным значением а, которое удовлетворяет данному неравенству.
Ответ: 13

3. Какое наименьшее натуральное значение а удовлетворяет неравенство а ≥ 12?

Решение.
Поскольку неравенство нестрогое, то число 12 является наименьшим натуральным значением а, которое удовлетворяет данному неравенству.
Ответ: 12.

4. Найдите все натуральные значения x, при которых является правильным неравенство 2 < x < 9

Решение.
Неравенство двойное (читают как «х больше от 2, но меньше от 9»), строгое, поэтому 3; 4; 5; 6; 7; 8 – натуральные решения данного двойного неравенства.
Ответ: х = {3; 4; 5; 6; 7; 8}

5. Найдите все натуральные значения x, при которых является правильным неравенство 2 < x ≤ 9.

Решение.
3; 4; 5; 6; 7; 8; 9 – натуральные решения данного двойного неравенства.
Ответ: х = {3; 4; 5; 6; 7; 8; 9}

6. Найти все целые числа, которые удовлетворяют неравенству| x | < 5.

Решение.
| x | < 5 (читаем как «расстояние от начала отсчёта до точки изображающей х меньше 5»).
Неравенство | x | < 5 эквивалентно (может быть также записано) –5 < x < 5. Неравенство двойное, строгое, поэтому данное неравенство будет правильным при таких значениях x: –4; –3; –2; –1; 0; 1; 2; 3; 4.
Ответ: х = {–4; –3; –2; –1; 0; 1; 2; 3; 4}

7. Найти все целые числа, которые удовлетворяют неравенству| x | ≤ 5.

Решение.
Неравенство | x | ≤  5 эквивалентно –5 ≤  x ≤  5. Неравенство двойное, нестрогое, поэтому числа –5 и 5 войдут в множество чисел, при которых данное неравенство будет правильным. Таким образом, данное неравенство будет правильным при таких значениях x: –5; –4; –3; –2; –1; 0; 1; 2; 3; 4; 5.
Ответ: х = {–5; –4; –3; –2; –1;  0;  1;  2;  3;  4;  5}

8. Найти все целые числа, которые удовлетворяют неравенству | x | > 2 и обозначте их на координатной прямой.

Решение.
Неравенство | x | > 2 эквивалентно x < – 2 или x > 2. Обозначим на координатной прямой точки, координаты которых удовлетворяют данному неравенству

Поскольку неравенство строгое, то числа – 2 и 2 не входят в множество целых чисел, при которых данное неравенство будет правильным. А на координатной прямой эти точки обозначаем в виде незакрашенной точки.

Ответ: х = {…–5; –4; –3;  3;  4;  5…}

9. Найти все целые числа, которые удовлетворяют неравенству | x | ≥ 2 и обозначте их на координатной прямой.

Решение.
Неравенство | x | ≥ 2 эквивалентно x ≤ – 2 или x ≥ 2. Обозначим на координатной прямой точки, координаты которых удовлетворяют данному неравенству

Поскольку неравенство нестрогое, то числа – 2 и 2 входят в множество целых чисел, при которых данное неравенство будет правильным. А на координатной прямой эти точки обозначаем в виде закрашенной точки.

Ответ: х = {…–5; –4; –3; –2;  2;  3;  4;  5…}

10. Найти все целые числа, которые удовлетворяют неравенству 1 < | x | ≤ 3 и обозначте их на координатной прямой.

Решение.
Рассмотрим сначала левую часть неравенства. Она означает, что расстояние от начала отсчёта до точек меньше 1. Рассмотрим правую часть неравенства: расстояние от начала отсчёта до этих же точек меньше или равно 3.
Построим эти точки на координатной прямой:

1 и – 1 не входят в множество целых чисел, которые удовлетворяют неравенству, потому что неравенство строгое.
3 и – 3 входят в множество целых чисел, которые удовлетворяют неравенству, потому что неравенство нестрогое.

Ответ: х = {–3; –2;  2;  3}

 

Модуль числа

Представим себе такую историю…

– Привет, Паша! Чем ты занимаешься? – спросил у друга Саша.

– Я собираюсь разгадать ребус, – ответил Паша. – Давай разгадаем его вместе.

– Давай, – сказал Саша.

– Смотри, – показал ребус другу Паша. – Здесь нарисован перевёрнутый дом и пульт с запятыми.

– А почему дом перевёрнут? – спросил Саша.

 – Это означает, что слово «дом» надо читать справа налево, – пояснил Паша. – То есть получаем слово «мод».

– Вторая картинка в ребусе – пульт. Что означают запятые перед и после картинки? – задал вопрос Саша.

– Запятые в ребусе означают, что из названия картинки нам нужно исключить столько букв, сколько стоит запятых, – объяснил Паша.

– Значит, в слове «пульт» мы уберём первую и последнюю буквы, – неуверенно сказал Саша.

– Верно! – отметил Паша. – Мы уберём буквы «п» и «т».

– И у нас останется слово «уль», – подсказал другу Саша.

– А теперь из получившихся слов «мод» и «уль» составим слово «модуль», – сказал Паша.

– А что оно означает? – спросил Саша.

– Не знаю. Давай спросим у Мудряша, – ответил Паша.

– Ребята, прежде чем я отвечу на ваш вопрос, давайте немного разомнёмся и выполним устные задания, – предложил Мудряш.

– Теперь сверимся! – сказал Мудряш. – Посмотрите, что у вас должно было получиться!

– А сейчас можем вернуться к вашему вопросу, – начал Мудряш. – Ребята, давайте на координатной прямой отметим точку

А (4) и точку В (). Эти точки имеют разные координаты, но и точка А, и точка В расположены на расстоянии 4 единичных отрезков от начала отсчёта.

Для такого расстояния и придумано название модуль числа. Тогда можно сказать, что числа 4 и  имеют одинаковые модули, равные 4. Записывают это вот таким образом:  и .

Обратите внимание! Так как расстояние не может быть отрицательным, то и модуль числа не может быть отрицательным.

– Запомните! – сказал Мудряш. – Модулем числа а называют расстояние от начала отсчёта до точки, изображающей это число на координатной прямой.

Модуль числа a обозначают так: . И читают: «модуль числа

а».

Модуль числа принимает только неотрицательные значения.

– Давайте найдём модули чисел 3; ; ; 0 и 2,5, – предложил Мудряш. – Начертим координатную прямую. Отметим на ней начало отсчёта точкой О. А за единичный отрезок возьмём 2 клеточки. Первое число у нас 3. Отметим его на координатной прямой. Расстояние от начала координат до него равно 3 единичным отрезкам, а значит, .

Второе число у нас . Отметим его на координатной прямой.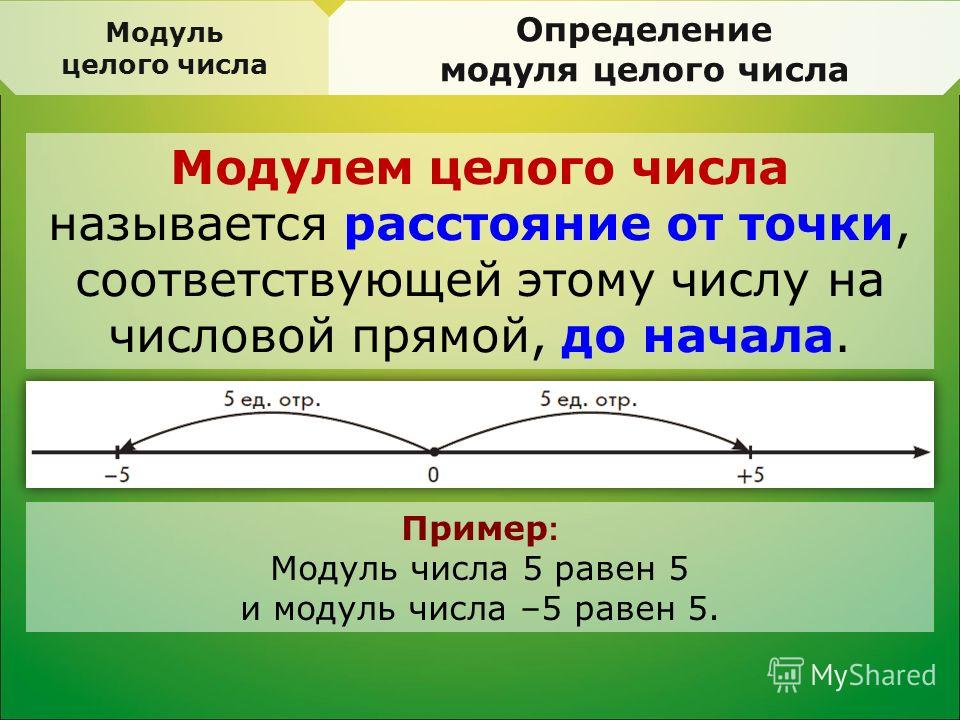 Расстояние от начала координат до него равно  единичного отрезка. А значит, .

Затем число . Отметим его. Расстояние до него от начала координат равно 3 единичным отрезкам, то есть .

Следующее число у нас 0. , так как точка с координатой 0 совпадает с началом отсчёта.

И ещё одно число – 2,5. Отметим его на нашей координатной прямой. Расстояние от начала отсчёта до него равно 2,5 единичным отрезкам, а значит, .

Обратите внимание, что модулями положительных чисел 3 и , а также 0 являются сами эти числа. А вот модулями отрицательных чисел  и  являются противоположные им числа  и 3. Причём модули противоположных чисел 3 и  равны.

– Запомните! – сказал Мудряш. – Модуль неотрицательного числа равен этому числу. То есть , если a – неотрицательное число. Модуль отрицательного числа равен противоположному числу. То есть , если a – отрицательное число. Модули противоположных чисел равны. То есть .

А теперь выполним несколько заданий.

Задание первое: найдите значения выражений:

а) ; б) ; в) ; г) .

Решение: в выражении  надо найти сумму модуля числа  и модуля числа . Найдём: ; . Сумма чисел 71 и 29 равна 100.

В выражении  надо вычислить разность модулей чисел 6,5 и . Найдём: ; . Разность чисел 6,5 и 0,8 равна 5,7.

В выражении  надо найти частное модуля  и модуля 7. Найдём: ; . Частное чисел 6,3 и 7 равно 0,9.

И в последнем выражении  надо найти произведение модулей дробей  и . Найдём: ; . Запишем произведение этих дробей: . Выполним сокращение числителя и знаменателя на 3 и на 7. И получим .

Второе задание: найдите:

а) положительное число, модуль которого равен 9; 7,1;

б) отрицательное число, модуль которого равен ; 85.

Решение: мы знаем, что . Воспользовавшись этим равенством справа налево, мы можем записать, что , а .

Модуль отрицательного числа равен противоположному числу, то есть . Воспользовавшись этим равенством справа налево, можем записать, что одна , а .

Следующее задание: расположите числа  в порядке возрастания их модулей.

Решение: сначала нам надо найти модули данных чисел. Итак, ; ; ; ; ; ; ;  и .

Нам надо расположить числа в порядке возрастания их модулей. Наименьший модуль имеет число 0. Запишем его первым. Следующее наименьшее значение модуля имеет число 0,15. Записываем его. Далее наименьший модуль у числа . Следующее наименьшее значение имеет модуль . Записываем . Затем записываем число , так как его модуль самый меньший из оставшихся. За ним будет идти . Следующее наименьшее значение модуля имеет число . Записываем его. Далее будет идти 7,14. Самое большое значение модуля имеет число .

Записываем его последним.

И последнее задание: решите уравнения:

а) ; б) ; в) .

Решение: для решения этих уравнений мы воспользуемся известными равенствами: , если a – неотрицательное число; , если a – отрицательное число.

Первое уравнение. Если модуль , то  или , так как  и .

Второе уравнение: . Решением этого уравнения является , так как только .

И последнее уравнение  не имеет решений, так как модуль не может быть отрицательным.

Divi Number Module — Elegant Themes

Divi Number Module — Elegant Themes

Модуль Number — это удобный инструмент для улучшения дизайна чисел на вашем сайте Divi. Модуль дает вам полный контроль над дизайном числового текста, позиционированием и дизайном фона, поэтому вы можете легко создавать выдающиеся дизайны цифровых блоков. Он даже имеет встроенную анимацию счетчика чисел.

Посмотреть демо-версию модуля Скачать этот модуль

Документация по модулю

Как использовать модуль Number

Это бесплатный модуль Divi, созданный Divi Torque. Divi имеет процветающую экосистему сторонних модулей, которые значительно расширяют потенциал Divi. Это одна из сильных сторон Divi! Чтобы использовать этот модуль, установите бесплатный плагин. Затем вы найдете числовой модуль в списке модулей Divi. Этот модуль полностью настраивается с использованием широкого диапазона настроек дизайна Divi.

Просмотр документации модуля

Часто задаваемые вопросы

• Что такое модуль Divi?

  Модули Divi — это элементы контента, которые можно использовать для создания страниц в Divi. Каждый модуль имеет уникальный набор функций, элементов и настроек дизайна, которые помогут вам создать что-то уникальное. Разные модули служат разным целям. Используя огромный набор модулей Divi, вы можете создать сайт практически любого типа.

  Развернуть менюСвернуть меню

• Включен ли этот модуль бесплатно в мое членство в Divi?

  Да, это бесплатные модули, разработанные Divi Torque и доступные для бесплатной загрузки. Как только вы установите бесплатный плагин WordPress, эти модули станут доступны внутри визуального конструктора Divi.

  Развернуть менюСвернуть меню

• Где я могу найти дополнительные модули Divi?

  Благодаря процветающему сообществу разработчиков Divi существует множество сторонних модулей Divi, доступных бесплатно и для покупки. Лучшее место, где можно найти дополнительные модули Divi, — это Divi Marketplace.

  Развернуть менюСвернуть меню

• Как я могу сделать свои собственные модули Divi?

  Да, API модулей Divi позволяет разработчикам легко создавать свои собственные модули! Создав модуль, вы сможете использовать его во всех своих будущих проектах или даже продать на Divi Marketplace. Чтобы узнать больше о том, как создавать собственные модули, посетите нашу документацию для разработчиков.

  Развернуть менюСвернуть меню

Ознакомьтесь с дополнительными бесплатными модулями от сообщества

Как и WordPress, Divi имеет процветающую экосистему сторонних плагинов, которые значительно расширяют функциональность Divi. Существуют десятки бесплатных элементов контента, созданных сообществом, которые вы можете установить и использовать для создания своего веб-сайта.

Просмотреть все модули

Разноцветные формы

881 346 клиентов уже создают потрясающие веб-сайты с помощью Divi. Присоединяйтесь к самому влиятельному сообществу WordPress в Интернете

Зарегистрируйтесь сегодня

Мы предлагаем 30-дневную гарантию возврата денег, так что присоединение без риска!

Фейсбук 156к Последователи группа в фейсбуке 73к Члены Твиттер 63k Последователи Новостная рассылка 325к Подписчики YouTube 173k Подписчики Дрибббл 6к Последователи

Авторские права © 2023 Elegant Themes ®

Нумерация версии модуля — язык программирования Go

Разработчик модуля использует каждую часть номера версии модуля для обозначения стабильность версии и обратная совместимость. Для каждого нового выпуска номер версии выпуска модуля конкретно отражает характер изменения по сравнению с предыдущим выпуском.

При разработке кода, использующего внешние модули, можно использовать версию цифры, чтобы понять стабильность внешнего модуля, когда вы рассматриваете обновление. Когда вы разрабатываете свои собственные модули, номера версий будут сообщить другим разработчикам о стабильности и обратной совместимости ваших модулей.

В этом разделе описывается, что означают номера версий модулей.

См. также

• Когда вы используете внешние пакеты в своем коде, вы можете управлять ими зависимости с помощью инструментов Go. Дополнительные сведения см. в разделе Управление зависимостями.
• Если вы разрабатываете модули для использования другими, вы применяете номер версии когда вы публикуете модуль, помечая модуль в его репозитории. Для большего, см. Публикация модуля.

Выпущенный модуль публикуется с номером версии в семантической версии модель, как на следующем рисунке:

В следующей таблице описано, как части номера версии обозначают стабильность модуля и обратная совместимость.

Этап версии	Пример	Сообщение разработчикам
В разработке	Автоматический номер псевдоверсии v 0 .x.x	Сигнализирует о том, что модуль все еще находится в состоянии . разработка и нестабильная версия . Этот выпуск не имеет обратной гарантии совместимости или стабильности.
Основная версия	v 1 .x.x	Signals обратно несовместимый общедоступный API меняется . Этот релиз не гарантирует, что он будет обратная совместимость с предыдущими основными версиями.
Дополнительная версия	вх. 4 .x	Signals общедоступный API с обратной совместимостью меняется . Этот выпуск гарантирует обратную совместимость и стабильность.
Исправление версии	вх.х. 1	Сигналы изменений, не влияющих на общедоступный API модуля или его зависимости. Этот выпуск гарантирует обратную совместимость и стабильность.
Предварительная версия	vx.x.x- бета.2	Сигнализирует о том, что это предварительная версия . веха, например альфа- или бета-версия . Этот релиз не несет гарантии стабильности.

В разработке

Сигнализирует о том, что модуль все еще находится в разработке и нестабилен . Этот выпуск не несет никаких гарантий обратной совместимости или стабильности.

Номер версии может принимать одну из следующих форм:

Номер псевдоверсии

v0.0.0-20170915032832-14c0d48ead0c

v0 номер

v0. x.x

Псевдоверсия номер

Если модуль не был помечен в своем репозитории, инструменты Go сгенерируют номер псевдоверсии для использования в файле go.mod кода, который вызывает функции в модуль.

Примечание: Рекомендуется всегда разрешать инструментам Go генерировать номер псевдоверсии, а не создавать свой собственный.

Псевдоверсии полезны, когда разработчик кода, использующего модуль функции должны разрабатываться против коммита, который не был помечен тегом тег семантической версии еще.

Номер псевдоверсии состоит из трех частей, разделенных тире, как показано на следующая форма:

Синтаксис

baseVersionPrefix — метка времени — идентификатор ревизии

Детали

• baseVersionPrefix (vX.0.0 или vX.Y.Z-0) — это значение, полученное либо из семантический тег версии, который предшествует ревизии или из vX.0.0, если нет такой тег.

• метка времени (ггммддччммсс) — это время создания ревизии в формате UTC. В git, это время фиксации, а не время автора.

• ревизионный идентификатор (abcdefabcdef) — 12-символьный префикс коммита. hash, или в Subversion, дополненный нулями номер версии.

v0 номер

Модуль, опубликованный с номером v0, будет иметь формальный семантический номер версии. с основной, второстепенной частью и частью исправления, а также необязательным предварительным выпуском идентификатор.

Хотя в рабочей среде можно использовать версию v0, она не обеспечивает стабильности или отсталости. гарантии совместимости. Кроме того, версиям v1 и более поздним разрешено нарушить обратную совместимость для кода, использующего версии v0. По этой причине разработчик с функциями потребления кода в модуле v0 отвечает за адаптация к несовместимым изменениям, пока не будет выпущена версия 1.

Предварительная версия

Сигнализирует о том, что это предварительная веха, например альфа- или бета-версия. Этот релиз не несет гарантий стабильности.

Пример

 vx.x.x-бета.2
 

Разработчик модуля может использовать предварительный идентификатор с любым major.minor.patch комбинации путем добавления дефиса и идентификатора предварительной версии.

Младшая версия

Сигнализирует об обратно совместимых изменениях в общедоступном API модуля. Этот выпуск гарантирует обратную совместимость и стабильность.

Пример

 вх.4.х
 

Эта версия изменяет общедоступный API модуля, но не нарушает код вызова. Это может включать изменения в собственных зависимостях модуля или добавление новых функций, методов, структурных полей или типов.

Другими словами, эта версия может включать улучшения за счет новых функций. которые другой разработчик может захотеть использовать. Однако разработчик, использующий предыдущие в противном случае младшим версиям не нужно менять свой код.

Версия исправления

Сигналы об изменениях, которые не влияют на общедоступный API модуля или его зависимости. Этот выпуск гарантирует обратную совместимость и стабильность.

Пример

 вх.х.1
 

Обновление, которое увеличивает этот номер, предназначено только для незначительных изменений, таких как ошибка исправления. Разработчики, использующие код, могут безопасно перейти на эту версию без необходимо изменить их код.

Основная версия

Сигнализирует об обратно несовместимых изменениях в общедоступном API модуля. Этот выпуск не дает никаких гарантий, что он будет обратно совместим с предыдущими основными версии.

Пример

v1.х.х

Номер версии v1 или выше указывает на то, что модуль стабилен для использования (с исключения для его предварительных версий).

Обратите внимание, что, поскольку версия 0 не обеспечивает стабильности или обратной совместимости гарантии, разработчик, обновляющий модуль с v0 до v1, несет ответственность за адаптация к изменениям, нарушающим обратную совместимость.

Разработчик модуля должен увеличивать это число после v1 только при необходимости.